2. 中国石油化工股份有限公司石油勘探开发研究院海外中心, 北京 100871;
3. 中国科学院大学, 北京 100049;
4. 中国地质大学, 北京 100083
2. Oversea Department of Sinopec Petroleum Exploration and Production Research Institute, Beijing 100871, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. China University of Geosciences, Beijing 100083, China
油气勘探目标的日趋复杂, 对勘探方法提出了更高的勘探精度要求。“两宽一高”地震数据采集方式是开展高精度勘探的有效途径, 且多个实例也证明了该采集方法在提高勘探精度方面的巨大优势。但由于昂贵的采集成本, 导致其很难得到大范围推广应用。
高效率地震数据采集通过缩短震源激发时间间隔、提高震源激发效率的方式提高数据采集效率, 实现高密度采集, 改善成像质量。高效率采集的发展包括多个方面。首先是震源的发展, 高效率采集关注更多的是:①更高密度、更大范围采集, 因此, 需要足够的震源能量保证更远偏移距的检波器接收; ②检波器的发展, 高效率采集需要对地震数据进行不间断地连续接收, 目前已经开始应用于实际生产的节点仪器, 适应了高效率采集的发展要求, 成为地震数据采集的必备检波器; ③数据处理方法的发展, 高效率采集获得的数据是多震源混叠的地震数据, 无法采用常规资料处理方式处理, 需要进行特殊方式处理。
本文主要介绍高效率采集地震数据分离处理方法的研究进展, 着重论述了噪声压制类方法、反演类方法和预测-相减类方法的内容及其在混采地震数据分离中的应用, 并对混采地震数据的分离处理方法的发展方向进行了展望。
1 高效率地震数据采集方式的发展高效率地震数据采集方式的研究始于20世纪70年代。1979年, SILVERMAN[1]提出采用多源激发的采集方式提高地震数据采集效率。1993年, 交替扫描试验首次出现在了可控震源地震数据采集中, 拉开了可控震源的高效率数据采集的序幕。BEASLEY[2]引入脉冲型震源, 进行多震源同时激发采集, 以期更好地分离混采地震数据。VAAGE[3]提出随机/伪随机时间延迟的海上地震采集方式, 有效提高了海上地震数据采集的效率; BERKHOUT等[4]提出对震源进行线性随机编码, 在提高采集效率的同时, 有助于混采数据的分离。在国内, 许多学者[5-7]也先后对高效率采集方式进行了研究和探索, 但在应用层面上还落后于国际水平。
目前, 基于陆上可控震源的高效率采集方式主要有4种:交替扫描[8]、滑动扫描[9]、距离分开的同步激发[10]和独立同步扫描[11]。其中, 独立同步扫描是目前效率最高的采集方式, 又称为同时震源激发或同步震源激发。这种采集方式可以在常规采集一炮地震记录的时间内采集到多炮地震记录, 从而大幅降低了采集时间和成本, 显著增加震源覆盖密度, 提高地下照明和地震数据的质量。因此, 在地震勘探中, 尤其是海上地震勘探, 受到广泛关注。
传统的地震数据采集方式是多炮之间分开激发, 炮与炮之间互不干扰, 排列只接收当前炮点能量。而高效率地震数据采集方式通过多炮同时激发, 大大缩短炮点激发时间, 因此, 在采集得到的记录中, 除主炮能量外, 还有很强的交涉炮干扰能量。目前, 针对混采地震数据的处理方法主要有两种[4]:①先进行混采数据的分离, 得到各单炮地震数据后进行常规地震数据处理; ②直接对混采地震数据进行偏移成像或反演处理。
2 混采地震数据分离对混采地震数据进行分离的根据是地震波场的线性叠加原理。目前, 最常用的分离方法主要有3类:①噪声压制类方法; ②反演类方法; ③预测-相减类方法。
2.1 噪声压制类方法噪声压制类方法是最常用的混采地震数据分离方法。基于混采地震数据在不同道集记录的不同特征, 进行数据的有效分离。根据高效率采集地震数据的特点, 当混合震源在不同位置上进行随机时间延迟激发时, 相同的排列接收来自不同震源不同激发时刻产生的直达波、折射波和反射波等。在共炮点道集, 除主炮能量具有相干性外, 其它炮点所产生的能量也都具有相干性; 而在共偏移距道集、共接收点道集或共中心点道集, 由于炮点激发时间的差异, 只有来自主炮点的能量具有相干性, 而来自交涉炮干扰的能量表现为随机噪声形式, 因而可以在这些道集上对交涉炮干扰能量进行压制。HAMPSON等[12]使用随机噪声压制方法对混采地震数据进行了初步分离, 获得了较好的效果; 随后, 有学者分别在共检波点道集[13-14]、共偏移距道集[15-16]进行了混采地震数据的分离研究; DOULGERIS等[17]进一步对比分析了不同去噪方法对混采地震数据的分离效果。
在中值滤波的基础上, 矢量中值滤波方法[18]被提出来用于混采地震数据的分离。中值滤波是一种有效压制随机噪声的方法, 基本原理是把数字序列或数字图像中某点的值用该点的某个邻域中各点值的中值来代替, 从而消除随机噪声。假设一组矢量为{ Xi|i=1, 2, …, N}, 则这组矢量的距离函数可以表示为:
| $ \begin{array}{*{35}{l}} D\left( {\mathit{\boldsymbol{X}}_{j}} \right)=\sum\limits_{i=1}^{N}{{{\left\| {\mathit{\boldsymbol{X}}_{j}}-{\mathit{\boldsymbol{X}}_{i}} \right\|}_{l}}} \\ {\mathit{\boldsymbol{X}}_{j}}\in \left\{ {\mathit{\boldsymbol{X}}_{i}}\mid i=1, 2, \cdots , N \right\} \\ \end{array} $ | (1) |
式中:l=0, 1, 2或∞。该组矢量对应的中值矢量Xm可以表示为:
| $ {\mathit{\boldsymbol{X}}_{m}}=\underset{{\mathit{\boldsymbol{X}}_{j}}}{\mathop{\operatorname{argmin}}}\, D\left( {\mathit{\boldsymbol{X}}_{j}} \right) $ | (2) |
基于矢量中值滤波, 建立矢量中值滤波器进行地震记录的干涉炮噪声去除。但矢量中值滤波需要一个假设前提, 即地下反射界面是水平的。通常情况下, 这样的假设很难满足。因此, HUO等[18]又提出多方向的矢量中值滤波方法, 表示如下:
| $ \begin{array}{*{35}{l}} D\left[ {\mathit{\boldsymbol{X}}_{j}}(p) \right]=\sum\limits_{i=1}^{N}{{{\left\| {\mathit{\boldsymbol{X}}_{j}}(p)-{\mathit{\boldsymbol{X}}_{i}}(p) \right\|}_{l}}} \\ {\mathit{\boldsymbol{X}}_{j}}(p)\in \left\{ {\mathit{\boldsymbol{X}}_{i}}(p)\mid i=1, \cdots , N;p={{p}_{\min }}, \cdots , {{p}_{\max }} \right\} \\ \end{array} $ | (3) |
式中:p代表倾角方向; Xj(p)为沿其中某一个方向p的矢量。同样, 公式(3)中的中值矢量Xm(p)可以表示为:
| $ {\mathit{\boldsymbol{X}}_{m}}(p)=\underset{{\mathit{\boldsymbol{X}}_{j}}(p)}{\mathop{\operatorname{argmin}}}\, D\left[ {\mathit{\boldsymbol{X}}_{j}}(p) \right] $ | (4) |
通过多方向的矢量中值滤波方法, 可以灵活地对干涉炮噪声进行有效压制。
多方向矢量中值滤波方法进一步改善了交涉炮干扰能量的压制效果。在此基础上, CHEN[19]提出变窗口中值滤波的方法, 通过控制每次迭代的窗口长度, 尽可能保留主炮的有效信号, 该方法适用于复杂地质构造的同步震源波场分离。MAHDAD等探讨了基于不同迭代滤波方法进行混采地震波场分离的效果, 并对不同道集地震记录分离算法的特性进行了分析[20-21]。王文闯等[22]提出基于Alpha-trimmed矢量中值滤波方法进行交涉炮干扰能量的压制, 效果改善明显。在中值滤波的基础上, 添加约束条件, 可进一步改善处理效果。GAN等[23]将局部斜率作为约束, CHEN等[24]则添加局部正交加权为约束, 对数据进行测试, 均取得了较好的分离效果。GAN等[25]提出结构导向的中值滤波方法, 通过对相邻道地震记录的同相轴进行预测并拉平, 再采用中值滤波方法压制混采噪声。周丽等[26]提出使用自适应迭代多级中值滤波方法实现混叠地震波场的分离, 在迭代过程中通过逐步修改中值滤波窗口提取波场细节信息。SHU等[27]提出将变频率中值滤波和均值滤波结合的方法应用于十字交叉道集, 有效压制了交涉炮干扰噪声。CHEN等[28]将局部正交加权约束[24]和结构导向中值滤波[25]结合, 实现对混叠地震波场的多重滤波, 效果明显。
除了矢量中值滤波类方法外, 还有其它一些噪声压制类的方法。基于地震信号的稀疏性, IBRAHIM等[29]通过对最小平方、稀疏和鲁棒3种拉冬变换进行测试和效果分析, 提出在混采数据处理中, 可以采用鲁棒拉冬变换提高干扰噪声的压制效果。JI等[30]提出一种迭代混合拉冬变换的方法, 适用于存在较强干扰噪声的非规则数据体, 并采用多个频率进行邻炮干扰的压制, 具有较好的鲁棒性, 同时对低频噪声压制效果明显。CAO等[31]通过双焦点变换, 结合一个高效的贪婪算子, 对同时震源采集中的干扰噪声进行快速有效分离, 利用合成数据和实际资料验证了算法的有效性。ZU等[32]认为在三维空间中考虑更多的稀疏约束可以更好地去除交涉炮干扰, 因此基于三维多尺度整形算子对同时震源数据进行邻炮干扰分离, 并利用合成数据和实际数据验证了算法的优越性。BAARDMAN等提出使用卷积神经网络的方法进行混采地震数据的分离, 并在合成地震记录上取得了良好的应用效果, 但应用于实际资料的研究还在继续[33-34]。在此基础上, SLANG等[35]提出使用深度卷积神经网络的方法去除地震记录中的干扰, 并应用于共接收点道集, 取得了较好的应用效果, 但该方法的结果受资料的信噪比影响较大, 并且需要消耗计算机的大量内存, 因此还有待进一步优化。ZU等[36]提出一种混合稀疏约束模型, 将其应用于混采数据分离中, 通过自适应字典学习识别非相干噪声, 然后采用稀疏变换框架实现信号与干扰的分离。但该方法计算量大, 需要进一步提高计算效率。RICHARDSON等[37]提出采用深度学习的方法在共偏移距道集进行混采数据的分离, 通过训练, 快速获取最优去噪参数, 大大节省了人工调整参数的时间, 但应用于实际数据处理时, 可能会伤及有效信号, 导致分离效果不理想。
噪声压制类方法分离混采地震数据, 基本上都是基于主炮能量和交涉炮能量在不同道集排列中的相干性差异进行数据分离。此类方法计算速度快、易实现、方法适应性强。但该类方法对有效弱信号的处理难度较大, 当选择的窗口较大时, 可以更好地抑制噪声, 但有可能损失有效弱信号; 当窗口较小时, 能够较好地保护信号的细节, 但压噪效果又不明显。因此, 该类方法的分离效果比较依赖于去噪方法的优劣和去噪参数的选择。并且, 当混采地震记录中的震源较多时, 干扰噪声能量可能数倍于有效信号, 在进行数据分离时, 有效信号容易受到伤害, 影响分离效果。
2.2 反演类方法反演类方法是用于混采地震数据分离的另一大类方法。将多震源激发用一个混合算子表示, 混采地震数据的分离就是一个欠定的反问题。IKELLE[38]从编码与解码的方面对该问题进行了初步研究, 并采用高阶统计思想进行了混采数据的分离。地震数据的稀疏性[39-41]也决定了该欠定反问题是一个地震数据的稀疏恢复问题[42-43]。基于稀疏反演的混采地震数据分离方法大多是基于Delphi提出的反演框架[4]进行的。把混采数据分离抽象成一个矩阵求解问题, 并且, 在求解的时候加上正则化条件进行约束。
采用多震源激发, 任一检波器接收到的地震记录可表示为[44]:
| $ \mathit{\boldsymbol{b}}=\mathit{\pmb{\Gamma\text{ f}}} $ | (5) |
式中: f表示常规共接收点道集记录; Γ表示震源混合算子。基于稀疏约束的混采地震数据分离问题可以表示为[45]:
| $ \begin{matrix} \mathop {\min v}\limits_{f,A} \|\mathit{\pmb{\Gamma\text{ f}}}-\mathit{\boldsymbol{b}}\|_{2}^{2}+\sum\limits_{ij}{\left\| {\mathit{\boldsymbol{R}}_{ij}}\mathit{\boldsymbol{f}}-\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{\alpha}}_{ij}} \right\|_{2}^{2}} \\ {{\left\| {\mathit{\boldsymbol{\alpha}}_{ij}} \right\|}_{0}}<{{\theta }_{0}}\quad \forall i, j \\ \end{matrix} $ | (6) |
式中:υ为权重系数, 其大小与资料信噪比有关, 如果信噪比较高, 则适当增大其取值, 反之则减小; Rij表示从待恢复地震记录中抽取的数据; i和j分别表示所选数据在整个地震记录上的时间和空间位置; C表示稀疏基; A表示分解系数矩阵; ‖ αij‖0表示分解系数向量的L0范数; θ0为一正数。
MOORE等[15, 46]和AKERBERG等[16]在拉冬域采用稀疏约束反演方法实现了混采地震记录的分离, 但拉冬变换适用于具有明显抛物线或双曲线特征的同相轴地震数据, 对复杂构造区的地震数据分离效果不明显。AYENI等[47]将倾角信息作为约束条件在拉冬域分离混采地震数据, 改善了分离效果。WASON等[43]通过曲波域L1范数稀疏反演进行混采地震数据的分离, 效果显著。LIN等[48]将震源编码技术和曲波变换相结合, 进一步优化了混采数据的分离效果。ZU等[49]提出以周期性变化代替随机性变化的震源编码方式, 增加了地震数据在曲波域的稀疏性, 获得了更高精度的结果。ZHANG等[50]采用加权τ-p变换对不同炮线信号能量进行交替增强, 进而分离OBN数据, 获得了良好的效果。
此外, 还有一些改进的方法也被应用于混采地震数据的分离。ZU等[49]提出了直接在炮点域对混采地震数据分离的反演方法, 通过引入两个卷积算子, 分别对信号和邻炮干扰进行分解, 然后用最小二乘意义下的共轭梯度算法求解, 并利用海上拖缆混采数据验证了方法的有效性。周松等[51]提出L1正则化和L0正则化混合迭代的稀疏反演方法, 对实际独立同步扫描地震资料进行了分离, 获得了比中值滤波方法更好的效果。ZHAO等[52]提出了一种鲁棒的混采地震数据分离方法, 其鲁棒性源于在正态分布置信区间定义的规范化整形算子, 该算子将异常横向最小化到正常水平, 以满足最小二乘整形正则化的假设, 方法效果显著, 收敛速度和最小二乘正则化方法接近。WANG等[53]选择在主频波数域对同时震源地震数据进行分离, 相较于时空域地震数据分离方法而言, 变换后的数据量更小, 分离效果更好。
目前, 适合地震数据的稀疏变换主要有拉冬变换[15-16]、曲波变换[15, 43, 48-49, 54]和Seislet变换[55]等。这类变换的稀疏基具有明确的表达式和几何特征。但由于这些变换的形式较为固定, 因此较难应用于复杂地震信号的稀疏表示。近年来发展较快的字典学习方法, 通过学习可以获得自适应分析信号的字典, 有望实现地震信号的更稀疏表示。
在混合震源采集框架下, 周艳辉等[45]提出一种基于字典学习的混采地震数据分离方法, 其核心是字典基的选择。基于L0范数稀疏约束的字典学习问题可以表示为[56]:
| $ \begin{matrix} \underset{\mathrm{D}, \mathrm{A}}{\mathop{\min }}\, \|\mathit{\boldsymbol{Y}}-\mathit{\boldsymbol{DA}}\|_{2}^{2} \\ {{\left\| {\mathit{\boldsymbol{\alpha}}_{i}} \right\|}_{0}}\le {{\theta }_{0}}\quad i=1, 2, \cdots , L \\ \end{matrix} $ | (7) |
式中: Y =[y1, y2, …, yL]∈ Rm×L包含L个信号, m表示向量化训练信号的维数; 字典D =[d1, d2, …, dp]∈ Rm×p包含p个字典原子; A =[a1, a2, …, aL]∈ Rp×L表示分解系数矩阵; ‖ αi‖0表示分解系数向量的L0范数。
周艳辉等[45]将未混叠的共炮点记录作为训练样本, 基于K-SVD[57-58]算法训练字典, 反映地震记录局部波形特征。由于共炮点道集和共接收点道集记录具有相似性, 将共炮点道集训练得到的稀疏字典应用于共接收点道集, 并基于稀疏反演构造反问题表达式, 利用交替迭代策略进行求解, 有效提高了分离结果的精度, 为后续地震信号处理提供了高质量的基础数据。ZHOU等[59]从含干扰信号的地震记录中进行字典学习, 并采用交替方向乘子算法进行字典的更新, 极大提高了地震信号的稀疏性, 模拟数据和实际资料的测试证明了方法具有更高的精度和鲁棒性。图 1分别为采用二维离散余弦变换(2D-DCT)、曲波变换和字典学习在共接收点道集进行混采地震数据的分离, 可以看出, 利用字典学习方法可以分离出最多的有用信息, 并且误差也是3种方法中最小。图 2展示了初始字典原子和更新后的字典原子, 可以看到, 字典原子的局部波形特征与分离出来的有效信号的特征具有良好的一致性。

|
图 1 利用3种方法在共接收点道集对实际混采地震数据进行分离的结果及分离后的残差[59] a 2D-DCT; b 2D-DCT分离后残差; c曲波变换; d曲波变换分离后残差; e字典学习; f字典学习分离后残差 |

|
图 2 实际混采地震数据的部分字典原子[59] a 初始字典原子; b 更新后的字典原子 |
目前, 基于字典学习的稀疏反演类方法展现了较强的方法优越性, 但从含噪声的地震记录中提取并优化字典原子, 仍需要较大的计算量和迭代次数, 因此, 提高精度的同时提高计算效率, 是该类方法的发展方向。
2.3 预测-相减类方法除了噪声压制类和反演类方法之外, 还可以采用预测-相减类方法进行混采地震数据的分离。对于高效率采集, 地震记录是各单个震源地震记录的叠加, 通过对各单个震源记录进行预测, 可逐一分离地震记录。SPITZ等[60]提出采用预测-相减法对两炮混采地震记录进行分离, 取得了较好的效果。考虑两个震源S1和S2, 这两个震源的混采地震记录可以表示为[60]:
| $ D={{D}_{1}}+{{D}_{2}}={{G}_{1}}*{{S}_{1}}+{{G}_{2}}*{{S}_{2}} $ | (8) |
式中:Di表示震源Si的地震记录; Gi表示震源在i位置的格林函数。混采地震数据的分离就是从混采地震记录D中将D1和D2分开。这类似于多次波压制的问题:
| $ D=P+M={{G}_{P}}*S+{{G}_{M}}*S $ | (9) |
式中:P表示一次波; M表示多次波。该问题的目标就是求解P, 常用解法是:
| $ P=D-M=D-f*\hat{M} $ | (10) |
式中:f表示匹配算子;
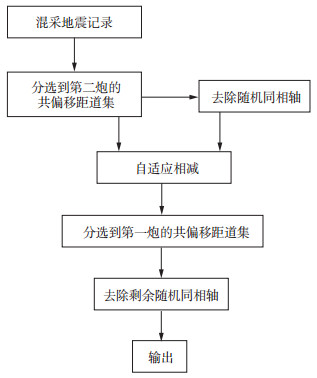
KIM等[61]针对海上OBC同时震源数据, 提出自适应去除混采噪声, 获得了与不含干扰噪声几乎相同的偏移成像结果, 很好地保留了有效弱信号成分。具体流程如图 3[61]所示。如果交涉炮震源的位置很近, 该方法的分离效果不够理想。因此, KIM等[61]建议采用该类方法进行数据分离时, 震源间距最好大于2 000 m。
|
图 3 两炮混采地震记录分离流程[61] |
此外, MAHDAD等[14]通过迭代的方法估计交涉炮能量, 然后采用自适应相减法对混采数据进行分离, 并将之应用于简单的实际数据处理中, 得到了较好的结果。WU等[62]提出一种海上炮集混合的方法, 采用迭代相减进行混采数据分离。该方法对震源间距没有限制, 但目前仅进行了数值模拟和实际数据的初步试验, 其实用性还有待检验。
不同于噪声压制类方法, 预测-相减类方法可以有效保护弱信号。但由于该类方法严重依赖预测波场的精度, 因而稳定性稍差。应用此类方法处理实际混采地震数据时, 会受到多种因素的影响, 导致分离效果不理想。因此, 该类方法仍有待进一步深入研究。
2.4 多方法联合用于混采地震数据分离混采地震数据的分离方法主要有3类:基于噪声压制类的方法, 此类方法效率高、稳定、易实现; 基于稀疏反演类的方法, 此类方法可以获得比噪声压制类信噪比和保真度更高的结果, 但计算效率稍低; 预测-相减类方法可以获得精度很高的分离效果, 但算法易受预测波场精度的影响, 稳定性较差。因此, 这3类方法各有优劣。如果能够将这3类方法有机地结合, 可以进一步提高混采地震数据的分离精度和效率。
KIM等[61]将噪声压制类方法与预测-相减类方法相结合, 提出中值滤波-预测误差联合的方法进行混采数据分离, 取得了良好的效果。BAGAINI等[63]结合拉冬域的稀疏约束反演方法和F-X滤波方法对混采数据进行了分离。WU等[62]在预测-相减的过程中采用稀疏反演方法, 增强混采数据分离的能力。CHEN等[64]提出Seislet变换和迭代阈值(ISTA)滤波结合的混采地震数据分离方法。王汉闯等[40]将噪声压制类方法和反演类方法相结合, 提出基于小窗口中值滤波与稀疏约束联合的混采地震数据分离方法, 先采用小窗口中值滤波压制大部分的随机噪声, 然后采用稀疏约束反演的方法进一步去除残余噪声, 很好地保留了地震数据中的有效弱信号, 取得了较好的去噪效果, 如图 4所示, 小窗口中值滤波与稀疏约束联合的方法可以在去除孤立随机噪声的同时保持地震数据中所需要的主要信息, 去噪效果良好。

|
图 4 不同方法对混采地震记录共接收点道集数据的分离结果[40] a 混采数据; b 中值滤波分离结果; c 小窗口中值滤波与稀疏约束联合去噪结果; d 最终分离结果 |
对混采地震数据的另一种处理方式是直接对其进行偏移成像处理。FROMYR等[65]进行了混采地震数据的直接成像试验, 得到了和常规采集方法精度相当的成像效果。但该试验的不足是混采数据的震源间距都在8 000 m以上, 距离过大, 与实际高效率采集方式差异较大。VERSCHUUR等[66]对混采地震数据和单震源地震数据成像进行了对比, 并指出最小二乘偏移是直接处理混采地震数据的有效方法。TANG等[67]讨论了基于波动方程的混采地震数据最小二乘成像/反演方法和流程, 在提高勘探精度的同时, 压制了交涉炮干扰噪声。DAI等[68]指出, 对混采地震数据直接进行叠加或偏移处理, 可以压制交涉炮干扰噪声, 并采用最小二乘逆时偏移对混采地震数据进行了处理[69], 改善了成像效果。
混采地震数据最小二乘偏移, 需要通过多次迭代优化成像效果, 巨大的计算量导致其很难应用于实际资料处理中。此外, 目前对混采地震数据直接进行偏移成像的方法, 适用于简单构造的情况, 对复杂构造地区的资料还不能获得理想的效果[2]。随着计算机能力的提高和偏移/反演算法的进一步优化, 直接进行成像将成为混采地震数据处理的发展方向, 从而真正实现高效率地震勘探。目前, 先分离再成像, 依旧是处理混采地震数据的最有效方法, 对混采地震数据的直接成像和反演仍有待进一步研究。
4 展望目前, 高效率采集方法依然是进行“两宽一高”采集的重要方式。今后的勘探目标, 会越来越精细, 而采集会向超高密度发展。因此, 提高野外采集效率依然具有重要的理论意义和实际价值。
针对高效率采集地震数据的处理, 进行直接的偏移成像具有重要的研究价值, 不仅在偏移的过程中可以压制噪声, 而且还节省了混采数据分离的时间, 进一步提升勘探效率。但就目前来看, 对混采数据进行直接的偏移成像, 依然存在数据计算量大、速度模型不准等问题。同时, 也会对属性反演等工作提出新的挑战。因此, 针对混采地震数据的处理, 目前仍推荐先进行数据分离、再进行偏移成像以及属性反演等后续处理的方式。
针对现有的混采地震数据分离的3类方法:噪声压制类方法是目前使用最广泛的一类方法, 该类方法计算效率高、算法稳定, 适合实际混采地震数据的分离; 反演类方法是目前研究最多的一类方法, 从各种变换域的反演方法, 到基于字典学习的稀疏反演方法等, 相比于噪声压制类方法, 该类方法可以获得更高信噪比和保真度的结果, 但由于该类方法对稀疏基的要求越来越高, 因此, 计算效率有待进一步提高; 预测-相减类方法与反演类方法类似, 可以获得精度更高的分离效果, 但由于受预测波场的影响较大, 因此, 算法稳定性较差。
目前, 混采地震数据分离的精度和效率仍然是国内高效率地震数据采集技术发展的瓶颈。研发能够适用于复杂地区的混采地震数据分离方法, 对国内高效率采集技术的发展具有重要意义。本文介绍的混采地震数据分离方法, 还无法完全满足国内复杂环境条件下的混采地震数据分离。因此, 基于目前混采数据分离的方法, 将它们进行有机结合, 将会进一步提高混采数据分离的精度和效率, 文中也介绍了部分学者在该领域的初步研究成果且已见良好效果, 但仍有待在计算精度、效率等方面进一步优化。因此, 多方法联合是混采地震数据分离处理的主要发展方向。
5 结束语混采地震数据分离方法目前主要有3类:噪声压制类方法、反演类方法和预测-相减类方法。本文对这3类方法进行了综合评述, 并指出多方法联合有助于进一步提高混采地震数据分离的精度和效率, 是高效率采集地震数据处理的主要发展方向。特别是针对我国复杂地区的地震勘探, 更是如此。
目前, 高效率采集方式主要应用于陆上可控震源, 其它类型震源使用较少。此外, 高效率采集正是海上进行宽方位角地震勘探的有效方法, 但目前发展较为缓慢。这其中的重要原因就在于混采地震数据分离的精度和效率达不到技术发展的要求。多方法联合的混采地震数据分离, 必将进一步提高数据处理的精度和效率, 并逐步满足高效率采集发展的需求, 从而提高勘探精度和效率, 推动“两宽一高”采集技术的发展。
| [1] |
SILVERMAN D.Method of three dimensional seismic prospecting[P].U.S.Patent, 4159463, 1979
|
| [2] |
BEASLEY C J. A new look at marine simultaneous sources[J]. The Leading Edge, 2008, 27(7): 914-917. DOI:10.1190/1.2954033 |
| [3] |
VAAGE S.Method and system for acquiring marine seismic data using multiple sources[P].U.S.Patent, 6906981B2, 2002
|
| [4] |
BERKHOUT A J, BLACQUIERE G, VERSCHUUR D J. Changing the mindset in seismic data acquisition[J]. The Leading Edge, 2008, 27(7): 924-938. DOI:10.1190/1.2954035 |
| [5] |
佘德平. 多震源地震正演数值模拟技术[J]. 地球物理学进展, 2012, 27(4): 1533-1540. SHE D P. A numerical modeling of simultaneous sources[J]. Progress in Geophysics, 2012, 27(4): 1533-1540. |
| [6] |
陈生昌, 马在田. 广义地震数据合成及其偏移成像[J]. 地球物理学报, 2006, 49(4): 1144-1149. CHEN S C, MA Z T. Generalized synthesis of seismic data and its migration[J]. Chinese Journal of Geophysics, 2006, 49(4): 1144-1149. |
| [7] |
陈生昌, 王汉闯, 陈林. 三维VSP数据高效偏移成像的超道集方法[J]. 地球物理学报, 2012, 55(1): 232-237. CHEN S C, WANG H C, CHEN L. A high efficient super-gather migration method for 3D VSP data[J]. Chinese Journal of Geophysics, 2012, 55(1): 232-237. |
| [8] |
BERTELLI L, SERVODIO R. New perspectives for multisource vibroseis technique for 3D land acquisition[J]. Expanded Abstracts of 55th EAGE Annual Conference, 1993, 1-2. |
| [9] |
ROZEMOND H J. Slip-sweep acquisition[J]. Expanded Abstracts of 66th Annual Internat SEG Mtg, 1996, 64-67. |
| [10] |
BOUSKA J. Distance separated simultaneous sweeping, for fast, clean, vibroseis acquisition[J]. Geophysical Prospecting, 2010, 58(1): 123-153. DOI:10.1111/j.1365-2478.2009.00843.x |
| [11] |
HOWE D, FOSTER M, ALLEN T, et al. Independent simultaneous sweeping - A method to increase the productivity of land seismic crews[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 2826-2830. |
| [12] |
HAMPSON G, STEFANI J, HERKENHOFF F. Acquisition using simultaneous sources[J]. The Leading Edge, 2008, 27(7): 918-923. DOI:10.1190/1.2954034 |
| [13] |
DOULGERIS P, MAHDAD A, BLACQUIERE G. Separation of blended impulsive sources using an iterative approach[J]. Expanded Abstracts of 72nd EAGE Annual Conference, 2010, B004. |
| [14] |
MAHDAD A, DOULGERIS P, BLACQUIERE G. Separation of blended data by iterative estimation and subtraction of blending interference noise[J]. Geophysics, 2011, 76(3): Q9-Q17. |
| [15] |
MOORE I, DRAGOSET W, OMMUNDSEN T, et al. Simultaneous source separation using dithered sources[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 2806-2809. |
| [16] |
AKERBERG P, HAMPSON G, RICHETT H, et al. Simultaneous source separation by sparse radon transform[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 2801-2804. |
| [17] |
DOULGERIS P, MAHDAD A, BLACQUIERE G. Iterative separation of blended marine data:discussion on the coherence-pass filter[J]. Expanded Abstracts of 81st Annual Internat SEG Mtg, 2011, 26-31. |
| [18] |
HUO S, LUO Y, KELAMIS P G. Simultaneous sources separation via multi-directional vector median filtering[J]. Geophysics, 2012, 77(4): V123-V131. |
| [19] |
CHEN Y. Deblending using a space-varying median filter[J]. Expanded Abstracts of 84th Annual Internat SEG Mtg, 2014, 82-87. |
| [20] |
MAHDAD A, DOULGERIS P, BLACQUIERE G. Iterative method for the separation of blended seismic data:discussion on the algorithmic aspects[J]. Geophysical Prospecting, 2012, 60(4): 782-801. DOI:10.1111/j.1365-2478.2012.01084.x |
| [21] |
MAHDAD A.Deblending of seismic data[D].Delft: Delft University of Technology, 2012
|
| [22] |
王文闯, 李合群, 赵波, 等. 基于Alpha-trimmed矢量中值滤波压制同步激发邻炮干扰[J]. 石油地球物理勘探, 2014, 49(6): 1061-1067. WANG W C, LI H Q, ZHAO B, et al. Suppression of crosstalk from simultaneous sources with alpha-trimmed vector median filtering[J]. Oil Geophysical Prospecting, 2014, 49(6): 1061-1067. |
| [23] |
GAN S, WANG S, CHEN Y, et al. Deblending using a structural-oriented median filter[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015, 59-64. |
| [24] |
CHEN Y, FOMEL S. Random noise attenuation using local signal-and-noise orthogonalization[J]. Geophysics, 2015, 80(6): WD1-WD9. |
| [25] |
GAN S, WANG S, CHEN Y, et al. Separation of simultaneous sources using a structural-oriented median filter in the flattened dimension[J]. Computers and Geosciences, 2016, 86(1): 46-54. |
| [26] |
周丽, 庄众, 成景旺, 等. 利用自适应迭代多级中值滤波法分离海上多震源混合波场[J]. 石油地球物理勘探, 2016, 51(3): 434-443. ZHOU L, ZHUANG Z, CHENG J W, et al. Multi-source blended wavefield separation for marine seismic based on an adaptive iterative multi-level median filtering[J]. Oil Geophysical Prospecting, 2016, 51(3): 434-443. |
| [27] |
SHU G, SHI T, DU X, et al. Simultaneous sources deblending via frequency-varying filter in cross-spread azimuth-offset domain[J]. Studia Geophysica et Geodaetica, 2018, 62(4): 648-659. DOI:10.1007/s11200-017-0374-6 |
| [28] |
CHEN Y, ZU S, WANG Y, et al. Deblending of simultaneous source data using a structure-oriented space-varying median filter[J]. Geophysical Journal International, 2019, 216(2): 1214-1232. DOI:10.1093/gji/ggy487 |
| [29] |
IBRAHIM A, SACCHI M D. Simultaneous source separation using a robust Radon transform[J]. Geophysics, 2013, 79(1): V1-V11. |
| [30] |
JI Y, WILLACY C, TANG Z, et al. Deblending of simultaneous source data using a non-uniform, Hybrid-Radon transform[J]. Expanded Abstracts of 81st EAGE Annual Conference, 2019, Tu_R09_11. |
| [31] |
CAO J, KONTAKIS A, VERSCHUUR D, et al. Deblending using the focal transformation with an efficient greedy inversion solver[J]. Journal of Applied Geophysics, 2019, 170(1): 1-11. |
| [32] |
ZU S, ZHOU H, MAO W, et al. 3D deblending of simultaneous source data based on 3D multi-scale shaping operator[J]. Journal of Applied Geophysics, 2018, 151(1): 274-289. |
| [33] |
BAARDMAN R. Classification and suppression of blending noise using CNN[J]. Extended Abstracts of 1st EAGE/PESGB Workshop Machine Learning, 2018, ML_11. |
| [34] |
BAARDMAN R, TSINGAS C. Classification and suppression of blending noise using convolutional neural networks[J]. SPE Middle East Oil and Gas Show and Conference, 2019, SPE-194731-MS. |
| [35] |
SLANG S, SUN J, ELBOTH T, et al. Using convolutional neural networks for denoising and deblending of marine seismic data[J]. Expanded Abstracts of 81st EAGE Annual Conference, 2019, Tu_R06_05. |
| [36] |
ZU S, ZHOU H, WU R, et al. Hybrid-sparsity constrained dictionary learning for iterative deblending of extremely noisy simultaneous-source data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(4): 2249-2262. DOI:10.1109/TGRS.2018.2872416 |
| [37] |
RICHARDSON A, FELLER C. Seismic data denoising and deblending using deep learning[J]. Image and Video Processing, 2019. |
| [38] |
IKELLE L. Coding and decoding:seismic data modeling acquisition and processing[J]. Expanded Abstracts of 77th Annual Internat SEG Mtg, 2007, 66-70. |
| [39] |
杜世通. 地震波动力学理论与方法[M]. 东营: 石油大学出版社, 2009: 1-290. DU S T. Seismic wave dynamics:Theory and method[M]. Dongying: China Petroleum University Press, 2009: 1-290. |
| [40] |
王汉闯, 陶春辉, 陈生昌, 等. 基于稀疏约束和多源激发的地震数据高效率采集方法[J]. 地球物理学报, 2017, 60(9): 3518-3538. WANG H C, TAO C H, CHEN S C, et al. Highly efficient methods of seismic data acquisition based on sparse constraints and blended-source excitation[J]. Chinese Journal of Geophysics, 2017, 60(9): 3518-3538. |
| [41] |
马坚伟. 压缩感知走进地球物理勘探[J]. 石油物探, 2018, 57(1): 24-27. MA J W. Compressive sensing in geophysical exploration[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 24-27. |
| [42] |
ABMA R, MANNING T, TANIS M, et al. High quality separation of simultaneous sources by sparse inversion[J]. Expanded Abstracts of 70th EAGE Annual Conference, 2008, B003. |
| [43] |
WASON H, HERRMANN F J, LIN T T. Sparsity-promoting recovery form simultaneous data:A compressive sensing approach[J]. Expanded Abstracts of 81st Annual Internat SEG Mtg, 2011, 6-10. |
| [44] |
MANSOUR H, WASON H, LIN T, et al. Random marine acquisition with compressive sampling matrices[J]. Geophysical Prospecting, 2012, 60(4): 648-662. DOI:10.1111/j.1365-2478.2012.01075.x |
| [45] |
周艳辉, 陈文超. 基于稀疏反演的同步震源地震数据分离方法[J]. 石油物探, 2018, 57(1): 33-38. ZHOU Y H, CHEN W C. Separation of simultaneous source data based on sparse inversion[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 33-38. |
| [46] |
MOORE I. Simultaneous sources-processing and applications[J]. Expanded Abstracts of 72nd EAGE Annual Conference, 2010, B001. |
| [47] |
AYENI G, ALMOMIN A, NICHOLS D. On the separation of simultaneous-source data by inversion[J]. Expanded Abstracts of 81st Annual Internat SEG Mtg, 2011, SEP-142. |
| [48] |
LIN T T, HERRMANN F J. Designing simultaneous acquisitions with compressive sensing[J]. Expanded Abstracts of 71st EAGE Annual Conference, 2009, B007. |
| [49] |
ZU S, ZHOU H, LI Q, et al. Shot-domain deblending using least-squares inversion[J]. Geophysics, 2017, 82(4): V241-V256. DOI:10.1190/geo2016-0413.1 |
| [50] |
ZHANG C, OLOFSSON B. Separating simultaneous source data using weighted tau-p transform[J]. Expanded Abstracts of 74th EAGE Annual Conference, 2012, B003. |
| [51] |
周松, 霍守东, 胡立新, 等. 可控震源独立同步扫描高效地震采集资料噪声压制方法[J]. 石油物探, 2018, 57(5): 691-696. ZHOU S, HUO S D, HU L X, et al. Denoising for seismic data from vibroseis independent simultaneous sweeping[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 691-696. |
| [52] |
ZHAO Q, DU Q, GONG X, et al. Normalized shaping regularization for robust separation of blended data[J]. Geophysics, 2019, 84(5): V281-V302. DOI:10.1190/geo2018-0557.1 |
| [53] |
WANG B, GENG J. Efficient deblending in the PFK domain based on compressive sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(2): 995-1003. DOI:10.1109/TGRS.2019.2942329 |
| [54] |
祖绍环, 周辉, 陈阳康, 等. 不规则采样的多震源数据整形正则化分离方法[J]. 石油地球物理勘探, 2016, 51(2): 247-253. ZU S H, ZHOU H, CHEN Y K, et al. Irregularly sampled multi-source data deblending based on shaping regularization[J]. Oil Geophysical Prospecting, 2016, 51(2): 247-253. |
| [55] |
CHEN Y. Deblending using a space-varying median filter[J]. Exploration Geophysics, 2015, 46(4): 332-341. DOI:10.1071/EG14051 |
| [56] |
唐刚, 马坚伟, 杨慧珠. 基于学习型超完备字典的地震数据去噪[J]. 应用地球物理, 2012, 9(1): 27-32. TANG G, MA J W, YANG H Z. Seismic data denoising based on learning-type overcomplete dictionaries[J]. Applied Geophysics, 2012, 9(1): 27-32. |
| [57] |
AHARON M, ELAD M, BRUCKSTEIN A. K-SVD:An algorithm for designing over-complete dictionaries for sparse representation[J]. IEEE Transaction on Signal Process, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
| [58] |
ELAD M, AHARON M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006, 15(12): 3736-3745. DOI:10.1109/TIP.2006.881969 |
| [59] |
ZHOU Y, GAO J, CHEN W, et al. Seismic simultaneous source separation via patchwise sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(9): 5271-5284. DOI:10.1109/TGRS.2016.2559514 |
| [60] |
SPITZ S, PICA A, HAMPSON G. Simultaneous source separation:a prediction-subtraction approach[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 2811-2815. |
| [61] |
KIM Y, GRUZINOV I, GUO M, et al. Source separation of simultaneous source OBC data[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 51-55. |
| [62] |
WU S, BLACQUIERE G. Shot repetition:an alternative approach to blending in marine seismic[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015, 48-52. |
| [63] |
BAGAINI C, BALY M, MOORE I. The acquisition and processing of dithered slip-sweep vibroseis data[J]. Geophysical Prospecting, 2012, 60(4): 618-639. DOI:10.1111/j.1365-2478.2012.01085.x |
| [64] |
CHEN H, CAO S, YUAN S, et al. Robust iterative deblending of simultaneous-source data[J]. Expanded Abstracts of 87th Annual Internat SEG Mtg, 2017, 4893-4897. |
| [65] |
FROMYR E, CAMBOIS G, LOYD R, et al. Flam-A simultaneous source wide azimuth test[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 2821-2825. |
| [66] |
VERSCHUUR D, BERKHOT A. Target-oriented least-squares imaging of blended data[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 2889-2893. |
| [67] |
TANG Y, BIONDI B. Least-squares migration/inversion of blended data[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 2859-2863. |
| [68] |
DAI W, WANG X, SCHUSTER G T. Least-squares migration of multisource data with a deblurring filter[J]. Geophysics, 2011, 76(5): R135-R146. DOI:10.1190/geo2010-0159.1 |
| [69] |
DAI W, FOWLER P, SCHUSTER G T. Multi-source least-squares reverse time migration[J]. Geophysical Prospecting, 2012, 60(4): 681-695. DOI:10.1111/j.1365-2478.2012.01092.x |




