2. 南方海洋科学与工程广东省实验室(湛江), 广东湛江 524088
2. Southern Marine Science and Engineering Guangdong Laboratory(Zhanjiang), Zhanjiang 524088, China
地震勘探系统由3个基本单元组成:震源、地下介质、检波器。震源和检波器的排列方式, 即观测系统, 是地震勘探系统中重要的组成部分。震源在整个油气地震勘探技术链条中占据重要位置, 对地震数据的质量有着决定性影响。地震勘探中主要有脉冲震源(炸药震源)和非脉冲震源(可控震源)。
美国大陆石油公司(CONOCO)于1952年开始进行连续振动地震作业方法试验, 并在1956年完成专利注册。同年, 世界上第1个可控震源地震队成立。早期的可控震源是一套由机械装置控制的连续振动系统, 并且其振动控制系统采用开环控制方式, 系统控制精度较低。1959年研制出了液压伺服控制的可控震源, 并开始对输出信号进行相位控制试验。1963年以控制振动平板输出信号相位为目的的现代可控震源开始投入使用。1967年研制成功用于海上勘探的可控震源。
陆上可控震源地震勘探采用一个与大地紧密耦合的振动平板, 以反作用方式向地下传送一组连续振动的弹性波信号(又称扫描信号), 再经过对地面接收到的反射波信号进行成像处理, 用于解释地下地质目标的构造形态与产状。这种扫描信号是一种连续的、频率变化的信号。不是所有的连续信号都可以用于地震勘探, 除伪随机信号外, 可控震源的扫描信号必须满足如下基本要求:①具有相应的起始与终了频率; ②具有相应的起始与终了镶边函数(斜坡); ③具有一定的扫描时间; ④扫描信号可以是(线性的)严格单调升频或降频, 也可以是非线性的扫描。
经过几十年的不断发展, 一般意义下的可控震源地震勘探技术已经发展得相当完善了。为什么最近十几年, 可控震源地震勘探技术, 无论是陆上或是海上的, 都重新受到重视[1]?
1) 可控震源是一种破坏性低的震源, 在环境保护意识逐渐提升的今天, 只要有可能, 油气地震勘探中都必然会采用绿色环保的激发方式。海上可控震源对海洋生物的干扰比气枪震源要小很多。工农业发达地区, 陆上可控震源对工农业基础设施的影响要弱很多。
2) 油气地震勘探的目标越来越小, 油藏描述的精度要求越来越高, 高精度反演成像(如全波形反演(FWI)和最小二乘逆时深度偏移(LS_RTM))成为必要的方法技术。这就促进了地震数据必须采用“两宽一高”的采集方式。其中, 能高效且廉价地激发出地震波场的震源是必须具备的条件。与炸药震源相比, 可控震源显然更具优势。
3) 宽带地震勘探是实现高精度成像和油藏描述的必由之路[2]。可控震源至少理论上可以通过人为控制激发出1~100 Hz频带范围的地震波, 或者说可以由客户定制震源激发子波, 甚至定制接收的反射子波。当前, 有的石油公司仅采集1~4 Hz的低频长偏移距数据, 用于FWI透射波层析反演以建立更精确的背景速度场, 这只有利用可控震源才能够实现[3]。
在当前技术及经济效益需求下, 尚有哪些与可控震源有关的问题值得关注和研究?
1) 与当今先进制造技术相关的新一代可控震源的设计、研发与制造。最近十几年, 几家大的西方石油公司投入大量人力和物力制造的新一代海上可控震源已经接近商业应用的程度[4-5]。对采集到低至1 Hz的地震波场的需求使得有必要发展新一代的可控震源。另外, 震源的小型化、轻便化、智能地感知介质和记录波场的变化从而调整扫描信号、自主移动等新需求不断出现, 促进了可控震源制造技术的变革。
2) 从理论上讲, 利用可控震源可以人为地控制反射子波的频谱, 产生客户希望的宽带地震子波。但是, 当前的可控震源与这样的期望还相差甚远。
3) “两宽一高”地震数据采集方式的真正实现中, 震源起到了至关重要的作用。所谓高密度地震勘探, 更重要的是实现炮点的高密度。巨量的炮点必然带来施工效率的大幅度降低和成本的大幅度提升, 目前多台可控震源同时激发是实现高密度地震勘探的必要措施。为提高采集效率, 同时方便混叠数据的解混叠, 高效采集中可控震源扫描方式、多台震源起震时间的设计还需要进一步研究[6]。
4) 可控震源的震动激发方式与脉冲(炸药)震源不同。由于与近地表介质的相互作用机制不同, 产生的噪声类型(实际上是在近地表区域传播的波的类型)差异很大[7]。在可控震源高效采集中, 由于涉及到后续地震数据的解混叠处理, 对噪声非常关注。但是, 不同近地表介质和地形条件下, 可控震源产生噪声的机制并不完全相同。
5) 混叠数据的解混叠, 尤其是当涉及到压缩感知理论下空间随机观测方式、近地表条件下相关噪声比较强、静校正问题很复杂、地下介质横向变化很剧烈时, 解混叠问题远没有得到很好地解决。
6) 可控震源高效采集方案的制订与实施, 原则上是一个最优化问题, 应该开发出一个最优化可控震源高效采集软件管理系统, 与自动化、智能化的可控震源系统一起, 发展出一套先进的可控震源地震数据高效采集系统, 从而大幅提升数据采集的效率和自动化与智能化程度, 显著降低数据采集成本[8-9]。
笔者认为, 上述6个方面的问题还需要进行深入的研究。
可控震源的本质是激发单频震动、采用时延积累震动能量、各单频震动满足线性叠加原理。在此理论基础上, 设计合理的扫描信号, 驱动可控震源机械系统, 在实际介质中激发不同频率的谐波地震波, 在地表接收反射的谐波地震波, 通过与扫描信号的互相关, 得到地表观测的波场。如何设计可控震源以激发出期望的谐波地震波, 超出了笔者的专业研究范围。本文重点讨论与分析当前可控震源地震勘探面临的问题, 提出相应的对策, 并重点阐述我们一直推崇的客户定制反射子波的可控震源地震勘探理念, 促进可控震源地震勘探技术的进一步深入研究和应用。
1 当前可控震源地震勘探面临的问题及解决方案 1.1 高效采集方案问题分析“两宽一高”地震数据采集过程中, 由于炮点密度和炮线密度的增加, 炮点数目大幅提升。保持检波器端的宽方位、长偏移距、合适的检波点距和线距的情形下, 必须提高每天的单炮道集采集数目才能在有限时间内完成一个工区数十万至百万炮道集的采集任务。
实践证明, 目前的炸药震源, 无论从成本和效率方面都远远无法满足真正的“两宽一高”地震数据采集的要求。比较而言, 可控震源更能满足“两宽一高”地震数据采集的要求。事实上, 要真正满足“两宽一高”地震数据采集的要求, 进而大幅度提升成像质量和勘探效益, 震源技术和检波器技术都需要有创新性的改变。
所谓的高效采集, 指的是若干台可控震源同时激发的地震数据采集方式。高效采集方案的设计既要考虑提高单位时间内所采集的单炮道集的数量, 又要尽量减少同时激发的不同震源之间的波场干扰。当然, 这中间还要注意野外施工时, 可控震源数量有限, 要重复使用这些震源就必须考虑震源移动问题。此处不考虑施工中的问题, 仅仅分析在尽可能好地分离出独立单源激发波场的情况下, 提升单位时间内能采集到的单炮道集数目。这显然是一个优化设计问题。
已有大量文献讨论过此问题[10-13], 此处我们分析想要尽可能好地分离出独立单源激发波场的影响因素, 正是它们在影响高效采集方案的制定。①单个可控震源之间的空间距离:距离越大, 相隔一定距离同时激发的两个可控震源激发波场之间的干扰越小, 甚至不存在干扰。②扫描方式:若干相邻的可控震源激发的谐波只要不重叠, 激发的波场就不相干。③随机起震时间:若干相邻的可控震源同时激发产生的混叠波场, 在进行解混叠时, 必须利用各可控震源之间的随机起震时间。④不同近地表条件与可控震源相互作用引起的噪声:噪声的类型和强弱, 直接影响混叠波场中的干扰情况, 影响后续混叠波场的分离。高效采集方案的设计中尽量不要让相邻炮激发的、在近地表传播的噪声波场干扰当前炮集中主要反射层对应的反射波场。
笔者认为, 高效采集方案的设计应该以尽可能好地分离出独立单源激发波场和预定的采集效率为目标提出一个优化问题, 而不是分散地考虑独立因素设计高效采集方案。
1.2 可控震源激发的与自由地表相关的噪声波场分析可控震源地震勘探中一个重要的问题是可控震源激发的噪声问题, 它与炸药震源明显不同。高效采集和高精度反演都非常重视噪声问题。可控震源地震勘探中已知的特殊噪声包括谐波噪声和可控震源车移动产生的噪声。关于谐波噪声的研究文献有很多[14]。可控震源车移动产生的噪声是一种常见的噪声类型。
遗憾的是, 目前可控震源与不同的地表介质作用产生噪声的机制仍没有研究清楚。譬如沙漠(干砂、湿砂、松软的砂、压实的砂、沙丘)、戈壁、农田、基岩出露、冲积砾石等地表介质类型, 包括不同地形特征, 可控震源(包括炸药震源)激发产生的在近地表传播的噪声波场特征差异很大。应该在不同介质情况下, 在可控震源周围一定范围内布设检波器, 观测并分析可控震源引起的在近地表传播的噪声波场特征, 分析总结其中的规律。
这些复杂的噪声对高效采集中混叠数据的解混叠效果有很严重的影响, 从而制约着高效采集技术的实际应用。笔者认为应该系统地分析这些噪声产生的机制与特点, 并基于此优化所设计的高效采集方案。
1.3 混叠数据的解混叠问题分析高效采集中混叠数据的解混叠是一个老问题。多炮同时激发的波场被任意一个检波器接收, 其记录的波场是一个混叠波场, 相当于每个检波器“听到几个人同时在讲话”, 这是一个典型的“鸡尾酒会”问题。根据记录的波场区分出每个震源激发的波场, 这是一个经典的盲反演问题。地震勘探中不会直接求解这种盲反演问题, 通常是设计一种若干可控震源随机起震的方式, 对若干可控震源进行时间上的随机编码。由于这种随机编码的引入, 使得解码(解混叠)变得相对简单。按照主索引重排数据, 主索引数据间没有随机时间差, 同相轴具有线性或非线性(譬如双曲或抛物)可预测性, 次索引数据由于可控震源激发时间的随机表现出时间上的随机性, 据此设计预测器(或滤波器), 就可以把主索引数据提取出来。这就是目前混叠数据解混叠的最核心做法, 其严格依赖于对若干可控震源进行时间上的随机编码。已有很多文献[15-19]对该时间上的随机编码方式进行过讨论。
混叠数据的解混叠效果, 还受主索引数据中同相轴是否具有线性或非线性(双曲或抛物)可预测性的制约。这显然与近地表条件引起的静校正、地下介质横向变化情况以及同时源激发数据的信噪比等有密切关系。目前该问题尚未引起足够重视。事实上, 制约高效采集的因素不仅仅是前文讨论的那4个方面, 还应包括这些问题。
1.4 压缩感知理论下空间随机采样与高效采集问题分析“两宽一高”代表了地震数据采集的技术发展方向, 高效采集可以说只是实现“两宽一高”地震数据采集的一种探索。如何高效率、低成本地采集到宽方位、高密度、宽频带、高信噪比的地震数据依然任重而道远。
Shannon采样理论是当前指导地震数据采集和处理的基本理论。但是, 按照Shannon采样理论采集到的数据(至少理论上看)大多是冗余的, 而且它也导引不出高效的采集方法。压缩感知采样提供了另一种采样理论。只要地震波场具备可稀疏表达的特点, 就可以对它进行压缩感知理论下的炮检点位置空间随机采样。
事实上, 高效采集所要求的若干可控震源同时激发时各震源之间起震时间的随机性已经在利用压缩感知理论, 基于此, 可以实现单位时间内获得更多炮道集的高效采集。更为高效的采集应该是使震源点和检波点的空间位置服从随机排布[20]。
理想的高效采集方式是:按高密度采集的要求, 基于解混叠效果最好的原则优化设计空间随机分布的炮检点位置和每个震源起震时间, 将同一探区所有震源和检波器按设计要求布设好, 按设计好的起震时间起震, 连续记录所有震源产生的波场。这样就可以用极高的效率进行地震数据采集。但是, 巨量的震源和检波器增加了硬件成本。
因此, 发展廉价、宽带响应、有自动传输功能的无线单点检波器以及小型化、廉价、可大量布置的宽带震源是实现高密度、宽方位、宽频带(尤其是低频端)数据高效采集的技术发展方向。
1.5 最优化理论下的高效采集软件控制系统分析根据上述讨论, 可控震源高效采集涉及多方面的影响因素, 但是目标是明确的:在尽可能短的时间内, 采集到更多高质量的单炮数据。这明显是一个最优化问题。在当前高性能计算、5G通讯等技术的支持下, 可以也应该研发出一个最优化可控震源高效采集软件管理系统, 统一管理各可控震源的扫描信号自适应变化、震源自动移动、随机激发时间等, 大幅提升数据采集的效率和自动化与智能化程度, 显著降低数据采集成本。
2 客户定制反射子波的可控震源对于高精度地震勘探, 激发和接收宽带子波具有极为重要的意义。当然, 保持频带的成像处理也十分重要。本文不讨论宽频处理, 而是着重分析激发和接收宽带子波的问题。
2.1 谐波叠加产生地震子波问题分析脉冲震源(炸药)激发出的地震子波频带和时间延续度有限、谱光滑变化。这种子波可以被分解为不同幅值和不同频率的谐波成分, 可控震源正是基于该理论研发的。
零相位子波可以由公式(1)进行描述。
| $ f(t) = \sum\limits_{j = 0}^N {{a_j}} \cdot {\rm{cos}}(2\pi {f_j} \cdot t) $ | (1) |
式中:aj为单频谐波的振幅; fj为单频谐波的频率, 其变化范围可以人为确定为[fmin, fmax], 其中fmin和fmax分别为子波频带的下限和上限。
为了控制子波振幅谱的能量展布, 可以加入一个振幅编码函数h(aj), j=0, 1, 2, …, N。这样, (1)式可以重写为:
| $ f(t) = \sum\limits_{j = 0}^N h ({a_j}) \cdot {\rm{cos}}(2\pi {f_j} \cdot t) $ | (2) |
其中, h(aj), j=0, 1, 2, …, N的选择可以满足构造宽带子波的要求, 根据需要人为调整振幅谱的分布特征。
更进一步地, 为了解决子波旁瓣过多和旁瓣能量较强的问题, 我们可以把窗函数施加到由(2)式得到的地震子波上。这样既兼顾了子波的局部性, 也考虑了宽带子波谱的特点。综上所述, 可以定义如下的子波形式:
| $ \begin{array}{l} {f^B}(t) = g(t)f(t) = g(t)[\sum\limits_{j = 0}^N h ({a_j}) \cdot \\ \;\;\;\;\;\;\;\;\;\;{\rm{cos}}(2{\rm{\pi }}{f_j} \cdot t)] \end{array} $ | (3) |
其中, 窗函数g(t)可以选不同的形式, 譬如高斯窗或Hanning窗等。理论上这样构造的地震子波可以兼顾宽频、零相位、小旁瓣的要求。设计可控震源扫描信号能比较容易地控制h(aj), j=0, 1, 2, …, N, 但控制窗函数g(t)就比较困难。一般情况下仅控制h(aj)以得到较为理想的地震子波, 尽量不考虑g(t)。
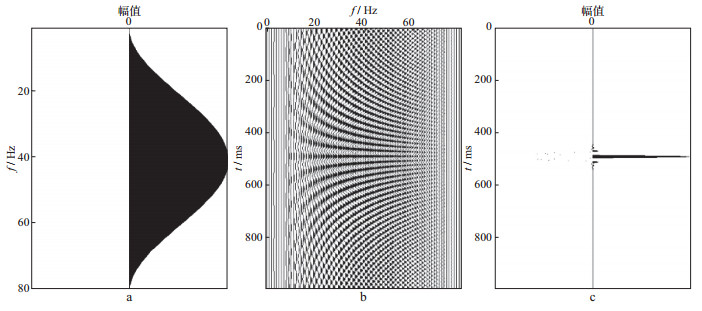
编码函数h(aj), j=0, 1, 2, …, N的设计很关键。图 1至图 5给出了不同形式的h(aj)对应的振幅谱、谐波成分以及零相位叠加产生的地震子波。其中, h(aj)定义为:
| $ h({a_j}) = 1 + {\rm{cos}}\left[ {\frac{{\pi ({f_j} + F)}}{T}} \right] $ | (4) |
|
图 1 h1(a)对应的振幅谱(a)、谐波成分(b)以及零相位叠加产生的地震子波(c) |
|
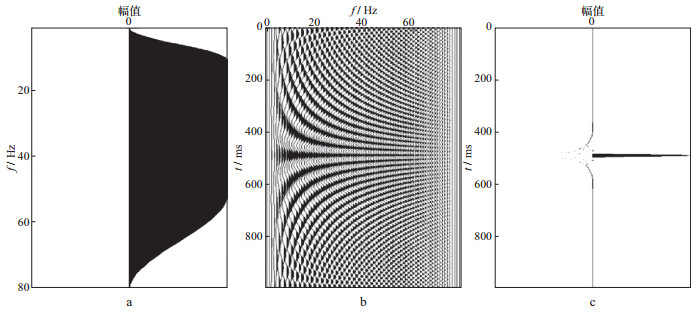
图 2 h2(a)对应的振幅谱(a)、谐波成分(b)以及零相位叠加产生的地震子波(c) |
|
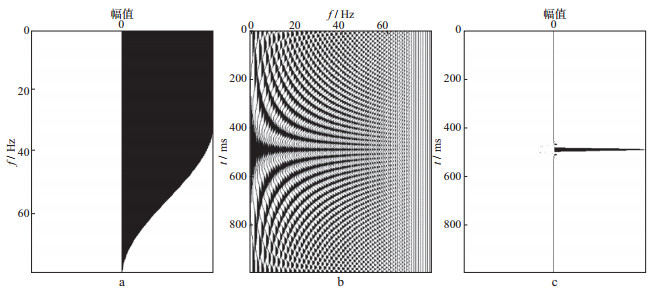
图 3 h3(a)对应的振幅谱(a)、谐波成分(b)以及零相位叠加产生的地震子波(c) |
|
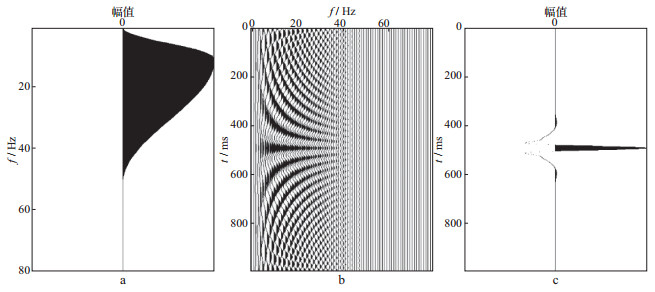
图 4 h4(a)对应的振幅谱(a)、谐波成分(b)以及零相位叠加产生的地震子波(c) |
|
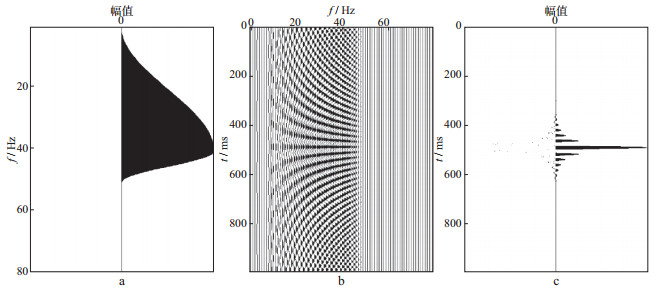
图 5 h5(a)对应的振幅谱(a)、谐波成分(b)以及零相位叠加产生的地震子波(c) |
其中, F是引入的控制振幅随频率变化的量。在可控震源中, h(aj)为扫描信号。在信号分析理论中, h(aj)也可选为其它窗函数的形式, 很多信号分析文献专门讨论了窗函数选择问题。
图 1a的振幅谱函数为:
| $ {h_1}(a) = 1 + {\rm{cos}}\left[ {\frac{{\pi (f - 40)}}{{40}}} \right]\quad f \in [0,80] $ |
图 2a的振幅谱函数为:
| $ {h_2}(a) = \left\{ {\begin{array}{*{20}{c}} {1 + {\rm{cos}}\left[ {\frac{{\pi (f - 10)}}{{10}}} \right]}&{0 \le f < 10}\\ 2&{10 \le f < 50}\\ {1 + {\rm{cos}}\left[ {\frac{{\pi (f + 10)}}{{30}}} \right]}&{50 \le f < 80} \end{array}} \right. $ |
图 3a的振幅谱函数为:
| $ {h_3}(a) = \left\{ {\begin{array}{*{20}{c}} 2&{0 \le f < 30}\\ {1 + {\rm{cos}}\left[ {\frac{{\pi (f - 30)}}{{50}}} \right]}&{30 \le f < 80} \end{array}} \right. $ |
图 4a的振幅谱函数为:
| $ {h_4}(a) = \left\{ {\begin{array}{*{20}{l}} {1 + {\rm{cos}}\left[ {\frac{{\pi (f - 10)}}{{10}}} \right]}&{0 \le f < 10}\\ {1 + {\rm{cos}}\left[ {\frac{{\pi (f - 10)}}{{40}}} \right]}&{10 \le f < 50} \end{array}} \right. $ |
图 5a的振幅谱函数为:
| $ {h_5}(a) = \left\{ {\begin{array}{*{20}{l}} {1 + {\rm{cos}}\left[ {\frac{{\pi (f - 40)}}{{40}}} \right]}&{0 \le f < 40}\\ {1 + {\rm{cos}}\left[ {\frac{{\pi (f - 40)}}{{10}}} \right]}&{40 \le f < 50} \end{array}} \right. $ |
从图 1至图 5可以清楚地看出, 地震子波的形状由振幅谱或每个单频余弦函数的振幅分布决定。当然也严重依赖于相位谱, 但此处我们已经界定所设计的子波是零相位的。低频的缺失是导致子波旁瓣电平水平高、延续时间长的重要原因; 优势的低频分量是产生高分辨率地震子波的重要因素。这也清楚地说明了地震数据处理过程中, 低频的重要性。高频成分的存在可以压缩地震子波主瓣宽度, 提高分辨率。勘探地震中, 丰富的(必须是有效的)低频成分的存在对提高分辨率的贡献很大。图 1至图 5的数值试验清楚地展示了子波振幅谱的整体形态决定地震子波的分辨率, 而不仅仅是频宽, 也不是优势频率。这才是对地震子波分辨率的完整描述。由于地震子波的整体振幅谱很难把握, 用地震子波频率范围的倍频程来刻画地震子波的分辨率更合适。高分辨率地震勘探中, 期望地震子波(激发子波、接收子波、成像子波)具有5个以上的倍频程。
在可控震源设计中, 图 1至图 5的数值试验具有特别明显的指导意义, 其关键是如何设计扫描信号。将公式(2)中对h(aj), j=0, 1, 2, …, N的控制转化为对扫描时间的控制, 扫描时间的累积决定单频谱幅值的大小, 从而得到比较理想的各单频信号的振幅分布。在可控震源高分辨率地震勘探中, 这是十分有意义的探索。用其它震源进行高分辨率地震勘探, 基本思想类似, 但是炸药和气枪震源不容易控制所激发子波的形态, 因此如何使脉冲震源产生高分辨率地震子波还要进行持续深入的探索。
2.2 客户定制地震子波的基本思想与方法高分辨率地震勘探需要高分辨率地震子波, 但理想子波构造标准的提出还是源于对实际子波特征的深入认识。最小相位、较光滑、频带较宽且较为平坦的谱是期望子波的频域特征; 主瓣较窄、旁瓣电平水平低、延续时间短的子波是期望子波的时域特征。
更为重要的, 我们希望在地震数据采集过程中真正能产生所期望的子波。因此, 在地震数据采集过程中, 原则上应该包括观测系统和地震子波的设计两个方面, 这样才能得到纵横向高分辨率的成像结果, 方便储层解释。目前, 地震数据采集过程中, 更多地关注观测系统设计, 很少关注地震子波的设计。这是因为客户定制地震子波实现难度非常大!
实现对期望地震子波的设计目前似乎只有可控震源能够做到。可控震源采用对不同的单频信号进行编码的方式产生扫描信号, 扫描信号控制振动装置进行激发。野外接收未相关的数据, 室内用扫描信号对未相关数据进行相关处理, 得到反射地震记录。
目前常用的扫描信号包括:线性扫描信号(升频或降频方法)、非线性扫描信号(DB/OCT和DB/Hz方法)和伪随机扫描信号。譬如线性扫描信号为:
| $ \begin{array}{*{20}{c}} {S(t) = A{\rm{sin}}2\pi \left( {{f_{\rm{s}}} + \frac{{{f_{\rm{e}}} - {f_{\rm{s}}}}}{{2T}}t} \right)t}\\ {0 \le t < T} \end{array} $ | (5) |
其瞬时相位为:
| $ \varphi (t) = 2\pi \left( {{f_{\rm{s}}} + \frac{{{f_{\rm{e}}} - {f_{\rm{s}}}}}{{2T}}t} \right)t $ | (6a) |
瞬时频率为:
| $ f(t) = \frac{{{\rm{d}}\varphi (t)}}{{{\rm{d}}t}} = {f_{\rm{s}}} + \frac{{{f_{\rm{e}}} - {f_{\rm{s}}}}}{{2T}}t $ | (6b) |
式中:fs为起始扫描频率; fe为终止扫描频率; T为扫描时长。
地震子波的分辨率主要由其整体振幅谱形态决定。对可控震源而言, 单频谐波的能量取决于时间累积的结果, 因此, 可以通过设计扫描信号得到期望的整体振幅谱形态, 最终得到期望的高分辨率子波。可控震源通过扫描信号和记录信号的自相关得到反射子波, 反射信号的振幅谱是扫描信号振幅谱的平方。精细地控制单频谐波的幅值, 线性扫描显然不是最好的方式, 应该用非线性扫描方法。
若期望设计反射子波的振幅谱, 得到高分辨率反射子波, 则必须考虑地下介质的变化, 这就需要一个反馈过程。基于实际介质中接收到的反射信号, 根据其与期望分辨率的偏差, 及时调整扫描信号, 使后续震动激发出期望的高分辨率地震子波。很显然这也是一个优化问题。在当前人工智能和机器学习应用逐渐普及的情况下, 可以将可控震源与地下介质视为一个系统, 在该系统输出理想高分辨率期望子波的约束下, 将实测反射子波与理想高分辨率期望子波的差异作为反馈量, 调整可控震源的非线性扫描方式, 使得最终的输出结果接近理想的高分辨率期望子波。
实际上, 可控震源宽带子波设计更现实的方案是由多台车组合完成[21]。我们知道, 不同类型震源车能够激发出频带不同的子波。箱体大的震源车激发的低频信号比较好, 箱体较小的震源车激发的高频信号比较好。以前为了使得单台震源车能够激发的频带足够宽, 常常需要折中, 这样使得扫描频带的低频端和高频端均受到了限制。如果每台震源车采用不同频带激发, 每种震源车的特征就可以得到更好的利用。这样做的另外一个优点在于激发出来的混叠子波频带可以更宽, 可以使地震记录的分辨率更高。但是, 这会使得设备维护过程更加复杂, 成本增加。到底是采用单台震源车兼顾所有频带, 还是利用不同频段的震源车进行组合, 要看今后的技术发展和应用情况[22-25]。
2.3 客户定制可控震源子波的数值试验扫描信号实际上是对单频信号的编码, 可以用(7)式来表达。
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{S_{{\rm{sc}}}}(\omega ,t) = s({\omega _1},\Delta {t_1}){{\rm{e}}^{ - {\rm{i}}{\varphi _1}}} + s({\omega _2},\Delta {t_2}){{\rm{e}}^{ - {\rm{i}}{\varphi _2}}} + \cdots + }\\ {s({\omega _n},\Delta {t_n}){{\rm{e}}^{ - {\rm{i}}{\varphi _n}}}} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = ({{\rm{e}}^{ - {\rm{i}}{\varphi _1}}},{{\rm{e}}^{ - {\rm{i}}{\varphi _2}}}, \cdots ,{{\rm{e}}^{ - {\rm{i}}{\varphi _n}}})\left[ {\begin{array}{*{20}{c}} {s({\omega _1},\Delta {t_1})}\\ {s({\omega _2},\Delta {t_2})}\\ \vdots \\ {s({\omega _n},\Delta {t_n})} \end{array}} \right] \end{array} $ | (7) |
其中, s(ωi, Δti), i=1, 2, …, n代表单频信号的时间域振动, Δti, i=1, 2, …, n代表单频(ωi)谐波的延续时间, e-iφj, j=1, 2, …, n代表每个单频扫描信号的相位移动函数, 所有函数组合形成一定的编码形式, 每个单频振动的时长不同, 这取决于扫描信号的编码方式, n代表扫描频率的个数, Ssc(ω, t)代表扫描信号, 它按一定的形式将不同频率的振动组合在一起。
用(7)式控制可控震源进行振动, 得到相关前的地震记录Sbc(ω, t), 它是上述扫描信号控制下震源车产生的振动在接收点接收的记录。用Ssc(ω, t)对Sbc(ω, t)进行相关处理, 得到常规地震数据。其过程可以描述为:
| $ \begin{array}{*{20}{l}} {{S_{{\rm{ ac }}}}(\omega ) = \sum\limits_t {S_{{\rm{ sc }}}^*} (\omega ,t){S_{{\rm{ bc }}}}(\omega ,t)}\\ { = \sum\limits_t {S_{{\rm{sc}}}^*} (\omega ,t){S_{{\rm{sc}}}}(\omega ,t)R(\omega )}\\ { = R(\omega )\sum\limits_t {S_{{\rm{ sc }}}^*} (\omega ,t){S_{{\rm{sc}}}}(\omega ,t)} \end{array} $ | (8) |
其中, Sac(ω)代表相关后地震记录的频谱, Ssc*(ω, t)是扫描信号Ssc(ω, t)的共轭, R(ω)为地下反射系数。应该注意的是, Sbc(ω, t)不会严格等于扫描信号与地下反射系数的褶积, 传播过程改变了震源激发的扫描信号, 但为了推导公式方便, 假定可以如此近似。
将(7)式中的扫描信号代入(8)式得到:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{S_{{\rm{ac}}}}(\omega ) = R(\omega )\sum\limits_t {S_{{\rm{sc}}}^*} (\omega ,t){S_{{\rm{sc}}}}(\omega ,t)}\\ { = R(\omega )\sum\limits_i \cdot } \end{array}\\ \left\{ \begin{array}{l} \\ {[s({\omega _1},\Delta {t_1})\quad s({\omega _2},\Delta {t_2})\quad \cdots \quad s({\omega _n},\Delta {t_n})]^*}\\ \; \end{array} \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left( {\begin{array}{*{20}{c}} {{{\rm{e}}^{ - {\rm{i}}{\varphi _1}}}}\\ {{{\rm{e}}^{ - {\rm{i}}{\varphi _2}}}}\\ \vdots \\ {{{\rm{e}}^{ - {\rm{i}}{\varphi _n}}}} \end{array}} \right)}^*}\quad \left( {\begin{array}{*{20}{l}} {{{\rm{e}}^{ - {\rm{i}}{\varphi _1}}}}&{{{\rm{e}}^{ - {\rm{i}}{\varphi _2}}}}& \cdots &{{{\rm{e}}^{ - {\rm{i}}{\varphi _n}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {s({\omega _1},\Delta {t_1})}\\ {s({\omega _2},\Delta {t_2})}\\ \vdots \\ {s({\omega _n},\Delta {t_n})} \end{array}} \right)} \right\}\\ = R(\omega )\sum\limits_t \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{{[s({\omega _1},\Delta {t_1})\quad s({\omega _2},\Delta {t_2})\quad \cdots \quad s({\omega _n},\Delta {t_n})]}^*}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} 1&0& \cdots &0\\ 0&1& \cdots &0\\ \vdots & \vdots &{}& \vdots \\ 0&0&0&1 \end{array}} \right]\left( {\begin{array}{*{20}{c}} {s({\omega _1},\Delta {t_1})}\\ {s({\omega _2},\Delta {t_2})}\\ \vdots \\ {s({\omega _n},\Delta {t_n})} \end{array}} \right)} \end{array}\\ = R(\omega )\sum\limits_t {[{s^*}({\omega _1},\Delta {t_1})s({\omega _1},\Delta {t_1}) + {s^*}({\omega _2},\Delta {t_2}) \cdot } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s({\omega _2},\Delta {t_2}) + \cdots + {s^*}({\omega _n},\Delta {t_n})s({\omega _n},\Delta {t_n})]\\ = R(\omega )S_{{\rm{sc}}}^{\rm{P}}(\omega ) \end{array} $ | (9) |
其中, SscP(ω)是扫描信号的功率谱。由维纳-辛钦定理可知, 扫描信号的功率谱与其自相关函数是一个傅里叶变换对。对(9)式进行傅里叶反变换得到:
| $ S(t) = W(t) * R(t) $ | (10) |
式中:W(t)是SscP(ω)的傅里叶反变换, 代表可控震源激发的地震子波。
理论上, W(t)是扫描信号的自相关结果, 是零相位的。实际上, 它是仪器记录的扫描信号与检波器记录的未相关信号的互相关结果。常规偏移成像时, 我们不太关注这一点, 但是在保真的反演成像中, W(t)的含义会影响我们对岩性油藏的解释。这一点在当今的高精度油气勘探中应该引起足够的重视。
(10) 式代表的是地震子波与反射系数R(t)的褶积产生地震记录的过程。理论上, W(t)应该具备自相关函数的特点, 它是对称的、零相位的。其频率成分由扫描信号确定, 频谱由扫描编码方式决定。
上述推导过程说明, 用扫描信号的自相关函数也可以构造一个地震子波, 而且是零相位的。与(2)式对比可以看出, 通过设计合适的扫描信号可以构造预想的地震子波, 达到高分辨率地震勘探的目的。因此, 根据上述分析, 客户定制地震子波在可控震源地震勘探中, 理论上是可行的。真正困难的是, 相关前的实际地震记录Sbc(ω, t)受地震波传播过程影响。这也是前面提出自适应介质变化进行动态非线性扫描信号设计的原因。
依据上述对可控震源激发方式的编码理论解释, 实际地震记录反射子波是编码扫描信号与地下反射系数褶积形成的, 但实际上还要与传播效应算子进行褶积, 并假设传播效应算子不改变扫描信号的相位关系。事实上, 介质的吸收衰减效应总会改变扫描信号的相位关系, 只是勘探实践表明, 这种改变不显著而已。据上述分析, 设计如下的数值实验, 证明从编码的角度可以分频段激发, 叠加形成宽频反射子波。分频段谐波激发可以由单一可控震源完成, 也可以由一组可控震源激发不同的频段完成。
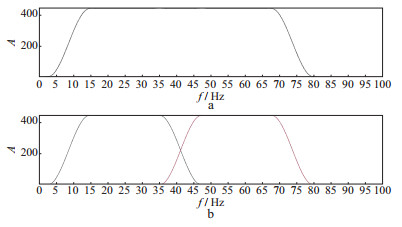
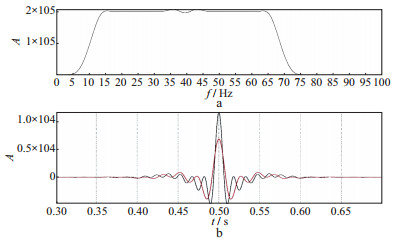
图 6a给出了常规单个宽带扫描信号的振幅谱。其频带范围为10~75 Hz, 扫描长度为10 s。图 6b给出了两个窄带扫描信号的振幅谱。图 7a显示了两个窄带扫描信号叠加后的振幅谱; 图 7b显示了单个宽带扫描信号和两个窄带扫描信号得到的相关子波。由图 6和图 7可知, 可以通过两个窄带扫描信号来实现单个宽带扫描信号所要达到的使相关子波分辨率更高的目的。这说明可以用一组不同的震源组合进行编码扫描, 得到高分辨率地震子波。
|
图 6 常规单个宽带扫描信号(a)与两个窄带扫描信号(b)的振幅谱 |
|
图 7 两个窄带扫描信号叠加后的振幅谱(a)以及常规单个宽带扫描信号(红色)和两个窄带扫描信号(黑色)得到的相关子波(b) |
前文分析过, 反射子波的分辨率取决于整个子波的振幅谱。如何控制扫描信号得到期望的反射子波振幅谱?当前的可控震源子波设计还没有建立起关于扫描信号的单频时长与单频能量之间的关系, 这需要很多野外试验工作。在实际地震数据采集过程中, 通过自适应地下介质变化反过来优化扫描信号的思想, 前面已经提到过。笔者认为这是下一代可控震源技术要解决的问题, 进入智能可控震源勘探是不可避免的!
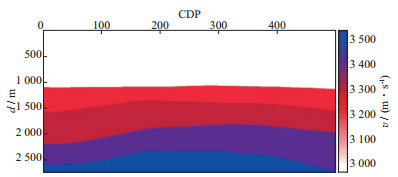
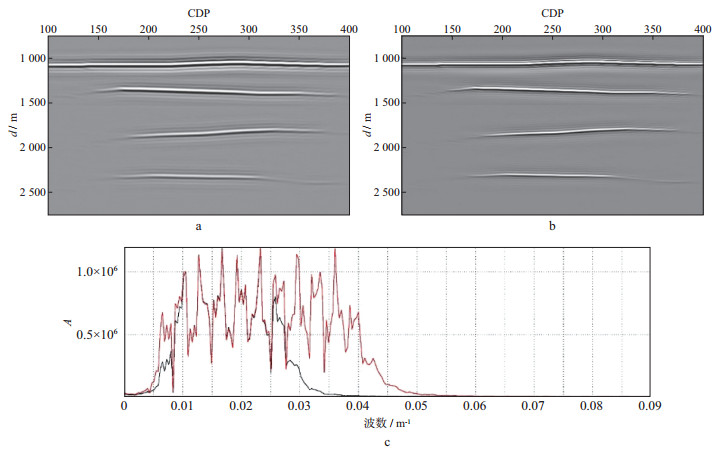
图 8显示了单个宽带扫描信号与两个窄带扫描信号对应的可控震源进行数据采集的速度模型。两个窄带扫描信号可控震源的采集系统如下:CDP100至CDP400, 总计采集100炮, 炮间隔15 m, 总记录时间为50×10.7=535 s。单个宽带扫描信号可控震源的采集系统如下:CDP100至CDP400, 总计采集50炮, 炮间隔30 m, 总的记录时间为50×11.7=585 s。在上述模型及采集数据的基础上, 进行叠前深度偏移成像, 其结果如图 9所示。图 9a是单个宽带扫描信号激发数据对应的偏移成像结果, 图 9b是两个窄带扫描信号激发数据对应的偏移成像结果, 图 9c显示了CDP250处两种偏移成像结果的振幅谱, 其中, 黑线代表图 9a偏移成像结果对应的振幅谱, 红线代表图 9b偏移成像结果对应的振幅谱。无论是对比成像剖面还是对比CDP250处地震道的振幅谱, 都可以清楚地看出, 利用不同扫描频率区间可控震源的组合可以实现高分辨率地震勘探。
|
图 8 单个宽带扫描信号与两个窄带扫描信号对应的可控震源进行数据采集的速度模型 |
|
图 9 单个宽带扫描信号激发数据得到的偏移成像结果(a)和两个窄带扫描信号激发数据得到的偏移成像结果(b)以及CDP250处两种偏移成像结果的振幅谱(c) |
该数值实验证明, 从编码的角度看, 一个完整的扫描过程, 可以由单台可控震源车完成, 也可以由不同的震源车组合完成, 理论上并不影响最后的成像效果。但是, 由不同的震源车实现不同频段的扫描并组合, 可以更精细地控制激发子波的振幅谱形态, 得到更理想的高分辨率反射子波。
与前面的子波设计方法对比可知, 实际地震数据采集过程中, 不同扫描频率区间可控震源车的组合激发是更为实际的宽带地震子波产生方式。
3 结论与讨论可控震源作为一种对环境友好、使用高效、方便控制的地震波激励源在当前绿色油气勘探理念、“两宽一高”地震数据采集技术和全波形反演(FWI)技术的推动下, 面临着新的发展机遇和新的问题。
本文从信号编码理论出发, 认为可控震源扫描信号是一组谐波的编码组合。在当前线性编码、非线性编码和随机编码的基础上, 认为不同谐波段可以在同一台可控震源车上按常规方法实现, 也可以分配到不同的可控震源车上组合实现, 后者从工程实现的角度更容易达到产生宽带数据的目的。从对地下反射子波同相叠加进行地震波成像的角度看, 都是可行的。这极大地提升了可控震源地震勘探的灵活性。另外, 分析结果指出, 反射子波的分辨率取决于其振幅谱的整体形态, 而不仅仅是优势频率和优势频宽。低频在高分辨率地震子波的形成中占据核心地位, 可以有效降低旁瓣的电平水平, 而高频分量的存在可以显著降低主瓣的宽度。扫描信号设计中应该以输出理想的高分辨率地震子波对应的振幅谱为目标。目前的线性扫描方式不可能产生期望的高分辨率子波, 非线性扫描信号的设计理论上也应该根据地下介质情况自适应地调整才能达到此目标。在分布式可控震源技术(不同震源控制不同频段的谐波扫描激发技术)基础上, 基于现代智能控制技术的发展, 实现客户定制反射子波完全是可实现的。
本文还分析了影响高效采集方案制定的5个关键因素; 讨论了可控震源引起的近地表区域传播的(噪声)波场对高效采集方案制定及地震波反演成像的影响; 解释了当前高效采集中混叠数据解混叠的思想与方法, 特别指出它们受近地表静校正量、信噪比和地下介质复杂性的影响; 提出压缩感知框架下真正的地震数据高效采集方案; 最后笔者认为, 应在最优化理论控制下, 以预定的宽带反射子波作为目标, 用接收到的地震反射子波与预定的宽带反射子波之间的差异作为反馈量, 修正扫描信号, 据此开发出一套高效采集软件控制系统, 统一管理各可控震源的扫描信号自适应变化、震源自动移动、随机激发时间等, 大幅提升数据采集的效率和自动化与智能化程度, 显著降低数据采集成本。
致谢: 感谢中石油勘探开发研究院及西北分院、中海油研究院和湛江分公司、中石化石油物探技术研究院和胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持。| [1] |
AMINE O, JIM K, CHRIS B, et al. Seismic Acquisition, what really matters?[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015, 6-11. |
| [2] |
TSINGAS C, KIM Y, YOO J. Broadband acquisition, deblending and imaging employing dispersed source arrays[J]. The Leading Edge, 2016, 35(4): 354-360. |
| [3] |
REUST D K, JOHNSTON O A, GILES J A, et al. Very low frequency seismic source[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015, 221-225. |
| [4] |
ROY D A, RUSSEL R, CRAIG B, et al. A marine vibrator to meet the joint industry project specification[J]. Expanded Abstracts of 88th Annual Internat SEG Mtg, 2018, 97-101. |
| [5] |
ROBERT P, CHINAEMEREM K, ANDREW B, et al. The wolfspar® field trial:design & execution of a low-frequency seismic survey in the gulf of Mexico[J]. Expanded Abstracts of 88th Annual Internat SEG Mtg, 2018, 91-96. |
| [6] |
王华忠. ""两宽一高""油气地震勘探中的关键问题分析[J]. 石油物探, 2019, 58(3): 313-324. WANG H Z. Key problem analysis in seismic exploration based on wide-azimuth, high-density, and broadband seismic data[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 313-324. |
| [7] |
WANG Y, BAKER G S, MILLER R D. Near-surface vibroseis signal enhancement using a fractional Fourier domain method[J]. Expanded Abstracts of 86th Annual Internat SEG Mtg, 2016, 2372-2376. |
| [8] |
DENNIS Y, PETER A, AJAY J, et al. An empirical assessment of deblending results on land vibroseis data[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 4024-4028. |
| [9] |
THOMAS J W, TOM P, KEVIN W, et al. Vibroseis sourcing methodology:A comparison of long, short, and slip-sweep 3D data image volumes acquired and constrained by equivalent source time[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 22-26. |
| [10] |
ABMA R D, HOWE M, FOSTER I, et al. Independent simultaneous source acquisition and processing[J]. Geophysics, 2015, 80(6): WD37-WD44. DOI:10.1190/geo2015-0078.1 |
| [11] |
BOUSKA J. Distance separated simultaneous sweeping, for fast, clean, vibroseis acquisition[J]. Geophysical Prospecting, 2009, 58(1): 123-153. |
| [12] |
HOWE D M, FOSTER T, ALLEN B, et al. Independent simultaneous sweeping - A method to increase the productivity of land seismic crews[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 2826-2830. |
| [13] |
MOLODVEANU N P, TOTTEN J S, ROSSO E. Vibroseis simultaneous shooting using encoded sweeps:A field experiment[J]. Expanded Abstracts of 87th Annual Internat SEG Mtg, 2017, 146-150. |
| [14] |
DENISOV M S, EGOROV A, KURIN E A, et al. Vibroseis harmonic noise elimination based on optimized recursive filtering[J]. Expanded Abstracts of 81st Annual Internat EAGE Conference & Exhibition, 2019, 1-5. |
| [15] |
ABMA R T, MANNING M, TANIS J, et al. High quality separation of simultaneous sources by sparse inversion[J]. Expanded Abstracts of 72nd Annual Internat EAGE Conference and Exhibition, 2010. DOI:10.3997/2214-4609.201400611 |
| [16] |
WILLACY C, TANG Z, JI S. Land vibroseis data deblending in the presence of strong coherent noise[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 87-91. |
| [17] |
DOULGERIS D, MAHDAD A, BLACQUIERE G. Separation of blended data by iterative estimation and subtraction of interference noise[J]. Expanded Abstracts of 80th Annual Internat SEG Mtg, 2010, 3514-3518. |
| [18] |
HUO S, LUO Y, KELAMIS P. Simultaneous sources separation via multi-directional vector-median filter[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 31-35. |
| [19] |
KIM Y I, GRUZINOV M G, SEN S. Source separation of simultaneous source OBC data[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 51-55. |
| [20] |
王华忠, 冯波, 王雄文, 等. 压缩感知及其在勘探地震中的应用[J]. 石油物探, 2016, 55(4): 467-474. WANG H Z, FENG B, WANG X W, et al. Compressed sensing and its application in seismic exploration[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 467-474. |
| [21] |
BERKHOUT A J. Blended acquisition with dispersed source arrays[J]. Geophysics, 2012, 77(4): A19-A23. DOI:10.1190/geo2011-0480.1 |
| [22] |
WEI Z H. A new low frequency vibrator enhances blended vibroseis acquisition[J]. Expanded Abstracts of 86th Annual Internat SEG Mtg, 2016, 203-207. |
| [23] |
WEI Z H. Vibroseis controllers:Are your low frequency sweeps in phase?[J]. Expanded Abstracts of 88th Annual Internat SEG Mtg, 2018, 211-215. |
| [24] |
WEI Z H, QI Y F, DUAN C P, et al. Improving vibroseis transmitted signal in desert areas[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 228-232. |
| [25] |
ZHONG H W, JASON C, ANDY B, et al. The low-frequency seismic vibrator:design and experimental verification[J]. First Break, 2018, 36(1): 77-84. |



