吸收衰减是地球介质的一种基本属性。面对复杂山前带地震成像中小尺度油气藏、深层油气藏以及非常规油气藏勘探, 高分辨率地震成像越来越成为业界关注的焦点。对于高分辨率成像, 地层的吸收衰减效应是一个重要的影响因素。有效的地震波吸收与衰减补偿是地震资料处理工作的一个重要环节。
地层的黏滞性会导致地震波传播过程中振幅衰减和相位变化, 传统的声波逆时偏移和最小二乘逆时偏移不能对其进行校正, 从而导致地下反射体能量不能得到有效的聚焦和归位。品质因子Q描述了介质的吸收衰减特性, 在地震勘探频谱范围内通常使用常Q衰减模型[1], 在此模型基础上发展了很多黏滞声波方程。在过去的20年中, 许多研究使用了频率域单程波方程来补偿上、下行波的衰减和频散效应[2-7]。这些方法通常将衰减项放在复相速度虚部, 以便实现反向补偿。与频率域黏滞声波方程相比, 时间域黏滞声波方程具有更高的计算效率。ZHU等[8-9]提出了一种吸收衰减介质的时间域黏弹性波动方程, 描述了常Q吸收衰减介质中的地震波传播, 且衰减和频散运算符在这个方程中能够被分离, 从而通过反转振幅算符符号而频散算符符号不变来补偿振幅衰减和相位频散[10]。ZHU等[11]提出了基于时间域黏弹性波动方程及其反向传播(时间反向)建模的黏弹性逆时偏移, 在黏弹性波动方程中解耦P波和S波的衰减特性, 从而在波场外推期间补偿P波和S波的衰减效应, 且设计了一种黏弹性逆时传播方法, 通过反转P波和S波振幅损失算子的符号, 来校正P波和S波的衰减效应。基于各向同性黏弹性公式, ZHU[12]将各向同性公式扩展到一般的各向异性黏弹性波动方程来模拟各向异性衰减介质, 且推导出了时间域位移-应力公式。
基于牛顿法的全波形反演方法和基于线性化的高斯-牛顿法的最小二乘偏移方法都需要求解Hessian核函数。Hessian核函数在数学上是反问题泛函对模型参数的二阶导数。而在物理学上, Hessian核函数叠合了地震波场正传播和算子反传播的所有信息[13]。Hessian核函数的敏感性更加能够体现对地下成像空间每个点的照明响应, 研究Hessian核函数对理解地震波场正、反演过程有着重要意义。在地震反演的研究中, Hessian算子有多种称谓, 如SCHUSTER等[14]提出的偏移格林函数、BOSCHI[15]提出的模型分辨率矩阵、FICHTNER等[16]提出的点传播矩阵、XIE等[17]提出的照明矩阵、YU等[18]提出的去模糊化算子、WANG等[19]提出的偏移反褶积算子。这些概念都是Hessian算子的各种变称。在局部线性化情况下, Hessian核函数又可以写为线性的Hessian矩阵, 当一个Hessian矩阵作用于最小二乘成像, 会使得成像结果模糊, 因此常规叠前偏移成像实际上是模糊的、振幅畸变的成像结果。点扩散函数(Point Spreading Function, PSF)是Hessian矩阵的一行, 对应于地下一个成像点, 反映了观测系统对该点的照明能力。通常, PSF体现为目标点周围的一个椭圆。反演理论证明, 常规偏移成像结果就是该函数对理论成像结果的“模糊化”[20]。CHEN等[21]利用一个去模糊化算子来实现黏声介质的最小二乘逆时偏移。研究带Q因子的Hessian核函数, 找出其在不同模型下的特征规律, 解决Hessian矩阵的求解与求逆问题, 是发展更高精度更高分辨率地震反演成像方法的理论基础, 可以为地球内部结构研究与油气勘探提供更有利的成像工具。Hessian核函数的求解及求逆策略可以通过Hessian点响应矩阵的求逆来开展。因此, 研究PSF, 发展带Q因子的PSF的求逆策略, 可以将其逆算子直接作用在成像结果上从而提高成像分辨率。
本文是在ZHU等[8-10]和罗文山等[22]的研究基础上, 利用常Q模型吸收衰减与补偿统一表达的一阶“速度-压力”黏声波方程实现黏声介质地震波场的格林函数计算, 对Hessian矩阵分解与求逆方法进行研究, 基于构建去模糊化算子, 开展点扩散函数的逆矩阵研究, 将逆Hessian点响应作用在成像结果上, 从而对原始成像结果有效地去模糊化, 提高了成像振幅均衡性和分辨率。最后用模型数据对方法的有效性进行了测试。
1 方法原理 1.1 黏声介质地震波格林函数有效的地震波吸收与衰减补偿首先要解决的问题是如何有效描述地震波吸收与衰减的过程。地震波场的互易性理论揭示, 地震波场传播的正、反过程可以统一利用格林函数来表达, 因此一个合理的、带吸收衰减效应的格林函数表达式是进行反演理论框架下的地震成像的基础。
1.1.1 黏声介质地震波波动方程吸收衰减介质中的应力-应变关系为:
| $ \left\{ \begin{array}{l} \sigma = {\psi _{1 - 2\gamma }}\left( t \right) * \frac{{{\rm{d}}\varepsilon }}{{{\rm{d}}t}} = \left( {\frac{{{M_0}}}{{t_0^{ - 2\gamma }}}} \right)\frac{{{\partial ^{2\gamma }}\varepsilon }}{{\partial {t^{2\gamma }}}}\\ p = - \sigma \end{array} \right. $ | (1) |
式中:σ为应力; ε为应变; p为压力; ψ1-2γ(t)为弛豫时间函数。且:
| $ \left\{ \begin{array}{l} {\psi _{1 - 2\gamma }}\left( t \right) = \frac{{{M_0}}}{{\mathit{\Gamma }\left( {1 - 2\gamma } \right)}}{\left( {\frac{t}{{{t_0}}}} \right)^{ - 2\gamma }}H\left( t \right),t > 0\\ {M_0} = \rho c_0^2{\cos ^2}\left( {\frac{{{\rm{ \mathsf{ π} }}\gamma }}{2}} \right)\\ {t_0} = \omega _0^{ - 1}\\ \gamma = \frac{1}{{\rm{ \mathsf{ π} }}}\arctan \left( {\frac{1}{Q}} \right) \end{array} \right. $ | (2) |
式中:M0和t0分别为弛豫体积模量和弛豫时间常数; Γ是欧拉γ函数; γ与Q有关; ρ, c0, Q分别为密度、参考角频率ω0对应的速度和地震品质因子。
基于ZHANG等[5]推导的时间域黏声波动方程, 可以写出吸收衰减介质地震波场衰减与补偿的统一公式:
| $ \frac{1}{{{c^2}}}\frac{{{\partial ^2}p}}{{\partial {t^2}}} = \eta {\left( { - {\nabla ^2}} \right)^{\gamma + 1}}p + \alpha \tau \frac{{\rm{d}}}{{{\rm{d}}t}}{\left( { - {\nabla ^2}} \right)^{\gamma + \frac{1}{2}}}p $ | (3) |
其中,
| $ \eta = - c_0^{2\gamma }\omega _0^{ - 2\gamma }\cos \left( {{\rm{ \mathsf{ π} }}\gamma } \right) $ |
| $ \tau = - c_0^{2\gamma - 1}\omega _0^{ - 2\gamma }\sin \left( {{\rm{ \mathsf{ π} }}\gamma } \right) $ |
| $ {c^2} = c_0^2{\cos ^2}\left( {\frac{{{\rm{ \mathsf{ π} }}\gamma }}{2}} \right) $ |
当α=1时, 公式(3)为衰减公式; α=-1时, 公式(3)为补偿公式[10]。(3)式的一阶速度-压力形式为:
| $ \left\{ \begin{array}{l} \frac{{\partial {v_x}}}{{\partial t}} = \frac{{\partial u}}{{\partial x}}\\ \frac{{\partial {v_z}}}{{\partial t}} = \frac{{\partial u}}{{\partial z}}\\ \frac{{\partial u}}{{\partial t}} = - {c^2}\left( {\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}}} \right)\left[ {\eta {{\left( { - {\nabla ^2}} \right)}^\gamma } + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\alpha \tau \frac{\partial }{{\partial t}}{{\left( { - {\nabla ^2}} \right)}^{\gamma - \frac{1}{2}}}} \right] \end{array} \right. $ | (4) |
其中, u=∂p/∂t, vx=∂p/∂x, vz=∂p/∂z。当Q趋向无穷大时, γ→0, η→-1, τ→0, 则(4)式退化为一阶速度-压力形式的纯声波方程。
1.1.2 数值计算方法采用交错网格有限差分进行波场模拟, 对于(4)式中的高阶项采用伪谱法进行计算。其公式为:
| $ \left\{ \begin{array}{l} \frac{{v_x^{k + 1/2} - v_x^{k - 1/2}}}{{\Delta t}} = \frac{{\partial {u^k}}}{{\partial x}}\\ \frac{{v_z^{k + 1/2} - v_z^{k - 1/2}}}{{\Delta t}} = \frac{{\partial {u^k}}}{{\partial z}}\\ {S^k} = \left( {\frac{{\partial v_x^{k + 1/2}}}{{\partial x}} + \frac{{\partial v_z^{k + 1/2}}}{{\partial z}}} \right)\\ {R^k} = \frac{1}{{\Delta t}}\left( {{S^k} - {S^{k - 1}}} \right)\\ \frac{{{u^{k + 1}} - {u^k}}}{{\Delta t}} = - {c^2}\left[ {\eta {{\left( { - {\nabla ^2}} \right)}^\gamma }{S^k} + \alpha \tau {{\left( { - {\nabla ^2}} \right)}^{\gamma - \frac{1}{2}}}{R^k}} \right] \end{array} \right. $ | (5) |
公式(5)中的上角标“k”为离散的时间坐标。对于分数阶拉普拉斯算子(-∇2)γ和
波场传播到计算区域的边界, 采用最佳匹配层(PML)吸收边界条件。由于PML是在非吸收衰减方程中得到的边界条件, 本质上也是对波场振幅的衰减。为了避免两种衰减效应刚性过渡造成的边界反射, 在计算区与PML之间添加一个过渡区, 在过渡区中两种吸收衰减线性过渡。
1.2 Hessian核函数的求解与求逆 1.2.1 点扩散函数与其逆函数的求取在背景介质中, 记炮点位置为xs, 检波点位置为xr, 由炮点传播到散射点的频率域格林函数定义为:
| $ \left( {{\nabla ^2} + {\omega ^2}{\mathit{\boldsymbol{\sigma }}^2}} \right)\mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}},\mathit{\boldsymbol{x}},\omega } \right) = - \delta \left( {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{x}}} \right) $ | (6) |
式中:σ(x)=1/v(x), 为介质点xs上的慢度, v(x)为介质点集合x上的速度。类似的可以定义由检波点到散射点的格林函数。在Born近似下, 观测系统的地震记录可以表示为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega } \right) = {\omega ^2}\sum\limits_x {\mathit{\boldsymbol{r}}\left( \mathit{\boldsymbol{x}} \right){f_{\rm{s}}}\left( \omega \right)\mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}},\mathit{\boldsymbol{x}},\omega } \right)} \cdot }\\ {\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega } \right)} \end{array} $ | (7) |
式中:fs(ω)为炮点xs处激发的能量在圆频率ω上的谱; r是一个与反射系数相关的量。用矩阵-向量记法, (7)式可写为:
| $ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{m}}_0} $ | (8) |
式中:L表示一个线性模拟算子, 与观测系统、震源子波和地下介质模型参数有关; m0是地下反射率模型。对应正演模拟算子L, 可以获得其伴随偏移算子LT, 则偏移成像结果m可表示为:
| $ \mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{m}}_0} $ | (9) |
(9) 式用格林函数表示为:
| $ \begin{array}{l} \mathit{\boldsymbol{m}}\left( \mathit{\boldsymbol{x}} \right) = {\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_\omega {{\omega ^4}\sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{s}}}} {\left[ {\left| {{f_{\rm{s}}}{{\left( \omega \right)}^2}} \right|\mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}},\mathit{\boldsymbol{x}},\omega } \right){\mathit{\boldsymbol{G}}^t}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}},} \right.} \right.} } } \right.\\ \;\;\;\;\;\;\left. {\left. {\left. {\mathit{\boldsymbol{y}},\omega } \right)\sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{r}}}} {\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega } \right){\mathit{\boldsymbol{G}}^t}\left( {\mathit{\boldsymbol{y}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega } \right)\mathit{\boldsymbol{m}}\left( {{\mathit{\boldsymbol{x}}_0}} \right)} } \right]} \right\}\\ \;\;\;\;\;\; = {\mathit{\boldsymbol{H}}_a}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right)\mathit{\boldsymbol{m}}\left( {{\mathit{\boldsymbol{x}}_0}} \right) \end{array} $ | (10) |
式中:Gt表示G的共轭函数; m(x0)为位于x0处的点散射体; Ha(x, y)为Hessian算子, 其表达式为:
| $ \begin{array}{l} {\mathit{\boldsymbol{H}}_a}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = {\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_\omega {{\omega ^4}\sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{s}}}} {\left[ {\left| {{f_{\rm{s}}}{{\left( \omega \right)}^2}} \right|\mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}},\mathit{\boldsymbol{x}},\omega } \right) \cdot } \right.} } } \right.\\ \left. {\left. {{\mathit{\boldsymbol{G}}^t}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}},\mathit{\boldsymbol{y}},\omega } \right)\sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{r}}}} {\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega } \right){\mathit{\boldsymbol{G}}^t}\left( {\mathit{\boldsymbol{y}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega } \right)} } \right]} \right\} \end{array} $ | (11) |
可以看出, Hessian矩阵的元素Ha(x, y)对应两组成像点, 分别为x和y。Hessian矩阵的线性项表达成了格林函数的函数。而线性Hessian矩阵的每一个元素对应地下的两个成像点, 即线性Hessian矩阵的元素个数为成像点个数的平方, 这个数量再加上矩阵求逆运算, 计算量巨大。Hessian核函数的敏感性能够更加体现在对地下成像空间每个点的照明。抽取线性Hessian矩阵的一行, 即点扩散函数:
| $ \begin{array}{l} {\mathit{\boldsymbol{H}}_a}\left( \mathit{\boldsymbol{y}} \right)\left| {_x} \right. = {\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_\omega {{\omega ^4}\sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{s}}}} {\left[ {\left| {{f_{\rm{s}}}{{\left( \omega \right)}^2}} \right|\mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}},\mathit{\boldsymbol{x}},\omega } \right) \cdot } \right.} } } \right.\\ \left. {\left. {{\mathit{\boldsymbol{G}}^t}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}},\mathit{\boldsymbol{y}},\omega } \right)\sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{r}}}} {\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega } \right){\mathit{\boldsymbol{G}}^t}\left( {\mathit{\boldsymbol{y}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega } \right)} } \right]} \right\} \end{array} $ | (12) |
(12) 式描述了对应于一个成像点x处的点扩散函数, 可以看到单点的PSF弥散到整个成像空间的所有点y, 反映了观测系统对该点的照明能力。正向传播的两个格林函数G(xs, x, ω)和G(x, xr, ω)描述了地震波场从震源传播到点x处经由散射传播到接收点的过程; 而反向传播(共轭即是反向传播)的两个格林函数Gt(xs, y, ω)和Gt(y, xr, ω)描述了地震波场从接收点反传到y处经由散射反传到震源点的过程。而整个正传、反传的过程恰好反映了地震波在背景介质中传播对于散射点的聚焦程度。
针对单个散射体来说, 其点扩散函数响应即为其偏移成像结果。GUITTON[23]提出了一种局部去模糊滤波器构建方法, 直接在空间域执行去模糊偏移成像。给定参考模型m0, 观测数据uobs, 可得到常规偏移成像结果m1:
| $ {\mathit{\boldsymbol{m}}_1} = {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{m}}_0} = {\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{u}}_{{\rm{obs}}}} $ | (13) |
对该结果进行反偏移, 得到新数据:
| $ {\mathit{\boldsymbol{u}}_1} = \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{m}}_1} $ | (14) |
对新数据u1再次进行成像, 获得新的偏移结果m2:
| $ {\mathit{\boldsymbol{m}}_2} = {\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{u}}_1} $ | (15) |
其中, 两次成像结果之间的关系为:
| $ {\mathit{\boldsymbol{m}}_2} = {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{m}}_1} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{m}}_1} $ | (16) |
也就是说, m2是m1经过Hessian算子模糊作用后的成像结果。
假设采用一组非平稳滤波器来解决以下优化问题:
| $ \arg {\min _B}{\left\| {{\mathit{\boldsymbol{m}}_1} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{m}}_2}} \right\|^2} $ | (17) |
则B就是(LTL)-1的一个最优化估计。将估计得到的B作用到成像结果m1上, 得到去模糊化的成像结果。
1.2.2 解析表达的PSF声学格林函数可以表示为如下解析表达式:
| $ \mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = \frac{{\exp \left( {{\rm{i}}\omega \left| {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{x}}} \right|/{v_0}} \right)}}{{\left| {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{x}}} \right|}} $ | (18) |
如果为黏性介质, 则将完全弹性介质中的实速度v0替换成复速度v(ω):
| $ v\left( \omega \right) = {v_0}\left( {1 + \frac{1}{{{\rm{ \mathsf{ π} }}Q}}\ln \frac{\omega }{{{\omega _0}}}} \right)\left( {1 - \frac{{\rm{i}}}{{2Q}}} \right) $ | (19) |
从而得到黏声介质的格林函数:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = \frac{1}{{\left| {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{x}}} \right|}}\exp \left( {{\rm{i}}\omega \frac{{\left| {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{x}}} \right|}}{{{v_0}\xi }}} \right) \cdot }\\ {\exp \left( { - \frac{{\omega \left| {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{x}}} \right|}}{{2Q{v_0}\xi }}} \right)} \end{array} $ | (20) |
其中, ξ={1+(1/πQ)[ln(ω/ω0)]}[1+(1/4Q2)]。因此, 可据此给出声学和黏声情况下的PSF:
| $ \begin{array}{l} {\mathit{\boldsymbol{H}}_Q} = {\rm{Re}}\left\{ {\sum\limits_s {\sum\limits_r {\exp \left\{ {{\rm{i}}\frac{\omega }{{{v_0}\xi }}\left[ {\left( {\left| {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{x}}} \right| + \left| {{\mathit{\boldsymbol{x}}_{\rm{r}}} - \mathit{\boldsymbol{x}}} \right|} \right) - \left( {\left| {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{y}}} \right| + \left( {{\mathit{\boldsymbol{x}}_{\rm{r}}} - } \right.\left. \mathit{\boldsymbol{y}} \right|} \right)} \right]} \right\}} } } \right.\;\;\\ \;\;\;\;\;\;\;\;\;\;\exp \left\{ { - \frac{\omega }{{2Q{v_0}\xi }}\left[ ({\left| {{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right. - \left. \mathit{\boldsymbol{x}} \right) + } \right.} \right.\;\;\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {\left. {\left. {\left| {{\mathit{\boldsymbol{x}}_{\rm{r}}} - \mathit{\boldsymbol{x}}} \right|} \right) + \left( {\left| {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{y}}} \right| + \left| {{\mathit{\boldsymbol{x}}_{\rm{r}}} - \mathit{\boldsymbol{y}}} \right|} \right)} \right]} \right\}/\left| {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{x}}} \right| \cdot \left| {{\mathit{\boldsymbol{x}}_{\rm{r}}} - \mathit{\boldsymbol{x}}} \right| \cdot \left| {{\mathit{\boldsymbol{x}}_{\rm{s}}} - \mathit{\boldsymbol{y}}} \right| \cdot \left| {{\mathit{\boldsymbol{x}}_{\rm{r}}} - \mathit{\boldsymbol{y}}} \right|} \right\} \end{array} $ | (21) |
利用与声介质情况相同的去模糊滤波器来求取黏声介质点扩散函数的逆, 然后作用于常规偏移成像结果上就能达到去模糊化的效果。
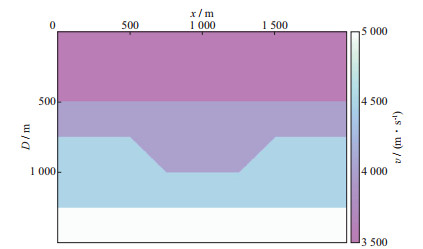
2 模型参数实验 2.1 黏声介质复杂模型逆时偏移成像测试针对简单模型的逆时偏移我们设计了一个凹陷速度模型, 如图 1所示, 模型大小为1 500 m×2 000 m, 水平、垂直网格间距都是5 m。速度范围为3 500~5 000 m/s。
|
图 1 凹陷速度模型 |
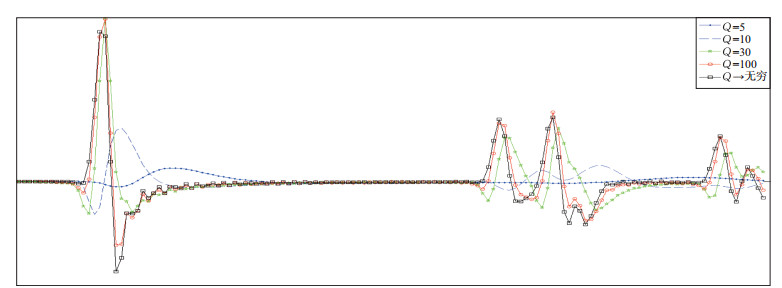
首先, 我们设Q值为常数, 分别对该模型整体设置Q=5, 10, 30, 100和无穷大, 图 2为不同Q值对应的地震记录。由图 2可以看出, Q值的变化会造成不同程度的振幅衰减, 且Q值越小衰减越严重。从图 2还可以看出, 由于Q值的影响, 地震记录有向下的时移, 这表明Q值对地震波传播具有相位畸变效应。图 3给出了不同Q值下的同一单道地震记录。从图 3可以看出, Q值除了引起振幅的衰减, 还使得相位发生了变化:Q越小相位越滞后。

|
图 2 不同Q值对应的地震记录 |
|
图 3 不同Q值的同一单道地震记录 |
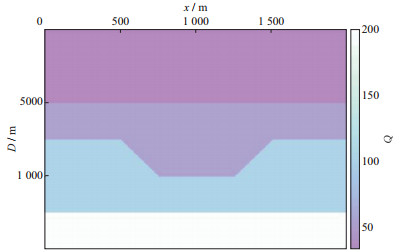
考虑地质构造特征, 我们重新设置Q值, 使得Q值结构与速度模型结构相对应, 模型的Q值设置如图 4所示。模拟100炮地震数据, 炮点位置从450 m开始, 炮间距为15 m。地表位置布满接收点, 总道数为400道, 道间距5 m, 记录长度0.88 s, 时间采样率1 ms。
|
图 4 凹陷Q模型 |
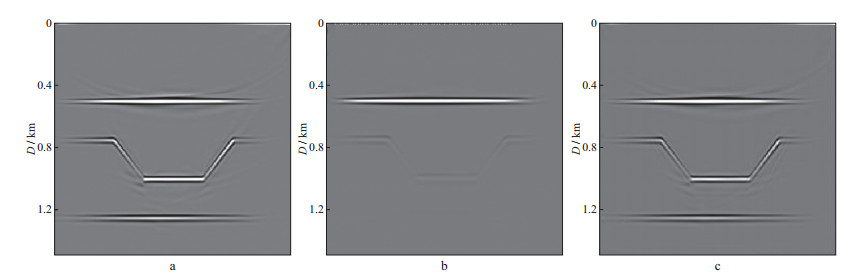
图 5给出了采用不同数据和成像方法得到的成像结果。图 5a为声介质成像结果; 图 5b为正演的衰减数据不加以补偿的逆时成像结果; 图 5c为正演的衰减数据给予补偿的逆时成像结果。由图 5可以看出, 与声介质成像结果相比, 偏移时如果不对衰减数据进行Q补偿, 地震波能量明显减弱, 图像分辨率变低, 衰减层越到下方成像效果越差, 图像层位也不准确, 层位略向上移动。当采用本文衰减与补偿统一表达的黏声介质传播方程对带吸收衰减数据进行补偿成像后, 成像结果的振幅得到补偿, 下方层位被有效地恢复出来, 图像层位也准确。该实验结果证明了吸收与衰减统一表达的黏声介质波动方程能够有效地计算黏声介质地震波场的格林函数。
|
图 5 不同数据和成像方法得到的成像结果 a 声介质成像结果; b 正演的衰减数据不加以补偿的逆时成像结果; c 正演的衰减数据给予补偿的逆时成像结果 |
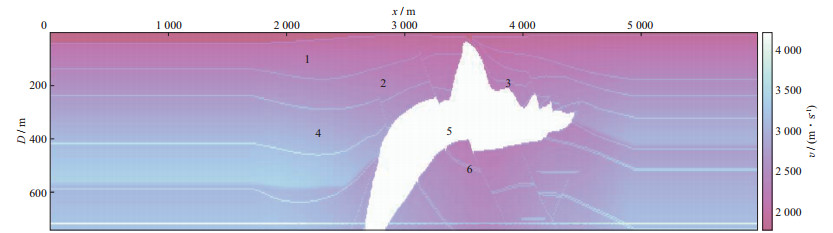
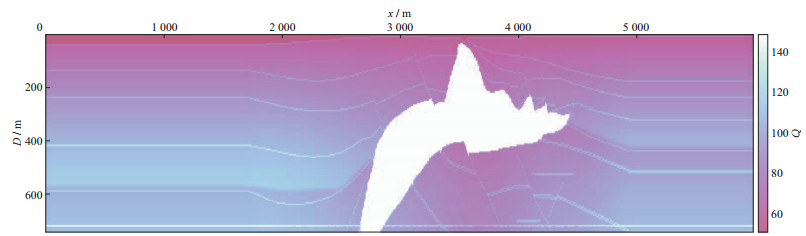
图 6为盐丘速度模型, 模型大小为6 000 m×750 m, 水平、垂直网格间距都是5 m。考虑常规地质构造中, Q值结构与速度模型结构相对应, 我们设置模型中的Q值分布如图 7所示。模拟325炮数据, 炮间距15 m。中间放炮, 两边接收, 每一炮覆盖总道数为200道, 道间距5 m, 记录长度2.5 s, 时间采样率0.3 ms。用数值实验来观测线性Hessian矩阵的单点响应。
|
图 6 SEG/EAGE盐丘模型 |
|
图 7 盐丘Q模型 |
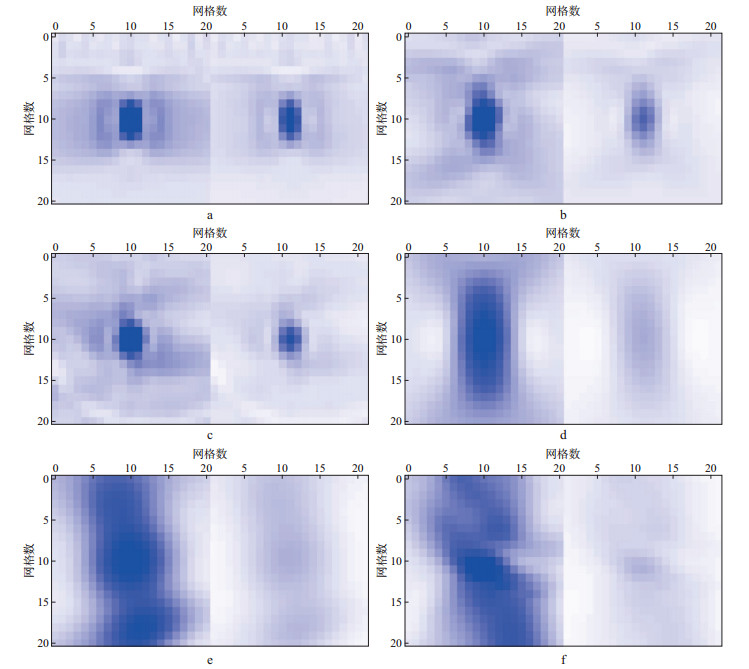
按照模型数据的观测系统和频带分布, 我们根据公式(21)计算其点扩散函数。将模型划分为231个网格大小为21×21的区域, 目标点位于网格区域中心。图 8给出了图 6中6个参考点的点扩散函数图(1~6号参考点的中心坐标分别为:[436, 10], [562, 31], [751, 31], [457, 73], [667, 73], [688, 94])。从图 8中可以看出, 点扩散函数集中在中心点周围区域。在这一区域之外, 单点响应相对区域内为极小值。另外, 由于浅层速度结构简单, 同时照明也较为均匀, 它们的PSF也是简单的椭圆形。而在速度变化剧烈的区域, PSF却是畸变的, 而且具有一定的方向特性。对比图 8中声介质单点PSF与黏声介质PSF可以发现:吸收衰减效应显著降低了照明振幅强度, 带吸收衰减的PSF明显比声介质PSF能量低, 在深层这种能量损耗更为强烈; 吸收衰减效应改变了观测系统对地下的照明图样, 即各点在两种情况下的分辨率相差较大。
|
图 8 图 6中6个参考点的PSF分布(左边为声介质的PSF分布, 右边为黏声介质的PSF分布) a 参考点1; b 参考点2; c 参考点3; d 参考点4; e 参考点5; f 参考点6 |
在中心点位置将PSF图样按照空间位置进行排列, 将全观测系统的PSF图样显示在图 9(声介质)和图 10(黏声介质)中。从图 9和图 10可以看出, 吸收衰减效应的影响体现在全空间中, 其显著降低了盐丘下方照明振幅。也可以看到, 线性Hessian矩阵在不同区域展示的单点响应不同。浅层速度结构简单, 同时照明也较为均匀, 它们的PSF是简单的椭圆形; 而在速度变化剧烈的区域PSF发生了畸变, 且有一定的方向特性, 图样更为分散; 在盐丘周围, 吸收衰减效应显著降低了成像分辨能力。

|
图 9 全观测系统点扩散函数分布(声介质) |

|
图 10 全观测系统点扩散函数分布(黏声介质) |
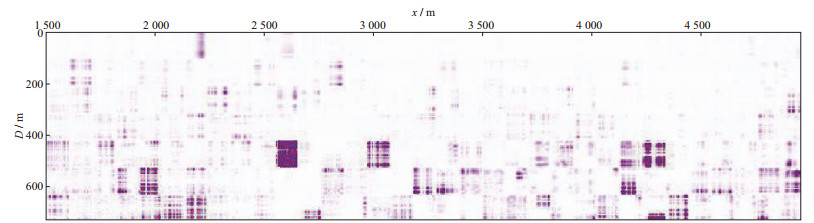
图 11和图 12分别给出了声介质和黏声介质的逆PSF成像结果。图 13给出了常规声介质偏移成像结果。虽然没有Q的影响, 但在高速体下方, 常规偏移成像并不能得到显著的层位信息。图 14给出了逆PSF作用在常规声介质偏移成像结果后的成像结果。可以看出, 逆PSF作用在常规声介质偏移成像结果上, 能够达到去模糊的作用, 特别是在盐丘下方, 能够有效恢复层位信息。图 15给出了采用黏声数据并加以补偿的常规偏移成像结果。由图 15可以看出, 衰减层及其下部反射体的成像振幅逐渐减弱, 成像分辨率逐渐降低。图 16给出了逆PSF作用在图 15成像结果后的成像结果。对比图 15和图 16可以看出, 逆PSF显著增强了深层成像的能量, 成像剖面振幅更加均衡, 吸收衰减效应能够通过逆PSF进行有效补偿。

|
图 11 声介质逆PSF成像结果 |
|
图 12 黏声介质逆PSF成像结果 |

|
图 13 直接偏移成像结果(声波数据+声波成像) |

|
图 14 逆点扩散函数作用后的成像结果(声波数据+声波成像+声波PSF) |

|
图 15 直接偏移成像结果(黏声数据+黏声成像) |

|
图 16 逆点扩散函数作用后成像结果(黏声数据+黏声成像+黏声PSF) |
本文从衰减与补偿统一表达的黏声介质传播方程出发, 利用交错网格有限差分方法和最佳匹配层吸收边界条件进行求解, 实现了黏声介质衰减与补偿的格林函数计算。基于地震反演成像理论和数值实验结果, 对点扩散函数的敏感性以及Q因子对点扩散函数数学、物理特征的影响进行了分析。结果表明, PSF反映了吸收衰减效应对波场穿透能力和角度照明能力的影响。利用去模糊滤波器对PSF进行求逆, 并将逆点扩散函数直接作用在成像结果上, 从而对原始成像结果有效地去模糊化, 并提高成像振幅的分辨率和均衡性。模型数据实验结果证明了该方法的有效性, 在黏声介质中的逆时偏移成像可以达到与声介质成像相当的精度。基于这一系列研究成果, 可以进一步开展迭代的最小二乘偏移成像和全波形反演方法研究。
致谢: 感谢同济大学海洋与地球科学学院波现象与反演成像研究组(WPI)对本研究工作的帮助。| [1] |
KJARTANSSON E. Constant Q wave propagation and attenuation[J]. Journal Geophysical Research, 1979, 84(4): 4737-4748. |
| [2] |
DAI N, WEST G F. Inverse Q migration[J]. Expanded Abstracts of 64th Annual Internat SEG Mtg, 1994, 1418-1421. |
| [3] |
MITTET R, SOLLIE R, HOKSTAD K. Prestack depth migration with compensation for absorption and dispersion[J]. Geophysics, 1995, 60(5): 1485-1494. DOI:10.1190/1.1443882 |
| [4] |
YU Y, LU R S, DEAL M D. Compensation for the effects of shallow gas attenuation with viscoacoustic wave-equation migration[J]. Expanded Abstracts of 72nd Annual Internat SEG Mtg, 2002, 2062-2065. |
| [5] |
ZHANG J, WAPENAAR K. Wavefield extrapolation and prestack depth migration in anelastic inhomogeneous media[J]. Geophysical Prospecting, 2002, 50(6): 629-643. DOI:10.1046/j.1365-2478.2002.00342.x |
| [6] |
MITTET R. A simple design procedure for depth extrapolation operators that compensate for absorption and dispersion[J]. Geophysics, 2007, 72(2): S105-S112. |
| [7] |
ZHANG J, WU J, LI X. Compensation for absorption and dispersion in prestack migration:an effective Q approach[J]. Geophysics, 2013, 78(1): S1-S14. |
| [8] |
ZHU T, CARCIONE J M. Theory and modeling of constant-QP-and S-waves using fractional spatial derivatives[J]. Geophysical Journal International, 2014, 196(3): 1787-1795. DOI:10.1093/gji/ggt483 |
| [9] |
ZHU T, HARRIS J M. Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional Laplacians[J]. Geophysics, 2014, 79(3): T105-T116. |
| [10] |
ZHU T, HARRIS J M, BIONDI B. Q-compensated reverse-time migration[J]. Geophysics, 2014, 79(3): S77-S87. DOI:10.1190/geo2013-0344.1 |
| [11] |
ZHU T, SUN J. Viscoelastic reverse time migration with attenuation compensation[J]. Geophysics, 2017, 82(2): S61-S73. DOI:10.1190/geo2016-0239.1 |
| [12] |
ZHU T. Numerical simulation of seismic wave propagation in viscoelastic-anisotropic media using frequency-independent Q wave equation[J]. Geophysics, 2017, 82(4): WA1-WA10. |
| [13] |
任浩然, 黄光辉, 王华忠, 等. 地震反演成像中的Hessian算子研究[J]. 地球物理学报, 2013, 56(7): 2429-2436. REN H R, HUANG G H, WANG H Z, et al. A research on the hessian operator in seismic inversion imaging[J]. Chinese Journal of Geophysics, 2013, 56(7): 2429-2436. |
| [14] |
SCHUSTER G T, HU J. Green's function for migration:continuous recording geometry[J]. Geophysics, 2000, 65(1): 167-175. |
| [15] |
BOSCHI L. Measures of resolution in global body wave tomography[J]. Geophysical Research Letters, 2003, 30(19): 379-394. |
| [16] |
FICHTNER A, TRAMPERT J. Hessian kernels of seismic data functionals based upon adjoint techniques[J]. Geophysical Journal International, 2011, 185(2): 775-798. DOI:10.1111/gji.2011.185.issue-2 |
| [17] |
XIE X B, JIN S, WU R S. Wave-equation based seismic illumination analysis[J]. Geophysics, 2006, 71(5): S169-S177. DOI:10.1190/1.2227619 |
| [18] |
YU J, HU J, SCHUSTER G T, et al. Prestack migration deconvolution[J]. Geophysics, 2006, 71(2): S53-S62. |
| [19] |
WANG Y, YANG C. Accelerating migration deconvolution using a nonmonotone gradient method[J]. Geophysics, 2010, 75(4): S131-S137. DOI:10.1190/1.3457923 |
| [20] |
REN H, WANG H, WU R S. Frequency domain wave equation based angular Hessian for amplitude correction[J]. Expanded Abstracts of 80th Annual Internat SEG Mtg, 2010, 3145-3148. |
| [21] |
CHEN Y, DUTTA G, DAI W, et al. Q-least squares reverse time migration with viscoacoustic deblurring filters[J]. Geophysics, 2017, 82(6): S425-S438. DOI:10.1190/geo2016-0585.1 |
| [22] |
罗文山, 陈汉明, 王成祥, 等. 时间域黏滞波动方程及其数值模拟新方法[J]. 石油地球物理勘探, 2016, 54(4): 707-713. LUO W S, CHEN H M, WANG C X, et al. A novel time-domain viscoacoustic wave equation and its numerical simulation[J]. Oil Geophysical Prospecting, 2016, 54(4): 707-713. |
| [23] |
GUITTON A. Fast 3D Least-Squares RTM by preconditioning with Non-Stationary matching filters[J]. Expanded Abstracts of 87th Annual Internat SEG Mtg, 2017, 4395-4399. |




