2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
2. National Laboratory for Marine Science and Technology, Qingdao 266071, China
微地震信号作为一种复杂的非线性、非平稳信号, 其噪声能量通常比有效信号能量高。微地震噪声通常包括随机噪声和相干噪声:随机噪声由多种方式产生, 混杂在一起, 没有规律; 相干噪声包括常见的多次波和面波, 在时空域和频率域具有一定规律。相较于常规地震资料, 微地震资料普遍存在压裂干扰。传统的滤波方法包括低通、高通和带通滤波方法, 不能很好地去除压裂干扰。COMON[1]首次引入独立分量分析(independent component analysis)的概念, 并提出最小化互信息的代价函数, 通过对概率密度函数的高阶近似实现了线性混合信号中独立分量的提取; HYVARINEN[2]提出固定点fast ICA算法, 该算法以批处理的方式快速迭代寻优, 其目的是寻找混合信号所组成矩阵的非高斯性最大值; 孙成禹等[3]将改进后的ICA算法应用于地震数据去噪, 去噪结果表明该方法能够很好地去除地震资料的随机噪声; 曹小玲等[4]提出了一种改进的M-fast ICA算法, 该算法能够很好地实现大地电磁数据的信噪分离; 邱玥等[5]以负熵为目标函数, 利用初值降敏感性和高阶收敛速度改进迭代公式, 对快速独立分量进行分析并优化算法, 从而实现盲源分离; 谭晓衡等[6]将高阶互累积量与小波变换相结合, 证明了在地震资料信噪比低的情况下, 该方法仍然能够有效地进行信噪分离。
由于微地震信号中有效信号与噪声之间存在时间差, 所以fast ICA算法分离信号和噪声时会受到干扰, 影响分离效果。本文采用四阶互累积量算法对微地震信号进行时差估计, 并根据计算结果将有效信号偏移到同一相位点, 最后利用fast ICA算法分离信号和噪声。微地震仿真实验和实际微地震资料处理结果证明了本文方法的正确性和有效性。
1 方法原理 1.1 互累积量算法设随机变量x的概率密度函数为p(x), 则其k阶原点矩mk定义为[7-8]:
| $ m_{k}=\mathrm{E}\left[x^{k}\right]=\int_{-\infty}^{+\infty} x^{k} p(x) \mathrm{d} x $ | (1) |
式中:k=1, 2, …, n, 表示原点矩的阶数; xk代表随机变量x的k阶原点矩; E代表数学期望。
随机变量x的特征函数φ(v)定义为:
| $ \varphi(v)=\mathrm{E}\left[\mathrm{e}^{\mathrm{j} v x}\right]=\int_{-\infty}^{+\infty} p(x) \mathrm{e}^{\mathrm{j} v x} \mathrm{d} x $ | (2) |
式中:v为实系数;
因为p(x)≥0, 所以φ(v)在原点有最大值, 即:
| $ |\varphi(v)| \leqslant \varphi(0)=\int_{-\infty}^{+\infty} p(x) \mathrm{d} x=1 $ | (3) |
对φ(v)求k阶导数, 得:
| $ \frac{\mathrm{d}^{k} \varphi(v)}{\mathrm{d} v^{k}}=\mathrm{j}^{k} m_{k} $ | (4) |
式中:mk=(-j)kdkφ(v)/dvk。
令ψ(v)=lnφ(v), 对ψ(v)进行泰勒级数展开, 求k阶导数, 得到x的k阶累积量Ck为:
| $ C_{k}=\left.(-\mathrm{j})^{k} \frac{\mathrm{d}^{k} \psi(v)}{\mathrm{d} v^{k}}\right|_{v=0} $ | (5) |
当随机变量序列{x1, x2, …, xn}的均值为0时, 它的原点矩和互累积量之间有如下关系[10]:
| $ \begin{array}{l} C\left[ {{x_1}, {x_2}, \cdots , {x_n}} \right] = \sum {{{( - 1)}^{p - 1}}} (p - 1)!\;\; \cdot \\ {\rm{E}}\left\{ {\prod_{i \in {s_1}} {x_i^k} } \right\}{\rm{E}}\left\{ {\prod_{i \in {s_2}} {x_i^k} } \right\} \cdots {\rm{E}}\left\{ {\prod_{i \in {s_p}} {x_i^k} } \right\} \end{array} $ | (6) |
式中:xik表示随机变量xi的k阶累积量; C[·]表示随机变量序列的互累积量; Si(i=1, 2, …, p)为整数集(1, 2, …, n)的子集; p为子集的个数。
在信号均值为0的情况下, 为兼顾计算精度和效率, 采用四阶互累积量, 其计算公式为:
| $ \begin{array}{*{20}{l}} {C\left[ {{x_1}, {x_2}, {x_3}, {x_4}} \right] = {\rm{E}}\left\{ {{x_1}{x_2}{x_3}{x_4}} \right\} - {\rm{E}}\left\{ {{x_1}{x_2}} \right\} \cdot }\\ {{\rm{E}}\left\{ {{x_3}{x_4}} \right\} - {\rm{E}}\left\{ {{x_1}{x_3}} \right\}{\rm{E}}\left\{ {{x_2}{x_4}} \right\} - {\rm{E}}\left\{ {{x_1}{x_4}} \right\}{\rm{E}}\left\{ {{x_2}{x_3}} \right\}} \end{array} $ | (7) |
根据各道四阶互累积量是否都具有相似的最大值可以判断各道是否存在与微地震子波类似的微地震信号, 通过提取四阶互累积量的时间点还可以检测初至时间[9-12]。检测出有效信号后, 计算各道有效信号极大值点, 可以得到各道有效信号的时间点; 计算得到各道的时间点后, 可以得到相对时差[13]。相对于初至时间点的计算, 有效信号的极大值点计算简便且误差小, 因此我们将有效信号极大值点作为时间点, 以第1道为参考点, 将其余各道按照相对时差进行偏移, 以消除相对时差, 从而得到相位一致的数据。
1.2 基于负熵的固定点fast ICA算法由于传统ICA算法无法确定所提取信号对应原始信号源中的哪个分量, 也无法将提取出的信号恢复到信号源的真实幅度[14-17], 所以我们选择基于负熵极大的fast ICA算法, 以改善传统ICA算法内在的不确定性, 具体如下。
首先定义负熵J(x′)为[16]:
| $ \boldsymbol{J}\left(\boldsymbol{x}^{\prime}\right)=\boldsymbol{H}\left(\boldsymbol{x}_{\mathrm{g}}\right)-\boldsymbol{H}\left(\boldsymbol{x}_{{\rm o}}\right) $ | (8) |
式中:H表示随机向量的微分熵; x′为随机向量; xg和xo均为具有同一个协方差矩阵的高斯随机向量。鉴于直接计算负熵比较困难, 本文采用改进的负熵估计算法, 这种算法计算过程相对简单[18-20], 其表达式为:
| $ \boldsymbol{J}\left(\boldsymbol{x}^{\prime}\right) \approx\left[\mathrm{E}\left\{G\left(\boldsymbol{x}_{\mathrm{g}}\right)\right\}-\mathrm{E}\{G(p)\}\right]^{2} $ | (9) |
式中:p符合正态分布且满足均值为0的要求; G为非二次函数, 不同类型的观测信号采用不同的G函数进行计算。将负熵估计的计算问题转化为求解使函数J(W)达到E{(WTX2)}最大的混矩阵W, 在约束条件E(XXT)=1的情况下, 牛顿迭代公式可以改写为:
| $ \begin{aligned} \boldsymbol{W}_{k+1}=& \boldsymbol{W}_{k}-\left[\mathrm{E}\left\{\boldsymbol{X}_{\boldsymbol{g}}\left(\boldsymbol{W}_{k}^{\mathrm{T}} \boldsymbol{X}\right)\right\}-\beta \boldsymbol{W}_{k}\right] / \\ &\left[\mathrm{E}\left\{g^{\prime}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{X}\right)-\beta\right\}\right] \end{aligned} $ | (10) |
式中:中间变量β=E{WKTXg(WkTX)}; g′表示函数G的导数; Xg表示观测信号; X表示观测信号构成的矩阵。(10)式可改写为:
| $ \boldsymbol{W}_{k+1}=\mathrm{E}\left\{\boldsymbol{X}_{{\rm g}}\left(\boldsymbol{W}_{k}^{\mathrm{T}} \boldsymbol{X}\right)\right\}-\mathrm{E}\left\{g^{\prime}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{X}\right)\right\} \boldsymbol{W}_{k} $ | (11) |
1) 预处理, 包括去均值、主成分分析和数据的白化处理, 目的是消除数据的相关性;
2) 以负熵为准则寻找到最大的非高斯性分离矩阵W, 得到信号的各个独立分量。
2 数据实验 2.1 四阶互累积量算法实验为验证四阶互累积量算法的准确性, 我们采用微地震子波和高斯噪声合成微地震信号, 如图 1a所示, 其背景噪声较强, 但是有效信号仍然依稀可见, 图 1b为微地震子波(假设检波点均匀分布)。图 2是经四阶互累积量算法计算后检测到的有效信号, 从图中可以看出仅微地震信号处有突变, 背景噪声处几乎没有任何“毛刺”信号, 图 1a中出现的高斯噪声干扰对检测结果几乎没有影响。

|
图 1 含有高斯噪声的合成微地震信号(a)和微地震子波(b) |

|
图 2 经四阶互累积量算法计算后检测到的有效信号 |
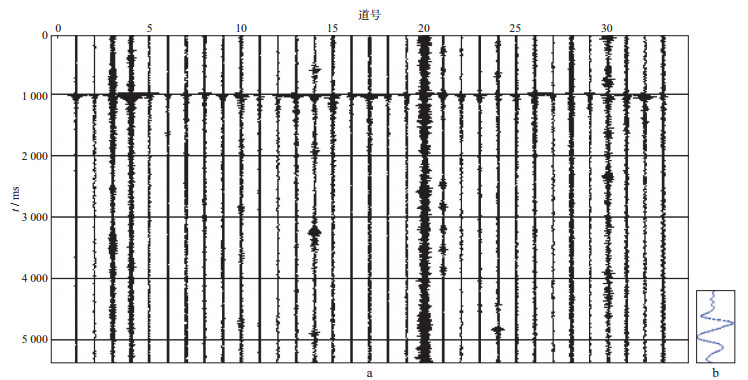
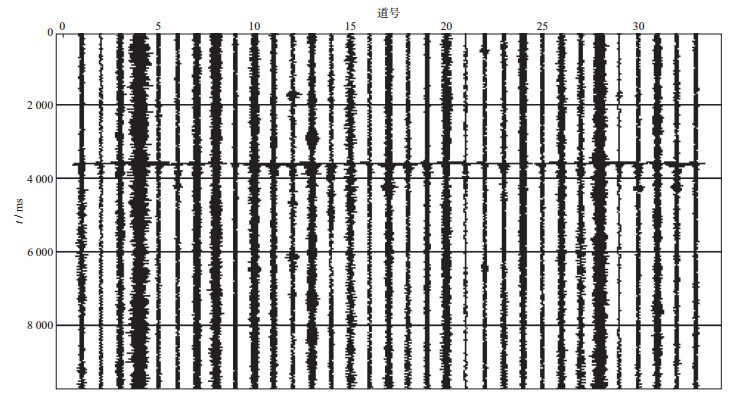
将四阶互累积量算法应用于实际微地震资料的信号检测时, 需要先从一段信噪比高的信号中提取微地震信号子波, 然后用该子波去检测相似信号。我们利用实际资料做进一步的验证。图 3为某段实际信号和从其中某一高信噪比道中提取的微地震子波。将提取的子波应用于检测图 4中的一段有效信号, 并计算四阶互累积量, 结果如图 5所示, 可以看出, 微地震信号的各道出现峰值信号, 背景噪声被压制。将计算得到的四阶互累积量用于检测有效信号的初至时间, 可为下一步计算不同道间有效信号的时差和信号校正奠定基础。
|
图 3 某段实际微地震信号(a)和提取的微地震信号子波(b) |
|
图 4 待检测的某段有效信号 |

|
图 5 对图 4中的信号应用四阶互累积量算法后检测出的有效信号 |
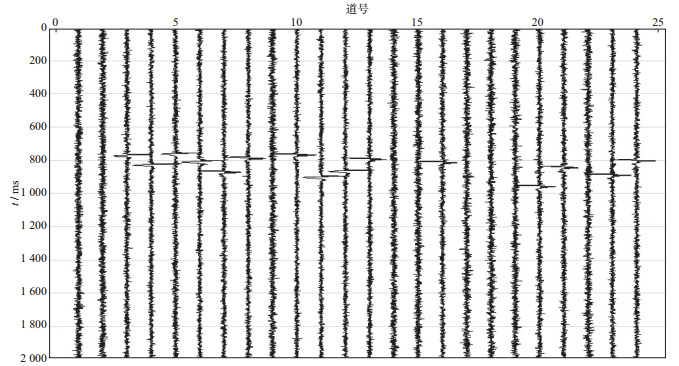
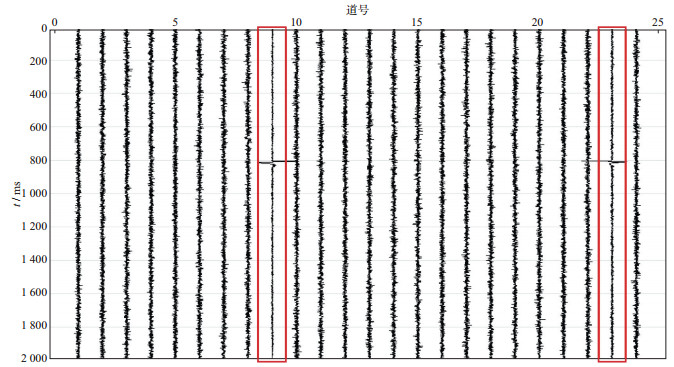
对图 1中的合成信号, 分别应用fast ICA算法以及基于四阶互累积量的fast ICA微地震数据噪声压制方法进行信噪分离。图 6为应用fast ICA算法进行信噪分离的结果, 可以看出多个道都含有有效信号, 但含有效信号的道中还含有高斯噪声, 这说明fast ICA算法并未完全实现噪声和信号的有效分离, 分离效果不理想, 无法分辨信号源和噪声源。图 7为应用基于四阶互累积量的fast ICA微地震数据噪声压制方法(经四阶互累积量计算时差偏移后的fast ICA算法)进行信噪分离的结果, 可以看出信号与噪声已明显分离, 第9道和第23道中是分离出的有效信号, 其余则为噪声, 分离出的信号中几乎不含有噪声, 分离效果较为理想。相对于仅应用fast ICA算法(未经四阶互累积量计算时差偏移的fast ICA算法)得到的结果中信号与噪声未分离的情况而言, 应用本文方法能够分离出两个有效信号, 说明本文方法能够更好地分离微地震混合信号, 并增强微地震混合信号的分离效果。
|
图 6 应用fast ICA算法进行信噪分离的结果 |
|
图 7 应用四阶互累积量的fast ICA算法进行信噪分离的结果(红色方框里为分离出的信号源) |
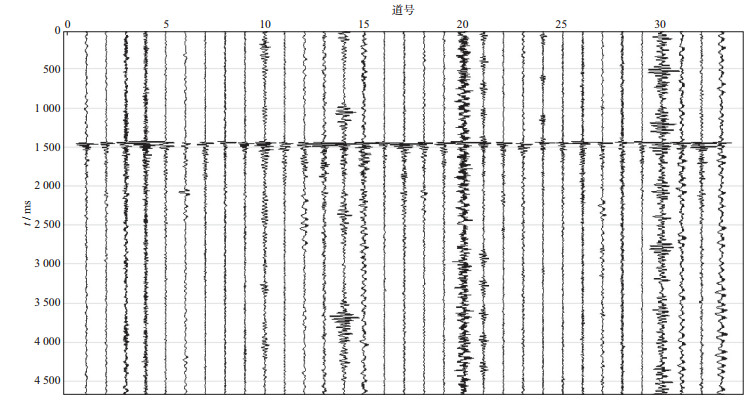
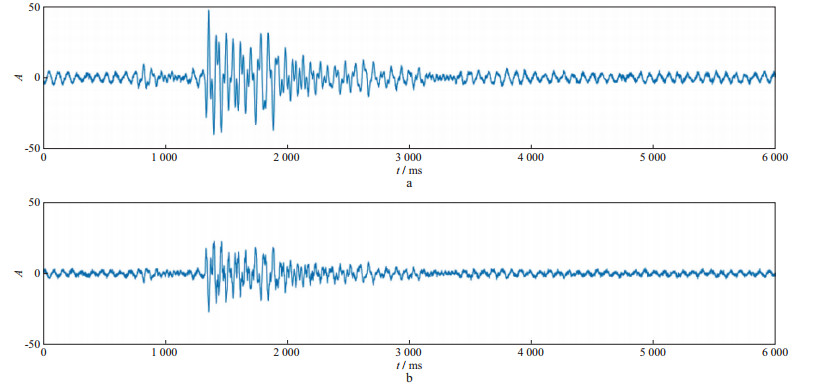
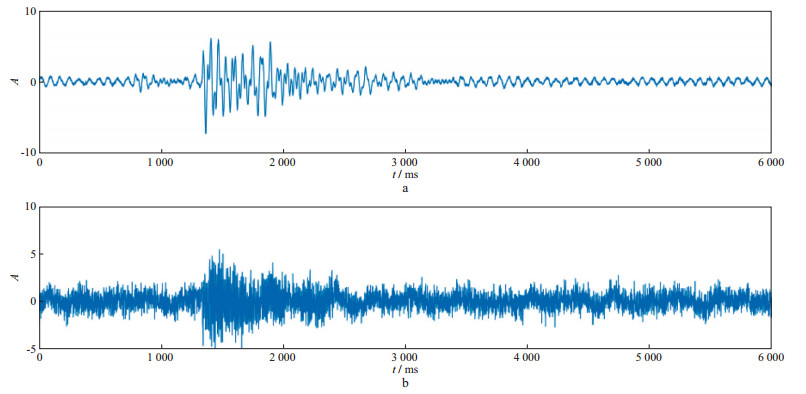
图 8所示为微地震监测得到的含有效信号的地面微地震资料。因为每道信号的噪声不同, 所以实际资料中不同道的微地震信号理论上是不相关的, 即信号是独立的, 这时可应用fast ICA算法分离信号。取两道相邻的微地震信号(图 9), 应用基于四阶互累积量的fast ICA微地震数据噪声压制方法对实际信号2进行信噪分离, 结果如图 10所示。将分离出的信号与实际信号2对比, 可以看出大部分的噪声已被分离, 分离出的有效信号具有很高的保真度。这说明该方法能够有效地对微地震数据进行信噪分离, 以实现去噪的目的。
|
图 8 含有效信号的实际微地震资料 |
|
图 9 两道相邻的实际微地震信号 a用于计算四阶互累积量的实际信号1; b用于信噪分离的实际信号2 |
|
图 10 应用基于四阶互累积量的fast ICA微地震数据噪声压制方法得到的信噪分离结果 a分离出的实际信号2; b分离出的噪声 |
由于微地震信号是复杂的非线性、非平稳信号, 且噪声能量通常比有效信号能量高, 因而传统的去噪方法不能很好地去除微地震资料中的噪声, 本文将fast ICA算法应用于微地震资料去噪。由于微地震资料中不同道有效信号之间存在时间差, 因而fast ICA算法不能很好地适应微地震资料。我们首先利用四阶互累积量算法检测出微地震资料中的有效信号, 再根据有效信号极大值所处的位置进行时差估计, 然后利用估算的时差将微地震信号偏移到同一个时间点, 最后应用fast ICA算法进行盲源分离。微地震仿真实验的结果证明四阶互累积量算法能够很好地检测出有效信号, 提高时差计算精度, 并在满足精度要求的同时具有较高的计算效率; 实际微地震资料的处理结果证明本文方法能够有效分离微地震信号中的有效信号与噪声, 具有良好的去噪效果。但由于实际微地震资料复杂, 很多时候应用高阶互累积量算法得到的震源位置精度不高, 并且噪声源的个数也无法确定, 所以只能不断地进行高阶互累积量算法测试, 以提高震源位置精度并进一步确定噪声源的个数, 这也是下一步研究中需要解决的问题。
致谢: 感谢中国石油大学(华东)SWPI课题组成员对本研究的帮助与支持。| [1] |
COMON P. Independent component analysis, A new concept?[J]. IEEE Sensors Journal, 1994, 36(3): 287-314. |
| [2] |
HYVARINEN A.A family of fixed-point algorithms for independent component analysis[C]//Acoutics Speech and Signal Processing Washington: IEEE Computer Society, 1997: 3917-3920
|
| [3] |
孙成禹, 邵婕, 蓝阳, 等. 基于独立分量分析基的地震随机噪声压制[J]. 石油物探, 2016, 55(2): 196-204. SUN C Y, SHAO J, LAN Y, et al. Seismic random noise suppression based on independent component analysis basis[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 196-204. DOI:10.3969/j.issn.1000-1441.2016.02.005 |
| [4] |
曹小玲, 严良俊. 一种改进的独立分量分析算法在大地电磁去噪中的应用[J]. 石油物探, 2017, 56(6): 890-897. CAO X L, YAN L J. An improved independent component analysis algorithm for magnetotelluric denoising[J]. Geophysical Prospecting for Petroleum, 2017, 56(6): 890-897. DOI:10.3969/j.issn.1000-1441.2017.06.015 |
| [5] |
邱玥, 孙成禹, 唐杰. 基于优化fast ICA盲源分离算法的地震属性融合方法研究[J]. 石油物探, 2018, 57(5): 101-111. QIU Y, SUN C Y, TANG J. Seismic attribute fusion method based on optimized fast ICA blind source separation algorithm[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 101-111. |
| [6] |
谭晓衡, 褚国星, 张雪静, 等. 基于高阶累积量和小波变换的调制识别算法[J]. 系统工程与电子技术, 2018, 23(3): 244-251. TAN X H, CHU G X, Zhang X J, et al. Modulation recognition algorithm based on higher order cumulant and wavelet transform[J]. Systems Engineering and Electronics, 2018, 23(3): 244-251. |
| [7] |
吴波, 潘树林, 陈辉. 用四阶累积量子函数改进剩余静校正量的计算[J]. 石油物探, 2010, 49(3): 227-239. WU B, PAN S L, CHEN H. Improving the calculation of residual static correction by using fourth-order cumulative quantum function[J]. Geophysical Prospecting for Petroleum, 2010, 49(3): 227-239. DOI:10.3969/j.issn.1000-1441.2010.03.003 |
| [8] |
王维强.独立分量分析在地震勘探中的应用研究[D].青岛: 中国石油大学(华东), 2012 WANG W Q.Application of independent component analysis in seismic exploration[D].Qingdao: China University of Petroleum (East China), 2012 http://cdmd.cnki.com.cn/Article/CDMD-10425-1014017539.htm |
| [9] |
吕文彪, 曹中林, 张华. 一种叠前地震资料单频噪声压制新方法[J]. 石油天然气学报, 2014, 36(3): 675-678. LV W B, CAO Z L, ZHANG H. A new method for single-frequency noise suppression of prestack seismic data[J]. Journal of Oil and Gas Technology, 2014, 36(3): 675-678. |
| [10] |
刘诚.基于独立分量分析的地震信号多次波盲分离方法研究[D].成都: 成都理工大学, 2008 LIU C.Seismic signal multiple-wave blind separation method based on independent component analysis[D].Chengdu: Chengdu University of Technology, 2008 http://cdmd.cnki.com.cn/Article/CDMD-10616-2008086377.htm |
| [11] |
蹇柯, 崔志涛. 一种基于四阶累积量的改进快速ICA算法[J]. 广东工业大学学报, 2008, 10(5): 112-118. JIAN K, CUI Z T. An improved fast ICA algorithm based on fourth-order cumulant[J]. Journal of Guangdong University of Technology, 2008, 10(5): 112-118. |
| [12] |
蔡连芳, 田学民. 基于互累积量的有噪独立分量分析方法[J]. 计算机工程, 2012, 16(6): 69-77. CAI L F, TIAN X M. A noisy independent component analysis method based on mutual cumulant[J]. Computer Engineering, 2012, 16(6): 69-77. |
| [13] |
刘洪林, 李海山. ICA及其在气液两相流辨识中的应用[J]. 吉林大学学报(地球科学版), 2009, 39(1): 33-38. LIU H L, LI H S. ICA and its application in gas-liquid two-phase flow identification[J]. Journal of Jilin University(Earth Science Edition), 2009, 39(1): 33-38. |
| [14] |
冯智慧, 刘财, 冯晅, 等. 基于高阶累积量一维切片的地震信号初至自动拾取方法[J]. 吉林大学学报(地球科学版), 2011, 41(2): 559-564. FENG Z H, LIU C, FENG H, et al. First-time automatic picking method for seismic signals based on high-order cumulant one-dimensional slicing[J]. Journal of Jilin University(Earth Science Edition), 2011, 41(2): 559-564. |
| [15] |
王维波, 周瑶琪, 春兰. 地面微地震监测SET震源定位特性研究[J]. 中国石油大学学报:自然科学版, 2012, 36(5): 45-50. WANG W B, ZHOU Y Q, CHUN L. Study on the location characteristics of ground micro-seismic monitoring SET[J]. Journal of China University of Petroleum:Natural Science Edition, 2012, 36(5): 45-50. |
| [16] |
魏巍.盲信号处理技术在地震数据处理中的应用研究[D].北京: 中国地质大学(北京), 2009 WEI W.Application of blind signal processing technology in seismic data processing[D].Beijing: China University of Geosciences (Beijing), 2009 http://cdmd.cnki.com.cn/Article/CDMD-11415-2009075390.htm |
| [17] |
王永涓.基于改进Fast ICA算法的地震信号去噪研究[D].成都: 成都理工大学, 2012 WANG Y J.Seismic signal denoising based on improved Fast ICA algorithm[D].Chengdu: Chengdu University of Technology, 2012 |
| [18] |
刘太伟.地面微地震资料去噪方法研究[D].青岛: 中国石油大学(华东), 2013 LIU T W.Research on denoising method of ground microseismic data[D].Qingdao: China University of Petroleum (East China), 2013 http://cdmd.cnki.com.cn/Article/CDMD-10425-1015024732.htm |
| [19] |
周德山, 韩文功, 李振春, 等. 基于相对走时计算的地面微地震监测SET定位算法[J]. 地球物理学进展, 2016, 31(6): 2495-2500. ZHOU D S, HAN W G, LI Z C, et al. SET localization algorithm for ground microseismic monitoring based on relative travel time calculation[J]. Progress in Geophysics, 2016, 31(6): 2495-2500. |
| [20] |
张山, 刘清林, 赵群, 等. 微地震监测技术在油田开发中的应用[J]. 石油物探, 2002, 41(2): 226-231. ZHAN S, LIU Q L, ZHAO Q, et al. Application of microseismic monitoring technology in oilfield development[J]. Geophysical Prospecting for Petroleum, 2002, 41(2): 226-231. DOI:10.3969/j.issn.1000-1441.2002.02.021 |
| [21] |
夏森, 王维波, 李树荣, 等. 微地震信号的参数辨识建模及其Kalman滤波[J]. 地球物理学进展, 2016, 31(5): 2005-2010. XIA S, WANG W B, LI S R, et al. Parametric identification modeling of microseismic signals and kalman filtering[J]. Progress in Geophysics, 2016, 31(5): 2005-2010. |
| [22] |
刘百红, 秦绪英, 郑四连, 等. 微地震监测技术及其在油田中的应用现状[J]. 油气藏评价与开发, 2005, 28(5): 325-329. LIU B H, QING X Y, ZHENG S L, et al. Microseismic monitoring technology and its application status in oilfields[J]. Research and Development of Oil and Gas Reservoirs, 2005, 28(5): 325-329. |
| [23] |
李智敏, 苟先太, 金炜东, 等. 微地震信号的频率特征[J]. 岩土工程学报, 2008, 30(6): 830-834. LI Z M, GOU X T, JING W D, et al. Frequency characteristics of microseismic signals[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(6): 830-834. DOI:10.3321/j.issn:1000-4548.2008.06.009 |
| [24] |
姜宇东, 杨勤勇, 何柯, 等. 基于曲波变换的地面微地震资料去噪方法研究[J]. 石油物探, 2012, 51(6): 620-624. JIANG Y D, YANG Q Y, HE K, et al. Research on denoising method of ground microseismic data based on curvelet transform[J]. Geophysical Prospecting for Petroleum, 2012, 51(6): 620-624. DOI:10.3969/j.issn.1000-1441.2012.06.011 |




