2. 中国石油化工股份有限公司胜利油田分公司物探研究院, 山东东营 257000;
3. 成都理工大学地球物理学院, 四川成都 610059;
4. 中国石油天然气股份有限公司西南油气田分公司, 四川成都 610059
2. Geophysical Research Institute, Shengli Oilfield Company, SINOPEC, Dongying 257000, China;
3. College of Geophysics, Chengdu University of Technology, Chengdu 610059, China;
4. PetroChina Southwest Oil & Gasfield Company, Chengdu 610051, China
静校正问题一直是制约复杂地区地震勘探的瓶颈, 处理不好会严重影响地震资料的成像效果[1]。针对复杂地区的静校正问题, 人们研究了折射静校正、层析静校正、波动方程静校正等各种技术, 在近地表变化较为复杂的地区往往要联合两种以上的静校正方法才能取得较好的效果[2]。沙漠地区是我国西部油气勘探的主战场, 沙漠对地震勘探的主要影响表现在起伏剧烈的地表引起严重的静校正问题。由于沙漠地区近地表近似为连续介质, 因此有人提出了基于折射波初至的连续介质速度模型反演静校正方法[3], 但是其应用效果并不理想。杨贵明等[4]根据微测井测量得到的初至时间与深度的关系, 拟合得到近地表时深关系量板(时深曲线), 根据该量板及高速层顶面计算出所有炮点和检波点的静校正量。该方法不需要拾取记录初至, 特别适用于当前高密度地震采集, 自推出以来凭借其经济高效的优势在沙漠地区地震勘探中得到了广泛应用, 成为沙漠地区主要的静校正技术。1996年, 许亚军等[5]在塔里木沙漠成功应用了时深曲线静校正技术。2010年, 张恒超等[6]在ZGE沙漠地区对时深曲线静校正、模型静校正和折射静校正的效果进行了对比, 认为时深曲线静校正方法能较好地解决沙漠区的静校正问题。2015年, 尚新民[7]在准中地区沙层地球物理性质研究的基础上, 综合应用时深曲线量板解决了该区沙丘引起的静校正问题。但是, 在一些沙丘成因复杂、表层物性差别大的地区, 特别是大沙漠的边缘地区, 根据简单的时深曲线获得的静校正量应用效果不理想。针对这一问题, 学者们提出了很多对策:王增明等[8]将模型约束技术与时深曲线结合计算静校正量, 在准噶尔盆地沙漠地区取得了一定的应用效果, 但该方法仍然需要拾取初至, 而且实现过程较为复杂;肖泽阳等[9]在塔里木沙漠地区对常见的几种静校正方法应用效果进行了对比, 提出按照沙层厚度或分区域建立时深曲线库的静校正方法, 取得了明显效果, 但该方法应用的效果依赖于分区策略, 对各分区之间如何实现静校正量的闭合则需要进一步研究;秦亚玲等[10-11]先后在2007年和2009年提出了利用多项式拟合速度和深度的关系进而计算静校正量的方法, 该方法是常规时深曲线静校正方法的另一种形式, 并没有考虑沙层物性空间上的差异。
虽然沙漠地区有些沙层物性空间上具有较大差异, 但是其纵向上仍然保持着连续介质的特性, 因此时深曲线静校正应用的前提条件依然满足。为了更好地应用时深曲线方法, 需要根据沙层物性空间差异对方法进行改进。受肖泽阳等[9]的方法启发, 本文以微测井测量数据的地质统计学分析结果为依据, 提出了一种逐点时深曲线静校正方法。通过克里金插值获得每个炮点和检波点处不同厚度的地震波垂直传播时间, 利用最小二乘法拟合得到每个炮点和检波点处的时深曲线量板, 进而计算静校正量。该方法通过沙层物性空间上的相关性, 采用地质统计学分析和处理手段, 实现了真正意义上的逐点时深曲线静校正量计算。
1 微测井数据的地质统计学分析借鉴CHAMBERS等[12-13]应用地质统计学的经验, 本文首先对微测井数据进行地质统计学分析, 明确了样本数据的统计特征。
1.1 数据来源S1X工区大部分地表为沙漠, 北部为盐碱滩, 南部为梭梭林浮土区, 古尔图河从工区中东部穿过。工区西部主要为高大的垄状沙丘, 东北部为高大的蜂窝状沙丘, 东南部为相对较小的沙丘。
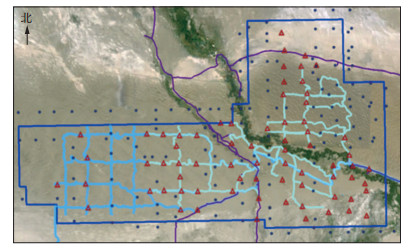
搜集S1X工区64口微测井(图 1)数据并拾取初至, 选取10m、30m两个激发深度, 分析同一深度地震波垂向传播时间的统计特征及空间分布特征, 以确定合适的空间数据插值方法。
|
图 1 S1X工区卫星图片及微测井分布(红色三角形为微测井位置) |
克里金插值法以变异函数理论和结构分析为基础, 利用对待插值点有影响的距离范围内的采样点来估计待插值点的属性值, 区域化变量存在空间相关性是克里金插值方法的应用条件[14-17]。在应用克里金插值方法之前, 需要对空间变量的变异函数进行分析, 根据变异函数分析区域化变量是否存在空间相关性。如果存在空间相关性, 则可以利用克里金方法进行插值。肖斌等[18]和李黎等[19]对克里金方法进行了较为系统的研究, 指出克里金插值方法要求样本数据符合正态分布, 不符合正态分布的数据应转化成为正态分布的形式。绘制正态分位数图(quantile-quantile plot)是评估待插值数据是否为正态分布的一种直观方式, 如果数据散点接近一条直线, 则表明它服从正态分布。
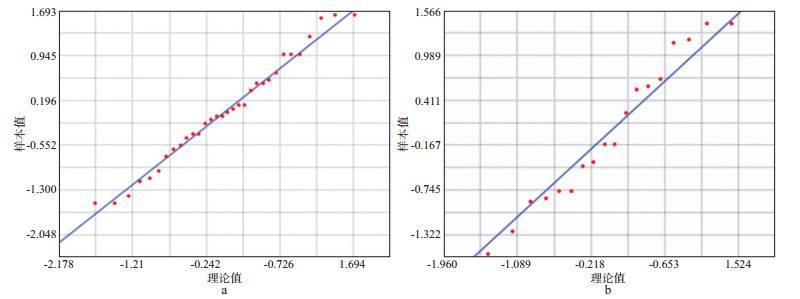
图 2分别为深度10m、30m处的垂直传播时间正态分位数图, 两个深度处的地震波垂直传播时间分位数散点均接近直线, 基本符合正态分布特征, 因此可用于后续的空间插值。
|
图 2 不同深度垂直传播时间正态分位数 a深度10m; b深度30m |
在使用克里金方法进行地质统计学插值之前, 必须对样本数据进行变异分析。实际计算时, 为了满足随机变量内在平稳的假设, 将样本数据配对分组为条柱单元, 取半变异函数值的平均值进行分析。变异函数定义为:
| $ \gamma_{{\rm d}}(h)=\frac{1}{2 n} \sum\limits_{i=1}^{n}\left[z\left(x_{i}\right)-z\left(x_{i}-h\right)\right]^{2} $ | (1) |
式中:h为成对位置相隔距离; n为距离h的样点对个数; z为与x相关的变量。
根据半变异函数图, 可检验随机变量是否具有空间相关性, 确定采用哪种变异函数模型进行插值计算。
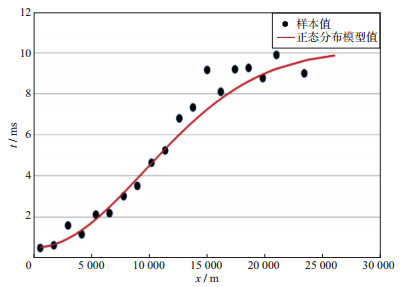
为便于分析, 选择各微测井20m深度测量的地震波垂直传播时间绘制全方向半变异函数图, 并利用正态分布模型进行拟合(图 3)。结果表明:垂直传播时间变程值在15000m之内变化小, 相关性大。利用正态分布模型得到的插值结果精度更高, 可将其作为本工区变异函数理论模型。正态分布模型表达式为:
|
图 3 全方向半变异函数与理论模型 |
| $ \gamma_{\mathrm{m}}(h)=c_{0}+c\left[1-\mathrm{e}^{-(h / a) 2}\right] $ | (2) |
式中, γm(h)为根据正态模型拟合的变异函数; h为距离; c0、c、a为待求系数, 本例拟合结果分别为0.585ms、9.628ms、13666.458m。
由上述分析可知, 研究区近地表同一深度地震波垂直传播时间的半变异函数存在且平稳, 因此本文将根据微测井测量值, 应用克里金插值方法完成所有炮点和检波点不同深度垂直传播时间的插值计算。
2 时深曲线静校正计算利用克里金插值方法计算出每个炮点和检波点处不同深度的地震波初至时间, 再对各个炮点和检波点处的深度-初至散点进行最小二乘法多项式拟合, 可以得到炮点和检波点的逐点时深曲线。
沙丘底(高速顶界面)足够稳定是可以采用时深曲线进行静校正的前提。当这一条件满足时, 可以通过小折射和微测井测量得到的高速顶高程进行插值, 得到整个工区沙丘底。静校正量的计算采用两步法, 首先将炮点和检波点校正到沙丘底, 然后使用统一的替换速度将炮点和检波点从沙丘底校正到最终基准面(或中间基准面)上。在炮点静校正量的计算中, 应考虑实际炮点对应的井深。
沙漠区受地表条件影响, 在沙丘厚的地方一般用浅井多井组合激发, 此时炮点位于沙丘底界之上; 在沙丘薄的地方采用单井深井激发, 这种情况下炮点位于沙丘底界之下。因此, 炮点和检波点静校正量的计算公式可以分为两种情况。
当炮点或检波点在沙丘底界之上时, 为:
| $ \Delta t=-\left[f\left(h_{1}\right)-f\left(h_{2}\right)\right]+\frac{d-b}{v_{\mathrm{R}}} $ | (3a) |
当炮点或检波点位于沙丘底界之下时, 为:
| $ \Delta t=\frac{d-e}{v_{\mathrm{R}}} $ | (3b) |
式中:f(h)为根据时深曲线量板计算的值, 单位为s; h1为沙丘底界离地表面的深度, h2为炮点或检波点的实际埋深, 单位为m; d为基准面高程, b为炮点或检波点处沙丘底界高程, 单位为m; vR为沙丘底界到基准面之间的替换速度, 单位为m/s; e为炮点高程, 单位为m。
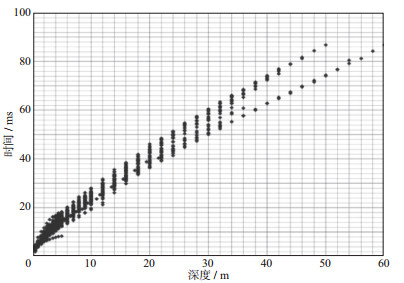
3 实际应用效果将S1X工区64口微测井测量得到的深度-时间散点叠合显示, 结果如图 4所示。可见沙丘深度-时间关系差异较大, 相同深度最大时差在10ms以上, 因此常规时深曲线静校正方法明显不适用。
|
图 4 S1X工区全部微测井测量的深度-时间散点 |
由于插值得到的每个炮点和检波点处的深度-时间散点是否准确决定了后续逐点时深曲线量板及静校正计算结果是否可靠, 因此本文采用交叉验证的方法, 对10m、30m两个深度点的克里金插值结果进行了交叉验证。方法如下:首先移除一个样本数据, 利用剩余样本数据进行克里金插值得到移除样本点的预测值, 然后将移除样本点的真实值与预测值比较; 对所有样本点进行同样处理, 将所有样本点预测值与真实值交会显示。
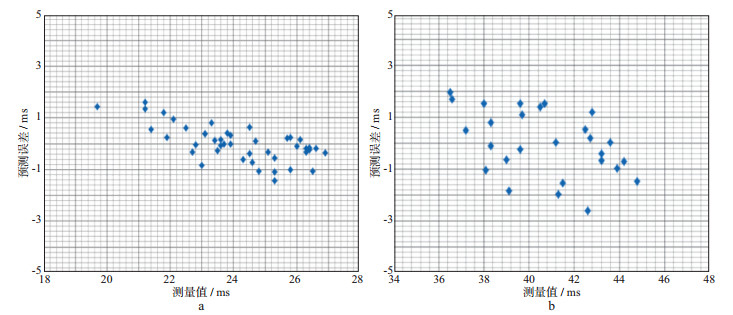
图 5为根据样本数据交叉验证的结果, 克里金插值得到的预测值与真实值高度逼近, 整体误差为[-2ms, 2ms], 满足静校正计算要求。即使存在剩余静校正量, 也能通过后续的反射波剩余静校正予以消除, 从而验证了方法的有效性。
|
图 5 不同深度地震波垂直传播时间克里金插值结果交叉验证误差分析 a深度10m; b深度30m |
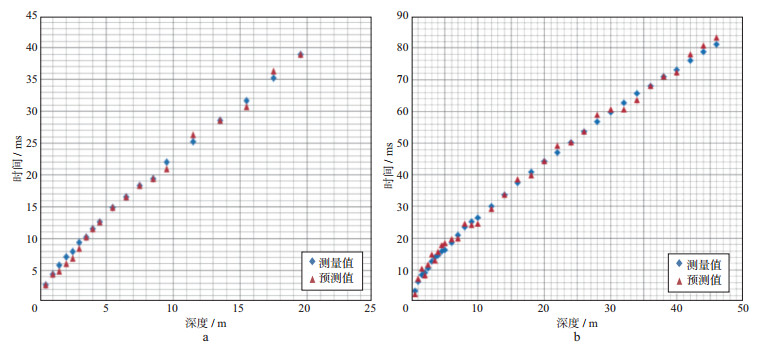
为了验证纵向上深度-时间散点插值结果的可靠性, 选取工区东部和西部两个样本点位置, 通过插值得到其深度-时间散点, 并将其与实测深度-时间散点进行对比, 结果如图 6所示。可以看出, 预测得到的深度-时间散点与实测值高度逼近, 只存在[-1ms, 2ms]的随机误差。由于后续求取逐点时深曲线时要进行多项式拟合, 因此深度-时间散点的随机误差并不会影响静校正量的计算。
|
图 6 工区不同位置微测井深度-时间散点插值结果与测量值的比较 a工区西部; b工区东部 |
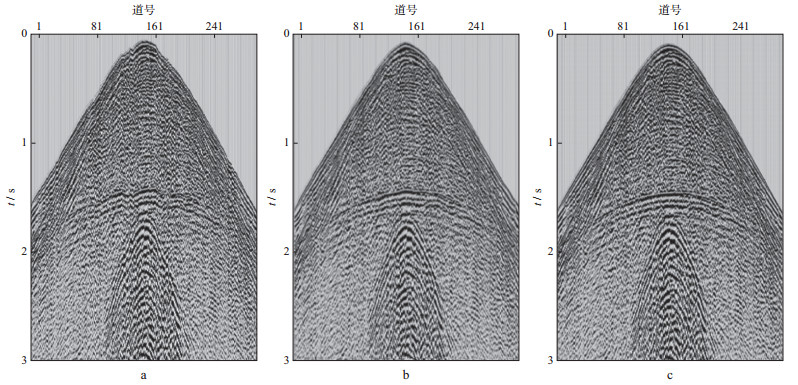
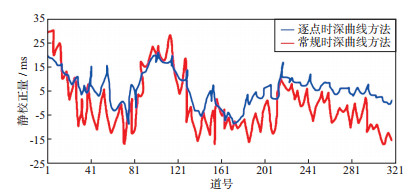
S1X工区内沙丘厚度从几米到70m左右均有, 其中30~40m厚度的大沙丘最为常见。为了验证逐点时深曲线静校正方法的应用效果, 选择工区内具有代表性的大沙丘区, 对不同方法静校正处理后的共炮点道集和叠加剖面进行了对比。图 7a展示了沙丘厚度在40m左右的共炮点道集, 图 7b和图 7c分别为常规时深曲线方法和逐点时深曲线方法静校正后的共炮点道集。可以看出, 常规时深曲线静校正方法虽然一定程度上校正了沙丘起伏造成的时差, 但是其初至和反射波同相轴上仍然存在明显的静校正问题, 这表明在大沙丘区应用常规时深曲线静校正方法效果有限(图 7b)。与常规时深曲线静校正结果相比, 使用逐点时深曲线静校正方法处理的结果初至平滑, 沙丘起伏引起的同相轴扭曲得到了有效恢复, 中短波长静校正问题得到了较好解决。图 8对比了两种方法计算的检波点静校正量曲线, 可以看出, 两种方法计算的静校正量总体趋势相同, 但受地表沙丘变化的影响, 局部细节上差别较大。
|
图 7 大沙丘区共炮点道集静校正效果对比 a原始记录; b常规时深曲线静校正; c逐点时深曲线静校正 |
|
图 8 大沙丘区不同静校正方法计算的检波点静校正量 |
采用同样的叠加速度对两种方法静校正后的道集叠加成像(图 9), 可以看出, 常规时深曲线静校正(图 9a)只是消除了一部分地表起伏引起的时差, 在沙丘较大处同相轴连续性较差, 由沙丘引起的时差仍然没有得到很好的校正。而用本文方法静校正处理后(图 9b), 同相轴连续性明显变好, 不存在明显的中长波长静校正问题, 虽然短波长静校正问题仍有残留, 但通过后续的剩余静校正基本可以将其消除。采用折射静校正方法进行了对比处理, 结果如图 9c所示。可以看出, 大沙丘区使用折射静校正方法处理的效果仍不理想, 甚至无法达到常规时深曲线静校正方法处理的效果。

|
图 9 大沙丘区叠加剖面静校正效果对比 a常规时深曲线静校正; b逐点时深曲线静校正; c折射静校正 |
本文将地质统计学方法应用于沙漠区静校正量的计算, 实现了一种逐点时深曲线静校正方法。通过计算变异函数和对微测井样本进行克里金插值, 获得时深曲线量板, 对实际资料进行逐点时深曲线静校正值计算, 克服了常规时深曲线静校正技术在沙丘物性差异较大地区计算误差大的问题, 进一步提高了时深曲线静校正方法的适用性, 为解决我国西部沙漠、黄土塬等地区的静校正问题提供了一条新的途径。S1X工区实际资料应用表明, 改进后的逐点时深曲线静校正方法比常规的时深曲线静校正方法和折射静校正方法的应用效果有明显改善。
| [1] |
王东, 李文卉, 熊登, 等. 静校正对波动方程叠前深度偏移成像效果的影响[J]. 石油地球物理勘探, 2017, 52(S2): 76-80. WANG D, LI W H, XIONG D, et al. Static corrections influence on wave equation prestack depth migration[J]. Oil Geophysical Prospecting, 2017, 52(S2): 76-80. |
| [2] |
高秦, 陈超群, 王智茹, 等. 多方法静校正融合技术在鄂尔多斯盆地黄土塬区中的应用[J]. 石油地球物理勘探, 2017, 52(S2): 38-44. GAO Q, CHEN C Q, WANG Z R, et al. Multiple statics fusion in loess tablelands, Ordos Basin[J]. Oil Geophysical Prospecting, 2017, 52(S2): 38-44. |
| [3] |
祖云飞, 李培明, 杨葆军, 等. 连续速度模型反演静校正技术的改进[J]. 石油地球物理勘探, 2005, 40(3): 295-299. ZU Y F, LI P M, YANG B J, et al. Improvement of static corrections technique using continuous velocity model for inversion[J]. Oil Geophysical Prospecting, 2005, 40(3): 295-299. DOI:10.3321/j.issn:1000-7210.2005.03.016 |
| [4] |
杨贵明, 钱荣钧, 严峰. 塔里木盆地大沙漠静校正方法[J]. 石油地球物理勘探, 1994, 29(S1): 110-124. YANG G M, QIAN R J, YAN F. Static correction method for desert in Tarim Basin[J]. Oil Geophysical Prospecting, 1994, 29(S1): 110-124. |
| [5] |
许亚军, 徐子伯, 魏庚雨, 等. 塔里木复杂地表区静校正问题的处理方法及效果[J]. 石油地球物理勘探, 1996, 31(4): 483-494. XU Y J, XU Z B, WEI G Y, et al. Processing methods for complicated-surface static correction in the Tarim basin and the application effects[J]. Oil Geophysical Prospecting, 1996, 31(4): 483-494. DOI:10.3321/j.issn:1000-7210.1996.04.003 |
| [6] |
张恒超, 李学聪. 模型法、扩展广义互换法(EGRM)、时深曲线静校正对比研究及在ZGE沙漠资料处理中的应用[J]. 地球物理学进展, 2010, 25(6): 2193-2198. ZHANG H C, LI X C. Study of static corrections by the model method extended generalized reciprocal method(EGRM) and sand dune curve method and their application to seismic data processing in the ZGE area[J]. Progress in Geophysics, 2010, 25(6): 2193-2198. DOI:10.3969/j.issn.1004-2903.2010.06.042 |
| [7] |
尚新民. 准中沙漠区近地表特征及针对性勘探技术[J]. 西南石油大学学报(自然科学版), 2015, 37(1): 65-75. SHANG X M. The research of near-surface characters and targeted exploration technology in the hinterland of Junggar basin desert area[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2015, 37(1): 65-75. |
| [8] |
王增明, 刘超敏, 刘斌, 等. 董1井区静校正方法研究与应用[J]. 石油物探, 2005, 44(4): 379-382. WANG Z M, LIU C M, LIU B, et al. Methodology research and application of seismic static data in Dong1 well area[J]. Geophysical Prospecting for Petroleum, 2005, 44(4): 379-382. DOI:10.3969/j.issn.1000-1441.2005.04.017 |
| [9] |
肖泽阳, 唐成鸽, 刘厚裕. 沙丘曲线静校正应用效果分析[J]. 勘探地球物理进展, 2007, 30(1): 52-56. XIAO Z Y, TANG C G, LIU H Y. Analysis on the application of dune curve statics correction[J]. Progress in Exploration Geophysics, 2007, 30(1): 52-56. |
| [10] |
秦亚玲, 王彦春, 王瑞祥, 等. 一种适合沙漠地区的静校正方法[J]. 地球物理学进展, 2007, 22(6): 1873-1878. QIN Y L, WANG Y C, WANG R X, et al. A method of static correction suitable to the desert area[J]. Progress in Geophysics, 2007, 22(6): 1873-1878. DOI:10.3969/j.issn.1004-2903.2007.06.030 |
| [11] |
秦亚玲, 王彦春, 王瑞祥, 等. 用多项式拟合求取沙漠地区表层速度的静校正方法[J]. 天然气工业, 2009, 29(6): 37-39. QIN Y L, WANG Y C, WANG R X, et al. A static correction method:To calculate the velocity of surface layer in the desert area by polynomial fitting[J]. Natural Gas Industry, 2009, 29(6): 37-39. DOI:10.3787/j.issn.1000-0976.2009.06.010 |
| [12] |
CHAMBERS R L, YARUS J M, HIRD K B. Petroleum geostatistics for nogeostatisticians part 1[J]. The Leading Edge, 2000, 19(5): 474-479. DOI:10.1190/1.1438630 |
| [13] |
CHAMBERS R L, YARUS J M, HIRD K B. Petroleum geostatistics for nogeostatisticians part 2[J]. The Leading Edge, 2000, 19(6): 592-596. DOI:10.1190/1.1438664 |
| [14] |
杨培杰. 地质统计学反演——从两点到多点[J]. 地球物理学进展, 2014, 29(5): 2293-2300. YANG P J. Geostatistics inversion—from two point to multiple point[J]. Progress in Geophysics, 2014, 29(5): 2293-2300. |
| [15] |
王雅春, 王璐. 地质统计学反演在杏北西斜坡区储层预测中的应用[J]. 地球物理学进展, 2013, 28(5): 2554-2560. WANG Y C, WANG L. Application of geostatistical inversion to reservoir prediction in the western slope of the northern Xingshugang oil field[J]. Progress in Geophysics, 2013, 28(5): 2554-2560. |
| [16] |
韩东, 胡向阳, 邬兴威, 等. 基于地质统计学反演的缝洞储集体物性定量评价[J]. 地球物理学进展, 2016, 31(2): 655-661. HAN D, HU X Y, WU X W, et al. Quantitative evaluation for porosity of the fracture-cavity reservoir based on geostatistical inversion[J]. Progress in Geophysics, 2016, 31(2): 655-661. |
| [17] |
耿美霞, 黄大年, 于平, 等. 基于协同克里金方法的重力梯度全张量三维约束反演[J]. 地球物理学报, 2016, 59(5): 1849-1860. GENG M X, HUANG D N, YU P, et al. Three-dimensional constrained inversion of full tensor gradiometer data based on Co-Kriging method[J]. Chinese Journal Geophysics, 2016, 59(5): 1849-1860. |
| [18] |
肖斌, 赵鹏大, 侯景儒. 地质统计学新进展[J]. 地球科学进展, 2000, 15(3): 293-296. XIAO B, ZHAO P D, HOU J R. New development of geostatistics[J]. Advances in Earth Science, 2000, 15(3): 293-296. DOI:10.3321/j.issn:1001-8166.2000.03.010 |
| [19] |
李黎, 王永刚. 地质统计学应用综述[J]. 勘探地球物理进展, 2006, 29(3): 163-169. LI L, WANG Y G. Review of applications of geostatistics[J]. Progress in Exploration Geophysics, 2006, 29(3): 163-169. |



