2. 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266580
2. Laboratory for Marine Mineral Resource, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266580, China
全波形反演(full waveform inversion, FWI)方法是一种基于波动方程正演模拟的反演方法, 该方法可在无需任何假设条件的情况下进行波动方程全波场数值模拟, 因此理论上可以提供最高分辨率的速度成像。随着计算机技术的发展, 全波形反演近年来逐渐成为勘探地球物理领域的研究热点。全波形反演通过建立实际观测记录与正演模拟记录的最小二乘目标函数, 利用全波场的信息获取全波数的速度模型, 反演结果理论上具有最高的分辨率[1-3]。但全波形反演的精度严重依赖于低频信息、长偏移距地震数据以及准确的初始速度模型。
将速度模型分为浅层速度模型和中、深层速度模型两部分。浅层模型存在的波主要包括直达波、潜水波等透射波, 该类型的波由于观测孔径大, 故可以很好地恢复浅层的低波数速度[4]。多尺度反演所采用的从低频逐步反演到高频的策略可以解决浅层背景速度的恢复问题, 同时多尺度反演还依赖于地震数据中的低频信息, 特别是1.5~2.0Hz的地震有效信号在恢复背景速度中起了非常关键的作用, 但在实际情况中, 传统的地震数据最低频约为5Hz, 低于2Hz的低频信息几乎不存在[5]。包络反演将地震信号解调重构得到地震数据包络用于更新大尺度的地震速度[6-7]。将地震数据进行包络变换后, 数据的频带移至超低频区域, 该低频区域独立于地震频带之外可有效反演大尺度的速度信息[8]。但是地震数据求取包络后, 以浅层直达波能量为主, 包络反演对浅层大尺度的速度信息恢复能力要优于对中、深层速度信息恢复能力。
中、深层速度更新主要依赖于反射波信息, 而反射波的观测孔径相对较小, 几乎只有高波数的速度得到了更新[9-10]。为了得到中、深层的背景速度, 一方面从梯度优化方面入手, 对深层能量进行补偿以提高中、深层反演精度[11-12], 另一方面, XU等[13]提出反射波全波形反演的方法旨在利用反射波更新中、深层的低波数速度参数, 并用格林函数表示反射波全波形反演中的雅可比矩阵及梯度。雅可比矩阵计算量大, 故多采用伴随状态法求取梯度[14]。雅可比矩阵被称为全波形反演的敏感核函数[15-18], 表征速度扰动与波场扰动之间的关系。将常规全波形反演的敏感核函数分解为4个子核, 不同子核表征不同位置不同尺度的速度更新量, 反射波只有沿着“兔耳”路径方可对中、深层的低波数速度进行更新[19]。散射理论也可用于表征全波形反演对不同波数速度的更新, 一般认为全波形反演包含偏移分量和层析分量[20], 对反射波数据而言, 偏移分量能量远大于层析分量能量, 而偏移分量对应着高波数速度的更新, 因此常规全波形反演的反射波对高波数速度的恢复能力更强。相同方向的正传波场与残差波场主要产生层析分量, 用于更新低波数速度, 相反方向的正传波场与残差波场主要产生偏移分量, 用于更新高波数速度[21]。按照不同的方向分解波场, 并更新偏移分量, 再计算层析分量也可以达到反演不同波数速度参数的目的[22]。
以上方法均存在两个问题:①包络反演对地震数据变换, 并未改变雅可比矩阵, 且能量集中在浅层, 对浅层背景速度的更新能力远大于对中、深层背景速度的更新能力; ②反射波全波形反演方法可改变雅可比矩阵, 且对中、深层背景速度更新能力更强, 但反演过程需要用到反射波, 偏移/反偏移计算可以有效地得到反射波, 但是每次迭代需要进行6次正演计算, 计算量巨大。因此本文提出一种基于包络反演的高低波数同步反演方法, 首先将线性初始速度作为一级速度, 利用希尔伯特变换将地震数据变换为包络数据, 重构低频数据用于浅层背景速度的恢复; 再将包络反演的速度作为二级速度进行高低波数同步反演, 采用坡印廷矢量波场分解方法分解得到偏移分量及层析分量, 根据偏移分量更新模型的扰动速度, 同时根据层析分量更新模型中、深层的背景速度; 最后利用Marmousi2模型数据的反演结果验证了本文方法的有效性。
1 方法原理 1.1 包络反演方法全波形反演方法受周波跳跃问题的影响, 易陷入局部极值。为解决低频信息缺失情况下的周波跳跃问题, 对地震数据进行非线性变换以重构低频信息, 从而为全波形反演提供合理的初始模型。地震数据包络包含丰富的低频信息, 利用Hilbert变换可得到观测数据和模拟数据的包络信息, 包络残差的L2范数即为包络反演的目标函数, 可表示为:
| $ \begin{aligned} C_{\mathrm{e}}(\boldsymbol{m}) &=\frac{1}{2} \sum\limits_{s, g} \int_{t}\left[e_{\mathrm{obs}}^{p}\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}_{\mathrm{g}}, t\right)-e_{\mathrm{cal}}^{p}\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}_{\mathrm{g}}, t\right)\right]^{2} \mathrm{d} t \\ &=\frac{1}{2} \sum\limits_{s, g} \int_{t} E^{2}\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}_{\mathrm{g}}, t\right) \mathrm{d} t \end{aligned} $ | (1) |
式中:m为模型参数; t表示时间; eobsp与ecalp分别表示观测数据和模拟数据的包络; xs和xg分别表示接收点和震源点位置; 参数p用于控制包络信号的能量, 一般情况下p=2;E为包络残差。
包络反演的梯度∇Ce可表示为:
| $ \begin{array}{l}{\nabla C_{\mathrm{e}}(\boldsymbol{m})=\sum\limits_{s, g} \int_{t} \frac{\partial \boldsymbol{u}}{\partial \boldsymbol{m}}\left[E\left(\boldsymbol{x}_{{\rm s}}, \boldsymbol{x}_{\mathrm{g}}, t\right) y\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}_{\mathrm{g}}, t\right) \cdot\right.} \\ {e_{\mathrm{cal}}^{p-2}\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}_{\mathrm{g}}, t\right)-H\left\{E\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}_{\mathrm{g}}, t\right) y_{\mathrm{H}}\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}_{\mathrm{g}}, t\right) \cdot\right.} \\ {\left.\left.e_{\mathrm{cal}}^{p-2}\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}_{\mathrm{g}}, t\right)\right\}\right] \mathrm{d} t}\end{array} $ | (2) |
式中:u表示波场; ∂u/∂m为雅可比矩阵; y表示模拟地震记录; H{·}表示希尔伯特变换; yH表示希尔伯特变换后的模拟地震记录。利用地震数据包络中所包含的丰富的低频信息可恢复介质的背景速度, 从而为常规全波形反演提供合理的初始速度模型。如图 1所示, 包络数据的能量集中于浅层的直达波, 因此其只对浅层的低波数速度具有良好的恢复能力。
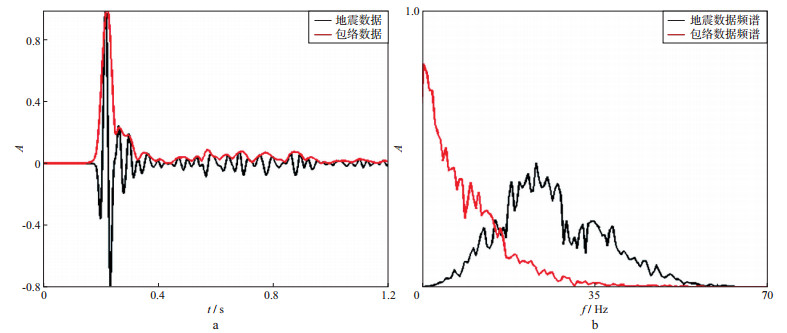
|
图 1 地震数据与包络数据的地震记录对比(a)和频谱对比(b) |
在全波形反演中, 速度模型包括背景速度和扰动速度:
| $ \boldsymbol{m}=\boldsymbol{m}_{0}+\Delta \boldsymbol{m} $ | (3) |
式中:m0为背景速度, 即低波数分量; Δm为扰动速度, 即高波数分量。相应的, 地震波场可分解为背景速度对应的地震波场及扰动速度对应的地震波场, 格林函数也可相应地分解成两部分:
| $ G=G_{0}+\Delta G $ | (4) |
式中:G为地震波场的格林函数; G0为平滑背景波场的格林函数, 用于描述直达波和潜波; ΔG为扰动波场的格林函数, 用于描述反射波等。在一阶Born近似假设下, 全波形反演敏感核函数可表示为[15]:
| $ \mathit{\boldsymbol{k}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{g}}}} \right) = \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial \mathit{\boldsymbol{m}}}} = {\omega ^2}G\left( {\mathit{\boldsymbol{x}}, t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)G\left( {{\mathit{\boldsymbol{x}}_{\rm{g}}}, t;\mathit{\boldsymbol{x}}} \right) $ | (5) |
式中:k(x; xs, xg)又称为Fréchet导数; u为地震波场; ω为圆频率; m为速度场; G(x, t; xs)为震源波场的格林函数; G(xg, t; x)为反转波场的格林函数。因为格林函数可分解为两部分, 故常规全波形反演的敏感核函数可分解为4个子核[19]:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{k}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{g}}}} \right) = {\mathit{\boldsymbol{k}}_1}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{g}}}} \right) + {\mathit{\boldsymbol{k}}_2}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{g}}}} \right) + }\\ {{\mathit{\boldsymbol{k}}_3}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{g}}}} \right) + {\mathit{\boldsymbol{k}}_4}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{g}}}} \right)} \end{array} $ | (6) |
式中:k1(x; xs, xg)=ω2G0(x, t; xs)G0(xg, t; x); k2(x; xs, xg)=ω2G0(x, t; xs)ΔG(xg, t; x); k3(x; xs, xg)=ω2ΔG(x, t; xs)G0(xg, t; x); k4(x; xs, xg)=ω2ΔG(x, t; xs)ΔG(xg, t; x)。不同的子核函数表征不同位置不同尺度的速度更新量, 核函数k1(x; xs, xg)表征直达波场之间的关系, 主要依赖于背景速度模型, 对于中、深层反射波而言, 主要贡献于高波数速度场[23]; 核函数k2(x; xs, xg)和k3(x; xs, xg)均表征背景波场及散射波场之间的关系, 对沿着“兔耳”路径即反射波路径传播的地震波场而言, 即为层析算子的脉冲响应, 对速度模型的低波数分量有贡献; 核函数k4(x; xs, xg)表征散射波场之间的关系, 主要依赖于扰动速度模型。分离直达波场和散射波场, 即可得到各个子核函数。
利用坡印廷矢量[21, 23]沿地震波传播方向进行地震波场分解, 可得到正向直达波场和背向散射波场。利用坡印廷矢量可将波形反演的核函数分为偏移分量和层析分量:
| $ {\mathit{\boldsymbol{k}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{g}}}} \right) = {\mathit{\boldsymbol{k}}_t}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{g}}}} \right) + {\mathit{\boldsymbol{k}}_m}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{g}}}} \right)} $ | (7) |
| $ \begin{array}{l}{\boldsymbol{k}_{t}\left(\boldsymbol{x} ; \boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}_{\mathrm{g}}\right)=\sum\limits_{\boldsymbol{x}_{\mathrm{s}}} \sum\limits_{\boldsymbol{x}_{\mathrm{g}}}\left[G_{\mathrm{U}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) \cdot\right.} \\ {\left.G_{\mathrm{U}}\left(\boldsymbol{x}_{\mathrm{g}}, t ; \boldsymbol{x}\right)+G_{\mathrm{D}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) G_{\mathrm{D}}\left(\boldsymbol{x}_{\mathrm{g}}, t ; \boldsymbol{x}\right)\right]}\end{array} $ | (8) |
| $ \begin{array}{l}{\boldsymbol{k}_{m}\left(\boldsymbol{x} ; \boldsymbol{x}_{{\rm s}}, \boldsymbol{x}_{\mathrm{g}}\right)=\sum\limits_{\boldsymbol{x}_{\mathrm{s}}} \sum\limits_{\boldsymbol{x}_{\mathrm{g}}}\left[G_{\mathrm{U}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) G_{\mathrm{D}}\left(\boldsymbol{x}_{\mathrm{g}}, t\right)\right.}; \\ {\left.\boldsymbol{x})+G_{\mathrm{D}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) G_{\mathrm{U}}\left(\boldsymbol{x}_{\mathrm{g}}, t ; \boldsymbol{x}\right)\right]}\end{array} $ | (9) |
式中:kt和km分别表示核函数的层析分量和偏移分量; GU和GD分别表示向上传播地震波场和向下传播地震波场的格林函数。图 2为层析分量与偏移分量, 分别对应恢复速度场中的背景速度与扰动速度。
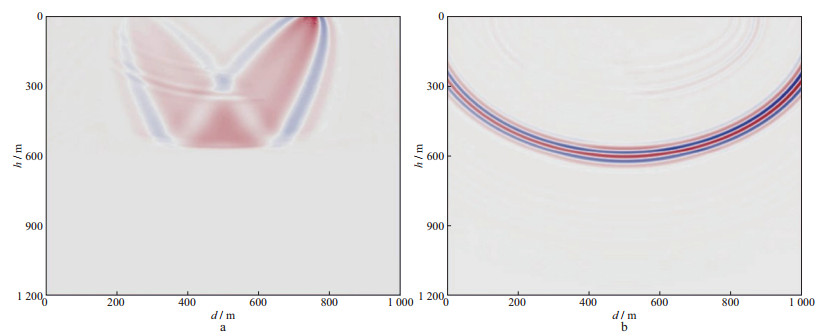
|
图 2 层析分量(a)与偏移分量(b) |
由于全波形反演的初始速度是平滑的, 只能产生较弱的扰动反射波场, 因此导致了全波形反演中k1(x; xs, xg)的贡献远大于k2(x; xs, xg)+k3(x; xs, xg)的贡献, 也导致了中、深层低波数速度分量更新能力有限。
图 3为高低波数同步反演流程, 在全波形反演过程中, 利用坡印廷矢量计算得到的层析分量和偏移分量, 可以实现梯度分解, 计算得到相应的速度更新量, 两者叠加即为迭代过程中的速度更新量。高低波数同步反演方法所采用的偏移分量和层析分量同步迭代的方式能够避免偏移分量和层析分量之间的耦合效应, 在实现扰动速度更新的同时, 加强了中、深层低波数背景速度的更新, 一定程度上降低了对初始速度的依赖, 提高了反演方法的稳定性, 反演结果较为理想。此外, 反射波波形反演方法引入偏移/反偏移构建层析分量[19], 每次迭代需要额外进行6次正演运算, 其运算消耗及内存消耗高; 而基于坡印廷矢量的高低波数同步反演方法, 无需偏移/反偏移计算即可得到层析分量, 计算效率高。
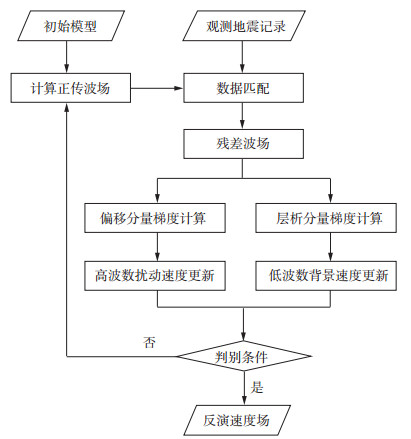
|
图 3 高低波数同步反演流程 |
本文基于包络反演及高低波数同步反演方法提出了分步多尺度全波形反演策略。图 4为分步多尺度全波形反演策略流程:以线性初始速度作为一级初始速度, 通过希尔伯特变换重构低频数据, 并进行包络反演以恢复浅层背景速度; 将包络反演结果作为二级初始速度, 进行高低波数同步反演。主要反演步骤如下:
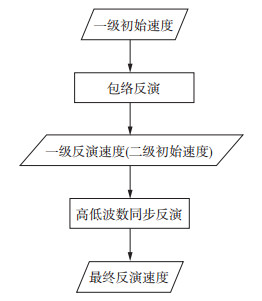
|
图 4 分步多尺度全波形反演策略流程 |
1) 线性初始速度作为一级初始速度;
2) 将一级初始速度作为一级反演的初始输入速度模型, 采用包络反演方法进行速度迭代更新, 主要实现浅层背景速度更新, 得到一级速度反演结果;
3) 将一级速度反演结果作为二级反演的初始输入速度模型, 采用高低波数交替更新迭代的反演策略, 实现扰动速度及中、深层背景速度更新, 得到最终反演速度。
2 模型测试利用图 5所示的Marmousi2速度模型进行测试, 模型参数如下:水平方向网格点数为301, 垂直方向网格点数为151, 水平方向和垂直方向网格间距均为8m, 时间采样间隔为0.5ms, 时间采样点数为1500, 子波采用雷克子波, 全波形反演子波主频为25Hz, 震源放置于地表, 第1炮的坐标为(56m, 0), 炮间距为56m, 检波点也放置于地表, 第1个检波点坐标为(0, 0), 检波点间隔为8m, 地表全孔径接收。
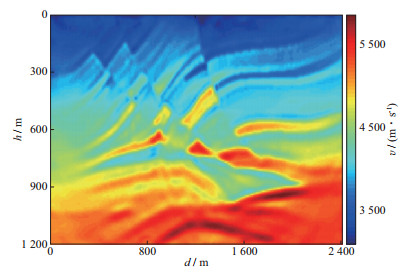
|
图 5 Marmousi2速度模型 |
将从浅层到深层速度值线性增加的速度模型作为包络反演的初始速度, 如图 6所示。首先进行包络反演, 地震数据的子波主频为25Hz, 对地震数据求取包络后, 频率向超低频方向移动, 主要集中在0~5Hz附近; 能量集中在浅层直达波处, 对浅层的背景速度更新能力强。这一步的包络反演为之后的全波形反演提供了背景速度更为准确的初始速度模型。
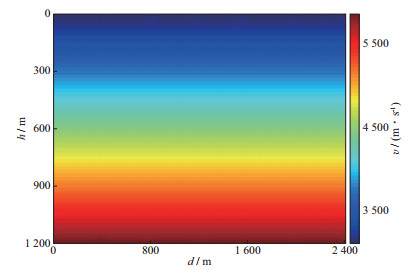
|
图 6 包络反演的线性初始速度模型 |
包络反演采用的子波主频为10Hz, 迭代30次后得到的速度模型如图 7所示, 可以看出包络算子可以解调出地震数据中的超低频信息并可以有效恢复速度模型的背景速度信息。分别抽取真实速度模型、线性初始速度模型以及包络反演速度模型中第120道, 第150道和第200道的速度并对比, 结果如图 8所示, 可以看出, 恢复的浅层背景速度接近真实速度, 而中、深层速度的更新量较小, 导致包络反演对背景速度的更新能力集中于浅层。
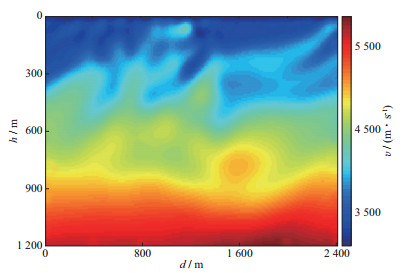
|
图 7 包络反演(迭代30次)得到的速度模型 |
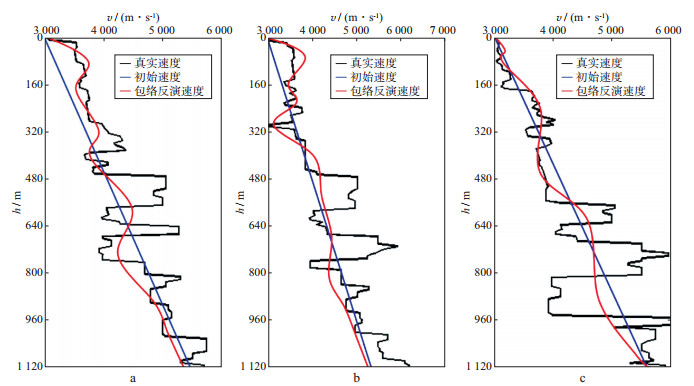
|
图 8 包络反演(迭代30次)得到的单道速度与真实速度、初始速度对比 a 120道; b 150道; c 200道 |
将图 7包络反演(迭代30次)得到的速度模型作为初始速度模型, 进行常规全波形反演, 子波主频25Hz, 误差迭代收敛后得到的速度模型如图 9所示。分别抽取真实速度模型和常规全波形反演速度模型中的第120道、第150道和第200道的速度进行对比, 结果如图 10所示, 可以看出, 以包络反演速度作为初始速度进行常规全波形反演可以较好地更新扰动速度, 黄色椭圆区域所在的浅层(贴近地表处震源会影响干扰速度的更新)背景速度准确, 速度恢复结果几乎与真实速度一致; 蓝色椭圆区域所在的中、深层, 误差收敛后的速度更新结果并不理想, 这主要是由于常规全波形反演的速度更新能力集中于扰动速度, 对中、深层背景速度的更新能力弱。
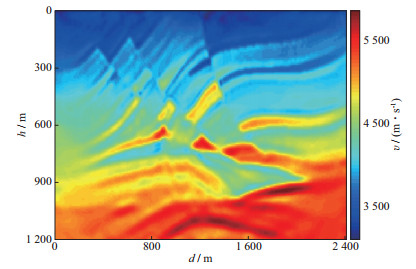
|
图 9 常规全波形反演得到的速度模型 |
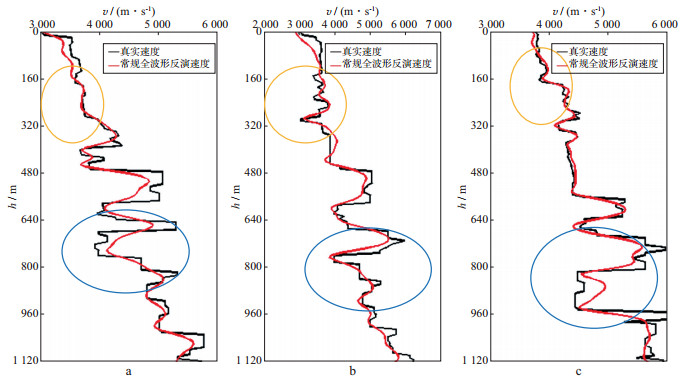
|
图 10 常规全波形反演得到的单道速度与真实速度对比 a 120道; b 150道; c 200道 |
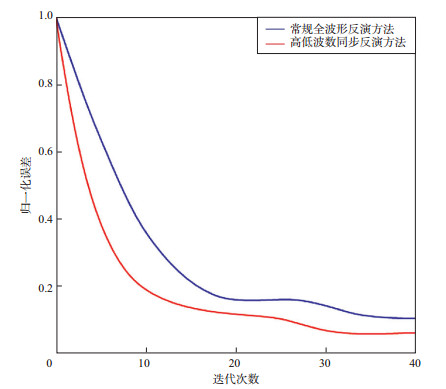
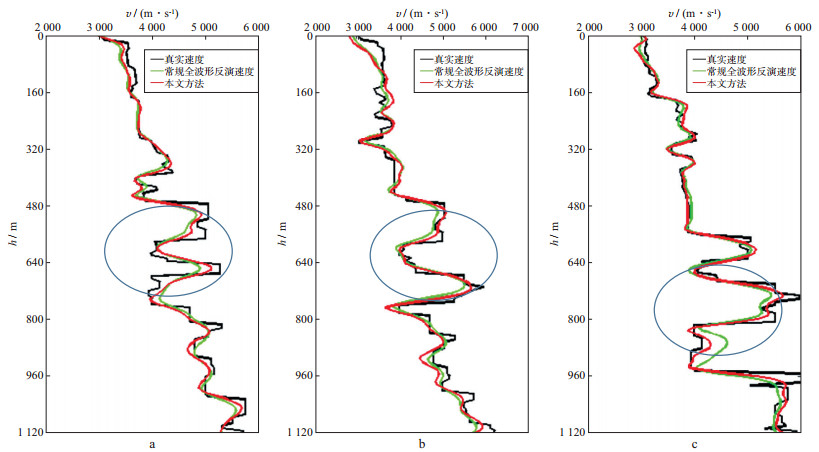
同样地, 将图 7包络反演(迭代30次)得到的速度作为初始速度, 进行高低波数同步反演, 子波主频25Hz, 误差迭代收敛后得到的速度模型如图 11所示。在反演迭代过程中, 利用偏移分量对扰动速度进行更新, 同步引入层析分量对中、深层的背景速度进行迭代更新, 迭代40次后根据优化的全波形反演结果确定反射界面, 并利用坡印廷矢量分离出上行波进而求取层析分量与偏移分量, 结果如图 12所示。图 13为采用不同方法反演得到的迭代误差曲线, 可以看出, 高低波数同步反演方法具有良好的收敛性, 随着迭代次数的增加, 误差稳定下降并收敛。分别抽取真实速度模型、高低波数同步反演速度模型以及常规全波形反演速度模型中第120道、第150道和第200道的速度进行对比, 结果如图 14所示。总体而言, 常规全波形反演及高低波数同步反演得到的反演速度均与真实速度吻合; 相对而言, 应用高低波数同步反演方法得到的反演速度与真实速度吻合得更好, 且在中、深层区域(图 11的黑色椭圆区域和图 14的蓝色椭圆区域)速度精度更高。
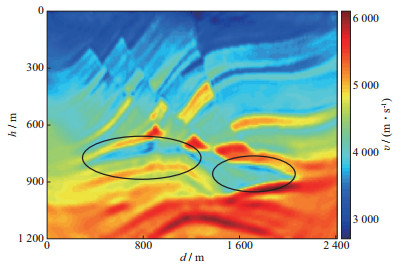
|
图 11 高低波数同步反演得到的速度模型 |
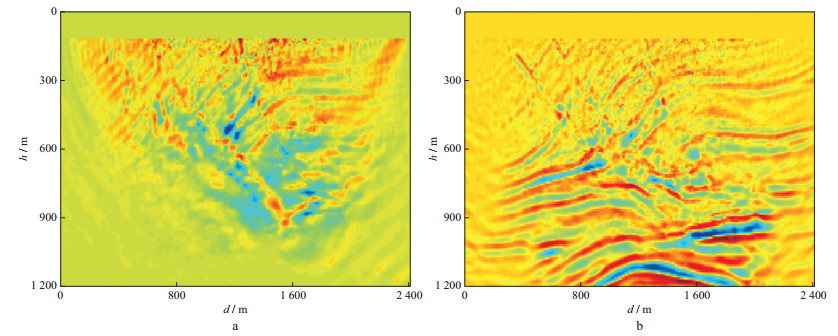
|
图 12 利用坡印廷矢量分解得到的层析分量(a)与偏移分量(b) |
|
图 13 采用不同方法反演得到的迭代误差曲线 |
|
图 14 采用不同方法反演得到的单道速度与真实速度对比 a 120道; b 150道; c 200道 |
我们利用坡印廷矢量进行梯度分解并构建了高低波数同步反演方法, 同时结合包络反演提出了分步多尺度反演策略。该策略引入包络反演实现浅层背景速度场更新, 然后将更新的背景速度场作为初始速度模型, 利用波印廷矢量分解反演梯度的偏移分量和层析分量, 交替更新小尺度扰动速度和中、深层处大尺度背景速度, 以达到不同尺度速度同步更新的目的。Marmousi2模型数据测试结果表明, 基于包络反演的高低波数同步反演方法可以准确稳定地恢复中、深层速度, 同时避免偏移/反偏移计算带来的计算消耗和内存消耗, 计算效率较高。采用基于包络反演的高低波数同步反演方法反演得到的速度模型, 为之后地震层位标定及油气预测奠定了基础。考虑到实际资料中初始速度模型不精确, 本文方法在三维实际资料中的应用还需深入研究。
| [1] |
LAILLY P.The seismic inverse problem as a sequence of before stack migrations[C]//Conference on inverse scattering: theory and application.Philadelphia: Society for Industrial and Applied Mathematics, 1983: 206-220
|
| [2] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [3] |
BIONDI B, ALMOMIN A. Simultaneous inversion of full data bandwidth by tomographic full-waveform inversion[J]. Geophysics, 2014, 79(3): WA129-WA140. DOI:10.1190/geo2013-0340.1 |
| [4] |
GAUTHIER O, VIRIEUX J, TARANTOLA A. Two-dimensional nonlinear inversion of seismic waveforms:Numerical results[J]. Geophysics, 1986, 51(7): 1387-1403. DOI:10.1190/1.1442188 |
| [5] |
BAETEN G, DE MAAG J W, PLESSIX R E, et al. The use of low frequencies in a full-waveform inversion and impedance inversion land seismic case study[J]. Geophysical Prospecting, 2013, 61(4): 701-711. DOI:10.1111/1365-2478.12010 |
| [6] |
WU R S, LUO J, WU B. Seismic envelope inversion and modulation signal model[J]. Geophysics, 2014, 79(3): WA13-WA24. DOI:10.1190/geo2013-0294.1 |
| [7] |
王官超, 杜启振. 基于包络目标函数的弹性波波形反演[J]. 石油物探, 2016, 55(1): 133-141. WANG G C, DU Q Z. Elastic full waveform inversion based on envelope objective function[J]. Geophysical Prospecting Petroleum, 2016, 55(1): 133-141. DOI:10.3969/j.issn.1000-1441.2016.01.017 |
| [8] |
包乾宗, 陈俊霓, 吴浩. 基于地震数据包络的多尺度全波形反演方法[J]. 石油物探, 2018, 57(4): 584-591. BAO Q Z, CHEN J N, WU H. Multi-scale full waveform inversion based on logarithmic envelope of seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 584-591. DOI:10.3969/j.issn.1000-1441.2018.04.012 |
| [9] |
RAVAUT C, OPERTO S, IMPROTA L, et al. Multiscale imaging of complex structures from multifold wide-aperture seismic data by frequency-domain full-waveform tomography:Application to a thrust belt[J]. Geophysical Journal International, 2004, 159(3): 1032-1056. DOI:10.1111/j.1365-246X.2004.02442.x |
| [10] |
SIRGUE L, BARKVED O I, DELLINGER J, et al. Thematic set:Full waveform inversion:The next leap forward in imaging at Valhall[J]. First Break, 2010, 28(4): 65-70. |
| [11] |
荣涛, 张凯, 李振春, 等. 梯度优化在多重网格法多尺度波形反演中的应用[J]. 石油地球物理勘探, 2017, 52(6): 1208-1217. RONG T, ZHANG K, LI Z C, et al. Gradient optimization in the multi-grid and multi-scale waveform inversion[J]. Oil Geophysical Prospecting, 2017, 52(6): 1208-1217. |
| [12] |
史才旺, 何兵寿. 基于主成分分析和梯度重构的全波形反演[J]. 石油地球物理勘探, 2018, 53(1): 95-104. SHI C W, HE B S. Full waveform inversion based on principal component analysis and gradient reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 95-104. |
| [13] |
XU S, CHEN F, LAMBARÉ G, et al. Full waveform inversion of reflected seismic data[J]. Journal of Seismic Exploration, 2013, 22(5): 449-462. |
| [14] |
PLESSIX R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 2006, 167(2): 495-503. DOI:10.1111/j.1365-246X.2006.02978.x |
| [15] |
WOODWARD M J. Wave-equation tomography[J]. Geophysics, 1992, 57(1): 15-26. DOI:10.1190/1.1443179 |
| [16] |
DAHLEN F A, HUNG S H, NOLET G. Fréchet kernels for finite-frequency traveltimes—I.Theory[J]. Geophysical Journal International, 2000, 141(1): 157-174. DOI:10.1046/j.1365-246X.2000.00070.x |
| [17] |
刘玉柱, 谢春, 杨积忠. 基于Born波路径的高斯束初至波波形反演[J]. 地球物理学报, 2014, 57(9): 2900-2909. LIU Y Z, XIE C, YANG J Z. Gaussian beam first-arrival waveform inversion based on Born wavepath[J]. Chinese Journal of Geophysics, 2014, 57(9): 2900-2909. |
| [18] |
刘玉柱, 王光银, 杨积忠, 等. 基于Born敏感核函数的VTI介质多参数全波形反演[J]. 地球物理学报, 2015, 58(4): 1305-1316. LIU Y Z, WANG G Y, YANG J Z. Multi-parameter full-waveform inversion for VTI media based on Born sensitivity kernels[J]. Chinese Journal of Geophysics, 2015, 58(4): 1305-1316. |
| [19] |
CHI B, DONG L, LIU Y. Correlation-based reflection full-waveform inversion[J]. Geophysics, 2015, 80(4): R189-R202. DOI:10.1190/geo2014-0345.1 |
| [20] |
MORA P. Inversion=migration+tomography[J]. Geophysics, 1989, 54(12): 1575-1586. DOI:10.1190/1.1442625 |
| [21] |
TANG Y, LEE S, BAUMSTEIN A, et al. Tomographically enhanced full wavefield inversion[J]. Expanded Abstracts of 83rd Annual Internat SEG Mtg, 2013, 1037-1041. |
| [22] |
IRABOR K, WARNER M. Reflection FWI[J]. Expanded Abstracts of 86th Annual Internat SEG Mtg, 2016, 1136-1140. |
| [23] |
XU S, WANG D, CHEN F, et al.Inversion on Reflected Seismic Wave[J].Expanded Abstracts of 82nd Annual Internat SEG Mtg, 2012: https://doi.org/10.1190/segam2012-1473.1
|




