2. 中国石油化工集团公司石油工程地球物理有限公司胜利分公司, 山东东营 257086;
3. 中国科学院地质与地球物理研究所, 北京 100029;
4. 中石化休斯顿研究开发中心, 休斯顿 77056
2. Shengli Branch, Sinopec Geophysical Corporation, Dongying 257086, China;
3. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
4. Sinopec Tech Houston LLC., Houston 77056, USA
近年来压缩感知理论因其特有的优点得到广泛关注。它利用数据可稀疏表达的性质, 采用远低于传统尼奎斯特采样率的稀疏随机采样, 通过稀疏约束的优化算法重建完整的数据信号[1-2]。该方法一方面突破了尼奎斯特采样定理的限制, 打散了采样假频的分布, 为拓宽信号的频率建立了理论基础; 另一方面, 采用了较少的采样, 减少了信号数据在采集、传输、存储等方面人力和物力的投入。由于地震波信号在不同的变换域具有稀疏性, 具备了压缩感知的应用条件, 因此地震勘探与压缩感知的结合, 能够实现基于压缩感知稀疏采样的高密度数据信号重建, 从而降低数据采集成本和提高勘探目标的分辨能力。
基于压缩感知的地震勘探技术, 目前国内外已经开展较多的应用研究和尝试, 特别是在随机欠采样的数据重建处理中得到了广泛研究与应用, HERRMANN等[3-4]研究了用较少的采样就能获取较多信息的随机稀疏采样方法, 并提出了一种基于Curvelet的多尺度非线性地震数据处理方法; 白兰淑等[5]提出了在Curvelet域基于压缩感知通过联合迭代进行地震数据重建的方法; CANDES等[6]根据鲁棒不确定性原理研究了高度不完整频率信息的精确信号重建; WU等[7]用dreamlet方法在压缩域进行成像; NAGHIZADEH等[8]从理论出发研究了采样函数和傅里叶重建方法; LI等[9]提出了用于地震资料重建的插值压缩感知方法; 张良等[10]、冯飞等[11]和王升超等[12]研究了基于Contourlet, Shearlet和Radon变换的地震数据重建方法; 刘争光等[13]和屠宁[14]提出了压缩感知理论下基于快速不动点连续算法的地震数据重建和快速最小二乘逆时偏移方法; MOSHER等[15]进行了较为深入的压缩感知成像研究; 周亚同等[16]研究了形态分量分析框架下基于DCT与曲波字典组合的地震信号重建。基于压缩感知的地震勘探数据采集方面, 关于观测系统设计和野外采集方面的文献相对较少; MOLDOVEANU[17]于2010年在海上利用随机观测方法采集数据; HENNENFENT等[18]提出了基于随机抖动的欠采样方案, 控制了相邻测点之间的最大距离, 便于野外施工; MOSHER等[19]提出并完善了一种在观测系统设计中基于约束条件的更优选择激发点和接收点位置的非均匀采样方法, 设计了非均匀优化采样观测系统, 并进行了海上和陆上数据采集, 通过数据重建, 取得了良好的效果; LEO等[20]于2015年在阿拉斯加陆上冰雪覆盖区用可控震源作为激发震源, 稀疏非规则三维观测系统采集, 通过数据重建, 获得了较常规采集更好的高密度地震成像资料。国内相关学者和地球物理工作者在理论和数值模拟方面开展了一些研究, 取得了不少认识, 如王华忠等[21]探讨了压缩感知技术基础理论方法、应用于地震勘探中面临的问题与难题、可行的应用方案及效果预期等; 崔永福等[22]研究了一种基于局部数据规则化的相干噪声压制技术, 通过在不规则观测系统局部区域利用五维插值技术求取最优解重建规则道集, 使噪声满足相干的假设条件, 从而实现去噪; 陈生昌等[23]设计了地震数据采集稀疏观测系统, 并进行了模型数据模拟和重建; LIN等[24]用压缩感知设计同步采集方法; 马坚伟等[25]综述了压缩感知的基本概念及其在地球物理勘探中的最新应用进展, 包括地震数据不规则采集、处理、成像、反演的新理论和新技术; 周松等[26]给出了较系统的技术解决方案, 设计了块状非规则观测系统, 进行了模拟验证; 舒国旭等[27]进一步给出了基于压缩感知的数据重建方案。总之, 目前国外在沙漠和海上只是采用激发点随机设计, 接收点大都是规则的采集方案; 国内主要停留在室内数据模拟和重建, 实际基于压缩感知的地震数据采集工作尚未见到相关报道。
本文在周松等[26]和舒国旭等[27]工作的基础上, 重点介绍了在中国西部沙漠某工区基于压缩感知的地震数据采集的实践及成果。在简要介绍压缩感知理论的基础上, 先阐述了基于压缩感知的地震数据采集观测系统设计的方法理论及实施步骤, 然后重点介绍了在该工区基于压缩感知的地震数据采集的实施情况并分析了应用效果。
1 压缩感知概述压缩感知理论包含3个层面:数据信号的稀疏表达、非相关的观测矩阵、非线性优化的数据重建。基于压缩感知理论, 高密度信号的恢复是通过采集得到的、包含了信号全部信息的、有限个选择的压缩数据, 来解一个某种范数下高度非线性的优化问题, 即使在不满足尼奎斯特采样定理要求的情况下, 仍然可以从压缩观测的数据中高概率地恢复原始信号。
实现压缩感知数据采集重建需要三步完成:
第一步重建数据x的稀疏采集:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} x}} $ | (1) |
式中: y代表采集的数据; x表示待恢复估计的数据; Φ表示随机采样矩阵。一般地, x向量的维数通常大于采集数据向量y的维数, 稀疏采集是一个数据降维的过程。
第二步重建数据x的稀疏表达: x在某个域内表现是稀疏的, 其稀疏变换为:
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{ \boldsymbol{\varPsi} s}} $ | (2) |
(2) 式中s即为x在变换域Ψ的稀疏系数。实际应用中通常采用傅里叶变换、小波变换、曲波变换、Radon变换等来稀疏表示地震数据。
第三步数据x的重建:
将方程(2)代入方程(1)可以写为:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} s}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varPsi} s}} $ | (3) |
式中: Θ为压缩感知矩阵。由于s是稀疏的, 使得该欠定方程有解。
实际数据y中往往包含信号和噪声两部分。数学上, 基于随机采样数据y估计稀疏表达系数向量s是一个稀疏反演问题。即:
| $ {\rm{min}}{\left\| \mathit{\boldsymbol{S}} \right\|_{\rm{P}}}约束于\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{ \boldsymbol{\varTheta} s}}} \right\| \le \varepsilon $ | (4) |
求解上述反问题, 估计出稀疏表达系数向量s后, 可以由(5)式恢复待重建的规则信号x。
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{ \boldsymbol{\varPsi} s}} $ | (5) |
根据压缩感知理论, 要实现压缩数据的精确重建必须满足观测矩阵的不相关性, 即:观测矩阵与变换矩阵不具备相关性, 具体为感知矩阵列向量的不相关性, 或者是感知矩阵列向量最大互相关值要足够小, 最优满足该条件的观测矩阵就是最佳的。
2.1 方法理论结合周松等的理论[26], 假设真实信号为x, 采用变换矩阵Ψ得到稀疏信号s, 可以得到公式(2)所示的表达式, 若采样矩阵Φ为单位矩阵I抽出的若干行组成的矩阵, 则有采样数据:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} x}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varPsi} s}} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} s}} $ | (6) |
式中: Θ = ΦΨ记为感知矩阵, 其列向量为Θi。列向量间的最大互相关值为:
| $ \mu = \mathop {{\rm{max}}}\limits_{i \ne j} \frac{{\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{\rm{H}} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_j}} \right|}}{{({{\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i}} \right\|}_2} \cdot {{\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_j}} \right\|}_2})}} $ | (7) |
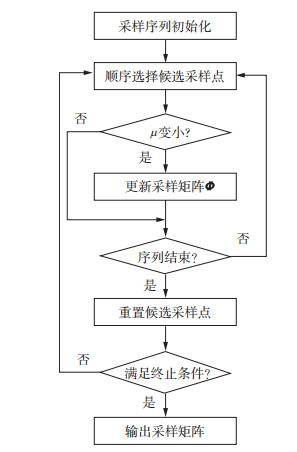
可以证明[26], 感知矩阵列向量间的最大互相关值即为非规则采样归一化频谱的最大非零频率振幅, 也就是因为非规则破坏稀疏基的正交性所引起的最大频率泄露。根据压缩感知理论, μ越小, 则信号在非规则采样后能够重建的概率就越高。为此, 我们采用贪心序贯算法(图 1)来优化采样点的位置, 通过改变非规则采样点的分布来降低最大互相关值, 进而构建采样矩阵:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = {\rm{argmin}}\;\mu $ | (8) |
|
图 1 贪心序贯算法示意流程 |
设计观测系统炮检点时, 对目标数量的随机采样点进行归一化傅里叶谱计算, 在压制假频的同时, 注意防止频率泄露, 以确保优化后的随机非规则采样在去假频程度上能够无限逼近规则充分采样时的去假频效果。
2.2 观测矩阵的设计步骤按照以上方法, 采用贪心序贯算法即逐个点增加的方式来确定检波点以及炮点的位置并构建观测矩阵。具体步骤如下:
1) 确定最终需要达到的目标采样密度以及稀疏采样的检波点、炮点的最大最小间距, 根据不同稀疏程度需求确定总的检波点数和炮点数, 再进行点位非规则设计;
2) 逐个加入采样点, 并计算加入采样点之后观测矩阵的最大互相关值。如果加入采样点使得最大互相关值变大, 需重新选择采样点位置, 直到加入该采样点使得最大互相关值最小时接受该采样点;
3) 重复步骤2)的计算与采样点位置的选取, 直到达到预先规定的采样点数;
4) 当检波点和炮点的位置初步确定之后, 进一步采用Jitter方法, 以(8)式为目标, 继续优化检波点、炮点的位置, 并最终确定观测矩阵。
2.3 观测系统设计根据上述设计步骤, 首先, 需要确定重建后规则化数据要达到的空间采样密度值。根据工区以往高精度拟确定的重建面元网格为15 m×15 m, 其检波点重建目标为44(线)×486(道/线), 重建线距为180 m, 重建道距为30 m, 炮点重建目标为7 888炮(炮线距90 m, 炮点距30 m)。
其次, 确定野外稀疏采样物理点的数量。根据工区以往地震资料信噪比的分析认为, 工区属于高信噪比地区, 确定采用重建目标一半左右的接收点进行接收和接近重建目标四分之一的激发点进行激发。根据实际运算, 具体的接收点数量为33(线)×365(道/线), 激发点为1 760炮。
第三步, 确定布设检波点和接收点位置的约束条件。为了保证采样的适当均匀, 避免出现较大的采集资料空白区, 需要对采样点进行适当约束, 同时, 也要考虑有线仪器的排列限制, 以及采集链长度的影响。最终确定约束条件为:接收点沿排列线方向道距控制在15~50 m、接收线距控制在60~540 m; 炮点距在排列方向控制在30~360 m, 垂直排列方向控制在15~90 m。
第四步, 计算采样点位置。根据确定的稀疏采样点数和约束条件, 按照公式(8)分别计算炮点、检波点位置的最大互相关值, 再根据公式(9)不断优化炮点、检波点位置, 当最大相关值为最小时, 即为最终的炮点、检波点位置。
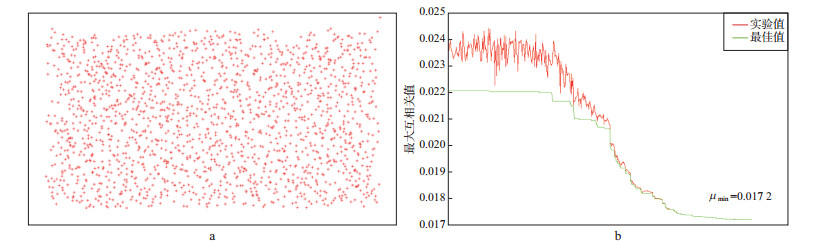
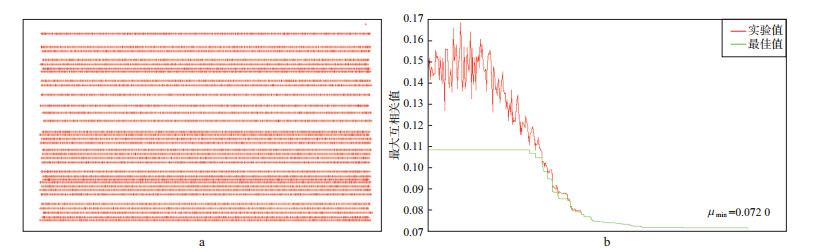
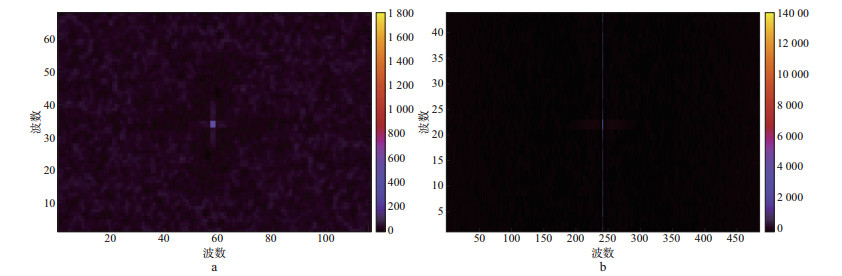
图 2显示了计算的炮点分布与其最大互相关值的收敛曲线, 可以看出, 炮点的最大互相关值最小可以达到0.017 2, 相关性非常低。图 3显示了检波点分布及其最大互相关值收敛曲线, 由于受接收线的限制, 其最大互相关值要比炮点大一些, 最小值仍可以达到0.072 0。炮点位置的频谱归一化后最大互相关值为0.046 7(如图 4a), 检波点位置的频谱归一化后最大互相关值为0.093 0(如图 4b)。综合炮检点布设结果, 最终确定的观测系统如图 5所示的块状观测系统, 每个炮点激发时, 所有检波点同时接收。
|
图 2 优化设计的非规则炮点分布(a)及最大互相关值收敛曲线(b) |
|
图 3 优化设计的非规则检波点分布(a)及最大互相关值收敛曲线(b) |
|
图 4 优化设计的非规则观测系统频谱 a 炮点; b 检波点 |

|
图 5 优化设计的非规则观测系统 |
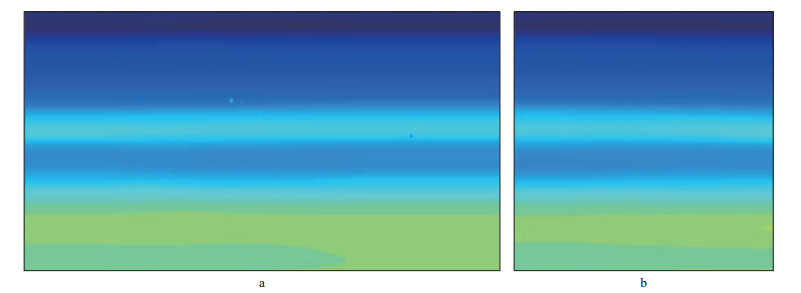
为了对设计的观测系统做进一步的分析验证, 建立了工区的速度模型(图 6), 并在模型上增加了一些不同尺度的溶洞, 如图 6a中的亮点和暗点, 利用前文设计的非规则观测系统进行正演模拟并分析验证。图 7a是486道接收、30 m道距规则采样的模拟记录, 图 7b是365道、15~75 m非规则道距采样的模拟记录, 图 7c是压缩感知规则化数据重建的结果, 图 7d是图 7a与图 7c的差值, 通过稀疏采样及重建前后模拟对比可以看出, 设计的观测系统能够较好地重建出高密度采样的数据。
|
图 6 工区速度模型剖面 a 沿排列方向; b 垂直排列方向 |

|
图 7 正演模拟、数据重建及其误差 a 486道接收(30 m道距)规则采样模拟记录; b 365道(15~75 m道距)接收不规则道距采样模拟记录; c 利用压缩感知规则化数据重建方法对图 7b进行数据重建的记录(486道, 30 m道距); d 图 7a与图 7c之间的差值 |
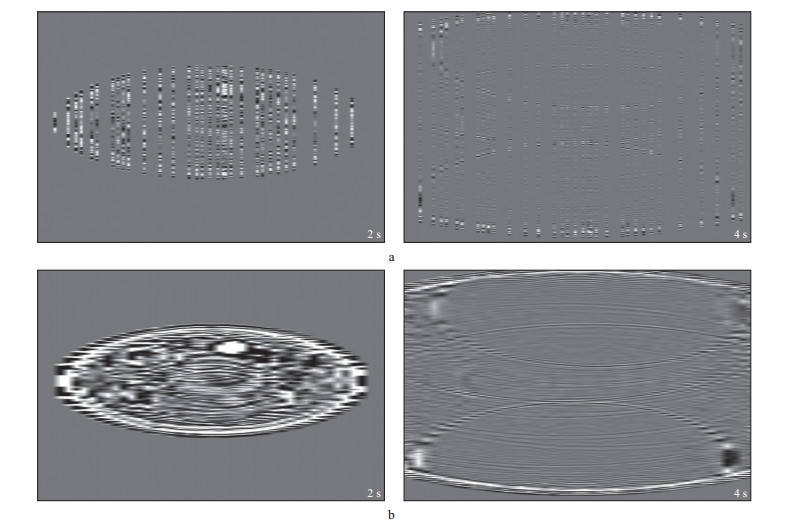
图 8展示了模拟的非规则稀疏采样和重建的高密度规则数据分别在2 s和4 s时的水平切片, 可以看出, 非规则稀疏采样能够较好地重建出高密度采样规则数据, 从2 s的数据切片上能够清晰地反应出模型上的溶洞(亮点和黑点的位置)。
|
图 8 非规则稀疏采样模拟记录(a)和重建数据水平切片(b) |
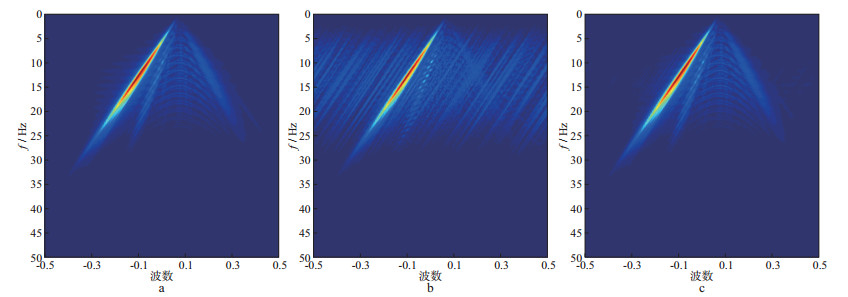
图 9显示了规则高密度采集、非规则稀疏采集和对应的重建数据F-K谱, 可以看出, 重建数据较好地去除了非规则采样产生的假频, 达到了与规则高密度采样相当的效果。通过以上模拟数据测试认为, 文中提出的非规则稀疏观测系统通过压缩感知方法, 能够较好地重建出规则高密度数据, 能够较好地在数据切片上反映模型中的缝洞体, 可以用于野外数据采集。
|
图 9 规则高密度采集(a)、非规则稀疏采集(b)以及对应的稀疏重建数据(c)的F-K谱 |
采用前文设计的观测系统在工区实施了非规则观测地震数据采集, 主要步骤如下。
1) 物理点位的定位。将不规则(随机)的物理点位落实到具体的大地位置, 利用GPS进行物理点位定位, 与规则点位定位方法类似, 不会带来较大的困难, 尤其检波点是在一条线上, 只是检波点距不均匀, 相对实施起来要比激发点更容易些。
2) 布设排列, 埋置检波器。道距在15~50 m之间, 检波点的位置与大线接头之间的距离太大时, 需要采用加长线将检波器与大线连接起来; 每道检波器两串24个检波器, 沙漠中挖坑埋置检波器; 共有12 045道接收。
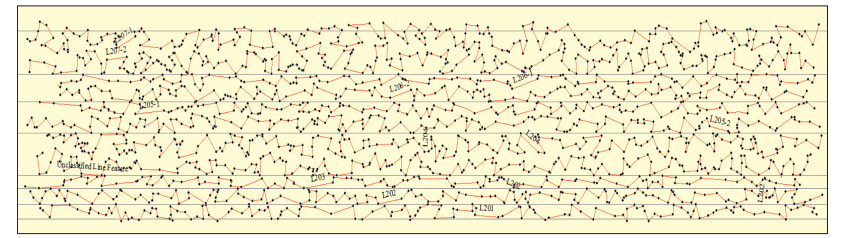
3) 可控震源耦合激发。激发点的随机分布造成了一定的布设难度。可控震源激发需要推土机将沙漠推平或沿着激发点推出一条路, 一是方便震源车的移动, 二是提高激发震板与沙漠间的耦合。由于激发点随机分布, 点距在15~90 m之间, 推路的目的是将激发点连接起来(见图 10), 且保证震源车组合中点较好地与激发点吻合, 这一点比规则激发点时困难得多。
|
图 10 实际施工的非规则炮点分布(黑点为炮点, 红线为可控震源移动轨迹) |
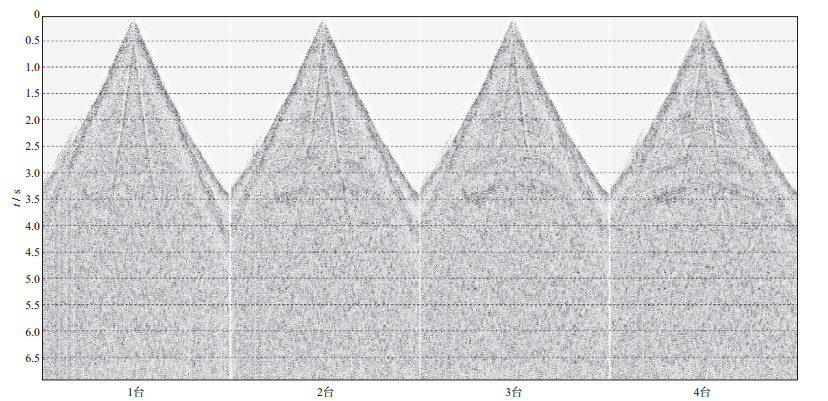
4) 激发因素试验。分别进行了不同震源台数的试验, 图 11所示是1至4台组合震源单次激发试验记录, 通过分析, 采用了2台1次的激发方式。
|
图 11 不同震源台数单次激发30~60 Hz扫描记录对比 |
采用上文设计的非规则采样观测系统和2台1次的激发参数, 完成了野外1 760炮的地震数据采集。为了便于参照和对比, 排列中增加了一条单点高密度检波线, 2 880道接收, 5 m道距, 与其它33条排列线同时接收, 总道数合计14 925道。
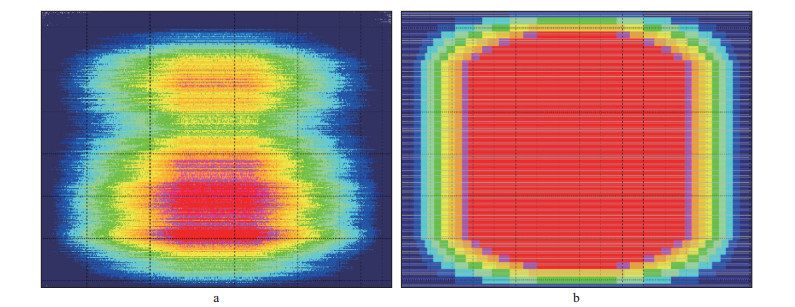
4 效果分析采用前文所述非规则观测系统进行地震数据采集, 本次采集实际资料三维面积约60 km2, 覆盖次数超过100次的面积约为22 km2。图 12a显示了稀疏非规则采集的覆盖次数分布情况, 可以看出, 覆盖次数分布非常不均匀。利用压缩感知技术, 对去噪后的数据进行重建, 得到了检波线距180 m, 检波点距30 m, 炮点距30 m, 炮线距90 m的规则化数据体, 数据重建后的覆盖次数分布情况如图 12b所示, 规则化后的满覆盖次数超过400次, 覆盖次数分布均匀, 满覆盖面积约47 km2。
|
图 12 压缩感知非规则采集覆盖次数分布(a)与重建后的覆盖次数分布(b) |
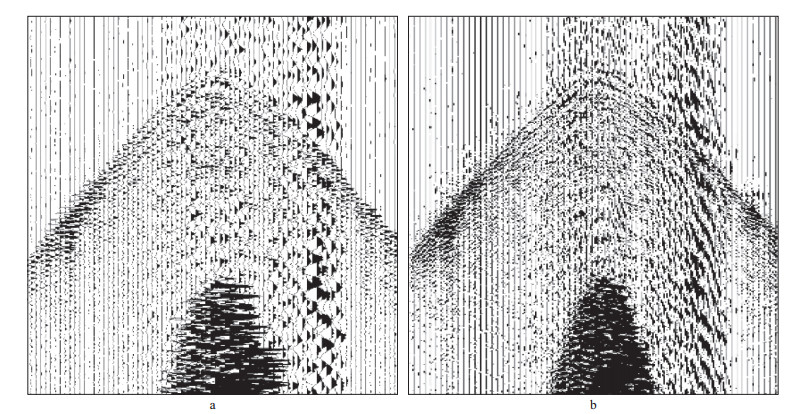
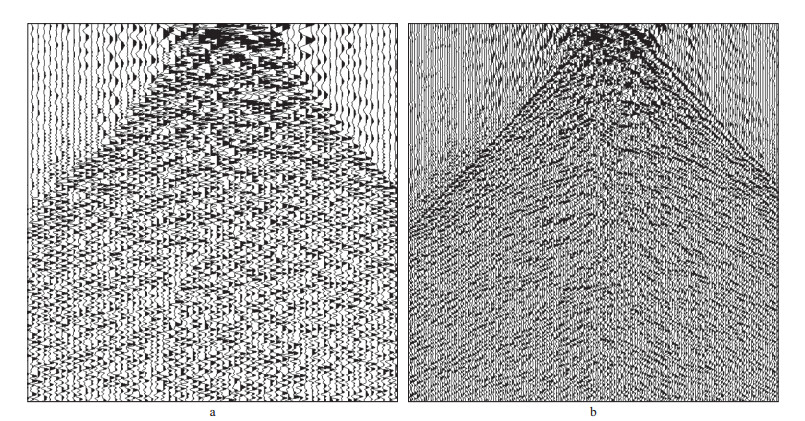
由于野外地震资料采集采用多组可控震源交替激发, 震源车移动对单炮记录产生了较大的干扰, 数据重建前如果不进行去噪处理, 会对重建结果产生比较大的影响。图 13对比了未去噪重建前后的远排列单炮记录, 可以看出, 用去噪前(图 13a)单炮记录进行数据重建, 重建记录(图 13b)上的可控震源移动噪声能量也得到一定程度的加强, 使重建效果不理想。对去噪后的单炮数据(图 14a)进行重建, 得到的记录(图 14b)效果改善明显。
|
图 13 未去噪重建前(a)、后(b)单炮记录对比 |
|
图 14 去噪后重建前(a)、后(b)单炮记录对比 |
对重建数据进行叠前时间偏移处理, 得到的三维偏移剖面(图 15)与同位置的井炮激发规则采集高精度三维地震剖面(图 16)及可控震源激发规则高密度二维剖面(图 17)进行对比, 可以看出, 重建的规则化剖面资料要好于规则高精度采集剖面, 层间的信息更加丰富; 与高密度二维剖面相比, 二者面貌和内部信息相当。

|
图 15 TFT南地区压缩感知三维采集重建数据叠前时间偏移剖面(重建面元为7.5 m×7.5 m) |

|
图 16 TFT南地区规则采集高精度三维叠前时间偏移剖面(15 m×15 m面元采集) |

|
图 17 TFT南地区规则高密度二维叠前时间偏移剖面(5 m线元采集) |
本文基于压缩感知的地震勘探采集技术首次成功应用于中国西部沙漠地区的野外地震数据采集, 获得了非规则稀疏采样下的地震数据, 为后续高密度数据重建研究提供了宝贵的实际资料。通过稀疏非规则数据的重建, 得到的偏移剖面达到了高密度采集数据偏移剖面的品质, 取得了较好的效果, 形成了完整的技术系列, 具备了实际应用的水平和能力。通过本文研究探索, 得出以下结论:
1) 非规则观测方式在野外的实施, 对于沙漠地区可控震源施工需要推路, 这会造成一些困难, 但若采用炸药震源, 则不会对野外施工带来困难; 也就是非规则的观测系统在野外不会给施工造成太大的影响;
2) 压缩感知地震数据采集技术, 可以大大减小野外采集的工作量, 降低地震勘探的成本, 且数据重建结果接近于高密度采集的效果, 提高了地震成像的精度;
3) 由于本次采用的是有线地震仪器, 因而制约了检波点布设, 不能设计更加理想的观测点位; 如果采用“节点仪器+压缩感知+可控震源”的组合方式, 将会取得更高的效益和更好的效果。
通过本次试验研究, 压缩感知地震勘探技术在沙漠地区取得了较好效果, 这种非规则的观测系统对于东部复杂障碍区的地震数据采集具有借鉴意义。另外, 还可以采用规则检波点接收和随机激发点激发的组合方式, 这样既采用了灵活的激发点位, 又降低了数据重建的难度, 是一种较好的应用方式。随着基于压缩感知的非规则数据采集技术的不断探索和发展, 必将带来较大效益和较好的效果。
致谢: 感谢中科院地质与地球物理研究所和中石化休斯顿研究开发中心相关人员在这项研究中的大力支持!| [1] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [2] |
CANDES E J, WAKIN M B. An introduction to compressive sampling:A sensing/sampling paradigm that goes against the common knowledge in data acquisition[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30. DOI:10.1109/MSP.2007.914731 |
| [3] |
HERRMANN F J. Randomized sampling and sparsity:Getting more information from fewer samples[J]. Geophysics, 2010, 75(6): :WB173-WB187. DOI:10.1190/1.3506147 |
| [4] |
HERRMANN F J., WANG D L, Hennenfent G, et al. Curvelet-based seismic data processing:A multiscale and nonlinear approach[J]. Geophysics, 2008, 73(1): A1-A5. |
| [5] |
白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报, 2014, 57(9): 2937-2945. BAI L S, LIU Y K, LU H Y, et al. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics, 2014, 57(9): 2937-2945. |
| [6] |
CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [7] |
WU R, WU B, GENG Y.Imaging in compressed domain using dreamlets[R]. Beijing 2009 International Geophysical Conference and Exposition, 2009: 212 https://www.researchgate.net/publication/268585252_Imaging_in_compressed_domain_using_dreamlets
|
| [8] |
NAGHIZADEH M, SACCHI M D. On sampling functions and Fourier reconstruction methods[J]. Geophysics, 2010, 75(6): WB137-WB151. DOI:10.1190/1.3503577 |
| [9] |
LI C B, CHALES C, MOSHER, et al. Interpolatated compressive sensing for seismic data reconstruction[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg, 2012, 6-12. |
| [10] |
张良, 韩立国, 刘争光, 等. 基于压缩感知和Contourlet变换的地震数据重建方法[J]. 石油物探, 2017, 56(6): 804-811. ZHANG L, HAN L G, LIU Z G, et al. Seismic data reconstruction based on compressed sensing and Contourlet transform[J]. Geophysical Prospecting for Petroleum, 2017, 56(6): 804-811. DOI:10.3969/j.issn.1000-1441.2017.06.005 |
| [11] |
冯飞, 王征, 刘成明, 等. 基于Shearlet变换稀疏约束地震数据重建[J]. 石油物探, 2016, 55(5): 682-691. FENG F, WANG Z, LIU C M, et al. Seismic data reconstruction based on sparse constraint in the Shearlet domain[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 682-691. DOI:10.3969/j.issn.1000-1441.2016.05.007 |
| [12] |
王升超, 韩立国, 巩向博. 基于各向异性Radon变换的叠前地震数据重建[J]. 石油物探, 2016, 55(6): 808-815. WANG S C, HAN L G, GONG X B. Prestack seismic data reconstruction by anisotropic Radon transform[J]. Geophysical Prospecting for Petroleum, 2016, 55(6): 808-815. DOI:10.3969/j.issn.1000-1441.2016.06.005 |
| [13] |
刘争光, 韩立国, 张良, 等. 压缩感知理论下基于快速不动点连续算法的地震数据重建[J]. 石油物探, 2018, 57(1): 50-57. LIU Z G, HAN L G, ZHANG L, et al. Seismic data reconstruction using FFPC algorithm based on compressive sensing[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 50-57. DOI:10.3969/j.issn.1000-1441.2018.01.007 |
| [14] |
屠宁. 基于压缩感知的快速最小二乘逆时偏移[J]. 石油物探, 2018, 57(1): 86-93. TU N. Fast least-squares reverse-time migration via compressive sensing[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 86-93. DOI:10.3969/j.issn.1000-1441.2018.01.012 |
| [15] |
MOSHER C C, KESKULA E, KAPLAN S T, et al. Compressive seismic imaging[J]. Expanded Abstracts of 82nd SEG Annual Internat Mtg, 2012, 1-5. |
| [16] |
周亚同, 刘志峰, 张志伟. 形态分量分析框架下基于DCT与曲波字典组合的地震信号重建[J]. 石油物探, 2015, 54(5): 560-568, 581. ZHOU Y T, LIU Z F, ZHANG Z W. Seismic signal reconstruction under the morphological component analysis framework combined with DCT and Curvelet dictionary[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 560-568, 581. DOI:10.3969/j.issn.1000-1441.2015.05.009 |
| [17] |
MOLDOVEANU N. Random sampling:a new strategy for marine acquisition[J]. Expanded Abstracts of 80th SEG Annual Internat Mtg, 2010, 51-55. |
| [18] |
HENNENFENT G, HERRMANN F J. Simply denoise:wavefield reconstruction via jittered undersampling[J]. Geophysics, 2008, 73(3): V19-V28. DOI:10.1190/1.2841038 |
| [19] |
MOSHER C C, KAPLAN S T, JANISZEWSKI F D. Non-uniform optimal sampling for seismic survey design[J]. Expanded Abstracts of EAGE Annual Conference, 2012, 77-84. |
| [20] |
LEO B, MOSHER C C, LI C B, et al. Application of compressive seismic imaging at Lookout Field, Alaska[J]. Expanded Abstracts of EAGE Annual Conference, 2017, 670-676. |
| [21] |
王华忠, 冯波, 王雄文, 等. 压缩感知及其在地震勘探中的应用[J]. 石油物探, 2016, 55(4): 467-474. WANG H Z, FENG B, WANG X W, et al. Compressed sensing and its application in seismic exploration[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 467-474. DOI:10.3969/j.issn.1000-1441.2016.04.001 |
| [22] |
崔永福, 郭念民, 吴国忱, 等. 不规则观测系统数据规则化及其在相干噪声压制中的应用[J]. 石油物探, 2016, 55(4): 524-532. CUI Y F, GUO N M, WU G C, et al. Regularization of irregular geometry seismic data and its application in the coherent noise suppression[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 524-532. DOI:10.3969/j.issn.1000-1441.2016.04.007 |
| [23] |
陈生昌, 陈国新, 王汉闯. 稀疏性约束的地球物理数据高效采集方法初步研究[J]. 石油物探, 2015, 54(1): 24-35. CHEN S C, CHEN G X, WANG H C. The preliminary study on high efficient acquisition of geophysical data with sparsity constraints[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 24-35. DOI:10.3969/j.issn.1000-1441.2015.01.004 |
| [24] |
LIN T T Y, HERRMANN F J. Designing simultaneous acquisitions with compressive sensing[J]. Expanded Abstracts of 71st EAGE Annual Conference, 2009, 4-9. |
| [25] |
马坚伟. 压缩感知走进地球物理勘探[J]. 石油物探, 2018, 57(1): 24-27. MA J W. Compressive sensing in geophysical exploration[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 24-27. DOI:10.3969/j.issn.1000-1441.2018.01.002 |
| [26] |
周松, 吕尧, 吕公河, 等. 基于压缩感知的非规则地震勘探观测系统设计与数据重建[J]. 石油物探, 2017, 56(5): 617-625. ZHOU S, LV Y, LV G H, et al. Irregular seismic geometry design and data reconstruction based on compressive sensing[J]. Geophysical Prospecting for Petroleum, 2017, 56(5): 617-625. DOI:10.3969/j.issn.1000-1441.2017.05.001 |
| [27] |
舒国旭, 吕公河, 吕尧, 等. 基于压缩感知的地震数据重建[J]. 石油物探, 2018, 57(4): 549-554. SHU G X, LV G H, LV Y, et al. Seismic data reconstruction based on compressive sensing[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 549-554. DOI:10.3969/j.issn.1000-1441.2018.04.008 |




