精准的层位信息是地震资料解释的基础, 是储层预测的重要依据。层位信息被广泛应用于各种地震处理方法中, 如速度分析和层析成像等, 但人工层位追踪需要巨大的人力成本, 且非常耗时, 影响了地震勘探的效率。因此, 开发一种稳定且高效的自动层位追踪技术对地震资料的处理和解释非常重要。
目前自动层位追踪的方法主要有三大类。第一类是基于相关的自动追踪技术, 主要利用第一代或第三代相干算法[1-2]。该方法通过道与道之间的相关性进行同相轴追踪, 其抗噪性和稳定性较好, 但计算量大, 而且当相邻层位存在相似波形时, 容易出现串层现象, 降低了结果的可靠性。第二类是基于人工神经网络的自动追踪技术, 由ALBERTS等[3]提出, 由于其在层位追踪中取得了较好的效果, 受到广泛关注[4-5], 但该技术需要大量的样本进行学习和训练, 计算量较大; 同时, 不同工区的地震数据具有不同的特征, 导致工区间不能共享学习。第三类是基于图像的自动追踪技术。HALE等[6]和NAEINI等[7]将结构张量应用于断层及层位识别, 利用一系列的方向滤波器, 提取特征方向, 进而获得层位发育的主方向。该方法计算效率高, 但当层位形态较复杂时, 会影响追踪结果的精度和稳定性。
本文利用希尔伯特变换对原始地震数据进行预处理, 降低假频和噪声的影响, 增强其信噪比和连续性, 进而提高结构张量算法估计角度信息的稳定性, 然后对角度信息进行预处理, 进一步改善角度信息的可靠性。在角度信息和一系列约束条件下, 沿层位发育方向进行双方向的层位匹配追踪, 获得优选结果。最后用理论沉积模型和实际数据进行了测试并与常规方法结果进行了对比, 以验证方法的稳定性和适应性。
1 方法原理 1.1 基于希尔伯特变换的数据预处理地震资料在采集过程中, 往往存在噪声干扰, 进而导致同相轴连续性弱和目的层位信噪比低等; 同时, 由于道间距较大等原因, 会出现空间假频现象。这些因素会降低结构张量估算角度信息的稳定性。为此, 利用希尔伯特变换进行预处理, 求取信号的包络, 提高数据的信噪比和同相轴连续性, 降低假频和噪声的影响, 再利用包络数据进行角度信息估计。
希尔伯特变换通常被用于时间域信号的处理, 这里采用基于希尔伯特变换的数据预处理技术对深度域成像剖面进行处理, 以提高剖面的连续性。深度域成像结果d(z)的希尔伯特变换为
| $ q\left( z \right) = d\left( z \right) + {\rm{i}}\tilde d\left( z \right) $ | (1) |
其深度域包络可表示为:
| $ I\left( z \right) = |q\left( z \right)| = \sqrt {{d^2}\left( z \right) + {{\tilde d}^2}\left( z \right)} $ | (2) |
包络数据突出了数据的低频信息, 可增强数据的连续性, 降低噪声及空间假频对结果的影响, 为角度信息的估计提供更好的基础数据。
1.2 结构张量算法在角度信息提取中, 常用的方法有结构张量算法、局部倾斜叠加和平面波分解法[8]等。就计算速度而言, 结构张量算法最优; 就分辨率而言, 结构张量算法虽然略低于局部倾斜叠加法, 但结构张量算法求取的是一个邻域内角度的平均值, 所以结果更光滑连续, 更利于同相轴稳定追踪[9]。所以, 我们选用结构张量算法进行角度信息提取, 同时, 为了提高其稳定性, 使用二维高斯函数进行迭代滤波处理, 并对其结果进行平滑处理, 以提高稳健性。最后采用WEICKER[10]提出的算子进行角度求取。
二维地震包络剖面可表示为一个M×N(M为地震道深度采样点, N为地震道数目)的矩阵I, 其某一元素的梯度向量为:
| $ \begin{array}{l} \mathit{\boldsymbol{G}}\left( {i, j} \right) = {[{I_x}\left( {i, j} \right), {I_z}\left( {i, j} \right)]^{\rm{T}}}\\ i = 1, 2, \cdots , M\;\;\;j = 1, 2, \cdots , N \end{array} $ | (3) |
式中:Ix(i, j)为剖面在x方向的梯度; Iz(i, j)为剖面在z方向的梯度。为了避免噪声等影响, VLIET等[11]提出了结构张量算法:
| $ \begin{array}{l} {\mathit{\boldsymbol{T}}_{\rm{S}}}\left( {i, j} \right) = \mathit{\boldsymbol{G}}\left( {i, j} \right) \times {\mathit{\boldsymbol{G}}^{\rm{T}}}\left( {i, j} \right) = \\ \;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {I_x^2\left( {i, j} \right)}&{{I_x}\left( {i, j} \right){I_y}\left( {i, j} \right)}\\ {{I_y}\left( {i, j} \right){I_x}\left( {i, j} \right)}&{I_y^2\left( {i, j} \right)} \end{array}} \right] \end{array} $ | (4) |
式中:TS(i, j)为点的结构张量。利用(4)式能消除局部平均的影响, 同时能增强同一方向的梯度矢量。进一步利用二维高斯函数((5)式)对结构张量进行滤波:
| $ \begin{array}{l} {T_{{\rm{S1}}}}_ = \left[ {\begin{array}{*{20}{c}} {{s_{11}}}&{{s_{12}}}\\ {{s_{12}}}&{{s_{22}}} \end{array}} \right] = \\ \;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{K_p} \cdot ({\mathit{\boldsymbol{I}}_\sigma })_x^2}&{{K_p} \cdot {{({\mathit{\boldsymbol{I}}_\sigma })}_x} \cdot {{({\mathit{\boldsymbol{I}}_\sigma })}_y}}\\ {{K_p} \cdot {{({\mathit{\boldsymbol{I}}_\sigma })}_x} \cdot {{({\mathit{\boldsymbol{I}}_\sigma })}_y}}&{{K_p} \cdot ({\mathit{\boldsymbol{I}}_\sigma })_y^2} \end{array}} \right] \end{array} $ | (5) |
式中:Kp=1/(2πρ2)·exp[-(x2+y2)/2ρ2]为二维高斯函数; ρ代表分析结构的邻域大小; Iσ=KσI为原始数据I经过高斯函数Kσ平滑后的结果; σ为标准方差。求解(6)式半正定矩阵TS1的最大特征向量即可获得方向信息:
| $ |\mathit{\boldsymbol{\lambda E}} - {\mathit{\boldsymbol{T}}_{{\rm{S1}}}}|\mathit{\boldsymbol{x}} = 0 $ | (6) |
其中, λ表示特征值向量; E为单位矩阵; x表示特征向量。特征值可解析表示为:
| $ {\lambda _{1, 2}} = \frac{1}{2}[{s_{11}} + \sqrt {{s_{22}} \pm {{({s_{11}} - {s_{22}})}^2} + 4{s_{12}}} ] $ | (7) |
定义结构一致性因子α和最大特征值向量的斜边距g为:
| $ \alpha = \sqrt {{{({s_{22}} - {s_{11}})}^2} + 4s_{12}^2} $ | (8) |
| $ g = \sqrt {{{({s_{22}} - {s_{11}} + \alpha )}^2} + 4s_{12}^2} $ | (9) |
进一步可得层位方向信息为[10]:
| $ v = \frac{{{s_{22}} - {s_{11}} + \alpha }}{{g + \varepsilon }} = \sin \theta $ | (10) |
| $ w = \frac{{2{s_{12}}}}{{g + \varepsilon }} = \cos \theta $ | (11) |
式中:v, w为方向向量的两个标量; ε为平滑系数; θ为该层位点处地层的发育角度。平滑处理能够提高角度值求取的稳定性, 进一步降低层位突变和噪声的影响。
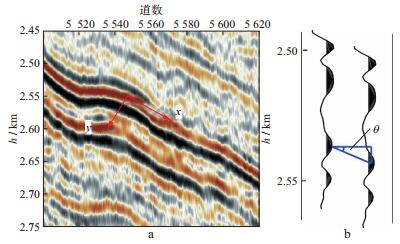
1.3 层位追踪HALE等[12]利用结构张量提取层位的主发育方向, 进而实现结构导向滤波。基于角度信息, 沿层位发育方向, 结合一系列约束条件进行层位追踪。如图 1所示, 首先在层位追踪的目的层处选定一个层位较清晰且同相轴较连续的点作为层位追踪的种子点, 然后对该种子点进行自动修正, 使其为准确的波峰点或波谷点。利用角度信息可确定该层位的相邻空间点位置, 由于层位的横向空间位置x可由数据道头获得, 因此层位追踪仅需获取层位的深度变化:
|
图 1 层位追踪示意 a角度方向示意; b角度导向示意 |
| $ {z_{j + 1}} = {z_j} + \Delta x \times \tan \theta $ | (12) |
式中:z为层位的深度值; Δx表示两道之间的间隔; θ为该层位点处地层的发育角度。为了提高相邻层位点的提取精度, 在上述计算的深度位置处沿深度方向取一定窗口, 优选层位结果。该深度时窗内的数据可表示为以下数据集合:
| $ \begin{array}{l} \{ I\left( {i - K/2, j + 1} \right), \cdots , I\left( {i, j + 1} \right), \cdots , \\ \;\;\;\;\;\;\;\;I\left( {i + K/2, j + 1} \right)\} \end{array} $ | (13) |
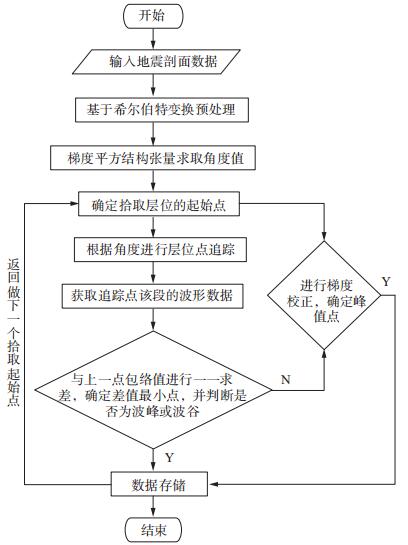
其中, I(i, j+1)为深度zj+1位置点对应的包络值, K为窗口长度。由于角度指向性强, 所以K值可相对较小(即小窗口数据), 它能有效缩短计算时间, 进而提高效率。在追踪层位时, 将上一层位点对应的包络值I(i, j)与窗口内地震数据集合进行一一求差, 选取差值最小点作为最终层位点。同时, 在层位追踪中, 通常沿波形的波谷或波峰(对应于数据中的极值点)进行追踪, 并进行点位自动修正, 使其为准确的波峰或者波谷点。在追踪波峰或波谷的一些特殊情况下, 还可加上额外的对比准则, 即将I(i, j)所对应的梯度信息G (i, j)与窗口内数据集的梯度信息进行一一对比, 选取包络值和梯度值差异最小的点作为最终层位点。层位自动追踪流程如图 2所示。
|
图 2 层位自动追踪流程 |
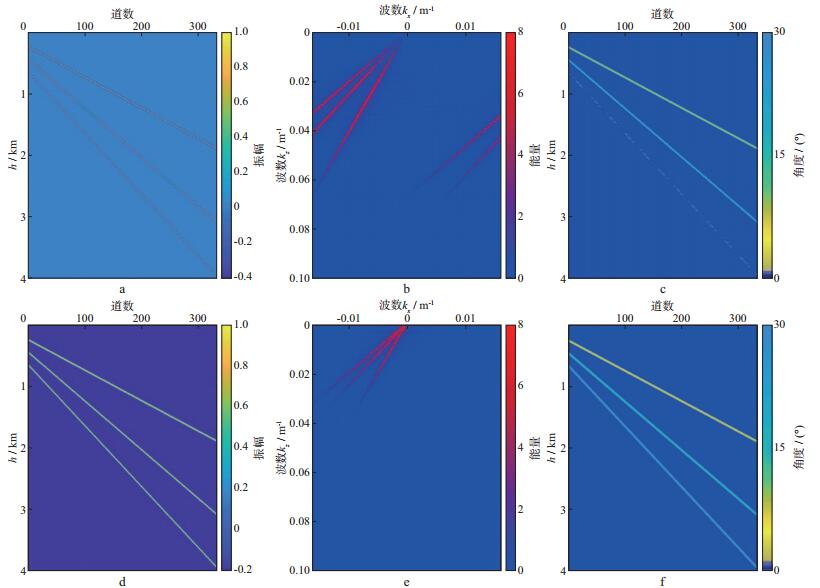
首先采用3层倾斜模型进行测试, 该模型深度域剖面如图 3a所示。3层的地层的倾斜度分别为10°, 15°和20°; 道间距为30 m, 水平距离为10 000 m; 深度采样间隔为10 m, 深度为4 000 m。道间距较大时会产生空间假频, 所以采用该模型来测试方法对假频的适应能力。对该模型原始数据进行频谱分析, 结果如图 3b所示, 可以看出, 该数据的空间假频明显。对原始数据进行角度提取, 结果如图 3c所示, 可以明显看出, 在倾斜层处角度提取结果不稳定。
|
图 3 模型及频谱结果对比 a原始模型深度域剖面; b原始剖面频谱; c原始剖面角度提取结果; d预处理后的模型深度域剖面; e经过变换后的剖面频谱; f预处理后剖面的角度提取结果 |
采用本文方法对原始数据进行处理, 结果如图 3d所示, 可以看出, 预处理后的数据连续性明显增强, 从其频谱(图 3e)可看出假频也被有效地消除。采用本文方法对预处理后的数据进行角度提取, 结果如图 3f所示。对比图 3c和图 3f可看出, 采用本文方法提取的角度结果更可靠。
再采用经典的深度域理论模型进行测试。该模型包含多种典型的地质特征, 如图 4a所示。由于理论模型数据不包含噪声, 为接近实际情况, 对该模型数据添加信噪比为0.3的高斯随机噪声, 如图 4b所示。经过预处理后, 数据的方向性和连续性均有所加强(图 4c)。从图 4中明显可以看出, 噪声导致同相轴不连续, 经过预处理后的数据连续性明显增强, 预处理后的数据与原始数据也有很好的一致性。
|
图 4 预处理前、后的理论沉积模型数据 a理论模型数据; b添加噪声后模型数据; c预处理后的模型数据 |
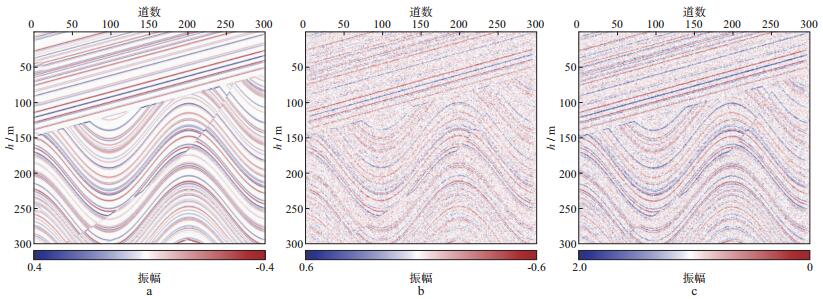
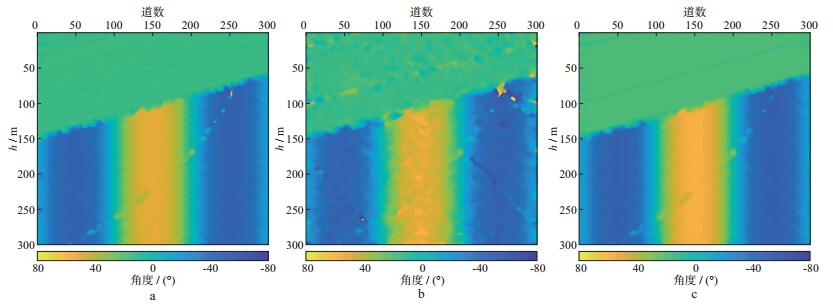
为进一步验证预处理的效果, 对图 4所示的3种数据分别进行角度提取, 结果如图 5所示。图 5a为对原始无噪数据进行角度提取的结果, 图 5b为对加噪后的模型数据进行角度提取的结果。相比于图 5a, 噪声的存在使得获取的角度有较大的误差, 并且存在不稳定现象。图 5c为对预处理后的模型数据进行角度提取的结果, 该结果与图 5a的结果具有高度一致性。经过预处理之后, 能够获得与无噪数据类似的角度估计结果, 说明该预处理方法有较强的抗噪性, 能够提高角度提取稳定性。
|
图 5 采用不同数据的角度提取结果 a原始数据; b加噪处理后的数据; c希尔伯特预处理后角度提取数据 |
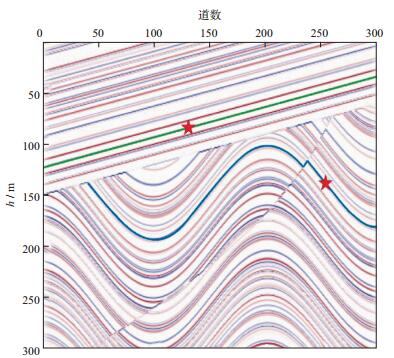
在该理论模型上选取两种地质特征的同相轴进行层位自动追踪, 结果如图 6所示, 图中, 红色五角星为在两种地质特征的同相轴上选取的种子点, 绿线为倾斜层位的追踪结果, 蓝线为褶皱层位的追踪结果。从图 6中可以看出, 层位追踪结果可靠, 特别是在有断层的地方, 能够准确地识别出断层的走向和位置。
|
图 6 理论沉积模型层位提取结果 |
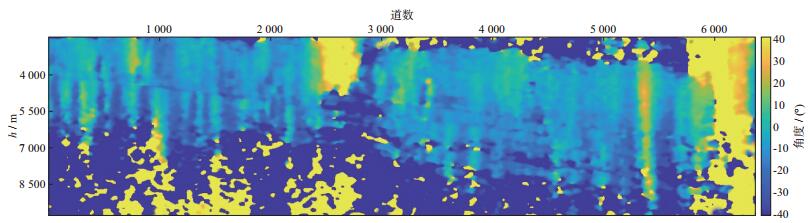
选取龙门山前陆盆地深层海相碳酸盐岩深度域叠后数据进行测试。龙门山前陆盆地海相地层主要为碳酸盐岩, 从震旦系到中三叠统, 其中缺失志留系、泥盆系和石炭系海相地层。图 7为该区原始地震剖面, 显示该区地震数据信噪比较低, 断层较多。在层位追踪时, 容易出现串层等现象, 追踪难度大。经过预处理后, 对该剖面进行角度提取, 结果如图 8所示, 可见, 提取的角度信息与构造角度吻合度较好, 断层在角度剖面上均有显示。

|
图 7 原始地震剖面 |
|
图 8 角度提取结果 |
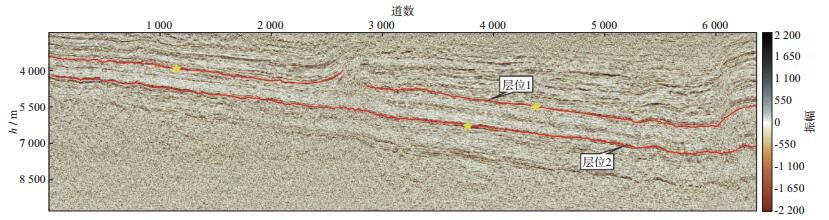
选取层位1和层位2作为目的追踪层位。采用本文方法的层位追踪结果如图 9所示, 图中黄色五角星为层位追踪的种子点。由于层位1的中间部分有较大的破碎带, 所以其种子点分别选在破裂带的两边。从图 9可以看出, 层位追踪结果与实际层位吻合度高。
|
图 9 层位追踪结果 |
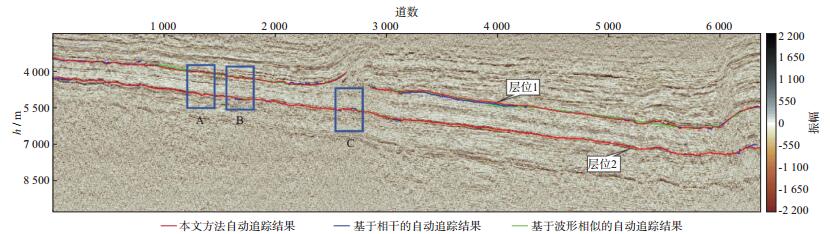
为了进一步检验层位追踪的结果, 将其与两种常用的层位自动追踪方法的结果进行了对比, 结果如图 10所示。基于相干的自动追踪方法利用相干算法在设定时窗范围中提取相关值最大的点作为层位点; 基于波形相似度的自动追踪方法通过衡量相邻地震道在时窗范围内的相似度, 同时加入断层等构造信息进行追踪。从图 10可以看出, 3种方法的结果基本相同。在使用方便程度方面, 本文方法仅需一个种子点进行追踪, 即可实现同相轴的双向追踪; 基于相干的自动追踪方法需给定追踪的方向和多个种子点; 基于波形相似的自动追踪方法也仅需一个种子点, 但当波形相似度变弱时会追踪停止, 在一些较大的断层区域, 追踪结果的连续性弱。
|
图 10 不同方法的自动追踪结果 |
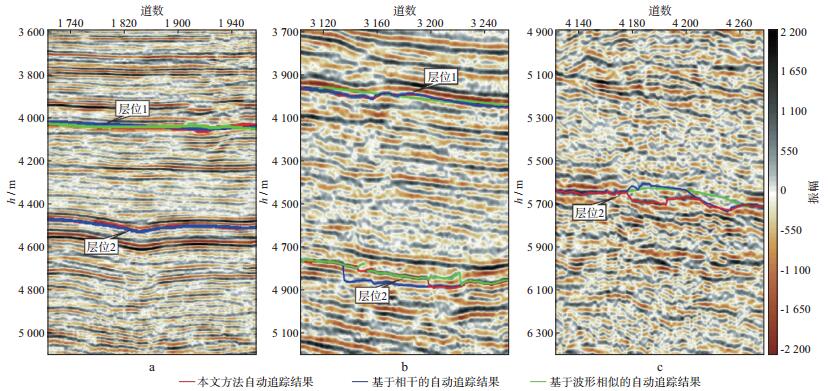
图 11为追踪结果的局部放大显示。从图 11a中可以看出, 层位1和层位2连续性好且信噪比高, 采用这3种方法都取得了较好的结果。图 11b中层位1发育一些小断层, 采用基于相干的方法时追踪结果出现串层现象, 采用基于相似度的方法时追踪结果未能在小断层处断开层位, 而采用本文方法能够很好地与断层信息相吻合; 层位2处的结果也显示采用本文方法的追踪结果更贴合层位的走势。图 11c为采用这3种方法在破碎带区域的追踪结果, 可以看出, 采用基于相干和基于相似度的两种方法的追踪结果出现明显的不贴合层位现象, 而采用本文方法的追踪结果在一定时窗内优选层位信息, 能够较好地贴合连续性强的层位信息, 为后续进一步修正层位信息提供依据。
|
图 11 不同方法自动追踪结果的局部放大显示 a区域A; b区域B; c区域C |
常用自动层位追踪算法通常存在稳定性不高且适应性不强的问题。本文结合结构张量算法, 提出了一种自动层位追踪方法。对地震剖面利用希尔伯特变换提取包络信息, 改善了结构张量方法求取方向信息的稳定性; 对结果进行经过高斯滤波和平滑等处理, 进一步提高角度信息的稳定度; 最后在角度信息和同相轴特征的约束下实现层位自动追踪。理论沉积模型及实际二维地震剖面数据的测试表明该方法结果相对稳定且与同相轴吻合度高。与基于相干和基于相似度的两种常用方法的对比结果表明, 本文方法在层位自动追踪中具有较高的稳定性。
| [1] |
BAHORICH M S, FARMER S L. 3-D seismic coherency for faults and stratigraphic features:the coherence cube[J]. The Leading Edge, 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [2] |
MARFURT K J, SUDHAKER V, GERSZTENKORN A, et al. Coherency calculations in the presence of structural dip[J]. Geophysics, 1999, 64(1): 104-111. DOI:10.1190/1.1444508 |
| [3] |
ALBERTS P, MOORFELD K. Artificial neural networks for simultaneous multi horizon tracking across discontinuities[J]. Expanded Abstracts of 61st EAGE Annual Conference, 1999, 6031-6034. |
| [4] |
HUANG K Y, CHANG C H, HSICH W S, et al.Cellular neural network for seismic horizon picking[C]//2005 9th International Workshop on Cellular Neural Networks and Their Applications.USA: IEEE, 2005: 219-222 http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1543200
|
| [5] |
张泉, 朱连章, 郭加树, 等. 地震DNA算法的改进及其在地震层位拾取中的应用[J]. 石油物探, 2017, 56(3): 400-407. ZHANG Q, ZHU L Z, GUO J S, et al. The improvement of seismic DNA algorithm and its application in automatic horizon pickup[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 400-407. DOI:10.3969/j.issn.1000-1441.2017.03.010 |
| [6] |
HALE D. Image-guided blended neighbor interpolation[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 1127-1131. |
| [7] |
NAEINI E Z, HALE D. Image and horizon-guided interpolation[J]. Geophysics, 2014, 80(3): V47-V56. |
| [8] |
穆立华, 杨国涛, 高文中, 等. 井震融合平面波分解地层倾角计算方法与应用[J]. 石油物探, 2017, 56(6): 820-826. MU L H, YANG G T, GAO W Z, et al. Formation dip calculation using plane-wave decomposition based on logging and seismic integration[J]. Geophysical Prospecting for Petroleum, 2017, 56(6): 820-826. DOI:10.3969/j.issn.1000-1441.2017.06.007 |
| [9] |
王宇翔, 杨锴, 杨小椿, 等. 基于梯度平方结构张量算法的高密度二维立体层析反演[J]. 地球物理学报, 2016, 59(1): 263-276. WANG Y X, YANG K, YANG X C, et al. A high-density stereo-tomography method based on the gradient square structure tensors algorithm[J]. Chinese Journal of Geophysics, 2016, 59(1): 263-276. |
| [10] |
WEICKER T J. Coherence-enhancing diffusion of colour images[J]. Image & Vision Computing, 1999, 17(3/4): 201-212. |
| [11] |
VLIET L J V, VERBEEK P W.Estimators for orientation and anisotropy in digitized images[R].Asci95 Proc First Conference of the Advanced School for Computing & Imaging, 1995: 442-450
|
| [12] |
HALE D. Structure-oriented bilateral filtering[J]. Expanded Abstracts of 81st Annual Internat SEG Mtg, 2011, 3596-3600. |
| [13] |
MARONI C S, QUINQUIS A, VINSON S. Horizon picking on subbottom profiles using multiresolution analysis[J]. Digital Signal Processing, 2001, 11(4): 269-287. DOI:10.1006/dspr.2001.0396 |
| [14] |
刘旭跃, 周巍, 张兵, 等. 一种基于图像学的地震层位自动追踪方法[J]. 物探化探计算技术, 2017, 39(1): 64-70. LIU X Y, ZHOU W, ZHANG B, et al. An automatic tracking method for seismic horizons based on image theory[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2017, 39(1): 64-70. DOI:10.3969/j.issn.1001-1749.2017.01.10 |
| [15] |
O'MALLEY S M, KAKADIARIS I A.Towards robust structure-based enhancement and horizon picking in 3-D seismic data[C]//Proceedings of the 2004 IEEE Computer Society Conference on.USA: IEEE, 2004: 1063-6919
|
| [16] |
王珂, 肖鹏峰, 冯学智, 等. 基于改进二维离散希尔伯特变换的图像边缘检测方法[J]. 测绘学报, 2012, 41(3): 421-427. WANG K, XIAO P F, FENG X Z, et al. The modified algorithm of image edge features detection hilbert transform[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 421-427. |
| [17] |
WU X M, HALE D. 3D seismic image processing for unconformities[J]. Geophysics, 2015, 80(2): IM35-IM44. DOI:10.1190/geo2014-0323.1 |
| [18] |
WU X M, HALE D. Horizon volumes with interpreted constraints[J]. Geophysics, 2015, 80(2): IM21-IM33. DOI:10.1190/geo2014-0212.1 |
| [19] |
张道兵, 张慧, 张正, 等. 一种稳健的道路主方向提取算法[J]. 光子学报, 2007, 36(增刊1): 326-330. ZHANG D B, ZHANG H, ZHANG Z, et al. Direction extraction method for road segment[J]. Acta Photonica Sinica, 2007, 36(S1): 326-330. |



