2. 油气资源研究院重点实验室, 中国科学院地质与地球物理研究所, 北京100029;
3. 中国石化石油工程地球物理有限公司胜利分公司, 山东东营257086;
4. 中国石化石油工程地球物理有限公司研发中心, 北京100020
2. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. Shengli Branch, Sinopec Geophysical Corporation, Dongying 257086, China;
4. Geophysical R & D Center, Sinopec Geophysical Corporation, Beijing 100020, China
“两宽一高”地震勘探可以大幅提高地震数据的覆盖次数和成像质量, 是未来地震勘探的重点发展方向。而地震采集需要在经济成本与数据质量之间进行权衡。传统采集方式是前一炮数据采集完成之后才进行下一炮的激发, 因而先后激发的炮之间的时间间隔较长。由于“两宽一高”的勘探方式需要进行高密度的炮检点排列, 因此, 若采用传统方式进行采集, 必然需要投入高昂的勘探成本。缩短采集周期、提高采集效率、降低采集成本, 成为野外地震数据采集的必然要求, 因此, 高效采集方式得到了广泛关注。
高效采集是通过缩短相邻炮之间的激发时间间隔来提高生产效率的一种野外数据采集方式。目前, 高效采集的震源激发方式主要有4种:交替扫描激发、滑动扫描激发、距离分离同步扫描激发和独立同步扫描激发[1]。这些采集方式, 通过缩短相邻震源激发的时间间隔, 提高了野外数据的采集效率。而独立同步扫描激发方式, 甚至无需考虑相邻炮的激发状态, 最大限度地提高了采集效率。
高效采集在提高采集效率的同时, 也给地震记录带来了严重的干涉炮能量干扰, 从而严重影响后续的数据处理, 因此, 需要对地震记录进行干涉炮噪声压制。目前, 对干涉炮噪声进行压制的方法主要有2类:基于噪声压制类的方法和基于稀疏反演类的方法。
基于噪声压制类方法的前提条件是地震信号的相干性。通常情况下, 对于独立同步扫描激发方式来说, 在原始炮集记录里, 干涉炮噪声和主炮信号类似, 具有较强的相干性。但是在其它道集, 比如共检波点道集、共偏移距道集或者共中心点道集, 干涉炮噪声则往往表现为随机噪声, 此时, 利用常规噪声压制方法, 便可对干涉炮噪声进行压制。HUO等[2]提出了利用矢量中值滤波进行干涉炮噪声压制的方法。在此基础上, CHEN[3]和王文闯等[4]分别提出了变窗口中值滤波和基于α-trimmed矢量中值滤波干涉炮能量压制的方法。HOOVER等[5]使用随机噪声衰减方法压制干涉炮噪声。MOORE等[6]和AKERBERG等[7]利用稀疏约束的拉冬变换实现了主炮信号与干涉炮噪声的数据分离; ZHANG等[8]采用加权τ-p变换的方法进行干涉炮噪声的压制; 曲英铭等[9]针对可控震源高效采集地震数据中的两种特征干扰噪声进行了噪声压制; 丁伟等[10]将高效地震采集技术应用于我国西部HS地区复杂山前带三维地震勘探, 有效提高了地震剖面的成像效果。
压制干涉炮噪声的另一大类方法是基于稀疏反演类的, WASON等[11]通过曲波域的L1范数稀疏反演进行了主炮信号与干涉炮噪声的分离; SPITZ等[12]和MAHDAD等[13]通过迭代方式对干涉炮能量进行估算, 并用自适应相减法实现干涉炮噪声的去除; ABMA等[14]将主炮信号的相干性作为约束条件进行反演, 取得了良好的信噪分离效果。
本文提出一种L1正则化和L0正则化混合迭代压制干涉炮噪声的方法。首先, 简单介绍了基于信号相干性的干涉炮噪声去除方法; 然后, 介绍了基于稀疏反演的干涉炮噪声去除方法, 利用实际资料干涉炮噪声的压制效果对比了2种方法的优劣; 最后, 采用稀疏反演方法对实际资料去噪结果进行叠加处理, 获得和常规采集相当的叠加结果, 但高效采集提高了效率, 从而降低了采集成本。
1 基于信号相干性的干涉炮噪声压制中值滤波法是一种有效压制随机噪声的信号处理方法, 其基本原理是把数字序列或数字图像中某点的值用该点的某个邻域中各点值的中值来代替, 从而压制随机噪声。矢量中值滤波为中值滤波的扩展, 下面介绍其定义。
假设一组矢量可表示为{Xi|i=1, 2, …, N}, 则对应地, 这组矢量的距离函数就可以表示为:
| $ \begin{array}{l} D({\mathit{\boldsymbol{X}}_j}) = \mathop \sum \limits_{i = 1}^N {\left\| {{\mathit{\boldsymbol{X}}_j} - {\mathit{\boldsymbol{X}}_i}} \right\|_l}\\ \;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{X}}_j} \in \{ {\mathit{\boldsymbol{X}}_\mathit{\boldsymbol{i}}}|i = 1, 2, \cdots , N\} \end{array} $ | (1) |
式中:l=0, 1, 2或∞, 本文中l取1和0。该组矢量的中值矢量Xm可以表示为:
| $ {\mathit{\boldsymbol{X}}_{\rm{m}}} = \mathop {\arg \min }\limits_{{\mathit{\boldsymbol{X}}_j}} D({\mathit{\boldsymbol{X}}_j}) $ | (2) |
基于矢量中值滤波的定义, 可以建立中值滤波器去除地震记录的干涉炮噪声。矢量元素可以通过在一个地震道内的滑动时窗获得。但矢量中值滤波需要有一个假设前提, 即地下反射界面是水平的。通常情况下, 这样的假设很难满足。因此, HUO等[2]提出了多方向的矢量中值滤波方法, 表示如下:
| $ \begin{array}{l} D[{\mathit{\boldsymbol{X}}_j}\left( p \right)] = \mathop \sum \limits_{i = 1}^N {\left\| {{\mathit{\boldsymbol{X}}_j}\left( p \right) - {\mathit{\boldsymbol{X}}_i}\left( p \right)} \right\|_l}\\ {\mathit{\boldsymbol{X}}_j}\left( p \right) \in \{ {\mathit{\boldsymbol{X}}_i}\left( p \right)|i = 1, 2, \cdots , N;p = {p_{\min }}, \cdots , {p_{\max }}\} \end{array} $ | (3) |
同样, 公式(3)中的中值矢量Xm(p)可以表示为:
| $ {\mathit{\boldsymbol{X}}_{\rm{m}}}\left( p \right) = \mathop {\arg \min }\limits_{{\mathit{\boldsymbol{X}}_j}\left( p \right)} D[{\mathit{\boldsymbol{X}}_j}\left( p \right)] $ | (4) |
式中:p代表倾角方向; Xj(p)为沿其中一个方向p的矢量。利用多方向的矢量中值滤波方法, 可以对干涉炮噪声进行有效压制。
2 基于稀疏反演的干涉炮噪声压制基于稀疏反演的干涉炮噪声压制方法, 通过地震记录的混叠延时数据构造混叠参数矩阵, 然后利用该矩阵将干涉炮噪声分离抽象成一个矩阵求解问题。由于混叠矩阵的逆往往不存在, 所以不能通过矩阵求逆直接得到干涉炮噪声压制后的地震数据, 而是将混叠参数矩阵的共轭转置与混叠数据矩阵的相乘结果作为反演初值进行迭代反演。由于该矩阵求解是一个欠定问题, 因此在求解的时候需要加上正则化条件进行约束反演。
对于不存在延迟时间的两个震源同时激发, 假设获得的地震记录S为:
| $ \mathit{\boldsymbol{S}} = {\mathit{\boldsymbol{S}}_1} + {\mathit{\boldsymbol{S}}_2} $ | (5) |
式中:S1, S2分别表示单一震源激发得到的地震记录。由于此方程欠定, 故存在多解性。如果引入时间延迟序列Γ, 便可得到方程组:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{S}} = {\mathit{\boldsymbol{S}}_1} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{S}}_2}\\ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}\mathit{\boldsymbol{S}} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}{\mathit{\boldsymbol{S}}_1} + {\mathit{\boldsymbol{S}}_2} \end{array} \right. $ | (6) |
上述方程组可简写为:
| $ \mathit{\boldsymbol{Fm}} = \mathit{\boldsymbol{\hat S}} $ | (7) |
式中:
建立目标函数:
| $ \mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{m}} \right) = \left\| {\mathit{\boldsymbol{Fm}} - \mathit{\boldsymbol{\hat S}}} \right\|_2^2 + \lambda \left\| {C\mathit{\boldsymbol{m}}} \right\| $ | (8) |
式中:C表示稀疏变换; λ表示拉格朗日乘子。
通常, 可采用L0和L1约束进行该目标函数的求取。本文采用L1正则化和L0正则化混合迭代的算法求解该目标函数, 完成干涉炮噪声的压制。首先, 应用软阈值迭代算法求解如下问题:
| $ \min \left\| {\mathit{\boldsymbol{Fm}} - \mathit{\boldsymbol{\hat S}}} \right\|_2^2 + \lambda {\left\| {C\mathit{\boldsymbol{m}}} \right\|_1} $ | (9) |
通过求解该问题, 可以为下一步的计算提供一个好的迭代初值, 并估计信号的稀疏水平。然后, 采用硬阈值迭代算法求解以下问题:
| $ \min \left\| {\mathit{\boldsymbol{Fm}} - \mathit{\boldsymbol{\hat S}}} \right\|_2^2 + \lambda {\left\| {C\mathit{\boldsymbol{m}}} \right\|_0} $ | (10) |
通过迭代反演, 直至获得最优的干涉炮噪声压制结果。
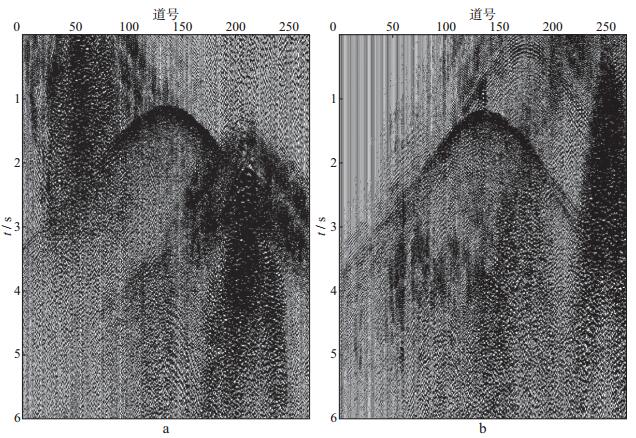
3 实际地震数据处理以西部沙漠某工区的三维可控震源分布式独立扫描高效采集地震数据为例。工区范围约200 km2, 设计20束段、151排炮, 总炮数为36 240炮, 共分12个区块进行可控震源的独立同步扫描。由于每个区块的震源扫描不考虑其它区块震源的工作状态, 因此干涉炮噪声成为影响地震记录质量的重要干扰。图 1为扫描信号与母记录相关后的某个排列的两炮地震记录, 对比有效信号和干扰的能量可以看出:干涉炮噪声能量强, 三角区噪声严重, 部分谐波干扰较强; 而有效信号较弱, 同相轴不够清晰连续, 部分同相轴被干涉炮噪声彻底淹没, 无法拾取初至走时。
|
图 1 可控震源独立同步扫描原始地震记录 a原始地震记录1; b原始地震记录2 |
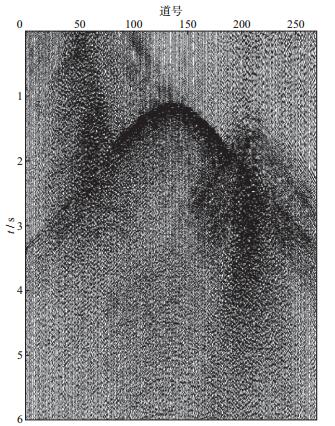
干涉炮噪声压制的主要流程:首先, 在共炮点道集对部分噪声进行压制; 然后, 将共炮点道集的地震记录分选为共接收点道集(或共中心点道集、共偏移距道集等), 在这些道集对干涉炮噪声做进一步压制; 最后, 将干涉炮噪声压制后的道集分选回共炮点道集, 获得最终干涉炮噪声压制后的结果。因此, 首先根据可控震源自主扫描获得地震记录的干涉炮噪声特征, 在共炮点道集对其进行压制, 同时一并去除三角区噪声、谐波干扰等噪声。图 1a所示的地震记录去噪后的结果如图 2所示。对比图 1a和图 2可以看出, 共炮点道集去噪后, 部分噪声得到了较为有效的压制, 但道集中还存在相当一部分的干涉炮噪声。
|
图 2 对图 1a地震记录进行共炮域去噪后的结果 |
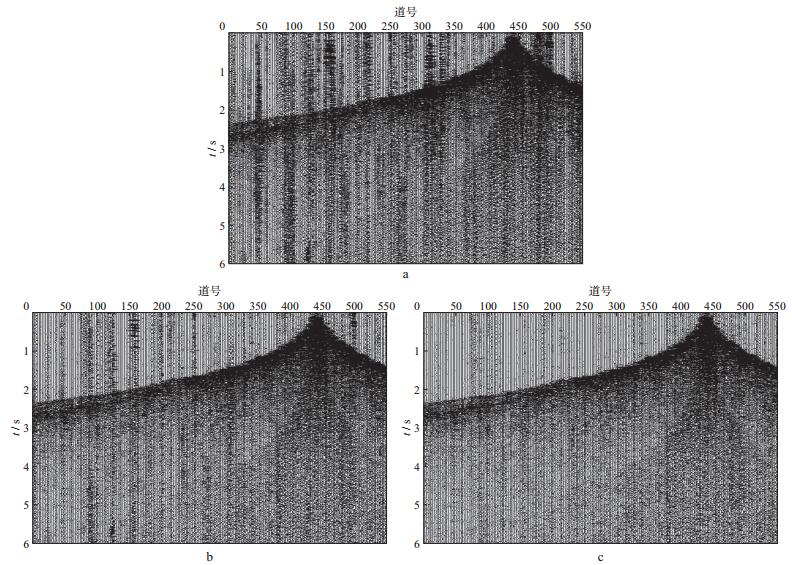
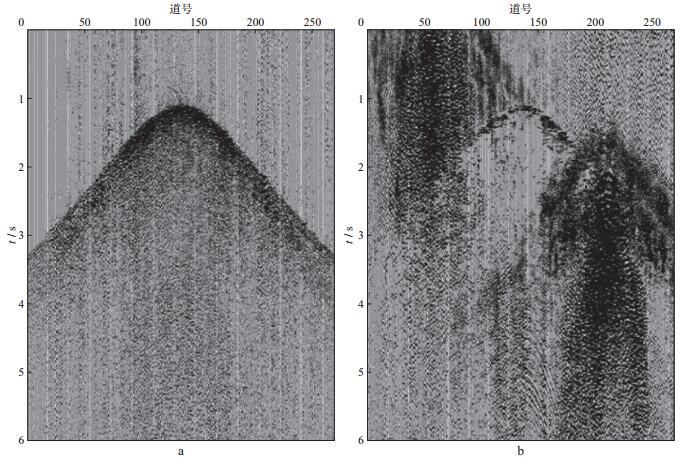
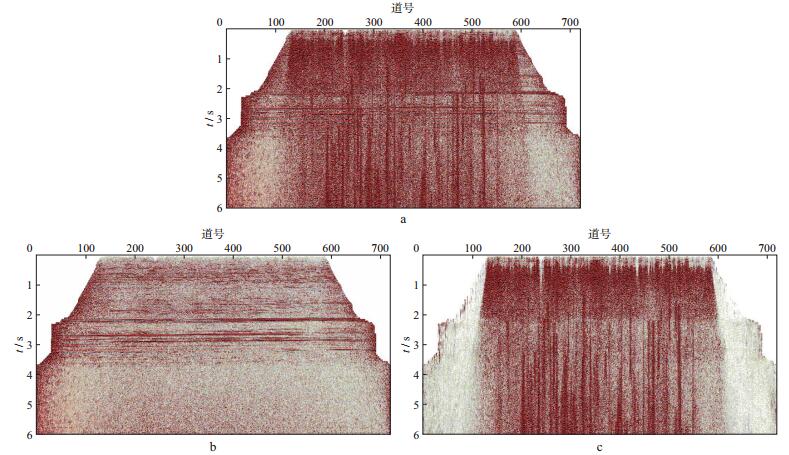
对去噪后的共炮点道集地震记录进行抽道集处理, 获得共中心点道集地震记录(图 3a)。分别采用基于信号相干性的矢量中值滤波干涉炮噪声压制方法和基于稀疏反演的干涉炮噪声压制方法, 对图 3a所示的共中心点道集地震记录进行干涉炮噪声压制, 结果如图 3b和图 3c所示。对比图 3b和图 3c可以看出, 在不伤害有效信号的情况下, 矢量中值滤波方法保留了较多的干涉炮噪声, 而基于稀疏反演的去噪方法可以将干涉炮噪声压制得比较干净, 其结果优于矢量中值滤波去噪的结果。经过在共炮点道集和共中心点道集两次去噪处理之后, 原始地震记录的干涉炮噪声基本上被压制。将共中心点道集的稀疏反演去噪结果分选到共炮点道集, 得到如图 4a所示的干涉炮噪声压制后的单炮地震记录(其去噪前记录见图 1a), 图 4b为去除的噪声。从图 4a可以看出, 干涉炮噪声得到了很好的压制, 并且去除的噪声(图 4b)中几乎不含有效信号。该处理方法最大程度地保留了原始记录中的有效信号。从图 4a还可以看出, 初至走时的拾取不再困难。
|
图 3 抽取的共中心点道集及其去噪结果 a抽取的共中心点道集; b矢量中值滤波去噪结果; c稀疏反演去噪结果 |
|
图 4 利用基于稀疏反演去噪方法对图 1a所示原始记录去噪后的单炮记录(a)和去除的噪声(b) |
将干涉炮噪声压制前后的地震记录分别进行叠加, 并抽取叠加剖面, 如图 5所示。图 5a为原始炮记录的叠加剖面, 图 5b为干涉炮噪声压制后的叠加剖面, 图 5c为图 5a与图 5b之差, 即为去除的噪声。对比该组叠加剖面可以看出, 干涉炮噪声能量得到了很好的压制, 地震剖面质量得到了极大提高。原始叠加剖面的很多同相轴被干涉炮噪声淹没, 浅层更甚, 基本无法追踪同相轴; 干涉炮噪声压制后的地震记录, 浅层同相轴清晰地显现出来, 中深层同相轴也更加清晰连续, 为后续处理提供良好的叠加数据。
|
图 5 叠加剖面对比 a原始叠加剖面; b干涉炮噪声压制后的叠加剖面; c去除的噪声 |
本文研究了可控震源独立同步扫描的地震记录干涉炮噪声压制方法。首先在共炮点道集进行去噪处理, 然后在共中心点道集做进一步的干涉炮噪声压制, 最终获得高质量的地震记录。比较了基于信号相干性的矢量中值滤波干涉炮噪声压制方法和基于稀疏反演的干涉炮噪声压制方法, 可以看出, 基于稀疏反演的干涉炮噪声压制方法可以获得更好的去噪效果。静校正问题的存在, 会降低主炮信号的相干性, 因此基于信号相干性的干涉炮噪声压制方法受静校正影响较为严重。而基于稀疏反演的干涉炮噪声压制方法, 可以不考虑静校正的影响, 并且在压制干涉炮噪声的同时不破坏初至波信息, 干涉炮噪声压制后仍旧可以对地震资料进行静校正处理。
| [1] |
倪宇东. 可控震源地震勘探采集技术[M]. 北京: 石油工业出版社, 2014: 52-97. NI Y D. Vibroseis seismic exploration acquisition technology[M]. Beijing: Petroleum Industry Press, 2014: 52-97. |
| [2] |
HUO S, LUO Y, KELAMIS P G. Simultaneous sources separation via multi-directional vector-median filtering[J]. Geophysics, 2012, 77(4): V123-V131. DOI:10.1190/geo2011-0254.1 |
| [3] |
CHEN Y K. Deblending using a space-varying median filter[J]. Exploration Geophysics, 2014, 46(4): 332-341. |
| [4] |
王文闯, 李合群, 赵波, 等. 基于α-trimmed矢量中值滤波压制同步激发邻炮干扰[J]. 石油地球物理勘探, 2014, 49(6): 1061-1067. WANG W C, LI H Q, ZHAO B, et al. Suppression of crosstalk from simultaneous sources with α-trimmed vector median filtering[J]. Oil Geophysical Prospecting, 2014, 49(6): 1061-1067. |
| [5] |
HOOVER G, SUBELETTE V, CARTER C, et al. Infield processing of an ISSTM dataset south-east Algeria[J]. Expanded Abstracts of 80th Annual Internat SEG Mtg, 2010, 468-472. |
| [6] |
MOORE I, DRAGOSET B, OMMUNDSEN T, et al. Simultaneous source separation using dithered sources[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 2806-2810. |
| [7] |
AKERBERG P, HAMPSON G, RICKETTE J, et al. Simultaneous source separation by sparse Radon transform[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 2801-2805. |
| [8] |
ZHANG C, OLOFSSON B. Separating simultaneous source data using weighted τ-p transform[J]. Expanded Abstracts of 74th EAGE Annual Conference, 2012, B003. |
| [9] |
曲英铭, 李振春, 韩文功, 等. 可控震源高效采集数据特征干扰压制技术[J]. 石油物探, 2016, 55(3): 395-407. QU Y M, LI Z C, HAN W G, et al. The elimination technology for special interference in vibroseis efficient acquisition data[J]. Geophysical Prospecting for Petroleum, 2016, 55(3): 395-407. DOI:10.3969/j.issn.1000-1441.2016.03.010 |
| [10] |
丁伟, 胡立新, 何京国, 等. 可控震源高效地震采集技术研究及应用[J]. 石油物探, 2014, 53(3): 338-343. DING W, HU L X, HE J G, et al. The research on vibrator high efficient simulation technology and its application[J]. Geophysical Prospecting for Petroleum, 2014, 53(3): 338-343. DOI:10.3969/j.issn.1000-1441.2014.03.012 |
| [11] |
WASON H, HERRMANN F J, LIN T T Y. Sparsity-promoting recovery from simultaneous data:a compressive sensing approach[J]. Expanded Abstracts of 81st Annual Internat SEG Mtg, 2011, 6-10. |
| [12] |
SPITZ S, HAMPSON G, PICA A.Simultaneous source separation using wave field modeling and PEF adaptive subtraction[R].EAGE Marine Seismic Workshop-Focus on Middle East and North Africa, 2009
|
| [13] |
MAHDAD A, DOULGERIS P, BLACQUIERE G. Separation of blended data by iterative estimation and subtraction of interference noise[J]. Geophysics, 2011, 76(3): Q9-Q17. DOI:10.1190/1.3556597 |
| [14] |
ABMA R L, MANNING T, TANIS M, et al. High quality separation of simultaneous sources by sparse inversion[J]. Expanded Abstracts of 72nd EAGE Annual Conference, 2010, B003. |



