2. 中海石油(中国)有限公司深圳分公司南海东部石油研究院, 广东深圳 518000
2. Nanhai East Petroleum Research Institute of CNOOC Ltd., Shenzhen 518000, China
全波形反演是一种基于数据拟合的高精度建模方法, 其分辨率可达到传播波场的二分之一[1], 被认为是建模精度最高的方法之一。该方法应用全波场信息, 无高频近似假设, 且同时利用波场的运动学和动力学特征, 理论上具备更高精度的建模能力。
20世纪80年代初, TARANTOLA[2]和LAILLY[3]分别提出了时间域的全波形反演方法。20世纪90年代, PRATT等[4]将其推广到频率域。近年来, 全波形反演受到越来越多学者的重视, 成为地球物理界的研究热点。高性能计算技术的飞速发展使得海量计算的全波形反演应用成为可能, 实际资料全波形反演的案例也越来越多[5-8]。国内全波形反演的实际资料应用已有较快的发展[9-10], 但常规陆上地震勘探采集的数据受偏移距和观测系统的限制, 很难满足全波形反演对数据和观测系统的要求。因此, 全波形反演在陆上实际资料应用中还面临很大的挑战[11]。
全波形反演是一个具有强非线性性的反问题, 观测数据与模型正演数据在L2范数约束下寻找全局最优解具有较大的难度。为了降低问题的非线性性, 王毓玮等[12]提出了分布反演的策略。张广智等[13]提出了一种快速共轭梯度方法, 加速了全波形反演的收敛。2008年, SHIN等[14]提出了拉普拉斯域的全波形反演方法, 利用波场的零频分量反演模型作为初始模型, 继而进行传统意义下的全波形反演, 一定程度上降低了问题的非线性性。工业界一般通过建立精度尽可能高的初始模型, 利用准确的先验信息等来实现陆地资料的全波形反演。
海上资料较陆地资料信噪比较高, 有稳定的震源和接收条件, 但海上资料也有其独特的处理难点, 如鬼波、多次波、浅水鸣震等干扰波压制问题。本文应用构造约束全波形反演技术, 在层析模型的基础上引入构造信息, 构建较为准确的速度模型, 重建断层位置, 成功解决了南海某海域实际资料存在的断层阴影带问题, 取得了较好的应用效果。
1 基于构造约束的全波形反演技术全波形反演是一个高度非线性性问题, 同时也是一个“病态”的反问题, 尤其在使用L2范数约束的情况下。传统全波形反演的目标泛函为:
| $ C\left( \mathit{\boldsymbol{m}} \right)=\frac{1}{2}{{L}^{2}}(\Delta \mathit{\boldsymbol{d}})=\frac{1}{2}\Delta {{\mathit{\boldsymbol{d}}}^{\text{T}}}\Delta {{\mathit{\boldsymbol{d}}}^{*}} $ | (1) |
其中:C(m)为误差函数, m为模型参数; L2为误差泛函; Δd为观测数据与模拟数据之间的残差。为解决问题的“病态”性, TIKHONOV等[15]提出了正则化思想。先验信息的引入有助于观测波场和模拟波场在L2范数的约束下快速拟合。在生产中最常用的先验模型来自测井信息, 利用测井信息得到的先验模型精度较高, 缺点是井的数量少, 仅能得到较为精确的局部信息。本文采用地质构造信息来构建先验模型, 首先定义误差泛函为:
| $ C\left( \mathit{\boldsymbol{m}} \right)={{\alpha }_{1}}{{C}_{\text{d}}}\left( \mathit{\boldsymbol{m}} \right)+{{\alpha }_{2}}\lambda {{C}_{\text{m}}}\left( \mathit{\boldsymbol{m}} \right) $ | (2) |
其中:Cd(m)为数据域残差; Cm(m)为构造约束模型项; λ为正则化项权重因子, 用来调节数据残差项和模型误差项之间的平衡; α1和α2为权重因子, 取α1+α2=1, 用来根据反演地质情况和先验信息精度调节数据项和模型项的比重, 并随着反演迭代次数的增加, 逐渐降低模型项的比重, 动态调整其在误差泛函中的比重, 最终回到完全数据驱动, 即传统的全波形反演。根据误差泛函形式获得最终的梯度表达式为:
| $ {{\mathit{\boldsymbol{g}}}_{\text{m}}}=-{{\alpha }_{1}}{{\left[ \frac{\partial \mathit{\boldsymbol{d}}\left( \mathit{\boldsymbol{m}} \right)}{\partial \mathit{\boldsymbol{m}}} \right]}^{\text{T}}}\mathit{\boldsymbol{W}}_{_{\bf{d}}}^{\text{T}}{{\mathit{\boldsymbol{W}}}_{\bf{d}}}\Delta \mathit{\boldsymbol{d}}+{{\alpha }_{2}}\lambda \mathit{\boldsymbol{Dm}} $ | (3) |
其中: gm为梯度; W为平滑算子; D为Laplace算子。为了避免Frechet矩阵的求解, 数据域梯度可利用伴随状态法求解[16]。
沿深度域层位进行各向异性高斯平滑得到先验模型m, 根据地层构造方向调节各向异性高斯平滑算子的平滑半径, 在沿地层走向方向上平滑尺度较大, 在垂直地层走向方向上平滑尺度较小, 进而构建出具有地质意义的先验模型。
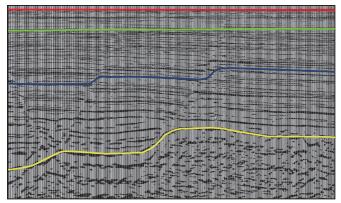
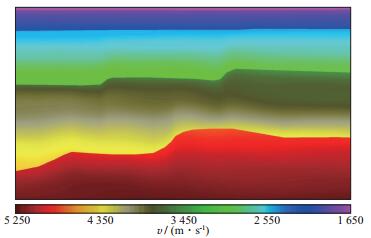
先验模型一般由深度域成像剖面获取。本文从偏移剖面上拾取了包括海底信息的主要4套反射层, 如图 1所示。经过各向异性高斯平滑得到的先验信息模型如图 2所示(根据资料方要求, 所有成像剖面隐去了坐标)。可以看出, 图 2中加入了有效的反射层信息。将这些信息引入目标泛函, 进而引入梯度信息, 有效避免了反演的错误收敛, 降低了反演的“病态”性。
|
图 1 从偏移剖面上拾取的主要反射层 |
|
图 2 基于构造信息建立的先验信息模型 |
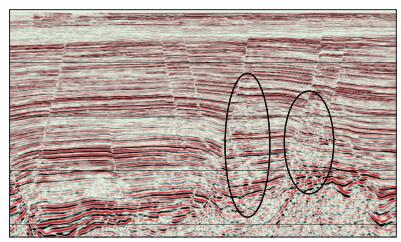
海上实际资料来自我国南海某油田, 区域水深100 m左右, 拖缆采集, 最大偏移距6 km, 目的层段深度1.5~2.5 km。该地区断层发育, 建模难度较大, 两期不同方式采集的资料成像时都存在不同程度的断层阴影问题。如图 3所示, 断层以下区域成像模糊、同相轴不连续、断点不清晰, 影响构造的落实。
|
图 3 传统建模模型的叠前深度偏移结果 |
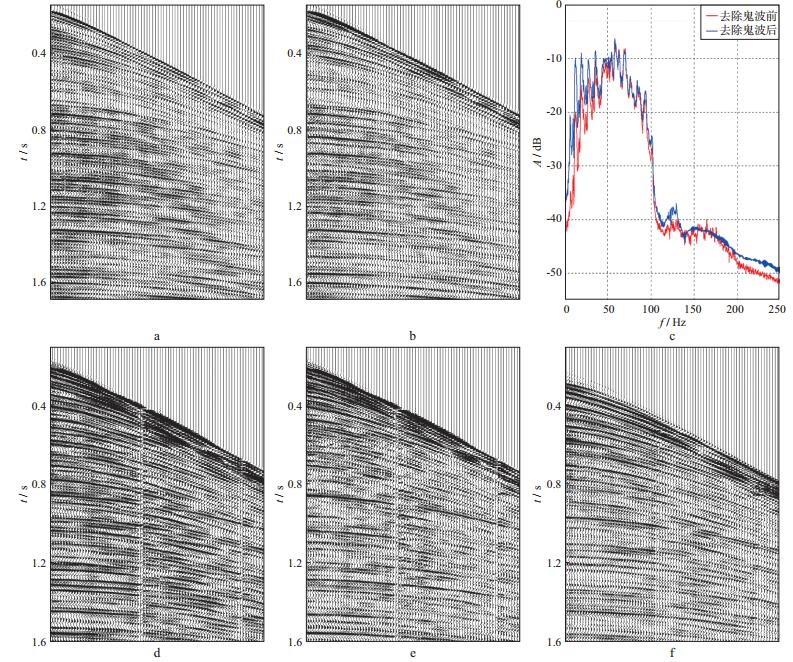
分析认为, 断层附近的速度反演是解决成像阴影问题的关键。本文采用构造约束全波形反演技术, 通过数据域拟合实现断层的自动控制, 从而实现高精度速度建模。虽然海上资料具有较高的信噪比, 炮点、检波点一致性较好, 但其相对陆地资料存在鬼波和多次波的压制问题。图 4对比了本次实际资料鬼波、多次波压制前后的结果。由图 4a~图 4c可见, 对鬼波进行压制后, 虚反射得到有效去除; 低频端有效波场能量得到很好改善, 有利于后续全波形反演的应用; 100 Hz附近的限波点也得到准确恢复。由图 4d~图 4f可见, 能量较强的主要多次波被基本压制。
|
图 4 鬼波、多次波压制效果对比 a鬼波去除前; b鬼波去除后; c频谱分析; d多次波压制前; e多次波压制后; f去除的噪声 |
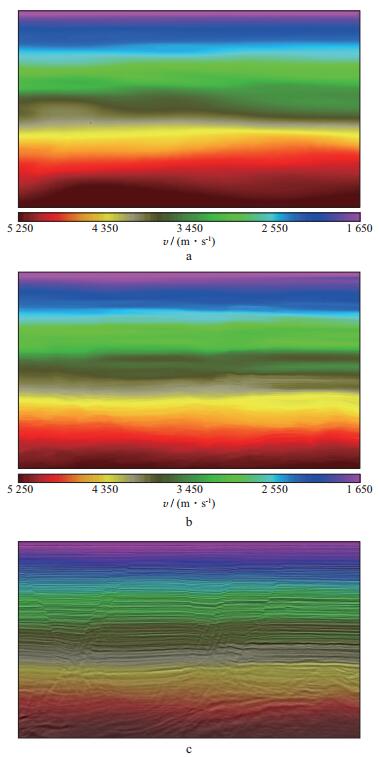
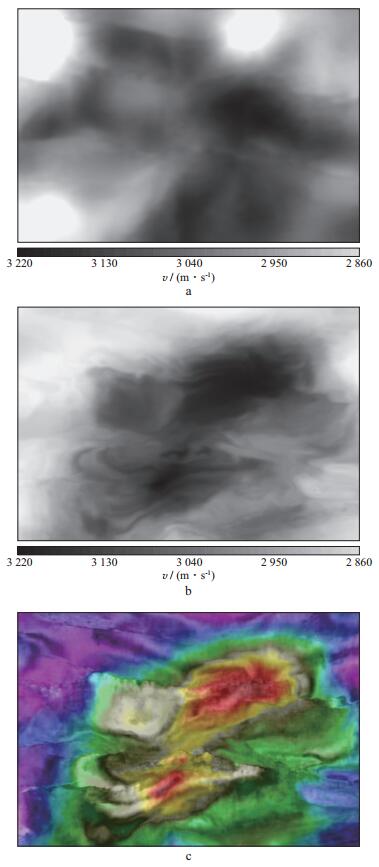
图 5对比了某测线方向反射层析模型与全波形反演模型, 其中图 5a为反射层析建模剖面, 图 5b为全波形反演得到的剖面, 图 5c为全波形反演模型与深度域成像剖面的叠加显示。可以看出, 全波形反演得到的速度模型分辨率明显提高, 且层位信息和断层信息较初始模型更加丰富; 全波形反演得到的各层信息与剖面构造信息吻合, 断层位置准确、清晰。图 6对比了反射层析模型与全波形反演模型在目的层的水平切片, 其中图 6a为反射层析建模模型, 图 6b为全波形反演模型, 图 6c为全波形反演模型与深度域成像剖面的叠加显示。层析反演可以得到大尺度的大套断层信息, 与层析模型相比, 全波形反演模型断裂系统更加丰富、断点更加干脆、断层更加清晰, 次级断层、小断层也得到了有效重建。与深度域成像剖面叠加显示的结果表明, 全波形反演得到的断层信息与深度域成像的断层信息吻合度较高。断裂处有明显的速度变化, 证明了全波形反演方法的可靠性和高精度建模的能力。
|
图 5 某测线方向反射层析模型与全波形反演模型对比 a反射层析模型; b全波形反演模型; c全波形反演模型与深度域成像剖面的叠加显示 |
|
图 6 反射层析模型与全波形反演模型在目的层的水平切片对比 a反射层析模型; b全波形反演模型; c全波形反演模型与深度域成像剖面的叠加显示 |
图 7是利用反射层析模型与全波形反演建模得到的偏移成像结果。以道集拉平的背景速度为初始模型进行全波形反演速度建模中, 为了得到地质意义更加明确的速度模型, 引入了准确的层位信息和断层信息, 很好地解决了成像的断层阴影问题, 基于构造约束全波形反演模型的成像剖面断点干脆, 断层以下三角区反射波同相轴更加连续。

|
图 7 反射层析模型(a)与全波形反演建模(b)得到的偏移成像结果 |
速度建模是改善地震成像的关键, 也是地球物理的核心问题。在构造复杂情况下, 全波形反演技术理论上具有更高精度的建模能力, 但其多解性不能保证成像道集拉平, 从而影响成像质量。本文从道集拉平的背景速度场出发, 在保证道集拉平的同时, 引入构造信息和断层信息约束, 进行全波形反演建模, 获得更加准确的速度场。在南海某油田实际资料应用中, 全波形反演得到的速度场重建了初始模型中缺失的断层分布及断层位置, 地质信息更加丰富, 且与偏移成像的构造信息更加吻合, 在不改变背景速度走时信息的同时, 引入构造信息准确反演了复杂断裂带的速度, 有效改善了断层阴影带的成像质量。
全波形反演技术采用波动理论和数据域拟合的思想, 是一个自动化的高精度建模手段, 但其对地震资料要求较高, 在陆地资料应用中存在很大困难。相对而言, 海上资料具有较高的信噪比, 炮点、检波点一致性较好, 全波形反演的实用化得到了较快的发展。除了偏移成像外, 全波形反演高精度建模技术在复杂构造建模成像、近海底水合物建模勘探、压力预测等方面的应用都得到了快速发展。随着全波形反演研究的深入和处理手段的进步, 全波形反演技术无论在海上还是在陆上都将发挥越来越重要的作用。
| [1] |
VIRIUEX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
| [2] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [3] |
LAILLY P. The seismic inverse problem as a sequence of before stack migrations[R]. Philadelphia: Conference on Inverse Scattering, Theory and Applications, 1984: 206-220
|
| [4] |
PRATT R G, WORTHINGTON M H. Inverse theory applied to multi-source cross-hole tomography, part Ⅰ:acoustic wave-equation method[J]. Geophysical Prospecting, 1990, 38(3): 287-310. DOI:10.1111/gpr.1990.38.issue-3 |
| [5] |
SIRGUE L, BARKVED O I, DELLINGER J, et al. Full waveform inversion:the next leap forward in imaging at Valhall[J]. First Break, 2010, 28(4): 65-70. |
| [6] |
PLESSIX R E, PERKINS C. Full waveform inversion:a deep water ocean bottom seismometer data set[J]. First Break, 2010, 28(4): 71-78. |
| [7] |
PLESSIX R E, GUIDO B, JAN B, et al. Full waveform inversion and distance separated simultaneous sweeping:a study with a land seismic data set[J]. Geophysical Prospecting, 2012, 60(4): 733-747. DOI:10.1111/gpr.2012.60.issue-4 |
| [8] |
胡光辉, 贾春梅, 夏洪瑞, 等. 3D声波全波形反演的实现及应用[J]. 石油物探, 2013, 52(4): 417-425. HU G H, JIA C M, XIA H R, et al. Implementation and validation of 3D acoustic full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2013, 52(4): 417-425. |
| [9] |
丁继才, 孙文博, 黄小刚, 等. 海上地震数据全波形反演实际应用[J]. 石油物探, 2017, 56(1): 75-80. DING J C, SUN W B, HUANG X G, et al. The strategies of FWI realization for marine seismic data[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 75-80. |
| [10] |
王杰, 胡光辉, 刘定进, 等. 陆上地震资料全波形反演策略研究[J]. 石油物探, 2017, 56(1): 81-88. WANG J, HU G H, LIU D J, et al. Strategy study on full waveform inversion for the land seismic data[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 81-88. |
| [11] |
杨勤勇, 胡光辉, 王立歆. 全波形反演研究现状及发展趋势[J]. 石油物探, 2014, 53(1): 77-83. YANG Q Y, HU G H, WANG L X. Research status and development trend of full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(1): 77-83. |
| [12] |
王毓玮, 董良国, 黄超, 等. 降低弹性波全波形反演强烈非线性的分步反演策略[J]. 石油地球物理勘探, 2016, 51(2): 288-294. WANG Y W, DONG L G, HUANG C, et al. A multi-step strategy for mitigating severe nonlinearity in elastic full-waveform inversion[J]. Oil Geophysical Prospecting, 2016, 51(2): 288-294. |
| [13] |
张广智, 孙昌路, 潘新朋, 等. 快速共轭梯度法频率域声波全波形反演[J]. 石油地球物理勘探, 2016, 51(4): 730-737. ZHANG G Z, SUN C L, PAN X P, et al. Acoustic full waveform inversion in the frequency domain based on fast conjugate gradient method[J]. Oil Geophysical Prospecting, 2016, 51(4): 730-737. |
| [14] |
SHIN C, HA W. A comparison between the behavior of objective functions for waveform inversion in the frequency and Laplace domains[J]. Geophysics, 2008, 73(5): 119-133. DOI:10.1190/1.2953978 |
| [15] |
TIKHONOV A, ARSENIN V. Solution of ill-posed problems[R]. Washington, DC: Winston & Sons, 1977
|
| [16] |
PLESSIX R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 2006, 167(2): 495-503. DOI:10.1111/gji.2006.167.issue-2 |



