2. 南京电子技术研究所, 中国电子科技集团公司智能感知技术重点实验室, 江苏南京 210029;
3. 西安交通大学数学与统计学院信息科学系, 陕西西安 710049;
4. 中国海洋石油总公司研究总院, 海洋石油勘探国家工程实验室, 北京 100029;
5. 大庆油田有限责任公司勘探开发研究院, 黑龙江大庆 163712
2. Nanjing Research Institute of Electronics Technology, Key Laboratory of IntelliSense Technology, CETC, Nanjing 210029, China;
3. Department of Information Science, School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an 710049, China;
4. CNOOC Research Institute and National Engineering Laboratory for Offshore Oil Exploration, Beijing 100029, China;
5. Exploration and Development Research Institute of Daqing Oilfield Company, Daqing 163712, China
薄互层储层是陆相沉积盆地中一种重要的储层类型, 在我国鄂尔多斯盆地、松辽盆地等盆地中, 薄互层储层发育, 因此, 这类储层具有重要研究意义。薄互层由多个薄层叠合而成。所谓薄层是相对于地震波波长来说的, 如果地层的厚度远小于地震波波长, 就称其为薄层。松辽盆地中、浅层地层的单层厚度一般仅为几米, 而地震波的波长为百米量级。鄂尔多斯盆地单层厚度仅为几米到十几米, 地震波波长也为百米量级。因此, 在此类盆地的地震勘探中, 地震波无法分辨单层的厚度及反射界面的位置。
来自薄互层的地震信号是一种包含频率和幅度快速变化的非平稳信号, 时频分析作为研究非平稳信号的一种有力工具[1], 已经被广泛应用于地震信号处理和解释领域。例如, PARTYKA等[2]将短时Fourier变换(STFT)用于墨西哥湾某区块实际地震资料的河道厚度刻画以及不连续性检测。CHAKRABORTY等[3]提出了基于小波变换(CWT)的地震信号谱分析方法。高静怀等[4-5]研究了利用小波变换对地震信号进行属性分析的方法, 并构造出适合于地震信号分析及瞬时属性分析的三参数小波[6]。ODEBEATU等利用S变换[7]检测与含气饱和度相关的异常现象[8]。高静怀等[9]提出一种广义S变换, 并将其用于薄互层的地震响应分析。LI等[10]利用Wigner-Ville分布(WVD)刻画了碳酸盐储层。LIU等[11]利用局域化属性检测河道和低频异常。时频分析还被广泛用于地震瞬时属性的提取, TANER等[12]首先提出了复地震道分析方法, 并给出了基于复地震道提取的地震瞬时属性的定义、物理意义及其在地震解释中的应用。CASTAGNA等[13]和MARFURT[14]将瞬时谱分别用于碳氢检测和地质结构刻画。HAN等[15]提出了结合经验模态分解(EMD)和瞬时频率的地震信号分析方法, 该方法能够更精细地刻画地质结构。
STFT由于窗函数在时间域及频率域宽度固定, 所以一旦选定窗函数, 它在时间和频率两个方向上的分辨率就不变。CWT克服了STFT的缺点, 在分析信号的缓变分量时利用长时窗以获得较高的频率分辨率; 分析快变分量时采用短时窗以获得较高的时间分辨率。CHAKRABORTY等[3]论证了CWT相比于STFT在地震信号谱分解上的优势。S变换用频率控制窗的宽度, 不仅具有小波变换的优点, 而且还能够直接得到时间-频率谱[7]。WVD虽然可以得到更集中的时频表示, 但是在分析多分量信号时, 会产生交叉项的干扰, 带来分析误差。为了提高时频分辨率, AUGER等在KODERA等[16]的研究基础上, 提出了利用STFT和WVD等时频分布的相位信息进行能量重排的时频分析方法[17]。重排时频分析方法已经得到了广泛的应用, PENG等[18]将基于CWT的重排方法用于旋转机械缺陷的特征提取, WU等[19]将基于WVD的重排方法用于地震资料的谱分解。然而这种时频重排方法没有给出重构公式, 限制了其应用。
综上所述, 各种时频分析方法虽然在地震信号分析中得到了成功的应用, 然而它们都有一定的局限性[16]。为了得到具有更高时频域分辨率的分析方法, HUANG等[20]提出了EMD的分析方法(称为Huang变换), 与上述时频分析方法不同, Huang变换是将待分析信号分解为若干个本征模态函数之和, 它在故障检测、地震信号分析等应用中具有显著效果[21], 但该变换缺乏严格的理论基础。
DAUBECHIES等[22]在研究EMD的基础上, 系统地提出了同步挤压小波变换, 并给出了一套完整的数学理论, 可实现待分析信号的本征模态函数分解。同步挤压变换已经被应用于语音信号、心电图、古气候学、降噪、故障检测及地震数据解释等领域[22-26]。LI等[26]提出了广义同步挤压变换, HERRERA等[27]研究了一般的同步挤压变换在地震信号解释中的应用, WANG等[28]将同步挤压变换应用于储层特征刻画。THAKUR等[29]将同步挤压变换推广到STFT以及用更一般的波形函数来替代余弦函数, HUANG等[30]提出了同步挤压S变换, 并用于地震信号谱分解。
本文聚焦薄互层型储层, 该类储层的地震响应信号往往具有频率和幅度变化都较快的特点, 常用的母小波函数(也称基本小波函数), 如Morlet小波等, 分析这种信号时分辨率较低, 相比之下高静怀等人提出的三参数小波[6]变换对薄层具有更强的刻画能力。然而, 与所有的小波变换类似, 三参数小波变换随着尺度的减小, 小波函数频域展宽, 导致频率分辨率降低。为了进一步提高三参数小波变换的分辨能力, 本文提出了同步挤压三参数小波变换, 进而提出了基于同步挤压三参数小波变换的薄互层组及其内部结构的谱分解分析方法。将该方法用于合成数据、薄互层模型合成数据及实际地震资料, 并与常用方法的结果进行了对比以说明方法的有效性。
1 同步挤压三参数小波变换 1.1 连续小波变换对于任意待分析信号s(t)∈L2(R), t为时间, R为实数集合, L2表示平方可积函数空间, 则其小波变换定义为:
| $ \begin{array}{l} {W_s}\left( {a,b} \right) = \frac{1}{{\left| a \right|}}\int {s\left( t \right)\bar \psi \left( {\frac{{t - b}}{a}} \right){\rm{d}}t} \\ \;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{{2{\rm{ \mathit{ π} }}}}\int_{ - \infty }^{ + \infty } {\hat s\left( \omega \right)\bar {\hat \psi} \left( {a\omega } \right){{\rm{e}}^{2{\rm{ \mathit{ π} i}}\omega b}}{\rm{d}}\omega } \end{array} $ | (1) |
式中, a是尺度因子或伸缩因子, 控制小波函数的宽度; b是时间平移, 控制小波函数的位置; ψ(t)是基本小波, ψ(t)是其复共轭, ψa, b(t)=|a|-pψ[(t-b)/a]是由基本小波ψ(t)通过平移和伸缩构成的小波族;
Morlet小波的时域表达式为:
| $ \psi \left( t \right) = k{{\rm{ \mathit{ π} }}^{ - \frac{1}{4}}}\left( {{{\rm{e}}^{ - \frac{1}{2}{t^2}}}{{\rm{e}}^{{\rm{i}}\sigma t}} - {{\rm{e}}^{ - \frac{1}{2}{\sigma ^2}}}{{\rm{e}}^{ - \frac{1}{2}{t^2}}}} \right) $ | (2) |
其中,
| $ \hat \psi \left( \omega \right) = k{{\rm{ \mathit{ π} }}^{ - \frac{1}{4}}}\left[ {{{\rm{e}}^{ - \frac{1}{2}{{\left( {\omega - \sigma } \right)}^2}}} - {{\rm{e}}^{ - \frac{1}{2}{\sigma ^2}}}{{\rm{e}}^{ - \frac{1}{2}{\omega ^2}}}} \right] $ | (3) |
基本小波函数如果要满足容许性条件, 就一定有
| $ \psi \left( t \right) = {{\rm{ \mathit{ π} }}^{ - \frac{1}{4}}}{{\rm{e}}^{ - \frac{1}{2}{t^2}}}{{\rm{e}}^{{\rm{i}}\sigma t}} $ | (4) |
三参数小波是针对地震信号的特点而提出的, 可以很好地匹配待分析信号, Morlet小波、改进的Morlet小波和匹配地震子波小波(BMSW)均为其特例, 它在地震信号分析中表现出很多优势, 并被广泛应用[5-6]。
三参数小波的时域表达式为:
| $ \begin{array}{l} \psi \left( {t;\mathit{\Lambda } } \right) = {{\rm{e}}^{ - \tau {{\left( {t - \beta } \right)}^2}}}\left\{ {p\left( \mathit{\Lambda } \right) \times \left[ {\cos \left( {\sigma t} \right) - k\left( \mathit{\Lambda } \right)} \right] + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\rm{i}}q\left( \mathit{\Lambda } \right)\sin \left( {\sigma t} \right)} \right\} \end{array} $ | (5) |
式中, Λ=(σ, τ, β)为参数集; σ为解析小波的调制频率; τ可以控制衰减快慢, 即控制小波的频率域宽度; β为能量延迟因子; 其它参数如下。
| $ k\left(\mathit{\Lambda } \right) = {{\rm{e}}^{ - \frac{{{\sigma ^2}}}{{4\tau }}}}\left[ {\cos \left( {\beta \sigma } \right) + i\frac{{q\left(\mathit{\Lambda } \right)}}{{p\left(\mathit{\Lambda } \right)}}\sin \left( {\beta \sigma } \right)} \right] $ | (6) |
| $ \begin{array}{l} p\left(\mathit{\Lambda } \right) = {\left( {\frac{{2\tau }}{{\rm{ \mathit{ π} }}}} \right)^{\frac{1}{4}}}\left[ {4\left( {{{\rm{e}}^{ - \frac{{{\sigma ^2}}}{{2\tau }}}} - {{\rm{e}}^{ - \frac{{3{\sigma ^2}}}{{8\tau }}}}} \right){{\cos }^2}\left( {\beta \sigma } \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;{\left. {1 - {{\rm{e}}^{ - \frac{{{\sigma ^2}}}{{2\tau }}}}} \right]^{ - \frac{1}{2}}} \end{array} $ | (7) |
| $ \begin{array}{l} q\left(\mathit{\Lambda } \right) = {\left( {\frac{{2\tau }}{{\rm{ \mathit{ π} }}}} \right)^{\frac{1}{4}}}\left[ {4\left( {{{\rm{e}}^{ - \frac{{{\sigma ^2}}}{{2\tau }}}} - {{\rm{e}}^{ - \frac{{3{\sigma ^2}}}{{8\tau }}}}} \right){{\sin }^2}\left( {\beta \sigma } \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;{\left. {1 - {{\rm{e}}^{ - \frac{{{\sigma ^2}}}{{2\tau }}}}} \right]^{ - \frac{1}{2}}} \end{array} $ | (8) |
三参数小波的频域表达式为:
| $ \begin{array}{l} \hat \psi \left( {\omega ;\mathit{\Lambda } } \right) = \sqrt {\frac{{\rm{ \mathit{ π} }}}{\tau }} \frac{{p\left(\mathit{\Lambda } \right) + q\left(\mathit{\Lambda } \right)}}{2}{{\rm{e}}^{ - {\rm{i}}\beta \left( {\omega - \sigma } \right) - \frac{{{{\left( {\omega - \sigma } \right)}^2}}}{{4\tau }}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sqrt {\frac{{\rm{ \mathit{ π} }}}{\tau }} \frac{{p\left(\mathit{\Lambda } \right) - q\left(\mathit{\Lambda } \right)}}{2}{{\rm{e}}^{ - {\rm{i}}\beta \left( {\omega + \sigma } \right) - \frac{{{{\left( {\omega + \sigma } \right)}^2}}}{{4\tau }}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;p\left(\mathit{\Lambda } \right)k\left(\mathit{\Lambda } \right)\sqrt {\frac{{\rm{ \mathit{ π} }}}{\tau }} {{\rm{e}}^{ - {\rm{i}}\beta \omega - \frac{{{\omega ^2}}}{{4\tau }}}} \end{array} $ | (9) |
Morlet小波的Heisenberg盒的面积最小, 具有最佳的时频联合域分辨率, 在实际中得到了广泛的应用, 但也存在着一定的局限性, 主要为:
1) Morlet小波要求调制频率较大, 一般取σ>5.33, 这就导致待分析信号中低频分量的时间分辨率较低, 为了提高低频分量的时间分辨率, 需降低调制频率, 但是此时Morlet小波在时域包络会由单峰变成双峰, 对待分析信号做小波变换会使信号在多个位置局域化, 小波变换得到的结果产生一些假象。
2) Morlet小波只有调制频率σ一个参数可调, 而且要求σ比较大时才是严格解析的小波函数, 自由度很低, 缺乏灵活性。在小波变换的实际应用中, 为了刻画奇异性, 需要度量待分析信号的局部正则性, 此时小波的消失矩非常重要。我们就需要根据实际需要来选取合适的小波函数, 不仅希望能调节调制频率, 还希望能够控制小波的消失矩等特性, 因此希望小波函数能有更大的自由度。
三参数小波由3个参数来控制, 有着很高的自由度, 不仅可以控制调制频率, 还可以控制小波包络的衰减速度, 此外, 在调制频率很低的时候, 依然保持时域的单峰特性, 具有良好的时频局域化特性。
1.3 同步挤压三参数小波变换在小波变换中, 由于基本小波函数在时频域支集(即Heisenberg盒)为一矩形, 因此待分析信号在小波变换域能量分布在某个区域内, 这不利于准确刻画快速时变信号的时频特性。为减小基本小波函数的影响, 通常在小波变换域进行能量重排, 以减少能量扩散带来的不利影响。常用的能量重排方法都需要解决两个基本问题:能量往哪个频率成分集中?能量如何往某个频率上集中?DAUBECHIES等[22]在小波变换的基础上, 通过同步挤压操作, 来解决上述两个基本问题。同步挤压操作分为两个步骤:第一步, 计算其瞬时频率ωs(a, b), 即重排准则; 第二步, 通过ωs(a, b)来对小波变换系数Ws(a, b)做频率重排。
为了理解DAUBECHIES等人所提方法的思想, 首先考虑一个单频余弦信号s(t)=Acos(ω0t)的连续小波变换结果, s(t)的Fourier变换为
| $ \begin{array}{l} {W_s}\left( {a,b} \right) = \frac{1}{{2{\rm{ \mathit{ π} }}}}\int_{ - \infty }^{ + \infty } {\hat s\left( \omega \right)\bar {\hat \psi} \left( {a\omega } \right){{\rm{e}}^{{\rm{i}}\omega b}}{\rm{d}}\omega } \\ = \frac{A}{{2{\rm{ \mathit{ π} }}}}\left[ {\bar {\hat \psi} \left( {a{\omega _0}} \right){{\rm{e}}^{{\rm{i}}{\omega _0}b}} + \bar {\hat \psi} \left( { - a{\omega _0}} \right){{\rm{e}}^{ - {\rm{i}}{\omega _0}b}}} \right] \end{array} $ | (10) |
如果我们选取的基本小波函数的负频率能量为0, 即
| $ {W_s}\left( {a,b} \right) = \frac{A}{{2{\rm{ \mathit{ π} }}}}\bar {\hat \psi} \left( {a{\omega _0}} \right){{\rm{e}}^{{\rm{i}}{\omega _0}b}} $ | (11) |
从公式(11)可以看到, 假如小波ψ(t)的峰值频率为ξM, 则小波变换的结果将在尺度a=ξM/ω0处取到最大值, 并以这个能量最大的尺度为中心形成一个尺度带, 造成能量扩散, 为了得到更集中的时频分布, 需要进行同步挤压操作, 具体如下:
1.3.1 计算瞬时频率瞬时频率有很多种定义方式, DAUBECHIES等[22]提出的信号s(t)的瞬时频率定义为:
| $ {\omega _s}\left( {a,b} \right) = \frac{{\frac{{\partial {W_s}\left( {a,b} \right)}}{{\partial b}}}}{{2{\rm{ \mathit{ π} i}}{W_s}\left( {a,b} \right)}} $ | (12) |
式中, 小波变换系数Ws(a, b)≠0。
根据公式(12), 对于一个单频余弦信号的小波变换会形成一个尺度带, 瞬时频率可表示为:
| $ {\omega _s}\left( {a,b} \right) = {\omega _0} $ | (13) |
从公式(13)可以看出, 公式(12)定义的瞬时频率就是余弦信号的频率。至此, 我们可归纳为:对于一个余弦信号, 它的小波变换得到的时间-尺度域结果会在某个能量最大的尺度邻域形成一个尺度带, 但是这些尺度对应的小波系数通过公式(12)计算出来的瞬时频率都为余弦信号的频率ω0, 因此我们可以设想将这些尺度的能量都集中到ω0上, 这就解决了前文提到的能量往哪个频率成分集中的问题。
还可以看到, 公式(12)是定义在Ws(a, b)≠0的位置, 如果某个信号有若干个频率成分, 那么得到的小波变换系数会形成若干个尺度带, 公式(12)在每个固定的时刻, 对相应的尺度都能算出一个瞬时频率, 于是可以在一个固定的时刻算出若干个瞬时频率。但这和通过Hilbert变换等方法定义的瞬时频率不同, Hilbert变换等方法是在每个固定的时刻只能算出一个瞬时频率, 因此, 这种方法类似于EMD方法, 它适用于分析多分量信号。
1.3.2 时间-尺度域到时间-频率域的映射由公式(12)计算得到瞬时频率, 意味着能量应该往这个频率上挤压(集中), 将小波变换系数累加到该频率成分上, 即(a, b)→(ω, b), 从而进行能量重排, 那么如何将对应在同一个频率成分上的小波系数累加到一起呢?
对于给定的信号s(t)∈L2(R)的小波变换Ws(a, b), 若选取的小波ψ(t)是解析小波, 则有表达式:
| $ \begin{array}{l} \int_0^{ + \infty } {{W_s}\left( {a,b} \right){a^{ - 1}}{\rm{d}}a} = \frac{1}{{2{\rm{ \mathit{ π} }}}}\int_{ - \infty }^{ + \infty } {\int_0^{ + \infty } {\hat s\left( \omega \right)\bar {\hat \psi} \left( {a\omega } \right){{\rm{e}}^{{\rm{i}}\omega b}}{a^{ - 1}} \cdot } } \\ \;\;\;\;\;\;{\rm{d}}a{\rm{d}}\omega = \frac{1}{{2{\rm{ \mathit{ π} }}}}\int_{ - \infty }^{ + \infty } {\int_0^{ + \infty } {\hat s\left( \omega \right)\bar {\hat \psi} \left( {a\omega } \right){{\rm{e}}^{{\rm{i}}\omega b}}{a^{ - 1}}{\rm{d}}a{\rm{d}}\omega } } \\ \;\;\;\;\;\; = \int_0^{ + \infty } {\frac{{\bar {\hat \psi} \left( \omega \right)}}{\omega }{\rm{d}}\omega } \frac{1}{{2{\rm{ \mathit{ π} }}}}\int_0^{ + \infty } {\hat s\left( \omega \right){{\rm{e}}^{{\rm{i}}\omega b}}{\rm{d}}\omega } \end{array} $ | (14) |
设
| $ \int_0^{ + \infty } {{W_s}\left( {a,b} \right){a^{ - 1}}{\rm{d}}a} = {C_\psi }{s_a}\left( b \right) $ | (15) |
因为sa(b)是s(b)的解析信号, 故有:
| $ s\left( b \right) = {\mathop{\rm Re}\nolimits} \left[ {{s_a}\left( b \right)} \right] = {\mathop{\rm Re}\nolimits} \left[ {C_\psi ^{ - 1}\int_0^{ + \infty } {{W_s}\left( {a,b} \right){a^{ - 1}}{\rm{d}}a} } \right] $ | (16) |
由公式(16)可以看出, 小波变换系数再乘以因子a-1得到的结果和原信号的解析信号只差一个常数因子, 因此可以容易地得到其反变换, 即公式(16)所示。同样, 如果将Ws(a, b)a-1都分配给公式(12)中相应的瞬时频率成分上, 则就得到挤压后的时频分布, 且存在简单严格的反变换。由此, 我们得出时间-尺度域到时间-频率域的映射如下:
| $ {T_s}\left( {\omega ,b} \right) = \int_{\left\{ {a:a > 0,\omega s\left( {a,b} \right) = \omega ,{W_s}\left( {a,b} \right) \ne 0} \right\}} {{W_s}\left( {a,b} \right){a^{ - 1}}{\rm{d}}a} $ | (17) |
通过公式(17), 在某个固定的时刻b, 且小波变换系数Ws(a, b)≠0时, 计算其瞬时频率ωs(a, b), 将所有瞬时频率都为某一频率ω的小波变换系数通过公式(17)累加, 就完成了能量的重分配, 得到了挤压后的时频分布。
1.3.3 阈值的选取公式(11)中当Ws(a, b)很小时, 计算瞬时频率时会出现不稳定的情况, 所以在数值计算时取|Ws(a, b)|>
| $ \tilde \varepsilon = \sqrt {2\log N} \cdot {\sigma _\eta } $ | (18) |
| $ \begin{array}{l} {\sigma _\eta } = {\rm{median}} \cdot \\ \frac{{\left\{ {\left| {{W_s}\left( {{a_{1:{n_v}}},b} \right) - {\rm{median}}\left[ {{W_s}\left( {{a_{1:{n_v}}},b} \right)} \right]} \right|} \right\}}}{{0.6745}} \end{array} $ | (19) |
式中, ση为与噪声水平相关的量, 可利用小波变换的前nv个尺度来估计; median代表取中值; 0.6745是针对高斯噪声的正则化因子。由于有N个时刻, 所以实际应用中, 可以对N个时刻求得的ση取均值, 即可得到最优的阈值。
2 模型算例分析 2.1 合成信号将本文方法用于合成信号, 以验证其有效性。图 1a中合成信号[27, 32]的表达式为:
| $ \begin{array}{l} f\left( t \right) = \\ \left\{ {\begin{array}{*{20}{c}} {\cos \left( {2{\rm{ \mathit{ π} }} \times 20t} \right)}&{0 \le t < 0.5}\\ {\cos \left\{ {2{\rm{ \mathit{ π} }} \times 30t + 3\sin \left[ {6{\rm{ \mathit{ π} }}\left( {t - 0.5} \right)} \right]} \right\}}&{0.5 \le t < 1.5} \end{array}} \right. \end{array} $ | (20) |
|
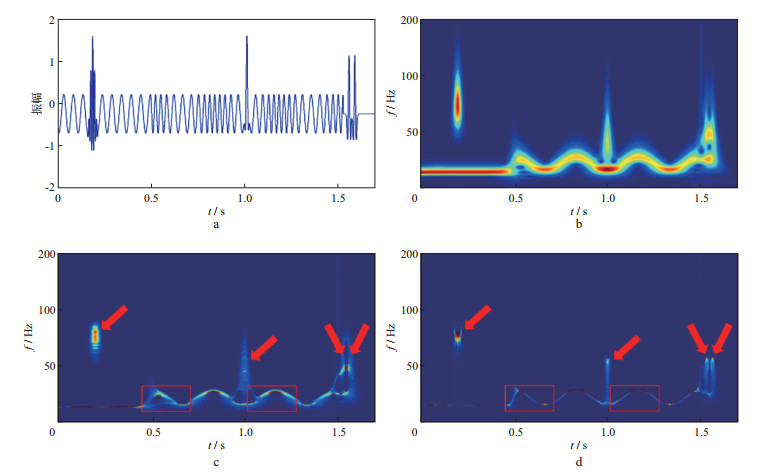
图 1 合成信号及其时频结果 a 合成信号; b 基于Morlet小波变换的时频结果; c 基于同步挤压变换的时频结果; d 基于本文方法的时频结果 |
该信号的前半段为一余弦信号, 其频率成分不随时间变化; 后半段的频率随时间而变化, 为典型的时变信号, 这为准确刻画其频率分布和频率变化带来了极大困难。此外, 在0.20s处有一个调制频率为100Hz的Morlet小波原子, 在1.00s, 1.53s和1.56s处分别有一个50Hz的Ricker子波, 三参数小波的参数选为Λ=(3, 0.5, 0)[6]。基于Morlet小波变换、Morlet小波同步挤压变换(后文简称为同步挤压变换)、本文提出的同步挤压三参数小波变换(下文称为本文方法)计算得到的时频结果分别如图 1b至图 1d所示。与连续小波变换方法相比, 看到图 1c和图 1d两个同步挤压变换的结果, 有着更高的时频分辨率。此外, 从红色矩形处可以看到, 在频率突变和频率变化较快的地方, 相比于同步挤压变换结果, 本文方法具有更高的时频分辨率, 时频局域性更好, 可以准确地刻画时变信号的频率分布和频率变化情况。从红色箭头所指处可以看出, 与同步挤压变换相比, 本文方法法可以更加准确地刻画单个Ricker子波; 即使当两个子波到达时间相近时, 本文方法法仍能清晰地分辨两个Ricker子波。
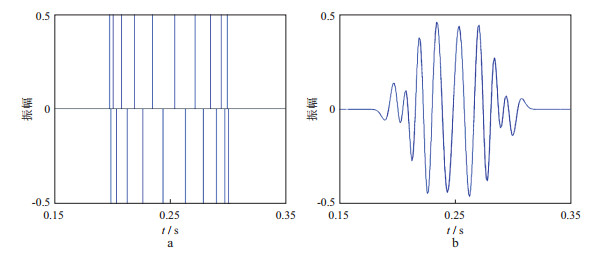
2.2 薄互层模型我们将不同时频分析方法用于经典的薄互层模型, 以验证本文方法的有效性和准确性。薄互层模型的反射系数序列和合成地震记录如图 2所示, 图 2a中反射系数的幅度大小都为0.5, 正负相间, 时间间隔从左往右依次为1, 2, 3, …, 9, 10, 9, …, 3, 2, 1ms, 薄层起始位置为200ms, 时间采样间隔为1ms。与主频为50Hz的Ricker子波卷积得到合成地震记录, 如图 2b所示。将不同时频分析方法用于该合成地震记录, 得到的时频结果如图 3所示。当选取Morlet小波为基本小波函数进行小波变换时, 由于Morlet小波的峰值频率较高, 对于低频来说, 对应的尺度较大, 所以其时间分辨率较低, 主能量带的中心频率(给定时刻主能量带中能量最大值对应的频率)对地层厚度的变化不灵敏, 导致对薄互层的时-频响应特性(调谐频率随着层的变薄而升高)刻画不够清晰准确。
|
图 2 反射系数序列(a)和合成地震记录(b) |
|
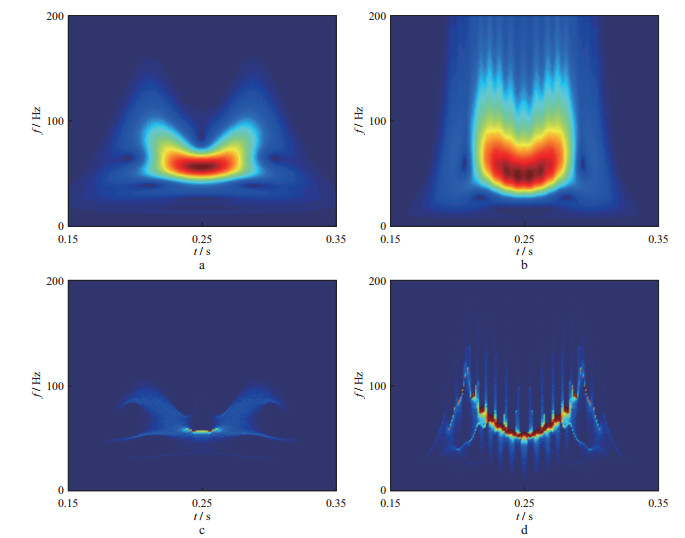
图 3 图 2b合成地震记录的时频结果 a 基于Morlet小波变换; b 基于三参数小波变换; c 基于同步挤压变换; d 基于本文方法 |
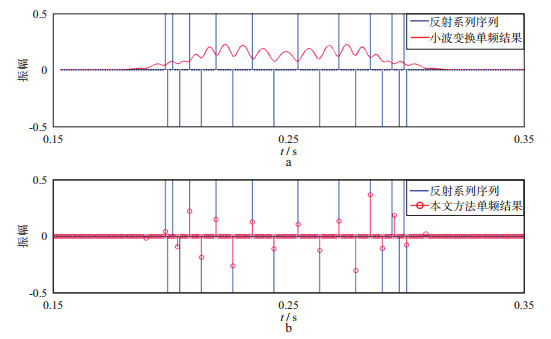
图 3c中同步挤压变换结果也可以看到, 尤其对于低频来说, 时间分辨率很低, 而此时的同步挤压效果也不好, 不足以刻画薄层的时频特征。图 3b和图 3d中, 三参数小波的参数选取为Λ=(3, 1, 0), 此时图 3b三参数小波变换结果的锥形条纹较为清晰, 但仍然不能清晰地刻画薄互层的局部结构特征。图 3d为本文方法的时频结果, 不仅可以清楚地反映主能量带, 这与薄互层的时-频响应特性是一致的, 而且可以清晰地揭示薄互层的局部结构, 即锥形条纹。我们提取了图 3b和图 3d中的单频(160Hz)结果, 如图 4所示, 其中蓝线是原始反射系数序列, 可见本文方法提取的单频分量的位置与反射系数序列的位置吻合较好, 从而可以准确地确定薄互层模型中反射系数的位置。但当反射系数间隔过小(小于3ms)时, 本文方法提取的单频分量的结果也不能准确地刻画薄层的位置。
|
图 4 自图 3时频结果中提取的单频(160Hz)分量 a 基于三参数小波变换; b 基于本文方法 |
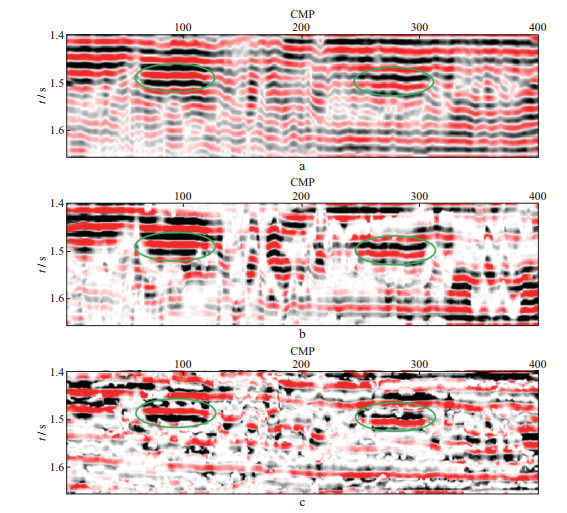
将本文方法应用于渤海地区某实际地震数据。首先, 将本文方法用于某二维地震叠后剖面, 共400道, 时间采样点数500, 时间采样间隔2ms, 如图 5所示, 图中绿色椭圆指示了河道所在位置。将不同的时频分析方法应用于该地震数据, 并提取30Hz的单频结果, 如图 6所示。图 6a中Morlet小波变换的单频切片过于粗糙, 不能有效地识别和定位绿色椭圆处的河道, 而图 6b和图 6c中同步挤压变换和本文方法均可以较为准确地定位河道。但对比图 6b和图 6c可见, 本文方法对于河道的位置和河道展布的刻画, 比同步挤压变换刻画得更加清晰和准确, 这是因为本文方法具有更高的时频分辨率, 可以得到更稀疏的时空表示。

|
图 5 二维实际地震剖面(绿色椭圆指示了河道) |
|
图 6 单频30Hz剖面 a 基于Morlet小波变换; b 基于同步挤压变换; c 基于本文方法 |
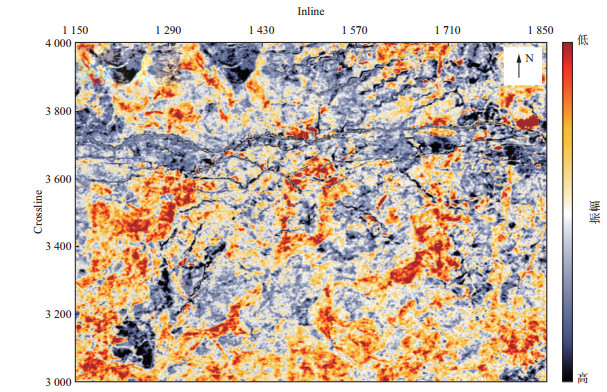
将不同的时频分析方法应用于渤海地区某三维实际地震数据, 对比其对河道等地质构造的刻画能力。图 7是该三维地震数据的沿层切片, 该层河流相薄砂体较为发育。原始地震数据分辨率较低, 不利于河道的期次划分, 河道之间的叠置关系也不够清楚。我们选取不同的时频分析方法, 提取单频30Hz沿层切片, 如图 8所示。图 8b为基于三参数小波变换提取的单频切片结果, 可见其对河道的刻画比图 8a中Morlet小波变换结果更为清晰。图 8c为同步挤压Morlet小波变换提取的单频切片结果, 虽然分辨率略高于三参数小波变换的结果, 但仍不能清晰地刻画河道叠置现象。图 8d为本文方法提取的单频切片结果, 对河道的刻画更为清晰, 也可以较为准确地刻画叠置的河道, 如红色箭头和红色矩形指示位置。
|
图 7 某工区三维原始地震数据体沿层切片 |

|
图 8 单频30Hz沿层切片结果(红色箭头和红色矩形指示了河道分布情况) a 基于Morlet小波变换; b 基于三参数小波变换; c 基于同步挤压变换; d 基于本文方法 |
本文提出了同步挤压三参数小波变换, 并用于薄互层型油气储层刻画, 该变换可以得到更稀疏的时频表示, 有利于精确刻画薄互层等地质结构。
合成地震记录算例表明, 本文方法具有更高的时频分辨率, 可以得到更稀疏的时频表示。薄互层模型算例表明, 本文方法不仅可以准确地刻画薄互层的时-频响应特性, 而且可以清楚地反映薄互层的局部结构; 本文方法提取的单频结果可以准确地定位薄互层模型中的反射界面。实际地震资料算例表明, 本文方法具有更稀疏的时空表示, 可以更加准确地刻画河道的位置及展布情况, 对于河道局部细节的刻画更为清晰。
同步挤压三参数小波变换可对薄互层组的整体特性(图 3d中的主能量带的变化趋势, 即先降低后升高)进行精细刻画, 该变化趋势与地层的韵律及沉积相密切相关, 需要进一步研究。同步挤压三参数小波变换也可对薄互层内部结构进行精细表征(图 3d中的垂向条纹), 这些与薄互层整体特征结合, 可表征薄互层的横向变换, 为储层预测提供帮助。
下一步的工作将根据我国松辽盆地和鄂尔多斯盆地的实际情况, 对薄互层类型进行分类, 建立数据库, 系统地研究其时频域的特征, 为储层预测提供依据。
| [1] |
刘光鼎, 李幼铭, 吴永刚, 等. 陆相油储地球物理学导论[M]. 北京: 科学出版社, 1998: 1-261. LIU G D, LI Y M, WU Y G, et al. An introduction to the continental oil reservoir geophysics[M]. Beijing: Science Press, 1998: 1-261. |
| [2] |
PARTYKA G, GRIDLEY J, LOPEZ J. Interpretational applications of spectral decomposition in reservoir characterization[J]. The Leading Edge, 1999, 18(3): 353-360. DOI:10.1190/1.1438295 |
| [3] |
CHAKRABORTY A, OKAYA D. Frequency-time decomposition of seismic data using wavelet-based methods[J]. Geophysics, 1995, 60(6): 1906-1916. DOI:10.1190/1.1443922 |
| [4] |
高静怀, 汪文秉, 朱光明, 等. 地震资料处理中小波函数的选取研究[J]. 地球物理学报, 1996, 39(3): 392-400. GAO J H, WANG W B, ZHU G M, et al. On the choice of wavelet functions for seismic data processing[J]. Chinese Journal of Geophysics, 1996, 39(3): 392-400. |
| [5] |
陈文超, 高静怀. 基于改进的最佳匹配地震子波的地震资料衰减特性研究[J]. 地球物理学报, 2007, 50(1): 837-843. CHEN W C, GAO J H. Characteristic analysis of seismic attenuation using MBMSW wavelets[J]. Chinese Journal of Geophysics, 2007, 50(1): 837-843. |
| [6] |
高静怀, 万涛, 陈文超, 等. 三参数小波及其在地震资料分析中的应用[J]. 地球物理学报, 2006, 49(6): 1802-1812. GAO J H, WAN T, CHEN W C, et al. Three parameter wavelet and its applications to seismic data processing[J]. Chinese Journal of Geophysics, 2006, 49(6): 1802-1812. |
| [7] |
STOCKWELL R G, MANSINHA L, LOWE R P. Localization of the complex spectrum:the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [8] |
ODEBEATU E, ZHANG J, CHAPMAN M, et al. Application of spectral decomposition to detection of dispersion anomalies associated with gas saturation[J]. The Leading Edge, 2006, 25(2): 206-210. |
| [9] |
高静怀, 陈文超, 李幼铭, 等. 广义S变换与薄互层地震响应分析[J]. 地球物理学报, 2003, 46(4): 526-532. GAO J H, CHEN W C, LI Y M, et al. Generalized S transform and seismic response analysis of thin interbeds[J]. Chinese Journal of Geophysics, 2003, 46(4): 526-532. |
| [10] |
LI Y, ZHENG X. Wigner-Ville distribution and its application in seismic attenuation estimation[J]. Applied Geophysics, 2007, 4(4): 245-254. DOI:10.1007/s11770-007-0034-7 |
| [11] |
LIU G, FOMEL S, CHEN X. Time-frequency analysis of seismic data using local attributes[J]. Geophysics, 2011, 76(6): P23-P34. DOI:10.1190/geo2010-0185.1 |
| [12] |
TANER M T, KOEHLER F, SHERIFF R. Complex seismic trace analysis[J]. Geophysics, 1979, 44(6): 1041-1063. DOI:10.1190/1.1440994 |
| [13] |
CASTAGNA J P, SUN S, SIEGFRIED R W. Instantaneous spectral analysis:detection of low-frequency shadows associated with hydrocarbons[J]. The Leading Edge, 2003, 22(2): 120-127. |
| [14] |
MARFURT K, KIRLIN R. Narrow-band spectral analysis and thin-bed tuning[J]. Geophysics, 2001, 66(4): 1274-1283. DOI:10.1190/1.1487075 |
| [15] |
HAN J, VAN DER BAAN M. Empirical mode decomposition for seismic time-frequency analysis[J]. Geophysics, 2013, 78(2): O9-O19. DOI:10.1190/geo2012-0199.1 |
| [16] |
KODERA K, VILLEDARY C D, GENDRIN R. A new method for the numerical analysis of non-stationary signals[J]. Physics of the Earth and Planetary Interiors, 1976, 12(2-3): 142-150. DOI:10.1016/0031-9201(76)90044-3 |
| [17] |
AUGER F, FLANDRIN P. Improving the readability of time-frequency and time-scale representations by the reassignment method[J]. IEEE Transaction on Signal Processing, 1995, 43(5): 1068-1069. DOI:10.1109/78.382394 |
| [18] |
PENG Z, CHU F, HE Y. Vibration signal analysis and feature extraction based on reassignment wavelet scalegram[J]. Journal of Sound and Vibration, 2002, 253(3): 1087-1100. |
| [19] |
WU X, LIU T. Spectral decomposition of seismic data with reassigned smoothed pseudo Wigner-Ville distribution[J]. Journal of Applied Geophysics, 2009, 68(3): 386-393. DOI:10.1016/j.jappgeo.2009.03.004 |
| [20] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A:Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995. DOI:10.1098/rspa.1998.0193 |
| [21] |
薛雅娟, 曹俊兴. 聚合经验模态分解和小波变换相结合的地震信号衰减分析[J]. 石油地球物理勘探, 2006, 51(6): 1148-1155. XUE Y J, CAO J X. Seismic attenuation analysis using the EEMD and CWT[J]. Oil Geological Prospecting, 2006, 51(6): 1148-1155. |
| [22] |
DAUBECHIES I, LU J, WU H T. Synchrosqueezed wavelet transforms:an empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243-261. DOI:10.1016/j.acha.2010.08.002 |
| [23] |
WU H T. Instantaneous frequency and wave shape functions (Ⅰ)[J]. Applied and Computational Harmonic Analysis, 2013, 35(2): 181-199. DOI:10.1016/j.acha.2012.08.008 |
| [24] |
THAKUR G, BREVDO E, FUČKAR N S, et al. The Synchrosqueezing algorithm for time-varying spectral analysis:robustness properties and new paleoclimate applications[J]. Signal Processing, 2013, 93(5): 1079-1094. DOI:10.1016/j.sigpro.2012.11.029 |
| [25] |
MEIGNEN S, OBERLIN T, MCLAUGHLIN S. A new algorithm for synchrosqueezing:With an application to multicomponent signals sampling and denoising[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5787-5795. DOI:10.1109/TSP.2012.2212891 |
| [26] |
LI C, LIANG M. Time-frequency signal analysis for gearbox fault diagnosis using a generalized synchrosqueezing transform[J]. Mechanical Systems and Signal Processing, 2012, 26(1): 205-217. |
| [27] |
HERRERA R H, HAN J, VAN DER BAAN M. Applications of the synchrosqueezing transform in seismic time-frequency analysis[J]. Geophysics, 2014, 79(3): 55-64. |
| [28] |
WANG P, GAO J H, WANG Z G. Time-frequency analysis of seismic data using synchrosqueezing transform[J]. IEEE Signal Process Letters, 2014, 11(12): 2042-2044. |
| [29] |
THAKUR G, WU H T. Synchrosqueezing-based recovery of instantaneous frequency from nonuniform samples[J]. SIAM Journal on Mathematical Analysis, 2011, 43(5): 2078-2095. DOI:10.1137/100798818 |
| [30] |
HUANG Z, ZHANG J, ZHAO T, et al. Synchrosqueezing S-transform and its application in seismic spectral decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 817-825. DOI:10.1109/TGRS.2015.2466660 |
| [31] |
DONOHO D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [32] |
LIU N H, GAO J H, ZHANG Z, et al. High-resolution characterization of geologic structures using the synchrosqueezing transform[J]. Interpretation, 2016, 5(1): T75-T85. |



