基于双程波动方程的逆时偏移方法, 无地层倾角限制, 适应于各种波现象, 是复杂地下构造成像的有效技术[1-3]。由于沉积地层中砂泥岩薄互层、灰岩页岩薄互层以及大块岩石中定向排列的垂直裂隙等常常引起地下地层各向异性[4], 在各向异性介质中地震波弹性特征随方向发生变化, 具体表现为地震波传播速度随着传播方向的变化而变化, 所以如果假设地下介质仍为各向同性, 势必影响地震波场模拟精度和逆时偏移成像分辨率。虽然各向异性介质弹性波偏移理论已经取得了一定突破[5-7], 但在应用过程中依然会遇到障碍。其一, 弹性波是由一个三分量的位移矢量表征, 包括两种模式即纵波和横波, 如利用有限差分法求解波场, 高昂的计算成本和巨大的存储量令人难以接受; 其二, 考虑横波速度较慢, 为了满足波场稳定延拓条件, 须采用较小时间步长和空间网格间距, 必然会影响计算效率; 其三, 纵波与横波分离以及实际弹性参数的确定等都是其制约因素[8]。因此, 对于地震波场在各向异性介质传播特征的研究聚焦于纵波[9-12]。
ALKHALIFAH[13]通过声学近似假设提出适用于VTI介质的四阶波动方程, 该方程qP波特征与弹性波方程纵波分量特征吻合。但是, 利用四阶波动方程不便于波场的求解, ZHOU等[14]引入一个辅助变量, 将qP波方程从四阶简化成两个耦合的二阶波动方程, 从而高效地对qP波进行数值模拟。基于上述研究, FLETCHER等[15-16]通过坐标变换将VTI介质qP波方程推广为TTI介质波动方程。随后, 许多研究学者在ALKHALIFAH提出的四阶qP波方程的基础上, 分别引入不同的辅助变量, 得到了一系列的二阶波动方程[17-19]。李博等[20]针对TTI介质逆时偏移算法的稳定性进行了详尽的探讨。
对于现有的二阶qP波方程, 尽管将方程中横波速度设置为0, 但是地震波场模拟仍出现伪横波分量, 并且, 当地质Thomsen参数变化剧烈时, qP波方程中的伪横波严重影响数值模拟的稳定性, 进而导致逆时偏移方法难以得到理想的成像结果。TSVANKIN[21]提出改变震源处Thomsen参数, 虽然压制了伪横波成分, 却改变了真实地下介质参数; ZHANG[22]提出的滤波投影法压制伪横波取得了理想效果; CHENG等[23]从物理学的角度, 利用波矢量方向与伪横波震动方向的偏差, 从耦合的波场中提取出标量的qP波; PESTANA[24]利用精确频散关系, 推导出波场的递推关系, 得到了解耦P波场。这些压制伪横波的方法提升了逆时偏移成像精度。
如果采用互相关成像条件实现TTI介质逆时偏移, 需要保存所有时刻的震源波场或检波点波场, 因此, 对存储空间的需求较大。SYMES[25]提出checkpiont方法, 仅存储部分时刻的地震波场, 互相关成像时再进行波场重建, 但是该方法仍然需要权衡计算效率和存储成本。从另一个角度讲, 王保利等[26]提出保存若干PML边界层, 再进行波场重建的存储策略, 并将该方法应用到了声波逆时偏移中, 但是该方法在重建时利用了PML边界层中经过衰减的波场信息, 理论上存在重建误差。
在计算机技术取得长足进步的背景下, GPU技术为高效的科学计算提供了强有力的工具。为了提高逆时偏移的计算效率, 逆时偏移算法与GPU硬件相结合成为了历史的必然, 形成的GPU/CPU并行加速计算方案满足了工业化生产的需求[27-29]。
本文在前人研究的基础上, 考虑地下介质的各向异性, 研究并实现了TTI介质波场传播特征的精确描述及逆时偏移成像方法, 并用BP2007模型数据进行了测试。
1 TTI介质qP波方程完全匹配吸收边界有限差分格式的推导刻画地震波在各向异性介质中传播的3个要素是波的震动方向、群速度和相速度。对于二维VTI介质, TSVANKIN[21]通过求解Christoffel方程得到qP-qSV波的精准相速度公式, 即:
| $ \begin{array}{l} \frac{{v_{{\rm{P}}z}^2\left( \varphi \right)}}{{v_{{\rm{P}}z}^2}} = 1 - \frac{1}{2}f + \varepsilon {\sin ^2}\varphi \pm \\ \;\;\;\;\;\;\;\frac{f}{2}\sqrt {{{\left( {1 + \frac{{2\varepsilon {{\sin }^2}\varphi }}{f}} \right)}^2} - \frac{{2\left( {\varepsilon - \delta } \right){{\sin }^2}2\varphi }}{f}} \end{array} $ | (1a) |
| $ f = 1 - v_{{\rm{S}}z}^2/v_{{\rm{P}}z}^2 $ | (1b) |
式中:vP(φ)是P波相速度; φ是相角; vPz和vSz分别为纵波和横波沿着对称轴方向的传播速度; ε和δ为Thomsen参数; “±”中正号对应qP波, 负号对应qSV波。利用相速度、频率和波数之间的关系, 可以得到VTI介质色散方程, 形式如下:
| $ \begin{array}{l} {\omega ^4} = \left[ {\left( {v_{{\rm{P}}x}^2 + v_{{\rm{S}}z}^2} \right)k_x^2 + \left( {v_{{\rm{P}}z}^2 + v_{{\rm{S}}z}^2} \right)k_z^2} \right]{\omega ^2} - \\ \;\;\;\;\;\;\;\;v_{{\rm{P}}x}^2v_{{\rm{S}}z}^2k_x^4 - v_{{\rm{P}}z}^2v_{{\rm{S}}z}^2k_z^4 + \left[ {v_{{\rm{P}}z}^2\left( {v_{{\rm{P}}n}^2 - v_{{\rm{P}}x}^2} \right) - } \right.\\ \;\;\;\;\;\;\;\;\left. {v_{{\rm{S}}z}^2\left( {v_{{\rm{P}}n}^2 + v_{{\rm{P}}z}^2} \right)} \right]k_x^2k_z^2 \end{array} $ | (2a) |
| $ {v_{{\rm{P}}x}} = \sqrt {1 + 2\varepsilon } {v_{{\rm{P}}z}} $ | (2b) |
| $ {v_{{\rm{P}}n}} = \sqrt {1 + 2\delta } {v_{{\rm{P}}z}} $ | (2c) |
式中:ω为角频率; kx和kz为波矢量; vPx为纵波沿垂直对称轴方向的速度; vPn为动校正速度。假设TTI介质的对称轴与垂直方向夹角为θ, (2)式中波矢量通过坐标变换为:
| $ \left( {\begin{array}{*{20}{c}} {{{\hat k}_x}}&{{{\hat k}_z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{k_x}}&{{k_z}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }\\ { - \sin \theta }&{\cos \theta } \end{array}} \right) $ | (3) |
将坐标变换后的波矢量代入(2)式有:
| $ \begin{array}{l} {\omega ^4} = \left[ {\left( {v_{{\rm{P}}x}^2 + v_{{\rm{S}}z}^2} \right){h_2} + \left( {v_{{\rm{P}}z}^2 + v_{{\rm{S}}z}^2} \right){h_1}} \right]{\omega ^2} - \\ \;\;\;\;\;\;\;\;v_{{\rm{P}}x}^2v_{{\rm{S}}z}^2h_2^2 - v_{{\rm{P}}z}^2v_{{\rm{P}}z}^2h_1^2 + \left[ {v_{{\rm{P}}z}^2\left( {v_{{\rm{P}}n}^2 - v_{{\rm{P}}x}^2} \right) - } \right.\\ \;\;\;\;\;\;\;\;\left. {v_{{\rm{S}}z}^2\left( {v_{{\rm{P}}n}^2 + v_{{\rm{P}}z}^2} \right)} \right]{h_1}{h_2} \end{array} $ | (4a) |
| $ {h_1} = k_x^2{\sin ^2}\theta + k_z^2{\cos ^2}\theta + {k_x}{k_z}\sin 2\theta $ | (4b) |
| $ {h_2} = k_x^2{\cos ^2}\theta + k_z^2{\sin ^2}\theta - {k_x}{k_z}\sin 2\theta $ | (4c) |
如果将(4)式两侧乘以频率波数域的波场, 再经过反傅里叶变换后可得到在时间方向上的四阶微分方程, 从而给数值模拟带来了困难。为了解决这一难题, FLETCHER等[15]引入一个频率波数域的辅助变量
| $ \hat q = \frac{{\left( {v_{{\rm{P}}n}^2 - v_{{\rm{S}}z}^2} \right){h_2}}}{{{\omega ^2} - v_{{\rm{S}}z}^2{h_2} - v_{{\rm{P}}z}^2{h_1}}}\hat p $ | (5) |
式中:
| $ {\omega ^2}\hat p = v_{{\rm{P}}x}^2{h_2}\hat p + v_{{\rm{S}}z}^2{h_1}\hat p + \left( {v_{{\rm{P}}z}^2 - v_{{\rm{S}}z}^2} \right){h_1}\hat q $ | (6) |
对方程(5)和方程(6)进行反傅里叶变换就将四阶微分方程转化为适用于TTI介质的两个二阶耦合微分方程:
| $ \frac{{{\partial ^2}p}}{{\partial {t^2}}} = v_{{\rm{P}}x}^2{H_2}p + v_{{\rm{P}}z}^2{H_1}q + v_{{\rm{S}}z}^2{H_1}\left( {p - q} \right) $ | (7a) |
| $ \frac{{{\partial ^2}q}}{{\partial {t^2}}} = v_{{\rm{P}}n}^2{H_2}p + v_{{\rm{P}}z}^2{H_1}q - v_{{\rm{S}}z}^2{H_2}\left( {p - q} \right) $ | (7b) |
对于各向同性介质, 方程(7)中的两式等价, 其二阶微分算子形式如下:
| $ {H_1} = {\sin ^2}\theta \frac{{{\partial ^2}}}{{\partial {x^2}}} + {\cos ^2}\theta \frac{{{\partial ^2}}}{{\partial {z^2}}} + \sin 2\theta \frac{{{\partial ^2}}}{{\partial x\partial z}} $ | (8a) |
| $ {H_2} = {\cos ^2}\theta \frac{{{\partial ^2}}}{{\partial {x^2}}} + {\sin ^2}\theta \frac{{{\partial ^2}}}{{\partial {z^2}}} - \sin 2\theta \frac{{{\partial ^2}}}{{\partial x\partial z}} $ | (8b) |
如果将(8)式中θ设置为0, 那么TTI介质方程就退化为VTI介质方程。
如果利用互相关成像条件, TTI介质逆时偏移成像过程需要对每一时刻的震源波场和检波点波场做互相关。因此, 地震波场的模拟精度直接影响最后成像结果的分辨率, 由于数值模拟只能在有限区域内计算, 存在截断边界, 而边界的内外两侧具有不同的波阻抗, 因而相当于人为增加了一个反射界面, 从而在界面产生虚假反射, 导致结果错误[30-31]。因此, 需要为偏移区域添加吸收层以避免能量反射。本文采用经典PML边界[32]吸收到达边界的波场能量。根据声波PML吸收边界条件的架构[33-35], 将(7)式变换为下列形式:
| $ \begin{array}{l} \frac{{{\partial ^2}p}}{{\partial {t^2}}} + 2d\left( {x,z} \right)\frac{{\partial p}}{{\partial t}} + {d^2}\left( {x,z} \right)p = \\ \;\;\;\;\;\;\;v_{{\rm{P}}x}^2{H_2}p + v_{{\rm{P}}z}^2{H_1}q + v_{{\rm{S}}z}^2{H_1}\left( {p - q} \right) \end{array} $ | (9a) |
| $ \begin{array}{l} \frac{{{\partial ^2}q}}{{\partial {t^2}}} + 2d\left( {x,z} \right)\frac{{\partial q}}{{\partial t}} + {d^2}\left( {x,z} \right)q = \\ \;\;\;\;\;\;\;v_{{\rm{P}}n}^2{H_2}p + v_{{\rm{P}}z}^2{H_1}q - v_{{\rm{S}}z}^2{H_2}\left( {p - q} \right) \end{array} $ | (9b) |
式中:d(x, z)为衰减因子。为了能够实现数值模拟, 时间方向上的二阶和一阶导数项采用公式(10)和公式(11)进行计算。
| $ \begin{array}{l} \frac{{{\partial ^2}p}}{{\partial {t^2}}} = \frac{{{p^{k + 1}} - 2{p^k} + {p^{k - 1}}}}{{\Delta {t^2}}}\\ \frac{{{\partial ^2}q}}{{\partial {t^2}}} = \frac{{{q^{k + 1}} - 2{q^k} + {q^{k - 1}}}}{{\Delta {t^2}}} \end{array} $ | (10) |
| $ \begin{array}{l} \frac{{\partial p}}{{\partial t}} = \frac{{{p^{k + 1}} - {p^{k - 1}}}}{{2\Delta t}}\\ \frac{{\partial q}}{{\partial t}} = \frac{{{q^{k + 1}} - {q^{k - 1}}}}{{2\Delta t}} \end{array} $ | (11) |
将(10)式和(11)式代入(9)式,得到TTI介质qP波方程有限差分格式如下:
| $ \begin{array}{l} {p^{k + 1}} = \frac{1}{{1 + \Delta td\left( {x,z} \right)}}\left\{ {\left[ {2 - \Delta {t^2}{d^2}\left( {x,z} \right)} \right]{p^k} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left[ {\Delta td\left( {x,z} \right) - 1} \right]{p^{k - 1}} + \Delta {t^2}\left[ {v_{{\rm{P}}x}^2{H_2}{p^k} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {v_{{\rm{P}}z}^2{H_1}{q^k} + v_{{\rm{S}}z}^2{H_1}\left( {{p^k} - {q^k}} \right)} \right]} \right\} \end{array} $ | (12a) |
| $ \begin{array}{l} {q^{k + 1}} = \frac{1}{{1 + \Delta td\left( {x,z} \right)}}\left\{ {\left[ {2 - \Delta {t^2}{d^2}\left( {x,z} \right)} \right]{q^k} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left[ {\Delta td\left( {x,z} \right) - 1} \right]{q^{k - 1}} + \Delta {t^2}\left[ {v_{{\rm{P}}n}^2{H_2}{p^k} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {v_{{\rm{P}}z}^2{H_1}{q^k} - v_{{\rm{S}}z}^2{H_2}\left( {{p^k} - {q^k}} \right)} \right]} \right\} \end{array} $ | (12b) |
由公式(12)可以得到波场重建的逆向延拓表达式,如公式(13)所示。
| $ \begin{array}{l} {p^{k - 1}} = \frac{1}{{1 - \Delta td\left( {x,z} \right)}}\left\{ {\left[ {2 - \Delta {t^2}{d^2}\left( {x,z} \right)} \right]{p^k} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left[ {\Delta td\left( {x,z} \right) + 1} \right]{p^{k + 1}} + \Delta {t^2}\left[ {v_{{\rm{P}}x}^2{H_2}{p^k} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {v_{{\rm{P}}z}^2{H_1}{q^k} + v_{{\rm{S}}z}^2{H_1}\left( {{p^k} - {q^k}} \right)} \right]} \right\} \end{array} $ | (13a) |
| $ \begin{array}{l} {q^{k - 1}} = \frac{1}{{1 - \Delta td\left( {x,z} \right)}}\left\{ {\left[ {2 - \Delta {t^2}{d^2}\left( {x,z} \right)} \right]{q^k} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left[ {\Delta td\left( {x,z} \right) + 1} \right]{q^{k + 1}} + \Delta {t^2}\left[ {v_{{\rm{P}}n}^2{H_2}{p^k} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {v_{{\rm{P}}z}^2{H_1}{q^k} - v_{{\rm{S}}z}^2{H_2}\left( {{p^k} - {q^k}} \right)} \right]} \right\} \end{array} $ | (13b) |
采用高阶中心有限差分方法求解(8)式中的空间导数项, 水平方向2N阶差分, 垂直方向2M阶差分, 形式如下:
| $ \begin{array}{l} {H_1}p = {\sin ^2}\theta \sum\limits_{n = 1}^N {{a_n}\left( {p_{i + n,j}^k + p_{i - n,j}^k} \right)/\Delta {x^2}} + \\ \;\;\;\;\;{\cos ^2}\theta \sum\limits_{m = 1}^M {{b_m}\left( {p_{i,j + m}^k + p_{i,j - m}^k} \right)/\Delta {z^2}} + \\ \;\;\;\;\;\sin 2\theta \sum\limits_{n = 1}^N {{c_n}\sum\limits_{m = 1}^M {{d_m}} } \left( {p_{i + n,j + m}^k - p_{i + n,j - m}^k - } \right.\\ \;\;\;\;\;\left. {p_{i - n,j + m}^k + p_{i - n,j - m}^k} \right)/\left( {\Delta x\Delta z} \right) \end{array} $ | (14a) |
| $ \begin{array}{l} {H_2}p = {\cos ^2}\theta \sum\limits_{n = 1}^N {{a_n}\left( {p_{i + n,j}^k + p_{i - n,j}^k} \right)/\Delta {x^2}} + \\ \;\;\;\;\;{\sin ^2}\theta \sum\limits_{m = 1}^M {{b_m}\left( {p_{i,j + m}^k + p_{i,j - m}^k} \right)/\Delta {z^2}} - \\ \;\;\;\;\;\sin 2\theta \sum\limits_{n = 1}^N {{c_n}\sum\limits_{m = 1}^M {{d_m}} } \left( {p_{i + n,j + m}^k - p_{i + n,j - m}^k - } \right.\\ \;\;\;\;\;\left. {p_{i - n,j + m}^k + p_{i - n,j - m}^k} \right)/\left( {\Delta x\Delta z} \right) \end{array} $ | (14b) |
| $ \begin{array}{l} {H_1}q = {\sin ^2}\theta \sum\limits_{n = 1}^N {{a_n}\left( {q_{i + n,j}^k + q_{i - n,j}^k} \right)/\Delta {x^2}} + \\ \;\;\;\;\;{\cos ^2}\theta \sum\limits_{m = 1}^M {{b_m}\left( {q_{i,j + m}^k + q_{i,j - m}^k} \right)/\Delta {z^2}} + \sin 2\theta \sum\limits_{n = 1}^N {{c_n}} \cdot \\ \;\;\;\;\;\sum\limits_{m = 1}^M {{d_m}} \left( {q_{i + n,j + m}^k - q_{i + n,j - m}^k - q_{i - n,j + m}^k + } \right.\\ \;\;\;\;\;\left. {q_{i - n,j - m}^k} \right)/\left( {\Delta x\Delta z} \right) \end{array} $ | (14c) |
| $ \begin{array}{l} {H_2}q = {\cos ^2}\theta \sum\limits_{n = 1}^N {{a_n}\left( {q_{i + n,j}^k + q_{i - n,j}^k} \right)/\Delta {x^2}} + \\ \;\;\;\;\;{\sin ^2}\theta \sum\limits_{m = 1}^M {{b_m}\left( {q_{i,j + m}^k + q_{i,j - m}^k} \right)/\Delta {z^2}} - \sin 2\theta \sum\limits_{n = 1}^N {{c_n}} \cdot \\ \;\;\;\;\;\sum\limits_{m = 1}^M {{d_m}} \left( {p_{i + n,j + m}^k - p_{i + n,j - m}^k - q_{i - n,j + m}^k + } \right.\\ \;\;\;\;\;\left. {q_{i - n,j - m}^k} \right)/\left( {\Delta x\Delta z} \right) \end{array} $ | (14d) |
式中:an, bm, cn, dm为差分系数。
如果采用声学近似的方法, 将方程(12)中横波沿对称轴的速度设置为0, 虽然能够提高计算效率, 但因横波沿着其它方向的速度并不为0, 仍有低振幅低波速的qSV波成分。当TTI介质的对称轴倾角较大或地下介质的对称轴倾角变化较大时, qSV波的存在将导致波场传播不稳定。虽然通过修改各向异性参数能够消除频散的影响, 但也会改变波场传播的动力学特征。为了避免地震波场异常传播, 并且能够准确地描述波场运动学传播特征, 在TTI介质波动方程中引入σ参数, 其数学描述如下:
| $ \sigma = \frac{{v_{{\rm{P}}z}^2}}{{v_{{\rm{S}}z}^2}}\left( {\varepsilon - \delta } \right) $ | (15) |
σ参数在很大程度上决定了qSV波的运动学特征。通过数值模拟, 当设置σ=0.75时, 频散得以压制, 确保波场的稳定传播。
2 基于checkpoint方法的TTI介质逆时偏移波场重建策略基于互相关成像条件的逆时偏移方法需要存储全部时刻震源波场, 或者存储全部时刻的检波点波场, 因而存储成本巨大。以BP2007模型为例, 重建试算截取模型水平方向2 000个网格点, 垂直方向1 801个网格点, 地震记录总时长9.2 s, 为了满足波场延拓稳定性条件, 选取时间步长0.5 ms, 需要延拓18 401次, 保存所有震源波场需要内存约246.9 GB。因此, SHI等[36]考虑存储较少的波场信息, 进而重建震源波场; 王保利等[26]利用存储若干PML吸收层信息实现了波场重建并将该方法应用到声波逆时偏移成像中。对于TTI介质, 逆时偏移成像对数据存储需求更高, 为了增强方法的实用性, 本文中提出了实用的TTI介质的checkpoint波场重建方法。
假定地震波场水平方向为Nx个网格, 垂直方向为Nz个网格, 为了避免边界反射噪声, 在有效波场外侧添加PML吸收衰减层(图 1中绿色区域), 在有效波场内部设置内边界层(图 1中蓝色区域)。内边界层数设定为有限差分阶数的一半, 如果采用空间12阶差分, 则内边界为6层。各向异性介质checkpoint波场重建由两次震源波场正传和一次波场反传组成。其中一次震源波场正传在最小时刻和最大时刻之间进行, 而另一次震源波场正传和一次震源波场反传逐个在两个checkpoint之间进行。具体如下。

|
图 1 波场存储示意 |
假设震源波场正向传播的时间点为N×m, N为在此传播过程中确定的checkpoint个数, m为每两个checkpoint间的时间点数。在波场正向延拓过程中, 保存每个checkpoint及其前一时间点处的p和q全部波场(图 1中PML吸收层、内边界层和内部区)至计算机内存, 图 2中黑点表示存储p和q全部波场的时间位置。例如, 当波场延拓至checkpoint N时, 记录(N×m-1)和N×m时间点对应的p和q全部波场。

|
图 2 checkpoint存储示意 |
以checkpoint(N-1)至checkpoint N期间的波场重建为例, 需从计算机内存中读取(N-1)×m-1及(N-1)×m时间点对应的p和q全部波场信息作为初值进行m次正向延拓, 并将每次延拓波场的内边界层(图 1中蓝色区域)信息保存至GPU的显存。利用公式(13)将N×m-1和N×m节点对应的p和q全部波场作为反向延拓的初值, 每延拓一次将上一步骤中保存至显存上p和q的内边界层(图 1中蓝色区域)信息载入到重建波场的对应位置, 延拓m次便可重建出checkpoint(N-1)至checkpoint N之间对应的震源波场。其它任两个checkpoint之间波场重建及内边界层的保存办法同上, 进而重建出N×m至最小时刻的震源波场。本文提出的TTI介质逆时偏移成像方法是在checkpoint框架下, 通过保存内边界层信息实现震源波场重建, 而非保存经过吸收衰减后的PML吸收层波场信息, 因此确保了波场重建精度。另外, 在波场重建过程中, 与保存所有波场相比, 仅保存两个checkpoint之间波场的内边界层信息, 虽然多了一次波场正向延拓的计算量, 但是GPU/CPU协同并行计算技术在本文方法中的应用, 较大地提高了计算效率, 充分补偿了由此带来的计算负担, 达到了以计算换存储的目的。需要指出的是在延拓时间点一定的情况下, checkpoint越多, GPU显存占用就越少, 虽然降低了对GPU硬件的要求, 但是增加了计算机内存与显存之间数据交换的次数, 这将导致计算耗时明显增长, 所以在确保两checkpoint间的波场内边界占用空间不超过GPU显存的情况下, 可适当减少checkpoint数, 以降低数据交换频率, 从而达到计算效率的优化。
3 各向异性介质模型数据测试 3.1 TTI介质正演数值模拟为了验证上述推导带有PML吸收边界qP波方程有限差分格式的正确有效性, 测试了均匀TTI介质的地震波场传播。假定模型在水平和垂直方向的网格数均为320, 水平方向和垂直方向的网格间距均为6.25 m, 沿对称轴方向的纵波速度vPz=3 000 m/s, Thomsen各向异性参数δ=0.1, ε=0.3, PML吸收边界层数为50, 震源位于模型的中央, 主频为30 Hz的雷克子波作为激发震源, 时间采样间隔为0.5 ms。
利用本文推导的公式(12)进行数值模拟得到的波场快照如图 3所示。图 3a为对称轴倾角θ=0, 沿着对称轴方向的横波速度为0, 波传播时间为200 ms时p的波场快照。图 3b为对称轴倾角θ=0, 沿着对称轴方向的横波速度为0, 波传播时间为350 ms时p的波场快照, 观察图 3b可知, PML边界对地震边界波场的吸收效果较为理想。图 3c为对称轴倾角θ=30°, 沿着对称轴方向的横波速度为0, 波传播时间为200 ms时p的波场快照。从图 3c可以看出, qSV波附近位置出现严重频散现象。图 3d为对称轴倾角θ=30°, 沿着对称轴方向的横波速度为1 500 m/s, 波传播时间为200 ms时的p的波场快照, 可见, 加入适当的横波速度或者引入σ参数后, 频散得到了有效抑制, TTI介质数值模拟精度较高。图 3a, 图 3b和图 3c中虽然横波沿对称轴方向的速度为0, 但是沿着其它方向的横波速度并不为0, 因此出现了qSV波, 如图中菱形状波场所示。

|
图 3 p的波场快照 a vSz=0, θ=0, t=200 ms; b vSz=0, θ=0, t=350 ms; c vSz=0, θ=30°, t=200 ms; d vSz=1 500 m/s, θ=30°, t=200 ms |
测试结果表明, 对于图 3d所示的数值模拟, 采用CPU算法共耗时7 min, 采用CPU/GPU协同并行加速算法耗时8.5 s, 计算效率提高约50倍。如果将模型的横、纵向网格点数由320增加至3 200, 数据量增加100倍, 采用CPU/GPU协同并行加速算法耗时40.9 s, 计算耗时是原数据的5倍。由此可见, 在波场正演模拟中引入CPU/GPU协同并行加速技术, 可以大幅提升计算效率, 随着模型网格点数的增大, 并行计算耗时也相应地增加, 但并不是线性增加。
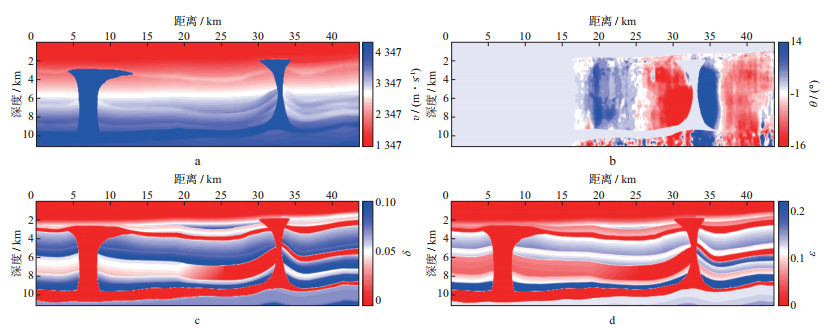
3.2 TTI介质逆时偏移试算利用BP2007复杂构造模型检验本文介绍的TTI介质逆时偏移成像方法。模型水平方向12 596个网格点, 垂直方向1 801网格点, 网格间距6.25 m, 水平长度78.70 km, 垂直深度11.25 km。该模型数据共1 641炮, 每炮800道, 最小偏移距37.5 m, 道间距12.5 m, 时间方向1 151个采样点, 采样间隔为8 ms。本文截取其水平方向43.70 km, 共626炮数据进行TTI介质逆时偏移成像测试, 截取部分模型参数如图 4所示。
|
图 4 TTI介质模型参数 a 纵波沿着对称轴的速度; b Thomsen参数θ; c Thomsen参数δ; d Thomsen参数ε |
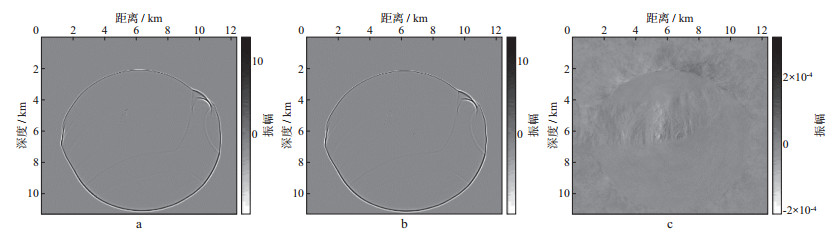
首先利用截取部分模型来测试基于checkpoint方法重建qP波的可行性和有效性。截取模型的水平方向2 000个网格点, 垂直方向1 801网格点, 时间采样间隔为0.5 ms, 利用主频为30 Hz的雷克子波作为激发震源, 激发点位于水平方向1 000网格点、垂直方向900网格点处。震源波场传播至1.5 s时的波场快照如图 5a所示, 震源波场传播至最大时刻后, 再根据本文提出的checkpoint方法和内边界保存技术对震源波场进行分时段的正向传播和逆向传播, 逆向传播至1.5 s时的震源波场如图 5b所示。正向传播的震源波场和逆向传播的震源重建波场在1.5 s时刻的波场误差如图 5c所示, 误差波场振幅与有效波场振幅相差5个数量级, 可忽略不计。由此可知, 在checkpoint方法框架下保存波场内边界的方法, 可以有效地进行波场重建, 丰富了逆时偏移算法的研究, 为TTI介质逆时偏移方法的工业化应用带来了更广阔的发展空间。
|
图 5 震源波场重建 a 正传震源波场; b 重建震源波场; c 重建震源波场误差 |
利用截取的BP2007模型进行偏移试算。单炮偏移区域水平方向2 000个网格点, 垂直方向1 801个网格点, 空间网格间距为6.25 m, 时间采样间隔为0.5 ms。先将震源子波和地层模型对震源波场正向延拓, 保存震源波场部分信息, 然后根据保存的波场信息, 基于checkpoint方法对震源波场重建, 与此同时将炮集数据加载到检波点得到沿时间逆向的检波点波场, 最后经震源归一化成像条件得到单炮偏移剖面。经单炮逆时偏移算法测试, 采用CPU/GPU协同并行加速算法耗时39 min, 从上述波场重建方法可知该时长受checkpoint数的影响, 而采用CPU算法耗时1 755 min, GPU硬件的应用可大幅提升逆时偏移的计算效率。对单炮偏移剖面利用拉普拉斯方法去除低频噪声后, 将626炮偏移结果进行多炮叠加得到最后的偏移剖面, 如图 6所示。从图 6可知, 基于qP波方程得到的剖面同相轴连续性好, 两个陡倾角盐丘与模型位置匹配。

|
图 6 逆时偏移剖面 |
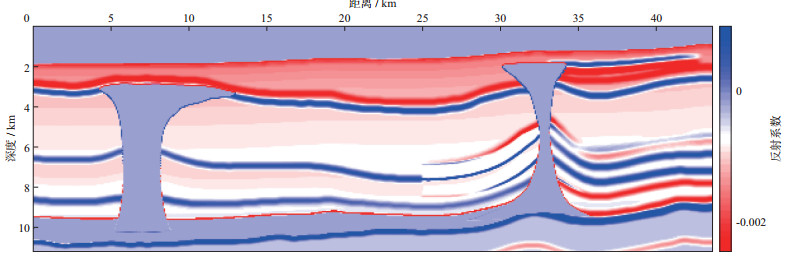
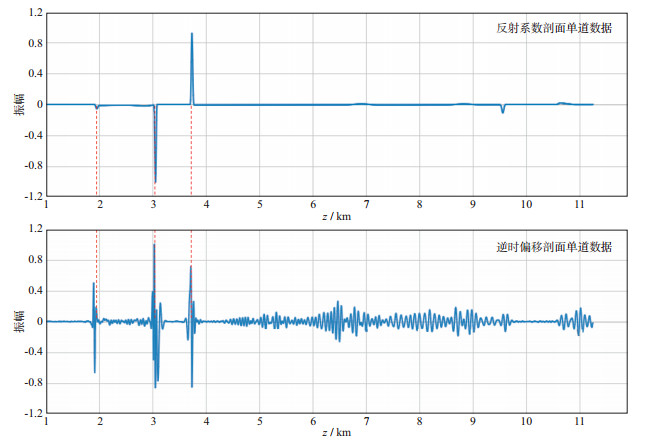
为了便于分析本文逆时偏移方法的精确性, 根据偏移速度场, 结合常密度参数, 计算得到反射系数模型, 如图 7所示。分别在图 6和图 7的水平方向11.25 km位置抽取单道数据如图 8所示(图中横轴为剖面的垂直深度, 纵轴是经归一化的单道振幅信息)。由图 8可知, 逆时偏移剖面包含了强反射系数信息, 同时弱反射系数也得以体现。因此, 本文的逆时偏移方法可以实现对地下各向异性构造体的精细刻画。
|
图 7 反射系数模型 |
|
图 8 水平方向11.25 km处单道数据对比 |
从精准相速度公式出发, 推导了基于有限差分数值解法的TTI介质qP波方程的PML吸收边界格式。由波场快照可知, 当波场能量传播至边界层后吸收效果良好。在波动方程中引入横波速度, 数值试验结果表明, 该方法有效地压制了qSV波频散, 能够解决波场传播不稳定的问题。为了解决算法无法在有限显存GPU端运行的问题, 本文在各向异性介质偏移成像过程中应用了基于checkpoint方法和保存内边界波场的存储策略, 极大地降低了存储, 虽然该策略增加了一次波场正向延拓计算量以及硬件之间数据的传输时间, 但是偏移成像过程中应用了GPU/CPU并行加速技术, 总体上大幅度提升了计算效率, 实现以计算换存储的目的, 从而降低对计算硬件的依赖, 为TTI介质逆时偏移成像的工业化应用开辟了有效的思路。
| [1] | BAYSAL E, KOSLOFF D, SHERWOOD J. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524 DOI:10.1190/1.1441434 |
| [2] | MCMECHAN G A. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 1983, 31(3): 413-420 DOI:10.1111/gpr.1983.31.issue-3 |
| [3] | WHITMORE N D. Iterative depth migration by backward time propagation[J]. Expanded Abstracts of 53rd Annual Internat SEG Mtg, 1983: 382-385 |
| [4] | THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966 DOI:10.1190/1.1442051 |
| [5] | YAN J, SAVA P. 3D elastic wave mode separation for TTI media[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009: 1197-1201 |
| [6] | YAN J, SAVA P. Elastic wave-mode separation for VTI media[J]. Geophysics, 2009, 74(5): 1954-1966 |
| [7] | HU X L, JIA X F, ZHANG W. A dynamic lattice method for elastic wave modeling and migration in TTI media[J]. Expanded Abstracts of 86th Annual Internat SEG Mtg, 2016: 447-451 |
| [8] |
秦海旭, 吴国忱. TTI介质弹性波随机边界逆时偏移的实现[J].
石油物探, 2014, 53(5): 570-578 QIN H X, WU G C. The implementation of elastic reverse time migration in TTI media based on random boundary[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 570-578 |
| [9] |
张千祥, 王德利, 周进举. 二维TTI介质的纯P波波动方程数值模拟[J].
石油物探, 2015, 54(5): 485-492 ZHANG Q X, WANG D L, ZHOU J J. Acoustic wave equation numerical simulation for pure P-wave in 2D TTI medium[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 485-492 |
| [10] |
张衡, 刘洪, 李博, 等. TTI介质声波方程分裂式PML吸收边界条件研究[J].
石油物探, 2017, 56(3): 349-361 ZHANG H, LIU H, LI B, et al. The research on split PML absorbing boundary conditions of acoustic equation for TTI media[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 349-361 |
| [11] | ALKHALIFAH T. Acoustic approximations media for processing in transversely isotropic[J]. Geophysics, 1998, 63(2): 623-631 DOI:10.1190/1.1444361 |
| [12] | HAN Q, WU R S. One-way dual-domain propagator for scalar qP-waves in VTI media[J]. Geophysics, 2005, 70(2): D9-D17 DOI:10.1190/1.1884826 |
| [13] | ALKHALIFAH T. An acoustic wave equation for anisotropic media[J]. Geophysics, 2000, 65(4): 1239-1250 DOI:10.1190/1.1444815 |
| [14] | ZHOU H B, ZHANG G Q, BLOOR R. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media[J]. Expanded Abstracts of 76th Annual Internat SEG Mtg, 2006: 194-198 |
| [15] | FLETCHER R P, DU X, FOWLER P J. Reverse time migration in tilted transversely isotropic(TTI) media[J]. Geophysics, 2009, 74(6): WCA179-WCA187 DOI:10.1190/1.3269902 |
| [16] | FLETCHER R P, DU X, FOWLER P J. Stabilizing acoustic reverse-time migration in TTI media[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009: 2985-2989 |
| [17] | DUVENECK E, MILCIK P, BAKKER P M. Acoustic VTI wave equations and their application for anisotropic reverse-time migration[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008: 2186-2190 |
| [18] | FOWLER P J, DU X, FLETCHER R P. Coupled equations for reverse-time migration in transversely isotropic media[J]. Geophysics, 2010, 75(1): S11-S22 DOI:10.1190/1.3294572 |
| [19] | ZHANG L B, RECTOR J W, HOVERSTEN G M. An acoustic wave equation for modeling in tilted TI media[J]. Expanded Abstracts of 73rd Annual Internat SEG Mtg, 2003: 153-156 |
| [20] |
李博, 李敏, 刘红伟, 等. TTI介质有限差分逆时偏移的稳定性探讨[J].
地球物理学报, 2014, 57(4): 1366-1375 LI B, LI M, LIU H W, et al. Stability of reverse time migration in TTI media[J]. Chinese Journal of Geophysics, 2014, 57(4): 1366-1375 |
| [21] | TSVANKIN I. Seismic signatures and analysis of reflection data in anisotropic media[M]. New York: Elsevier, 2001: 1-454. |
| [22] | ZHANG H Z. Removing S-wave noise in TTI reverse time migration[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009: 2849-2853 |
| [23] | CHENG J B, KANG W. Simulating propagation of separated wave modes in general anisotropic media, part Ⅱ:qS-wave propagators[J]. Geophysics, 2016, 81(2): C39-C52 DOI:10.1190/geo2015-0253.1 |
| [24] | PESTANA R C. Separate P-and SV-wave equations for VTI media[J]. 12th International Congress of the Brazilian Geophysical Society & EXPOGEF SEG, 2011: 1227-1232 |
| [25] | SYMES W W. Reverse time migration with optimal checkpointing[J]. Geophysics, 2007, 72(5): SM213-SM221 DOI:10.1190/1.2742686 |
| [26] |
王保利, 高静怀, 陈文超, 等. 地震叠前逆时偏移的有效边界存储策略[J].
地球物理学报, 2012, 55(7): 2412-2421 WANG B L, GAO J H, CHEN W C, et al. Efficient boundary storage strategies for seismic reverse migration[J]. Chinese Journal of Geophysics, 2012, 55(7): 2412-2421 |
| [27] |
刘国峰, 刘洪, 李博, 等. 山地地震资料叠前时间偏移方法及其GPU实现[J].
地球物理学报, 2009, 52(12): 3101-3108 LIU G F, LIU H, LI B, et al. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation[J]. Chinese Journal of Geophysics, 2009, 52(12): 3101-3108 |
| [28] |
李博, 刘红伟, 刘国峰, 等. 地震叠前逆时偏移算法的CPU/GPU实施对策[J].
地球物理学报, 2010, 53(12): 2938-2943 LI B, LIU H W, LIU G F, et al. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU[J]. Chinese Journal of Geophysics, 2010, 53(12): 2938-2943 |
| [29] |
刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现[J].
地球物理学报, 2010, 53(7): 1725-1733 LIU H W, LI B, LIU H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J]. Chinese Journal of Geophysics, 2010, 53(7): 1725-1733 |
| [30] |
柯璇, 石颖, 宋利伟, 等. 基于褶积完全匹配吸收边界的声波方程数值模拟[J].
石油物探, 2017, 56(5): 637-643 KE X, SHI Y, SONG L W, et al. Numerical modeling of acoustic wave equations based on convolutional perfectly matched layer absorbing boundary condition[J]. Geophysical Prospecting for Petroleum, 2017, 56(5): 637-643 |
| [31] |
柯璇, 石颖, 张莹莹, 等. 地震叠前逆时偏移衰减随机边界条件研究[J].
石油物探, 2017, 56(4): 523-533 KE X, SHI Y, ZHANG Y Y, et al. A damped random boundary condition for prestack reverse time migration[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 523-533 |
| [32] | BERENGER J P. A Perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200 DOI:10.1006/jcph.1994.1159 |
| [33] |
孙林洁, 印兴耀. 基于PML边界条件的高倍可变网格有限差分数值模拟方法[J].
地球物理学报, 2011, 54(6): 1614-1623 SUN L J, YIN X Y. A finite-difference scheme based on PML boundary condition with high power grid step variation[J]. Chinese Journal of Geophysics, 2011, 54(6): 1614-1623 |
| [34] | LIU Q H, TAO J P. The perfectly matched layer for acoustic waves in absorptive media[J]. Journal of the Acoustical Society of America, 1997, 102(4): 2072-2082 DOI:10.1121/1.419657 |
| [35] | CHEW W C, LIU Q H. Perfectly matched layers for elastodynamics:a new absorbing boundary condition[J]. Journal of Computational Acoustics, 1996, 4(4): 341-359 DOI:10.1142/S0218396X96000118 |
| [36] | SHI Y, WANG Y H. Reverse time migration of 3D vertical seismic profile data[J]. Geophysics, 2016, 81(1): S31-S38 DOI:10.1190/geo2015-0277.1 |




 ,
,