野外地震数据不可避免地含有各种噪声, 尤其是随机噪声, 会影响偏移、反褶积、插值、多次波消除等处理的结果^[1], 消除随机噪声、获得高信噪比的地震数据, 对于后期地震数据处理、解释和反演非常重要。随机噪声消除方法有f-x域去噪方法^[2]、局部奇异值分解法^[3]、Karhunen-Loeve(K-L)变换法^[4]、Cadzow滤波法^[5]、经验模态分解法^[6]、基于独立分量分析的去噪方法^[7]、基于稀疏反演的去噪方法^[8-9]等等。近年来字典学习方法^[10]也被用于地震数据去噪。这些方法大都假设地震记录的相邻道含有随机噪声, 并且仅适合线性同相轴记录, 基于这些方法去噪需要对数据进行分块处理。基于稀疏反演的方法利用解的某种先验信息建立反演模型, 通过求解该模型实现去噪的目的。先验信息有全变差极小^[5]、地震数据在某个变换域的稀疏性约束^[8-9]等。常用的变换有小波变换^[11]、曲波变换^[12]、Radon变换^[13]、物理小波框架^[14]、S变换^[15]等。当采用曲波变换^[9]等多尺度变换时, 基于稀疏反演的方法可以解决非线性同相轴记录的去噪问题。稀疏反演模型确定后, 还需估计一个合适的正则参数(阈值参数、噪声能量)才能得到可靠的解^[16-17]。而估计一个合适的正则参数往往需要进行多次人工调试, 这会耗费很多计算成本和时间。目前反演领域中获得正则参数(阈值)的方法主要有广义交叉检验准则和L曲线法。广义交叉检验准则定义函数${\rm{GCV}}(\delta ) = \frac{1}{M}{(\frac{M}{{{M_0}}})^2}{\left\| {{\omega _\delta } - \omega } \right\|^2}$, 其中δ为变换域的阈值, ω_δ为经过阈值处理后的变换域的系数, ω为阈值运算之前的变换域的系数, M为变换域系数的个数, M₀为经过阈值处理后被置为0的变换域的系数个数。调整阈值δ的大小使得GCV函数取极小时, 经过阈值去噪后的信号均方根误差逼近最小, 从而获得合适的正则参数。L曲线方法以目标函数和相应的约束项函数的对数为坐标得到一条参数曲线, 该曲线一般是L形状, 在曲率最大点处对应的正则参数一般被当作最优正则参数。但是上述两种方法都是针对2范数为正则项的反演模型提出的, 并且在某些情况下会失效^[18]。本文基于稀疏变换的去噪原理, 针对地震数据去噪问题的1范数正则化模型, 提出一种适合该模型的自适应随机噪声消除方法, 利用理论模型数据和实际地震数据对方法进行了测试。

1 方法技术

含随机噪声的地震数据可表示为有效信号和随机噪声之和:

$ \mathit{\boldsymbol{d}} + \mathit{\boldsymbol{n}} = {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} $

(1)

式中:d表示有效信号, d_obs代表观测数据, n表示加性随机噪声。假设有效信号d经过某个变换后有稀疏的表达, 则公式(1)可以表示为:

$ \mathit{\boldsymbol{ \boldsymbol{\varPsi} x}} + \mathit{\boldsymbol{n}} = {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} $

(2)

式中:Ψ为稀疏变换, x是信号在变换域的稀疏表示。基于x的稀疏性, 当噪声的能量已知时, 可以通过求解模型(3)得到x:

$ {\rm{min}}{\left\| \mathit{\boldsymbol{x}} \right\|_{\;1}}\;\;\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} x - }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|_{\;2}} \le \sigma $

(3)

其中σ表示噪声能量。由于σ的估计一般比较困难, 因此通常求解与模型(3)等价的稀疏反演模型:

$ {\rm{min}}\frac{1}{2}\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} x - }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|\;_2^2 + \lambda {\left\| x \right\|_{\;1}} $

(4)

其中λ＞0是正则参数, 用来平衡拟合误差${\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}_k}\mathit{\boldsymbol{ - }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|_{\;2}}$和x的稀疏性。求解模型(4)得到x后, 通过变换Ψ将x变换到时间-空间域即可实现去噪的目的。基于该反演模型去噪的关键是选择合适的λ, 当随机噪声能量较弱时, 应选择较小的λ, 当随机噪声的能量较强时, 应选择较大的λ, 只有当λ选择合适时, 才能达到解的精度和去噪效果的最佳平衡, 当λ选择不合适时, 即使再优秀的算法也得不到最优解。同时, 理论上λ和σ存在一一对应关系, 即对于某个σ, 存在一个λ使得模型(3)和模型(4)的解相同。由于不同数据的噪声能量不同, 因此需要针对具体的数据来估计λ。

在求解模型(4)实现去噪时, 一般先给模型(4)赋予较大的正则参数, 然后逐渐减小正则参数, 以较大正则参数确定的模型的解作为较小正则参数确定的模型的初始解, 以此类推直到确定出合适的最小正则参数。当采用迭代软阈值法求解模型(4)时, 正则参数与阈值相对应, 基于该方法去噪的关键是获得合适的最小阈值。当噪声能量未知时, 一般通过人工调节获得较为准确的最小阈值, 这会耗费大量的人力和计算资源。为了实现自适应去噪, 固定某个正则参数λ_k或者阈值τ_k, 解模型(4)得到解x_k。定义一个新的参数:

$ {P_k} = {\rm{lg}}({\left\| {{\mathit{\boldsymbol{x}}_k}} \right\|_1}) \cdot {\rm{lg}}({\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}_k}\mathit{\boldsymbol{ - }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|_{\;2}}) $

(5)

随着正则参数或者阈值的下降, ${\left\| {{\mathit{\boldsymbol{x}}_k}} \right\|_{\;1}}$逐渐增加, 而拟合误差${\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}_k}\mathit{\boldsymbol{ - }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|_{\;2}}$逐渐减小, P_k逐渐增大, 直到出现最大极值后逐渐减小。多次数值试验表明, 当P_k达到极大值时, 所对应的阈值即为一个较合适的阈值, 利用该阈值能够获得较好的去噪结果^[12]。基于上述发现, 本文给出一种自适应去噪方法的具体实现步骤。

步骤1:输入观测数据d_obs, 稀疏变换Ψ, 定义迭代次数N和最小阈值τ, 令k=0。

步骤2:定义初始解为x₀=0, 初始残差为r₀=d_obs, 初始阈值为${\tau _0} = {\rm{max}}{\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{\rm{H}}}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|_\infty }$, Ψ^H为Ψ的共轭转置或者逆变换, 令${P_0} = {\rm{lg}}({\left\| {{\mathit{\boldsymbol{x}}_0}} \right\|_{\;1}}) \cdot {\rm{lg}}({\left\| {{\mathit{\boldsymbol{r}}_0}} \right\|_{\;2}})$。

步骤3:通过软阈值运算更新变换域的系数, 即${\mathit{\boldsymbol{x}}_{k + 1}} = {\mathit{\boldsymbol{H}}_{{\tau _k}}}[{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{\rm{H}}}({\mathit{\boldsymbol{r}}_k} + \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}_k})]$, 其中H_τk(·)为软阈值运算。定义${\mathit{\boldsymbol{r}}_{k + 1}} = {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}_{k + 1}}$, 令

$ {P_{k + 1}} = {\rm{lg}}({\left\| {{\mathit{\boldsymbol{x}}_{k + 1}}} \right\|_{\;1}})\cdot{\rm{lg}}({\left\| {{\mathit{\boldsymbol{r}}_{k + 1}}} \right\|_{\;2}}) $

(6)

步骤4:如果P_k－1＜P_k＞P_k+1, 则转步骤5;否则通过指数法将阈值降低为τ_k+1, 令k=k+1, 转步骤3。

步骤5:输出最终解${\mathit{\boldsymbol{d}}_{{\rm{final}}}} = \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}_k}$。

由于线性阈值下降方法的阈值下降太快, 为防止阈值变化剧烈错过最合适的阈值, 本文采用指数下降方法来降低阈值, 使得迭代后期阈值下降缓慢。设定在迭代N次内下降到最小阈值, 实际则依靠步骤4终止迭代。本文算法针对每个τ_k对模型(4)进行一次迭代软阈值运算, 求出的结果作为阈值为τ_k+1时模型(4)的初始解, 这样会显著地减小计算量, 提高计算效率。为了使得变换域的系数更加稀疏, 本文采用曲波变换^[12]为稀疏变换。曲波变换不需要对数据进行分块, 比小波变换和傅里叶变换有更加稀疏的表达, 并且对曲波变换进行转置即可实现求逆运算, 因此是较理想的稀疏变换。关于曲波变换更加详细的内容见参考文献[12]。

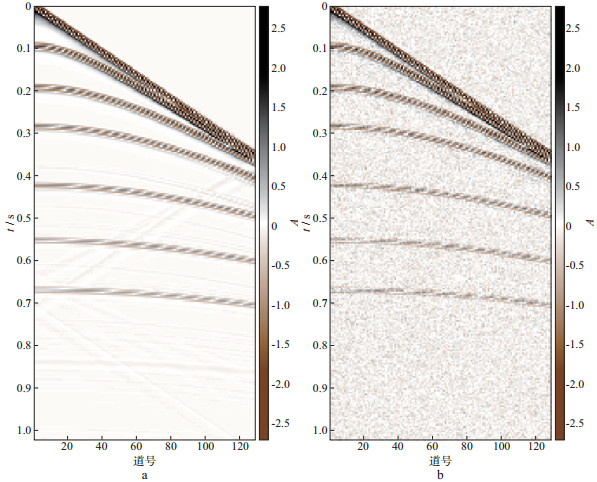
2 数值实验 2.1 模拟数据

利用图 1所示模拟数据对本文方法进行了测试。图 1a是一个模拟地震单炮数据, 共128道, 时间采样点数为256, 时间采样率为4ms; 图 1b为图 1a加入随机噪声的结果, 信噪比为6.7325dB。信噪比的定义为${R_{{\rm{SN}}}} = 10{\rm{lg}}(\left\| \mathit{\boldsymbol{x}} \right\|\;_2^2/\left\| {\mathit{\boldsymbol{x - }}{\mathit{\boldsymbol{x}}_{{\rm{nosie}}}}} \right\|\;_2^2)$, 其中x_noise表示含有噪声的数据, x表示不含噪声的数据。

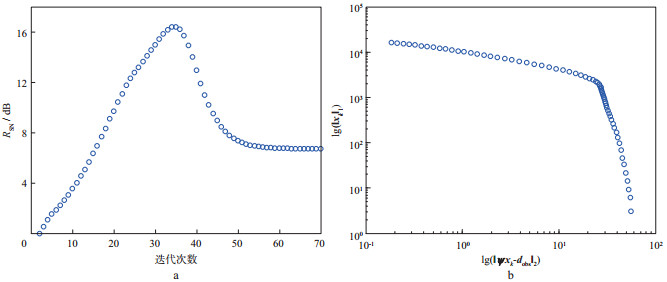
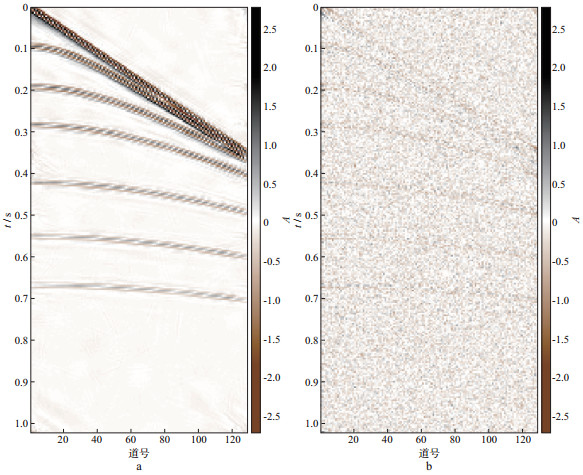
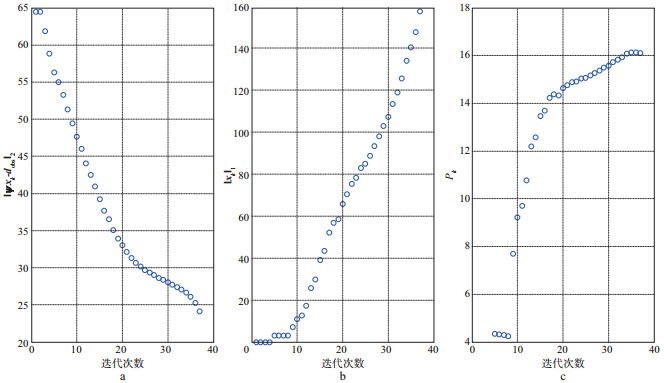
首先采用软阈值方法去噪。令阈值从变换域的最大系数开始, 按照指数方式下降到一个很小的阈值, 由于原始数据已知, 因此可以求出每个阈值所对应的去噪结果的信噪比。令总的阈值下降次数为70, 信噪比随阈值的变化如图 2a所示, 可以看出在第35次迭代(对应的阈值为0.153)时, 得到的信噪比最高。模型(4)的L曲线如图 2b所示, 此曲线与基于2范数正则化的L曲线差异很大, 因此按照L曲线法不能获得适合模型(4)的正则参数。图 3a是本文自适应去噪方法获得的结果, 信噪比为12.666dB, 经过36次迭代后算法停止(对应的阈值为0.1543), 确定的阈值与图 2a中信噪比最大时的阈值吻合。由此可见, 采用本文算法能够得到一个合适的阈值, 并且自动终止迭代, 获得较好的去噪结果。图 3b是图 1b和图 3a之间的差值剖面, 表示滤掉的噪声。图 3b中除含有随机噪声外, 还存在一定程度的有效信号, 原因是基于稀疏变换和阈值运算的去噪方法将变换域中小于阈值的系数都作为噪声, 当变换域有效信号的系数小于阈值时, 此方法不仅去掉了噪声, 而且去掉了一部分有效信号。这是基于稀疏变换的阈值去噪方法自身存在的问题, 需要研究出更加合适的稀疏表达方式来解决。图 4a, 图 4b和图 4c分别是模拟数据去噪过程中拟合误差${\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}_k}\mathit{\boldsymbol{ - }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|_{\;2}}$、解的1范数${\left\| {{\mathit{\boldsymbol{x}}_k}} \right\|_{\;1}}$和参数P_k随迭代次数的变化情况。随着阈值的下降, ${\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}_k}\mathit{\boldsymbol{ - }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|_{\;2}}$逐渐减小, 而${\left\| {{\mathit{\boldsymbol{x}}_k}} \right\|_{\;1}}$逐渐增大, P_k在迭代开始阶段逐渐增大, 在第36次迭代时开始降低, 因此取此时的阈值最为合适。MONTE-FUSCO等^[19]提出了H曲线方法, 该方法通过计算H曲线曲率最大的点确定正则参数, 需要计算出所有的正则参数确定的反演模型才能得到合适的正则参数, 因此计算量较大。

2.2 实际地震数据

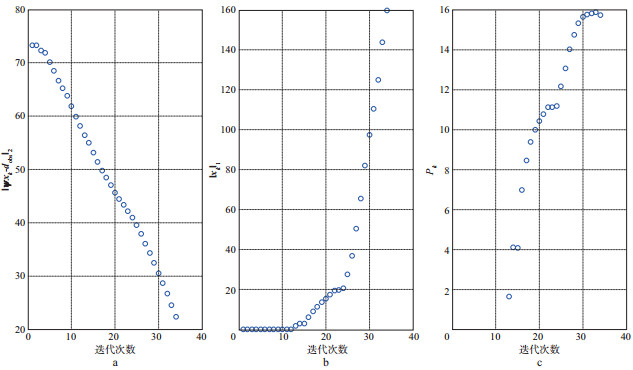
采用实际地震数据验证了本文方法的有效性。图 5a是我国西北某地区含随机噪声的叠后地震数据, 由于噪声的存在, 同相轴模糊, 断层划分困难。图 5b是利用本文方法对其去噪的结果, 设定的最大迭代次数为60次, 最小阈值为0.004。经过34次迭代后算法自动终止, 得到的阈值为0.097。由图 5b可见, 利用本文方法去噪后同相轴变得清晰连贯, 能够清楚地确定断层位置。图 5c是图 5b与原始含噪声数据(图 5a)的差值剖面, 该剖面没有明显的有效信号, 说明本文去噪方法去掉的基本上为随机噪声。图 6a, 图 6b和图 6c分别是该地区实际地震数据去噪过程中拟合误差${\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}_k}\mathit{\boldsymbol{ - }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|_{\;2}}$、解的1范数${\left\| {{\mathit{\boldsymbol{x}}_k}} \right\|_{\;1}}$和参数P_k随迭代次数的变化情况, 可见本文提出的自适应去噪方法能够自动获得阈值, 进而有效去除随机噪声。

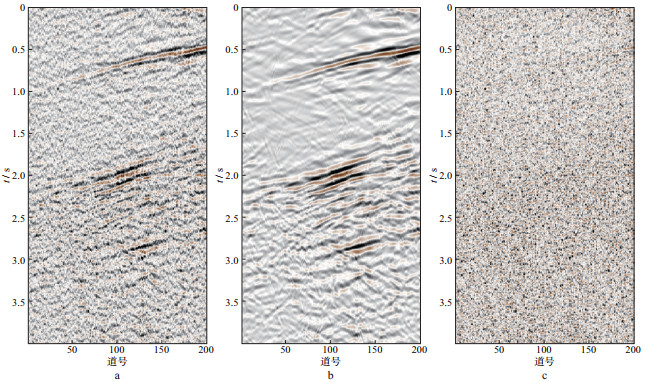
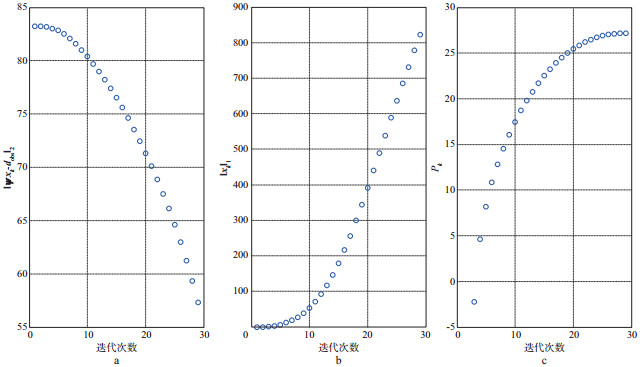
图 7a为我国东部某地区含噪声地震数据, 同相轴连续性差, 随机噪声强。图 7b是本文方法对该数据去噪的结果, 设定的最大迭代次数为60, 最小阈值为0.006。经过29次迭代后算法自动终止, 确定的阈值为0.1756。由图 7b可见, 利用本文方法去噪后, 一些不连续和不稳定的同相轴可以得到清楚的判识, 说明本文方法取得了较好的去噪效果。图 7c是图 7a与图 7b之间的差值剖面, 几乎看不到有效信号, 说明本文方法能在去噪的同时, 不损伤有效信号。图 8a, 图 8b和图 8c分别是该地区实际地震数据去噪过程中拟合误差${\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}_k}\mathit{\boldsymbol{ - }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|_{\;2}}$、解的1范数${\left\| {{\mathit{\boldsymbol{x}}_k}} \right\|_{\;1}}$和参数P_k随迭代次数的变化情况, 在P_k开始下降时迭代停止, 再次说明本文提出的自适应去噪方法能够自动获得阈值, 有效去除随机噪声。

3 结束语

本文提出一种自适应地震数据随机噪声消除方法, 采用曲波变换作为稀疏变换, 利用解的稀疏性和拟合误差之间的内在关系自动获得合适的正则参数(阈值), 只需要选择初始阈值和迭代次数就能够实现迭代去噪过程的自动终止, 实现噪声的有效去除。由于不需要对所有固定正则参数的模型进行求解就能够获得较好的去噪结果, 因此计算成本大大减少。

需要注意的是, 为了防止初始迭代时解的不稳定, 前几次迭代结果不能作为判断终止迭代的标准。另外, 若采用三维曲波变换为稀疏变换, 则本文算法可用于三维地震数据去噪。

致谢: 衷心感谢长安大学包乾宗老师和中国石油大学(北京)袁三一老师对本文研究的指导和帮助。