近年来, 压缩感知理论在地震勘探中受到越来越多的关注, 在地震数据去噪、数据压缩、采集系统设计与评价等方面得到广泛应用。王华忠等[1]系统概括了压缩感知思想的各个方面, 并且从叠前地震数据和叠前偏移成像结果两个方向说明了压缩感知理论在地震勘探中的应用效果。刘伟等[2]提出了一种基于压缩感知和全变差(total variation, TV)准则约束的曲波变换地震资料去噪方法。该方法指出, 只要信号可压缩或在某个变换域内稀疏, 则可以使用一个与字典变换矩阵不相关的观测矩阵将变换得到的高维信号投影到一个低维空间, 然后通过求解一个优化问题, 从这些少量的投影中以高概率重构原始信号[3]。地震勘探中所研究的沉积地层模型参数和地下介质的反射波场均可视为可压缩的, 这些条件使得压缩感知理论能够应用于地震勘探中。
在分析与应用压缩感知理论时, 常见的稀疏表示方法有傅里叶变换、小波变换和曲波变换[4]等。傅里叶变换是一种全局变换, 将时域特征与频率域特征紧密结合在一起[5-6]; 小波变换与曲波变换具有很好的局部特征识别能力, 不同的是曲波变换能更好地稀疏表示曲线状信号。
地震数据重建方法一般可归纳为3类:基于滤波器的重建方法[7-8]、基于波场算子的重建方法[9]以及基于数学变换的重建方法[10]。基于滤波器的重建方法将不规则数据视为规则数据进行处理, 导致重建结果误差较大; 基于波场算子的重建方法可以处理非规则数据, 但其计算量过大, 且需要采样率高的数据; 基于数学变换的重建方法将数据进行正变换, 在变换域内进行插值, 再进行反变换, 该方法计算效率高, 且能获得较好的重建结果。
重建方法的核心是重建算法。好的重建算法不仅计算效率高, 而且能取得高精度的结果。近年来, 研究人员提出了多种重建算法, 大致可分为以下3类[11]:
1) 贪婪追踪算法。该算法通过选择局部最优解来寻找非零解的位置, 包括匹配追踪(Matching Pursuit, MP)算法、正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法和分段正交匹配追踪(Stagewise Orthogonal Matching Pursuit, StOMP)算法。
2) 组合算法。该算法要求信号的采样支持分组测试快速重构, 包括傅里叶采样、链式追踪及HHS(Heavg Hitter on Steroids)追踪等。该算法对信号的结构要求较高。
3) 凸松弛算法。该算法通过求解凸优化问题的最优解, 找到信号的最佳逼近, 包括基追踪(Basis Pusuit, BP)算法、迭代阈值法和投影梯度法等。BP算法采用L1范数来衡量信号的稀疏度, 并将信号的稀疏问题转换为L1范数的最小值问题来求解, 该算法精度高但计算复杂; 迭代阈值法在迭代中对近似解做阈值处理来逼近信号, 该算法因结构简单、计算复杂度低得到广泛应用; 投影梯度法以迭代点的负梯度方向为下降方向搜索最优解, 该算法计算效率高, 适合处理大尺度数据[12]。BIRGIN等[13]提出非单调谱投影梯度方法, 在步长选择和线搜索方面对投影梯度法进行了改进, 在处理大规模数据时能获得更好的效果。
不同领域的算法均存在参数选取的问题[14-16], 参数的选取决定了算法性能的好坏, 影响最终的实验结果。目前, 对算法中参数的选取都是经验性或先验性的, 通过选取不同参数建立数学模型, 对比结果, 可以获得参数选取的部分规律特征。
本文选择基于数学变换的重建方法, 选择的稀疏变换基为傅里叶变换, 采样方式为Jitter下采样[17]。Jitter下采样方法优于纯随机采样, 可根据需要控制随机性, 既能保证不会出现数据过密或过稀疏的情况, 又能保留其随机特征。本文使用L1范数谱投影梯度(SPGL1)算法实现地震数据的重建, 并对算法中参数的选取进行多次试验, 着重讨论该算法中选取不同参数对地震数据重建效果的影响, 总结参数选择对重建效果的影响规律。
1 压缩感知理论概述奈奎斯特采样定理指出, 只有在采样频率不低于信号最大带宽的两倍时, 才能不失真地恢复出原信号。而压缩感知理论突破了奈奎斯特采样定理的限制, 在一定条件下, 仅需少量数据即可实现对地震数据的重建。
地震数据采集的数学表达式为:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\varphi f}} $ | (1) |
其中, f∈RN为原始数据, φ为采样矩阵, y∈RM(
若存在某种变换, 使得f在该变换域中是稀疏的, 即:
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{\psi f}} $ | (2) |
其中, Ψ为变换矩阵, x为变换域中数据。f具有可压缩特征, 即其具备幂指数衰减特征[18]。
则:
| $ \mathit{\boldsymbol{f}} = {\mathit{\boldsymbol{\psi }}^{ - 1}}\mathit{\boldsymbol{x}} $ | (3) |
(1) 式可表示为:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\varphi }}{\mathit{\boldsymbol{\psi }}^{ - 1}}\mathit{\boldsymbol{x}} = \mathit{\boldsymbol{Ax}} $ | (4) |
式中:A为感知矩阵; Ψ-1为变换矩阵Ψ的逆矩阵。
所谓的重建算法, 就是在上述前提下寻找最稀疏解的过程。此时, 公式(1)可表示为约束极小化问题, 表达式如下:
| $ \min {\left\| \mathit{\boldsymbol{x}} \right\|_0}\;\;{\rm{s}}.{\rm{t}}.\;\;\;\mathit{\boldsymbol{\varphi f}} = \mathit{\boldsymbol{y}} $ | (5) |
式中:零范数‖·‖0表示非零元素的个数。如果非零系数有K个, 其余N-K个系数均为零, 则称信号在变换域Ψ内是K稀疏的, 或称其稀疏度为K。用这K个基函数的线性组合就可完整表示信号[19]。(5)式是典型的NP-hard非凸优化问题, 不易求解。因此, 通常用L1范数代替L0范数。即求解(6)式:
| $ \min {\left\| \mathit{\boldsymbol{x}} \right\|_1}\;\;{\rm{s}}.{\rm{t}}.\;\;\;\mathit{\boldsymbol{\varphi f}} = \mathit{\boldsymbol{y}} $ | (6) |
基追踪(BP)问题可用于对欠定系统Ax=y求稀疏解。其中, A是M×N的矩阵, y是M×1的列向量。特别地,
| $ {\rm{BP}}:\min {\left\| \mathit{\boldsymbol{x}} \right\|_1}\;\;{\rm{s}}.{\rm{t}}.\;\;\;\mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{y}} $ | (7) |
但是, 含噪的或者不完整的数据不满足线性系统。可以通过基追踪中的约束条件获得基追踪去噪(BPDN)问题:
| $ {\rm{B}}{{\rm{P}}_\sigma }:\min {\left\| \mathit{\boldsymbol{x}} \right\|_1}\;\;{\rm{s}}.{\rm{t}}.\;\;\;\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{y}}} \right\| \leqslant \sigma $ | (8) |
参数σ用于衡量数据中的噪声等级。当σ=0时, 对应于BP问题的解。
(8) 式可变为求解二阶最优化问题, 其无约束优化形式为:
| $ {\rm{Q}}{{\rm{P}}_\lambda }:\min \left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{y}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{x}} \right\|_1} $ | (9) |
式中:λ为拉格朗日乘子。可用内点法、投影梯度法及同伦算法等求解(9)式[20]。
| $ {\rm{L}}{{\rm{S}}_{\rm{ \mathsf{ τ} }}}:\min {\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{y}}} \right\|_2}\;\;\;\;{\rm{s}}.{\rm{t}}.\;\;\;\;{\left\| \mathit{\boldsymbol{x}} \right\|_1} < \tau $ | (10) |
式中:τ为阈值。(10)式称为最小收缩和选择操作(LASSO)问题[22]。当选取合适的σ, λ, τ时, BPσ和QPλ的解一致。CHEN等[23]认为在噪声水平σ已知的情况下, 选择
SPGL1的思想是将BP或BPσ问题化为一系列LASSO子问题, 对其进行迭代求解。由于SPGL1将BPσ分解为一系列的LASSO子问题, 因此LASSO子问题的数目越少, 则SPGL1执行得越快。换言之, LASSO问题的计算量就是SPGL1的核心部分。该算法可应用于处理大尺度数据, 也可应用于复数域。
令xτ表示LSτ的最优解, 定义函数如下:
| $ \varphi \left( \tau \right) = {\left\| {{\mathit{\boldsymbol{r}}_\tau }} \right\|_2}\;\;\;\;{\mathit{\boldsymbol{r}}_\tau }: = \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_\tau } $ | (11) |
(11)式对所有τ>0给出LSτ的最优解。φ(τ)有如下性质:
1) φ是凸函数, 并且单调递减;
2) φ连续可微, 其导数为
| $ \begin{gathered} \varphi '\left( \tau \right) = - {\lambda _\tau }\;\;\;\;{\lambda _\tau }{\left\| {{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{y}}_\tau }} \right\|_\infty } \hfill \\ {\mathit{\boldsymbol{y}}_\tau } = {\mathit{\boldsymbol{r}}_\tau }/{\left\| {{\mathit{\boldsymbol{r}}_\tau }} \right\|_2} \hfill \\ \end{gathered} $ | (12) |
3) 对于τ∈[0, τBP], ‖x‖1=τ, 函数φ严格单调递减。
然后用牛顿法求解(13)式的根:
| $ \varphi \left( \tau \right) = \sigma $ | (13) |
(13)式定义正则化参数τk→τσ的顺序, τσ是使LSτ和BPσ有相同解的参数, xτσ是BPσ问题的解。用投影梯度法求出LSτ的解xτ, 再通过Pareto曲线来更新τ, 通过解新的LSτ问题逐渐逼近BPσ的准确解。
梯度投影法的步骤如下。
步骤1):初始化, x0←Pτ[x] r0←y-Ax0 g0←-ATr0 l←0。
步骤2):计算对偶间隙, 若满足精度则停止。
步骤3):梯度投影, x←Pτ[xl-αgl], α为搜索步长。
步骤4):线性搜索, 计算残差r←y-Ax, 若:
步骤5):更新迭代, 令xl+1←x, rl+1←r, gl+1←ATrl+1。
步骤6):更新搜索步长, 令αl+1←αmax。
步骤7):返回步骤2)。
步骤8):输出解, xτ←xl rτ←rl。
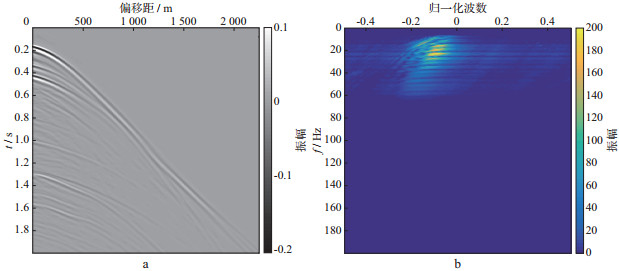
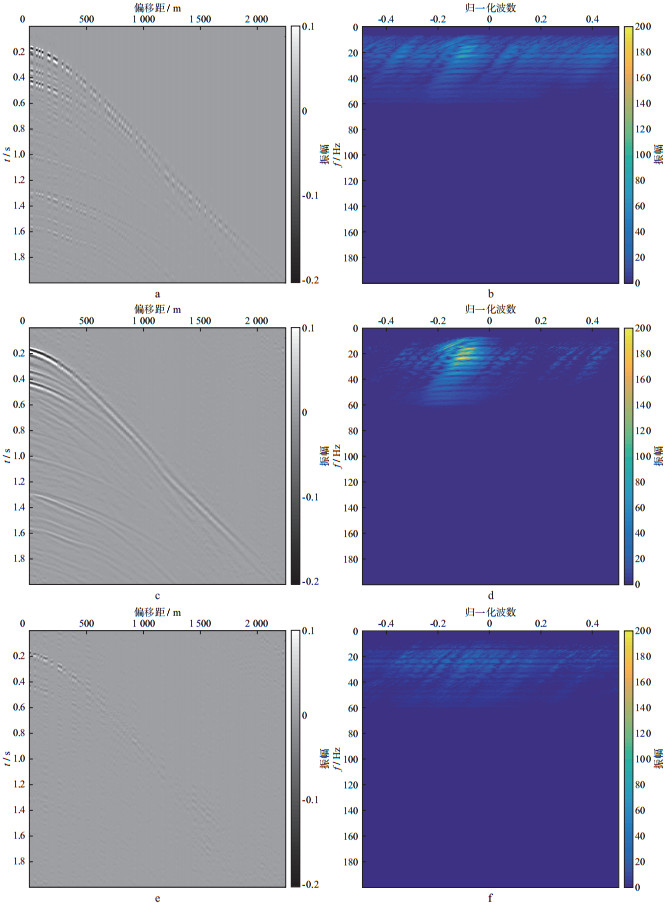
3 数值试验 3.1 基于Jitter采样、傅里叶变换的数值模拟选取一组实际数据进行数值试验。该数据共180道, 道间距12.5m, 时间采样间隔为1ms, 总采样时间为2s。图 1a和图 1b分别为原始单炮数据及其频谱。图 2给出了Jitter下采样数据、重建数据和误差及其频谱。本次实验的参数为:迭代50次, σ=0.01。本次重建结果的信噪比为7.0258dB, 重建效果良好。对比图 1a与图 2c可以看出, 原始数据的基本特征能够体现在重建数据中, 但在细节方面有所欠缺。从图 2e中可以看出, 重建数据在偏移距0~500m, 时间0.2~0.4s区域内误差较大。对比图 1b与图 2d可见, 有效信息得以保留。由此可知, SPGL1算法能获得较好的地震数据重建结果, 但其精度尚有欠缺, 有待改进。
|
图 1 原始单炮数据(a)及其频谱(b) |
|
图 2 Jitter下采样数据、重建数据和误差及其频谱 a Jitter下采样数据; b Jitter下采样数据频谱; c 重建数据; d 重建数据频谱; e 重建数据误差; f 重建数据误差频谱 |
自SPGL1算法提出以来, 学者们对其特性进行了深入研究, 证明该算法具有较好的重建能力, 能够得到令人满意的重建效果[24]。本节将讨论SPGL1的参数选取对于重建效果的影响。
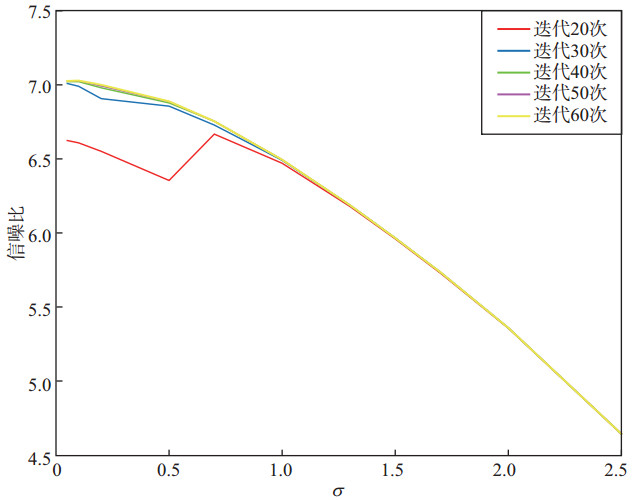
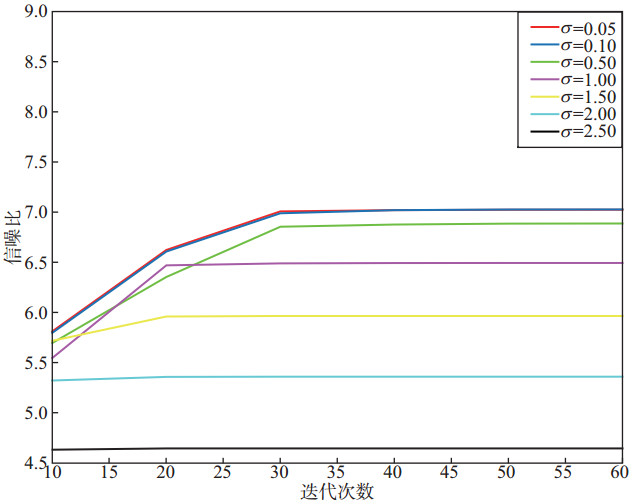
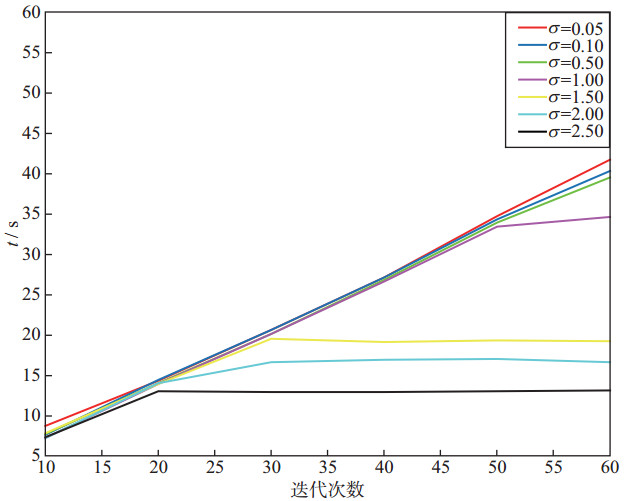
图 3是迭代次数分别选取20, 30, 40, 50和60次时, 信噪比随噪声水平σ的变化曲线。从图 3可以看出, 变化曲线随噪声水平增加呈递减趋势, 并且当迭代次数为20, σ=0.5时信噪比急剧降低, 随后又急剧升高, 说明迭代次数较少时, 收敛不稳定, 当迭代次数增加后, 曲线变化平稳光滑, 呈单调递减趋势。图 4是σ为0.05, 0.10, 0.50, 1.00, 1.50, 2.00, 2.50时, 信噪比随迭代次数的变化曲线。由图 4可见, σ=0.05, σ=0.10, σ=0.50在迭代次数小于30时曲线呈递增趋势, 之后趋于稳定; σ=1.00, σ=1.50, σ=2.00, σ=2.50在迭代次数小于20时曲线呈递增趋势, 但在20次迭代后就趋于稳定。由此可见, 在一定范围内信噪比与迭代次数呈正比, 迭代次数越大, 信噪比越高, 但是超出这个范围后, 信噪比趋于稳定, 不再变化。图 5给出了计算时间随迭代次数的变化曲线。当σ较小时, 时间曲线基本重合, 计算时间基本一致, 且随着迭代次数增多, 计算时间也增长; 当σ较大时, 算法收敛到局部最优解。如图 5中σ=2.50的曲线, 在迭代20次处有明显拐点, 此后迭代次数增加但时间不再改变, 因为在第19次迭代时便找到了理想的解, 迭代自动终止。当迭代停止, 计算结束时, 算法运行时间不再增加。由图 3、图 4和图 5可知, 在选取σ值时, 应尽可能小, 选择迭代次数时不应太大也不应太小, 迭代次数太大将增加计算时间, 太小则迭代不稳定, 且信噪比低。
|
图 3 信噪比随σ的变化曲线 |
|
图 4 信噪比随迭代次数的变化曲线 |
|
图 5 计算时间随迭代次数的变化曲线 |
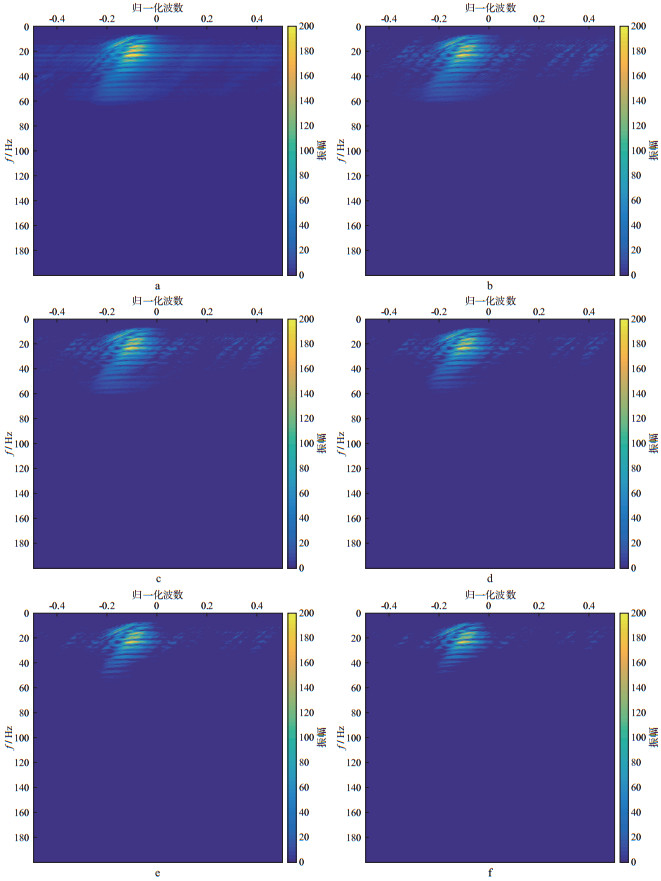
图 6对比了50次迭代、不同σ的重建数据频谱。图 6a为原始数据频谱图, 图 6b至图 6f分别为σ=0.1, σ=0.5, σ=1.0, σ=1.5, σ=2.0的重建数据频谱图。对比图 6a与图 6b可以看出, 在重建数据谱中出现了少许假频。对比图 6b, 图 6c, 图 6d, 图 6e和图 6f可以看出, 随着噪声水平的增加, 假频消失, 但是重建数据谱中有效信息缺失越来越多。
|
图 6 50次迭代重建数据频谱对比 a 原始数据谱; b σ=0.1; c σ=0.5; d σ=1.0; e σ=1.5; f σ=2.0 |
因此, 在利用SPGL1方法进行数据重建时, 选择合理的重建参数可以获得信噪比较高的重建结果, 且能够减少计算时间, 提高运算效率。
4 结论与认识本文重点介绍了L1范数谱投影梯度算法原理及其参数评估。选取不同σ值和迭代次数, 对地震数据的重建结果进行了讨论, 并评估不同参数对重建结果的影响。
研究结果表明, σ值和迭代次数均会影响算法计算时间, σ越小且迭代次数越多, 计算时间越长, 迭代次数较σ而言对计算时间的影响更大。σ值和迭代次数均会影响算法的重建结果, σ越小且迭代次数越多, 重建效果越好, 但迭代次数不能无限增加, 超出某个范围后, 对重建结果的影响甚微。
| [1] |
王华忠, 冯波, 王雄文, 等. 压缩感知及其在地震勘探中的应用[J].
石油物探, 2016, 55(4): 467-474 WANG H Z, FENG B, WANG X W, et al. Compressed sensing and its application in seismic exploration[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 467-474 |
| [2] |
刘伟, 曹思远, 崔震. 基于压缩感知和TV准则约束的地震资料去噪[J].
石油物探, 2015, 54(2): 180-187 LIU W, CAO S Y, CUI Z. Random noise attenuation based on compressive sensing and TV rule[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 180-187 |
| [3] |
白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重建[J].
地球物理学报, 2014, 57(9): 2937-2945 BAI L S, LIU Y K, LU H Y, et al. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics, 2014, 57(9): 2937-2945 DOI:10.6038/cjg20140919 |
| [4] |
唐刚. 基于压缩感知和稀疏表示的地震数据重建与去噪[D]. 北京: 清华大学, 2010
TANG G. Seismic data reconstruction and denoising based on compressive sensing and sparse representation[D]. Beijing: Tsinghua University, 2010 |
| [5] | LUSTIG M, DONOHO D L, SANTOS J, et al. Compressed sensing MRI[J]. IEEE Signal Processing Magazine, 2008, 25(2): 72-82 DOI:10.1109/MSP.2007.914728 |
| [6] | OKA A, LAMPE L. A compressed sensing receiver for UWB impulse radio in bursty applications like wireless sensor network[J]. Physical Communication, 2009, 30(14): 2802-2811 |
| [7] | SPITZ S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794 DOI:10.1190/1.1443096 |
| [8] | CLAERBOUT J F, FOMEL S. Image estimation by example:geophysical soundings image construction(GEE)[M]. California: Stanford Exploration Project, 2004: 1-312. |
| [9] | CANNING A, GARDNER G H F. Regularizing 3D data sets with DMO[J]. Geophysics, 1996, 61(4): 1103-1114 DOI:10.1190/1.1444031 |
| [10] | ZWARTJES P M, SACCHI M D. Fourier reconstruction of nonuniformly sampled, aliased data[J]. Geophysics, 2007, 72(1): V21-V32 DOI:10.1190/1.2399442 |
| [11] | NEEDELL D, TROPP J A. Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301-321 DOI:10.1016/j.acha.2008.07.002 |
| [12] | FIGUEIREDO M A T, NOWAK R D, WRIGHT S J. Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 1(4): 586-597 |
| [13] | BIRGIN E G, MARTINEZA J M, RAYDAN M. Nonmonotone spectral projected gradient methods on convex sets[J]. SIAM Journal on Optimization, 2000, 10(4): 1196-1211 DOI:10.1137/S1052623497330963 |
| [14] | YUAN X F, WANG Y N. Parameter selection of support vector machine for function approximation based on chaos optimization[J]. Journal of Systems Engineering and Electronics, 2008, 19(1): 191-197 DOI:10.1016/S1004-4132(08)60066-3 |
| [15] |
郭东伟, 周春光, 吕慧英, 等. 参数选取对遗传算法动力学形态的影响[J].
小型微型计算机系统, 2004, 25(2): 220-224 GUO D W, ZHOU C G, LV H Y, et al. Effects of parameters selection on global dynamical shape of genetic algorithms[J]. Mini-micro Systems, 2004, 25(2): 220-224 |
| [16] |
曾小牛, 李夕海, 陈鼎新, 等. 基于径向谱的位场向下延拓正则参数选取方法[J].
石油地球物理勘探, 2015, 50(4): 749-754 ZENG X N, LI X H, CHEN D X, et al. New regularization parameter selection for potential field downward continuation based on the radial spectrum[J]. Oil Geophysical Prospecting, 2015, 50(4): 749-754 |
| [17] |
张华, 陈小宏. 基于Jitter采样和曲波变换的三维地震数据重建[J].
地球物理学报, 2013, 56(5): 1637-1649 ZHANG H, CHEN X H. Seismic data reconstruction based on jittered sampling and Curvelet transform[J]. Chinese Journal of Geophysics, 2013, 56(5): 1637-1649 DOI:10.6038/cjg20130521 |
| [18] | DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306 DOI:10.1109/TIT.2006.871582 |
| [19] | CANDES E J, ROMBERG J, TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Math, 2010, 59(8): 1207-1223 |
| [20] |
曹静杰, 王彦飞, 杨长春. 地震数据压缩重构的正则化与零范数稀疏最优化方法[J].
地球物理学报, 2012, 55(2): 596-607 CAO J J, WANG Y F, YANG C C. Seismic data restoration based on compressive sensing using the regularization and zero-norm sparse optimization[J]. Chinese Journal of Geophysics, 2012, 55(2): 596-607 |
| [21] | CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 33-61 DOI:10.1137/S1064827596304010 |
| [22] | EWOUT V D B, FRIEDLANDER M P. Probing the pareto frontier for basis pursuit solutions[J]. Society for Industrial and Applied Mathematics, 2008, 31(2): 890-912 |
| [23] | CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129-159 DOI:10.1137/S003614450037906X |
| [24] | CAI R, ZHAO Q, SHE D P. Bernoulli-based random undersampling schemes for 2D seismic data regularization[J]. Applied Geophysics, 2014, 11(3): 321-330 DOI:10.1007/s11770-014-0447-z |




 ,
,