2. 中国科学院地球化学研究所, 矿床地球化学国家重点实验室, 贵州 贵阳 550081
2. State Key Laboratory of Ore Deposit Geochemistry, Institute of Geochemistry, Chinese Academy of Sciences, Guiyang 550081, China
Radon变换在地震信号处理中备受关注, 被广泛应用于提取波场信息和波场分离等。Radon变换是二维地震数据在特定路径t=φ(p, τ, x)上的曲线积分[1-2], 其目的是将数据中规律排列信号分解为Radon域内稀疏的系数, 以便识别和分离信号。依据积分路径, Radon变换可分为线性Radon变换、抛物Radon变换、双曲Radon变换等[3]; 依据算子类型, Radon变换又可分为时变Radon变换和时不变Radon变换[3]。线性Radon变换、抛物Radon变换属于时不变Radon变换, 而双曲Radon变换属于时变Radon变换[4]。
实际处理过程中往往先定义Radon反变换, 再由反变换推出正变换[5]。Radon反变换公式[6-7]为d=Lm。式中:d为时空域地震数据; m为Radon变换系数; L为变换算子。Radon反变换可以理解为模型m在算子L的作用下生成数据响应d, 那么, 相应的Radon变换是反问题:由数据求解Radon模型[8]。起初, 采用最小平方反演Radon模型, 此方法称为最小二乘Radon变换[9-10]。后来, 为提高Radon模型的分辨率, 引入稀疏约束, 提出了高分辨率Radon变换[6, 11]。高分辨率Radon变换是非线性反演问题, 通常采用迭代重加权共轭梯度算法求解[12], 并在受限模型空间中求解以减少计算量。近年来, 结合正交多项式变换对信号振幅变化信息的描述, 提出了高阶Radon变换, 重建信号的同时保持了信号的AVO特性[13]。
Radon变换在传统纵波勘探信号处理中已有很多应用, 如地震信号去噪[14-15]、多次波消除[16-17]、地震道重建[18-19]等。线性Radon变换提供了不同速度下纵波、转换横波、面波的到时信息, 这些信息可用于转换波静校正[20]、面波频散曲线提取[21]、鬼波压制[22]等; 抛物Radon变换常用于去除经NMO处理后的CMP道集数据中的多次波; 而双曲Radon变换常用于地震反射波场分离[17]。随着多波地震勘探和微震监测技术在非常规油气藏勘探开发中的迅猛发展, 地震数据矢量场处理技术也得到快速发展。但是Radon变换在矢量场处理中的应用仍处于探索阶段, 如何通过Radon变换获得良好的处理效果并保持信号的矢量场特性是研究的重点之一。近年来, 国内外的很多学者从不同的角度对Radon变换进行改进以适应矢量场处理, 取得了很多成果[23-24]。本文梳理了Radon变换研究成果, 主要讨论了其在稀疏正则化、高效计算等方面的研究历史与现状, 最后介绍了Radon变换在地震矢量数据处理中的应用情况, 希望研发出更适于矢量场数据处理的新方法。
1 Radon变换及其特点Radon变换离散形式定义为[25]:
| $ \mathit{\boldsymbol{m}}\left( {p,\tau } \right) = \sum\limits_x {\mathit{\boldsymbol{d}}\left[ {x,\varphi \left( {p,\tau ,x} \right)} \right]} $ | (1) |
式中:d(x, φ)为时空域地震数据; x是偏移距, 单位m; φ是地震波双程旅行时, 单位s; τ为时间截距, 单位s; m(p, τ)为Radon变换系数; p是斜率或者曲率。此定义为伴随Radon变换, 记为:m=LH d, LH称为伴随算子。
1.1 不同域Radon变换Radon变换可以在时间域、频率域、时频混合域中进行[8], 三者在分辨率和计算效率上差异明显, 见表 1。
| 表 1 不同域Radon变换的对比 |
时间域与频率域Radon变换的计算效率不同:时间域Radon变换所有时间分量相互耦合, 叠加算子矩阵过大, 致使计算成本较高; 频率域Radon变换不同频率分量相互解耦, 降低了变换矩阵的维数, 且可以只在有效信号的频带内计算, 提高了计算效率[26]。再者Radon模型分辨率也有差异:SACCHI等[11]提出的频率域高分辨率Radon变换, 只在斜率方向(或曲率方向)有约束[27-28], CARY[28]称其为高分辨率的必要非充分条件; 而THORSON[29]提出的时间域高分辨率Radon变换, 在斜率方向和时间方向都有约束, Radon模型更稀疏, 分辨率更高[8, 28]。
TRAD等[8]结合时间域方法与频率域方法, 提出时频混合域Radon变换:在时间域内进行稀疏约束, 利用迭代重加权法求高分辨率解; 在频率域内进行算子矩阵与单频向量乘积, 避免大矩阵运算。时频混合域方法具有较高的分辨率和计算效率, 受到国内外学者广泛关注[8, 26-27]。但是需要指出, 时频混合域求解方法并不适用于所有积分路径, 例如时变Radon变换就只能在时间域求解[26]。
1.2 不同积分路径Radon变换通过改变积分路径, 可追踪地震记录上不同形态的同相轴。双曲Radon变换常用来表示反射波同相轴。TRAD等[6]认为沿着Dix动校正公式
Dix动校正双曲线的顶部位于零偏移距, 故传统双曲Radon变换不能稀疏表示顶部偏移的反射同相轴, 因此多次波压制效果不佳[30]。为解决此问题, TRAD[31]提出顶偏双曲Radon变换:假设双曲线顶部偏移量α, 沿路径
另外, Dix动校正公式在水平多层介质近偏移距假设下近似成立[35], 在远偏移距时不能正确描述反射波的到时, 为解决这一问题, CASTLE[36]提出了相移双曲NMO公式:
| $ t = {\tau _s} + \sqrt {\tau _0^2 + \frac{{{x^2}}}{{{v^2}}}} $ | (2) |
式中:
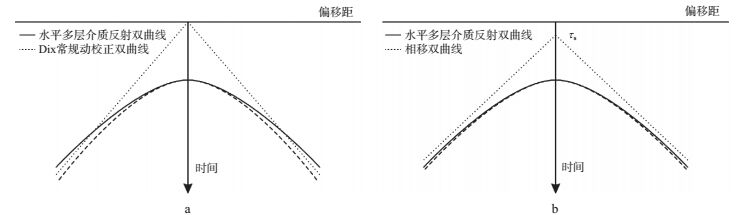
|
图 1 Dix常规动校正双曲线(a)与相移双曲线(b)分别与反射同相轴的对比 |
BICKEL[37]对抛物Radon变换变形, 提出伪双曲Radon变换。取路径:
| $ t = \tau + p\left( {\sqrt {{x^2} + {z^2}} - z} \right) $ | (3) |
式中:z=vresT0, 称为参考深度, 与波速和层深度相关, vres为剩余时差速度; p为慢度。参数z的取值控制反射同相轴在Radon域的稀疏性, z过大或过小都不能将反射同相轴稀疏表示[37]。建立如图 2所示的反射波模型, 其伪双曲Radon变换结果见图 3, 可见此例中只有当z取500 m左右时, Radon模型是稀疏的; 而z取其它值时, Radon模型不稀疏。通过速度扫描, 求取目标层反射波的对应z值, 可将目标层反射波在Radon域稀疏表示。由于CMP道集中不同反射界面的多种反射波进行Radon变换所需最优的z值都不相同, 贾春梅等[3]提出在变换中加入动态时窗, 在不同截距处选取不同的参考深度的方法加以解决。伪双曲Radon变换积分路径具有时不变性, 可以在频率域或时频混合域中求解, 相对于前述时变双曲Radon变换计算效率更高。
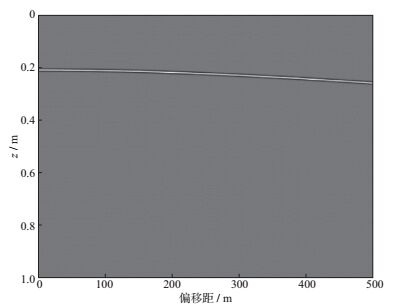
|
图 2 反射波模型 |
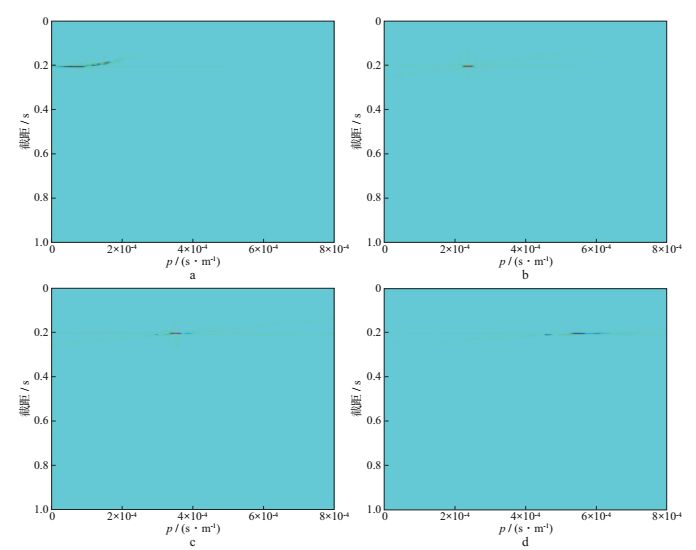
|
图 3 对反射波模型进行伪双曲Radon变换 a z=100 m; b z=500 m; c z=800 m; d z=1300 m |
伴随Radon变换无法实现信号保真[38]。在标准同相轴假设下, 高分辨率Radon变换有很好的保幅性。但是, Radon变换的分辨率和AVO特性相互矛盾[39-40]。为解决此问题, 李晶晶等[41]基于抛物Radon变换, 根据AVO特征对不同偏移距的地震道采用不同的均衡系数, 实现相对保幅地震道重建; 薛亚茹等[13]利用正交多项式谱表征AVO与Radon变换结合得到高阶Radon变换。高阶Radon变换包含了不同方向同相轴的振幅信息与振幅变化信息, 常用于地震数据保幅重建[13, 42]。高阶Radon变换定义式:
| $ {\mathit{\boldsymbol{m}}^{\left( j \right)}}\left( {p,\tau } \right) = \sum\nolimits_x {\mathit{\boldsymbol{d}}\left[ {x,\varphi \left( {p,\tau ,x} \right)} \right]{P_j}\left( x \right)} $ | (4) |
式中:Pj(x)表示j阶单位正交多项式; m(j)表示j阶的Radon变换系数, j=0, 1, 2。高阶Radon反变换的时间域形式:
| $ \mathit{\boldsymbol{d}}\left[ {x,\varphi \left( {p,\tau ,x} \right)} \right] = \sum\nolimits_p {\sum\nolimits_{j = 0}^2 {{\mathit{\boldsymbol{m}}^{\left( j \right)}}\left( {p,\tau } \right){P_j}\left( x \right)} } $ | (5) |
简记为:
| $ \mathit{\boldsymbol{d}} = {\mathit{\boldsymbol{L}}_0}{\mathit{\boldsymbol{m}}^{\left( 0 \right)}} + {\mathit{\boldsymbol{L}}_1}{\mathit{\boldsymbol{m}}^{\left( 1 \right)}} + {\mathit{\boldsymbol{L}}_2}{\mathit{\boldsymbol{m}}^{\left( 2 \right)}} = \mathit{\boldsymbol{Lm}} $ | (6) |
式中:L0, L1, L2分别为叠加算子、梯度算子、曲率算子[13]。与常规Radon变换求解思路一致, 高阶Radon变换也采用稀疏反演的方法提高分辨率。不同的是, 高阶Radon变换采用Radon域的能量来确定模型加权矩阵:
| $ {\left[ {{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{m}}}} \right]_{i,i}} = \frac{1}{{\sqrt {\left| {{E_i}} \right|} }} $ | (7) |
式中:
对于反问题d=Lm, 其解不全满足存在性、唯一性和稳定性, 故反问题是不适定的[11]。借助于某些先验信息而构建一个唯一且稳定的解, 这种方法就是正则化[11]。最常见的是二次正则化, 先验信息以固定形式给出, 作用是平滑模型, 避免观测随机误差被放大。利用二次正则化得到的反问题d=Lm的解, 就是最小二乘Radon变换。最小二乘Radon变换分辨率不高, 并不适用于波场分离。为此, 引入模型相关信息来得到稀疏正则解, 这就是高分辨率Radon变换。由于数据的高分辨率Radon变换系数更稀疏, 所以波场分离效果比较理想[43]。本文总结了高分辨率Radon变换的两种推导方法。
2.1 基于贝叶斯原理的高分辨率Radon变换此方法基于贝叶斯原理以概率形式给出先验信息, 常用到的先验概率分布为广义高斯分布和柯西分布[6, 44]。
柯西分布:
| $ f\left( {\mathit{\boldsymbol{m}},{\sigma _c}} \right) = \frac{1}{{{\rm{ \mathsf{ π} }}{\sigma _c}\left( {1 + \frac{{{{\left| \mathit{\boldsymbol{m}} \right|}^2}}}{{\sigma _c^2}}} \right)}} $ | (8) |
式中:σc为柯西分布参数。
广义高斯分布:
| $ f\left( {\mathit{\boldsymbol{m}},{\sigma _p},p} \right) = \frac{{{p^{1 - 1/p}}}}{{2{\sigma _p}\Gamma \left( {{p^{ - 1}}} \right)}}{{\rm{e}}^{ - \frac{1}{p} \cdot \frac{{{{\left| \mathit{\boldsymbol{m}} \right|}^p}}}{{\sigma _p^p}}}} $ | (9) |
式中:p是形状参数; σp是尺度参数。当p=1时, 为Laplace双指数分布, 表示稀疏模型; 当p=2时, 为正态分布, 表示平滑模型; 当p=∞时, 为均匀分布。
SACCHI等[11]推导了基于柯西正则化的高分辨率Radon变换; 1996年, SACCHI[44]提出了基于广义高斯分布和柯西分布的高分辨率Radon变换; TRAD等[6]利用双指数分布和柯西分布估计稀疏模型。
| $ \begin{array}{l} f\left( {\mathit{\boldsymbol{m}}\left| \mathit{\boldsymbol{d}} \right.} \right) = K\exp \left[ { - {\lambda _0} - {\lambda _1}S\left( \mathit{\boldsymbol{m}} \right) - \frac{1}{2}\left( {\mathit{\boldsymbol{Lm}} - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left. \mathit{\boldsymbol{d}} \right)}^{\rm{H}}}\mathit{\boldsymbol{C}}_n^{ - 1}\left( {\mathit{\boldsymbol{Lm}} - \mathit{\boldsymbol{d}}} \right)} \right] \end{array} $ | (10) |
式中:S(m)是模型的全局约束[11]; λ0, λ1分别为拉格朗日乘数。假设噪声满足正态分布, 则(10)式中K为归一化常数, Cn为噪声的协方差矩阵[44], 使后续分布取得最大值的解m称为最大先验(maximum a posterior, MAP)解[11], 也是稀疏解。MAP解等价于求如下目标函数的最小化问题:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \lambda S\left( \mathit{\boldsymbol{m}} \right) + {\left( {\mathit{\boldsymbol{Lm}} - \mathit{\boldsymbol{d}}} \right)^{\rm{H}}}\mathit{\boldsymbol{C}}_n^{ - 1}\left( {\mathit{\boldsymbol{Lm}} - \mathit{\boldsymbol{d}}} \right) $ | (11) |
式中:λ=2λ1。对目标函数(11)最小化, 得到方程:
| $ \left( {\lambda {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{m}}} + {\mathit{\boldsymbol{L}}^{\rm{H}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{n}}^{ - 1}\mathit{\boldsymbol{L}}} \right)\mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{L}}^{\rm{H}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{n}}^{ - 1}\mathit{\boldsymbol{d}} $ | (12) |
式中:对角阵Qm是与先验信息相关的模型加权矩阵。当先验信息满足柯西分布时, 有:
| $ {\left[ {{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{m}}}} \right]_{i,i}} = \frac{1}{{\sigma _c^2\left( {1 + \frac{{{{\left| {{m_i}} \right|}^2}}}{{\sigma _c^2}}} \right)}} $ | (13) |
当先验信息满足Laplace双指数分布时, 有:
| $ {\left[ {{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{m}}}} \right]_{i,i}} = \frac{1}{{2{\sigma _p}}}\frac{1}{{\left| {{m_i}} \right|}} $ | (14) |
由于高分辨率解对参数σc, σp的取值不灵敏, 可采用估计方法取值:先将模型向量m归一化, 然后选择其为0到1之间的值。σc, σp越小, 模型越稀疏[6]。
2.2 基于L1范数稀疏约束的高分辨率Radon变换在反演理论中, 对于不适定问题, 为获得唯一且稳定的解, 更直接的方法是加入正则项[44]。对于d=Lm, 可构造目标函数:
| $ \mathit{\boldsymbol{J}} = \left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Lm}}} \right\|_q^q + \lambda \left\| \mathit{\boldsymbol{m}} \right\|_p^p $ | (15) |
式中:‖m‖pp为正则项; ‖d-Lm‖qq为误差项, 下标p和q分别表示向量的Lp和Lq范数, 且p>0, q≤2。若正则项和误差项都采用L2范数(即p=2且q=2), 则对应最小二乘Radon变换。SCALES等[45]认为误差项采用L2范数, 夸大了奇异值的影响, 使得求解不稳定, 他将误差项改用L1范数, 稳定了反问题的求解; 但由于其未考虑解的稀疏性, 导致分辨率不高。TRAD等[8]将正则项使用L1范数得到了Laplace双指数稀疏解, 但文中未解释数据加权矩阵的由来。IBRAHIM等[25]利用不同约束下的4种Radon变换测试压制邻炮干扰的效果, 认为稀疏正则的稳健Radon变换(即p=1且q=1)处理效果最优。
为求稀疏解, 正则项和误差项都使用L1范数。取p=1, q=1, 则:
| $ \begin{array}{l} \left\| \mathit{\boldsymbol{m}} \right\|_1^1 = \sum\nolimits_i {\left| {{m_i}} \right|} = \sum\nolimits_i {{{\left| {{m_i}} \right|}^{ - 1}}\left| {{m_i}} \right|\left| {{m_i}} \right|} \\ \;\;\;\;\;\;\; = {\mathit{\boldsymbol{m}}^{\rm{H}}}\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{m}}^{\rm{H}}{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{m}}}\mathit{\boldsymbol{m}} = \left\| {{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{m}}}\mathit{\boldsymbol{m}}} \right\|_2^2 \end{array} $ | (16) |
| $ \begin{array}{l} \left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Lm}}} \right\|_1^1 = \sum\nolimits_i {\left| {{{\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Lm}}} \right)}_i}} \right|} = \left( {\mathit{\boldsymbol{d}} - } \right.\\ {\left. {\mathit{\boldsymbol{Lm}}} \right)^{\rm{H}}}\mathit{\boldsymbol{W}}_d^{\rm{H}}{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}}\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Lm}}} \right) = \left\| {{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}}\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Lm}}} \right)} \right\|_2^2 \end{array} $ | (17) |
其中, 对角矩阵Wd称为数据加权矩阵, 反映数据的标准差[8]; 对角矩阵Wm称为模型加权矩阵, 决定模型稀疏性[8, 46]。Wm和Wd元素分别为:
| $ {\left[ {{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{m}}}} \right]_{i,i}} = \frac{1}{{\sqrt {\left| {{m_i}} \right|} }} $ | (18) |
| $ {\left[ {{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}}} \right]_{i,i}} = \frac{1}{{\sqrt {\left| {{{\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Lm}}} \right)}_i}} \right|} }} $ | (19) |
则d=Lm可表述为新的目标函数:
| $ \mathit{\boldsymbol{J}} = \left\| {{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}}\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Lm}}} \right)} \right\|_2^2 + \lambda \left\| {{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{m}}}\mathit{\boldsymbol{m}}} \right\|_2^2 $ | (20) |
(20)式优化问题的解即为Radon变换高分辨率解:
| $ \left( {\lambda \mathit{\boldsymbol{W}}_\mathit{\boldsymbol{m}}^{\rm{H}}{\mathit{\boldsymbol{W}}_m} + {\mathit{\boldsymbol{L}}^{\rm{H}}}\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}^{\rm{H}}{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{L}}} \right)\mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{L}}^{\rm{H}}}\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}^{\rm{H}}{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{d}} $ | (21) |
为加快收敛, 可以使用预条件[6, 8]
| $ \left( {\lambda \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{W}}_\mathit{\boldsymbol{m}}^{ - {\rm{H}}}{\mathit{\boldsymbol{L}}^{\rm{H}}}\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}^{\rm{H}}{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{LW}}_\mathit{\boldsymbol{m}}^{ - 1}} \right)\mathit{\boldsymbol{\tilde m}} = \mathit{\boldsymbol{W}}_\mathit{\boldsymbol{m}}^{ - {\rm{H}}}{\mathit{\boldsymbol{L}}^{\rm{H}}}\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}^{\rm{H}}{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{d}} $ | (22) |
式中:参数λ用于平衡数据拟合和模型稀疏的比重[8]。λ越大, 模型越稀疏; 反之, 越接近最小二乘解。
(22)式与贝叶斯原理导出的Laplace双指数正则解形式一致。SACCHI [44]认为:两种推导方法实质联系密切, 且有近似的目标函数。基于贝叶斯原理导出的高分辨率解更能说明模型分布特性, 但是没有解释清楚“为何先验概率使用广义高斯分布或者柯西分布而不是其它分布”[44]; 推导过程中假定噪声的协方差矩阵Cn已知, 但实际数据中Cn不容易获取。基于L1范数稀疏约束的高分辨率解更实用, 每次迭代容易计算加权矩阵Wm和Wd。
3 Radon变换的计算效率问题计算高分辨率Radon变换((12)式、(21)和(22)式)可归纳为求解非线性方程:
| $ \mathit{\boldsymbol{Am}} = \mathit{\boldsymbol{y}} $ | (23) |
式中:系数矩阵A是稀疏度高的厄米特(Hermite)矩阵, 且系数矩阵A与模型和数据相关。此类方程需要迭代求解, 且随Radon系数的元素个数增多, 计算成本急剧升高。目前此方程的高效解法是在受限模型空间[47]中运用迭代重加权共轭梯度(iteratively reweighted conjugate gradient, IRCG)算法[6, 8]。
3.1 迭代重加权共轭梯度算法在每次迭代中, 更新加权矩阵, 将方程(23)转化为线性方程, 并利用共轭梯度法求解。内层共轭梯度迭代次数可由广义交叉校验(generalized cross validation, GCV)函数设定[8, 26], 外层迭代一般为3~7次[6]。以方程(21)的时频混合域解法为例, 总结迭代IRCG算法。
1) 给定初始平衡参数λ, 最大迭代次数n, 初始迭代变量k=1。
2) 二维地震剖面做关于时间的傅里叶变换, 提取单频向量, 并计算Radon算子矩阵L及伴随算子矩阵LH。先求频率域最小二乘解, 并对其做傅里叶反变换到时间域作为初始解m0。
3) 在迭代变量k=1, 2, …, K时, 执行下述迭代过程:
a) 更新模型加权矩阵Wm和数据加权矩阵Wd;
b) 计算
c) 共轭梯度法解方程Amk=y, 得到第k次迭代解mk;
d) 修改平衡参数λ。
4) 得到Radon系数向量m=mk。
5) 对所有频率的数据做前述相同的运算, 得到数据的高分辨率Radon变换系数。
3.2 受限模型空间Radon变换前述经典高分辨率Radon变换使用的是Radon变换的全部系数, 计算成本高[47]。LIU等[48]提出压缩计算域, 提高了计算效率, 但每次迭代时更新算子, 影响算法的收敛性。LU[27]采用迭代收缩阈值算法提高反演的收敛速度, 但只有阈值可以控制系数的稀疏性, 需要屡次尝试才能选到合适的阈值。WANG等[49]运用贪婪算法, 依据每次迭代模型的残差幅值选取子空间。SABBIONE等[47]直接在受限模型空间中运用共轭梯度算法, 保证了目标函数不会随迭代而改变, 并通过试验证明了受限模型空间中的Radon变换系数足以表示地震数据。
受限模型空间在迭代前就被选取, 它是指伴随Radon变换系数高于阈值的部分构成的空间, 不随迭代进行而改变, 这使得受限模型空间方法计算效率优于贪婪最小二乘方法。而在结果分辨率方面, 受限模型空间方法优于迭代收缩方法, 稀疏性不仅由阈值控制, 而且受概率先验信息的约束; 从另一个角度看, 此阈值选取较为随意[23]。受限模型空间
| $ \mathbb{A}\mathit{\boldsymbol{ = }}\left[ {\left( {\tau ,p} \right):\frac{1}{{{N_x}}}\left| {{\mathit{\boldsymbol{L}}^{\rm{H}}}\mathit{\boldsymbol{d}}} \right| > T} \right] $ | (24) |
式中:T是阈值, 取值范围0<T<1。在受限模型空间中求解d=Lm有:
| $ \left( {\tilde \lambda \mathit{\boldsymbol{W}}_{{\mathit{\boldsymbol{m}}_\mathbb{A}}}^{\rm{H}}{\mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{m}}\mathbb{A}}} + \mathit{\boldsymbol{L}}_\mathbb{A}^{\rm{H}}\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}^{\rm{H}}{\mathit{\boldsymbol{W}}_d}{\mathit{\boldsymbol{L}}_\mathbb{A}}} \right){\mathit{\boldsymbol{m}}_\mathbb{A}} = \mathit{\boldsymbol{L}}_\mathbb{A}^{\rm{H}}\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}^{\rm{H}}{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{d}}}\mathit{\boldsymbol{d}} $ | (25) |
方程(25)同样采用IRCG算法求解。
4 Radon变换在地震矢量数据处理中的应用Radon变换已广泛应用于传统纵波勘探地震数据处理的多次波压制、地震数据保幅重建、去噪、邻炮干扰压制以及波场走时信息提取等。随着多波地震勘探和微震监测技术在非常规油气藏勘探开发中的大量应用, 急需研发针对多分量地震数据的Radon变换方法, 如何通过Radon变换获得良好的处理效果并保持信号的矢量场特性是研究的重点。
4.1 纵横波分离PP波和PS波的分离是多波多分量地震勘探技术中一个重要的处理环节。基于PP波和PS波的运动学和动力学特征, 目前分离方法主要有:Radon变换法[50-52]、极化滤波法[24]、波动方程法[53]、散度和旋度法[54]等。Radon变换法分离PP波和PS波直接利用了二者的视速度差异, 基本思想为:地震剖面上相互交叉的PP波和PS波双曲同相轴, 在双曲Radon域中可以稀疏表示, 易于分离。但是, Radon变换只考虑了PP波和PS波的速度和走时信息, 对于复杂介质, 地震反射波的时距曲线不再是标准的双曲线, 即使采用高分辨率高阶双曲Radon变换也未必能将波场稀疏表示, 此时无法有效分离波场。对此, WANG等[24]提出基于τ-p域下的空间矢量旋转波场分离方法, 利用了PP波和PS波的速度差异和偏振特性, 波场分离精度更高。
4.2 微震信号提取与噪声压制Radon变换在反射同相轴的识别、压制随机噪声方面有良好的效果[14]。薛昭等[38]证明了高分辨率Radon变换去噪方法的相对保幅性。目前, 针对多分量地震数据去噪问题, 普遍采用分量单独处理, 而联合处理的技术应用较少[55]。实际上, 多分量地震数据是一个矢量波场, 接收器接收到的各个分量数据是位移矢量在不同坐标方向的投影。若不考虑多分量地震数据的矢量特性, 各个分量单独做Radon变换去噪处理会导致弱分量信号被压制。FORNASIER等[56]认为各个分量有效信号的稀疏表示系数具有相同的稀疏分布模式, 并提出组稀疏阈值准则; VERA RODRIGUEZ等[57]证明了基于组稀疏表示的去噪方法可以有效地保持多分量地震数据分量之间的振幅相对关系。对于三分量微震信号, 由变换域同一位置的各分量稀疏系数组成向量g, 其L2范数‖g‖2的大小决定系数是否为组稀疏。
与组稀疏的思想相近, 三分量微震信号的均方根包络[58]为:
| $ \begin{array}{l} e\left( {x,t} \right) = \sqrt {{e_x}{{\left( {x,t} \right)}^2} + {e_y}{{\left( {x,t} \right)}^2} + {e_z}{{\left( {x,t} \right)}^2}} \\ \;\;\;\;\;\;\;\;\;\; = {\left\| \mathit{\boldsymbol{g}} \right\|_2} \end{array} $ | (26) |
式中:g={ex(x, t), ey(x, t), ez(x, t)}, ex, ey, ez为3个分量的包络。均方根包络常被用于识别微震事件。为避免震源辐射花样的影响[23], SABBIONE等[59]对微震信号的均方根包络进行顶偏Radon变换, 识别微震事件。各个分量分别进行高分辨率顶偏Radon变换, 根据微震事件截取信号、压制噪声。为高效计算, 可采用两种措施:在时空窗中扫描事件以限制变换的道数; 在受限空间中计算Radon变换[59]。即便用于处理低信噪比的微震数据, 此方法依然能成功检测微震事件并压制噪声。
5 结束语Radon变换在地震学领域获得了广泛的应用, 并已在多次波压制、纵横波分离、地震数据保幅重建、去噪以及微震检测等方面取得良好的应用效果。本文总结了Radon变换目前的研究成果, 着重讨论了稀疏正则化、高效计算等方面的研究历史与现状; 并简单介绍了Radon变换在地震矢量数据处理中的应用。高分辨率Radon变换常用于地震波场分离; 受限模型空间Radon变换在海量地震数据处理提高计算效率方面获得了应用尝试。但这些方法改进和应用是以地震标量波场单分量数据处理为主, 未考虑到多分量地震信号的矢量特征, 也无法保持多分量地震信号处理中的矢量特性不畸变, 真正针对Radon变换在地震矢量场处理中的应用研究很少。
本文认为可将组稀疏约束的概念与高分辨率Radon变换相结合, 发展适合于多分量矢量场的Radon变换处理方法。但基于组稀疏约束的Radon变换也只是利用了地震矢量场的振幅信息, 未兼顾矢量场的方向性。因此, 探索基于矢量场数据处理的Radon变换方法, 利用矢量场的方向特性、偏振特性等改进现有的Radon变换方法将是以后重点研究方向之一。此外, 随着Radon变换方法的发展, 变换系数的维度也越来越高, 运算成本过高限制了Radon变换的实际应用, 因此, 基于CPU或GPU并行加速的Radon变换方法也是未来的发展方向之一。
| [1] |
王有新.
应用地震数据处理方法[M]. 北京: 石油工业出版社, 2009: 81-85.
WANG Y X. Applied seismic data processing method[M]. Beijing: Publishing House of Oil Industry, 2009: 81-85. |
| [2] |
刘法启, 张关泉. 借助广义Radon变换进行方位角校正[J].
石油物探, 1996, 35(4): 43-51 LIU F Q, ZHANG G Q. Azimuth correction with the aid of the generalized Radon transform[J]. Geophysical Prospecting for Petroleum, 1996, 35(4): 43-51 |
| [3] |
贾春梅, 姜国庆, 刘志成, 等. 频域稀疏双曲Radon变换去噪方法[J].
物探与化探, 2016, 40(3): 527-533 JIA C M, JIANG G Q, LIU Z C, et al. Denoising method based on sparse hyperbolic Radon transform in the frequency domain[J]. Geophysical and Geochemical Exploration, 2016, 40(3): 527-533 |
| [4] |
巩向博, 韩立国, 王升超. 混合域高分辨率双曲Radon变换及其在多次波压制中的应用[J].
石油物探, 2016, 55(5): 711-718 GONG X B, HAN L G, WANG S C. High-resolution hyperbolic Radon transform and its application in multiple suppression[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 711-718 |
| [5] | HAMPSON D. Inverse velocity stacking for multiple elimination[J]. Expanded Abstractes of 56thAnnual Internat SEG Mtg, 1986: 422-424 |
| [6] | TRAD D, ULRYCH T, SACCHI M. Accurate interpolation with high-resolution time-variant Radon transforms[J]. Geophysics, 2002, 67(2): 644-656 DOI:10.1190/1.1468626 |
| [7] |
谢俊法, 孙成禹, 韩文功. 迭代抛物Radon变换法分离一次波与多次波[J].
石油地球物理勘探, 2014, 49(1): 76-81 XIE J F, SUN C Y, HAN W G. Primary and multiple separation based on iterative parabolic Radon transform[J]. Oil Geophysical Prospecting, 2014, 49(1): 76-81 |
| [8] | TRAD D, ULRYCH T, SACCHI M. Latest views of the sparse Radon transform[J]. Geophysics, 2003, 68(1): 386-399 DOI:10.1190/1.1543224 |
| [9] | KOSTOV C. Toeplitz structure in slant-stack inversionJ][J]. Expanded Abstractes of 60thAnnual Internat SEG Mtg, 1990: 1618-1621 |
| [10] | ANDERSON J E.Parabolic and linear 2D tau-p transforms using the generalized radon transform:center for wave phenomena[R].CWP Report, 1993:109-120 |
| [11] | SACCHI M D, ULRYCH T J. High-resolution velocity gathers and offset space reconstruction[J]. Geophysics, 1995, 60(4): 1169-1177 DOI:10.1190/1.1443845 |
| [12] | SACCHI M D, PORSANI M. Fast high resolution parabolic Radon transform[J]. Expanded Abstracts of 69th Annual Internat SEG Mtg, 1999: 1477-1480 |
| [13] |
薛亚茹, 唐欢欢, 陈小宏. 高阶高分辨率Radon变换地震数据重建方法[J].
石油地球物理勘探, 2014, 49(1): 95-100 XUE Y R, TANG H H, CHEN X H. Seismic data reconstruction based on high order high resolution Radon transform[J]. Oil Geophysical Prospecting, 2014, 49(1): 95-100 |
| [14] |
徐彦凯, 曹思远, 何元. 双曲Radon-ASVD方法压制叠前地震数据随机噪声[J].
石油地球物理勘探, 2017, 52(3): 451-457 XU Y K, CAO S Y, HE Y. Prestack seismic random noise attenuation with a hyperbolic Radon-ASVD[J]. Oil Geophysical Prospecting, 2017, 52(3): 451-457 |
| [15] |
王立歆, 李强, 姬小兵, 等. 用Radon变换法消除沙丘鸣震的应用及效果分析[J].
石油物探, 2002, 41(1): 88-91 WANG L X, LI Q, JI X B, et al. Application of Radon transformation to elimination of dune ringing and its effect analysis[J]. Geophysical Prospecting for Petroleum, 2002, 41(1): 88-91 |
| [16] |
范景文, 李振春, 宋翔宇, 等. 各向异性高分辨率Radon变换压制多次波[J].
石油地球物理勘探, 2016, 51(4): 665-669 FAN J W, LI Z C, SONG X Y, et al. Multiple attenuation with anisotropic high-resolution Radon transform[J]. Oil Geophysical Prospecting, 2016, 51(4): 665-669 |
| [17] |
谢玉洪, 李列, 刘玉金, 等. 基于共散射点道集的多次波压制方法研究[J].
石油地球物理勘探, 2015, 50(2): 232-237 XIE Y H, LI L, LIU Y J, et al. Multiple elimination in common scattering gathers[J]. Oil Geophysical Prospecting, 2015, 50(2): 232-237 |
| [18] |
张红梅, 刘洪. 基于稀疏离散τ-p变换的非均匀地震道重建[J].
石油物探, 2006, 45(2): 141-145 ZHANG H M, LIU H. Sparseness discrete τ-p transform in irregular seismic trace reconstruction[J]. Geophysical Prospecting for Petroleum, 2006, 45(2): 141-145 |
| [19] |
王升超, 韩立国, 巩向博. 基于各向异性Radon变换的叠前地震数据重建[J].
石油物探, 2016, 55(6): 808-815 WANG S C, HAN L G, GONG X B. Prestack seismic data reconstraction by anisotropic Radon transform[J]. Geophysical Prospecting for Petroleum, 2016, 55(6): 808-815 |
| [20] | COVA R, HENLEY D, INNANEN K. Addressing shear wave static corrections in the ray parameter domain:a non-stationary interferometric approach[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015: 2129-2133 |
| [21] |
邵广周, 李庆春. 联合应用τ-p变换法和相移法提取面波频散曲线[J].
石油地球物理勘探, 2010, 45(6): 836-840 SHAO G Z, LI Q C. S Joint application of τ-p and phase-shift stacking method to extract ground wave dispersion curve[J]. Oil Geophysical Prospecting, 2010, 45(6): 836-840 |
| [22] |
张威, 韩立国, 李洪建. 基于起伏海水表面的拖缆鬼波压制方法[J].
石油物探, 2017, 56(4): 500-506 ZHANG W, HAN L G, LI H J. Deghosting method based on a variable sea surface for conventional streamer seismic data[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 500-506 |
| [23] | SABBIONE J I, VELIS D R, SACCHI M D. Microseismic data denoising via an apex-shifted hyperbolic Radon transform[J]. Expanded Abstracts of 83rd Annual Internat SEG Mtg, 2013: 2155-2161 |
| [24] | WANG Y, SINGH S C, BARTON P J. Separation of P-and SV-wavefields from multi-component seismic data in the τ-p domain[J]. Geophysical Journal International, 2002, 151(2): 663-672 DOI:10.1046/j.1365-246X.2002.01797.x |
| [25] | IBRAHIM A, SACCHI M D. Simultaneous source separation using a robust Radon transform[J]. Geophysics, 2014, 79(1): V1-V11 DOI:10.1190/geo2013-0168.1 |
| [26] |
熊登, 赵伟, 张剑锋. 混合域高分辨率抛物Radon变换及在衰减多次波中的应用[J].
地球物理学报, 2009, 52(4): 1068-1077 XIONG D, ZHAO W, ZHANG J F. Hybrid-domain parabolic Radon transform and its application to demultiple[J]. Chinese Journal of Geophysics, 2009, 52(4): 1068-1077 |
| [27] | LU W. An accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on iterative 2D model shrinkage[J]. Geophysics, 2013, 78(4): V147-V155 DOI:10.1190/geo2012-0439.1 |
| [28] | CARY P W. The simplest discrete Radon transform[J]. Expanded Abstracts of 68th Annual Internat SEG Mtg, 1998: 1999-2002 |
| [29] | THORSON J R. Velocity-stack and slant-stack stochastic inversion[J]. Geophysics, 1985, 50(12): 2727-2741 DOI:10.1190/1.1441893 |
| [30] | HARGREAVES N, VERWEST B, WOMBELL R, et al. Multiple attenuation using an apexshifted radon transform[J]. Expanded Abstracts of 73rd Annual Internat SEG Mtg, 2003: 1929-1932 |
| [31] | TRAD D. Interpolation and multiple attenuation with migration operators[J]. Geophysics, 2003, 68(6): 2043-2054 DOI:10.1190/1.1635058 |
| [32] | TRAD D, SILIQI R, POOLE G, et al. Fast and robust deblending using Apex Shifted Radon transform[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg, 2012: 1-5 |
| [33] | IBRAHIM A, SACCHI M D. Fast simultaneous seismic source separation using Stolt migration and demigration operators[J]. Geophysics, 2015, 80(6): WD27-WD36 DOI:10.1190/geo2015-0044.1 |
| [34] | GONG X B, YU C X, WANG Z H. Separation of prestack seismic diffractions using an improved sparse apex-shifted hyperbolic Radon transform[J]. Exploration Geophysics, 2016 |
| [35] | MOLDOVEANU-CONSTANTINESCU C, SACCHI M D. Enhanced resolution in Radon domain using the shifted hyperbola equation[J]. Expanded Abstracts of 75th Annual Internat SEG Mtg, 2005: 2277-2280 |
| [36] | CASTLE R J. A theory of normal moveout[J]. Geophysics, 1994, 59(6): 983-999 DOI:10.1190/1.1443658 |
| [37] | BICKEL S H. Focusing aspects of the hyperbolic Radon transform[J]. Geophysics, 2000, 65(2): 652-655 DOI:10.1190/1.1444762 |
| [38] |
薛昭, 董良国, 单联瑜. Radon变换去噪方法的保幅性理论分析[J].
石油地球物理勘探, 2012, 47(6): 858-867 XIE Z, DONG L G, SHAN L Y. Amplitude preservation theoretical analysis of Radon transform de-noise method[J]. Oil Geophysical Prospecting, 2012, 47(6): 858-867 |
| [39] |
薛亚茹, 陈小宏, 马继涛. 多方向正交多项式变换压制多次波[J].
地球物理学报, 2012, 55(10): 3450-3458 XUE Y R, CHEN X H, MA J T. Multiples attenuation based on directional orthogonal polynomial transform[J]. Chinese Journal of Geophysics, 2012, 55(10): 3450-3458 DOI:10.6038/j.issn.0001-5733.2012.10.028 |
| [40] | SCHONEWILLE M, ZWARTJES P. High-resolution transforms and amplitude preservation[J]. Expanded Abstracts of 72nd Annual Internat SEG Mtg, 2002: 2066-2069 |
| [41] |
李晶晶, 孙成禹, 谢俊法, 等. 相对保幅的抛物线Radon变换法地震道重建[J].
石油物探, 2014, 53(2): 181-187 LI J J, SUN C Y, XIE J F, et al. Seismic trace reconstruction by relative amplitude-preserved parabolic Radon transform[J]. Geophysical Prospecting for Petroleum, 2014, 53(2): 181-187 |
| [42] |
唐欢欢, 毛伟建. 3D高阶抛物Radon变换地震数据保幅重建[J].
地球物理学报, 2014, 57(9): 2918-2927 TANG H H, MAO W J. Amplitude preserved seismic data reconstruction by 3D high-order parabolic Radon transform[J]. Chinese Journal of Geophysics, 2014, 57(9): 2918-2927 DOI:10.6038/cjg20140917 |
| [43] |
曾有良, 乐友喜, 单启铜. 基于高分辨率Radon变换的VSP波场分离方法[J].
石油物探, 2007, 46(2): 115-119 ZENG Y L, LE Y X, SHAN Q T. VSP wavefield separation based on high-resolution Radon transform[J]. Geophysical Prospecting for Petroleum, 2007, 46(2): 115-119 |
| [44] | SACCHI M D.Aperture compensated Radon and Fourier transforms[D].Vancouver:The University of British Columbia, 1996 |
| [45] | SCALES J A, GERZTENKORN A, TREITEL S. Fast Ip solution of large, sparse, linear systems:application to seismic travel time tomography[J]. Journal of Computational Physics, 1988, 75(2): 314-333 DOI:10.1016/0021-9991(88)90115-5 |
| [46] | GORODNITSKY I F, RAO B D. Sparse signal reconstruction from limited data using FOCUSS:a re-weighted minimum norm algorithm[J]. IEEE Transactions on Signal Processing, 1997, 45(3): 600-616 DOI:10.1109/78.558475 |
| [47] | SABBIONE J I, SACCHI M D. Restricted model domain time Radon transforms[J]. Geophysics, 2016, 81(6): A17-A21 DOI:10.1190/geo2016-0270.1 |
| [48] | LIU Y, SACCHI M D. De-multiple via a fast least squares hyperbolic radon transform[J]. Expanded Abstracts of 72nd Annual Internat SEG Mtg, 2002: 2182-2185 |
| [49] | WANG J F, NG M, PERZ M. Fast high-resolution Radon transforms by greedy least-squares method[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009: 3128-3132 |
| [50] |
刘财, 杨庆节, 耿美霞. 多波多分量地震资料速度扫描法转换波识别技术[J].
石油物探, 2013, 52(4): 383-387 LIU C, YANG Q J, GENG M X. P-SV wave identification technique by velocity scanning for multi-wave multi-component seismic data[J]. Geophysical Prospecting for Petroleum, 2013, 52(4): 383-387 |
| [51] |
冯晅, 张先武, 刘财, 等. 带有多道相关的抛物线Radon变换法分离P-P、P-SV波[J].
地球物理学报, 2011, 54(2): 304-309 FENG X, ZHANG X W, LIU C, et al. Saparating P-P and P-SV wave by parabolic Radon transform with multiple coherence[J]. Chinese Journal of Geophysics, 2011, 54(2): 304-309 |
| [52] |
陶春辉, 何樵登. 地面多分量地震资料纵横波分离方法[J].
石油物探, 1993, 32(2): 47-55 TAO C J, HE Q D. Separation of P-and S-waves in multicomponent surface seismic data[J]. Geophysical Prospecting for Petroleum, 1993, 32(2): 47-55 |
| [53] |
马德堂, 朱光明. 弹性波波场P波和S波分解的数值模拟[J].
石油地球物理勘探, 2003, 38(5): 482-486 MA D T, ZHU G M. Numerical modeling of P-wave and S-wave separation in elastic wavefield[J]. Oil Geophysical Prospecting, 2003, 38(5): 482-486 |
| [54] | DELLINGER J, ETGEN J. Wave-field separation in two-dimensional anisotropic media[J]. Geophysics, 1990, 55(7): 914-919 DOI:10.1190/1.1442906 |
| [55] |
寻超, 汪超, 王赟. 多方向矢量中值滤波在多分量地震数据中的应用[J].
石油物探, 2016, 55(5): 703-710 XUN C, WANG C, WANG Y. The application of multi-directional vector median filtering in multi-component seismic data[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 703-710 |
| [56] | FORNASIER M, RAUHUT H. Recovery algorithms for vector valued data with joint sparsity constraints[J]. SIAM Journal on Numerical Analysis, 2008, 46(2): 577-613 DOI:10.1137/0606668909 |
| [57] | VERA RODRIGUEZ I, BONAR D, SACCHI M. Microseismic data denoising using a 3C group sparsity constrained time-frequency transform[J]. Geophysics, 2012, 77(2): 21-29 |
| [58] | MICHAUD G, LEANEY S. Continuous microseismic mapping for real-time event detection and location[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008: 1357-1361 |
| [59] | SABBIONE J I, SACCHI M D, VELIS D R. Radon transform-based microseismic event detection and signal-to-noise ratio enhancement[J]. Journal of Applied Geophysics, 2015, 113(1): 51-63 |



 ,
,