海洋可控源电磁法勘探包括海底高阻油气资源勘探[1-5]、深海热液硫化物矿勘探[6]、海底工程检测[7]等, 能够有效进行油气层识别和海上油气储层定量评价[1-4], 2000年以来得到了大力发展[8-9]。针对不同水深和油气藏规模, 海洋电磁法发展了多种不同的电磁勘探装置[10-16], 如频率域深拖拽发射-接收装置、频率域浅拖拽发射-接收装置、时间域深拖拽发射-接收装置、时间域浅拖拽发射-接收装置、时间域海底垂直发射-垂直接收装置等。国内外学者对不同海洋电磁法勘探装置的高阻目标体探测能力进行了很多对比研究, 如SHANTSEV等[17]、GUO等[18]比较了频率域深拖拽和浅拖拽装置在不同水深情况下对海底高阻目标体的探测能力, 建议在深水域采用深拖拽装置, 浅水域采用浅拖拽装置。GOLDMAN等[19]比较了频率域深拖拽水平发射-固定阵列接收装置、时间域海底垂直发射-垂直接收装置、时间域回线源装置对海底高阻目标体的探测能力, 建议在深水域采用频率域方法, 浅水域以及横向小目标体探测采用时间域方法。MACGREGOR等[10]对各类装置探测海底高阻目标体的优缺点进行了较为系统的总结。
深海热液硫化物矿[20]广泛分布于深海的大洋扩张脊和火山构造带等区域, 具有显著的经济开采价值。日益增长的资源需求推动着海底矿产勘探的发展, 海洋可控源电磁法在深海热液硫化物矿勘探中的应用得到越来越多的关注[6, 21-23]。深海热液硫化物矿是一种典型的低阻目标体, 相应的深海低阻目标体电磁法探测主要采用时间域海底中心回线或重叠回线装置[6, 21-22]。而目前广泛应用的海洋电磁法各类装置[11-16]主要应用于海底高阻油气探测, 关于深海低阻目标体探测能力的讨论和分析较少。本文研究分析了目前广泛应用的海洋电磁法装置对深海低阻目标体(以热液硫化物矿为例)的探测能力。考虑深海区域的目标体探测采用浅拖拽装置接收信号时需要经过两次厚的海水层吸收, 会导致电磁信号幅值过小[17], 同时考虑到海底操作的效率, 本文主要针对工作效率较高的频率域深拖拽发射-接收装置[12]和时间域深拖拽发射-接收装置[14]进行讨论。通过计算典型的深海三维低阻目标体模型的电场响应, 分析这两类海洋电磁法勘探装置对深水域低阻目标体的探测能力。
1 正演理论三维频率域正演电磁响应采用耦合势有限体积法计算[24]。频率域电磁法满足的控制方程为:
| $ \nabla \times \nabla \times E + {\rm{i}}\omega {\mu _0}\sigma \mathit{\boldsymbol{E}} = - {\rm{i}}\omega {\mu _0}\mathit{\boldsymbol{J}} $ | (1) |
式中:E为频率域电场强度矢量, J为外加电性源, ω为圆频率, μ0为真空磁导率, σ为地层电导率。引入电场的矢势A和标势φ, 将电场分解为无散场和无旋场之和:
| $ \mathit{\boldsymbol{E}} = \mathit{\boldsymbol{A}} + \nabla \varphi $ | (2) |
控制方程转换为关于矢势与标势的混合Helmholtz方程:
| $ {\nabla ^2}{A_x} + {\rm{i}}\omega {\mu _0}\left[ {\sigma \left( {{A_x} + \frac{{\partial \varphi }}{{\partial x}}} \right)} \right] = - {\rm{i}}\omega {\mu _0}{J_x} $ | (3a) |
| $ {\nabla ^2}{A_y} + {\rm{i}}\omega {\mu _0}\left[ {\sigma \left( {{A_y} + \frac{{\partial \varphi }}{{\partial y}}} \right)} \right] = - {\rm{i}}\omega {\mu _0}{J_y} $ | (3b) |
| $ {\nabla ^2}{A_z} + {\rm{i}}\omega {\mu _0}\left[ {\sigma \left( {{A_z} + \frac{{\partial \varphi }}{{\partial z}}} \right)} \right] = - {\rm{i}}\omega {\mu _0}{J_z} $ | (3c) |
| $ \nabla \cdot \sigma \left( {\mathit{\boldsymbol{A}} + \nabla \varphi } \right) = - \nabla \cdot \mathit{\boldsymbol{J}} $ | (3d) |
式中:Ax, Ay和Az为矢势A在直角坐标系中的3个分量; Jx, Jy和Jz为电性源J在直角坐标系中的3个分量。选择足够大的计算区域Ω, 则在区域外边界∂Ω上的电磁场将非常小, 因此可以采用简单的截断边界条件:
| $ \begin{array}{l} \mathit{\boldsymbol{n}} \times \mathit{\boldsymbol{A}}\left| {_{\partial \mathit{\Omega }}} \right. = 0\\ \mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{A}}\left| {_{\partial \mathit{\Omega }}} \right. = 0\\ \;\;\;\;\varphi \left| {_{\partial \mathit{\Omega }}} \right. = 0 \end{array} $ | (4) |
其中, n为边界单位矢量。为了求解控制方程(3)在边界条件(4)下的数值解, 采用Yee氏交错网格对求解区域进行空间离散, 利用高斯定理对旋度和散度算子进行离散处理, 发射源采用直接离散方法, 最终得到关于矢势A和标势φ的离散控制方程:
| $ \mathit{\boldsymbol{FX}} = \mathit{\boldsymbol{Q}} $ | (5) |
式中:系数矩阵F为大型非对称稀疏复矩阵, X为离散网格上的未知数, Q为离散的源项。采用直接法求解器PARDISO [25]求解该离散方程, 得到三维频率域正演电磁响应。
三维时间域正演电磁响应采用基于隐式时间步迭代的拟态有限体积法计算。忽略位移电流, 回线源瞬变电磁法对应的时间域Maxwell方程为:
| $ \frac{{\partial \mathit{\boldsymbol{b}}}}{{\partial t}} = - \nabla \times \mathit{\boldsymbol{e}} $ | (6a) |
| $ \nabla \times \mu _0^{ - 1}\mathit{\boldsymbol{b}} - \sigma \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{s}} $ | (6b) |
式中:e是时间域电场强度矢量, b是时间域磁感应强度矢量, t是时间, s是时间域外加源项。采用简单的自然边界条件
| $ \begin{array}{l} \mathit{\boldsymbol{b}} \times \mathit{\boldsymbol{n}} = 0\\ \mathit{\boldsymbol{n}} \times \mathit{\boldsymbol{e}} = 0 \end{array} $ | (7) |
则回线源瞬变电磁法在t=0时刻空间中只存在稳定的磁场分布, 即初始条件为:
| $ \mathit{\boldsymbol{b}}\left( {t = 0} \right) = {\mathit{\boldsymbol{b}}^0} $ | (8) |
式中, b0为t=0时刻空间中的磁场分布。将(8)式采用弱形式表示, 并采用Yee氏交错网格进行空间离散, 利用积分形式的斯托克斯定理处理电场旋度的离散, 得到控制方程空间离散的矩阵表示。采用关断源, 并采用无条件稳定的欧拉后向差分格式进行时间步离散, 得到最终的离散控制方程为:
| $ \left( {\mathit{\boldsymbol{C}}_{{\rm{URL}}}^{\rm{T}}{\mathit{\boldsymbol{M}}_\mu }{\mathit{\boldsymbol{C}}_{{\rm{URL}}}} + \Delta {t^{ - 1}}{\mathit{\boldsymbol{M}}_\sigma }} \right){\mathit{\boldsymbol{e}}^n} = \Delta {t^{ - 1}}\mathit{\boldsymbol{C}}_{{\rm{URL}}}^{\rm{T}}{\mathit{\boldsymbol{M}}_\mu }{\mathit{\boldsymbol{b}}^{n - 1}} $ | (9a) |
| $ {\mathit{\boldsymbol{b}}^n} = {\mathit{\boldsymbol{b}}^{n - 1}} - \Delta t{\mathit{\boldsymbol{C}}_{{\rm{URL}}}}{\mathit{\boldsymbol{e}}^n} $ | (9b) |
式中:CURL为旋度算子的离散形式, Mμ和Mσ分别为磁导率μ0和电导率σ离散形成的矩阵, Δt为迭代时间步长, en和bn分别为第n次时间步迭代得到的电场和磁场。先通过解析求得初始场b0, 然后通过求解时间步迭代的线性方程组(9), 即可得到不同时刻的电磁场响应。本文采用直接法求解器PARDISO[25]求解线性方程组(9), 同时, 为了保证计算精度和效率, 选取分段等间隔的时间步长。
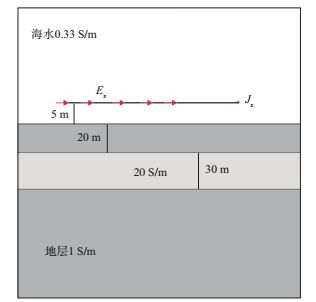
2 探测能力分析频率域和时间域深拖拽发射-接收装置探测深海三维低阻目标体模型设置参考文献[6]中的一维热液硫化物矿模型。当海水深度大于1000m时认为是深海域[8], 可以忽略空气层, 因此可以设置如图 1所示的正演模型。该模型上半空间为海水层, 电导率为3S/m; 海底地层电导率为1S/m, 海底下方20m存在一个电导率为20S/m的三维矩形低阻目标体, 其x方向长度为500m, y方向长度为500m, z方向厚度为30m。采用海底深拖拽水平发射-水平接收装置, 发射源与接收机位于同一高度, 操作方便, 距离海底上方5m, 发射源水平方向距离海底下方三维目标体边界100m(图 1)。
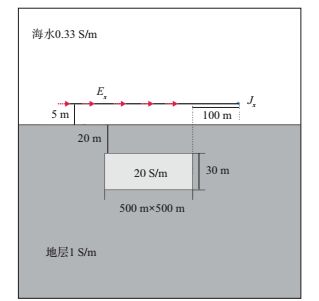
|
图 1 三维模型 |
在探测埋深较大的高阻油气藏时, 一般采用较低的发射频率(0.1~10.0Hz)。由于本文研究的低阻目标体埋深较浅, 因此采用相对高的发射频率(100Hz)[11]。深海域海洋电磁法在100Hz时的噪声水平为2×10-15V/Am2[11]。发射源位置水平方向距离海底下方三维目标体边界100m, 如图 1所示, 随船拖拽的多个接收机与发射机位于同一高度。图 2为不同偏移距时频率域深拖拽水平发射-接收装置的响应振幅和归一化振幅。图 2a中黑色圆圈为采用开源软件Dipole 1D[26]计算的不含异常体的一维模型的解析解, 红色曲线为采用三维耦合势有限体积算法计算的不含异常体的一维模型的数值解, 蓝色曲线为采用三维耦合势有限体积算法计算的三维模型(如图 1所示)的数值解, 黑色虚线为噪声水平; 图 2b为存在3D低阻体的电场响应相对不含低阻体的半空间模型的归一化振幅。图 2a中黑色圆圈与红色曲线重合, 说明本文算法的计算结果是有效的。图 2a中红色曲线和蓝色曲线对比可知, 该装置对于海底低阻目标体存在显著异常, 最小归一化振幅小于0.02, 最大异常响应位于偏移距500m处(图 2b), 其主要的异常响应均大于噪声水平, 说明该装置能够有效地探测海底低阻异常。
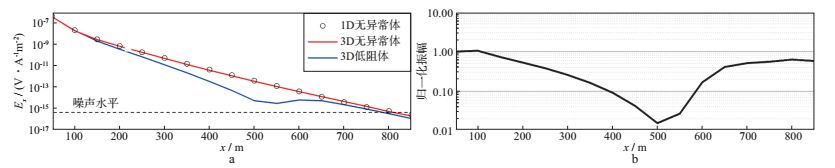
|
图 2 三维模型频率域深拖拽水平发射-接收装置电场响应(a)和归一化振幅(b) |
为了更清晰地理解频率域深拖拽水平发射-接收装置对海底低阻体的探测原理, 绘制了含有低阻目标体和不含低阻目标体两种情况三维模型的电流和电场分布图。图 3为不含低阻异常体的半空间模型的电场幅值(即
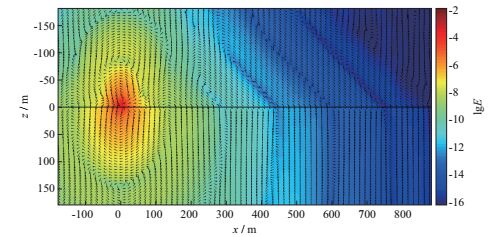
|
图 3 不含低阻异常体模型电场幅值及电流分布(等值线表示电场分布, 箭头表示电流方向) |
|
图 4 不含低阻异常体的三维模型x方向电场Ex幅值分布 |
|
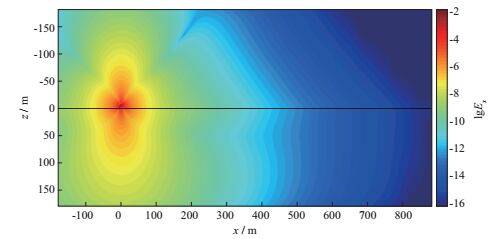
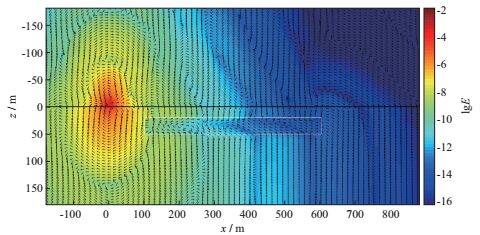
图 5 含有低阻异常体模型的电场幅值及电流分布(等值线表示电场分布, 箭头表示电流方向) |
|
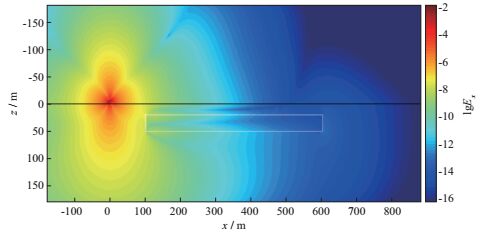
图 6 含有低阻异常体的三维模型x方向电场Ex幅值分布 |
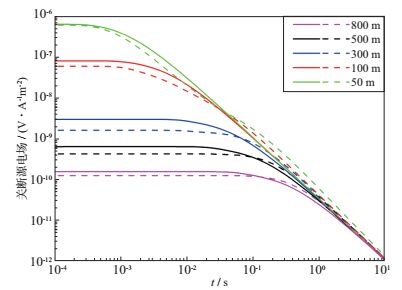
采用时间域深拖拽发射-接收装置探测深海三维低阻热液硫化物矿目标体类似于长偏移距瞬变电磁法[27-29], 存在最优化偏移距选取问题。本文通过对比不同偏移距情况下一维低阻模型的瞬变电磁响应, 得到近似最优化的偏移距。图 7为一维低阻层状模型, 分别计算偏移距为50, 100, 300, 500, 800m的模型地层响应, 如图 8所示。其中实线为不含低阻层的半空间地层响应, 虚线为含有低阻层的地层响应。由图 8可见, 当偏移距为300m时, 低阻层的异常响应最大。当偏移距逐渐大于300m或者小于300m时, 低阻层的异常响应都表现为逐渐减小, 可知图 7所示的一维低阻层状模型最优化偏移距在300m左右。因此, 本文在随后计算图 1所示三维模型的瞬变电磁响应时, 偏移距选取300m。
|
图 7 一维低阻层状模型 |
|
图 8 一维低阻层状模型的时间域深拖拽水平发射-接收装置响应(实线为不含低阻层的半空间地层响应, 虚线为含有低阻层的地层响应) |
采用三维有限体积正演算法计算图 1所示三维模型的正演响应。图 9为时间域深拖拽水平发射-接收装置的电场响应振幅和归一化振幅, 其中图 9a中黑色圆圈为采用开源软件Dipole1D结合正余弦数字滤波算法[30]计算得到的不含低阻异常体的一维模型的解析解, 红色曲线为采用三维有限体积算法计算的不含低阻异常体的一维模型的数值解, 蓝色曲线为采用三维有限体积算法计算的三维低阻模型的数值解, 黑色虚线为噪声水平[31]; 图 9b为存在三维低阻体的电场响应相对不含低阻异常体的一维模型的归一化振幅。图 9a中黑色圆圈与红色曲线重合, 说明本文算法的计算结果是有效的。图 9a中红色曲线和蓝色曲线对比可知, 时间域深拖拽水平发射-接收装置对于海底低阻目标体存在明显异常, 最小归一化振幅为0.55, 最大异常响应位于5×10-3s时刻。其主要异常响应均大于噪声水平, 说明该装置能够有效探测海底低阻异常。

|
图 9 三维低阻模型的时间域深拖拽水平发射-接收装置电场响应(a)与归一化振幅(b) |
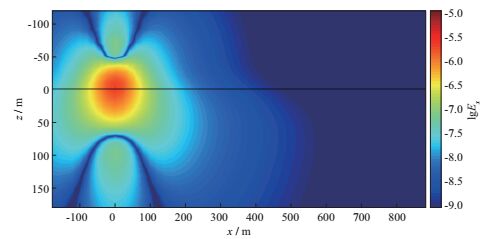
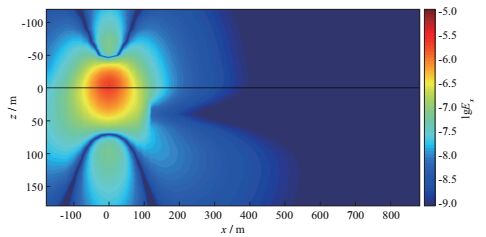
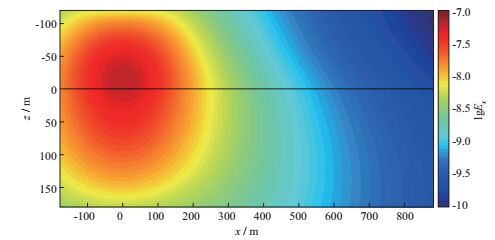
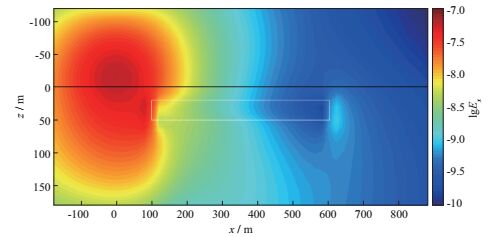
为了清晰地理解时间域深拖拽水平发射-接收装置对海底低阻体的探测原理, 绘制了含有低阻目标体和不含低阻目标体的三维模型电流和电场分布图。图 10为不含低阻异常体的模型在10-5s时刻x方向电场Ex幅值分布图, 图 11为含有低阻异常体的模型在10-5s时刻x方向电场Ex幅值分布图; 图 12为不含低阻异常体的模型在10-2s时刻x方向电场Ex幅值分布图, 图 13为含有低阻异常体的模型在10-2s时刻x方向电场Ex幅值分布图。由图 10和图 11可知, 在10-5s时刻, 三维低阻异常体的存在虽然能够导致其所在区域场值减小, 从而导致空间中的电场分布产生畸变, 但由于能量主要集中在发射源附近, 因此三维低阻异常体的存在对于300m接收点处的电场分布影响甚微, 表现为图 9中10-5s时刻存在三维低阻异常体和不存在三维低阻异常体两种情况的电场幅值|Ex|相同。随着时间增加, 能量逐渐向外扩散, 三维低阻异常体对接收点信号的影响逐渐增大, 表现为图 9中归一化振幅随时间增加逐渐减小, 到5×10-3s时刻三维低阻异常体对接收点信号的影响达到最大, 此后随着时间增加, 三维低阻异常体的影响逐渐减小, 对应接收点处的归一化振幅逐渐增大。对比图 12和图 13可知, 在10-2s时刻, 三维低阻异常体的存在导致电场幅值|Ex|的分布产生较大畸变, 三维低阻异常体对能量的强吸收作用导致接收点处的电场幅值低于不含三维低阻异常体时的电场幅值, 对应图 9中10-2s时刻电场的归一化振幅小于1.0。
|
图 10 不含低阻异常体的模型在10-5s时刻x方向电场Ex幅值分布 |
|
图 11 含有低阻异常体的模型在10-5s时刻x方向电场Ex幅值分布 |
|
图 12 不含低阻异常体的模型在10-2s时刻x方向电场Ex幅值分布 |
|
图 13 含有低阻异常体的模型在10-2s时刻x方向电场Ex幅值分布 |
本文研究了频率域和时间域深拖拽发射-接收装置对于深海三维低阻目标体的探测能力。通过计算典型的深水域三维低阻目标体模型的电场响应、归一化电场响应和空间中电场分布特点, 分析了两种不同海洋电磁方法的应用效果, 取得以下成果:
对于本文所计算的三维模型, 频率域响应的最大异常位于偏移距500m处, 时间域响应的最大异常位于偏移距300m处。频率域和时间域深拖拽发射-接收装置均能够在小偏移距观测到深海三维低阻目标体的电场异常, 频率域响应的最小归一化振幅小于0.02, 时间域响应的最小归一化振幅为0.55, 频率域电磁法的异常幅值要明显大于时间域电磁法。
本文研究内容能够为海洋电磁法勘探, 特别是小目标体和深海热液硫化物矿勘探提供一定的参考。
| [1] | EIDESMO T, ELLINGSRUD S, MACGREGOR L, et al. Sea bed logging (SBL), a new method for remote and direct identification of hydrocarbon filled layers in deepwater areas[J]. First Break, 2002, 20(3): 144-152 |
| [2] | ELLINGSRUD S, EIDESMO T, JOHANSEN S, et al. Remote sensing of hydrocarbon layers by seabed logging (SBL):results from a cruise offshore Angola[J]. The Leading Edge, 2002, 21(10): 972-982 DOI:10.1190/1.1518433 |
| [3] |
沈金松, 陈小宏. 海洋油气勘探中可控源电磁探测法(CSEM)的发展与启示[J].
石油地球物理勘探, 2009, 44(1): 119-127 SHEN J S, CHEN X H. Development and enlightenment of controlled-source electromagnetic (CSEM) surveying method in marine oil/gas exploration[J]. Oil Geophysical Prospecting, 2009, 44(1): 119-127 |
| [4] |
汤文武, 李耀国, 柳建新, 等. 基于二次电场的可控源电磁法三维矢量有限元正演模拟[J].
石油物探, 2015, 54(6): 665-673 TANG W W, LI Y G, LIU J X, et al. Three-dimensional controlled-source electromagnetic forward modeling by edge-based finite element using secondary electric field[J]. Geophysical Prospecting for Petroleum, 2015, 54(6): 665-673 |
| [5] |
李肃义, 蒋善庆, 王跃洋, 等. 海洋可控源电磁数据中海水扰动噪声的小波校正方法研究[J].
石油物探, 2016, 55(5): 657-663 LI S Y, JIANG S Q, WANG Y Y, et al. A wavelet correction method for the seawater turbulence noise in marine controlled-source electromagnetic data[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 657-663 |
| [6] | SWIDINSKY A, HÖLZ S, JEGEN M. On mapping seafloor mineral deposits with central loop transient electromagnetics[J]. Geophysics, 2012, 77(3): E171-E184 DOI:10.1190/geo2011-0242.1 |
| [7] |
刘长胜. 海底可控源电磁探测数值模拟与实验研究[D]. 长春: 吉林大学, 2009
LIU C S.Numerical simulation and experimental study on marine controlled-source electromagnetic methods[D].Changchun:Jilin University, 2009 http://cdmd.cnki.com.cn/Article/CDMD-10183-2009093520.htm |
| [8] | CONSTABLE S. Ten years of marine CSEM for hydrocarbon exploration[J]. Geophysics, 2010, 75(5): A67-A81 |
| [9] |
何展翔, 孙卫斌, 孔繁恕, 等. 海洋电磁法[J].
石油地球物理勘探, 2006, 41(4): 451-457 HE Z X, SUN W B, KONG F S, et al. Marine electromagnetic approach[J]. Oil Geophysical Prospecting, 2006, 41(4): 451-457 |
| [10] | MACGREGOR L, TOMLINSON J. Marine controlled-source electromagnetic methods in the hydrocarbon industry:a tutorial on method and practice[J]. Interpretation, 2014, 2(3): SH13-SH32 DOI:10.1190/INT-2013-0163.1 |
| [11] | CONSTABLE S. Review paper:instrumentation for marine magnetotelluric and controlled source electromagnetic sounding[J]. Geophysical Prospecting, 2013, 61(S1): 505-532 |
| [12] | CONSTABLE S, KANNBERG P K, WEITEMEYER K. Vulcan:a deep-towed CSEM receiver[J]. Geochemistry, Geophysics, Geosystems, 2016, 17(3): 1042-1064 DOI:10.1002/2015GC006174 |
| [13] | ANDERSON C, MATTSON J. An integrated approach to marine electromagnetic surveying using a towed streamer and source[J]. First Break, 2010, 28(5): 71-75 |
| [14] | EDWARDS N. Marine controlled source electromagnetics:principles, methodologies, future commercial applications[J]. Surveys in Geophysics, 2005, 26(6): 675-700 DOI:10.1007/s10712-005-1830-3 |
| [15] | HOLTEN T, FLEKK∅Y E G, SINGER B, et al. Vertical source, vertical receiver, electromagnetic technique for offshore hydrocarbon exploration[J]. First Break, 2009, 27(5): 89-93 |
| [16] |
李予国, STEVENCONSTABLE. 浅水区的瞬变电磁法:一维数值模拟结果分析[J].
地球物理学报, 2010, 53(3): 737-742 LI Y G, CONSTABLE S. Transient electromagnetic in shallow water:insights from 1D modeling[J]. Chinese Journal of Geophysics, 2010, 53(3): 737-742 |
| [17] | SHANTSEV D, ROTH F, RAMSFJELL H. Surface towing versus deep towing in marine CSEM[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg, 2012: 1-5 |
| [18] | GUO Z W, DONG H F, LIU J X. Comparison of marine controlled-source electromagnetic data acquisition systems by a reservoir sensitivity index:analyzing the effect of water depths[J]. Acta Oceanologica Sinica, 2016, 35(11): 113-119 DOI:10.1007/s13131-016-0954-2 |
| [19] | GOLDMAN M, MOGILATOV V, HAROON A, et al. Signal detectability of marine electromagnetic methods in the exploration of resistive targets[J]. Geophysical Prospecting, 2015, 63(1): 192-210 DOI:10.1111/gpr.2015.63.issue-1 |
| [20] | RONA P A. Hydrothermal mineralization at seafloor spreading centers[J]. Earth-Science Reviews, 1984, 20(1): 1-104 DOI:10.1016/0012-8252(84)90080-1 |
| [21] | JANG H, KIM H J. Mapping deep-sea hydrothermal deposits with an in-loop transient electromagnetic method:insights from 1D forward and inverse modeling[J]. Journal of Applied Geophysics, 2015, 123: 170-176 DOI:10.1016/j.jappgeo.2015.10.003 |
| [22] |
李瑞雪, 王鹤, 席振铢, 等. 深海热液硫化物矿体3D瞬变电磁正演[J].
地球物理学报, 2016, 59(12): 4505-4512 LI R X, WANG H, XI Z Z, et al. The 3D transient electromagnetic forward modeling of volcanogenic massive sulfide ore deposits[J]. Chinese Jounal of Geophysical, 2016, 59(12): 4505-4512 DOI:10.6038/cjg20161213 |
| [23] | CORSERI R, SENGER K, SELWAY K, et al. Magnetotelluric evidence for massive sulphide mineralization in intruded sediments of the outer Vøring Basin, mid-Norway[J]. Tectonophysics, 2017, 706-707: 196-205 DOI:10.1016/j.tecto.2017.04.011 |
| [24] |
周建美, 张烨, 汪宏年, 等. 耦合势有限体积法高效模拟各向异性地层中海洋可控源的三维电磁响应[J].
物理学报, 2014, 63(15): 159101 ZHOU J M, ZHANG Y, WANG H N, et al. Efficient simulation of three-dimensional marine controlled-source electromagnetic response in anisotropic formation by means of coupled potential finite volume method[J]. Acta Physica Sinica, 2014, 63(15): 159101 DOI:10.7498/aps.63.159101 |
| [25] | SCHENK O, GÄRTNER K. Solving unsymmetric sparse systems of linear equations with pardiso[J]. Future Generation Computer Systems, 2004, 20(3): 475-487 DOI:10.1016/j.future.2003.07.011 |
| [26] | KEY K. 1D inversion of multicomponent, multi-frequency marine CSEM data:methodology and synthetic studies for resolving thin resistive layers[J]. Geophysics, 2009, 74(2): F9-F20 DOI:10.1190/1.3058434 |
| [27] | SCHOLL C.Resolving an onshore gas-hydrate layer with long-offset transient electromagnetics (LOTEM)[C]//RIEDEL M, WILLOUGHBY E C, CHOPRA S.Geophysical Characterization of Gas Hydrates.[S.l.]:Society of Exploration Geophysicists, 2010:163-177 |
| [28] |
谢兴兵, 周磊, 严良俊, 等. 时移长偏移距瞬变电磁法剩余油监测方法及应用[J].
石油地球物理勘探, 2016, 51(3): 605-612 XIE X B, ZHOU L, YAN L J, et al. Remaining oil detection with time-lapse long offset & window transient electromagnetic sounding[J]. Oil Geophysical Prospecting, 2016, 51(3): 605-612 |
| [29] |
王显祥, 底青云, 邓居智. 多通道瞬变电磁法油气藏动态检测[J].
石油地球物理勘探, 2016, 51(5): 1021-1030 WANG X X, DI Q Y, DENG J Z. Reservoir dynamic detection based on multi-channel transient electromagnetic[J]. Oil Geophysical Prospecting, 2016, 51(5): 1021-1030 |
| [30] |
王华军. 正余弦变换的数值滤波算法[J].
工程地球物理学报, 2006, 1(4): 329-335 WANG H J. Digital filter algorithm of the sine and cosine transform[J]. Chinese Journal of Engineering Geophysics, 2006, 1(4): 329-335 |
| [31] | SCHOLL C, MIR R, WILLOUGHBY E, et al.Resolving resistive anomalies due to gas hydrate using electromagnetic imaging methods[R].Vancouver, Canada:Proceedings of the 6th International Conference on Gas Hydrates, 2008 |


