2. 大庆油田有限责任公司第六采油厂, 黑龙江 大庆 163712
2. NO.6 Oil Production Plant of Daqing Oilfield Company Ltd., Daqing 163712, China
近年来, 成功实现了以页岩气、致密油气等为代表的非常规油气资源规模开发, 推动了全球油气工业进入了常规资源与非常规资源并重发展的新阶段[1]。针对致密油储层的精细勘探开发, 目前国内外主要采取大规模水平井部署的方法, 这对致密薄储层地震预测提出了更高的要求[2]。因此, 国内外专家学者将地震岩石物理分析与储层预测、多波勘探以及四维地震油藏监测紧密结合起来。特别是对于非常规油气藏勘探开发, 地震岩石物理已经成为基于地震信息进行储层描述的基础和核心[3]。DAVID等[4]利用AVO反演得到的纵横波速度比描述了致密砂岩气储层属性。MERLETTI等[5]利用测井与叠前振幅数据联合随机反演技术刻画了薄砂岩沉积层序, 并且用正演模拟数据证明了该技术的适用性, 为利用叠前地质统计学反演进行薄砂体储层预测提供了非常好的借鉴。
松辽盆地北部齐家地区青山口组致密砂岩油是大庆探区非常规致密油勘探的重要领域。该区致密油形成具备良好的烃源岩、储集层、源储配置及地层压力条件, 属于源内致密油, 在平面上主要分布于凹陷中心部位与凹陷周边斜坡、阶地, 纵向上主要分布在青山口组的高三、高四油层。随着水平井和压裂改造技术的进步及规模化应用, 该区致密油资源的经济有效动用成为现实。
齐家地区青山口组高三、高四油层平均埋深2000m左右, 属于三角洲前缘沉积环境。三角洲内前缘与外前缘相带内砂体类型主要有河口坝和席状砂, 单砂体厚度1~5m, 平面上砂体连续性较好, 孔隙度3%~15%, 渗透率(0.1~1.0)×10-3μm2。储集层主要为方解石胶结或泥质胶结长石细砂岩, 少量为介形虫屑灰岩。岩石的矿物组成复杂, 不同类型的岩性及储层弹性参数特征不明, 储层薄互砂泥岩声阻抗叠置, 以往基于叠后信息的属性分析、稀疏脉冲反演和地质统计学反演无法精细刻画井间“甜点”分布, 不能满足该区致密油勘探资源评价和水平井部署要求。本文根据实际致密油勘探需求, 分析致密储层岩石物理规律, 结合地震岩石物理和叠前地质统计学反演实现井间砂体及“甜点”有效预测, 为齐家地区青山口组致密油勘探提供技术支撑。
1 地震岩石物理分析地震岩石物理分析主要是建立孔隙介质弹性参数与岩石属性之间的关系, 为地震储层特征描述奠定基础。三维地震采集处理及地震叠前弹性参数反演的发展, 促进了地震岩石物理分析方法技术的进步和实际应用[6]。以下从岩心数据和测井曲线两个尺度分析目的层段岩石物理基本规律, 建立岩石物理模型并形成地震岩石物理定量解释图版, 确定“甜点”储层弹性响应特征。
1.1 岩样声学测试数据分析岩心测试数据直观准确, 已成为分析孔隙介质声学特征与岩石属性之间关系的有效手段。本文通过基础岩心参数测试和声学参数测量, 重点分析岩石弹性特征与岩性、孔隙度的变化规律。岩心样品取自齐家地区高三和高四油层组, 岩性为粉砂岩、钙质粉砂岩、泥质粉砂岩、含钙泥质粉砂岩。
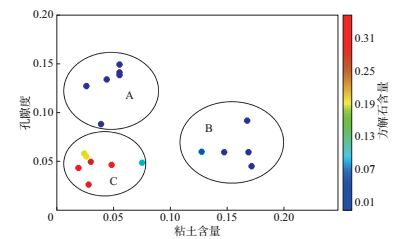
图 1为孔隙度与粘土含量交会图, 色标为方解石含量, 可以看到比较明显的3个分区:A区孔隙度最高, 粘土含量和方解石含量均较低; B区孔隙度其次, 粘土含量最高; C区孔隙度最低, 方解石含量高。这说明对储集层质量影响最大的成岩作用是方解石(钙质)胶结, 其含量直接影响孔隙度大小。砂岩胶结物中泥质含量适度增加将导致方解石含量降低或储集层质量变好(孔隙度增高)。
|
图 1 孔隙度与粘土含量交会分析 |
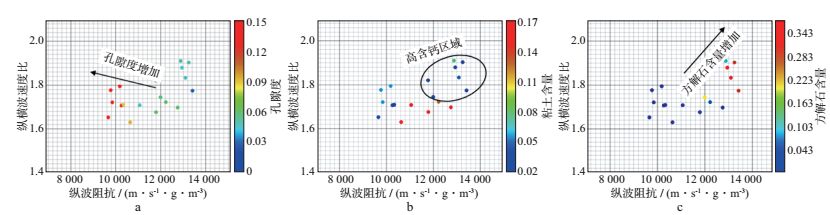
采用超声透射法测试岩样声学性质, 在实际地层条件下得到饱水岩石的纵、横波速度。在储层基本参数和声学参数测试的基础上, 通过不同组合分析研究发现, 规律最明显的是纵波阻抗与纵横波速度比弹性参数交会结果(图 2)。孔隙度增加以及方解石含量增加导致的岩样纵波阻抗和纵横波速度比变化表现出明显的规律, 孔隙度增加引起纵波阻抗减小和纵横波速度比增加。这里需要说明的是, 测井解释上的泥质含量与矿物分析中的粘土含量不同, 泥质含量的变化能够体现出实际应用中的岩性(或岩相)变化, 在后面的岩石物理分析中将给出具体的分析。
|
图 2 岩样数据纵波阻抗与纵横波速度比交会分析 a孔隙度; b粘土含量; c方解石含量 |
岩样数据分析给出了重要的岩石物理规律认识, 但测试对象的尺度小且是在高频情况下测试的结果。为进一步扩展岩石物理规律认识, 分析岩性和流体对弹性参数的影响, 下面对测井资料目的层段进行岩石物理交会分析。
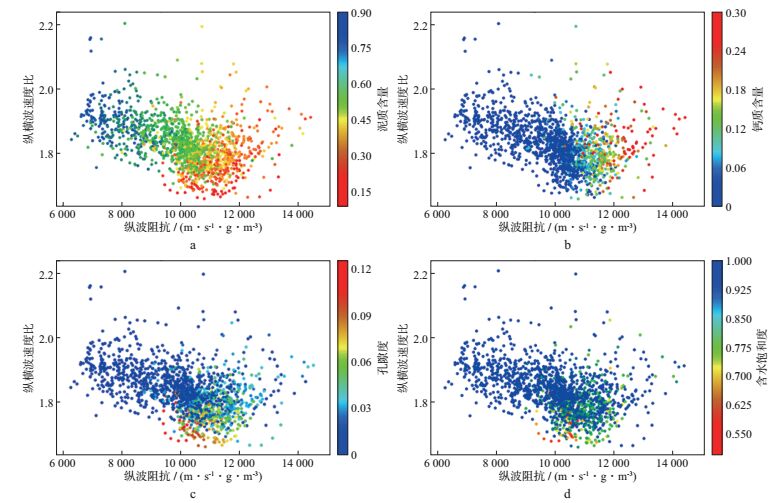
图 3给出了测井数据的纵波阻抗与纵横波速度比交会结果(图 3a至图 3d色标分别为泥质含量、钙质含量、孔隙度和含水饱和度), 交会图中数据使用了实测的交叉偶极测井资料。图 3与图 2的主要不同体现在, 后者分析的对象主要是粉砂岩类样品, 而前者包含更多岩性信息(如泥岩和过渡岩性)。图 3显示, 钙质含量(方解石含量)(图 3b)和孔隙度(图 3c)的影响与图 2一致, 泥质含量增加的影响表现为纵波阻抗降低和纵横波速度比增高(图 3a)。对比图 3c和图 3d可以看出, 孔隙度高的样点对应着高含油饱和度, 即孔隙度越高, 含油性越好。与其它储层参数相比, 本区致密砂岩(钙质含量少的砂岩)孔隙流体变化(油水相对含量变化)对纵波阻抗和纵横波速度比的影响不大(图 3d), 但总体趋势表现为纵波阻抗和纵横波速度比均随含油性增加而降低。
|
图 3 测井资料纵波阻抗与纵横波速度比交会分析 a泥质含量; b钙质含量; c孔隙度; d含水饱和度 |
理论分析与测井岩石物理分析的结合是岩石物理分析应用于地震储层预测的主流手段, 可以克服测井岩石物理交会分析直接应用带来的片面性[7]。在上述岩心和测井数据定性分析的基础上, 本节将理论研究与实际数据结合起来进行系统分析, 一方面建立合适的岩石物理模型, 以描述弹性参数响应与储层参数之间的定量关系; 另一方面, 在岩石物理机制下形成定量解释图版, 确立地质储层评价类别在弹性参数交会域中的分布特征, 为“甜点”地震预测奠定基础。
岩石物理模型大致可分为经验模型[8-10]和理论模型[11-13], 其中理论模型主要有等效介质理论和波传播理论。相比经验模型, 理论模型考虑岩石微观结构, 在一定的假设条件下通过内在的物理学原理建立通用关系, 更具有可推广性。考虑到实际应用的可操作性, 等效介质理论应用更为广泛, 如HS界限模型[14]、常数胶结模型[15]、未胶结砂岩模型[16]、自相容模型[17]和DEM模型[18]等。由于胶结和压实作用, 研究区目的层段砂岩固结致密, 颗粒呈点—线接触, 处于中成岩阶段[19]。为描述研究区致密砂岩储层, 本文通过分析对比, 采用硬砂岩等效介质模型[20]来模拟介质的弹性性质。
假设开始未成岩砂岩的骨架是孔隙度为φ0=0.36和平均配位数c=9的等同球体颗粒紧密任意排列。在该孔隙度下, 由Hertz-Mindlin理论给出静水压力(P)条件下等同球体颗粒紧密任意排列的骨架有效体积模量和剪切模量:
| $ {K_{{\rm{HM}}}} = {\left[ {\frac{{{c^2}{{\left( {1 - {\varphi _0}} \right)}^2}{G^2}}}{{18{{\rm{ \mathsf{ π} }}^2}{{\left( {1 - \sigma } \right)}^2}}}P} \right]^{\frac{1}{3}}} $ | (1) |
| $ {G_{{\rm{HM}}}} = \frac{{5 - 4\sigma }}{{5\left( {2 - \sigma } \right)}}{\left[ {\frac{{3{c^2}{{\left( {1 - {\varphi _0}} \right)}^2}{G^2}}}{{2{{\rm{ \mathsf{ π} }}^2}{{\left( {1 - \sigma } \right)}^2}}}P} \right]^{\frac{1}{3}}} $ | (2) |
式中:KHM和GHM是由Hertz-Mindlin理论计算出来的有效体积模量和剪切模量; σ是颗粒泊松比; G是颗粒剪切模量。对于不同孔隙度φ的有效模量, 采用Hashin-Strikman上边界[12]求取:
| $ {K_{{\rm{eff}}}} = {\left[ {\frac{{\frac{\varphi }{{{\varphi _0}}}}}{{{K_{{\rm{HM}}}} + \frac{4}{3}G}} + \frac{{1 - \frac{\varphi }{{{\varphi _0}}}}}{{K + \frac{4}{3}G}}} \right]^{ - 1}} - \frac{4}{3}G $ | (3) |
| $ \begin{array}{l} {G_{{\rm{eff}}}} = \\ {\left[ {\frac{{\frac{\varphi }{{{\varphi _0}}}}}{{{G_{{\rm{HM}}}} + \frac{G}{6}\left( {\frac{{9K + 8G}}{{K + 2G}}} \right)}} + \frac{{1 - \frac{\varphi }{{{\varphi _0}}}}}{{G + \frac{G}{6}\left( {\frac{{9K + 8G}}{{K + 2G}}} \right)}}} \right]^{ - 1}} - \\ \;\;\;\;\;\;\;\;\;\;\frac{G}{6}\left( {\frac{{9K + 8G}}{{K + 2G}}} \right) \end{array} $ | (4) |
式中:K是颗粒体积模量; Keff和Geff分别是采用HS模型上限计算出来的岩石等效体积模量和剪切模量。这里也是硬砂岩模型与未胶结砂岩模型的不同之处, 后者采用的是Hashin-Strikman下边界(构建的有效模量偏软)。
对于饱和岩石的有效弹性模量(或低频声波速度), 采用Gassmann公式求取:
| $ \begin{array}{l} {K_{{\rm{sat}}}} = {K_{{\rm{eff}}}} + \frac{{{{\left( {1 - \frac{{{K_{{\rm{eff}}}}}}{K}} \right)}^2}}}{{\frac{\varphi }{{{K_{{\rm{fluid}}}}}} + \frac{{1 - \varphi }}{K} - \frac{{{K_{{\rm{eff}}}}}}{{{K^2}}}}}\\ {G_{{\rm{sat}}}} = {G_{{\rm{eff}}}} \end{array} $ | (5) |
式中:Ksat和Gsat分别表示饱和岩石的有效体积模量和剪切模量; Geff表示饱和岩石的等效剪切模量; Kfluid表示流体的有效体积模量。实际应用中, 岩石骨架颗粒并非一种矿物成分, 通常有多种矿物成分存在。对于多矿物情况, 上述公式中的颗粒泊松比及模量由均匀混合模型得到。
体积模量、剪切模量与速度、密度的关系如下:
| $ {v_{\rm{P}}} = \sqrt {\frac{{{K_{{\rm{sat}}}} + \frac{4}{3}{G_{{\rm{sat}}}}}}{{{\rho _{{\rm{sat}}}}}}} $ | (6) |
| $ {v_{\rm{S}}} = \sqrt {\frac{{{G_{{\rm{sat}}}}}}{{{\rho _{{\rm{sat}}}}}}} $ | (7) |
| $ {\rho _{{\rm{sat}}}} = {\rho _{{\rm{eff}}}}\left( {1 - \varphi } \right) + {\rho _f}\varphi $ | (8) |
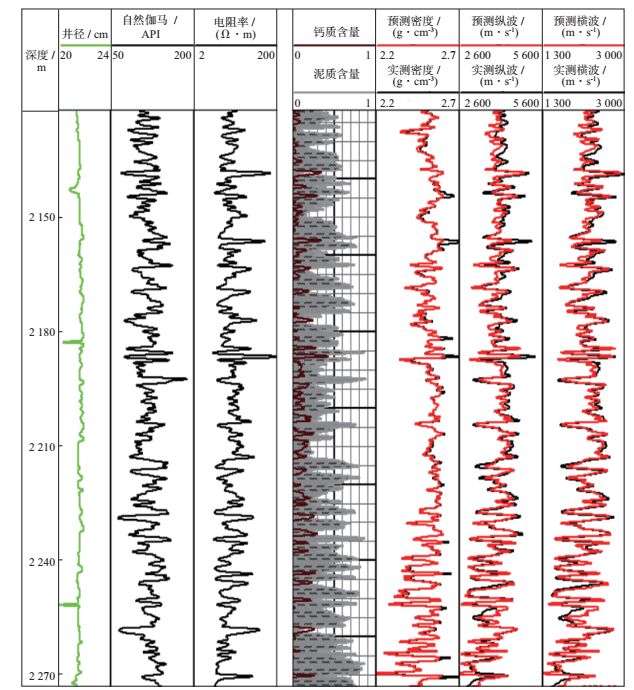
式中:vP表示纵波速度, vS表示横波速度, ρsat表示饱和岩石的密度, ρeff表示骨架密度, ρf表示流体密度。图 4对比了硬砂岩等效介质模型的预测结果(红色实线)和实际测井数据(黑色实线), 其中考虑到实际测井解释结果, 骨架颗粒由泥质、砂岩、钙质组成。图中预测结果和实测结果匹配良好, 说明岩石物理建模合理。
|
图 4 硬砂岩等效介质模型预测结果和实测结果对比 |
硬砂岩等效介质模型可用于研究区叠前反演所需的横波预测, 更重要的是在该模型理论指导下建立合适的岩石物理定量解释图版, 明确“甜点”弹性参数特征, 与叠前反演配套进行“甜点”地震预测。岩石物理定量解释图版具有明确的地质信息和地震信息, 作为地震定量解释的基石在常规和非常规油气储层预测中有着十分广泛的应用[21-23]。
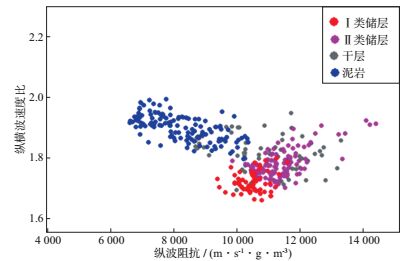
图 5显示了研究区地质评价分类储层在纵波阻抗和纵横波速度比双弹性交会域中的分布, 有Ⅰ类储层(孔隙度大于8%, 渗透率大于0.10×10-3μm2)、Ⅱ类储层(孔隙度4%~8%, 渗透率(0.02~0.50)×10-3μm2)、干层(孔隙度小于4%, 渗透率小于0.02×10-3μm2)及泥岩。图中的数据点取的是每段储层的代表性特征点, 而非全井段数据点, 这种做法主要是为了更清晰地分析储层的弹性特征。Ⅱ类储层与干层数据点叠置, 二者整体与Ⅰ类储层和泥岩可分离, 分布区间为高阻抗和中等纵横波速度比。Ⅰ类储层与其它储层和泥岩有较好的分离, 分布区间表现为中等阻抗和低纵横波速度比。
|
图 5 典型井储层纵波阻抗与纵横波速度比交会分析 |
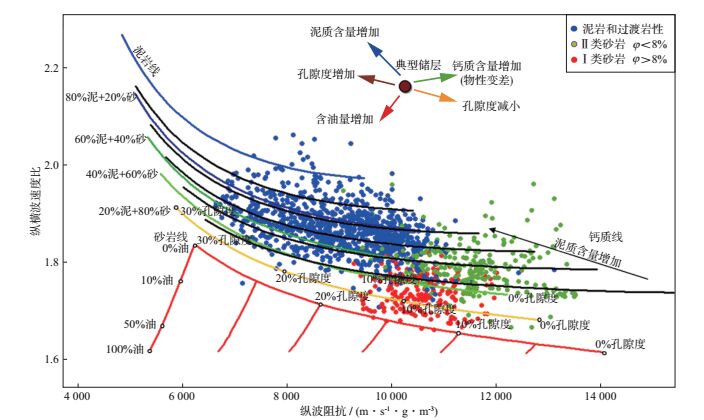
为便于地震储层预测, 在上述地震地质综合岩石物理分析的基础上, 给出了图 6所示的地震岩石物理解释图版(数据点为全井段数据), 将孔隙度大于8%的粉砂岩定义为Ⅰ类砂岩, 孔隙度小于8%的泥质、钙质粉砂岩定义为Ⅱ类砂岩。Ⅰ类砂岩对应Ⅰ类储层, Ⅱ类砂岩对应Ⅱ类储层和干层(二者在弹性参数交会域中无法区分)。图中的蓝色点为泥岩和过渡岩性(图 5中无过渡岩性是由于仅取了储层和泥岩段特征点), 过渡岩性指的是泥质含量高的粉砂岩和钙质粉砂岩, 将泥岩和过渡岩性作为一个岩相类别主要考虑到二者均是无效储层, 同时有利于叠前反演的地质统计分析。
|
图 6 研究区目的层地震岩石物理定量解释图版 |
图 6中的Ⅰ类砂岩与地质评价Ⅰ类储层对应, 孔隙度高、含油性好, 且分布趋势与理论分析的含油性增加趋势一致(含油饱和度增加, 纵波阻抗和纵横波速度比均降低)。另外, 岩样全矿物成分显示, 相对高孔粉砂岩的硅质矿物和碳酸盐岩含量较高, 利于水力压裂横向裂缝延展产生缝网。综合分析结果, Ⅰ类砂岩为研究区目的层段的“甜点”。
2 储层预测方法目前, 通过地震叠前AVO(或AVA)反演获取弹性参数的技术得到了广泛应用。叠前AVO反演问题的求解有两种主要方法[24]:一种是确定性反演; 另一种是统计性反演。确定性反演利用最优化目标函数来求解, 主要有稀疏脉冲反演和基于模型的反演。统计性反演也称为随机反演, 通过对后验概率密度的采样求解, 主要包括蒙特卡洛(Monte Carlo, MC)和序贯模拟方法。由于序贯模拟过程在网格被全部填充后即得到近似的结果, 所以任何应用序贯模拟的随机反演方法在统计学意义上都不是严格正确的。相比而言, 蒙特卡洛算法更加适用于模拟。
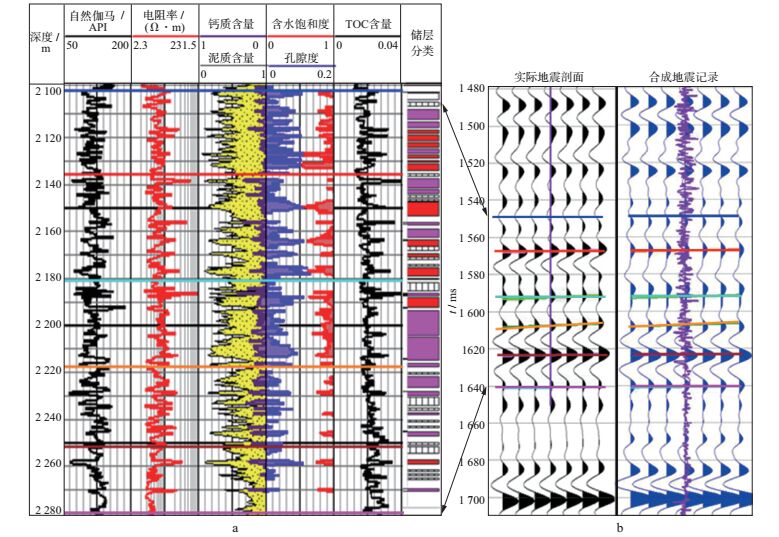
研究区目的层段地震剖面仅有7个相位, 对应160m层段范围内不同储层类别的叠置砂体(图 7), 叠前确定性反演受地震频带控制, 反演弹性参数纵向分辨率低, 显然无法用于薄储层刻画。叠前地质统计学反演综合了地震横向高密度和测井垂向精细尺度, 包含了地震的中频信息和测井的低频、高频信息, 能够提高弹性参数反演结果的纵向分辨率, 利于薄储层的预测。本文采用基于马尔科夫链蒙特卡洛算法(Markov Chain Monte Carlo, MCMC)的叠前地质统计学反演方法, 同时求得岩性和弹性参数属性体。先通过贝叶斯理论建立后验全局概率密度函数(probability density function, PDF), 该PDF包含所有关于储层的已知信息(地质、油藏、测井、地震), 然后利用MCMC方法获得符合后验PDF的统计意义上正确的样点集。
|
图 7 典型井井震对比 a测井曲线; b地震剖面和合成记录 |
从概率统计的角度, 任何反演问题都可以看成是一种贝叶斯估计问题, 在已有观测信息的基础上不断更新先验知识, 得到问题的解。一般性公式描述为:
| $ {P_{{\rm{post}}}}\left( \mathit{\boldsymbol{m}} \right) \propto {P_{{\rm{data}}}}\left[ {\mathit{\boldsymbol{d}} - f\left( \mathit{\boldsymbol{m}} \right)} \right] \cdot {P_{{\rm{prior}}}}\left( \mathit{\boldsymbol{m}} \right) $ | (9) |
式中:m是待估计的参数空间; Ppost(m)是后验概率密度函数; Pprior(m)是先验概率密度函数; Pdata[d-f(m)]是似然概率函数, 用来测量观测数据与计算数据的匹配程度。地震正演过程定义为:
| $ \mathit{\boldsymbol{d}} = f\left( \mathit{\boldsymbol{m}} \right) + \mathit{\boldsymbol{n}} $ | (10) |
式中:d是地震数据; f(m)为正演算子; n为噪声。
对于目前所讨论的叠前AVO反演, 在贝叶斯理论框架下构建的后验概率密度分布类似于公式(9):
| $ \begin{array}{l} P\left( {{\mathit{\boldsymbol{m}}_{{\rm{elastic}}}},{\mathit{\boldsymbol{m}}_{{\rm{litho}}}}} \right) \propto P\left( {\mathit{\boldsymbol{s}}\left| {{\mathit{\boldsymbol{m}}_{{\rm{elastic}}}}} \right.} \right) \cdot P\left( {{\mathit{\boldsymbol{m}}_{{\rm{elastic}}}}\left| {{\mathit{\boldsymbol{v}}_{{\rm{elastic}}}}} \right.,} \right.\\ \left. {{\mathit{\boldsymbol{w}}_{{\rm{elastic}}}},{\mathit{\boldsymbol{m}}_{{\rm{litho}}}}} \right) \cdot P\left( {{\mathit{\boldsymbol{m}}_{{\rm{litho}}}}\left| {{\mathit{\boldsymbol{v}}_{{\rm{litho}}}},{\mathit{\boldsymbol{w}}_{{\rm{litho}}}}} \right.} \right) \end{array} $ | (11) |
式中:melastic代表弹性参数模型, 弹性参数为纵波阻抗、横波阻抗和密度; mlitho代表岩性或岩相模型; s为地震叠前道集或者多个部分叠加数据体; P(s|melastic)是似然概率函数, 代表地下介质弹性参数模型melastic下地震道集数据的概率, 用来测量弹性参数模型melastic下合成道集数据与观测道集数据的匹配度, 由地震数据的信噪比控制; P(melastic|velastic, welastic, mlitho)是弹性参数的先验PDF, 以条件概率的形式给出; velastic为弹性参数的变差函数; welastic代表弹性参数测井曲线(传递到后验概率体现出弹性参数测井曲线的无偏约束); P(mlitho|vlitho, wlitho)是岩性的先验PDF, vlitho为岩性的变差函数, wlitho代表岩性测井曲线(传递到后验概率体现出岩性测井曲线的无偏约束)。
采用褶积模型正演合成数据, 利用Zoeppritz方程的Fatti近似公式[25]求取反射系数:
| $ \begin{array}{*{20}{c}} {R\left( \theta \right) = \left( {1 + {{\tan }^2}\theta } \right){R_{\rm{p}}} - 8{\gamma ^2}{{\sin }^2}\theta {R_{\rm{s}}} + }\\ {\left( {4{\gamma ^2}{{\sin }^2}\theta - {{\tan }^2}\theta } \right){R_{\rm{d}}}} \end{array} $ | (12) |
式中:R(θ)为不同入射角θ的反射系数; γ是界面两侧纵横波速度的均值; Rp, Rs, Rd分别是纵波阻抗、横波阻抗和密度反射系数。
公式(11)的概率分布极其复杂, 不能解析求解, 可应用MCMC方法进行概率评价。MCMC方法通常用于解决多峰、多维复杂贝叶斯判别问题, 对贝叶斯推断中的后验概率分布函数抽样, 获取收敛于后验分布的随机样本, 再统计这些样本, 得到后验分布的一些性质。MCMC方法的核心是马尔科夫链的构建, 以确定样本点接受或拒绝的转移概率。张广智等[26]采用Metropolis-Hastings算法生成马尔科夫链, 建议分布取为均匀分布, 该分布函数满足对称的随机游走, 因此转移概率表示为:
| $ \alpha \left( {{r_i},{r^ * }} \right) = \min \left\{ {1,\frac{{{\rm{ \mathsf{ π} }}\left( {{r^ * }} \right)}}{{{\rm{ \mathsf{ π} }}\left( {{r_i}} \right)}}} \right\} $ | (13) |
式中:ri和r*分别是当前样本点和由建议分布给出的随机样本点(候选点); π代表后验概率分布函数。
MCMC反演算法的基本步骤如下:①利用岩性先验PDF得到岩性的先验实现; ②采用弹性参数的先验条件PDF得到弹性参数的实现; ③利用弹性参数模型计算合成地震记录; ④根据Metropolis-Hastings准则接受或拒绝岩性和弹性参数的实现, 即根据公式(13)判断候选点和当前样本点的取舍。经过不断迭代, 使得马尔科夫链最终收敛于未知参数的后验PDF。
2.2 反演效果分析在上述地震岩石物理分析指导下, 反演中定义Ⅰ类砂岩、Ⅱ类砂岩和泥岩(定义的泥岩岩相包括过渡岩性)3种岩相进行地质统计分析。对保幅高分辨率处理的CRP道集进行分角度叠加, 增加叠加体数量可以提高AVO反演算法的稳定性, 但势必会同时减小单个叠加体的覆盖次数, 从而降低叠加体的信噪比, 影响反演质量。因此, 对于不同品质的地震数据, 合理选择叠加体个数十分必要。根据实际情况, 为保证反演的稳定性, 研究区使用了4个叠加体作为叠前反演的输入, 反演得到储层预测所需的纵波阻抗、纵横波速度比和岩相体。
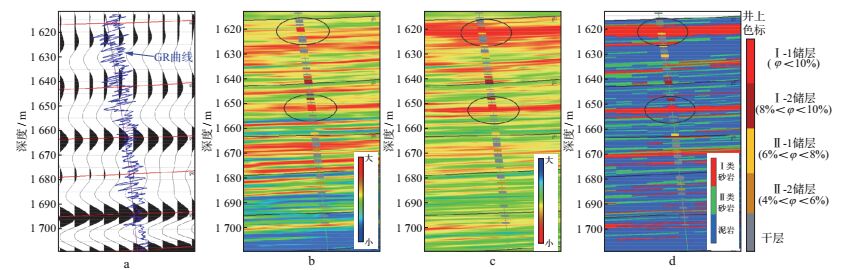
图 8给出了后验井叠前地质统计学反演剖面, 包括地震剖面、纵波阻抗、纵横波速度比及岩相反演剖面, 最右侧为地质储层评价结果。与地震剖面相比, 叠前地质统计学反演剖面纵向分辨率得到了较大程度的提高, 这对于薄储层预测, 特别是水平井设计和随钻地震地质导向十分有益。从岩相剖面上看, 叠前地质统计学反演对3m以上砂层预测符合率较高, 可达到80%以上, 对主力的“甜点”层(图中以椭圆标示)也有较好的预测效果。
|
图 8 后验井叠前地质统计学反演剖面 a地震剖面; b纵波阻抗; c纵横波速度比; d岩相 |
综合地震岩石物理与叠前地质统计学反演的致密薄储层预测技术在齐家地区南部致密油勘探中发挥了重要的支撑作用。
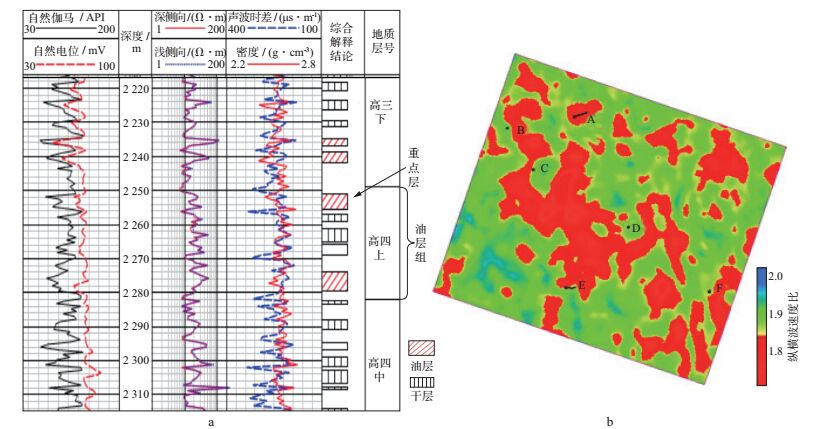
1) 分层段“甜点”地震预测结果用于实施水平井目标区和目标层的优选, 如图 9所示。图 9a为A井综合柱状图, 按照地震尺度, 测井在青山口组可分为5个油层组, 油层组内还可以细分若干个重点层。首先利用由地震岩相体得到的层间砂体厚度预测油层组级别“甜点”分布, 确定水平井部署的重点油层组和有利区, 然后在油层组内对重点层进行局部属性切片分析及重点层“甜点”分布预测(图 9b), 确定水平井轨迹。图 9b是沿A井重点层提取的纵横波速度比切片, 红色代表油层发育, A~E六口井中, A井综合解释为油层, 其余井为干层, 地震预测结果与钻井吻合较好。通过这样分层段进行地震预测, 可以逐步定位目标层, 有利于更好地设计井位。
|
图 9 分层段“甜点”地震预测 a A井综合柱状图; b A井重点层纵横波速度比切片 |
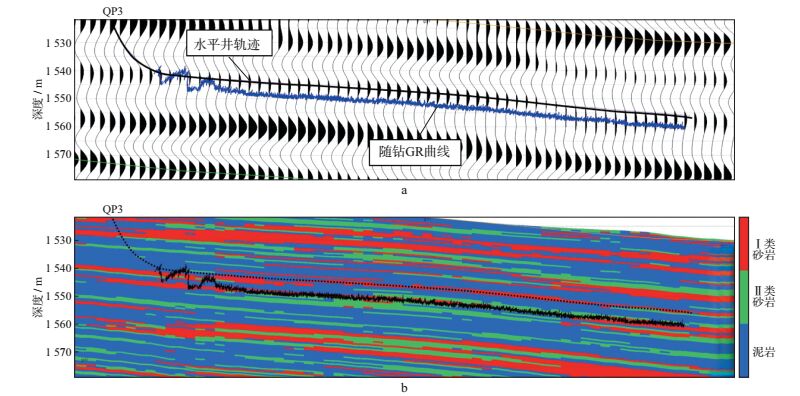
2) 利用预测的模型优化水平井轨迹的设计, 利用高分辨率的储层预测结果指导现场随钻数据解释和地震地质导向(图 10)。图 10b为过QP3井叠前地质统计学反演岩相剖面, 该井水平段进尺1230m, 砂岩及油层钻遇率分别为100%和99%, 地震预测与水平井实钻有着良好的一致性。整体上, 在近3年致密油勘探中, 部署实施的4口直井和5口水平井均取得了良好的钻探效果。4口直井中, 有2口井进行了储层压裂改造后获得工业油流。5口水平井油砂钻遇率平均95%以上, 通过多段压裂改造后, 试油初期产量为4.6~32.0t/d, 平均产量为17.6t/d, 与周边直井平均产量相比, 平均提产10倍。水平井实钻的成功带动了区块致密油控制储量的升级。
|
图 10 过QP3井的叠前地质统计学反演结果与水平井实钻对比 a地震剖面; b岩相剖面 |
本文针对齐家地区青山口组致密油勘探中井间砂体及“甜点”预测问题, 基于岩心和测井数据多尺度岩石物理交会分析形成了岩石物理机制下地震岩石物理解释图版, 明确了岩性、孔隙度和流体对致密孔隙介质弹性参数的影响规律, 确定了“甜点”储层的弹性参数特征, 为储层预测方法选取、叠前反演地质统计分析及反演成果定量解释提供了地球物理基础和重要依据。
研究区三角洲前缘沉积相对稳定(储层横向连续性较好), 地质统计学反演技术显示出良好的适用性, 能大幅提高反演结果的纵向分辨率, 对井间砂体及“甜点”储层有较好的预测能力, 为井间“甜点”目标优选和水平井轨迹设计及随钻地震地质导向提供了技术支撑。
致密油勘探部署的直井和水平井检验表明, 综合地震岩石物理分析的叠前地质统计学反演技术是齐家地区薄储层预测的有效手段, 可在地质条件类似的其它地区推广应用。
| [1] |
赵政璋, 杜金虎.
致密油气[M]. 北京: 石油工业出版社, 2012: 1-10.
ZHAO Z Z, DU J H. The tight oil and gas[M]. Beijing: Petroleum Industry Press, 2012: 1-10. |
| [2] |
迟唤昭, 刘财, 单玄龙, 等. 谱反演方法在致密薄层砂体预测中的应用研究[J].
石油物探, 2015, 54(3): 337-344 CHI H Z, LIU C, SHAN X L, et al. Application of spectral inversion for tight thin-bed sand body prediction[J]. Geophysical Prospecting for Petroleum, 2015, 54(3): 337-344 |
| [3] |
夏竹, 李中超, 贾瑞忠, 等. 井震联合薄储层沉积微相表征实例研究[J].
石油地球物理勘探, 2016, 51(5): 1002-1011 XIA Z, LI Z C, JIA R Z, et al. Thin reservoir sedimentary microfacies characterization based on well logging and seismic data:a case study[J]. Oil Geophysical Prospecting, 2016, 51(5): 1002-1011 |
| [4] | DAVID C, SIMON S. Tight gas geophysics:AVO inversion for reservoir characterization[J]. CSEG Recorder, 2010, 35(5): 28-35 |
| [5] | MERLETTI G D, TORRES-VERDIN C. Detection and spatial delineation of thin-sand sedimentary sequences with joint stochastic inversion of well logs and 3D prestack seismic amplitude data[J]. Spe Reservoir Evaluation & Engineering, 2010, 13(2): 246-264 |
| [6] | SENA A, CASTILLO G, CHESSER K. Seismic reservoir characterization in resource shale plays:stress analysis and sweet spot discrimination[J]. The Leading Edge, 2011, 30(6): 758-764 |
| [7] |
赵万金, 杨午阳, 赵伟. 地震储层及含油气预测技术应用进展综述[J].
地球物理学进展, 2014, 29(5): 2337-2346 ZHAO W J, YANG W Y, ZHAO W. The review of technical progress in application of seismic reservoir and hydrocarbon prediction[J]. Progress in Geophysics, 2014, 29(5): 2337-2346 DOI:10.6038/pg20140552 |
| [8] | CASTAGNA J P, BATZLE M L, EASTWOOD R L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks[J]. Geophysics, 1985, 50(4): 571-581 DOI:10.1190/1.1441933 |
| [9] | GARDNER G H F, GARDNER L W, GREGORY A R. Formation velocity and density:the diagnostic basics for stratigraphic traps[J]. Geophysics, 1974, 39(6): 770-780 DOI:10.1190/1.1440465 |
| [10] | BERRYMAN J G. Long-wavelength propagation in composite elastic media Ⅰ[J]. Journal of the Acoustical Society of America, 1980, 68(6): 1809-1819 DOI:10.1121/1.385171 |
| [11] | XU S, WHITE R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118 DOI:10.1111/gpr.1995.43.issue-1 |
| [12] | MAVKO G, JIZBA D. Estimating grain-scale fluid effects on velocity dispersion in rocks[J]. Geophysics, 1991, 56(12): 1940-1949 DOI:10.1190/1.1443005 |
| [13] |
巴金, CARCIONEJ M, 曹宏, 等. 非饱和岩石中的纵波频散与衰减:双重孔隙介质波传播方程[J].
地球物理学报, 2012, 55(1): 219-231 BA J, CARCIONE J M, CAO H, et al. Velocity dispersion and attenuation of P waves in prtially-saturated rocks:wave propagation equations in double-porosity medium[J]. Chinese Journal of Geophysics, 2012, 55(1): 219-231 |
| [14] | HASHIN Z, STRIKMAN S. A variantional approach to the elastic behavior of multiphase materials[J]. Journal of the Mechanics and Physics of Solids, 1963, 11(2): 127-140 DOI:10.1016/0022-5096(63)90060-7 |
| [15] | AVSETH P, DVORKIN J, MAVKO G, et al. Rock physics diagnostic of North Sea sands:link between microstructure and seismic properties[J]. Geophysical Research Letters, 2000, 27(17): 2761-2764 DOI:10.1029/1999GL008468 |
| [16] | DVORKIN J. Elasticity of high-porosity sandstones:theory for two North Sea datasets[J]. Geophysics, 1996, 61(5): 1363-1370 DOI:10.1190/1.1444059 |
| [17] | BERRYMAN J G. Long-wavelength propagation in composite elastic media, II:ellipsoidal inclusions[J]. Journal of the Acoustical Society of America, 1980, 68(6): 1820-1831 DOI:10.1121/1.385172 |
| [18] | BERRYMAN J G. Single-scattering approximations for coefficients in Biot's equations of poroelasticity[J]. Journal of the Acoustical Society of America, 1992, 91(2): 551-571 DOI:10.1121/1.402518 |
| [19] |
曾洪流, 朱筱敏, 朱如凯, 等. 砂岩成岩相地震预测——以松辽盆地齐家凹陷青山口组为例[J].
石油勘探与开发, 2013, 40(3): 266-274 ZENG H L, ZHU X M, ZHU R K, et al. Seismic prediction of sandstones diagenetic facies:applied to cretaceous Qingshankou formation in Qijia depression, Songliao Basin[J]. Petroleum Exploration and Development, 2013, 40(3): 266-274 DOI:10.11698/PED.2013.03.02 |
| [20] | MAVKO G, MUKERJI T, DVORKIN J. The rock physics handbook:tools for seimsic analysis of porous media[M]. New York: Cambridge University Press, 2009: 260-262. |
| [21] | CHI X G, HAN D H. Lithology and fluid differencetiation using a rock physics template[J]. The Leading Edge, 2009, 28(1): 60-69 DOI:10.1190/1.3064147 |
| [22] | REVERON J, ROOMER J. Probabilities facies discrimination from simultaneous seismic inversion results in clastics reservoir in southwest Venezuela[J]. Expanded Abstracts of 81st Annual Internat SEG Mtg, 2011: 1714-1718 |
| [23] | GOODWAY B, REREZ M, VARSEK J, et al. Seismic petrophysics and isotropic-anisotropic AVO methods for unconventional gas exploration[J]. The Leading Edge, 2010, 29(12): 1500-1508 DOI:10.1190/1.3525367 |
| [24] | BOSCH M, MUKERJI T, GONZALEZ E F. Seismic inversion for reservoir properties combining statistical rock physics and geostatistics:a review[J]. Geophysics, 2010, 75(5): A165-A176 |
| [25] | FATTI J L, SMITH G C, VAIL P J, et al. Detection of gas in sandstone reservoirs using AVO analysis:a 3D seismic case history using the geostack technique[J]. Geophysics, 1994, 59(9): 1362-1376 DOI:10.1190/1.1443695 |
| [26] |
张广智, 王丹阳, 印兴耀, 等. 基于MCMC的叠前反演方法研究[J].
地球物理学报, 2011, 54(11): 2926-2932 ZHANG G Z, WANG D Y, YIN X Y, et al. Study on prestack seismic inversion using markov chain monte carlo[J]. Chinese Journal of Geophysics, 2011, 54(11): 2926-2932 DOI:10.3969/j.issn.0001-5733.2011.11.022 |



