2. 中国石油大学(北京), 北京 102249;
3. 海洋石油勘探国家工程实验室, 北京 100028
2. China University of Petroleum, Beijing 102249, China;
3. National Engineering Laboratory for Offshore Oil Exploration, Beijing 100028, China
储层流体识别是油气勘探的关键环节, 识别精度关系到油气藏开发的成败。地震数据中包含的诸多信息都被用于指示储层流体性质, 弹性参数因其明确的物理意义和稳定的估计方法成为较常用的一类参数。地下岩石的速度、密度、阻抗等参数由于较容易获得, 因而最早用于判别储层性质。20世纪七八十年代, 泊松比因对含气砂岩储层的良好指示而被广泛应用, 至今仍然在含气储层预测中发挥重要作用[1]。GOODWAY[2]提出拉梅参数和密度的乘积是储层流体性质的良好指示参数。GRAY[3]认为拉梅参数本身就可以区分流体性质, 推导了可以用于拉梅参数直接反演的方程。QUAKENBUSH等[4]指出在复杂储层条件下可以通过组合纵、横波阻抗得到泊松阻抗来区分储层的岩性和流体性质。RUSSELL等指出流体项ρf和Gassmann流体项f对于流体性质的变化都比较敏感, 而且可以利用地震反演技术对其进行估计[5-6]。ZONG等[7]建立了利用纵横波模量表示的孔隙弹性理论和反射系数近似方程, 并发展了基于纵横波模量反演的流体识别方法。郝前勇等[8]提出基于体积模量和剪切模量的组合弹性模量流体因子可以降低流体识别的多解性。刘立峰等[9]利用多种地震属性的不同角度叠加数据体组合流体识别因子进行碳酸盐岩储层流体识别。李超等[10]提出利用孔隙流体模量作为流体因子可以降低固体骨架的影响, 提高流体识别精度。
精确估计流体因子是流体识别过程必不可少的步骤[11]。叠前地震反演技术极大地促进了地震流体识别技术的发展。BULAND等[12]和DOWNTON[13]分别提出了不同的AVO反演方法, 用于直接反演纵横波波阻抗; YOUNG等[14]采用LMR反演方法将拉梅参数用于储层流体识别; ZONG等[15]提出了一种叠前同步反演方法用于Gassmann流体项的估计; ZONG等[16]提出了泊松比和杨氏模量的直接反演方法, 用于页岩储层的脆性评价; LI等[17]基于入射角近似方程提出了Russell流体项的叠前反演方法; 桂金咏等[18]提出了致密储层流体因子的叠前同步反演方法。这些常用的叠前反演方法大都利用三项反射系数近似方程, 因此需要从小角度到大角度的叠前道集数据才能获得稳定的反演结果。
Zoeppritz方程的线性近似方程是目前叠前反演中较为常用的反射系数方程。这些近似方程以三项方程为主, 且第3项通常是密度项。要进行密度的稳定反演, 则需要大角度的叠前地震数据[19-20]。深部地层中蕴含有大量的石油天然气, 但是由于埋深较大, 深层油气藏勘探采集到的地震数据质量远不及中浅层, 最突出的表现就是大角度(大偏移距)的叠前地震道集品质低下, 从而限制了常规的基于叠前地震反演的油气预测技术的应用。
本文提出了一种可以在缺少大角度地震道集数据的情况下精确估计流体因子的叠前地震反演方法。基于Zoeppritz方程的线性近似方程和岩石物理理论推导出一个两项反射系数近似方程, 其包含Gassmann流体项和剪切模量。该近似方程仅有两项, 而且不包含密度项, 因而利用其进行叠前反演不需要大角度叠前地震数据。基于贝叶斯反演理论构建了叠前地震反演的目标方程和相应的反演算法来直接反演流体项, 并利用得到的流体项实现深部储层的流体识别。最后用模型数据和实际地震数据验证了方法的正确性和实用性。
1 流体因子反演方法 1.1 反射系数方程Zoeppritz反射系数方程可以精确描述反射、透射波的振幅, 但是由于本身的强非线性性, 用其进行反演稳定性较差。因此在叠前地震反演中, 常采用反射系数方程的近似方程。Aki和Richards给出的Zoeppritz方程近似公式如下:
| $ \begin{array}{l} R\left( \theta \right) = \frac{1}{2}\left( {1 + {{\tan }^2}\theta } \right)\frac{{\Delta {v_{\rm{P}}}}}{{{v_{\rm{P}}}}} - 4{\gamma ^2}{\sin ^2}\theta \frac{{\Delta {v_{\rm{S}}}}}{{{v_{\rm{S}}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\left( {1 - 4{\gamma ^2}{{\sin }^2}\theta } \right)\frac{{\Delta \rho }}{\rho } \end{array} $ | (1) |
其中, ΔvP=vP2-vP1, ΔvS=vS2-vS1, Δρ=ρ2-ρ1, vP=(vP1+vP2)/2, vS=(vS1+vS2)/2, ρ=(ρ1+ρ2)/2, γ=vS/vP。vP1, vS1, vP2, vS2, ρ1, ρ2分别为界面两侧地层的纵波速度、横波速度和密度, θ为入射角和透射角的平均值。
GARDNER等[21]研究了地下岩石的纵波速度与密度之间的关系, 将其提出的方程改写为差分形式:
| $ \frac{{\Delta \rho }}{\rho } = \frac{1}{c}\frac{{\Delta {v_{\rm{P}}}}}{{{v_{\rm{P}}}}} $ | (2) |
其中, c为常系数。
根据孔隙弹性介质理论, Gassmann流体项对孔隙流体性质的变化非常敏感, 可以作为储层孔隙流体的指示因子[6, 11, 15]。Gassmann流体项(f)、剪切模量(μ)与纵、横波速度、密度之间存在如下关系:f=(vP2-γdry2vS2)ρ, μ=vS2ρ。表示成差分形式为:
| $ \frac{{\Delta f}}{f} = \left( {\frac{2}{{1 - \gamma _{{\rm{dry}}}^2{\gamma ^2}}} + \frac{1}{c}} \right)\frac{{\Delta {v_{\rm{P}}}}}{{{v_{\rm{P}}}}} - \frac{{2\gamma _{{\rm{dry}}}^2{\gamma ^2}}}{{1 - \gamma _{{\rm{dry}}}^2{\gamma ^2}}}\frac{{\Delta {v_{\rm{S}}}}}{{{v_{\rm{S}}}}} $ | (3) |
| $ \frac{{\Delta \mu }}{\mu } = 2\frac{{\Delta {v_{\rm{S}}}}}{{{v_{\rm{S}}}}} + \frac{{\Delta \rho }}{\rho } $ | (4) |
其中, γdry为干燥岩石纵横波速度比。
综合方程(2), (3), (4)可以得到:
| $ \frac{{\Delta {v_{\rm{P}}}}}{{{v_{\rm{P}}}}} = \frac{{c\gamma _{{\rm{dry}}}^2{\gamma ^2}}}{{2c + 1}}\frac{{\Delta \mu }}{\mu } + \frac{{c\left( {1 - \gamma _{{\rm{dry}}}^2{\gamma ^2}} \right)}}{{2c + 1}}\frac{{\Delta f}}{f} $ | (5) |
| $ \begin{array}{l} \frac{{\Delta {v_{\rm{S}}}}}{{{v_{\rm{S}}}}} = \frac{1}{{2\left( {2c + 1} \right)}}\left[ {\left( {2c + 1 - \gamma _{{\rm{dry}}}^2{\gamma ^2}} \right)\frac{{\Delta \mu }}{\mu } - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left( {1 - \gamma _{{\rm{dry}}}^2{\gamma ^2}} \right)\frac{{\Delta f}}{f}} \right] \end{array} $ | (6) |
将方程(2), (5), (6)代入方程(1), 可以得到:
| $ \begin{array}{*{20}{c}} {R\left( \theta \right) = \frac{{\left( {1 - \gamma _{{\rm{dry}}}^2{\gamma ^2}} \right)}}{{2\left( {2c + 1} \right)}}\left( {c{{\sec }^2}\theta + 1} \right)\frac{{\Delta f}}{f} + \frac{{{\gamma ^2}}}{{2\left( {2c + 1} \right)}} \cdot }\\ {\left( {c\gamma _{{\rm{dry}}}^2{{\sec }^2}\theta + \gamma _{{\rm{dry}}}^2 - 8c{{\sin }^2}\theta - 4{{\sin }^2}\theta } \right)\frac{{\Delta \mu }}{\mu }} \end{array} $ | (7) |
方程(7)是一个两项近似方程, 基于此方程建立叠前地震反演方法, 可以在不需要大角度地震数据的情况下反演Gassmann流体项和剪切模量。
需要注意的是, 方程(7)中的参数都需要根据实际工区的具体地质情况确定, 这些参数的准确与否对于方法的精度有很大影响。其中, γdry2和γ2需要根据岩石骨架模量、流体模量进行计算, 具体计算公式为:
| $ \gamma _{{\rm{dry}}}^2 = \frac{{{K_{{\rm{dry}}}}}}{\mu } + \frac{4}{3} $ | (8) |
| $ {\gamma ^2} = \frac{f}{\mu } + \gamma _{{\rm{dry}}}^2 $ | (9) |
其中, Kdry为干燥岩石的体积模量。
1.2 方程精度验证为了检验方程(7)的精度, 选用如表 1所示的两个经典模型(Ostrander模型和Goodway模型), 计算模型中地层界面处的纵波反射系数, 并与Zoeppritz精确方程和Russell近似方程(包含Gassmann流体项的三项近似方程[6, 22])的计算结果进行对比。
| 表 1 两个模型的模型参数 |
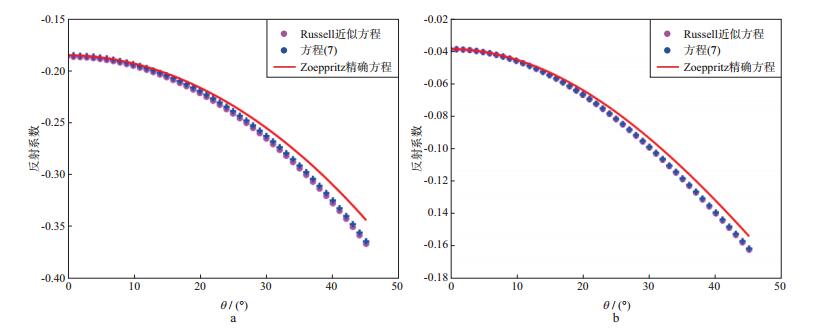
图 1a和图 1b分别给出了Ostrander模型和Goodway模型利用不同方程的计算结果。从图 1可以看出, 蓝色线和粉色线均与红色线接近, 而且蓝色线与红色线的距离更近, 说明方程(7)的精度略高于Russell近似方程, 因此其精度满足叠前反演的要求。
|
图 1 两个模型的计算结果对比 a Ostrander模型; b Goodway模型 |
叠前地震反演是综合利用叠前地震数据、测井数据和地质先验信息的地震反演方法。基于贝叶斯反演理论框架, 建立一种可以稳定估计流体因子的叠前反演方法[23]。首先考虑1个界面、m个角度的情况, 将方程(7)写成矩阵形式:
| $ \left[ {\begin{array}{*{20}{c}} {a\left( {{\theta _1}} \right)}&{b\left( {{\theta _1}} \right)}\\ {a\left( {{\theta _2}} \right)}&{b\left( {{\theta _2}} \right)}\\ \vdots&\vdots \\ {a\left( {{\theta _m}} \right)}&{b\left( {{\theta _m}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\frac{{\Delta f}}{f}}\\ {\frac{{\Delta \mu }}{\mu }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {R\left( {{\theta _1}} \right)}\\ {R\left( {{\theta _2}} \right)}\\ \vdots \\ {R\left( {{\theta _m}} \right)} \end{array}} \right] $ | (10) |
其中, a(θ)=[(1-γdry2γ2)]/[2(2c+1)](csec2θ+1), b(θ)=γ2/[2(2c+1)](cγdry2sec2θ+γdry2-8csin2θ-4sin2θ)。
在n个界面、m个角度的情况下, 基于褶积理论添加子波矩阵W, 将矩阵变成块化矩阵方程:
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{A}}_1}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{B}}_1}}\\ {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{A}}_2}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{B}}_2}}\\ \vdots&\vdots \\ {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{A}}_m}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{B}}_m}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{m}}_f}}\\ {{\mathit{\boldsymbol{m}}_\mu }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{d}}_1}}\\ {{\mathit{\boldsymbol{d}}_2}}\\ \vdots \\ {{\mathit{\boldsymbol{d}}_m}} \end{array}} \right] $ | (11) |
其中, A, B, m, d分别为方程(10)中对应项的矩阵形式。
矩阵方程(11)可以简写成以下形式:
| $ \mathit{\boldsymbol{Gm}} = \mathit{\boldsymbol{d}} $ | (12) |
根据贝叶斯理论, 待反演数据的后验概率密度分布可以表示为:
| $ P\left( {\mathit{\boldsymbol{m}}\left| \mathit{\boldsymbol{d}} \right.} \right) = \frac{{P\left( {\mathit{\boldsymbol{d}}\left| \mathit{\boldsymbol{m}} \right.} \right)P\left( \mathit{\boldsymbol{m}} \right)}}{{P\left( \mathit{\boldsymbol{d}} \right)}} $ | (13) |
其中, P(m|d)是后验概率密度, P(d|m)是似然函数, P(m)是先验概率密度, P(d)是边缘概率密度。
由于观测到的地震数据中包含的噪声通常服从高斯分布, 因此假设似然函数服从高斯分布。为了更好地保护弱小反射, 得到高分辨率的反演结果, 假设先验分布服从两参数柯西分布, 则后验概率密度函数可以表示为:
| $ \begin{array}{l} P\left( {\mathit{\boldsymbol{m}}\left| \mathit{\boldsymbol{d}} \right.} \right) = a\exp \left[ {\left( { - \frac{3}{2}} \right)\sum\limits_{i = 1}^n {\ln \left( {1 + {\mathit{\boldsymbol{m}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^i}\mathit{\boldsymbol{m}}} \right)} } \right] \cdot \\ \;\;\;\;\;\;\;\exp \left[ {\frac{{ - {{\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gm}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gm}}} \right)}}{{2\sigma _{\rm{m}}^2}}} \right] \end{array} $ | (14) |
式中:σm2是噪声的方差; Φi=(Di)TΨ-1Di, [Dqli]=
对方程(14)待反演参数求导并取极值, 可以得到如方程(15)的初始目标函数:
| $ J\left( \mathit{\boldsymbol{m}} \right) = {\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gm}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gm}}} \right) + \frac{3}{2}\mathit{\boldsymbol{Qm}} $ | (15) |
式中:
为了提高反演结果的横向连续性并补偿低频信息, 在目标函数中加入模型约束项, 得到:
| $ \begin{array}{l} J\left( \mathit{\boldsymbol{m}} \right) = {\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gm}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gm}}} \right) + \frac{3}{2}\mathit{\boldsymbol{Qm}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\alpha {\left\| {\mathit{\boldsymbol{Cm}} - \xi } \right\|^2} \end{array} $ | (16) |
式中:α是权重因子; C和ξ由低频模型计算得到。
方程(16)的最大后验概率解为:
| $ \left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}} + \lambda \mathit{\boldsymbol{Q}} + \alpha {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}}} \right)\mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{d}} + \alpha {\mathit{\boldsymbol{C}}^{\rm{T}}}\xi $ | (17) |
利用迭代重加权最小二乘方法可以求解方程(17), 然后利用方程(18)对结果积分即可得到最终反演结果。
| $ \left\{ \begin{array}{l} f\left( t \right) = f\left( {{t_0}} \right)\exp \left[ {2\int_0^t {{m_f}\left( \tau \right){\rm{d}}\tau } } \right]\\ \mu \left( t \right) = \mu \left( {{t_0}} \right)\exp \left[ {2\int_0^t {{m_\mu }\left( \tau \right){\rm{d}}\tau } } \right] \end{array} \right. $ | (18) |
式中:t0为第1个采样点的时间。
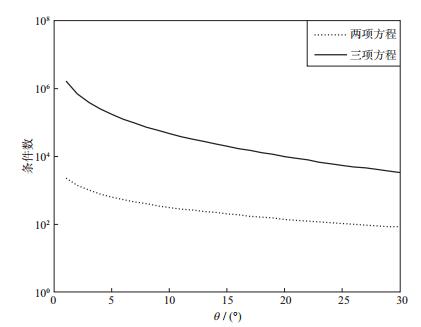
两项近似方程的优势不仅在于其不需要大角度地震道集数据, 而且由于方程的项数减少, 其系数矩阵的稳定性也大大提高。计算方程(7)与三项方程(Russell方程)在不同角度情况下系数矩阵的条件数, 来比较两个方程的稳定性(图 2)。图 2中实线和虚线分别是方程(7)和三项方程的条件数, 可以看出前者的条件数更小, 即稳定性更好, 抗噪能力更强。
|
图 2 两项和三项方程的条件数对比 |
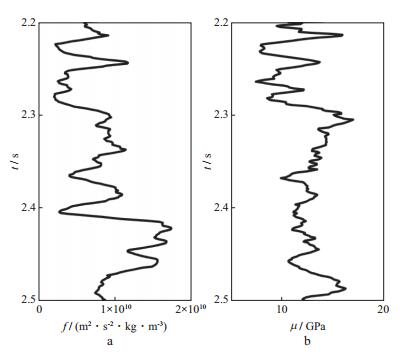
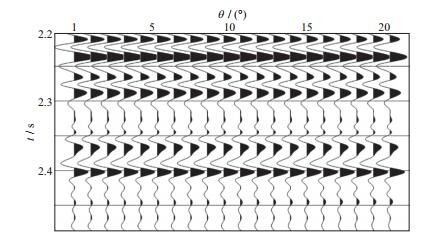
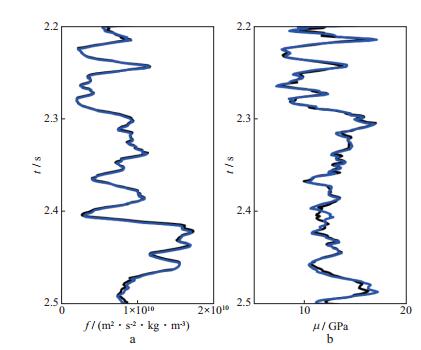
为了检验本文反演方法的有效性, 建立典型模型, 利用合成地震记录进行试算。图 3给出了利用实际测井数据建立的模型数据。利用褶积理论和精确Zoeppritz方程可以合成不同角度的叠前地震数据。图 4是无噪声的合成地震记录。对叠前数据进行分角度叠加得到小角度叠加数据(1°~10°)和中角度叠加数据(11°~20°), 利用本文方法进行反演, 结果如图 5所示。图 5中黑色曲线为原始模型, 蓝色曲线为反演结果。从图 5可以看出, 反演得到的Gassmann流体项和剪切模量与模型数据十分接近。
|
图 3 模型数据 a Gassmann流体项; b剪切模量 |
|
图 4 无噪声的合成地震记录 |
|
图 5 无噪声合成地震记录的反演结果对比 a Gassmann流体项; b剪切模量 |
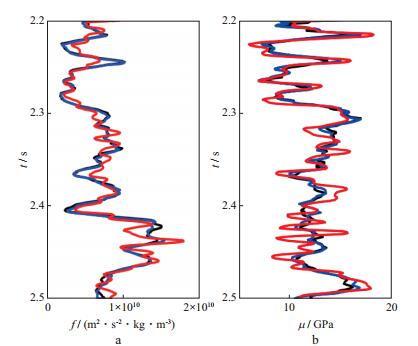
为了进一步说明本文方法的有效性, 利用含噪声的数据测试无大角度数据的叠前地震反演。首先利用前述正演方法得到1°~30°的叠前地震数据, 然后在1°~20°的地震数据中加入信噪比为2:1的高斯噪声, 用于模拟正常包含噪声的中小角度数据。实际生产中采集到的大角度地震数据质量往往较差, 因而在21°~30°的地震数据中加入信噪比为1:1的高斯噪声。加噪声后的地震记录如图 6所示。将1°~20°的地震数据采用本文方法进行反演, 为了进行对比说明, 将1°~30°的地震数据用基于Russell近似方程的贝叶斯反演方法进行了反演。反演结果如图 7a和图 7b所示, 图中黑色曲线是原始模型, 蓝色曲线是本文方法反演结果, 红色曲线是基于Russell近似方程的贝叶斯反演方法的反演结果。从图 7可以看出, 红色曲线与真实模型曲线相差比较大, 说明大角度数据的低信噪比对反演结果的影响较大, 这种情况下依然利用大角度数据进行反演得到的Gassmann流体项不能用于流体识别; 而蓝色曲线误差较小, 说明虽然受噪声的影响, 本文方法反演结果的精度略有下降, 但是仍然在可以接受的范围内, 仅利用中小角度叠前地震数据进行反演也可以得到准确的Gassmann流体项, 从而进行流体识别, 同时也证明本文方法具有较好的稳定性。

|
图 6 加入高斯噪声的合成地震记录 |
|
图 7 有噪声合成地震记录的反演结果对比 a Gassmann流体项; b剪切模量 |
利用东部某油田实际工区地震资料进行应用研究。研究的目标储层位于东营组二段, 埋深约为3400m。由于储层埋深较大, 且受采集条件限制得到的大角度道集信噪比较低, 不适合用于地震反演。为了开展储层特性的研究, 将本文提出的流体识别方法应用于该工区储层流体识别研究。
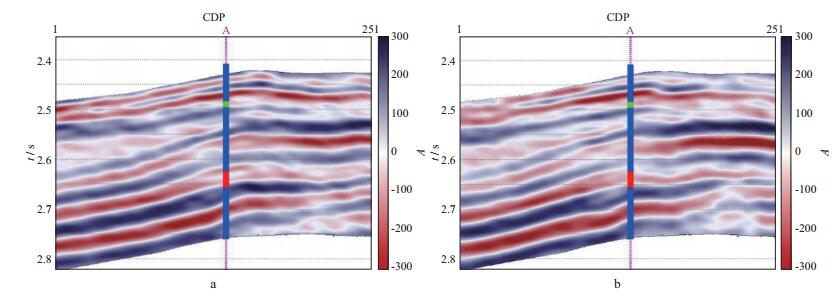
开展叠前地震反演前各种数据都要进行必要的预处理, 地震数据主要的预处理是保幅处理, 测井数据的主要预处理是曲线校正。之后, 将地震道集转换到角度域, 数据角度范围为3°~23°, 将其分别叠加为中心角为8°的小角度部分角度叠加数据(3°~13°)和中心角为18°的中角度部分角度叠加数据(13°~23°), 如图 8所示。利用工区的测井、地质、岩心资料开展岩石物理研究, 计算出本文方法中所需的γdry2, γ2, c参数值。
|
图 8 实际工区地震叠加剖面 a小角度道集叠加; b中角度道集叠加 |
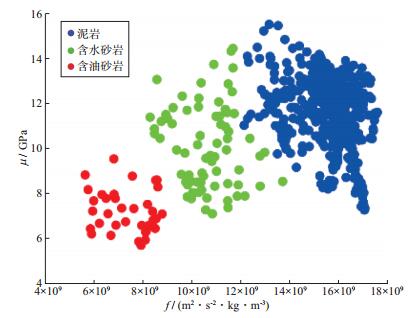
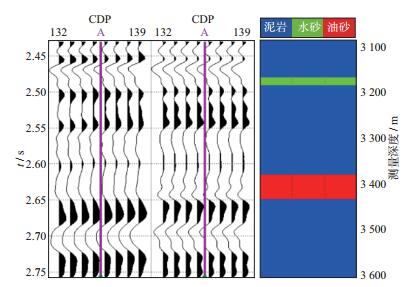
在图 8所示地震剖面的CDP136处有一口井(A井), 井位置处有一条测井曲线, 该柱状曲线表示测井解释结果, 红色、绿色和蓝色部分分别表示含油砂岩、含水砂岩和泥岩。利用工区内井数据进行Gassmann流体项和剪切模量的交会分析, 结果如图 9所示。从图 9可以看出, Gassmann流体项可以较好地识别含油砂岩和含水砂岩, 而剪切模量识别效果差于前者。反演前, 综合工区的地震数据、测井数据和地质资料进行了井震标定, 图 10是A井的井震标定结果。
|
图 9 岩石物理交会分析结果 |
|
图 10 A井井震标定结果 |
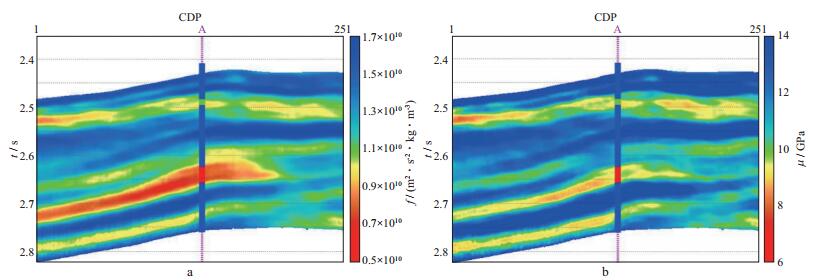
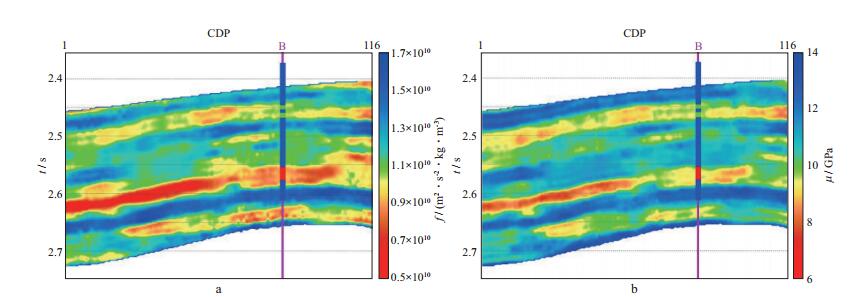
对该工区资料利用本文方法进行叠前地震反演, 得到的Gassmann流体项和剪切模量分别如图 11a和图 11b所示。图 11a中在2.65s处有低值异常, 与井上的含油砂岩对应, 而2.49s处有另一低值异常, 与井上的含水砂岩对应。而且前者Gassmann流体项值明显低于后者, 因此Gassmann流体项可以清晰地区分出含油、含水储层, 与测井解释结果和钻井资料一致。图 11b中在2.49s和2.65s处也有低值异常, 但是二者差别不大, 这是因为孔隙流体的性质对于剪切模量的影响不大。另外, 使用未参与反演过程的B井作为验证井, 过B井的Gassmann流体项和剪切模量剖面分别如图 12a和图 12b所示。图 12a中2.46s和2.56s处的含水砂岩和含油砂岩所对应的低值异常有明显差别, 而且与测井、钻井资料相符合, 说明反演得到的Gassmann流体项可以识别含油砂岩, 与图 11中A井过井剖面结论一致。
|
图 11 实际工区反演结果过井剖面 a Gassmann流体项; b剪切模量 |
|
图 12 反演结果过验证井的剖面 a Gassmann流体项; b剪切模量 |
为了在缺乏大角度叠前地震数据的情况下实现深部储层的流体识别, 本文推导了包含Gassmann流体项的两项地震反射系数近似方程, 并基于此方程构建了贝叶斯叠前地震反演方法, 用于直接、稳定地反演Gassmann流体项。利用该方法可以使用不含大角度的叠前道集数据进行流体项的直接反演, 并开展深部储层的流体识别。模型实验和实际工区应用结果均证明了该方法的有效性、稳定性和实用性。
本文提出的流体识别策略可以扩展到其它类型储层的预测中, 只需要选择合适的弹性参数作为流体因子, 推导包含该弹性参数的两项近似方程, 建立相应的反演方法进行反演和流体识别。另外需要注意的是, 本文方法综合多种理论提出, 涉及的参数较多, 在实际应用中需要根据工区实际情况计算出准确的参数, 如γdry2, c等, 才可以使方法得到有效应用。
| [1] | SHUEY R T. A simplification of the Zoeppritz equations[J]. Geophysics, 1985, 50(4): 609-614 DOI:10.1190/1.1441936 |
| [2] | GOODWAY B. AVO and Lamé constants for rock parameterization and fluid detection[J]. CSEG Recorder, 2001, 26(6): 39-60 |
| [3] | GRAY D. Bridging the gap:using AVO to detect changes in fundamental elastic constants[J]. Expanded Abstracts of 69th Annual Internat SEG Mtg, 1999: 852-855 |
| [4] | QUAKENBUSH M, SHANG B, TUTTLE C. Poisson impedance[J]. The Leading Edge, 2006, 25(2): 128-138 DOI:10.1190/1.2172301 |
| [5] | RUSSELL B H, HEDLIN K, HILTERMAN F J, et al. Fluid-property discrimination with AVO:a Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39 DOI:10.1190/1.1543192 |
| [6] | RUSSELL B H, GRAY D, HAMPSON D P. Linearized AVO and poroelasticity[J]. Geophysics, 2011, 76(3): C19-C29 DOI:10.1190/1.3555082 |
| [7] | ZONG Z, YIN X, WU G. AVO inversion and poroelasticity with P-and S-wave moduli[J]. Geophysics, 2012, 77(6): 29-36 DOI:10.1190/geo2012-0111.1 |
| [8] |
郝前勇, 印兴耀, 王玉梅, 等. 弹性模量流体因子在永新工区储层预测中的应用[J].
石油物探, 2012, 51(5): 502-507 HAO Q Y, YIN X Y, WANG Y M, et al. Application of elastic modulus fluid factor in the reservoir prediction in Yongxin area[J]. Geophysical Prospecting for Petroleum, 2012, 51(5): 502-507 |
| [9] |
刘立峰, 孙赞东, 韩剑发, 等. 量子粒子群模糊神经网络碳酸盐岩流体识别方法研究[J].
地球物理学报, 2014, 57(3): 991-1000 LIU L F, SUN Z D, HAN J F, et al. A carbonate fluid identification method based on quantum particle swarm fuzzy neural network[J]. Chinese Journal of Geophysics, 2014, 57(3): 991-1000 DOI:10.6038/cjg20140328 |
| [10] |
李超, 印兴耀, 张广智, 等. 基于贝叶斯理论的孔隙流体模量叠前AVA反演[J].
石油物探, 2015, 54(4): 467-476 LI C, YIN X Y, ZHANG G Z, et al. Prestack AVA inversion for pore fluid modulus based on the Bayesian theory[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 467-476 |
| [11] |
印兴耀, 宗兆云, 吴国忱. 岩石物理驱动下地震流体识别研究[J].
中国科学:地球科学, 2015, 45(1): 8-21 YIN X Y, ZONG Z Y, WU G C. Research on seismic fluid identification driven by rock physics[J]. China Science:Earth Science, 2015, 45(1): 8-21 |
| [12] | BULAND A, OMRE H. Bayesian linearized AVO inversion[J]. Geophysics, 2003, 68(3): 184-198 |
| [13] | DOWNTON J E.Seismic parameter estimation from AVO inversion[D]. Canada:University of Calgary, 2005 |
| [14] | YOUNG K T, TATHAM R H. Lambda-mu-rho inversion as a fluid and lithology discriminator in the Columbus Basin, offshore Trinidad[J]. Expanded Abstracts of 77th Annual Internat SEG Mtg, 2007: 214-218 |
| [15] | ZONG Z, YIN X, WU G. Direct inversion for a fluid factor and its application in heterogeneous reservoirs[J]. Geophysical Prospecting, 2013, 61(5): 998-1005 DOI:10.1111/gpr.2013.61.issue-5 |
| [16] | ZONG Z, YIN X, WU G. Elastic impedance parameterization and inversion with Young's modulus and Poisson's ratio[J]. Geophysics, 2013, 78(6): N36-N42 |
| [17] | LI C, YIN X, ZHANG G, et al. Fluid elastic impedance inversion based on the incident-angle approximation[J]. Expanded Abstracts of 84th Annual Internat SEG Mtg, 2014: 1980-1984 |
| [18] |
桂金咏, 高建虎, 雍学善, 等. 致密储层敏感弹性参数叠前同步反演方法[J].
石油物探, 2015, 54(5): 541-550 GUI J Y, GAO J H, YONG X S, et al. A prestack simultaneous inversion method for sensitive elastic parameters of tight reservoir[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 541-550 |
| [19] | BEHURA J, KABIR N, CRIDER R, et al. Density extraction from P-wave AVO inversion:tuscaloosa trend example[J]. The Leading Edge, 2010, 29(7): 772-777 DOI:10.1190/1.3462777 |
| [20] | KHARE V, RAPE T. Density inversion using joint PP/PS data:sensitivity to the angle range[J]. Expanded Abstracts of 77th Annual Internat SEG Mtg, 2007: 965 |
| [21] | GARDNER F, GARDNER W, GREGORY R. Formation velocity and density-the diagnostic basics for stratigraphic traps[J]. Geophysics, 1974, 39(6): 770-780 DOI:10.1190/1.1440465 |
| [22] |
张世鑫, 杜向东, 韩文明, 等. 适于Russell流体因子提取的孔隙弹性介质反射系数近似方程[J].
石油物探, 2016, 55(2): 178-187 ZHANG S X, DU X D, HAN W M, et al. A reflection coefficient approximation equation of poroelastic media for Russell fluid factor estimation[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 178-187 |
| [23] | LI C, ZHANG J, ZHU Z. Bayesian AVO inversion with consistent angle parameters[J]. Journal of Applied Geophysics, 2017, 139: 246-256 DOI:10.1016/j.jappgeo.2017.02.020 |


