2. 青岛国家海洋科学技术实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
3. 中国海洋大学海底科学与探测技术教育部重点实验室, 山东青岛 266100
2. Laboratory for Marine Mineral Resource, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China;
3. Key Lab of Submarine Geosciences and Prospecting Techniques Ministry of Education, Qingdao 266100, China
在地震资料采集过程中, 受野外施工条件所限, 常常会出现近偏移距道缺失甚至中间部分道缺失的现象, 使采集到的地下信息不完整, 严重影响后续地震数据处理的效果。在自由界面多次波衰减(SRME)等[1-2]基于多道信号的去噪处理中, 数据的缺失(尤其是近偏移距道的缺失)将直接导致无法预测到部分道的多次波信号[1], 进而影响到多次波的整体衰减效果。在速度分析或波动方程偏移成像处理中, 地震道的缺失会严重降低速度分析或偏移成像的精度, 从而降低最终成果剖面的成像质量。因此, 实际地震数据处理时, 必须对缺失的地震道进行重建。
为了重建缺失的地震道, 人们提出了多种波场插值方法:①基于波动理论的地震道插值方法, 包括正常时差校正(NMO)和倾角时差校正(DMO)交替进行的地震道插值[3]、基于方位角时差校正(AMO)的三维数据规则化[4]、基于NMO结果的趋势样条法[1]等, 此类方法通常无法对多次波同相轴进行插值; ②频率域插值方法, 包括f-x域预测滤波插值[5-6]、f-k域反假频地震道插值[7-8]、Fourier变换域信号重建方法[9-10]等, 其中f-x域预测滤波方法主要用于叠后数据的插值处理, f-k域反假频地震道插值与Fourier变换域信号重建方法虽可用于叠前数据的插值, 但要求地震数据的空间采样均匀, 且难以应用于道外推; ③基于数学变换的插值方法, 如抛物线或双曲拉冬变换插值方法[11-14]、基于曲波变换的地震道重建方法[15-16]、基于频率域奇异值分解的地震数据插值方法[17]等; ④基于稀疏反演的插值方法[18-19], 包括稀疏约束最小二乘反演、非二次模型权函数的稀疏反演傅里叶重建方法以及基于Shearlet变换的稀疏约束地震数据重建[20]等; ⑤基于自由界面多次波的地震数据插值方法[21-23], 利用原始数据的自由界面多次波建立缺失地震道中的低阶多次波与一次波。上述基于数学变换、稀疏反演以及基于自由界面多次波的地震数据插值方法均需引入复杂的数学变换或波场重构, 导致计算效率较低, 理论上也难以保证插值同相轴道间振幅的动力学特征。
对于来自同一波阻抗界面的反射波同相轴, 其各道信号的振幅与偏移距存在一定关系, 即AVO效应, 可用于描述插值同相轴道间振幅的动力学特征。谭军等[24]提出了共中心点(CMP)域同相轴追踪技术, 利用等值线追踪方法获得的高分辨率叠加速度谱中的强能量团来确定CMP道集中的反射波同相轴, 为将AVO分析技术引入道外推与内插处理奠定了基础。本文在此基础上提出了一种基于速度加权叠加与AVO分析技术的叠前CMP道集外推与内插方法, 基于CMP道集中反射波同相轴满足双曲线规律的假设条件, 先通过速度扫描叠加计算速度加权因子, 并通过AVO分析获得振幅校正因子, 然后在时空域将输入地震道信号加权叠加, 得到插值结果。该方法不但能使CMP记录中的双曲同相轴依据其几何规律得到重建, 而且应用AVO分析技术对插值结果进行振幅校正可在一定程度上恢复野外记录的相对振幅关系。
1 基于速度加权叠加的地震道外推与内插在水平层状介质条件下, CMP道集中的反射波同相轴满足双曲线规律, 甚至在复杂地质环境中, 诸如倾斜波阻抗界面、尖灭点等的反射波同相轴也可近似看作双曲线, 这是基于速度扫描叠加进行地震道外推与内插的理论依据。
对于叠加速度为v, 零偏移距时(即“零偏移距道的双程旅行时”, 下同)为τ的CMP域双曲同相轴, 其时距曲线方程可表示为:
| $ {t^2} = {\tau ^2} + \frac{{{x^2}}}{{{v^2}}} $ | (1) |
式中:x为偏移距, t为旅行时。
设插值道的道号和偏移距分别为k与xk, 输入道的道号和偏移距分别为m和xm, 根据公式(1), 输入道的旅行时tm与插值道的旅行时tk应满足以下关系式:
| $ {t_m} = \sqrt {t_k^2 + \frac{{x_m^2 - x_k^2}}{{{v^2}}}} $ | (2) |
对于来自同一波阻抗界面的反射波同相轴, 其各道信号的波形相差不大, 因此可利用输入道中旅行时为tm的信号创建插值道中旅行时为tk的信号。若信号振幅亦不变, 则可通过输入道信号的叠加得到插值道信号, 即
| $ {d_k}\left( {{t_k}} \right) = \frac{1}{M}\sum\limits_{m = 1}^M {{d_m}\left( {{t_m} = \sqrt {t_k^2 + \frac{{x_m^2 - x_k^2}}{{{v^2}}}} } \right)} $ | (3) |
式中:dk和dm分别表示插值道与输入道信号; M为输入道数。
在已知同相轴叠加速度的情况下, 公式(3)即为根据输入道信号估计插值道信号的关系式。但是, CMP道集中各同相轴的叠加速度是未知量, 应在地震道插值之前予以确定。叠加速度通常可根据人机交互叠加速度分析获得, 但人机交互速度分析降低了数据处理的效率, 并且对于基于叠加速度的地震道插值而言, 用于生成速度谱的CMP道集中通常不止含有一次波信号, 还存在大量的多次波信号(对于SRME方法而言, 原始地震记录中的多次波是进行多次波预测所不可缺少的信号), 这也增加了人机交互速度拾取的难度。本文采用“速度加权叠加”方法实现地震道插值, 先给定叠加速度扫描范围及间隔, 然后针对每一个扫描速度计算一个权重因子, 最后根据各个叠加速度的权重因子, 将所有速度值的重建信号加权叠加, 达到重建缺失地震道的目的。
令起始的叠加速度和速度间隔分别为v0及Δv, 且扫描次数为i(1≤i≤I), 则各叠加速度为:
| $ {v_i} = {v_0} + i\Delta v $ | (4) |
针对公式(4)中的vi计算速度加权因子, 计算公式为[13]:
| $ b\left( {{v_i},\tau } \right) = \frac{{\sum\limits_L {{{\left[ {\sum\limits_{m = 1}^M {{d_m}\left( {\sqrt {{\tau ^2} + \frac{{x_m^2}}{{v_i^2}}} } \right)} } \right]}^\lambda }} }}{{\sum\limits_L {\left[ {\sum\limits_{m = 1}^M {d_m^\lambda \left( {\sqrt {{\tau ^2} + \frac{{x_m^2}}{{v_i^2}}} } \right)} } \right]} + C}} $ | (5) |
式中:λ(λ≥2)表示阶数, λ值越大, b(vi, τ)的分辨率越高; L表示时窗长度; C为保证分母不为零的常量, 一般取平均振幅的0.001~0.010倍。由(4)式可知, 当CMP道集中不存在以vi为叠加速度的同相轴时, 加权因子为一个接近于零的值, 否则, 加权因子是一个较大的数值。
将速度加权叠加过程引入公式(3)中, 则最终的插值信号可表示为:
| $ {d_k}\left( {{t_k}} \right) = \frac{1}{s}\sum\limits_{i = 1}^I {\left\{ {b\left( {{v_i},\tau } \right)\sum\limits_{m = 1}^M {\left[ {{d_m}\left( {{t_m}} \right)} \right]} } \right\}} $ | (6) |
式中, s为叠加系数之和:
| $ s = M\sum\limits_{i = 1}^I {b\left( {{v_i},\tau } \right)} $ | (7) |
在实际数据处理中, 需以零偏移距时τ为基准, 基于一定的时窗长度, 应用公式(6)由上至下逐点进行插值运算。因此, 插值道中的每个样点都经历了多次速度加权叠加, 大样本的统计过程保证了重建信号的稳定性和精度。然而, 由(6)式可知, 最终得到的插值信号dk(tk)本质上是速度加权情况下所有输入道信号叠加的平均值, 其无法反映地震道间的振幅变化规律。为使重建信号更好地反映原地震道间的动力学特征, 还需要对插值结果进行道间振幅校正。
2 基于AVO分析技术的反射振幅校正对于来自同一波阻抗界面的反射波同相轴, 其各道信号振幅与偏移距之间存在一定的关系(AVO效应), 因此理论上可通过AVO分析来确定包括缺失道在内的地震道间振幅变化规律, 并以此进行缺失道的振幅校正。本文首先借助CMP域同相轴追踪技术[22]获得各反射波同相轴的旅行时信息, 然后利用短时窗F-K滤波法提取各同相轴信息, 据此统计分析地震道中各同相轴的反射振幅, 最后利用AVO分析技术确定包括缺失道在内的地震道间振幅变化规律。
若忽略几何扩散以及吸收衰减的影响, 且由于透射系数随偏移距的变化幅度远小于反射系数, 因此, 可以利用反射系数来描述同相轴的道间振幅变化规律。理论上, 可以基于Zoeppritz方程组求解纵波入射到平界面上的反射系数[25], 但由于该方程求解过程极为复杂, 实际处理中一般采用Zoeppritz方程近似公式[26], 其中应用最广的是SHUEY提出的近似公式[27], 即:
| $ \begin{array}{*{20}{c}} {R\left( \theta \right) \approx {R_0} + \left[ {{A_0}{R_0} + \frac{{\Delta \sigma }}{{{{\left( {1 - \sigma } \right)}^2}}}} \right]{{\sin }^2}\theta + }\\ {\frac{1}{2}\frac{{\Delta {v_{\rm{P}}}}}{{{v_{\rm{P}}}}}\left( {{{\tan }^2}\theta - {{\sin }^2}\theta } \right)} \end{array} $ | (8) |
式中:R为待求反射系数; θ为入射角度; R0与A0分别为法向入射的反射系数与振幅; σ为泊松比; vP为纵波速度。
公式(8)描述了反射系数R随入射角θ的变化关系。对于给定反射点而言, R0, A0, σ及vP均为常量, (8)式可简写为:
| $ R\left( \theta \right) \approx A + B{\sin ^2}\theta + C{\tan ^2}\theta $ | (9) |
式中:
公式(8)与公式(9)中的自变量均为入射角度θ, 在实际处理中需将振幅与偏移距x的关系(AVO)转换为振幅与入射角度θ的关系(AVA)。最简便可行的方法是进行直射线模型的射线追踪, 即利用以下关系式估计θ[26]:
| $ \theta = {\tan ^{ - 1}}\left( {\frac{x}{{v\tau }}} \right) $ | (10) |
式中:τ为目标同相轴的零偏移距时, v表示该同相轴的叠加速度。
对于所追踪并提取的目标同相轴, 将其已知地震道中的振幅极值作为反射系数, 求解公式(9)中的未知系数A, B和C。设已知地震道的偏移距与振幅分别为xm与Fm(m为道号), 则θm=tan-1[xm/(vτ)]。将其代入公式(9)可得:
| $ \left[ {\begin{array}{*{20}{c}} 1&{{{\sin }^2}{\theta _1}}&{{{\tan }^2}{\theta _1}}\\ 1&{{{\sin }^2}{\theta _2}}&{{{\tan }^2}{\theta _2}}\\ \vdots&\vdots&\vdots \\ 1&{{{\sin }^2}{\theta _M}}&{{{\tan }^2}{\theta _M}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} A\\ B\\ C \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_1}}\\ {{F_2}}\\ \vdots \\ {{F_M}} \end{array}} \right] $ | (11) |
基于最小二乘理论即可解出A, B, C。(11)式中M(M≥3)为输入地震道的道数。理论上道数越多解越精确, 但超过临界角度的地震道强振幅值会对求解产生干扰, 因此实际应用中仅采用近偏移距未超过临界角度的地震道求解。求出A, B和C后, 即可根据缺失道的偏移距计算其反射振幅Fk。
为使公式(6)中的插值信号dk(tk)在一定程度上具备野外记录的振幅特征, 可利用反射系数的变化规律对插值结果进行振幅校正。相应的振幅校正因子可表示为:
| $ a\left( {\tau ,{x_k},{x_m}} \right) = \frac{{{F_k}}}{{{F_m}}} $ | (12) |
式中:k与xk分别为插值道的道号和偏移距; m和xm分别为输入道的道号和偏移距; τ表示双曲同相轴的零偏移距时。
利用公式(12)所示的振幅校正因子对各输入道信号校正后再加权叠加, 则公式(6)可转化为:
| $ {d_k}\left( {{t_k}} \right) = \frac{1}{s}\sum\limits_{i = 1}^I {\left\{ {b\left( {{v_i},\tau } \right)\sum\limits_{m = 1}^M {\left[ {a\left( {\tau ,{x_k},{x_m}} \right){d_m}\left( {{t_m}} \right)} \right]} } \right\}} $ | (13) |
式中:a(τ, xk, xm)为各同相轴的振幅校正因子基于零偏移距时τ的线性插值; s为叠加系数之和, 计算过程见公式(7)。基于公式(13)得到的重建地震道充分考虑了地震信号的动力学特征, 因而在一定程度上保持了实际地震信号的相对振幅关系, 从而更有利于后续的地震数据处理。
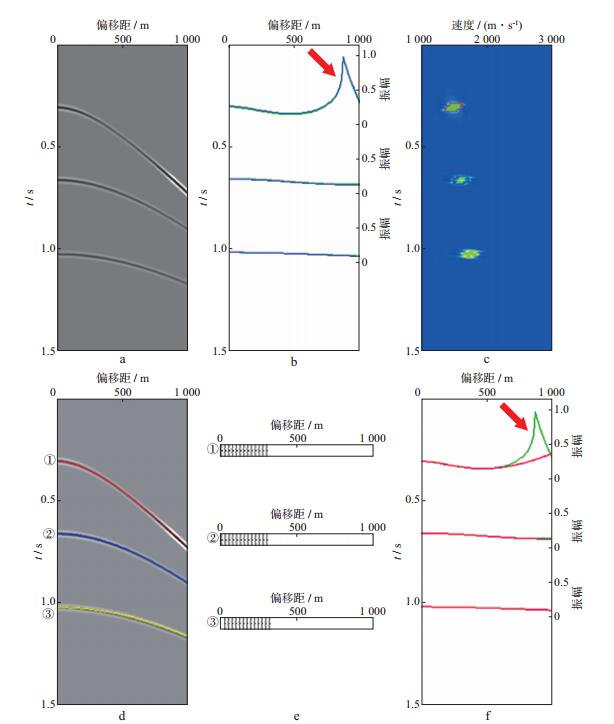
3 模型数据试验 3.1 基于简单模型的反射振幅估计建立一个包含4套地层的水平层状介质模型, 其速度与厚度由浅至深分别为(1500m/s, 230m)、(1700m/s, 300m)、(1950m/s, 350m)以及(2200m/s, 400m), 然后以主频35Hz的雷克子波为震源, 采用射线追踪方法模拟81道、偏移距间隔为12.5m的理论CMP记录, 如图 1a所示。在射线追踪过程中, 基于Zoeppritz方程计算各同相轴的反射系数与反射振幅(在忽略几何扩散与吸收衰减影响时为反射系数与透射系数的乘积), 如图 1b所示。两条曲线几乎完全重合, 说明道间透射系数基本不变, 因而可利用反射系数来描述同相轴的道间振幅变化规律。
|
图 1 基于简单模型的反射振幅估计 a理论CMP记录; b反射系数曲线与反射振幅曲线; c叠加速度谱; d追踪的反射波同相轴; e提取的反射波同相轴; f基于AVO分析技术估计的反射振幅曲线 |
基于理论CMP记录创建同相轴追踪的叠加速度谱(图 1c), 通过等值线追踪获得各同相轴叠加能量团的范围, 搜索其中的极值可确定出CMP记录中相应的同相轴(图 1d中彩色曲线①~③)。提取各反射波同相轴(图 1e), 取其近偏移距位置13道(道号为奇数)反射信号的振幅极值作为输入, 基于公式(9)~(11)计算出反射振幅曲线(图 1f中的红色曲线)。与理论反射振幅曲线(图 1f中的绿色曲线)相比, 估计的反射振幅在箭头指向位置(发生全反射)存在显著误差, 但在实际资料处理中这里因混杂有强折射波干扰会被直接切除, 因此并不影响最终的处理效果。
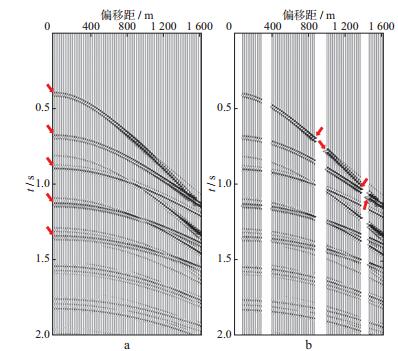
3.2 基于简单模型的地震道外推与内插建立一个包含6套地层的水平层状介质模型, 其速度与厚度由浅至深分别为(1500m/s, 300m)、(2000m/s, 280m)、(2500m/s, 258m)、(2000m/s, 240m)、(2600m/s, 280m)以及(3100m/s, 300m), 第4套地层存在明显的速度反转。以主频为30Hz的雷克子波为震源, 将模型上边界设置为自由边界, 采用声波方程有限差分法模拟得到含有多次波的地震记录。该地震记录共500炮, 每炮含有160道, 炮间距与道间距均为10m, 最小偏移距是0。图 2a为该炮集记录对应的第500个CMP记录, 除箭头指向的同相轴之外其余均为多次波干扰。由于全反射作用, 其强反射波同相轴的信号波形在中、远偏移距位置发生了明显的突变。将该CMP记录中序号为1~4, 16~20, 45~50及70~73的地震道充0, 得到存在缺失道的CMP记录, 见图 2b。图 2b中箭头指向的位置地震信号的波形变化较为剧烈, 因混杂有强直达波及折射波干扰在实际资料处理中会被直接切除, 但本实验中仍然展示了这些信号的插值结果。
|
图 2 理论CMP记录(a)与存在缺失道的CMP记录(b) |
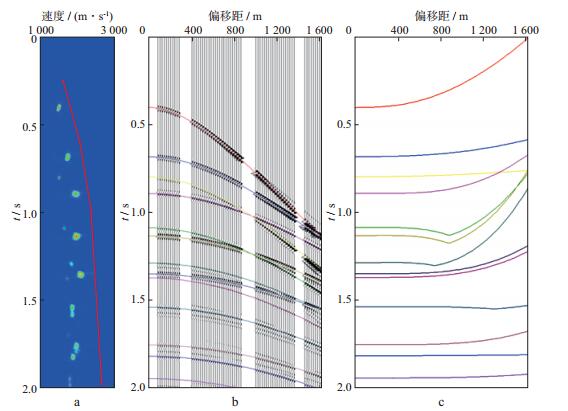
应用本文方法进行地震道外推与内插时, 须给定适当的叠加速度扫描范围及速度间隔, 一般要求速度采样能够涵盖所有同相轴的叠加速度值。基于图 2a所示理论CMP记录创建高分辨率叠加速度谱后[28-29], 拾取一条速度值明显高于谱中各能量团的叠加速度曲线(图 3a中的红色曲线), 其速度误差介于200~600m/s。在进行地震道插值之前, 首先利用同相轴追踪技术[24]获得速度谱中强能量团, 据此确定图 3b中彩色曲线所指示的反射波同相轴, 再利用AVO分析方法根据道号为5~15的已知地震道估计各同相轴的反射振幅曲线(图 3c)。为避免超过临界角度的地震道强振幅值对求取的反射振幅曲线产生干扰, 这里仅用近道进行计算。
|
图 3 基于同相轴追踪技术与AVO分析的反射振幅曲线估计 a叠加速度谱及拾取的存在明显偏差的叠加速度曲线; b追踪的反射波同相轴; c估计的反射振幅曲线 |
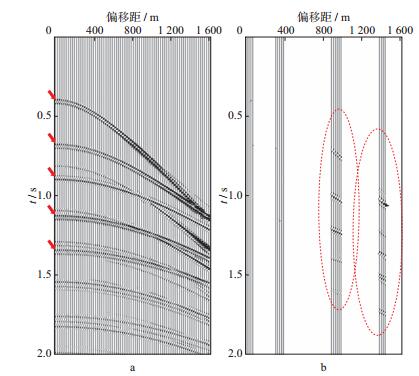
基于图 3c所示各同相轴的反射振幅曲线, 以所拾取速度曲线(图 3a中红色曲线)为准向低速方向扫描, 截止扫描速度为1500m/s, 速度扫描间隔是25m/s。此外, 输入所有已知地震道计算速度加权因子, 取左右与缺失道最为邻近的已知地震道(共4道)参与信号叠加运算, 信号时窗长度为30ms。经过地震道插值的CMP记录如图 4a所示。为探讨波场插值精度, 计算原始CMP记录(图 2a)与重建CMP记录的所有样点的差值, 得到如图 4b所示的误差记录, 其幅值明显小于原始记录中的信号幅值。对比分析可知, 中、远偏移距道中的插值误差(图 4b中椭圆区域)明显大于近道位置, 原因在于:①采用Zoeppritz方程近似公式计算的反射振幅在中、远偏移距位置存在一定误差; ②强直达波及折射波干扰导致地震信号波形变化较为剧烈; ③插值过程在时间域中进行, 相交同相轴之间会相互影响插值精度。
|
图 4 重建的CMP记录(a)及其与原始CMP记录的误差记录(b) |
某海域二维测线ML_A数据采集于硬海底地区, 沿观测方向水深由150m增加至1100m, 相应的原始炮集记录中发育有强自由界面多次波, 且在海底陡降位置多次波特征尤为复杂。该测线原始数据共2699炮, 每炮240道接收, 道间隔及炮间隔均为25m, 最小偏移距为100m(缺失4道)。近偏移距道的缺失对该测线自由界面多次波衰减的影响极为严重, 直接导致无法预测部分道中的多次波信号。而且, 由于传统SRME依赖于原始记录中的多次波信息, 因此除一次波外还需要针对多次波同相轴进行插值。
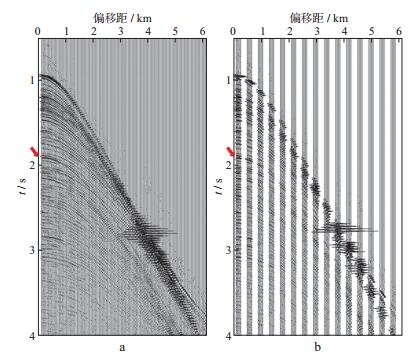
在进行地震道插值之前, 首先对ML_A测线的原始炮集进行了预处理:①切除各炮记录中的直达波信号; ②通过带通滤波消除原始地震记录中5Hz以下的低频信号; ③为增强炮集记录中深部较弱的反射信息, 进行了球面扩散补偿处理。经过预处理的CMP记录如图 5a所示, 箭头指向位置附近存在明显的海底全程多次波, 其叠加速度明显低于同时段的一次波。对于野外地震记录, 一般要先切除中、远偏移距道上混杂有强直达波及折射波干扰的信号, 但为了全面检验基于速度加权叠加和AVO分析的地震道插值方法对复杂地震波场的插值效果, 本次试验中将其保留。人为舍弃原始CMP记录中的部分地震道, 即在3~112道之间每隔4道舍弃4道, 存在缺失道的CMP记录如图 5b所示。
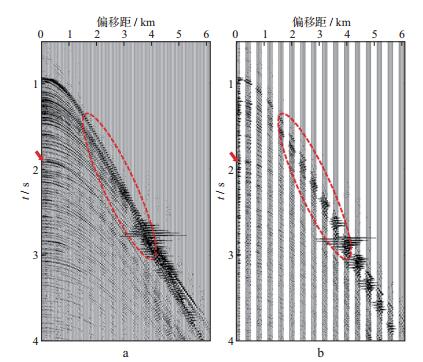
利用本文方法针对缺失道进行波场插值处理时, 需给定较大的叠加速度扫描范围方可有效构建低速的多次波信号。设拾取的一次波叠加速度为v(τ), 则相应的速度扫描范围为1500~v(τ)+400m/s, 速度间隔为25m/s, 图 6a显示了波场插值的结果。计算原始记录与插值记录的差值, 得到如图 6b所示误差记录, 该记录的振幅明显小于原始记录的振幅。对比分析图 5和图 6可知, 除因混杂有强直达波及折射波干扰导致地震信号波形变化较为剧烈的位置外, 图 5a所示CMP记录中同相轴(包括明显低速的多次波同相轴)得到了有效重建。
|
图 5 原始CMP记录(a)与舍弃部分地震道的CMP记录(b) |
|
图 6 重建的CMP记录(a)与误差记录(b) |
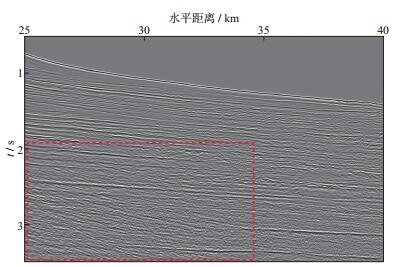
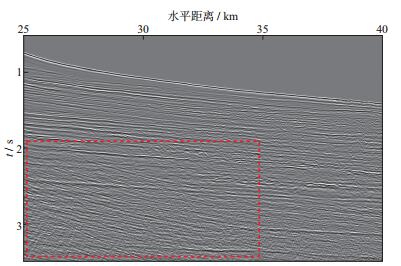
利用一次波的偏移速度场, 对原始记录和插值记录进行克希霍夫叠前时间偏移处理, 结果如图 7和图 8所示。为便于比较分析, 本文仅选取了起伏海底位置部分剖面, 其水平距离为25~40km, 旅行时为0.5~3.5s。在利用一次波偏移速度进行成像的过程中, 多次波信息受到了一定压制, 但剖面中矩形区域内仍存在较强的倾斜多次波同相轴。对比原始记录的偏移剖面与插值记录的偏移剖面可见, 二者构造形态几乎完全一致, 倾斜多次波同相轴亦较为接近, 这很好地证明了本文地震道插值方法的准确性。
|
图 7 原始CMP记录的偏移剖面 |
|
图 8 插值CMP记录的偏移剖面 |
本文提出一种新的叠前CMP道集插值和外推方法, 通过速度扫描叠加计算速度加权因子, 通过AVO分析获得振幅校正因子, 在时空域基于输入地震道信号的加权叠加重建缺失地震道中的反射信号。该方法在重建缺失地震道的同时, 充分考虑了地震信号的动力学特征, 从而使重建的地震信号在一定程度上保持了野外记录的相对振幅关系。理论模型和实际资料试验结果表明, 无论是对一次波还是多次波, 该方法均可实现缺失道的高精度重建。此外, 该方法在时间域内实现波场插值, 无须借助复杂的数学变换, 因而具有较高的计算效率。
然而, 当地震记录中存在交叉同相轴时, 时间域插值会在一定程度上影响地震道的重建精度, 因此目前该方法更适用于近偏移距地震道的重建。进一步研究高精度插值算法, 使其能够适用于远偏移距地震道的重建并将其推广应用到三维地震数据的规则化处理, 将是我们下一步的研究目标。
| [1] | VERSCHUUR D J.Surface-related multiple elimination, an inversion approach[D]. Netherlands:Delft University of Technology, 1991 |
| [2] | BERKHOUT A J, VERSCHUUR D J. Estimation of multiple scattering by iterative inversion, part Ⅰ:theoretical considerations[J]. Geophysics, 1997, 62(5): 1586-1595 DOI:10.1190/1.1444261 |
| [3] | RONEN J. Wave-equation trace interpolation[J]. Geophysics, 1987, 52(7): 973-984 DOI:10.1190/1.1442366 |
| [4] | CHEMINGUI N, BIONDI B. Handling the irregular geometry in wide-azimuth surveys[J]. Expanded Abstracts of 66th Annual Internat SEG Mtg, 1996: 32-35 |
| [5] | SPITZ S. Seismic trace interpolation in f-x domain[J]. Geophysics, 1991, 56(6): 785-794 DOI:10.1190/1.1443096 |
| [6] |
钱忠平, 陈海峰, 黄少卿, 等. 一种高效稳定的三维叠前插值技术及应用[J].
石油物探, 2016, 55(4): 506-515 QIAN Z P, CHEN H F, HUANG S Q, et al. An efficient and stable 3D prestack trace interpolation technique and its application[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 506-515 |
| [7] | GULUNAY N, CHAMBERS R E. Unaliased f-k domain trace interpolation (UFKI)[J]. Expanded Abstracts of 66th Annual Internat SEG Mtg, 1996: 1461-1464 |
| [8] |
刘喜武, 刘洪, 刘彬. 反假频非均匀地震数据重建方法研究[J].
地球物理学报, 2004, 47(2): 299-305 LIU X W, LIU H, LIU B. A study on algorithm for reconstruction of de-alias uneven seismic data[J]. Chinese Journal of Geophysics, 2004, 47(2): 299-305 |
| [9] | DUIJNDAM A J W, SCHONEWILLE M, HINDRIKS C. Reconstruction of band-limited signals, irregularly sampled along one spatial direction[J]. Geophysics, 1999, 64(2): 524-538 DOI:10.1190/1.1444559 |
| [10] | GULUNAY N. Seismic trace interpolation in the Fourier transform domain[J]. Geophysics, 2003, 68(1): 355-369 DOI:10.1190/1.1543221 |
| [11] | DARCHE G. Spatial interpolation using a fast parabolic Radon transform[J]. Expanded Abstracts of 60th Annual Internat SEG Mtg, 1990: 1647-1650 |
| [12] | KABIR M M N, VERSCHUUR D J. Restoration of missing offsets by parabolic Radon transform[J]. Geophysical Prospecting, 1995, 43(3): 347-368 DOI:10.1111/gpr.1995.43.issue-3 |
| [13] | TRAD D O, ULRYCH T J, SACCHI M D. Accurate interpolation with high-resolution time-variant Radon transforms[J]. Geophysics, 2002, 67(2): 644-656 |
| [14] |
王升超, 韩立国, 巩向博. 基于各向异性Radon变换的叠前地震数据重建[J].
石油物探, 2016, 55(6): 808-815 WANG S C, HAN L G, GONG X B. Prestack seismic data reconstruction by anisotropic Radon transform[J]. Geophysical Prospecting for Petroleum, 2016, 55(6): 808-815 |
| [15] |
周亚同, 刘志峰, 张志伟. 形态分量分析框架下基于DCT与曲波字典组合的地震信号重建[J].
石油物探, 2015, 54(5): 560-568 ZHOU Y T, LIU Z F, ZHANG Z W. Seismic signal reconstruction under the morphological component analysis framework combined with discrete cosine transform (DCT) and curvelet dictionary[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 560-568 |
| [16] |
王本锋, 陈小宏, 李景叶, 等. POCS联合改进的Jitter采样理论曲波域地震数据重建[J].
石油地球物理勘探, 2015, 50(1): 20-28 WANG B F, CHEN X H, LI J Y, et al. Seismic data reconstruction based on POCS and improved Jitter sampling in the curvelet domain[J]. Oil Geophysical Prospecting, 2015, 50(1): 20-28 |
| [17] |
马继涛, 王建花, 刘国昌. 基于频率域奇异值分解的地震数据插值去噪方法研究[J].
石油物探, 2016, 55(2): 205-213 MA J T, WAN J H, LIU G C. Seismic data noise attenuation and interpolation using singular value decomposition in frequency domain[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 205-213 |
| [18] | WANG Y H. Sparseness-constrained least-squares inversion:application to seismic wave reconstruction[J]. Geophysics, 2003, 68(5): 1633-1638 DOI:10.1190/1.1620637 |
| [19] | ZWARTJES P, GISOLF A. Fourier reconstruction with sparse inversion[J]. Geophysical Prospecting, 2007, 55(2): 199-221 DOI:10.1111/gpr.2007.55.issue-2 |
| [20] |
冯飞, 王征, 刘成明, 等. 基于Shearlet变换稀疏约束地震数据重建[J].
石油物探, 2016, 55(5): 682-691 FENG F, WANG Z, LIU C M, et al. Seismic data reconstruction based on sparse constraint in the Shearlet domain[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 682-691 |
| [21] | BERKHOUT A J. Transformation of multiples into primary reflections[J]. Expanded Abstracts of 73rd Annual Internat SEG Mtg, 2003: 1925-1928 |
| [22] | VERSCHUUR D J, BERKHOUT A J. Transforming multiples into primaries:experience with field data[J]. Expanded Abstracts of 75th Annual Internat SEG Mtg, 2005: 2103-2106 |
| [23] |
郭书娟, 方伍宝, 徐兆涛. 基于表层多次波的地震数据插值方法研究[J].
石油物探, 2013, 52(6): 636-641 GUO S J, FANG W B, XU Z T. Interpolation of near offset seismic trace using surface-related multiples[J]. Geophysical Prospecting for Petroleum, 2013, 52(6): 636-641 |
| [24] |
谭军, 王修田. 基于同相轴追踪的多次波衰减[J].
中国海洋大学学报:自然科学版, 2012, 42(6): 99-106 TAN J, WANG X T. Multiple attenuation based on event tracing[J]. Periodical of Ocean University of China, 2012, 42(6): 99-106 |
| [25] |
SHERIF R E, GELDART L P. 勘探地震学[M]. 初英, 李程楚, 译. 北京: 石油工业出版社, 1999: 98-102
SHERIF R E, GELDART L P.Exploration seismology[M]. CHU Y, LI C C, translator.Beijing:Petroleum Industry Press, 1999:98-102 |
| [26] |
周锦明, 熊翥.
地震数据精细处理[M]. 北京: 石油工业出版社, 2003: 98-109.
ZHOU J M, XIONG Z. Fine processing of seismic data[M]. Beijing: Petroleum Industry Press, 2003: 98-109. |
| [27] | SHUEY R T. A simplification of the Zoeppritz equations[J]. Geophysics, 1985, 50(4): 609-614 DOI:10.1190/1.1441936 |
| [28] |
谭军, 李金山, 宋鹏, 等. 基于同相轴优化追踪的多次波匹配衰减方法[J].
中国石油大学学报:自然科学版, 2016, 40(6): 40-49 TAN J, LI J S, SONG P, et al. Multiple matching attenuation method based on optimized event tracing[J]. Journal of China University of Petroleum:Edition of Natural Science, 2016, 40(6): 40-49 |
| [29] | TAN J, SONG P, LI J S, et al. Combined adaptive multiple subtraction based on optimized event tracing and extended wiener filtering[J]. Journal of Ocean University of China, 2017, 16(3): 411-421 DOI:10.1007/s11802-017-3279-7 |



 ,
,