地震数据的缺失重建是地震数据处理的主要任务之一。目前, 地震数据缺失重建的方法有三大类:预测滤波法、波动方程法以及数学变换法。预测滤波法有F-X域预测误差滤波法[1]以及基于加权最小二乘回归的F-X域预测滤波插值法等[2], 该类方法不仅计算量偏大, 而且较容易引入误差。波动方程法有AMO局部叠加法[3]以及NMO与逆DMO联合法[4]等, 该类方法需要地下介质速度参数且计算量大。数学变换法有基于曲波变换的地震数据重建方法[5]、基于傅里叶变换的地震数据重建方法[6]以及字典学习地震数据重建方法[7-8], 该类方法理论公式直观, 计算结果偏差较小, 比较适用于实际生产。
由压缩感知理论可知:倘若数据具有稀疏性, 那么只要采集少量的数据, 就可以利用合适的重建算法准确地重建原始数据[9-10]。而地震信号可以通过数学变换进行稀疏表示, 满足压缩感知应用于地震数据重建的先决条件, 因此, 压缩感知技术在基于傅里叶变换[11]、小波变换[12]、曲波变换[13]和Shearlet变换[14]的地震数据重建中得到了较大发展。其中, 选择一个合适的稀疏基十分重要, 它直接影响到地震数据的重建效果[15]。傅里叶变换缺乏描述地震信号局部时频特征的能力; 短时傅里叶变换能够解决局部时频问题, 但是窗口难以完全自适应; 小波变换虽然弥补了窗口难以自适应的缺陷, 但是对于二维图像中线性特征的描述能力较弱。DO等[16]提出了Contourlet变换, 首先利用拉普拉斯金字塔结构对信号进行多尺度分解并捕获奇异点, 然后利用方向滤波器合成Contourlet域中的稀疏系数。相对小波变换和短时傅里叶变换, 它能够更好地描述地震信号中的线性特征。目前, Contourlet变换已被广泛应用于地震数据处理, 如:在Contourlet域中对地震数据的稀疏系数进行阈值处理, 从而完成地震数据重建[17];采用Contourlet和Curvelet相结合的方法对地震数据进行稀疏表示, 再通过正则化方法对地震数据进行去噪及重建[18];采用Contourlet变换来增强地震剖面的横向连续性[19]。本文提出一种基于压缩感知和Contourlet变换的地震数据重建方法, 通过合成数据测试分析和实际地震数据重建验证了方法的有效性。
1 基本原理 1.1 压缩感知根据压缩感知理论, 地震数据的缺失重建是将M维不完整的地震数据f(f∈RM)恢复为N维完整的地震数据y(y∈RN, N>M):
| $ \mathit{\boldsymbol{f}} = \mathit{\phi} \mathit{\boldsymbol{y}} $ | (1) |
式中, ϕ(ϕ∈RM×N)为测量矩阵算子。压缩感知技术针对稀疏信号, 因此将y在可变域上变稀疏:
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{\varphi y}} $ | (2) |
式中:φ为稀疏变换算子, s为y在可变域上的稀疏系数。将(1)式和(2)式合写为:
| $ \mathit{\boldsymbol{f}} = \phi {\mathit{\boldsymbol{\varphi }}^{\rm{H}}}\mathit{\boldsymbol{s}} $ | (3) |
式中:φH为稀疏逆变换算子。引入重构算子A=ϕφH, 将其代入(3)式中, 有如下表示:
| $ \mathit{\boldsymbol{f}} = \mathit{\boldsymbol{As}} $ | (4) |
公式(4)中的未知量个数大于方程个数(N>M), 所以为病态方程, 无法进行求解。CANDES等[20]指出, 在s具有稀疏性和A满足有限等距性质(restricted isometry property, RIP)的情况下, 可以对欠定方程(4)进行求解。即对于稀疏度为k的任意稀疏信号s, 存在常数νk∈(0, 1), 使A满足:
| $ \left( {1 - {\nu _k}} \right){\left\| \mathit{\boldsymbol{s}} \right\|_2} \le {\left\| {\mathit{\boldsymbol{As}}} \right\|_2} \le \left( {1 - {\nu _k}} \right){\left\| \mathit{\boldsymbol{s}} \right\|_2} $ | (5) |
一般情况下, A是否满足RIP很难由(5)式判定。BARANIUK[21]提出, 当φH与ϕ不相干时, A很大概率上满足RIP。因为A=ϕφH, φH与ϕ的相干性可以定义为[22]:
| $ \mu \left( \mathit{\boldsymbol{A}} \right) = \mathop {\max }\limits_{i,j,i \ne j} \frac{{\left\langle {\mathit{\boldsymbol{a}}_i^{\rm{T}},{\mathit{\boldsymbol{a}}_j}} \right\rangle }}{{\left\| {{\mathit{\boldsymbol{a}}_i}} \right\| \cdot \left\| {{\mathit{\boldsymbol{a}}_j}} \right\|}} $ | (6) |
式中, ai为A的第i列向量。在地震数据采集中, 因为各个方位的检波器采集的是点震源发出的脉冲, 所以ϕ是一个单位矩阵, 它与φH不相干。当该地震道未采集到数据时, ϕ的ai列元素为0, 采集到数据时, ϕ的ai列元素为1[23]。
此时, 求解方程(4)等价于求解下述模型:
| $ \mathit{\boldsymbol{\tilde s}} = \arg \min {\left\| \mathit{\boldsymbol{s}} \right\|_0}\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{\left\| {\mathit{\boldsymbol{As}} - \mathit{\boldsymbol{f}}} \right\|_2} \le \varepsilon $ | (7) |
式中:
| $ \mathit{\boldsymbol{\tilde s}} = \arg \min {\left\| \mathit{\boldsymbol{s}} \right\|_1}\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{\left\| {\mathit{\boldsymbol{As}} - \mathit{\boldsymbol{f}}} \right\|_2} \le \varepsilon $ | (8) |
(8) 式是一个凸优化问题, 可改写为:
| $ \mathit{\boldsymbol{\tilde s}} = \arg \min \frac{1}{2}{\left\| {\mathit{\boldsymbol{As}} - \mathit{\boldsymbol{f}}} \right\|_2} + \lambda {\left\| \mathit{\boldsymbol{s}} \right\|_1}\;\;\;\;\lambda > 0 $ | (9) |
式中:λ为正则化参数。本文采用快速迭代收缩阈值算法(FISTA)求解(9)式, 得到
| $ \mathit{\boldsymbol{\tilde y}} = {\mathit{\boldsymbol{\varphi }}^{\rm{H}}}\mathit{\boldsymbol{\tilde s}} $ | (10) |
在压缩感知技术中, 稀疏变换阶段及重建阶段的算法选择十分重要, 直接影响到重建效果。
1.2 Contourlet变换本文在压缩感知的稀疏变换阶段选择Contourlet变换[26]。该变换主要由拉普拉斯金字塔分解和方向滤波器组采集两部分组成。拉普拉斯金字塔分解即将待分解的地震数据y与低通滤波算子d卷积, 第l层的低频信息yl可以表示为:
| $ \begin{array}{l} {\mathit{\boldsymbol{y}}_l} = \left( {g,h} \right) = \sum\limits_{m = - 2}^2 {\sum\limits_{n = - 2}^2 {d\left( {m,n} \right)y\left( {2g + m} \right)\left( {2h + n} \right)} } \\ l \in \left( {0,F} \right]\;\;\;g \in \left( {0,{A_l}} \right]\;\;\;h \in \left( {0,{B_l}} \right] \end{array} $ | (11) |
式中:F为金字塔分解总层数, Al为地震数据的行, Bl为地震数据的列。第l层的高频信息ylh可以表示为:
| $ {\mathit{\boldsymbol{y}}_{l{\rm{h}}}} = \mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{y}}_l} $ | (12) |
方向滤波器组的采集矩阵Epl可以表示为:
| $ \mathit{\boldsymbol{E}}_p^l = \left\{ \begin{array}{l} {\rm{diag}}\left( {{2^{l - 1}},2} \right)\;\;\;\;0 \le p \le {2^{l - 1}}\\ {\rm{diag}}\left( {2,{2^{l - 1}}} \right)\;\;\;\;{2^{l - 1}} \le p \le {2^l} \end{array} \right. $ | (13) |
式中:p为方向角度。方向滤波器组对每一层的ylh进行分解, 得到相应的稀疏系数sl, 以内积形式表示为:
| $ {\mathit{\boldsymbol{s}}_l} = \left\langle {{\mathit{\boldsymbol{y}}_{l{\rm{h}}}},\mathit{\boldsymbol{\gamma }}} \right\rangle $ | (14) |
式中:γ为Contourlet系数空间RZ(Z=0, 1, …, 2l-1)的基函数。
1.3 快速迭代收缩阈值算法本文在压缩感知的重建阶段采用快速迭代收缩阈值算法FISTA)[27-28], 它是ISTA[29]的一种改进算法。ISTA的迭代形式为:
| $ {{\mathit{\boldsymbol{\tilde s}}}_{n + 1}} = {\rm{soft}}\left[ {{{\mathit{\boldsymbol{\tilde s}}}_n} + \frac{1}{\alpha }{\mathit{\boldsymbol{A}}^{\rm{H}}}\left( {\mathit{\boldsymbol{f}} - \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\tilde s}}}_n}} \right),\frac{\lambda }{{2\alpha }}} \right] $ | (15) |
式中:
| $ {\rm{soft}}\left( {\mathit{\boldsymbol{\tilde s}},T} \right) = \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde s}} - T}&{\mathit{\boldsymbol{\tilde s}} > T}\\ 0&{ - T \le \mathit{\boldsymbol{\tilde s}} \le T}\\ {\mathit{\boldsymbol{\tilde s}} + T}&{\mathit{\boldsymbol{\tilde s}} < T} \end{array}} \right. $ | (16) |
式中:T为阈值。FISTA和ISTA的区别在于每一步迭代时初始点的选择不同, 当迭代到n+1次时, ISTA选择
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{n + 1}} = {{\mathit{\boldsymbol{\tilde s}}}_n} + \frac{{{\beta _n} - 1}}{{{\beta _{n + 1}}}}\left( {{{\mathit{\boldsymbol{\tilde s}}}_n} - {{\mathit{\boldsymbol{\tilde s}}}_{n - 1}}} \right) $ | (17) |
式中:βn+1是一个迭代更新的参量, 定义为:
| $ {\beta _{n + 1}} = \frac{{1 + \sqrt {1 + 4\beta _n^2} }}{2} $ | (18) |
βn+1的初始值为1。将(15)式中的
| $ {{\mathit{\boldsymbol{\tilde s}}}_{n + 1}} = {\rm{soft}}\left[ {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{n + 1}} + \frac{1}{\alpha }{\mathit{\boldsymbol{A}}^{\rm{H}}}\left( {\mathit{\boldsymbol{f}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{n + 1}}} \right),\frac{\lambda }{{2\alpha }}} \right] $ | (19) |
本文采用信噪比RSN来衡量地震数据的重建效果:
| $ {R_{{\rm{SN}}}} = 10\lg \frac{{\left\| \mathit{\boldsymbol{y}} \right\|_2^2}}{{\left\| {\mathit{\boldsymbol{\tilde y}} - \mathit{\boldsymbol{y}}} \right\|_2^2}} $ | (20) |
式中:
|
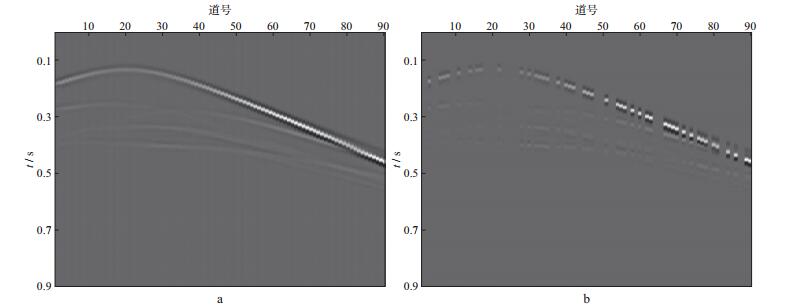
图 1 原始合成炮集数据(a)和随机缺失50%的合成炮集数据(b) |
采用压缩感知技术对图 1b中随机缺失50%地震道的合成炮集数据进行重建。图 2a至图 2c分别为采用傅里叶稀疏基、小波稀疏基和Contourlet稀疏基重建的结果。重建过程中90%较小的稀疏系数被阈值滤除, 前后两次迭代的信噪比相对误差小于1%时停止迭代。
|
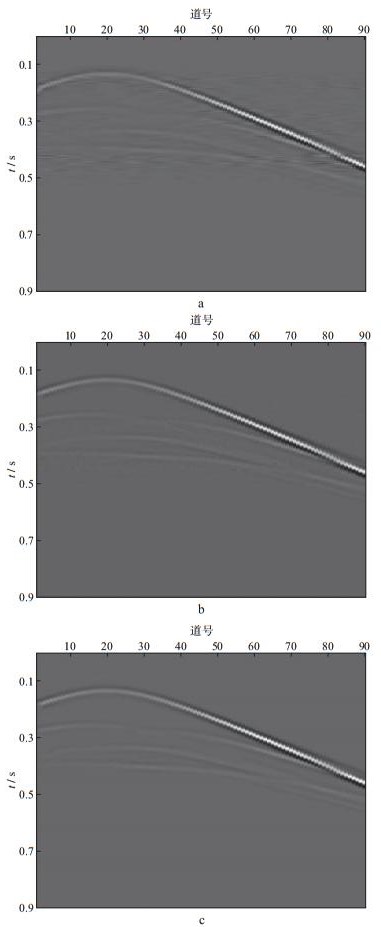
图 2 不同稀疏基重建的合成炮集数据对比 a傅里叶稀疏基; b小波稀疏基; c Contourlet稀疏基 |
从图 2可以看出, 基于压缩感知技术的各稀疏基都可以完成合成数据的重建。其中傅里叶稀疏基的重建用时最短, 为10.003s, 但是重建结果稍差, 含有部分分布在同相轴周围的噪声, 能量较弱的同相轴湮没在噪声之中, 勉强能识别出来。小波稀疏基的重建用时为11.193s, 重建结果比傅里叶稀疏基好, 只含有微量噪声, 同相轴几乎都能识别。而Contourlet稀疏基重建的结果最好, 同相轴清晰可见, 几乎不含噪声, 重建用时为14.751s。图 3对比了本文方法不同迭代次数重建的合成炮集数据Contourlet域中最外层稀疏系数; 图 4为不同稀疏基重建的合成炮集数据采样率和信噪比关系曲线; 表 1对比了本文方法不同迭代次数重建随机缺失50%地震道的合成炮集数据信噪比。

|
图 3 本文方法不同迭代次数重建的合成炮集数据Contourlet域中最外层稀疏系数 a 5次迭代; b 10次迭代; c 15次迭代; d 20次迭代 |
|
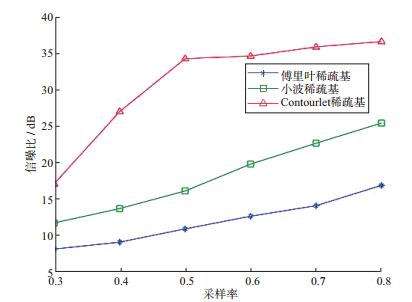
图 4 不同稀疏基重建的合成炮集数据采样率和信噪比关系曲线 |
| 表 1 本文方法不同迭代次数重建的合成炮集数据信噪比 |
从图 3可以看出, 随着迭代次数的增加, Contourlet域中最外层稀疏系数显示的信息逐渐增加, 对数据细节的描述越来越清晰。当迭代次数达到15次后, 最外层稀疏系数不再有明显变化。
利用压缩感知技术对随机缺失20%~70%地震道的合成炮集数据进行重建的结果均表明, 采用Contourlet稀疏基比采用傅里叶稀疏基和小波稀疏基重建的结果信噪比高。
3 实际地震数据重建及分析采用如图 5a所示实际炮集数据测试了本文方法对实际地震数据的重建性能。该炮集有100个地震道, 每道有1000个采样点, 时间采样率为0.001s。图 5b为随机缺失50%地震道的实际炮集数据。

|
图 5 实际炮集数据(a)和随机缺失50%地震道的炮集数据(b) |
采用压缩感知技术对图 5b中随机缺失50%地震道的实际炮集数据进行重建。图 6a至图 6c分别为采用傅里叶稀疏基、小波稀疏基和Contourlet稀疏基重建的结果, 重建过程中90%较小的稀疏系数被阈值滤除, 前后两次迭代的信噪比相对误差小于1%时停止迭代。

|
图 6 不同稀疏基重建的实际炮集数据对比 a傅里叶稀疏基; b小波稀疏基; c Contourlet稀疏基 |
从图 6可以看出, 基于压缩感知技术的各稀疏基都能完成实际地震数据的重建。其中傅里叶稀疏基的重建用时为11.848s, 重建结果一般, 含有微量噪声, 重建同相轴能量较弱, 模糊不清。小波稀疏基的重建用时为13.786s, 重建结果稍好, 所含噪声较少, 能识别出能量较强的同相轴。Contourlet稀疏基的重建用时为18.044s, 重建结果比前两者好, 几乎不含噪声, 能量很弱的同相轴也可以识别出来。图 7对比了本文方法不同迭代次数重建的实际炮集数据Contourlet域中最外层稀疏系数, 图 8为不同稀疏基重建的实际炮集数据采样率和信噪比关系曲线, 表 2对比了本文方法不同迭代次数重建随机缺失50%地震道的实际炮集数据信噪比。

|
图 7 本文方法不同迭代次数重建的实际炮集数据Contourlet域中最外层稀疏系数 a 10次迭代; b 15次迭代; c 18次迭代; d 20次迭代 |
|
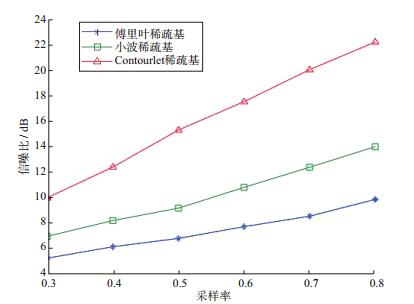
图 8 不同稀疏基重建的实际炮集数据采样率和信噪比关系曲线 |
| 表 2 本文方法不同迭代次数重建的实际炮集数据信噪比 |
从图 7可以看出, 随着迭代次数的增加, Contourlet域中最外层稀疏系数对实际地震数据的细节描述越来越丰富, 当迭代次数达到18次后, Contour-let域中最外层稀疏系数不再有明显增加。
利用压缩感知技术对随机缺失20%~70%地震道的实际地震数据进行重建的结果均表明, 采用Contourlet稀疏基比采用傅里叶稀疏基和小波稀疏基重建的结果信噪比高。
4 结束语本文在压缩感知技术框架下引入Contourlet稀疏基, 提出了一种基于压缩感知和Contourlet变换的地震数据重建方法。
合成数据和实际地震数据测试结果表明, 在随机缺失20%~70%地震道时, 利用压缩感知技术能够完成地震数据的重建, Contourlet稀疏基相比傅里叶稀疏基和小波稀疏基具有更好的重建效果, 所增加的耗时有限, 在可接受的范围之内。
虽然本文方法重建的地震数据信噪比要比压缩感知技术常用的稀疏基高, 但还不能令人完全满意, 因此, 我们下一步的研究方向是构造重建效果更好的稀疏基。
| [1] | SPITZ S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 789-794 |
| [2] | NAGHIZADEH M, SACCHI M D. F-X adaptive seismic trace interpolation[J]. Geophysics, 2009, 74(1): V9-V16 DOI:10.1190/1.3008547 |
| [3] | CHEMINGUI N, BIONDI B. Handling the irregular geometry in wide-azimuth surveys[J]. Expanded Abstracts of 66th Annual Internat SEG Mtg, 1996: 32-35 |
| [4] | RONEN J. Wave equation trace interpolation[J]. Geophysics, 1987, 52(7): 973-984 DOI:10.1190/1.1442366 |
| [5] | HENNENFENT G, FENELON L, HERRMANN F J. Nonequispaced Curvelet transform for seismic data reconstruction:a sparsity-promoting approach[J]. Geophysics, 2010, 75(6): WB203-WB2010 DOI:10.1190/1.3494032 |
| [6] | NAGHIZADEH M, INNANEN K A. Seismic data interpolation using a fast generalized Fourier transform[J]. Geophysics, 2011, 76(1): V1-V10 DOI:10.1190/1.3511525 |
| [7] | YU S, MA J, ZHANG X, et al. Interpolation and denoising of high-dimensional seismic data by learning a tight frame[J]. Geophysics, 2015, 80(5): V119-V132 DOI:10.1190/geo2014-0396.1 |
| [8] | YU S, MA J, OSHER S. Monte Carlo data-driven tight frame for seismic data recovery[J]. Geophysics, 2016, 81(4): V327-V340 DOI:10.1190/geo2015-0343.1 |
| [9] | CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509 DOI:10.1109/TIT.2005.862083 |
| [10] | DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2005, 51(4): 1289-1306 |
| [11] | ZHANG H, CHENG X H, WU X M. Seismic data reconstruction based on CS and Fourier theory[J]. Applied Geophysics, 2013, 10(2): 170-180, 236 DOI:10.1007/s11770-013-0375-3 |
| [12] |
郭念民, 李海山, 冯雪梅, 等. 非抽样离散小波变换叠前地震数据重建方法[J].
石油地球物理勘探, 2014, 49(3): 508-516 GUO N M, LI H S, FENG X M, et al. Pre-stack seismic data reconstruction based on the undecimated wavelet transform[J]. Oil Geophysical Prospecting, 2014, 49(3): 508-516 |
| [13] |
白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重建[J].
地球物理学报, 2014, 57(9): 2937-2945 BAI L S, LIU Y K, LU H Y, et al. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics, 2014, 57(9): 2937-2945 DOI:10.6038/cjg20140919 |
| [14] |
冯飞, 王征, 刘成明, 等. 基于Shearlet变换稀疏约束地震数据重建[J].
石油物探, 2016, 55(5): 682-691 FENG F, WANG Z, LIU C M, et al. Seismic data reconstruction based on sparse constraint in the Shearlet domain[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 682-691 |
| [15] |
王华忠, 冯波, 王雄文, 等. 压缩感知及其在地震勘探中的应用[J].
石油物探, 2016, 55(4): 467-474 WANG H Z, FENG B, WANG X W, et al. Compressed sensing and its application in seismic explpration[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 467-474 |
| [16] | DO M N, VETTERLI M. The Contourlet transform:an efficient directional multiresolution image representation[J]. IEEE Transaction on Image Processing, 2005, 14(12): 2091-2106 DOI:10.1109/TIP.2005.859376 |
| [17] |
徐旋, 赵亮, 张翠芳. 非下采样Contourlet自适应的地震信号插值方法[J].
西南科技大学学报, 2012, 27(1): 70-73 XU X, ZHAO L, ZHANG C F. Adaptive of non-subsampled Contourlet transform for seismic data interpolating[J]. Journal of Southwest University of Science and Technology, 2012, 27(1): 70-73 |
| [18] | SHAN H, MA J, YANG H. Comparisons of wavelets, contourlets and curvelets in seismic denoising[J]. Journal of Applied Geophysics, 2009, 69(2): 103-115 DOI:10.1016/j.jappgeo.2009.08.002 |
| [19] | WEN X, ZHOU D, HE Z. Impedance inversion based on basis pursuit decomposition and contourlet transform[J]. Expanded Abstracts of 84th Annual Internat SEG Mtg, 2014: 3211-3215 |
| [20] | CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30 DOI:10.1109/MSP.2007.914731 |
| [21] | BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121 DOI:10.1109/MSP.2007.4286571 |
| [22] | BARANIUK R, DAVENPORT M, DEVORE R, et al. A simple proof of the restricted isometry property for random matrices[J]. Constructive Approximation, 2008, 28(3): 253-263 DOI:10.1007/s00365-007-9003-x |
| [23] |
周亚同, 刘志峰, 张志伟. 形态分量分析框架下基于DCT与曲波字典组合的地震信号重建[J].
石油物探, 2015, 54(5): 560-568, 581 ZHOU Y T, LIU Z F, ZHANG Z W. Seismic signal reconstruction under the morphological component analysis framework combined with DCT and Curvelet dictionary[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 560-568, 581 |
| [24] |
刘伟, 曹思远, 崔震. 基于压缩感知和TV准则约束的地震资料去噪[J].
石油物探, 2015, 54(2): 180-187 LIU W, CAO S Y, CUI Z. Random noise attenuation based on compressive sensing and TV rule[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 180-187 |
| [25] | DONOHO D L. For most large underdetermined systems of linear equations, the minimal L1-norm near-solution approximates the sparsest near-solution[J]. Communications on Pure & Applied Mathematics, 2006, 59(6): 797-829 |
| [26] | LI Q, GAO J. Contourlet based seismic reflection data non-local noise suppression[J]. Journal of Applied Geophysics, 2013, 95(9): 16-22 |
| [27] |
王升超, 韩立国, 巩向博. 基于各向异性Radon变换的叠前地震数据重建[J].
石油物探, 2016, 55(6): 808-815 WANG S C, HAN L G, GONG X B. Prestack seismic data reconstruction by anisotropic Radon transform[J]. Geophysical Prospecting for Petroleum, 2016, 55(6): 808-815 |
| [28] | PEREZ D O, VELIS D R, SACCHI M D. High-resolution prestack seismic inversion using a hybrid FISTA least-squares strategy[J]. Geophysics, 2013, 78(5): R185-R195 DOI:10.1190/geo2013-0077.1 |
| [29] | DAUBECHIES I, DEFRISE M, MOL C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure & Applied Mathematics, 2004, 57(11): 1413-1457 |


