2. 南方科技大学, 广东深圳 518055
2. Southern University of Science and Technology, Shenzhen 518055, China
复杂的近地表环境对地震波传播特性影响显著, 地形特征对地震波能量的放大与衰减具有重要作用[1]。实际观察与数值模拟分析发现, 2008年汶川地震中山脊对地震波能量的放大作用是造成一些地区受灾严重的主要原因[2-3]。地震面波作为近地表波场中重要组成成分, 在大地震中对地表造成破坏的同时, 也提供了一种了解地球内部结构的重要手段。了解地震面波在复杂地形条件下的传播特性, 不仅可以为防灾减损提供建议, 也可以指导面波勘探观测系统设计, 尽量避开不利地形[4-5], 或者进行面波噪声压制[6]。
关于面波地形效应的研究已有很多, KNOPOFF[7]和FUJII[8]通过实验观测研究了瑞雷面波通过楔形地形时反射系数和透射系数的影响因素; HUDSON等[9]与MAL等[10]从理论上研究了楔形地形对瑞雷面波反射系数和透射系数的影响; 陈伟等[4]采用势函数方法模拟并讨论了正、负楔形体角度对瑞雷面波传播特征的影响; 周红等[11]采用局域离散波数法探讨了瑞雷面波穿过凹陷地形时能量、频率等参数的变化; 汪利民[12]采用交错网格有限差分法并结合声学/弹性界面近似与阶梯近似起伏地形方法对瑞雷面波传播特征进行模拟分析, 并且讨论了不同陡峭程度的起伏地形对瑞雷面波传播特性的影响[13];巴振宁等[14-15]采用间接边界元方法对瑞雷面波入射含凸起与凹陷层状地层模型的响应进行分析; 刘中宪等[16]采用有限元-间接边界积分耦合方法, 对盆山耦合地形二维P波、P-SV波和瑞雷面波的散射波场进行了模拟研究。
当模型简单时, 可采用解析或半解析方法求解面波记录。该方法计算量较小且可以获得较准确的解, 但当复杂模型时, 如存在起伏地表或低速体等情况则方法的适应性较差, 所以需要采用对模拟区域格点离散的数值模拟技术[17-18]。采用格点离散方式进行近地表波场模拟关键是如何实现地表处的自由边界条件。有限元方法网格划分灵活, 自由边界条件实现也比较容易、直接, 但其计算量较大; 而有限差分法求解波动方程实现较容易且计算量适中。但若采用矩形网格则需要对起伏地表进行阶梯状近似, 要用较大的网格密度来压制地表处网格散射[19]。曲线网格为解决起伏地表问题提供了一个有效手段[20-21]。
本文采用曲线网格有限差分方法研究了瑞雷面波通过起伏地形时的传播特性。首先介绍了曲线网格有限差分法结合牵引力镜像法处理起伏自由地表的模拟方法; 然后讨论了地形的凹凸、高(深)度、跨度等对瑞雷面波波形、能量、频散等参数的影响。
1 方法原理起伏地形网格剖分拟合有两种方式:一是ROBERTSSON[19]所采用的阶梯状网格近似方式, 汪利民[12]结合声学/弹性界面近似与Robertsson方法对面波传播特征进行模拟分析; 二是通过网格变换方式, 采用曲线网格来拟合地形的起伏, 从而避免了阶梯状近似方法需大量格点压制虚假散射问题[22]。
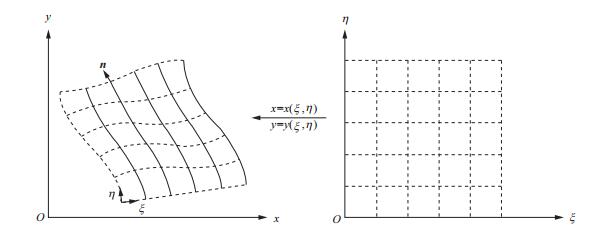
本文采用张伟[20]提出的曲线网格(图 1), 该网格可以很好地拟合起伏地形。其思想是在物理空间内采用与物理边界重合的曲线网格进行离散, 然后将网格坐标变换到均匀的计算网格空间, 最后在计算网格空间对波动方程进行求解。
|
图 1 曲线网格坐标变换示意[20] |
在二维笛卡尔坐标系中, 一阶速度-应力P-SV波动方程表达式为:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} = \mathit{\boldsymbol{A}}\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial x}} + \mathit{\boldsymbol{B}}\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial y}} + \mathit{\boldsymbol{F}} $ | (1) |
式中:U为速度-应力矢量; F为震源项; A, B为系数矩阵。
| $ \mathit{\boldsymbol{U}} = {\left( {{v_x},{v_y},{\sigma _{xx}},{\sigma _{yy}},{\sigma _{xy}}} \right)^{\rm{T}}} $ | (2) |
| $ \mathit{\boldsymbol{F}} = {\left( {\frac{{{f_x}}}{\rho },\frac{{{f_y}}}{\rho }, - {\mathit{\boldsymbol{M}}_{xx,t}}, - {\mathit{\boldsymbol{M}}_{yy,t}}, - {\mathit{\boldsymbol{M}}_{xy,t}}} \right)^{\rm{T}}} $ | (3) |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&0&{\frac{1}{\rho }}&0&0\\ 0&0&0&0&{\frac{1}{\rho }}\\ {\lambda + 2\mu }&0&0&0&0\\ \lambda &0&0&0&0\\ 0&\mu &0&0&0 \end{array}} \right] $ | (4) |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{\frac{1}{\rho }}\\ 0&0&0&{\frac{1}{\rho }}&0\\ 0&\lambda &0&0&0\\ 0&{\lambda + 2\mu }&0&0&0\\ \mu &0&0&0&0 \end{array}} \right] $ | (5) |
其中, vx, vy为速度分量; σxx, σyy, σxy为应力分量; T表示矩阵转置; fx, fy为体力项; Mxx, Myy, Mxy分别为地震矩张量; ρ为密度; λ, μ为拉梅常数。
物理空间与计算空间的坐标映射方程为:
| $ \begin{array}{l} x = x\left( {\xi ,\eta } \right)\\ y = y\left( {\xi ,\eta } \right) \end{array} $ | (6) |
式中:(x, y)为物理空间坐标; (ξ, η)为计算空间坐标。通过链式求导法则, 可得到在计算空间坐标系中P-SV波动方程表达式:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} = \mathit{\boldsymbol{\tilde A}}\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial \xi }} + \tilde B\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial \eta }} + \mathit{\boldsymbol{F}} $ | (7) |
其中, 系数矩阵
| $ \mathit{\boldsymbol{\tilde A}} = \left[ {\begin{array}{*{20}{c}} 0&0&{\frac{{{\xi _{,x}}}}{\rho }}&0&{\frac{{{\xi _{,y}}}}{\rho }}\\ 0&0&0&{\frac{{{\xi _{,y}}}}{\rho }}&{\frac{{{\xi _{,x}}}}{\rho }}\\ {{\xi _{,x}}\left( {\lambda + 2\mu } \right)}&{{\xi _{,y}}\lambda }&0&0&0\\ {{\xi _{,x}}\lambda }&{{\xi _{,y}}\left( {\lambda + 2\mu } \right)}&0&0&0\\ {{\xi _{,y}}\mu }&{{\xi _{,x}}\mu }&0&0&0 \end{array}} \right] $ | (8) |
| $ \mathit{\boldsymbol{\tilde B}} = \left[ {\begin{array}{*{20}{c}} 0&0&{\frac{{{\eta _{,x}}}}{\rho }}&0&{\frac{{{\eta _{,y}}}}{\rho }}\\ 0&0&0&{\frac{{{\eta _{,y}}}}{\rho }}&{\frac{{{\eta _{,x}}}}{\rho }}\\ {{\eta _{,x}}\left( {\lambda + 2\mu } \right)}&{{\eta _{,y}}\lambda }&0&0&0\\ {{\eta _{,x}}\lambda }&{{\eta _{,y}}\left( {\lambda + 2\mu } \right)}&0&0&0\\ {{\eta _{,y}}\mu }&{{\eta _{,x}}\mu }&0&0&0 \end{array}} \right] $ | (9) |
交错网格是目前地震波数值模拟中比较流行的网格结构, 但其在自由界面格点处应力或速度分量缺失, 需要在该格点处进行插值等处理, 因而降低了计算精度。而本文所采用的曲线网格是基于同位网格, 可很好地避免这一点, 本文空间差分采用低频散低耗散的DRP/opt MacCormack(Dispersion Relation Preserving/optimized MacCormack)格式[23]:
| $ \left\{ \begin{array}{l} L_\xi ^F\left( {{\mathit{\boldsymbol{U}}_i}} \right) = \frac{1}{{\Delta \xi }}\sum\limits_{n = - 1}^3 {{a_n}{\mathit{\boldsymbol{U}}_{i + n}}} \\ L_\xi ^B\left( {{\mathit{\boldsymbol{U}}_i}} \right) = \frac{{ - 1}}{{\Delta \xi }}\sum\limits_{n = - 1}^3 {{a_n}{\mathit{\boldsymbol{U}}_{i - n}}} \end{array} \right. $ | (10) |
式中:LξF为前向差分算子; LξB为后向差分算子; an为系数, 其中, a-1=-0.3087, a0=-0.6326, a1=1.2330, a2=0.3334, a3=0.04168。在ξ和η两个方向求导可任意采用上述两种差分格式之一, 例如同时采用前向差分求解(7)式等号右项, 记为:
| $ {{\hat L}^{FF}} = \mathit{\boldsymbol{\tilde A}}L_\xi ^F\left( \mathit{\boldsymbol{U}} \right) + \mathit{\boldsymbol{\tilde B}}L_\eta ^F\left( \mathit{\boldsymbol{U}} \right) + \mathit{\boldsymbol{F}} $ | (11) |
这里,
在时间迭代过程中, 采用了四阶精度的Runge-Kutta格式[24]。为避免偏心差分算子带来的频散和不稳定性, 在Runge-Kutta格式中交替使用前向与后向差分格式:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{k}}^1} = {{\hat L}^{FF}}\left( {{\mathit{\boldsymbol{U}}^n}} \right)\\ {\mathit{\boldsymbol{k}}^2} = {{\hat L}^{BB}}\left( {{\mathit{\boldsymbol{U}}^n} + \Delta t{\alpha _2}{\mathit{\boldsymbol{k}}^1}} \right)\\ {\mathit{\boldsymbol{k}}^3} = {{\hat L}^{FF}}\left( {{\mathit{\boldsymbol{U}}^n} + \Delta t{\alpha _3}{\mathit{\boldsymbol{k}}^2}} \right)\\ {\mathit{\boldsymbol{k}}^4} = {{\hat L}^{BB}}\left( {{\mathit{\boldsymbol{U}}^n} + \Delta t{\alpha _4}{\mathit{\boldsymbol{k}}^3}} \right)\\ {\mathit{\boldsymbol{U}}^{n + 1}} = {\mathit{\boldsymbol{U}}^n} + \Delta t\sum\limits_{i = 1}^4 {{\beta _i}{\mathit{\boldsymbol{k}}^i}} \end{array} \right. $ | (12) |
其中, 系数α2=0.5, α3=0.5, α4=1.0;β1=1/6, β2=1/3, β3=1/3, β4=1/6。为方便讨论, 将(12)式简写为:
| $ {\mathit{\boldsymbol{U}}^{n + 1}} = {{\hat L}^{BB}}{{\hat L}^{FF}}{{\hat L}^{BB}}{{\hat L}^{FF}}{\mathit{\boldsymbol{U}}^n} $ | (13) |
对前向和后向差分的各种选择, (13)式有多种组合方式, 本文在时间迭代过程中采用了4个计算时间步长为一个循环的处理方式:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{U}}^{n + 1}} = {{\hat L}^{BB}}{{\hat L}^{FF}}{{\hat L}^{BB}}{{\hat L}^{FF}}{\mathit{\boldsymbol{U}}^n}\\ {\mathit{\boldsymbol{U}}^{n + 2}} = {{\hat L}^{FB}}{{\hat L}^{BF}}{{\hat L}^{FB}}{{\hat L}^{BF}}{\mathit{\boldsymbol{U}}^{n + 1}}\\ {\mathit{\boldsymbol{U}}^{n + 3}} = {{\hat L}^{FF}}{{\hat L}^{BB}}{{\hat L}^{FF}}{{\hat L}^{BB}}{\mathit{\boldsymbol{U}}^{n + 2}}\\ {\mathit{\boldsymbol{U}}^{n + 4}} = {{\hat L}^{BF}}{{\hat L}^{FB}}{{\hat L}^{BF}}{{\hat L}^{FB}}{\mathit{\boldsymbol{U}}^{n + 3}} \end{array} \right. $ | (14) |
LEVANDER[25]首先在交错网格中采用应力镜像法对水平自由地表进行处理, 但该方法并不适应于任意曲线网格。ZHANG等[26]将该思想引入到贴体网格中并提出牵引力镜像法, 解决了曲线网格中起伏地表自由边界条件处理问题。当网格在自由地表处正交时, 牵引力镜像法可以退化为应力镜像法[20-21]。本文采用ZHANG等[26]提出的牵引力镜像法来实现自由边界条件。
1) 速度导数求取。在地表自由边界处, 要求地表外法向牵引力T为零, 即:
| $ \mathit{\boldsymbol{T}} = \mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{\sigma }} = 0 $ | (15) |
式中:n为地表某点的法向矢量; σ为点的应力张量。将(7)式代入(15)式整理后可得:
| $ \left[ {\begin{array}{*{20}{c}} {{v_{x,\eta }}}\\ {{v_{y,\eta }}} \end{array}} \right] = - {\mathit{\boldsymbol{X}}^{ - 1}}\mathit{\boldsymbol{Y}}\left[ {\begin{array}{*{20}{c}} {{v_{x,\xi }}}\\ {{v_{y,\xi }}} \end{array}} \right] $ | (16) |
矩阵X, Y的具体表达式为:
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {\chi {\eta _{,x}}{\eta _{,x}} + \mu {\eta _{,y}}{\eta _{,y}}}&{\lambda {\eta _{,x}}{\eta _{,y}} + \mu {\eta _{,y}}{\eta _{,x}}}\\ {\lambda {\eta _{,y}}{\eta _{,x}} + \mu {\eta _{,x}}{\eta _{,y}}}&{\chi {\eta _{,y}}{\eta _{,y}} + \mu {\eta _{,x}}{\eta _{,x}}} \end{array}} \right] $ | (17) |
| $ \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {\chi {\eta _{,x}}{\xi _{,x}} + \mu {\eta _{,y}}{\xi _{,y}}}&{\lambda {\eta _{,x}}{\xi _{,y}} + \mu {\eta _{,y}}{\xi _{,x}}}\\ {\lambda {\eta _{,y}}{\xi _{,x}} + \mu {\eta _{,x}}{\xi _{,y}}}&{\chi {\eta _{,y}}{\xi _{,y}} + \mu {\eta _{,x}}{\xi _{,x}}} \end{array}} \right] $ | (18) |
其中, χ=λ+2μ。
由(16)式可以看出, 自由地表网格层速度的η方向导数可以通过速度ξ方向导数获得。对于地表下两层网格, 为避免使用地表以上虚拟格点上的速度值, 本文采用4/4-MacCormack紧致差分格式[27]。
2) 应力分量导数的求取。由于在自由地表处格点上牵引力为零:
| $ \left\{ \begin{array}{l} {T_x}\left| {_{{j_f}}} \right. = 0\\ {T_y}\left| {_{{j_f}}} \right. = 0 \end{array} \right. $ | (19) |
利用牵引力镜像法, 自由地表以上3层格点上的应力值可以通过(20)式得到:
| $ \left\{ \begin{array}{l} {T_x}\left| {_{{j_f} + j}} \right. = {T_x}\left| {_{{j_f} - j}} \right.\\ {T_y}\left| {_{{j_f} + j}} \right. = {T_y}\left| {_{{j_f} - j}} \right. \end{array} \right. $ | (20) |
式中:jf为自由地表处对应的η方向格点坐标, j=1, 2, 3。在文献[26]中详细讨论对比了采用牵引力镜像法处理起伏自由地表的结果与边界元等方法得到的结果, 验证了该方法的准确性, 本文采用该方法研究地形效应对面波传播过程的影响。
另外, 吸收边界处理方式是影响长时程面波模拟稳定性的一个重要因素。这里我们采用的是ZHANG等[28]提出的ADE CFS-PML(Auxiliary Differential Equation Complex Frequency Shifted Perfectly Matched Layer)吸收边界。该方法分析了PML吸收层内的自由表面情况, 修改PML方程以满足吸收层的自由表面条件, 消除了PML层和自由地表条件不相容导致的不稳定问题。
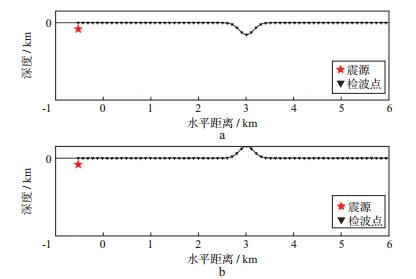
2 地形效应模拟与分析 2.1 模型设计模型设计的目的是为了讨论地形不同的深(高)度和跨度对面波传播特性的影响。本文所采用的介质为泊松体, 其纵波速度vP=4000m/s, 横波速度vS=2310m/s, 密度ρ=2300kg/m3, 瑞雷波速度vR≈2123m/s; 采用炸药震源, 地震子波为Ricker子波, 主频为20Hz。为了充分激发面波, 震源位于地表附近(-500m, -80m)处, 距地形起伏处有一定距离。这样可以使瑞雷波与P波能够充分分离, 方便时间窗口截取瑞雷波进行后续讨论; 地表检波器排列间距为20m, 如图 2所示。网格离散空间步长Δx≈5m, 离散最小波长所用格点数约为8.5。但由于曲线网格存在一定扭曲, 最大空间步长约为5.75m, 最小空间步长约为4.25m;时间步长Δt=0.5ms。
|
图 2 高斯形谷模型(a)与高斯形山模型(b) |
模型的水平距离为7km, 深度为1km。地形采用高斯形山(谷)模型, 其计算公式为:
| $ D = \pm {D_0}\exp \left[ { - \frac{{{{\left( {x - {x_0}} \right)}^2}}}{{2{w^2}}}} \right] $ | (21) |
式中:D0为控制起伏程度(高度或深度); w为控制水平宽度参数(跨度); x0=3km为起伏地形中心位置; “±”中的“+”表示山形地形, “-”表示谷形地形。以D0=150m, w=150m为例, 其形态如图 2所示。采用高斯形山(谷)模型主要是为了使自由表面从水平地形到山(谷)体平滑过渡, 避免采用圆形或多边形(三角形或梯形)模型在过渡区域的拐点。当面波通过拐点时, 会产生很强的散射现象, 模拟结果可能会影响到面波传播规律的讨论。
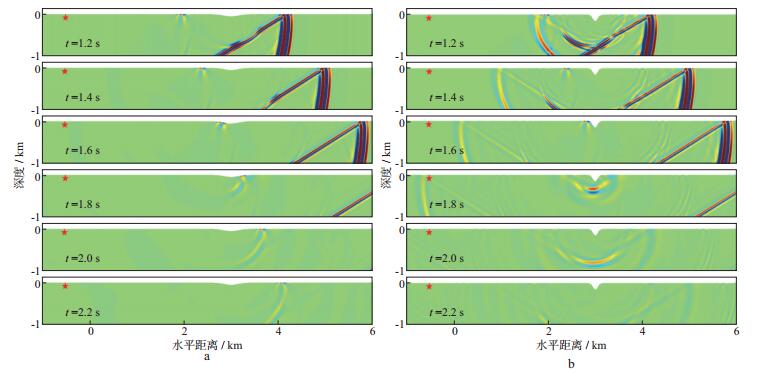
2.2 凹陷模型结果对不同深度(25~150m, 间隔25m)和跨度(50~150m, 间隔25m)共计30个凹陷模型进行模拟。图 3显示了其中两种情形(D0=50m, w=150m;D0=150m, w=50m)的波场快照, 可以看出, 不同的深度和跨度凹陷地形对面波波场传播的影响。当地形较为平缓时(图 3a), 面波穿过地形畸变较小, 但会产生转换波(P波和S波)向下传播; 当地形较为陡峭时(图 3b), 面波在地形凹陷处产生很强的散射现象, 并且出现反射面波, 透射面波能量出现显著衰减, 转换波能量较强。在实际地震勘探中, 如果地表起伏较为剧烈, 向下方传播的面波转换波也可能是造成波场复杂的一个重要原因。图 4为不同的深度和跨度凹陷地形附近(1~5km)截取的面波地震记录(1.5~3.0s)。当地形较为陡峭时, 可以看到清晰的反射面波和透射面波以及转换波(散波P波和S波)(图 4b)。
|
图 3 不同深度和跨度凹陷地形模型波场快照(vx分量) a D0=50m, w=150m; b D0=150m, w=50m |
|
图 4 凹陷地形地表处面波的地震记录(vx分量) a D0=50m, w=150m; b D0=150m, w=50m |
在凹陷地形两侧面波与散射波传播较为稳定处取两点(1km与5km处), 分别计算反射和透射面波能量, 来讨论地形对面波能量分配的影响。面波能量计算公式为:
| $ E = {A_0}\int_{{t_1}}^{{t_2}} {\left[ {v_x^2\left( t \right) + v_y^2\left( t \right)} \right]{\rm{d}}t} $ | (22) |
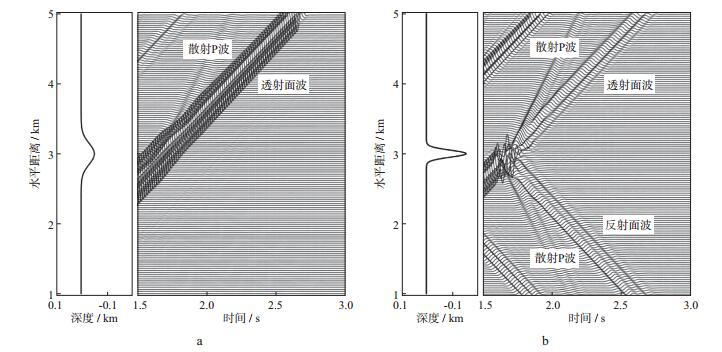
式中:vx(t)和vy(t)为速度分量, 面波波形位于时间[t1, t2]区间内, 区间长度略大于面波波形长度; A0为归一化系数; E为所求面波能量。图 5中所示红框为计算直达瑞雷面波和反射瑞雷面波的时间区间, 其中二次瑞雷面波为来自与P波经过地形时产生的散射瑞雷面波。
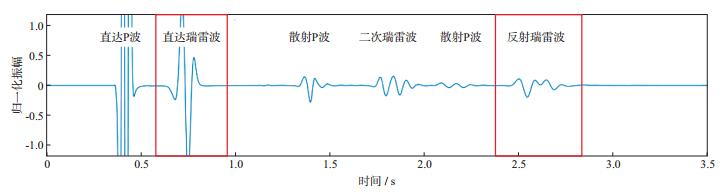
|
图 5 面波波形截取 D0=150m, w=50m模型vx分量地震记录, 检波点位于(1km, 0)处 |
图 6显示了经过不同的深度和跨度凹陷地形面波能量分配情况, 可以看出, 对于相同的高度, 随跨度的减小反射面波能量逐渐增强(图 6a), 透射面波能量逐渐减弱(图 6b), 转换波能量呈整体逐渐增强趋势(转换波能量为入射面波减去反射面波和透射面波能量)(图 6c); 而对于相同的跨度(图 6a, 图 6b, 图 6c), 随高度的增加, 同样出现反射面波能量增强、透射面波能量逐渐减弱和转换波能量增强的现象。值得注意的是, 当深度大于某个数值时(100m, 与波长相关), 转换波能量随跨度减小而略微减小, 主要原因是反射面波急剧增强分配了部分能量。图 7给出了1km与5km处反射与透射面波的频谱, 可以看出, 地形对面波具有滤波效应, 体现为反射和透射面波频谱上出现陷波点。其陷波点频率受深度和跨度的影响, 当深度与跨度增加时, 陷波点向低频移动。
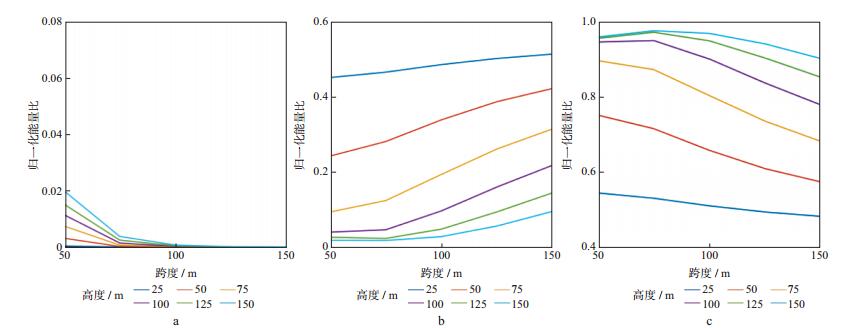
|
图 6 经过凹陷地形后面波能量变化 a反射面波能量; b透射面波能量; c转换波能量 |
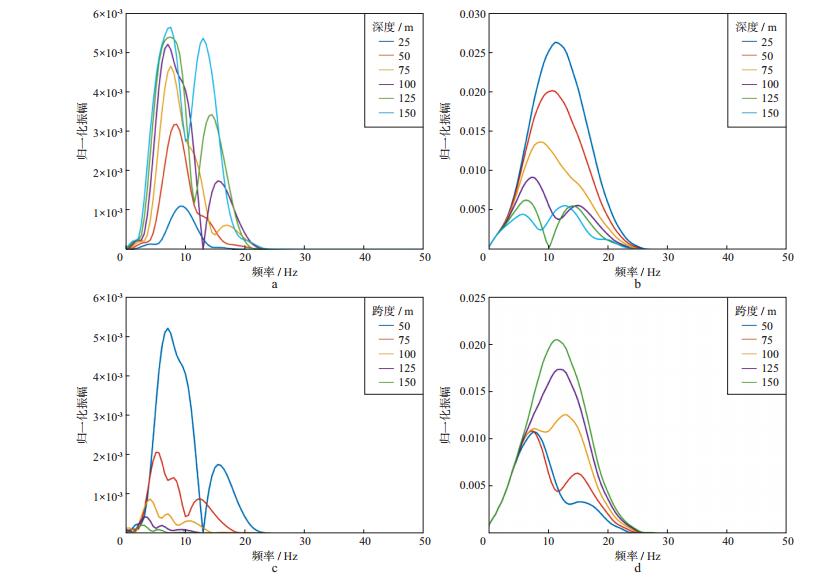
|
图 7 反射面波与透射面波频谱(凹陷地形) a反射面波频谱(跨度50m); b透射面波频谱(跨度50m); c反射面波频谱(深度100m); d透射面波频谱(深度100m) |
为讨论不同高度和跨度的凸起地形对面波传播的影响, 我们共设计30个凸起模型进行模拟(高度为25~150m, 跨度为50~150m, 间隔25m), 介质参数和震源参数与凹陷地形模型相同, 其中两种情形的波场快照如图 8所示。图 9为凸起地形地表处面波的地震记录。从图 9可以看出, 当地形较为平缓时, 对面波传播影响较小(图 9a), 但也会产生向下传播的转换波; 当地形变化较为剧烈时, 其波场变得较为复杂, 并产生反射面波和透射面波以及转换波(图 9b)。
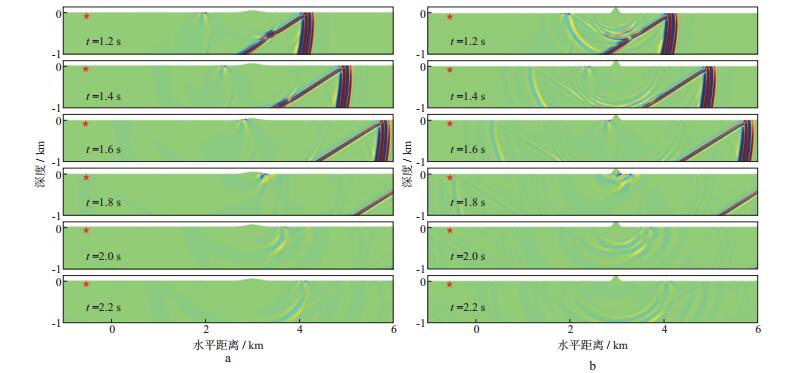
|
图 8 不同深度和跨度凸起地形模型波场快照(vx分量) a D0=50m, w=150m; b D0=150m, w=50m |
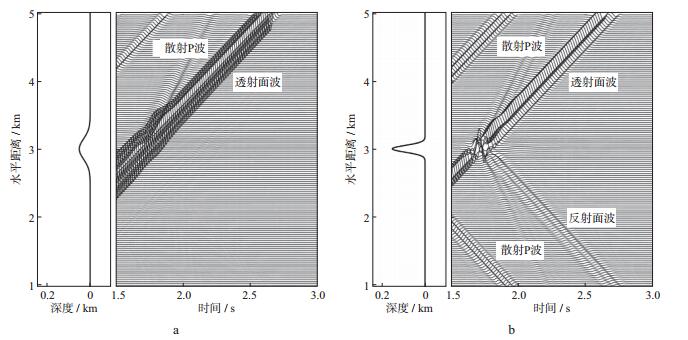
|
图 9 凸起地形地表处面波的地震记录(vx分量) a D0=50m, w=150m; b D0=150m, w=50m |
同样, 在面波与其散射波传播较为稳定的1km与5km两点处分析反射和透射面波能量的变化情况。图 10显示了经过凸起地形的面波能量变化情况, 可以看出, 影响能量分配的受控因素较为复杂。整体看, 当跨度减小时, 其反射面波与转换能量增强, 透射面波能量减弱, 但当高度大于某个阈值(100m), 跨度小于某个阈值(75~100m)时, 情况出现反转。其原因是当跨度小于面波横向波长时, 面波可以不沿凸起地形表面传播, 直接穿过凸起地形, 这与凹陷情形不同。
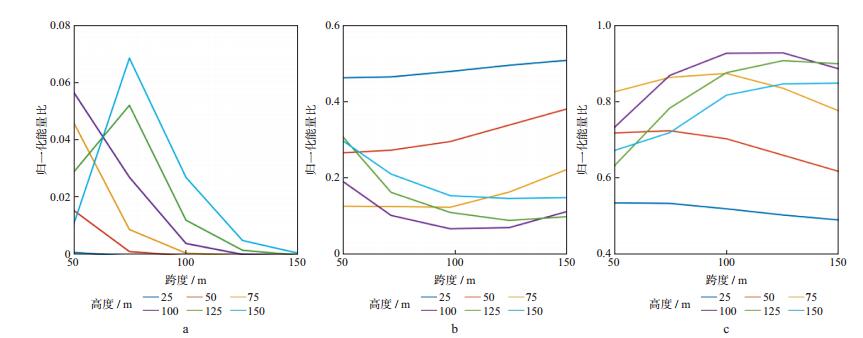
|
图 10 经过凸起地形后面波能量变化 a反射面波能量; b透射面波能量; c转换波能量 |
图 11显示了1km与5km处反射面波和透射面波的频谱, 可以看出, 其形态变化也较为复杂。随着高度不同, 透射面波频谱出现了陷波现象, 其陷波点频率随高度增加有减小趋势(图 11b)。对于相同高度凸起地形(150m), 当跨度小于某个阈值时(50m), 其频谱形态产生本质变化, 其反射能量急剧减弱并出现陷波点(图 11c), 透射能量增强(图 11d)。
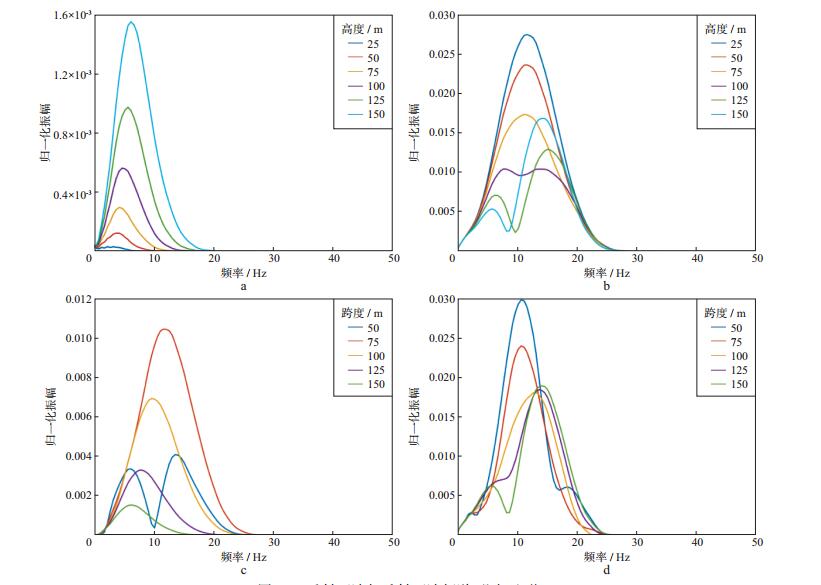
|
图 11 反射面波与透射面波频谱(凸起地形) a反射面波频谱(跨度150m); b透射面波频谱(跨度150m); c反射面波频谱(高度150m); d透射面波频谱(高度150m) |
本文采用贴体网格有限差分方法研究了瑞雷面波经过起伏地形时的传播特性, 讨论了地形的凹凸、高(深)度和跨度等因素对面波波形、能量、频散等参数的影响。
对于凹陷地形, 地表起伏平缓时, 面波可以平滑地绕过地形; 地表起伏剧烈时, 面波产生严重的散射现象。地形不仅对面波的高频部分有影响, 对低频部分还存在滤波效应, 表现为在频谱上出现陷波点, 陷波点的频率与地形的高度、跨度以及面波横向波长有一定关系。
对于凸起地形, 地表起伏平缓时对面波传播影响较小, 起伏剧烈时波场变得复杂; 当跨度较小、起伏较大时, 面波通过凸起地形的机理与凹陷地形不同, 而且表现形式更加复杂。凹陷地形表现为阻挡, 产生较强反射面波, 而凸起地形表现为面波直接穿过地形, 此时透射面波能量增大, 其能量分配规律与频谱表现也更加复杂。
从模拟结果看, 可能存在纯地形与瑞雷波能量陷波的经验关系, 我们将在下一步研究工作中讨论该问题。另外, 贴体网格有限差分方法结合牵引力镜像法可以很好地处理起伏地表问题, 为研究更复杂的近地表条件下地震波传播规律提供有效手段。
| [1] | WEN Y Y, MA K F, OGLESBY D D. Variations in rupture speed, slip amplitude and slip direction during the 2008 Mw 7.9 Wenchuan earthquake[J]. Geophysical Journal International, 2012, 190(1): 379-390 DOI:10.1111/gji.2012.190.issue-1 |
| [2] | SHEN Z K, SUN J, ZHANG P, et al. Slip maxima at fault junctions and rupturing of barriers during the 2008 Wenchuan earthquake[J]. Nature Geoscience, 2009, 2(10): 718-724 DOI:10.1038/ngeo636 |
| [3] | WEN J, CHEN X. Variations in f_max along the Ruptured Fault during the Mw 7.9 Wenchuan earthquake of 12 May 2008[J]. Bulletin of the Seismological Society of America, 2012, 102(3): 991-998 DOI:10.1785/0120110105 |
| [4] |
陈伟, 徐义贤, 张煜. 瑞雷面波在弹性楔状体中的传播特性研究[J].
工程地球物理学报, 2009, 6(2): 143-149 CHEN W, XU Y X, ZHANG Y. Study of transmission characteristics of Rayleigh waves on an elastic wedge[J]. Chinese Journal of Engineering Geophysics, 2009, 6(2): 143-149 |
| [5] |
沈鸿雁, 李庆春, 严月英, 等. 多道瞬态面波相速度分析[J].
石油物探, 2016, 55(5): 692-702 SHEN H Y, LI Q C, YAN Y Y, et al. Phase velocity analysis of multi-channel transient surface wave[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 692-702 |
| [6] |
岳龙, 刘怀山, 尹燕欣, 等. 基于连续小波变换的面波衰减方法研究[J].
石油物探, 2016, 55(2): 214-222 YUE L, LIU H S, YIN Y X, et al. Attenuation of ground roll based on continuous wavelet transform[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 214-222 |
| [7] | KNOPOFF L. Transmission and reflection of Rayleigh waves by wedges[J]. Geophysics, 1960, 25(6): 1203-1214 DOI:10.1190/1.1438807 |
| [8] | FUJⅡ K. Rayleigh-wave scattering at various wedge corners:investigation in the wider range of wedge angles[J]. Bulletin of the Seismological Society of America, 1994, 84(6): 1916-1924 |
| [9] | HUDSON J A, KNOPOFF L. Transmission and reflection of surface waves at a corner, 2, Rayleigh waves (theoretical)[J]. Journal of Geophysical Research Atmospheres, 1964, 69(2): 281-289 DOI:10.1029/JZ069i002p00281 |
| [10] | MAL A K, KNOPOFF L. Transmission of Rayleigh waves at a corner[J]. Bulletin of the Seismological Society of America, 1966, 56(2): 455-466 |
| [11] |
周红, 陈晓非. 凹陷地形对Rayleigh面波传播影响的研究[J].
地球物理学报, 2007, 50(4): 1182-1189 ZHOU H, CHEN X F. A study on the effect of depressed topography on Rayleigh surface wave[J]. Chinese Journal of Geophysics, 2007, 50(4): 1182-1189 |
| [12] |
汪利民. 起伏地表三维高频瑞雷面波传播特性研究[D]. 武汉: 中国地质大学, 2013
WANG L M.Propagation of high-frequency Rayleigh waves in 3d medium with topography[D]. Wuhan:China University of Geoscience, 2013 |
| [13] | WANG L M, XU Y X, XIA J H, et al. Effect of near-surface topography on high-frequency Rayleigh-wave propagation[J]. Journal of Applied Geophysics, 2015, 116: 93-103 DOI:10.1016/j.jappgeo.2015.02.028 |
| [14] |
巴振宁, 梁建文. Rayleigh波斜入射下层状场地中凸起地形的三维响应分析[J].
中国科学:技术科学, 2015, 45(8): 874-888 BA Z N, LIANG J W. Three dimensional responses of a hill in a layered half-space for obliquely incident Rayleigh waves[J]. Scientia Sinica Techolgica, 2015, 45(8): 874-888 |
| [15] |
巴振宁, 梁建文. 层状场地中凹陷地形Rayleigh波斜入射下三维地震响应分析[J].
振动工程学报, 2015, 28(5): 809-821 BA Z N, LIANG J W. 3-D seismic responses for oblique incident Rayleigh waves of a canyon cut in a layered half-space[J]. Journal of Vibration Engineering, 2015, 28(5): 809-821 |
| [16] |
刘中宪, 武凤娇, 王冬. 沉积盆地-山体耦合场地对平面P波、SV波和Rayleigh波的二维散射分析[J].
工程力学, 2016, 33(2): 160-171 LIU Z X, WU F J, WANG D. Two dimensional scattering analysis of plane P, SV, and Rayleigh waves by coupled alluvial basin-mountain terrain[J]. Engineering Mechanics, 2016, 33(2): 160-171 |
| [17] |
朱多林, 白超英. 基于波动方程理论的地震波场数值模拟方法综述[J].
地球物理学进展, 2011, 26(5): 1588-1599 ZHU D L, BAI C Y. Review on the seismic wavefield forward modelling[J]. Progress in Geophysics, 2011, 26(5): 1588-1599 |
| [18] |
张明财, 熊章强, 张大洲. 基于MPI的三维瑞雷面波有限差分并行模拟[J].
石油物探, 2013, 52(4): 354-362 ZHANG M C, XIONG Z Q, ZHANG D Z. 3D finite difference parallel simulation of Rayleigh wave based on message passing interface[J]. Geophysical Prospecting for Petroleum, 2013, 52(4): 354-362 |
| [19] | ROBERTSSON J O A. A numerical free-surface condition for elastic/viscoelastic finite-difference modeling in the presence of topography[J]. Geophysics, 1996, 61(6): 1921-1934 DOI:10.1190/1.1444107 |
| [20] |
张伟. 含起伏地形的三维非均匀介质中地震波传播的有限差分算法及其在强地面震动模拟中的应用[D]. 北京: 北京大学, 2006
ZHANG W.Finite difference seismic wave modelling in 3D heterogeneous media with surface topography and its implementation in strong ground motion study[D]. Beijing:Peiking University, 2006 |
| [21] |
丘磊. 正交曲线坐标系下的地震波数值模拟技术研究[D]. 杭州: 浙江大学, 2011
QIU L.Study on seismic wave simulations in orthogonal curvilinear coordinate system[D]. Hangzhou:Zhejiang University, 2011 |
| [22] |
裴正林. 任意起伏地表弹性波方程交错网格高阶有限差分法数值模拟[J].
石油地球物理勘探, 2004, 39(6): 629-634 PEI Z L. Numerical modeling using staggered-grid high-order finite-difference of elastic wave equation on arbitrary relief surface[J]. Oil Geophysical Prospecting, 2004, 39(6): 629-634 |
| [23] | HIXON R.On increasing the accuracy of MacCormack schemes for aeroacoustic applications[J/OB]. AIAA, 1997:1-33[2017-05-12]. https://www.researchgate.net/publication/24298166 |
| [24] | HU F Q, HUSSAINI M Y, MANTHEY J L. Low-dissipation and low-dispersion runge-kutta schemes for computational acoustics[J]. Journal of Computational Physics, 1996, 124(1): 177-191 DOI:10.1006/jcph.1996.0052 |
| [25] | LEVANDER A R. Fourth-order finite-difference P-SV seismograms[J]. Geophysics, 1988, 53(11): 1425-1436 DOI:10.1190/1.1442422 |
| [26] | ZHANG W, CHEN X. Traction image method for irregular free surface boundaries in finite difference seismic wave simulation[J]. Geophysical Journal International, 2006, 167(1): 337-353 DOI:10.1111/gji.2006.167.issue-1 |
| [27] | LELE S K. Compact finite difference schemes with spectral-like resolution[J]. Journal of Computational Physics, 1992, 103(1): 16-42 DOI:10.1016/0021-9991(92)90324-R |
| [28] | ZHANG W, SHEN Y. Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling[J]. Geophysics, 2010, 75(4): T141-T154 DOI:10.1190/1.3463431 |


