储层静态建模实现了对地下地质体的三维定量表征, 是油藏评价、动态模拟和剩余油预测的技术基础, 其与地下实际情况的吻合程度直接影响油田的开发效果[1]。因此, 如何使地质模型更贴近地下的真实情况, 即提高储层静态建模的精度, 一直是国内外学者研究的重点之一。
构造建模是储层静态建模的主要手段之一, 1989年MALLET[2]采用离散光滑插值方法实现了构造建模; 针对复杂构造建模的需求, 1998年EULER[3]提出了表征断层和层面空间拓扑关系的解决方案; 杨钦等[4]将Delaunary三角剖分算法应用于构造建模; 魏嘉等[5]提出了适用于复杂地质体的曲面拟合技术, 并发展了适应地层沉积特点的三维地层网格剖分方法; 孙波等[6]进一步完善了复杂地质界面的三维重构方法, 使其能更好地表征复杂地质体的结构。三维构造建模技术较为成熟, 随着层序地层学的发展, 结合层序地层建立表征地层尖灭、剥蚀和超覆等接触关系的层面框架模型成为研究重点。在明确地层接触关系之后, 根据不同的地层接触关系分别采用平行于顶面、平行于底面、在顶底间等比例插值这3种方法来垂向划分层面框架模型。董建华等[7]以地震解释的层序界面作为顶底约束, 通过倾角体的引导进行层间的垂向划分, 得到了等时的层序界面。属性模型表征了地下储层及流体, 其表征精度直接影响井位部署和开发效果, 因此属性建模方法也是国内外学者的研究重点。HALDORSON等[8]于1984年提出了基于井数据的储层随机建模方法; 1992年ARAKTINGI等[9]联合地震和测井资料进行了属性建模研究; 此后, YANG等[10]和TJOLSEN等[11]研究了采用地震反演约束属性建模的方法; DOYEN等[12]基于贝叶斯理论实现了地震约束的储层参数预测; 李绪宣等[13]基于地震属性的空间变化代表了储层的空间变化规律这一特点, 利用与储层参数相关性高的地震属性来取代变差函数, 提出了地震驱动建模方法, 提高了井网稀疏时储层参数预测的精度; 郭智等[14]将地震反演自然伽马和地质约束条件加入到建模过程中, 提高了井间储层参数预测精度; 胡勇等[15]采用地震反演数据约束储层参数建模, 以地震正演来验证地质模型的可靠性, 提高了建模精度。
当层间存在与顶、底面不一致的起伏变化, 尤其顶、底界面为不整合类型时, 上述方法难以得到等时的层面框架模型, 降低了构造模型的精度。地震驱动建模方法提高了井网稀疏时储层参数预测的精度, 但是没有解决三维地层网格模型不等时的问题。本文在地震驱动建模方法的基础上, 利用地震倾角体来引导垂向网格的划分, 建立等时的三维地层网格模型, 以井数据为已知点, 利用敏感地震属性的变化规律来估计井间储层参数, 形成基于地震等时格架的倾角导向储层静态建模方法。理论模型的数据测试和海上油田的实际应用表明, 该方法能进一步提高建模精度。
1 基本原理 1.1 倾角导向三维地层网格模型建立方法利用相干估计倾角扫描计算方法计算倾角体[16-17]。以倾角体为导向建立三维地层网格模型, 选择各小层种子点的时间(或深度)和局部倾角, 根据不同点之间倾角值的关系计算出小层下一点的时间(或深度)值, 采用这种逐点递推的方式完成小层的导向追踪。主要过程为:① 在断层模型的基础上, 以地震解释的层面作为关键层面; ② 以关键层面作为顶、底趋势面, 以顶、底面间的倾角体为导向, 对其内部的小层进行追踪内插; ③ 根据储层表征的需要, 在内插小层基础上, 以层间的倾角体为导向, 采用逐点递推计算的方式从起始点开始追踪小层内的网格层, 最后建立三维地层网格模型。
倾角导向小层追踪的具体算法为:
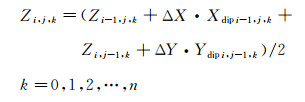
|
(1) |
式中:Zi, j, k表示(i, j)位置处第k层的深度; ΔX和ΔY分别为X和Y方向上的采样间隔; Xdip i, j, k和Ydip i, j, k分别为X方向和Y方向(i, j)位置处第k层的视倾角。
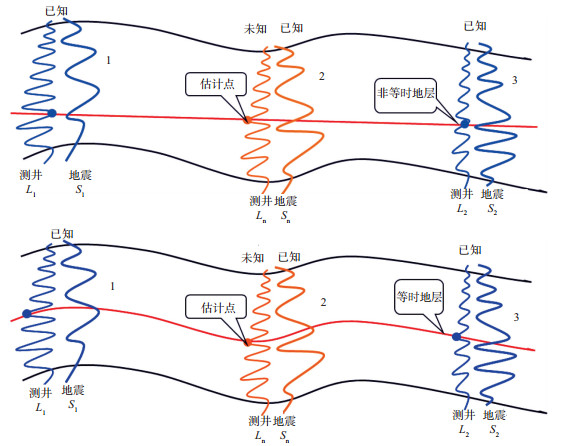
1.2 基于地震等时格架的储层静态建模方法反映相同地质体的地震属性和储层参数联系紧密[18], 因此对储层参数敏感的地震属性可以揭示储层参数的变化[19-21], 再联合已知井就可以定量预测储层参数值。基于地震等时格架的倾角导向储层静态建模方法的原理就基于此, 如图 1所示。已知点1, 2, 3处的地震属性(S1, Sn, S2)和点1, 3处的测井数据(L1, L2), 根据地震属性的空间变化规律预测点2处的储层参数值。在不等时的地层网格里提取数据时, 地震属性和测井数据之间的线性相关性差, 预测的储层参数值精度低。因此需要倾角导向建立的三维地层网格模型来约束, 非等时地层内的测井数据和地震属性不参与该地层的建模, 这样建模结果更准确。
|
图 1 基于地震等时格架倾角导向储层静态建模原理示意 |
根据地震属性的空间相关性:
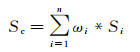
|
(2) |
式中:Sc代表未知点的地震属性; Si代表已知井的井旁道地震属性; ωi代表不同井点处的转换函数。井点处的地震数据和测井数据分别从不同尺度反映储层变化情况, 当地震属性与储层参数之间具有较好线性相关性时, 有:
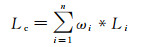
|
(3) |
式中:Lc为未知点的储层参数值; Li为已知井的储层参数值。
由(2) 式、(3) 式可知, 通过地震属性求取反映储层参数空间变化规律的转换函数, 结合已知井点的测井数据, 就可以预测出未知点的储层参数值, 不需要求取变差函数。其中, 转换函数的求取是实现基于地震等时格架倾角导向储层静态建模的关键。
采用多道最小化均方误差来求取转换函数ωi。以两口井为例介绍多道最小化均方误差计算转换函数的方法。这两口井分别对应两个转换函数ω1, j和ω2, j(j=0, 1, …, m)。k时刻的误差为:
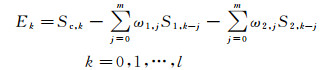
|
(4) |
平方误差为:
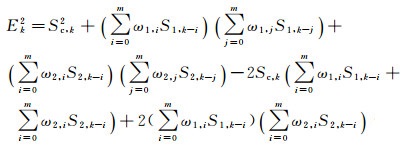
|
(5) |
总的平方误差为:
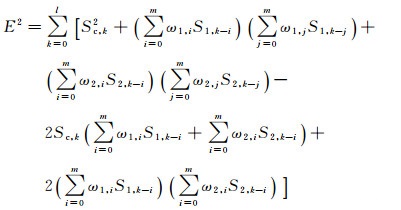
|
(6) |
当E2最小时有:
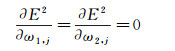
|
(7) |
E2对ω1, j和ω2, j分别求偏导, 得:
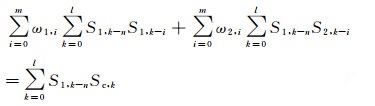
|
(8) |
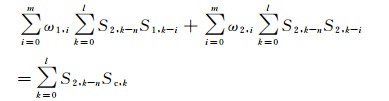
|
(9) |
利用互相关和相关计算来化简方程并求解, 得到转换函数ω1, j和ω2, j。多口井时上述过程同理扩展。
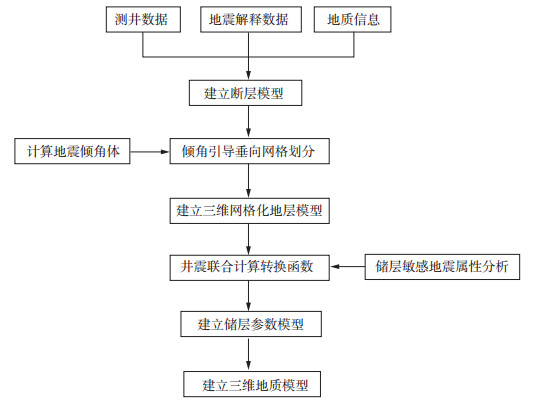
1.3 技术流程在三维地层网格模型不等时的情况下, 井震之间的线性相关性变差, 相当于用地震属性去预测非同一时期的储层参数, 预测精度下降。因此, 需要通过倾角导向建立一个等时的三维地层网格模型, 在其约束下, 提取的地震属性和测井数据才能反映同一时期沉积的储层, 敏感地震属性才能真正反映储层参数的变化, 从而取代变差函数, 有效避免变差函数在井较少或井网稀疏时难以得到稳定结果的缺点[13]。因此, 基于地震等时格架的倾角导向储层静态建模对井间储层参数预测的精度要高于地质统计学建模方法。主要步骤(图 2)如下:
|
图 2 基于地震等时格架的倾角导向储层静态建模技术流程 |
1) 根据断层数据建立断层模型, 基于地震数据计算地震倾角体, 在断层模型基础上, 利用倾角体引导建立三维地层网格模型;
2) 对测井数据进行质量检查, 确保无误后将建模用到的测井数据按照厚度加权的方法粗化到三维网格中;
3) 确定需要建立的储层参数模型, 寻找对该参数最敏感的地震属性, 将地震属性数据投影到三维地层网格模型中, 为建模做好准备;
4) 在一个等时的小层内提取层内的地震属性与井数据, 通过地震属性计算转换函数, 利用该函数从井出发估计层内未知点的储层参数值;
5) 根据步骤4) 对下一个等时小层内每个网格的储层参数值进行预测, 不断循环, 最终建立三维储层参数模型。
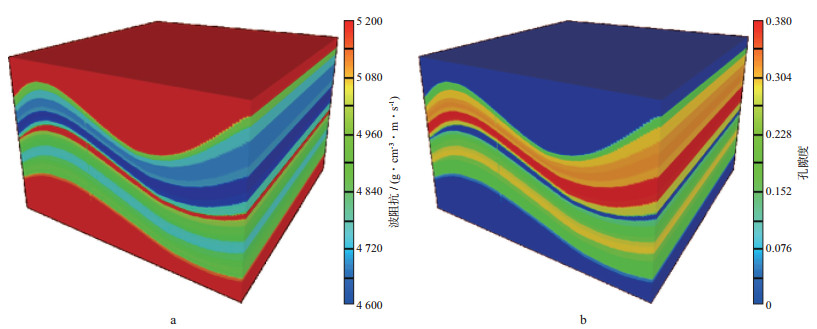
2 模型试验采用由一个背斜和一个向斜组成的褶皱构造模型对本文方法进行测试。沿褶皱构造方向划分为100个网格, 步长为10m;走向方向划分为5个网格, 步长为20m。纵向由19个小层组成, 划分为550个网格, 步长为1m。设定理论波阻抗对理论孔隙度有很高的敏感性, 将波阻抗作为基于地震等时格架倾角导向储层静态建模的地震数据。给每个小层填充孔隙度参数和波阻抗参数, 从而得到理论孔隙度三维模型和理论波阻抗三维模型(图 3)。参与孔隙度建模的井数据从理论孔隙度模型中抽取, 一共提取了4口井数据。
|
图 3 理论三维模型示意 a 理论波阻抗模型; b 理论孔隙度模型 |
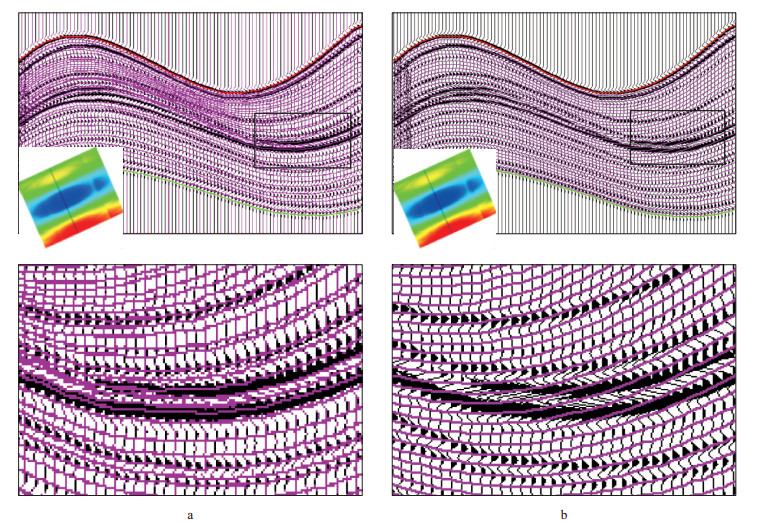
在采用50Hz雷克子波与理论模型褶积正演得到的地震数据中, 将解释为褶皱顶、底的层位作为关键层面。在地震剖面中拾取稳定连续的波峰为顶界面, 拾取稳定连续的波谷作为底界面, 对每条测线都进行解释。基于地震数据分别计算Inline方向和Xline方向的视倾角体, 其中Xline方向沿走向方向, 所以其视倾角值都为0。以解释的顶、底层位作为趋势面, 基于Inline方向和Xline方向计算的倾角体进行导向追踪细分, 得到细分后的网格层。地震反射同相轴具有等时意义, 将细分后的网格层与地震同相轴进行叠合对比, 分析其等时性。与地震同相轴一致的网格层等时性好; 与地震同相轴趋势不一致, 发生斜交的网格层不等时。图 4a和图 4b分别给出了采用倾角导向方法和线性等分方法细分的小层与地震剖面叠合结果。由图 4可以看到, 倾角导向细分的网格层等时性很好, 而线性等分的网格层在局部不等时。
|
图 4 细分小层与地震剖面叠合结果 a 倾角导向细分小层; b 线性等分小层 |
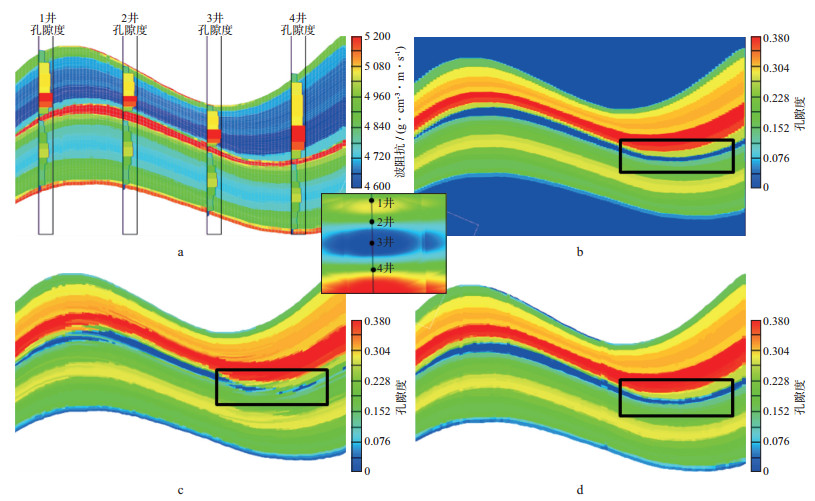
波阻抗从与网格无关的反演中得到, 将波阻抗和井数据重采样到倾角导向的三维网格中, 基于波阻抗的空间变化来预测孔隙度, 建立三维孔隙度模型。通过对比预测孔隙度与理论孔隙度来评价预测精度。图 5给出了理论波阻抗模型、理论孔隙度模型以及不同地层模型约束的孔隙度模型剖面。由图 5可以看出, 基于地震等时格架倾角导向储层静态建模的预测孔隙度分布和理论孔隙度基本一致, 预测精度很高。线性等分方法建立的三维地层网格模型存在局部穿时, 在其约束下地震驱动建立的孔隙度模型在地层模型穿时位置预测孔隙度值与理论孔隙度值差异较大(图 5中黑色框线内), 预测精度较低。
|
图 5 理论模型与不同地层模型约束的预测孔隙度模型剖面 a 理论波阻抗模型; b 理论孔隙度模型; c 线性等分地层格架地震驱动预测孔隙度模型; d 地震等时格架倾角导向储层静态建模预测孔隙度模型 |
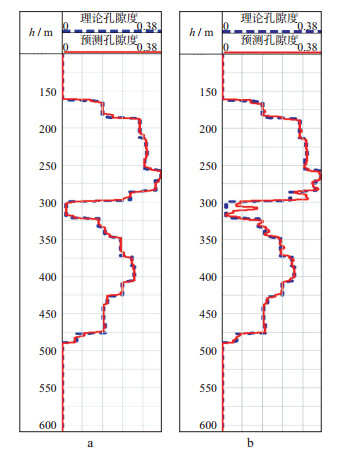
采用不参与建模的检验井来检验孔隙度模型的预测精度。将检验井设置在x=200m处, 对比该检验井的预测孔隙度与理论孔隙度。图 6给出了基于不同地层模型的预测孔隙度与理论孔隙度。由图 6可以看出, 在检验井处, 地震等时格架倾角导向储层静态建模预测的孔隙度与理论孔隙度的相对误差在5%以内, 两者几乎相同; 线性等分地层格架地震驱动模型的预测孔隙度与理论孔隙度的相对误差局部超过了10%。这是因为线性等分三维地层网格模型存在局部不等时, 导致了孔隙度模型预测精度下降。基于地震等时格架的倾角导向储层静态建模建立了等时的三维地层网格模型, 建立的孔隙度模型准确地预测了理论孔隙度值, 建模的精度有了进一步提高。
|
图 6 检验井处基于不同地层模型的预测孔隙度与理论孔隙度对比 a 地震等时格架倾角导向储层静态建模预测孔隙度模型; b 线性等分地层格架地震驱动预测孔隙度模型 |
A油田位于渤海湾地区, 为海上稠油油田, 主要目的层为新近系明化镇组Nm Ⅰ—Nm Ⅳ, 总共有4个油组。储层沉积类型为河流相沉积, 储层横向变化快, 开发井井距在350~450m, 相对陆上油田井距较大。传统地质统计学建模方法对井间储层的预测存在较大的不确定性, 难以精细表征井间储层参数的变化, 无法满足油田中后期开发调整的需求。采用倾角导向建立一个等时的三维地层网格模型, 在其约束下, 基于敏感地震属性计算转换函数来表征储层参数的变化[22]。在井数据的基础上, 结合转换函数估计储层参数, 建立三维地质模型。
选择A油田解释了孔隙度的46口井参与孔隙度模型的建立。分析哪种地震属性对孔隙度的变化最敏感, 以便确定采用此种地震属性进行基于地震等时格架的倾角导向储层静态建模。结果表明, 目的层段低速度、低密度对应砂岩, 高速度、高密度对应泥岩。利用波阻抗可以区分砂、泥岩, 而泥岩是低孔隙度, 砂岩是高孔隙度, 所以高孔隙度对应低阻抗, 低孔隙度对应高阻抗。46口井的数据都体现了这一特点。因此采用油田的地震反演波阻抗数据来进行基于地震等时格架的倾角导向储层静态建模。其中, A10井作为检验井, 不参与建模, 而用于检验模型与实际情况的吻合程度。
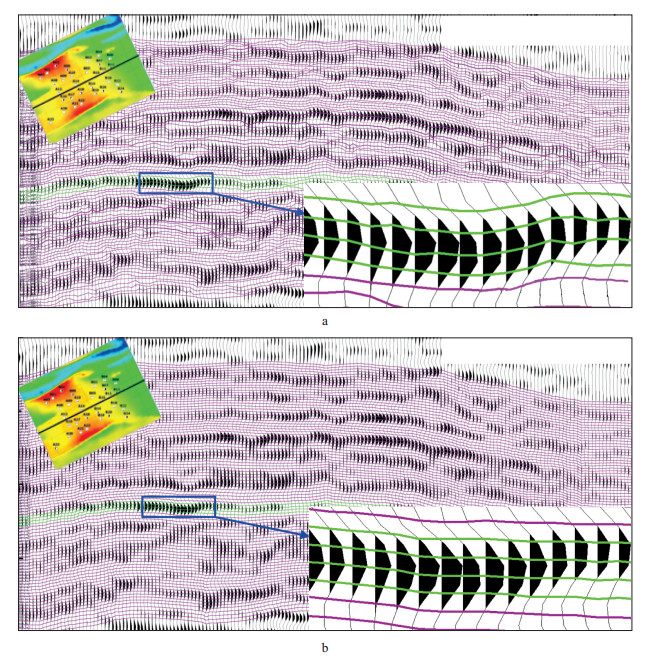
基于地震数据计算Inline方向和Xline方向的倾角体。选择目的层段稳定、连续的地震反射同相轴, 解释8个关键层位。这些关键层位都是等时界面, 作为顶、底面约束, 分别利用倾角导向方法和线性等分方法追踪网格层, 形成三维网格, 如图 7所示。从图 7可以看到, 倾角导向方法基于地震反射同相轴进行追踪细分来建立三维地层网格模型, 得到的网格层面与地震反射同相轴一致, 具有良好的等时性。线性等分方法通过等比例内插得到内部的网格层, 内插出来的网格层与地震反射同相轴存在交叉现象, 所建立的三维地层网格模型不完全等时。
|
图 7 采用不同方法建立的三维地层网格模型 a 倾角导向方法; b 线性等分方法 |
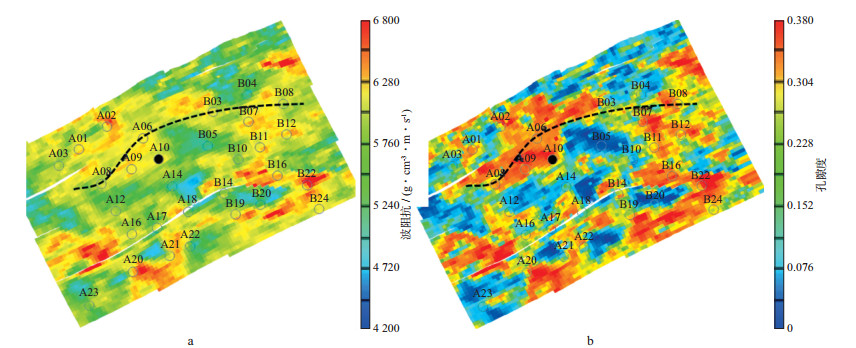
将参与建模的测井数据和地震属性粗化到三维网格中。在网格化的等时小层内, 提取已知井的井旁地震属性, 采用多道最小化均方误差方法计算反映孔隙度空间变化的转换函数。基于计算得到的转换函数, 从小层内已知井的孔隙度出发, 估计该小层内未知点的孔隙度, 最终建立三维孔隙度模型。基于波阻抗的空间变化规律对孔隙度进行预测, 所以孔隙度模型的空间变化与波阻抗的空间变化一致(图 8)。从模型提取的Nm31小层等时切片(图 9)清晰地反映了河流相储层的平面展布特征, 表明基于地震等时格架倾角导向储层静态建模建立的三维地层网格更等时。孔隙度模型的分辨率明显高于地震反演波阻抗, 因为基于地震等时格架倾角导向储层静态建模综合了测井数据垂向分辨率高的优势, 所以对细节的刻画比波阻抗更精细, 对砂体的空间展布特征描述更清晰。

|
图 8 波阻抗模型(a)与基于地震等时格架倾角导向储层静态建模预测的孔隙度模型(b) |
|
图 9 Nm31小层波阻抗等时切片(a)与基于地震等时格架倾角导向储层静态建模预测的孔隙度等时切片(b) |
用检验井数据来验证地震等时格架倾角导向储层静态建模方法对储层参数的预测精度。A10井作为检验井不参与建模, 沿检验井的井轨迹提取模型孔隙度, 并与测井孔隙度进行对比, 评价两种孔隙度之间的相对误差。相对误差越小, 表明建模方法的预测精度越高。
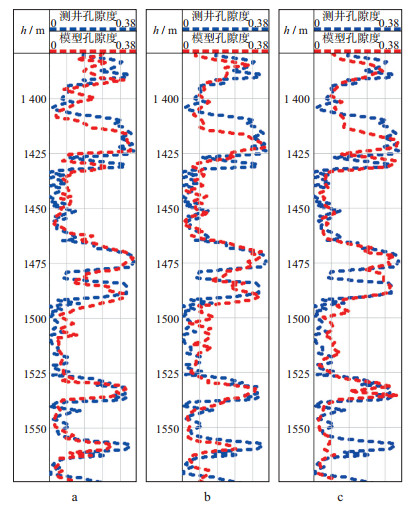
图 10给出了评价井A10井基于不同方法预测得到的模型孔隙度与测井孔隙度的对比结果。从图 10可以看到, 地震等时格架倾角导向储层静态建模方法的模型孔隙度变化趋势与测井孔隙度相同, 两者孔隙度值的相对误差小于10%。线性等分划分网格方法的模型孔隙度与测井孔隙度吻合程度要差一些, 12%的孔隙度值相对误差大于10%。配置协克里金序贯高斯方法模拟的孔隙度值在局部与测井孔隙度值差异较大, 28%的孔隙度值的相对误差大于10%。因此, 配置协克里金序贯高斯方法对孔隙度的预测精度最差。这是因为配置协克里金序贯高斯方法以井数据为储层参数预测的核心, 敏感地震属性仅起到辅助作用; 而基于地震等时格架倾角导向储层静态建模方法能够充分利用敏感地震属性来表征储层参数的空间变化, 地震属性与井数据都是储层参数预测的核心。因此基于地震等时格架倾角导向储层静态建模方法对储层的表征精度更高, 比地质统计学方法具有优越性, 采用倾角导向的方法自动追踪形成的网格层, 比常规方法建立的网格层更接近于等时。基于地震等时格架倾角导向储层静态建模方法比常规方法建立的地层模型约束的地震驱动建模精度更高, 在井网稀疏的条件下能更好地表征储层的非均质性, 为油田开发井网部署和开发方案的调整优化提供了坚实的技术支持。
|
图 10 评价井A10井基于不同方法预测得到的模型孔隙度与测井孔隙度对比 a 地震等时格架倾角导向储层静态建模方法; b 线性等分划分网格方法; c 配置协克里金序贯高斯方法 |
当层间存在与顶、底面不一致的起伏变化时, 常规方法划分的垂向网格层等时性较差。尝试采用地震倾角体来引导垂向网格层的划分, 建立等时的三维地层网格模型, 更好地反映了储层的层序结构和沉积特征, 对提高属性建模的精度具有现实意义。在此基础上, 利用敏感地震属性来求取转换函数, 以井数据为已知点, 采用转换函数来估计井间储层参数, 不再采用变差函数来预测储层参数的变化, 降低了井网稀疏时地质统计学方法对井间储层参数预测的不确定性, 形成了一种基于地震等时格架的倾角导向储层静态建模方法。
理论模型测试和实际应用表明, 倾角导向三维地层网格模型比常规方法建立的三维地层网格模型更接近等时, 提高了属性建模的精度。在井网稀疏的条件下, 与传统地质统计学方法相比, 基于地震等时格架的倾角导向储层静态建模方法能更精细地描述储层的非均质性, 降低了井间储层预测的不确定性。该方法在地震属性与储层参数线性相关性好的地区具有较好的推广应用价值。
| [1] |
吴胜和, 李宇鹏. 储层地质建模的现状与展望[J].
海相油气地质, 2007, 12(3): 53-60 WU S H, LI Y P. Reservoir modeling:current situation and development prospect[J]. Marine Origin Petroleum Geology, 2007, 12(3): 53-60 |
| [2] | MALLET J L. Discrete smooth interpolation[J]. ACM-Transactions on Graphics, 1989, 8(2): 121-144DOI:10.1145/62054.62057 |
| [3] | EULER N. A new tool to seal 3D earth model:a cut with constraint[J]. Expanded Abstracts of 68th Annual Internat SEG Mtg, 1998: 321-324 |
| [4] |
杨钦, 徐永安, 陈其明, 等. 三维约束Delaunay三角化的研究[J].
计算机辅助设计与图形学学报, 2000, 12(8): 590-594 YANG Q, XU Y A, CHEN Q M, et al. Research on 3D constrained delaunay triangulation[J]. Journal of Computer-Aided Design & Computer Graphics, 2000, 12(8): 590-594 |
| [5] |
魏嘉, 唐杰, 岳承祺, 等. 三维地质构造建模技术研究[J].
石油物探, 2008, 47(4): 319-326 WEI J, TANG J, YUE C Q, et al. Study of 3-D geological structure model building[J]. Geophysical Prospecting for Petroleum, 2008, 47(4): 319-326 |
| [6] |
孙波, 刘大安. 复杂地质界面三维重构与评价方法[J].
岩石力学与工程学报, 2015, 34(3): 556-564 SUN B, LIU D A. Three-dimensional reconstruction of complex geological interfaces and its evaluation method[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(3): 556-564 |
| [7] |
董建华, 范廷恩, 高云峰, 等. 真地层切片的拾取及应用[J].
石油地球物理勘探, 2010, 45(S1): 150-153 DONG J H, FAN T E, GAO Y F, et al. Pickup and application of the true stratal slice[J]. Oil Geophysical Prospecting, 2010, 45(S1): 150-153 |
| [8] | HALDORSON H, LAKE L A. New approach to shale management in field scale simulation models[J]. Society of Petroleum Engineers Journal, 1984, 24(4): 447-457DOI:10.2118/10976-PA |
| [9] | ARAKTINGI U G, BASHORE W M. Effects of properties in seismic data on reservoir characterization and consequent fluid-flow predictions when integrated with well logs[J]. SPE Technical Conference & Exhibition, 1992: 913-926 |
| [10] | YANG C T, CHOPRA A K. Integrated geostatistical reservoir description using petrophysical, geological, and seismic data for Yacheng 13-1 gas field[J]. SPE Technical Conference & Exhibition, 1995: 357-372 |
| [11] | TJOLSEN C B, JOHNSEN G, HALVORSEN G, et al. Seismic data can improve the stochastic facies modeling[J]. SPE Formation Evaluation, 1996, 11(3): 141-146DOI:10.2118/30567-PA |
| [12] | DOYEN P M, PSAILA D E, DEN BOER L D, et al. Reconciling data at seismic and well log scales in 3D earth modeling[J]. SPE Technical Conference & Exhibition, 1997: 465-474 |
| [13] |
李绪宣, 胡光义, 范廷恩, 等. 基于地震驱动的海上油气田储层地质建模方法[J].
中国海上油气, 2011, 23(3): 143-147 LI X X, HU G Y, FAN T E, et al. A method of geological reservoir modeling based on seismic drive for offshore fields[J]. China Offshore Oil and Gas, 2011, 23(3): 143-147 |
| [14] |
郭智, 孙龙德, 贾爱林, 等. 辫状河相致密砂岩气藏三维地质建模[J].
石油勘探与开发, 2015, 42(1): 76-83 GUO Z, SUN L D, JIA A L, et al. 3D geological modeling for tight sand gas reservoir of braided river facies[J]. Petroleum Exploration and Development, 2015, 42(1): 76-83DOI:10.11698/PED.2015.01.09 |
| [15] |
胡勇, 于兴河, 李胜利, 等. 应用地震正反演技术提高地质建模精度[J].
石油勘探与开发, 2014, 41(2): 190-197 HU Y, YU X H, LI S L, et al. Improving the accuracy of geological model by using seismic forward and inversion technique[J]. Petroleum Exploration and Development, 2014, 41(2): 190-197DOI:10.11698/PED.2014.02.08 |
| [16] | MARFURT K J, KIRLIN R L, FARMER S L. 3D seismic attributes using a semblance-based coherency algorithm[J]. Geophysics, 1998, 63(4): 1150-1165DOI:10.1190/1.1444415 |
| [17] | MARFURT K J. Robust estimates of 3D reflector dip and azimuth[J]. Geophysics, 2006, 71(4): 29-40 |
| [18] |
刘伟, 尹成, 王敏, 等. 河流相砂泥岩薄互层基本地震属性特征研究[J].
石油物探, 2014, 53(4): 468-476 LIU W, YIN C, WANG M, et al. Study on the characteristics of basic seismic attributes in fluvial sand-shale interbedded layers[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 468-476 |
| [19] |
张营革. 能量半衰时属性在浊积岩储层预测中的应用研究[J].
石油物探, 2013, 52(6): 662-668 ZHANG Y G. The application of energy half-time attribute to turbidite reservoir prediction[J]. Geophysical Prospecting for Petroleum, 2013, 52(6): 662-668 |
| [20] |
毕俊凤, 顾汉明, 刘书会, 等. 河道砂体地震响应特征及影响因素分析——以垦东1地区馆陶组上段河道砂为例[J].
石油物探, 2013, 52(1): 97-103 BI J F, GU H M, LIU S H, et al. Analysis on seismic response characteristics of channel sands and its influence factors:case study of Upper Guantao Formation in KD1 area[J]. Geophysical Prospecting for Petroleum, 2013, 52(1): 97-103 |
| [21] |
唐湘蓉, 蔡涵鹏, 贺振华. 地震波高频信息在薄层砂体预测中的应用[J].
石油物探, 2012, 51(3): 244-250 TANG X R, CAI H P, HE Z H. Thin-bed sand body prediction based on seismic wave high-frequency information[J]. Geophysical Prospecting for Petroleum, 2012, 51(3): 244-250 |
| [22] |
张建宁, 韩文功. 东营凹陷浊积砂体叠后地震属性与储层物性相关性研究[J].
石油物探, 2012, 51(2): 204-212 ZHANG J N, HAN W G. Correlative analysis on post-stack seismic attributes and physical properties of reservoir in turbidite sandstone of Dongying Depression[J]. Geophysical Prospecting for Petroleum, 2012, 51(2): 204-212 |


