常规地震反演(不包括全波形反演)能够从叠后地震资料中求取波阻抗, 从叠前数据中求取纵、横波速度和密度等岩性参数, 在地层岩性识别、岩相分析、储层描述中起着十分重要的作用[1]。理论上, 叠前地震反演能够获取岩性的多参数信息, 然而在实际生产中, 受叠前地震资料品质、入射角度求取精度和范围以及系数矩阵求取精度的影响, 叠前地震反演结果的可靠性相对较差, 在复杂岩性油气藏勘探中的应用效果不甚理想[2-5]。相比之下, 叠后波阻抗反演由于地震叠后资料可靠性高, 无需求取入射角和筛选入射角范围, 应用方便且效果较好, 在实际生产中得到了广泛的应用, 在地震反演中具有特殊的地位[6-7]。
目前, 波阻抗反演主要分为直接反演和基于模型的迭代反演两大类。直接反演主要分为道积分反演和递推反演。道积分反演受地震有效频宽的限制, 分辨率低, 无法满足薄层解释的需求, 不能求取地层的绝对波阻抗, 难以直接用于岩性识别。递推反演受反射系数递推时累计误差大的影响, 难以保证反演结果的可靠性[8-9]。基于模型的迭代反演需要利用大量测井资料和地质资料建立较为准确的初始模型(包含地震资料本身缺失的部分高频和低频信息), 在井少的工区, 难以保证应用效果; 且当反演参数和初始模型设置不理想时, 容易陷入局部最优, 反演结果难以反映真实的地下地质情况[10]。因此, 在勘探初期测井资料较少的情况下, 如何从有限带宽的叠后地震数据中求取可靠的高分辨率声波阻抗,是叠后波阻抗反演方法研究需要重点考虑的问题。IVAN等[11]基于频率域维纳滤波反褶积公式,提出了将反褶积和道积分通过一步计算实现的一步法地震波阻抗直接反演的方法, 但由于没有考虑到地震原始数据中失真的低频和高频信号对反演结果的影响, 导致反演结果出现低频和高频异常噪声, 其稳健性及可解释性大大降低。
我们在IVAN工作的基础上, 对一步法地震波阻抗直接反演的方法进行改造, 即利用Tukey窗函数的带通滤波器压制地震原始数据中失真的低频和高频信息, 建立稳健的一步法地震波阻抗直接反演计算方法。但由于缺失较多的低频和高频成分, 反演结果的分辨率较低。为了提高该反演结果的分辨率, 在实施一步法地震波阻抗直接反演前, 利用基于压缩感知的稀疏脉冲反射系数谱反演方法(CSSRI法)重构原始地震数据缺失的低频和高频成分, 使得用于频率域一步法地震波阻抗直接反演的地震数据频带拓宽, 带通滤波器压制的频带成分大大降低, 最终得到含有更多低频和高频成分的高分辨率地震波阻抗数据, 实现对薄层波阻抗异常的识别。
1 方法原理假设地层波阻抗Z(t)随时间深度连续可微, 则地层反射系数r(t)可近似等价为[12]:
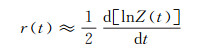
|
(1) |
式中:lnZ(t)通常定义为地层的相对波阻抗。显然, (1) 式的频率域表达式为:
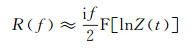
|
(2) |
式中:R(f)为地层反射系数r(t)的频谱; f为频率; i为虚数单位, 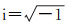
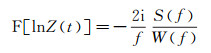
|
(3) |
式中:S(f)是地震道s(t)的频谱; W(f)是地震子波w(t)的频谱。
考虑到实际地震资料的频谱是有限带宽的, 低于最低截止频率fl和高于最高截止频率fh的频谱成分(信噪比谱小于1) 通常是缺失或失真的, 从地震资料中估计的地震子波同样具有类似性质。因此, 要稳定求解(3) 式, 必须引入正则化项, 则(3) 式可改写为:
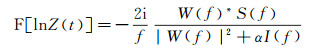
|
(4) |
式中:“*”为复共轭算子, 即W(f)*为W(f)的复共轭; I(f)>0为正则化项; α>0为正则化因子。(4) 式在形式上与IVAN等[11]提出的频率域一步法地震波阻抗直接反演公式一致。考虑到(4) 式分母存在频率项f, 显然对于高频成分, (4) 式是稳定的, 而对于低频成分则不稳定, 因此, 正则化项的设计应针对低频情况。由于前文假设地层波阻抗Z(t)随时间深度连续可微, 为了保证结果的光滑性, 则可引入Tikhonov光滑化算子I(f)=1/|f|p作为正则化项[13-14]。为了保证极限情况f→0时, (4) 式稳定, 则p应该大于1, 这里p取2即可。尽管通过(4) 式可稳定求得相对波阻抗的频谱, 但其低于最低截止频率fl和高于最高截止频率fh的频谱成分同样不可靠, 通过傅里叶逆运算F-1(·)得到的相对波阻抗会受到影响, 因此, 在逆运算前需要加入一步带通滤波运算, 消除这些频谱的影响。基于Tukey窗函数[15], 设计的带通滤波器b(f)为:
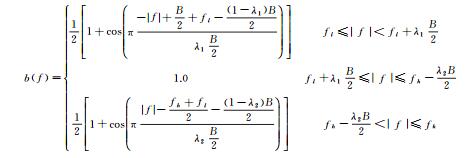
|
(5) |
其中, 带通滤波器的频带范围B=fh-fl, 在实际工作中, fl和fh的取值通常可以采用分频扫描或信噪比谱估算[16]来确定; λ1, λ2∈(0, 1) 为带通滤波器余弦镶边长度与所在滤波器长度的比例。由于中低频信息对反演结果整体格架起着控制作用, 因此, 为了降低中低频能量的损失, λ1取值通常较小, 且小于λ2。由此, 根据绝对声波阻抗公式Z(t)=Z0(t)elnZ(t), 可以推导出常规的频率域波阻抗直接反演方法(简称为FIDI法):
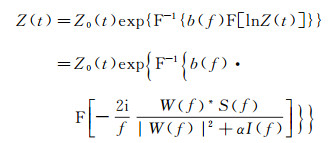
|
(6) |
式中:Z0(t)为声波阻抗低频背景模型。(6) 式即是对IVAN等[11]提出的频域一步法地震波阻抗直接反演公式进行改进的结果。
尽管(6) 式可以避免常规直接反演法反射系数递推时的累积误差, 稳定求取声波阻抗, 但由于缺少低频和高频信息, 反演结果的分辨率仍然相对较低。因此, 需要首先获得包含相对可靠的低频和高频成分的高分辨率地震记录, 从而求取高分辨率声波阻抗。
稀疏反演理论能够重构相对可靠的地震低频和高频数据[17-20], 拓宽原始地震数据的频带宽度, 获取高分辨率的地震数据, 因此, 可以利用该理论得到的地震数据作为(6) 式的输入, 进一步提高频率域波阻抗直接反演的分辨率。我们采用陈祖庆等[21]提出的基于压缩感知的稀疏脉冲反射系数谱反演方法来稳健重构高分辨率地震数据,并获取相应的宽带Morlet理论子波作为频率域波阻抗直接反演法的输入数据。基本理论公式为:
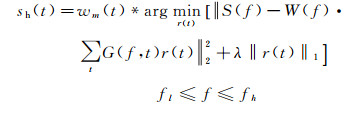
|
(7) |
式中: 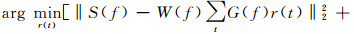
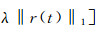
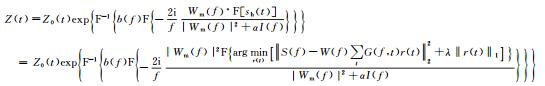
|
(8) |
式中:Wm(f)为宽带Morlet理论子波wm(t)的频谱; Wm(f)*为Wm(f)的复共轭。事实上, (8) 式是对FIHDI法实现过程的数学表达, 具体实现过程是先用CSSRI法对地震原始数据进行谱反演拓频, 再用Tukey窗函数的带通滤波器滤波, 最后进行频率域波阻抗计算。对于(8) 式, 由于输入的是高分辨率地震数据sh(t), 其有效频带范围比原始地震数据s(t)的频带大, 因此, 选取的带通滤波器b(f)的频带宽度[f′l, f′h]比输入原始地震数据时的[fl, fh]大, 即截止频率的低频更低, 高频更高, f′l < fl, f′h > fh, 具体取值可以通过试验确定。显然, 求解(8) 式可以获得比原始地震数据更宽频带的高分辨率地震波阻抗数据。
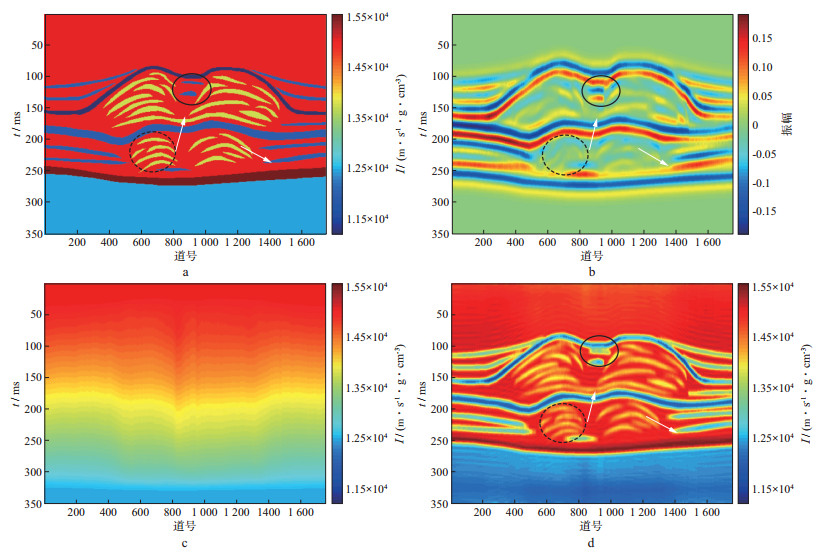
2 应用分析 2.1 理论模型试验为了验证频率域高分辨率地震波阻抗直接反演方法(FIHDI法)的可行性和识别薄层的能力, 设计了含有薄层结构的发育两期叠置的礁滩波阻抗模型, 如图 1a所示。采用主频为25Hz雷克子波合成地震记录(图 1b), 可以大致反映发育两期叠置的礁滩模型的基本轮廓, 但难以区分礁滩地层的具体叠置关系(黑色虚线椭圆部位)、判别礁滩生长的尖灭位置(白色箭头部位)以及分辨相邻两独立礁体的地震响应(黑色实线椭圆所示), 难以满足复杂薄层岩性圈闭的精细识别。基于图 1c所示的波阻抗低频背景模型, 采用FIHDI法对合成地震记录(图 1b)进行反演, 结果如图 1d所示。从图 1d可以看出, 薄层礁滩模型的多层礁滩叠置关系、礁滩的生长尖灭位置和相邻两独立礁体的特征均得到了精细刻画, 与图 1a所示的礁滩模型在整体形态和细节特征上均保持了一致。以上分析表明, 频率域高分辨率地震波阻抗直接反演方法可以获取高分辨率地震波阻抗反演结果。该方法只需输入地震数据的优势频带的频谱信息, 能够在一定程度上回避地震数据失真的低、高频成分的影响。
|
图 1 礁滩波阻抗模型的数值试验 a 礁滩波阻抗模型; b 合成地震记录(主频25Hz); c 波阻抗低频背景模型; d FIHDI的反演结果 |
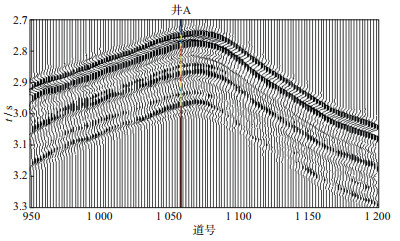
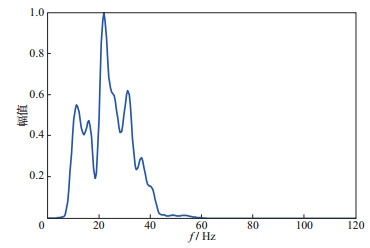
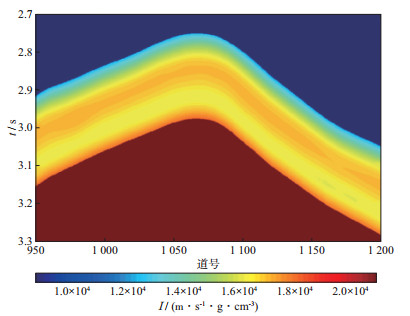
采用FIHDI法对川东北地区过井A的某地震测线海相地层的地震资料进行处理, 结果如图 2所示(测井曲线计算的声波阻抗投影在道号1059处)。图 3为图 2所示的地震剖面的频谱, 从频谱特征上看, 该地震剖面的频带较窄, 主频较低, 缺失可靠的高频和低频信息(5Hz以下和75Hz以上的频率成分主要是噪声, 失真明显), 地震分辨率较低, 难以有效识别具有薄层结构的储层地震响应和刻画圈闭形态。根据测井曲线计算的声波阻抗和地震剖面标志层的构造形态(层位数据), 采用沿层外推、高阶多点圆滑的办法, 可以建立该海相地层的波阻抗低频背景模型, 如图 4所示。
|
图 2 某工区过井A的实际地震剖面(井A测井计算的声波阻抗投影在道号1059处) |
|
图 3 图 2所示的地震剖面的频谱 |
|
图 4 图 2所示的地震剖面对应的波阻抗低频背景模型 |
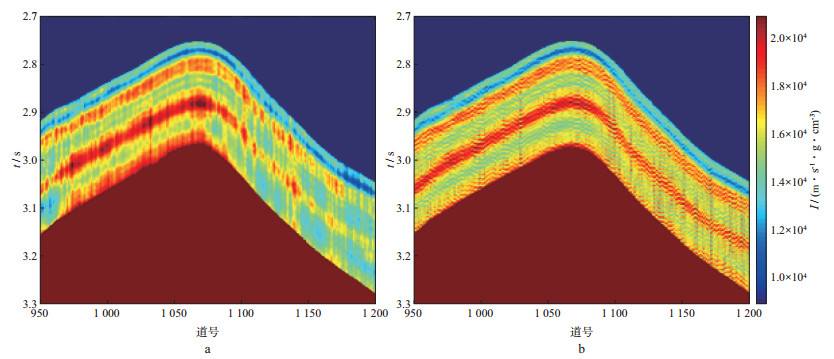
为了测试实际地震资料被噪声污染的低频和高频信息对反演结果的影响, 采用FIDI法((6) 式)对图 2所示的地震剖面进行反演, 结果如图 5所示。图 5a选取的频带带通范围[fl, fh]为1~75Hz, 实际地震资料失真的低频参与了反演, 反演结果存在“面条状”低频噪声, 出现了许多虚假的高阻抗和低阻抗异常, 给解释工作带来不确定性。类似地, 图 5b选取的频带带通范围[fl, fh]为5~120Hz, 实际地震资料失真的高频参与了反演, 反演结果存在“锯齿状”的高频噪声, 严重干扰了反演结果对真实波阻抗异常的识别。上述分析结果表明, 实际地震资料失真的低频和高频信息不能直接用于反演。因此, 只能利用有效频带内的部分谱信息来获取反演结果。
|
图 5 实际地震数据失真的低频和高频成分对反演结果的影响 a 失真的低频成分; b 失真的高频成分 |
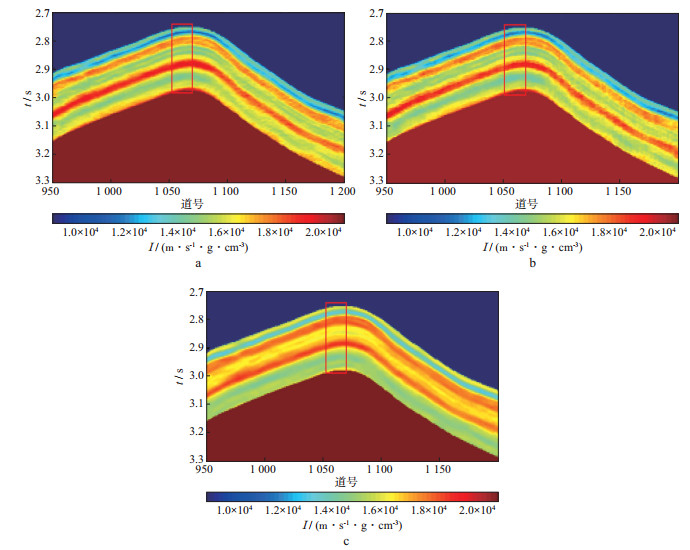
图 6a和图 6b分别为利用地震资料有效频带内的部分谱(5~75Hz)信息采用FIDI法((6) 式)和FIHDI法((8) 式)进行反演的结果。从图 6a和图 6b中可以看到, 失真的低频( < 5Hz)和高频(>75Hz)信息不参与反演后, 反演结果不存在“面条状”低频噪声和“锯齿状”的高频噪声, 稳定可靠。图 6c为采用商业软件的约束稀疏脉冲反演模块反演的结果。对比图 6a, 图 6b和图 6c可以看出, 采用FIDI法和FIHDI法的结果整体上能够反映波阻抗地层的更多异常细节, 分辨率较商业软件的反演结果(图 6c)高。
|
图 6 实际地震数据应用不同波阻抗反演方法的反演结果 a FIDI法; b FIHDI法; c 商业软件的约束稀疏脉冲反演模块 |
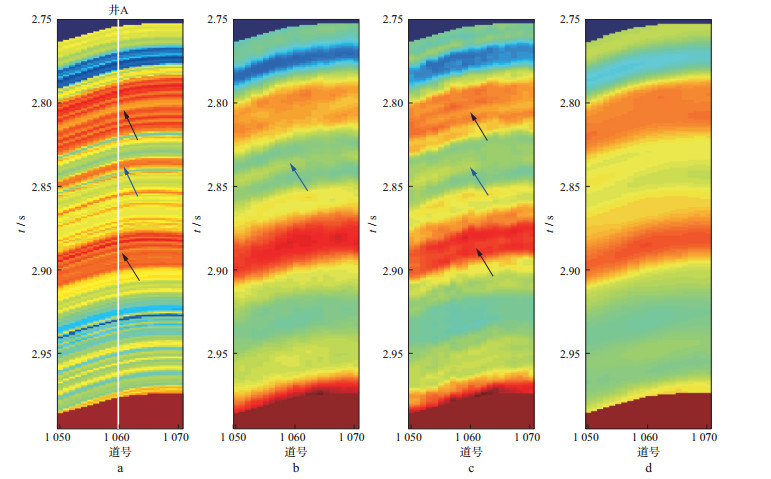
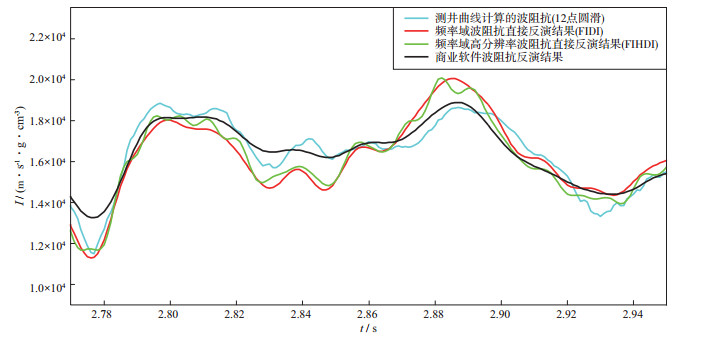
图 7a为井A测井波阻抗沿井旁道地震反射地层构造产状外推的结果。图 7b, 图 7c和图 7d分别为图 6a, 图 6b和图 6c中红色矩形框区域放大显示的结果。对比图 7a, 图 7b, 图 7c和图 7d可以清楚地看出, 采用本文提出的FIHDI法(图 7c)的反演结果能够在一定程度上反演测井波阻抗中的高阻背景下的低阻薄层的异常响应(图 7a和图 7c中黑色箭头所示)和低阻背景下的高阻薄层的异常响应(图 7a和图 7c中蓝色箭头所示); 采用FIDI法(图 7b)只能反映低阻背景下的高阻薄层的异常响应(图 7b中蓝色箭头所示); 采用商业软件的约束稀疏脉冲反演模块的反演结果(图 7d)尽管能够正确反演波阻抗地层的整体变化趋势, 但无法精细反映图 7a中箭头所示的薄层波阻抗异常特征。在井A位置, 从图 7a至图 7d中分别抽取一道波阻抗曲线, 结果如图 8所示。从图 8可以看出, 采用FIHDI法的结果光滑性最低, 对波阻抗异常细节的刻画能力较FIDI法和商业软件反演的结果强, 与测井计算的波阻抗曲线(12点圆滑)对薄层波阻抗异常细节的刻画能力相当。综上所述, FIHDI法对薄层波阻抗异常细节的刻画能力最强, 分辨率最高, FIDI法次之, 商业软件相对较低。
|
图 7 图 2中井A测井波阻抗沿地震反射层外推的结果和图 6中红色矩形框区域放大的结果 a 图 2中井A测井波阻抗沿地震反射层外推结果; b 图 6a中红色矩形框区域放大的结果; c 图 6b中红色矩形框区域放大的结果; d 图 6c中红色矩形框区域放大的结果 |
|
图 8 不同方法的反演结果在井A位置抽取的波阻抗曲线 |
在改进频率域一步法地震波阻抗反演方法的基础上, 引入具有良好拓频性能的CSSRI法, 提出了利用地震资料有效频带内的部分谱信息实现频率域高分辨率地震波阻抗直接反演的方法。理论模型和实际地震资料的试验结果表明, 相对于传统的地震波阻抗反演方法, 本文提出的FIHDI法不仅可以避免原始地震数据失真的低频和高频成分对反演结果的影响, 而且可以获取包含更多低频和高频成分的宽频带地震波阻抗, 明显提高波阻抗反演结果的分辨率, 更加清晰地识别薄(互)层波阻抗异常的细节特征, 一定程度上满足了复杂多变的岩性精细解释的要求。
| [1] |
撒利明, 杨午阳, 姚逢昌, 等. 地震反演技术回顾与展望[J].
石油地球物理勘探, 2015, 50(1): 184-202 SA L M, YANG W Y, YAO F C, et al. Past, present, and future of geophysical inversion[J]. Oil Geophysical Prospecting, 2015, 50(1): 184-202 |
| [2] |
殷文. 叠前地震反演关键技术及影响因素分析与研究[J].
地球物理学进展, 2013, 28(6): 2958-2968 YIN W. The analysis on the key techniques and influence factors of pretack seismic inversion[J]. Progress in Geophysics, 2013, 28(6): 2958-2968DOI:10.6038/pg20130617 |
| [3] |
晓宇, 凌云, 孙德胜, 等. 叠前地震反演应用研究[J].
石油物探, 2010, 49(4): 384-389 XI X Y, LING Y, SUN D S, et al. Application research of prestack seismic inversion[J]. Geophysical Prospecting for Petroleum, 2010, 49(4): 384-389 |
| [4] |
陈建江, 朱兴卉. AVO反演的不确定性分析[J].
地球物理学进展, 2009, 24(4): 1461-1467 CHEN J J, ZHU X H. Uncertainty analysis for AVO inversion[J]. Progress in Geophysics, 2009, 24(4): 1461-1467 |
| [5] |
张广智, 王文, 印兴耀, 等. 基于射线理论的角度道集提取方法综述[J].
地球物理学进展, 2011, 26(5): 1696-1707 ZHANG G Z, WANG W, YIN X Y, et al. Overview of extraction methods of angle gathers based on ray theory[J]. Progress in Geophysics, 2011, 26(5): 1696-1707 |
| [6] |
张永刚. 地震波阻抗反演技术的现状和发展[J].
石油物探, 2002, 41(4): 385-390 ZHANG Y G. The present and future of wave impedance inversion technique[J]. Geophysical Prospecting for Petroleum, 2002, 41(4): 385-390 |
| [7] |
卢占武, 韩立国. 波阻抗反演技术研究进展[J].
世界地质, 2002, 21(4): 372-377 LU Z W, HAN L G. The Development of the research of the wave impedance inversion technique[J]. World Geology, 2002, 21(4): 372-377 |
| [8] |
栾颖, 冯晅, 刘财, 等. 波阻抗反演技术的研究现状及发展[J].
吉林大学学报(地球科学版), 2008, 38(S1): 94-98 LUAN Y, FENG X, LIU C, et al. The research present and future of wave impedance inversion technique[J]. Journal of Jilin University (Earth Science Edition), 2008, 38(S1): 94-98 |
| [9] |
刘喜武, 年静波, 吴海波. 几种地震波阻抗反演方法的比较分析与综合应用[J].
世界地质, 2005, 24(3): 270-275 LIU X W, NIAN J B, WU H B. Comparison of seismic impedance inversion methods and an application case[J]. World Geology, 2005, 24(3): 270-275 |
| [10] |
王延光. 储层地震反演方法以及应用中的关键问题与对策[J].
石油物探, 2002, 41(3): 299-304 WANG Y G. Seismic reservoir inversion algorithm and the key problems and policies in its application[J]. Geophysical Prospecting for Petroleum, 2002, 41(3): 299-304 |
| [11] | IVAN P, AARON S. Robust one-step (deconvolution+integration) seismic inversion in the frequency domain[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg, 2012: 1-5 |
| [12] | OLDENBURG D W, SCHEUER T, LEVY S. Recovery of the acoustic impedance from reflection seismograms[J]. Geophysics, 1983, 48(10): 1318-1337DOI:10.1190/1.1441413 |
| [13] | TIKHONOV A N. Solution of incorrectly formulated problems and the regularization method[J]. Soviet Mathematical Doklady, 1963, 4(5): 1035-1038 |
| [14] | TIKHONOV A N, GONCHARSKY A V, STEPANOV V V, et al. Numerical methods for the solution of ill-posed Problems[M]. Nauka, Moscow: Kluwer Academic Publishers, 1990: 34-44. |
| [15] | HARRIS F J. On the use of windows for harmonic analysis with the discrete Fourier transform[J]. Proceedings of the IEEE, 1978, 66(1): 51-83DOI:10.1109/PROC.1978.10837 |
| [16] |
梁光河. 信噪比的估算及其在高分辨率处理中的应用[J].
石油物探, 1998, 37(3): 64-71 LIANG G H. The estimation of signal-to-noise ratio and its use in high-resolution processing[J]. Geophysical Prospecting for Petroleum, 1998, 37(3): 64-71 |
| [17] |
管路平, 唐权钧. 地震信号的高低频成分补偿[J].
石油物探, 1990, 29(3): 35-45 GUAN L P, TANG Q J. High/low frequency compensation of seismic signal[J]. Geophysical Prospecting for Petroleum, 1990, 29(3): 35-45 |
| [18] |
韩立国, 张莹, 韩利, 等. 基于压缩感知和稀疏反演的地震数据低频补偿[J].
吉林大学学报(地球科学版), 2012, 43(S1): 259-265 HAN L G, ZHANG Y, HAN L, et al. Compressed sensing and sparse inversion based low-frequency information compensation of seismic data[J]. Journal of Jilin University (Earth Science Edition), 2012, 43(S1): 259-265 |
| [19] | LI G F, QIN D H, PENG G X. Experimental analysis and application of sparsity constrained deconvolution[J]. Applied Geophysics, 2013, 10(2): 191-200DOI:10.1007/s11770-013-0377-1 |
| [20] | WANG J, WANG S, YUAN S, et al. Stochastic spectral inversion for sparse-spike reflectivity by presetting the number of non-zero spikes as a prior sparsity constraint[J]. Journal of Geophysics & Engineering, 2014, 11(1): 1-14 |
| [21] |
陈祖庆, 王静波. 基于压缩感知的稀疏脉冲反射系数谱反演方法研究[J].
石油物探, 2015, 54(4): 459-466 CHEN Z Q, WANG J B. A spectral inversion method of sparse-spike reflection coefficients based on compressed sensing[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 459-466 |



 ,
,