2. 北京博豪罗根石油技术有限公司, 北京 100085
2. Beijing Borehole Logging Petroleum Technology Co., Ltd., Beijing 100085, China
利用零偏VSP资料求取地震时深关系、标定地震层位和预测钻前地层是零偏VSP的三大主要任务, 时深关系和层位标定是地震资料解释最基础、最重要的工作。利用零偏VSP资料求取地震时深关系被认为是各种时深关系求取方法精度最高的方法[1-2]。层位标定是地震资料解释中可靠识别地震反射波组的地质层位的一项非常重要的基础工作, 目前地震剖面纵波层位标定最主要、最直接的方法是通过与零偏VSP上行反射纵波的走廊叠加记录对比加以实现。同时VSP还可以直接将钻井、测井资料和地面地震剖面上的地震波组有效地联系在一起(即零偏VSP桥式标定或桥式对比), 因此常被业界誉为地震-地质的桥梁。严格意义上的零偏VSP桥式标定需要对上行反射波场做拉平处理, 使来自于井筒附近同一反射界面的VSP上行反射纵波同相轴得到充分拉平。水平地层情况下, 零偏VSP上行反射纵波经纵波初至时间静校正后, 可以得到充分拉平, 然后再进行走廊叠加, 就可得到精确的纵波走廊叠加记录[3]。
当地层倾斜时, 经纵波初至时间静校正后的零偏VSP上行反射纵波无法得到拉平, 因此, 走廊叠加出现误差[4-5]。孟恩等[4]和王保利等[5]将上述误差归结为地层倾角的影响, 并讨论了VSP观测井段之内地层倾角对零偏VSP上行反射纵波误差(倾角时差)的影响, 推导出了可用于分析地层倾角和进行走廊叠加倾角时差校正的公式。两者的主要区别是:孟恩等[4]利用倾角测井资料计算地层倾角; 王保利等[5]则利用了VSP本身的上、下行反射波通过迭代自动计算地层倾角。
此外, 传统求取VSP时深关系时并未考虑地层倾角的影响, 当地层较平或地层倾角很小时, 对地震资料解释而言, 这种时深关系是准确的。但当地层倾角较大时, 这种由VSP初至波走时所求取的时深关系存在很大误差, 导致地震资料解释不准确, 出现钻井误差, 因此, 需对上述时深关系进行倾角时差校正处理[6-7]。姜本厚等[6]和殷文等[7]在将井筒附近地层简化为倾斜层状介质模型并在已知地层倾角的情况下, 根据Snell定律, 对VSP时深关系进行倾角时差校正, 取得实际应用效果。
对复杂高陡构造, 零偏VSP波场相当复杂, 已不属于一维地震的范畴, 初至波不是下行直达波, 其射线路径无法用简单的直射线或折线精确表示, 上行反射波场来自于井筒附近一定范围内的地层, 属于二维甚至是三维地震, 因此可对零偏VSP上行反射波场进行二维地震成像处理[8]。但更多情况下, 业界更愿意将零偏VSP当作一维地震处理, 因此, 上述相关文献所述时深关系校正和倾角时差校正方法, 已经无法适应复杂高陡构造零偏VSP资料处理, 特别对钻前(或VSP观测井段之下)地层的上行反射波场, 已无法将其成像到走廊叠加记录的正确位置。
近年来, 随着我国油气勘探开发由构造油气藏转向非构造油气藏, 非构造油气藏的研究对时深关系精度及其层位标定精度的要求比构造油气藏高[9], 因此, VSP资料在地震勘探开发中的应用越来越广泛, VSP资料作为地面地震资料处理最理想的井控处理资料之一发挥着越来越重要的作用[10]。
本文在梁向豪等[8]的基础上, 利用零偏VSP自身的上、下行波场所包含的反射界面倾角信息, 建立高陡构造零偏VSP上行反射成像所需要的二维层速度模型, 采用常速度梯度射线追踪方法, 对零偏VSP上行波场进行拉平处理, 经过多次迭代修正速度模型, 使来自于复杂连续构造形态上的零偏VSP上行反射波也能得到充分拉平。最后用实际资料验证了本文方法的有效性。
1 方法原理 1.1 利用零偏VSP资料计算反射界面倾角利用VSP资料估算井筒附近反射界面倾角在国外研究较早, 方法很多, 主要包括解析法、倾斜时差法、模型法和偏振测量法等[11-15]。KENNETT等[11]推导出了利用零偏VSP资料同一界面上的两道反射时差计算地层倾角的解析公式, CONN等[12]进一步指出了上述解析公式计算出来的地层倾角与倾角测井值有较好的吻合性。
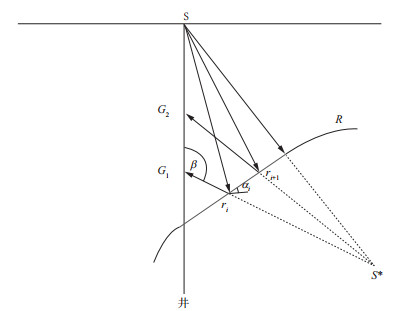
如图 1所示, 对于单一地层倾角空间变化的复杂反射界面, 设界面以上介质速度为常速, S*为炮点S的虚震源, t1和t2分别为震源到接收点G1和G2的直达波初至时间, t3和t4分别为震源到接收点G1和G2的一次上行反射波时间, t5为震源S到虚震源S*的旅行时间, αi为反射地层R上反射段riri+1的倾角, β为震源到接收点G1一次上行反射与井筒所形成的张角。根据函数的三角关系, 可得到αi的计算公式如下:
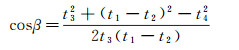
|
(1a) |
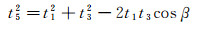
|
(1b) |
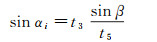
|
(1c) |
|
图 1 零偏VSP上行反射波估算地层倾角示意 |
通过拾取反射界面上所有相邻反射点的上行波场, 就可计算出沿反射界面R不同空间位置的地层倾角, 从而构造出倾角空间变化的复杂反射界面R的构造形态。
1.2 复杂高陡构造零偏VSP时深关系及空变倾角时差校正的基本概念如图 2所示, 假设井孔为直井, S为地面井口, 亦即零偏VSP激发点, R为井下某检波点, 地下为复杂高陡构造, r1至rn分别为井下不规则复杂反射界面。根据费马原理, 零偏VSP初至波一定是从地层速度偏高的上倾方向一侧沿图中所示某曲线(如图中粗线)从S点最先到达R, 而不是从S点沿井筒(直线)最先到达R点。所谓时深关系校正就是将上述沿曲线从S传播到R的初至波时间校正到沿铅直线(井筒)从S传播到R的直达波传播时间。
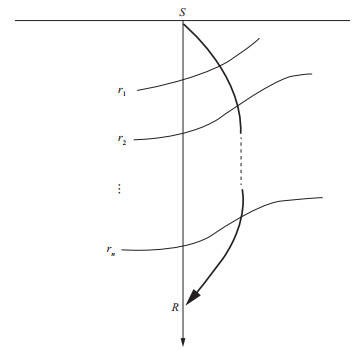
|
图 2 复杂高陡构造零偏VSP初至射线路径示意 |
图 3为零偏VSP纵波初至时间静校正后的上行反射纵波剖面示意图。图中3条粗黑实线表示3个上行反射纵波同相轴, 同一反射同相轴(如图中第2条粗黑实线)内、外切除线之间的时间差(Δt)即为文献[4]和文献[5]所定义的倾斜地层零偏VSP倾角时差。可以看出:该倾角时差仅限于观测井段之内; 受到切除宽度的影响; 复杂情况下无法将整个零偏VSP记录的上行波场拉平; 未涉及钻前地层预测问题和时深关系校正处理问题, 即, 走廊叠加记录的时深关系并不能代表沿井筒铅直向下的时深关系, 而仅仅是如图 2所示沿某曲线传播的时深关系。
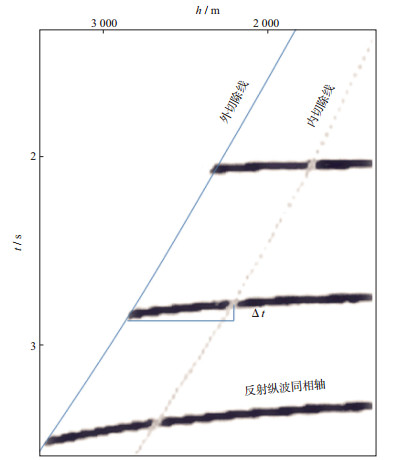
|
图 3 零偏VSP静校正后的上行纵波及走廊切除示意 |
所谓空变倾角时差校正, 是指来自于复杂连续高陡构造界面上的零偏VSP上行波场(包括观测井段之下的上行波场)经空变倾角时差校正后得到充分拉平, 并经时深关系校正处理, 再对拉平后的上行反射波场进行走廊叠加。这样, 不仅观测井段之内, 而且观测井段之下, 不仅井筒附近与井筒相交地层, 而且远离井筒地层的地震反射, 即二维空间中全井段记录的地震反射均可得到充分拉平。同时, 上行反射波场和走廊叠加记录的时深关系真正代表从井口铅直向下传播的时深关系。
1.3 复杂高陡构造零偏VSP钻前地层预测问题钻前地层预测是零偏VSP三大主要任务之一。在地层水平情况下, 无论是观测井段之内, 还是观测井段之下, 零偏VSP上行反射总是来自于与垂直井筒轨迹相交地层上的地震反射, 属一维地震范畴。
如图 4所示, R为钻前倾斜地层, S为垂直井井口也是零偏VSP激发点, G1至Gn为井中接收检波器。由于地层倾斜, 井中检波器观测不到井筒与地层交点r处的地震反射, 而只能得到从r1到rn地层段的地震反射。因此, 要获得r处的地震反射属于钻前(或观测井段之下)地层预测问题。
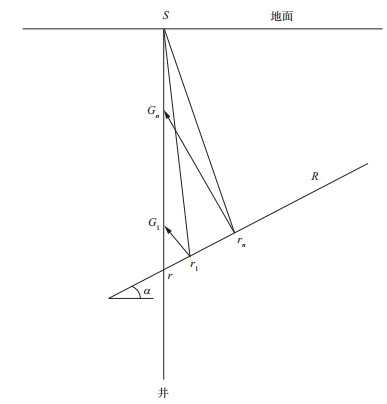
|
图 4 倾斜地层零偏VSP反射位置示意 |
对零偏VSP上行反射波场, 经纵波初至时间校正和空变倾角时差校正处理后, 可将r1到rn地层段上的反射拉平, 并使之成像到r点处反射时间位置, 再对上述拉平后的上行反射波场进行走廊叠加处理, 获得高精度走廊叠加记录。这样, 对观测井段之下的地层, 不仅完成了地层深度的精确预测, 也实现了地震反射波组特征的精确预测。
1.4 时深关系校正和空变倾角时差校正的实现方法从上述分析可以看出, 无论是下行波场的时深关系校正还是上行波场的空变倾角时差校正, 均涉及射线路径的追踪问题。射线路径追踪主要基于费马原理, 波在界面上的反射、透射和折射遵循Snell定律, 已知射线的始点(震源点)和终点(接收点)位置, 求旅行时最小射线路径(射线轨迹), 即两点射线追踪问题[16]。
有关两点射线追踪的基本原理, 我们沿用文献[8]所述的常速度梯度射线追踪方法, 在此不再赘述, 仅给出以下实现步骤和方法。
1) 拾取零偏VSP纵波初至和一定数量的上行反射纵波同相轴。求取初至时深关系拟合曲线和上行反射波场同相轴时深关系拟合曲线的交点, 得到一个时深关系对。按照此方法求出每个上行反射同相轴的时深关系对, 进而求得观测井段之下地层的层速度, 加上观测井段之内由初至时间得到的层速度, 就可得到整个记录深度的层速度, 再根据公式(1) 建立井筒附近地层构造模型, 将上述层速度场根据构造模型沿层外推得到整个二维初始层速度模型。
2) 采用三次样条函数描述地质界面并对速度场进行平滑处理。几何地震学是波动地震学的高频近似, 射线追踪要求地质界面和速度场具有一定的平滑度, 宜采用三次样条函数描述地质界面并对速度场进行一定程度的平滑处理, 使其充分光滑。
3) 对上述速度模型进行网格化处理, 再对网格内速度进行常速度梯度处理。
4) 采用常速度梯度射线追踪法分别从炮点和每个检波点进行双向射线追踪。
当网格或速度梯度满足λ·r/v0 < 1, 其中, λ为速度梯度, r为射线在单元内路径s处的坐标, v0为单元入口处的速度, 相当于网格或速度梯度足够小时, 借助Taylor级数展开, 得到恒定速度梯度场射线追踪近似公式[17-18]:
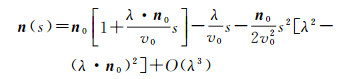
|
(2a) |
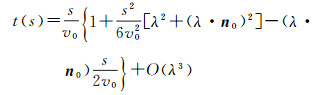
|
(2b) |
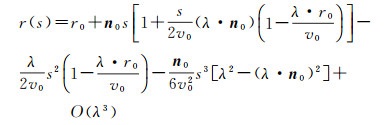
|
(2c) |
式中:r0为射线在每个单元入口处的坐标; n0为单元入口处的射线方向; n(s)为单元内路径s处的射线方向; t(s)为射线在单元内沿路径s传播的旅行时间。
5) 求取炮点的每条射线与每个检波点每条射线在成像范围内的交点。
6) 求取从炮点到每个检波点的旅行时最小射线路径。
7) 根据每个检波器接收到的最小传播时间精度误差, 加密射线或网格。
8) 对纵波初至静校正后的VSP上行纵波进行排齐处理。如果反射纵波无法得到有效排齐, 说明速度场(或地层倾角)存在误差, 通过计算上行反射纵波拉平时每个点的时差来控制和修正二维层速度场。分以下两种情况:① 由于观测井段之内的上行反射同相轴与下行直达波在初至连线相交, 则该上行反射同相轴在与井筒相交点的射线追踪所得到的反射时间, 就是该点的初至时间, 我们称之为井筒交点反射时间; ② 对于观测井段之下地层的上行反射同相轴, 如果步骤1) 中所求拟合交点准确, 则该上行反射同相轴射线追踪所得到的井筒交点反射时间即为拟合交点反射时间。
假设某一上行反射同相轴的井筒交点反射时间为tdij, i表示VSP道号, j表示所拾取的上行反射纵波序号, 经射线追踪得到的上行反射时间为tpij, 则根据以下公式, 得到该同相轴拉平到tdij时的时间误差(Δtij)为:
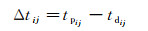
|
(3a) |
给定速度场一个小的扰动δvij, 得到:
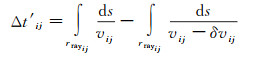
|
(3b) |
则:
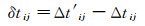
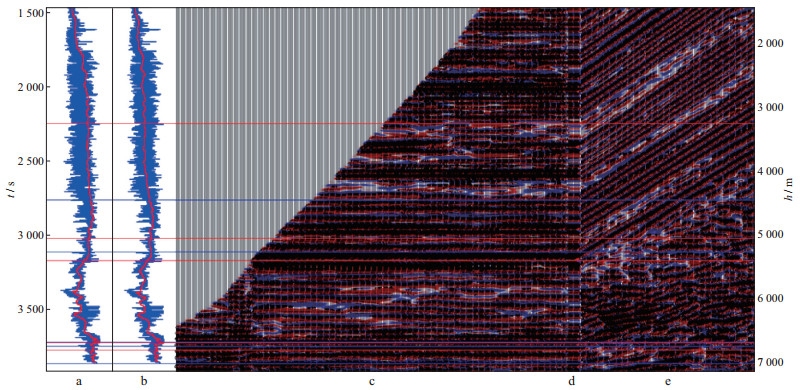
|
(3c) |
式中:rrayij表示射线路径; vij表示地震速度。根据δvij修正速度模型, 继续完成步骤2) 到步骤8) 的处理, 直到上行反射纵波得到充分拉平, 即‖δtij‖趋于最小。
9) 对时深关系(速度)、上行波拉平剖面及其走廊叠加记录进行时深关系校正处理, 使传播时间校正到从井口铅直传播到井中检波器的旅行时间。
2 实际资料处理效果图 5为塔里木库车地区某零偏VSP数据经波场分离和初至时间静校正后得到的上行纵波波场(图 5a)及其走廊叠加记录(图 5b)与过井地面地震剖面(图 5c)的对比。可以看出, 因地层倾斜(且地层倾角在离开井筒的上倾方向横向有所变化), 经纵波初至时间静校正后, 上行反射纵波波场无法拉平, 不进行倾角时差校正的走廊叠加记录与地面地震剖面的吻合效果很差。
|
图 5 零偏VSP初至静校正后的上行纵波(a)及其走廊叠加记录(b)与地震剖面(c)对比 |
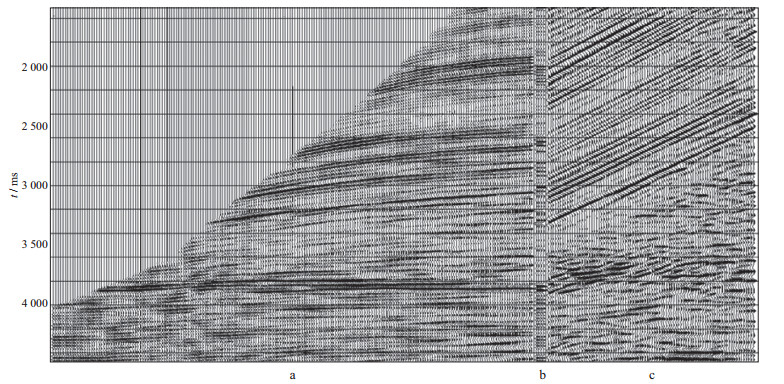
图 6为图 5所示上行纵波波场经空变倾角时差校正后(图 6a)及其走廊叠加记录(图 6b)与过井地面地震剖面(图 6c)的对比。可以看出, 上行反射纵波波场得到有效拉平, 走廊叠加记录精度得到大幅提高, 与地面地震剖面吻合很好。
|
图 6 经空变倾角时差校正后的上行纵波(a)及其走廊叠加记录(b)与地震剖面(c)对比 |
图 7a和图 7b分别给出了零偏VSP上行纵波波场经空变倾角时差校正和未经空变倾角时差校正的走廊叠加记录与过井地震剖面。可以清楚地看出, 未经空变倾角时差校正处理的走廊叠加记录不仅与地面地震剖面吻合很差, 信噪比也比空变倾角时差校正处理后的走廊叠加记录低很多。

|
图 7 空变倾角时差校正(a)和未经空变倾角时差校正(b)的走廊叠加记录与过井地震剖面的对比 |
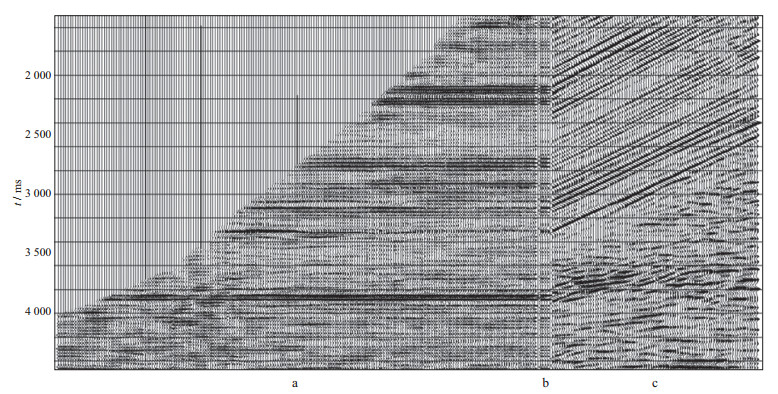
图 8为零偏VSP记录经空变倾角时差校正前、后的VSP速度(图 8a, 图 8b中红线)、声波测井速度(图 8a, 图 8b中蓝线)、上行纵波拉平地震剖面(图 8c)及其走廊叠加记录(图 8d)和过井地面地震剖面(图 8e)。可以看出, 在地层陡倾角部分, 零偏VSP速度(图 8a中红线)明显高于声波测井速度(图 8a中蓝线)。经空变倾角时差校正处理后的零偏VSP速度(图 8b中红线)与声波测井速度(图 8b中蓝线)吻合很好。
|
图 8 倾角时差校正前(a)、后(b)的VSP速度、测井速度与上行纵波拉平地震剖面(c)、走廊叠加记录(d)及地震剖面(e) |
图 8中的零偏VSP上行纵波拉平剖面(或走廊叠加记录)有效地将地面地震剖面和测井曲线关联到一起, 为大多现代软件所采用的零偏VSP桥式标定, 可在地震资料的综合解释中发挥重要作用。
图 9为塔里木库车探区另一口井的零偏VSP上行波场的空变倾角时差校正处理实例。图 9a和图 9b对比了VSP倾角时差校正前、后的上行波场及其走廊叠加记录与地震剖面。可以看出, 未经倾角时差校正的上行波场由于地层倾角较大, 初至波静校正无法使之有效拉平, 经空变倾角时差校正后, 即使倾角横向变化地层的上行反射同相轴也能得到充分拉平, 提高了走廊叠加记录的精度。特别对观测井段之下的地震反射, 如图 9a中3.1s附近的上行倾斜强反射, 如果不进行空变倾角时差校正处理, 被直接叠加到走廊叠加记录3.1s附近(图 9a中红色箭头所指), 不仅无法达到同相叠加且成像位置错误。经空变倾角时差校正处理后, 上述倾斜强反射被校正到3.18s附近强反射水平同相抽(图中黄色箭头所指), 并使走廊叠加记录正确成像, 波组特征与地面地震剖面吻合很好, 不仅实现了观测井段之下(钻前)地层深度的精确预测, 也实现了钻前波组特征的预测。
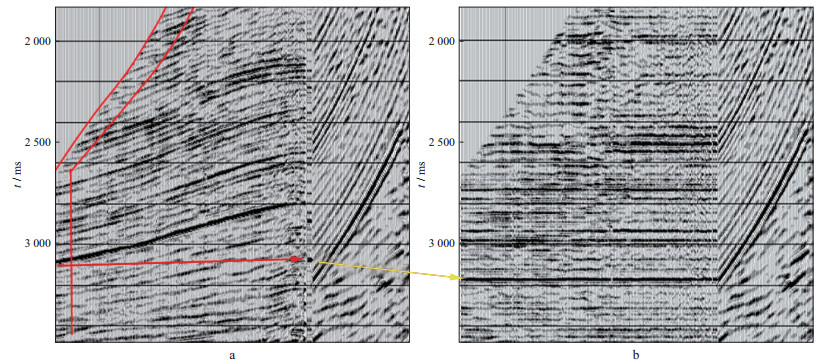
|
图 9 VSP倾角时差校正前(a)、后(b)的上行波场及其走廊叠加记录与地震剖面的对比 |
复杂高陡构造零偏VSP时深关系校正及空变倾角时差校正技术及其对实际资料的处理结果表明:
1) 复杂高陡构造零偏VSP空变倾角时差校正处理技术不仅可以提高零偏VSP走廊叠加记录精度, 还实现了观测井段之下(钻头前)地层深度的精确预测和波组特征预测。同时, 还将复杂的地震波传播时深关系校正到从激发点铅直向下传播到接收点的传播时深关系, 有助于降低钻井误差。
2) 目前的VSP资料常规处理流程无法满足复杂高陡构造零偏VSP资料处理要求, 地层倾角对零偏VSP资料的影响不可忽视, 特别是复杂高陡构造, 空变倾角时差校正是解决复杂高陡构造零偏VSP资料时深关系和层位标定精度的有效手段。
3) 对于地层倾角特别大或断层发育的复杂高陡构造, 建议对零偏VSP上行反射波场同时进行一维和二维地震成像处理。
| [1] |
姜本厚, 张凯, 张平平, 等. 时深标定中VSP时深关系调整影响因素分析[J].
石油地质与工程, 2014, 28(4): 62-66 JIANG B H, ZHANG K, ZHANG P P, et al. Influence factors and comparative analysis of VSP's time depth relationship adjustment in time depth calibration[J]. Petroleum Geology and Engineering, 2014, 28(4): 62-66 |
| [2] |
何惺华. 从VSP资料求取速度参数的方法[J].
石油物探, 1991, 30(1): 97-108 HE X H. Method for obtaining the speed parameter from VSP[J]. Geophysical Prospecting for Petroleum, 1991, 30(1): 97-108 |
| [3] |
田晶莹, 鬲寿和. 应用VSP资料进行地震特征波组的地质层位标定[J].
石油物探, 2000, 39(4): 100-106 TIAN J Y, GE S H. Geologic horizon calibration of seismic characteristic wave group using VSP data[J]. Geophysical Prospecting for Petroleum, 2000, 39(4): 100-106 |
| [4] |
孟恩, 牟风明, 赵彦青, 等. VSP走廊叠加倾角时差校正[J].
石油地球物理勘探, 2005, 40(6): 700-702 MENG E, MOU F M, ZHAO Y Q, et al. VSP corridor stack dip correction[J]. Oil Geophysical Prospecting, 2005, 40(6): 700-702 |
| [5] |
王保利, 朱广明. 零井源距VSP数据地层倾角分析和倾角时差校正[J].
石油地球物理勘探, 2009, 44(3): 282-287 WANG B L, ZHU G M. Formation dip analysis and corridor stack dip correction of zero-offset VSP[J]. Oil Geophysical Prospecting, 2009, 44(3): 282-287 |
| [6] |
姜本厚, 沈章洪, 张平平, 等. 倾斜地层的VSP时深标定研究[J].
石油地球物理勘探, 2012, 47(4): 598-604 JIANG B H, SHEN Z H, ZHANG P P, et al. Study on time depth calibration of VSP in inclined strata[J]. Oil Geophysical Prospecting, 2012, 47(4): 598-604 |
| [7] |
殷文, 唐建云, 朱剑兵, 等. VSP时差分析及时深关系校正[J].
地球物理学进展, 2014, 29(6): 2823-2830 YING W, TANG J Y, ZHU J B, et al. VSP first break time difference analysis and time depth relationship correction[J]. Progress in Geophysics, 2014, 29(6): 2823-2830DOI:10.6038/pg20140651 |
| [8] |
梁向豪, 罗斌, 张新东. 复杂高陡构造零井源距VSP资料常速度梯度射线追踪法VSP-CDP成像[J].
石油地球物理勘探, 2014, 49(2): 271-277 LIANG X H, LUO B, ZHANG X D. Complicated dipping structure zero-offset VSP data's VSP-CDP imaging using constant velocity gradient ray-tracing method[J]. Oil Geophysical Prospecting, 2014, 49(2): 271-277 |
| [9] |
康有元, 马丰臣, 满红霞, 等. 面向油田开发的井控地震资料处理技术及应用[J].
石油物探, 2013, 52(4): 402-408 KANG Y Y, MA F C, MAN H X, et al. Well control seismic data processing method and application for oil-field development[J]. Geophysical Prospecting for Petroleum, 2013, 52(4): 402-408 |
| [10] |
郭栋, 韩文功, 杨玉龙. 车西高分辨率地震资料精细层位标定方法[J].
石油地球物理勘探, 2001, 36(5): 533-539 GUO D, HAN W G, YANG Y L. Fin seismic layer identification using high resolution seismic data in Che Xi area[J]. Oil Geophysical Prospecting, 2001, 36(5): 533-539 |
| [11] | KENNETT P, IRESON R L, CONN P J, et al. Vertical seismic profiles:their applications in exploration geophysics[J]. Geophysical Prospecting, 1980, 28(5): 676-699DOI:10.1111/gpr.1980.28.issue-5 |
| [12] | CONN P J, BUCK S J. Use a zero-offset VSP to image a complex structure:a case history[J]. Expanded Abstracts of 57th Annual Internat SEG Mtg, 1987: 704-706 |
| [13] | WYATT K D, WYATT S B. The determination of subsurface structural information using the vertical seismic Profiles[J]. Expanded Abstracts of 51st Annual Internat SEG Mtg, 1981: 1915-1949 |
| [14] | MALLOY J M, SPENCER T W. A VSP transformation technique for the determination of subsurface structure[J]. Expanded Abstracts of 55th Annual Internat SEG Mtg, 1985: 32-34 |
| [15] | NOPONEN I. Application of slant moveout on VSP data to display reflector dips[J]. Expanded Abstracts of 58th Annual Internat SEG Mtg, 1988: 809-811 |
| [16] |
郭立鹏, 杨勤勇, 李振春, 等. 复杂各向异性介质初至波射线追踪[J].
石油物探, 2016, 55(1): 18-24 GUO L P, YANG Q Y, LI Z C, et al. First arrival ray tracing in complex anisotropic medium[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 18-24 |
| [17] | LANGAN R T, LERCHE I, CUTLER R T. Tracing of rays through heterogeneous media:an accurate and efficient procedure[J]. Geophysics, 1985, 50(9): 1456-1465DOI:10.1190/1.1442013 |
| [18] |
吴国忱, 王华忠, 马在田. 常速度梯度射线追踪与二维层速度反演[J].
石油物探, 2003, 42(4): 434-440 WU G C, WANG H Z, MA Z T. Ray tracing with constant velocity gradient and inversion of 2-D interval velocity[J]. Geophysical Prospecting for Petroleum, 2003, 42(4): 434-440 |


