2. 中国科学院地质与地球物理研究所, 北京100029;
3. 中国地质大学地球物理与信息技术学院, 北京100083
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. School of Geophysics and Information Technology, China University of Geosciences, Beijing 100083, China
多分量地震勘探能够同时获得纵波与转换横波资料, 既包含了地下构造信息, 也包含了反映岩性、流体特征以及裂缝信息, 因而可以降低常规纵波勘探的多解性[1-3]。20世纪末, 海上转换波地震技术使多分量地震勘探进入发展高潮, 从理论研究阶段开始转入工业化应用阶段[4-6]。国内在莺歌海盆地进行了海上多分量地震勘探的工业化应用, 在浅层气藏构造成像方面取得了良好效果[7-8]。近年来, 在陆上多分量地震勘探迅速发展的同时[9-12], 海上多分量地震勘探在采集和处理等方面也取得很大进展[13-14]。与陆上相比, 海底环境噪声低, 而且降速带比较简单, 噪声和静校正影响较小, 有利于转换波的记录及后期处理。但另一方面, 海上多分量地震勘探一般采用海底电缆四分量检波器(4C-OBC)记录数据, 包括一个水检H分量、一个陆检垂直分量Z和两个相互正交的水平分量X, Y[4], 不仅能够记录到上行纵波和横波, 也能记录到水层多次波等下行波, 波场分离和多次波去除远比陆上复杂。因此, 波场分离是海上多分量资料处理的关键问题。
常用波场分离方法包括平面波分解[15]、Radon变换[16]、偏振滤波[17]、波动方程法[18]等。与其它方法相比, 平面波分解法基于入射波在海底界面发生反射与透射时振幅响应与入射角的关系, 不仅可以分离纵波和横波, 也可以分离上行波和下行波, 因而成为海底多分量地震波场分离的主要方法。由于水检记录海水中的压力, 可以视为放置在海底之上, 而陆检三分量记录海底介质的质点偏振速度, 可以视为放置在海底之下[15], 因此海底多分量波场分离包括海底之上的声波分解和海底之下的弹性波分解两部分。
海底之上的声波分解也就是双检合成, 可以得到水检记录的上行和下行声波分量, 从而去除检波点端水层多次波。在地震波垂直入射的假设下, BARR[19]发展了x-t域双检合成的方法; BALL等[20]、BALE[21]、SOUBARAS[22]、OSEN等[23]在其基础上进行了改进。海底之下的弹性波分解即分离上行纵波和上行横波。基于透射和反射时的振幅响应以及纵横波的偏振特性, AMUNDSEN等[24]、DONATI等[25]、SOUBARAS[26]和WANG等[27]发展了多种分离方法, 这些方法求取的物理量是纵波势和横波势, 一般在τ-p域或ω-k域进行。近年来, SCHALKWIJK等[28]和EDME等[29]分别提出了不同的波场分离公式, 既包含海底之上的声波分解, 也包含海底之下的弹性波分解, 代表了海底波场分离的最新进展。为了发展更完善的波场分离方法, 我们通过正演获得波场分离的理论解, 测试两种方法的分离结果与理论解的差异, 并针对其存在的问题进行改进。
本文首先介绍了SCHALKWIJK和EDME提出的两种波场分离公式, 然后采用旋转交错网格和混合边界条件模拟得到一个海底水平多层模型的多分量记录, 同时在波场延拓的每一步采用亥姆霍兹算子和坡印廷矢量分离的方法得到上行和下行纵、横波理论记录, 并将两种方法的分离结果与理论解进行对比; 最后, 通过剥离水检上行分量的微屈反射和上行纵波分量的转换纵波, 对现有方法进行了补充完善。
1 两种海底多分量波场分离公式如果不考虑海底界面上的反射、透射和波型转换, 海底电缆四分量检波器能够记录的入射波包括水中下行声波、地下反射界面上行纵波和横波。如果考虑到水检可以视为放置在海底之上, 陆检三分量视为放置在海底之下, 那么上述3种入射波在海底之上和海底之下存在的所有透射、反射和波型转换关系如图 1所示。其中, “+”表示下行波, “-”表示上行波, “R”表示反射, “T”表示透射。由图 1可以看到, 位于海底之上的水检不仅可以记录到由水层多次波和检波点端多次波组成的下行声波Pw+, 也可以记录到由上行纵波透射形成的纵波、上行横波透射形成的转换纵波以及下行声波反射形成的微屈反射Ppegw-组成的上行声波Pw-, 前两者包含地下反射界面的有效信息, 可以记为上行声波有效分量Ppriw-。位于海底之下的陆检三分量不仅可以记录到上行纵波P-和上行横波S-, 也可以记录到由上行纵波在海底界面反射形成的纵波、上行横波反射形成的转换纵波与下行声波透射形成的纵波组成的下行纵波P+, 以及由上行纵波反射形成的转换横波、上行横波反射形成的横波与下行声波透射形成的转换横波组成的下行横波S+。综上所述, 经过海底界面上的反射、透射和波型转换, 海底四分量检波器可以记录上行和下行的纵/横波, 上行波和下行波的组成十分复杂, 但其中的有效信号只有上行纵波和横波。
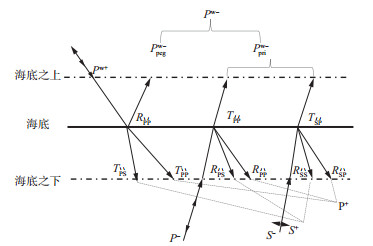
|
图 1 海底之上和海底之下的透射、反射和波型转换关系 |
根据上行和下行纵/横波在海底四分量检波器上的振幅响应关系, SCHALKWIJK等[28]提出了一种在ω-p域进行波场分离的公式, 即在海底之上进行声波分解:
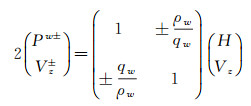
|
(1) |
同时在海底之下进行弹性波分解的公式为:
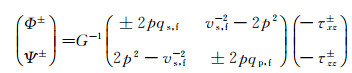
|
(2) |
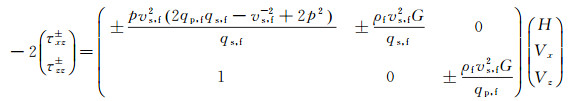
|
(3) |
式中:G=4p2vs, f2qp, fqs, f+vs, f2(qs, f2-p2)2; Φ是纵波势; Ψ是横波势; H为水检分量; Vx为陆检水平分量; Vz为陆检垂直分量; τzz为检波点附近海底介质的正应力; τxz为剪应力; p为水平慢度; qw为水中声波的垂直慢度; qp, f, qs, f是海底介质中纵波和横波的垂直慢度; ρw为海水密度; vp, f, vs, f, ρf分别表示海底检波点处的纵、横波速度和密度。
根据上行纵波、上行横波和下行声波在海底界面上的透射、反射和波型转换关系, EDME等[29]提出了在τ-p域进行波场分离的公式:

|
(4) |
公式(4) 上面两行表示海底之上的声波分解, 下面两行表示海底之下的弹性波分解。
可以看到, 两种波场分离公式的主要区别为:SCHALKWIJK公式既可以求取陆检记录的上行纵波和横波, 也可以求取下行纵波和横波; EDME公式考虑到陆检分量的所有下行纵波和横波都是由入射波反射或透射形成, 公式推导时将其振幅响应归溯到入射波分量, 因而没有计算下行纵波和横波。
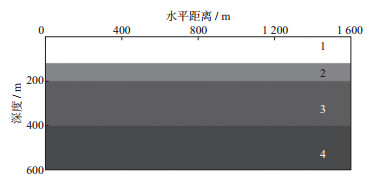
2 模型试算以海底水平多层各向同性介质模型为例, 模拟得到水检H分量、陆检X分量和Z分量的地震记录, 计算上行和下行纵/横波记录的理论解并作为波场分离测试的基础。模型尺寸为1600m×600m, 如图 2所示, 第1层为海水, 水深120m, 其它层为各向同性介质, 具体物理参数如表 1所示。如此设置模型参数, 是为了分离直达波、反射波、转换波以及多次波, 以便在炮记录上识别。在x=800m, z=8m网格点上震源激发纯纵波, 并将检波点等间隔布置在海底界面上, x和z方向的空间采样间隔为2m, 时间采样间隔为0.5ms, 记录时长为1.0s。采用时间二阶、空间十阶差分精度旋转交错网格[30]进行波场延拓计算, 在左、右、下边界构造完全匹配层进行吸收衰减, 同时采用应力镜像法在上边界构造自由界面[31-32], 最终得到中间放炮多分量地震记录, 如图 3所示。
|
图 2 海底水平多层介质模型 |
| 表 1 海底水平多层模型参数 |
|
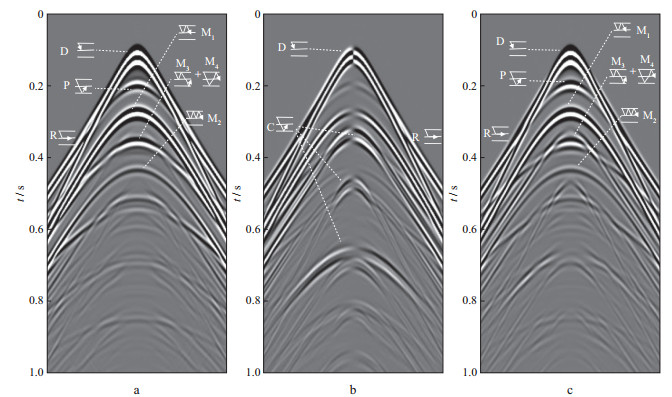
图 3 海底水平多层介质模型多分量记录 a水检H分量; b陆检X分量; c陆检Z分量 |
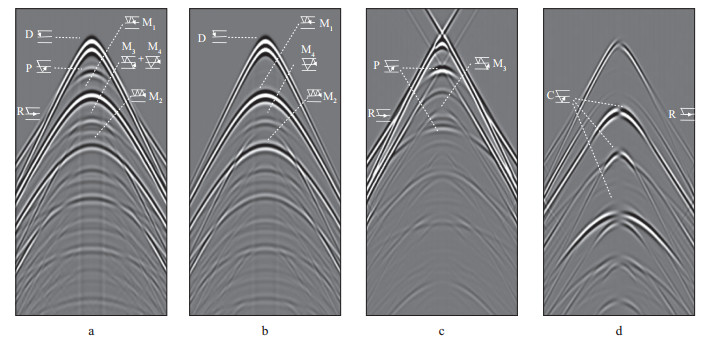
为便于分析, 对图 3中的直达波、折射波、反射纵波、转换波以及水层多次波进行了标注, 其中, D代表直达波, R代表折射波, P代表反射纵波, C代表转换横波, M1和M2分别代表 1阶和2阶水层多次波, M3和M4分别代表炮点端和检波点端多次波。可以看到:下行的水层多次波和检波点端多次波以及上行的炮点端多次波在海底四分量记录上都存在, 表现出明显的周期性; 陆检水平和垂直分量同时存在上行和下行的纵、横波, 波组相互混杂。
为了计算上行和下行纵/横波记录的理论解, 在波场正向延拓的每一步, 都将矢量波场分离成上行和下行的纵、横波波场, 并由布置在海底的检波器记录, 最终得到上行和下行的纵、横波炮记录。由于纵波是一种散度场, 横波是一种旋度场, 根据亥姆霍兹分解理论, 可以应用散度算子“∇·”和旋度算子“∇×”来求取弹性波场中的纵波和横波成分[33]:
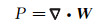
|
(5) |
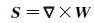
|
(6) |
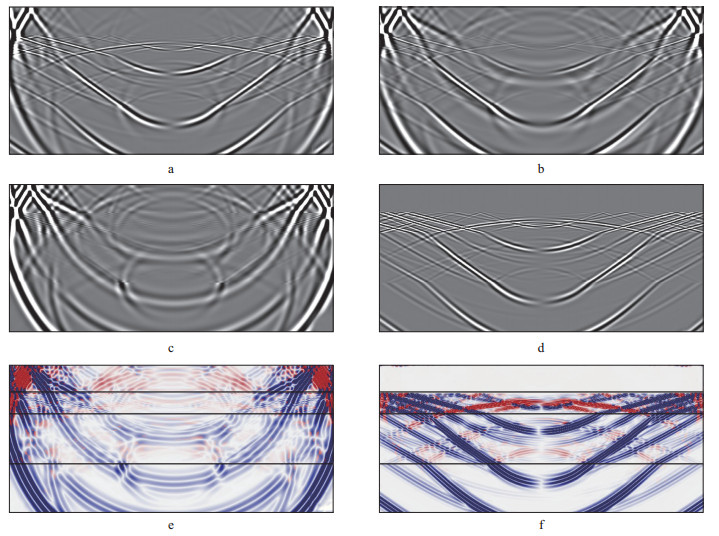
其中, ∇=(∂/∂x)i+(∂/∂z)k, W表示原有矢量波场。图 4为海底水平多层介质模型在t=600ms时的波场分离快照。其中, 图 4a和图 4b分别为原X和Z分量; 图 4c和图 4d分别为采用亥姆霍兹分解得到的纵波分量和横波分量。可以看到, 纵波与横波得到很好分离, 没有波型残留。坡印廷矢量法[34]分离上行波和下行波, 可以指示波场的能量流动方向。在二维弹性介质中, 坡印廷矢量F计算公式为:
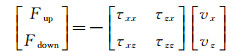
|
(7) |
|
图 4 海底水平多层介质模型t=600ms时的波场分离快照 a原X分量; b原Z分量; c纵波分量; d横波分量; e纵波的上、下行波分量; f横波的上、下行波分量 |
其中, Fup表示上行波, Fdown表示下行波。图 4e和图 4f分别为采用坡印廷矢量法分解得到的纵波和横波的上、下行波分量(其中, 红色表示上行波, 蓝色表示下行波)。可以看到, 除上、下行波相交时以一方为主而造成同相轴截断, 波场的上、下行波分量都能得到很好分离。
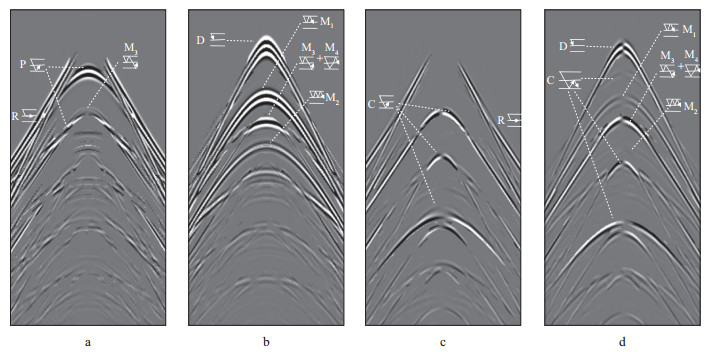
在波场正向延拓的每一步都进行上述分离计算, 最后得到波场分离炮记录如图 5所示。由图 5可以看到:原来连续的直达波和折射波被准确分离到上行波和下行波炮记录; 上行纵波炮记录以反射纵波为主, 但仍然存在炮点端多次波, 下行纵波炮记录以直达波、水层多次波和检波点端多次波为主; 与X分量相比, 上行横波记录没有上行纵波和下行多次波干扰, 此时上行横波记录中的折射波为转换折射波, 在折射纵波之后到达, 与其存在时差, 同理下行横波记录中的转换波主要由上行横波在海底界面反射形成, 与上行横波也存在时差。
|
图 5 海底水平多层介质模型波场分离炮记录理论解 a上行纵波; b下行纵波; c上行横波; d下行横波 |
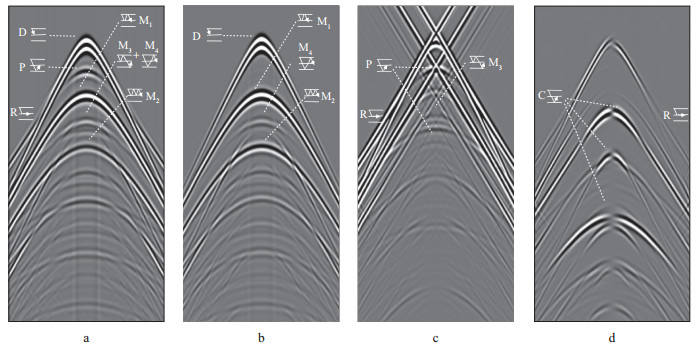
我们分别采用SCHALKWIJK公式和EDME公式进行波场分离试算, 结果如图 6和图 7所示。可以看到, 两种方法计算的上行声波和下行声波基本一致, 下行声波没有反射纵波和折射波, 以下行多次波为主, 表明声波分解准确; 两种方法得到的上行横波与理论解基本一致, 转换波的到达时与上行横波相同, 并保留了转换折射波, 残留的下行直达波主要由τ-p变换对波组的补偿效应引起; 如果不考虑“剪刀差”现象, 两种方法得到的上行纵波与理论解也基本一致, 但是由于分别将连续的直达波和折射波分配到上行波和下行波分量, 从而造成了波组截断, 所以容易引起“剪刀差”现象[35], 而且SCHALKWIJK公式的“剪刀差”问题更为严重, 这可能是由公式具体形式引起。
|
图 6 应用SCHALKWIJK公式进行波场分离的结果 a上行声波; b下行声波; c上行纵波; d上行横波 |
|
图 7 应用EDME公式进行波场分离的结果 a上行声波; b下行声波; c上行纵波; d上行横波 |
SCHALKWIJK公式和EDME公式的声波分解虽然准确, 但并不彻底, 从图 6和图 7可以看到, 上行声波仍然存在较强的多次波, 这是直达波、水层多次波和检波点端多次波下行到海底形成的上行微屈反射, 即图 1中的Ppegw-, 它与地下界面的有效反射Ppriw-共同组成了上行声波Pw-, 由于它不能直接反映海底地层信息, 因而也是一种干扰波, 需要进一步剥离。
考虑到上行声波包括上行微屈反射和有效反射, 下行声波包括直达波和下行多次波, 而所有的上行微屈反射均由下行波在海底反射形成, 若以Pdirw+表示直达波, Pmulw+表示下行多次波, Rpp表示海底反射系数, 那么可以得到以下关系式:
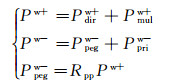
|
(8) |
将公式(8) 代入公式(4), 可以得到上行声波有效反射Ppriw-的τ-p域计算公式:
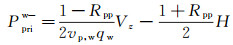
|
(9) |
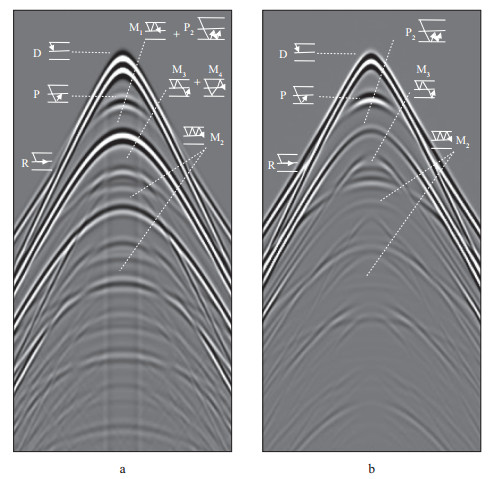
图 8对比了采用公式(9) 求取的上行声波有效反射与SCHALKWIJK和EDME公式求取的上行声波。可以看到, 由下行多次波引起的微屈反射M1和M2基本被剥离, 表明公式(9) 准确; 上行声波以有效反射为主, 还包括地层间多次波P2和炮点端上行多次波M3, 此时在一阶水层多次波M1的位置残留的波组是同时到达的地层间多次波P2, 由于剥离了一阶水层多次波, 因而振幅大幅减弱。
|
图 8 应用SCHALKWIJK和EDME公式求取的上行声波分量(a)和公式(9) 求取的上行有效反射(b) |
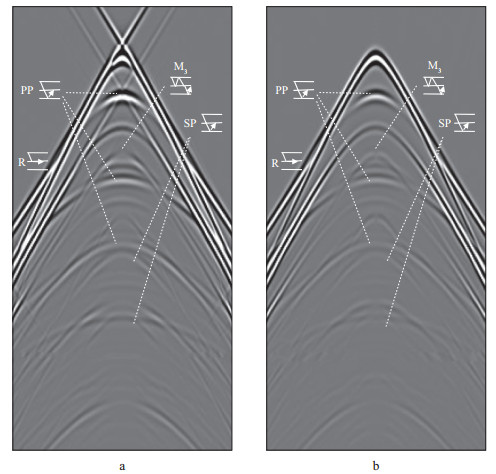
目前的波场分离方法存在的另一个问题是分离后的上行纵波中仍然存在SP型纵波, 如图 9所示, 它与全程都以纵波形式传播的PP型纵波共同组成了上行纵波, 但是其射线路径不对称, 从而影响了速度分析和偏移。
|
图 9 应用EDME公式求取的上行纵波(a)和公式(11) 求取的上行纯纵波(b) |
由于SP型纵波与PS型横波一般同时到达, 上行横波包括PS型和SS型, 而上行声波有效反射由PP, SP, PS和SS入射波透射形成, 即:
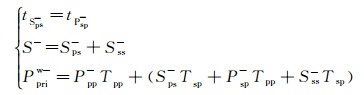
|
(10) |
式中:t表示旅行时; Sps-和Sss-分别表示上行PS型和SS型横波; Psp-和Ppp-分别表示上行SP型和PP型纵波; Ppriw-表示上行声波有效反射; Tsp和Tpp分别表示SP型和PP型纵波的透射系数。
因此, 在准确求取上行横波的前提下, 我们提出一种剥离SP型纵波从而得到纯PP型纵波的策略, 假设上行声波有效反射中由SP, PS以及SS入射波形成的波组与同时到达的上行横波在振幅上存在一定的比值, 那么可以由(11) 式计算上行纯纵波:
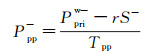
|
(11) |
其中, r表示PS入射波所在时窗内上行声波有效反射与上行横波的振幅比值。图 9对比了采用公式(11) 计算得到的上行纯纵波与EDME公式求取的上行纵波。可以看到, 部分SP型纵波被剥离, 而且不会出现“剪刀差”问题, 表明求取上行纯纵波的策略有效。
4 结束语由于海上降速带比较简单, 可以采集到比陆上信噪比更高的多分量地震资料, 因此, 海上多分量地震勘探的发展和应用前景更为广阔。但是, 多次波去除和波场分离是海上多分量地震勘探的关键。本文采用模型正演的方式, 得到了上行和下行纵/横波炮记录的理论解, 并与两种常用波场分离公式的处理效果进行了对比, 具体分析了分离前、后不同波组的变化, 并针对存在的问题进行了改进。获得以下3点结论:
1) SCHALKWIJK公式和EDME公式都可以准确分离上行声波、下行声波、上行纵波和横波, 但是由于将连续的直达波和折射波分离成下行和上行分量, 造成了波组截断, 因而在τ-p域计算得到的上行纵波存在“剪刀差”现象, 且SCHALKWIJK公式的“剪刀差”问题更为严重。
2) 原有波场分离公式计算的上行声波并不彻底, 在下行多次波的位置仍然存在微屈反射, 根据微屈反射均由下行波在海底反射形成的原理, 推导了从上行声波中剥离微屈反射的公式, 从而得到了更纯净的上行有效反射。
3) 提出一种由上行声波有效反射和上行横波计算上行纯纵波的方法, 可以剥离部分SP型纵波, 并避免了“剪刀差”问题。
下一步研究方向为将改进后的波场分离方法用于实际资料处理。
| [1] |
张永刚, 王赟, 王妙月. 目前多分量地震勘探中的几个关键问题[J].
地球物理学报, 2004, 47(1): 151-155 ZHANG Y G, WANG Y, WANG M Y. Some key problems in the multi-component seismic exploration[J]. Chinese Journal of Geophysics, 2004, 47(1): 151-155 |
| [2] |
黄中玉, 曲寿利, 王于静, 等. 三维多分量地震资料处理技术研究[J].
石油物探, 2010, 49(2): 140-146 HUANG Z Y, QU S L, WANG Y J, et al. The studies on 3-D multi-component seismic data processing techniques[J]. Geophysical Prospecting for Petroleum, 2010, 49(2): 140-146 |
| [3] |
赵波, 王赟, 芦俊. 多分量地震勘探技术新进展及关键问题探讨[J].
石油地球物理勘探, 2012, 47(3): 506-519 ZHAO B, WANG Y, LU J. Recent advances of multi-component seismic and some of its key issues[J]. Oil Geophysical Prospecting, 2012, 47(3): 506-519 |
| [4] | CALDWELL J. Marine multicomponent seismology[J]. The Leading Edge, 1999, 18(11): 1274-1282DOI:10.1190/1.1438198 |
| [5] | STEWART R R, GAISER J E, BROWN R J, et al. Converted-wave seismic exploration:methods[J]. Geophysics, 2002, 67(5): 1348-1363DOI:10.1190/1.1512781 |
| [6] | BARKVED O, BARTMAN B, GAISER J, et al. The many facets of multicomponent seismic data[J]. Oilfield Review, 2004, 16(2): 42-56 |
| [7] |
张树林, 李绪宣, 姜立红. 海上多波多分量地震技术新进展与发展方向[J].
物探化探计算技术, 2000, 22(2): 97-107 ZHANG S L, LI X X, JIANG L H. Improvement and development of China offshore multiwave and multi-component seismic technique[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2000, 22(2): 97-107 |
| [8] |
傅旦丹, 刘一峰, 沈丽丽, 等. 南海某构造二维多分量地震资料处理[J].
石油物探, 2004, 43(2): 181-184 FU D D, LIU Y F, SHEN L L, et al. Processing the 2D multicomponent seismic data of a structure in South China Sea[J]. Geophysical Prospecting for Petroleum, 2004, 43(2): 181-184 |
| [9] | LI X Y, ZHANG Y G. Seismic reservoir characterization:how can multicomponent data help?[J]. Journal of Geophysics and Engineering, 2011, 8(2): 123-141DOI:10.1088/1742-2132/8/2/001 |
| [10] |
程冰洁, 唐建明, 徐天吉. 转换波三维三分量地震勘探技术的研究现状及发展趋势[J].
石油天然气学报, 2008, 30(2): 235-238 CHENG B J, TANG J M, XU T J. Status and development of converted wave 3D-3C seismic technologies[J]. Journal of Oil and Gas Technology, 2008, 30(2): 235-238 |
| [11] |
陈海峰, 李向阳, 赵波, 等. 三维转换波处理技术研究及应用[J].
石油物探, 2013, 52(5): 512-518 CHEN H F, LI X Y, ZHAO B, et al. Study on 3D converted wave data processing method and application[J]. Geophysical Prospecting for Petroleum, 2013, 52(5): 512-518 |
| [12] | DONATI M, PIAZZA J L, ROLLET A, et al. 3D-3C multicomponent seismic-a successful fracture characterization case study in Algeria[J]. First Break, 2016, 34(1): 35-47 |
| [13] | PACAL E E.Seismic imaging with ocean-bottom nodes(OBN):new acquisition designs and the ATLANTIS 4C OBN survey[D]. Houston:University of Houston, 2012 |
| [14] | AMUNDSEN L, ROBERTSSON J O. Wave equation processing using finite-difference propagators, part 1:wavefield dissection and imaging of marine multicomponent seismic data[J]. Geophysics, 2014, 79(6): T287-T300DOI:10.1190/geo2014-0151.1 |
| [15] | MUIJS R, ROBERTSSON J O, HOLLIGER K. Data-driven adaptive decomposition of multi-component seabed seismic recordings[J]. Geophysics, 2004, 69(5): 1329-1337DOI:10.1190/1.1801949 |
| [16] | JIANG X X, LIN J, YE F, et al. Separation of P-P and P-SV wavefields by high resolution parabolic Radon transform[J]. Journal of Applied Geophysics, 2015, 119: 192-201DOI:10.1016/j.jappgeo.2015.05.011 |
| [17] | LU J, WANG Y, YAO C. Separating P-and S-waves in an affine coordinate system[J]. Journal of Geophysics and Engineering, 2012, 9(1): 12-18DOI:10.1088/1742-2132/9/1/002 |
| [18] | SUN R, MCMECHAN G A, HSIAO H H, et al. Separating P-and S-waves in prestack 3D elastic seismograms using divergence and curl[J]. Geophysics, 2004, 69(1): 286-297DOI:10.1190/1.1649396 |
| [19] | BARR F J. Dual sensor OBC technology[J]. The Leading Edge, 1997, 16(1): 45-51DOI:10.1190/1.1437427 |
| [20] | BALL V, CORRIGAN D. Dual sensor summation of noisy ocean-bottom data[J]. Expanded Abstracts of 66th Annual Internat SEG Mtg, 1996: 28-31 |
| [21] | BALE R. Plane wave deghosting hydrophone and geophone data[J]. Expanded Abstracts of 68th Annual Internat SEG Mtg, 1998: 730-733 |
| [22] | SOUBARAS R. Ocean botton hydrophone and geophone processing[J]. Expanded Abstracts of 66th Annual Internat SEG Mtg, 1996: 24-27 |
| [23] | OSEN A, AMUNDSEN L, REITAN A. Removal of water-layer multiples from multi-component sea-bottom data[J]. Geophysics, 1999, 64(3): 838-851DOI:10.1190/1.1444594 |
| [24] | AMUNDSEN L, REITAN A. Decomposition of multicomponent sea-floor data into upgoing and downgoing P-and S-waves[J]. Geophysics, 1995, 60(2): 563-572DOI:10.1190/1.1443794 |
| [25] | DONATI M S, STEWART R R. P and S wave separation at a liquid-solid interface[J]. Journal of Seismic Exploration, 1996, 5(2): 113-127 |
| [26] | SOUBARAS R. Multiple attenuation and P-S decomposition of multi-component ocean-bottom data[J]. Expanded Abstracts of 68th Annual Internat SEG Mtg, 1998: 1336-1339 |
| [27] | WANG Y, SINGH S C, BARTON P J. Separation of P and SV wavefields from multi-component seismic data in the τ-p domain[J]. Applied Geophysics, 2006, 3(3): 163-168DOI:10.1007/s11770-006-0024-1 |
| [28] | SCHALKWIJK K M, WAPENAAR C P A, VERSCHUUR D J. Adaptive decomposition of multicomponent ocean-bottom seismic data into downgoing and upgoing P-and S-waves[J]. Geophysics, 2003, 68(3): 1091-1102DOI:10.1190/1.1581081 |
| [29] | EDME P, SINGH S C. Receiver function decomposition of OBC data:theory[J]. Geophysical Journal International, 2009, 177(3): 966-977DOI:10.1111/gji.2009.177.issue-3 |
| [30] | SAENGER E H, GOLD N, SHAPIRO S A. Modeling the propagation of elastic waves using a modified finite-difference grid[J]. Wave Motion, 2000, 31(1): 77-92DOI:10.1016/S0165-2125(99)00023-2 |
| [31] |
杜启振, 孙瑞艳, 张强. 组合边界条件下二维三分量TTI介质波场数值模拟[J].
石油地球物理勘探, 2011, 46(2): 187-195 DU Q Z, SUN R Y, ZHANG Q. Numerical simulation of three-component elastic wavefield in 2D TTI media in the condition of the combined boundary[J]. Oil Geophysical Prospecting, 2011, 46(2): 187-195 |
| [32] | JASTRAM C, TESSMER E. Elastic modelling on a grid with vertically varying spacing[J]. Geophysical Prospecting, 1994, 42(4): 357-370DOI:10.1111/gpr.1994.42.issue-4 |
| [33] | DELLINGER J, ETGEN J. Wave-field separation in two-dimensional anisotropic media[J]. Geophysics, 1990, 55(7): 914-919DOI:10.1190/1.1442906 |
| [34] | DU Q Z, ZHU Y T, BA J. Polarity reversal correction for elastic reverse time migration[J]. Geophysics, 2012, 77(2): S31-S41DOI:10.1190/geo2011-0348.1 |
| [35] |
巩向博. 高精度Radon变换及其应用研究[D]. 吉林: 吉林大学, 2008
GONG X B.High precision Radon transform and its application[D]. Jilin:Jilin University, 2008 |



