地震波场数值模拟是由已知的岩石结构和物理参数建立地震地质模型, 依据不同的算法模拟地震波在地下介质中的传播过程, 计算在地面或地下各观测点的地震记录的一种方法, 是勘探地震学和地震波理论的重要基础。目前, 常用的数值模拟方法主要有射线追踪法[1]和波动方程法, 其中, 波动方程法有伪谱法[2-3]、有限元法[4]、边界元法[5]、谱元法[6]和有限差分法。自20世纪60年代ALTERMAN等[7]首先将有限差分方法用于地震波场的数值模拟以来, 该方法已经成为地震波场数值模拟中应用最为广泛的一种方法, 差分格式也由早期的低阶差分发展到高阶差分, 由常规网格发展到交错网格、旋转交错网格、可变网格等[8-16]。近似解析离散化(Nearly-Analytic Discrete, 以下简称NAD)[17-18]方法是近些年发展起来的一种有限差分数值模拟方法, 基本思想是在时间上采用泰勒公式展开, 在空间上利用截断的泰勒公式构造高阶插值函数来逼近空间偏导数, 与其它有限差分法的根本区别是该方法利用空间节点的位移和梯度来共同逼近变量的空间偏导数, 从而提高计算精度, 在粗网格下可有效地压制数值频散, 提高计算效率。YANG等[19-22]、卢明[23]、宋国杰[24-25]和TONG等[26]对该方法进行了研究和改进, 使得该方法逐步完善。
粘弹性介质是介于流相粘滞性介质和固相完全弹性介质之间的一种介质。开尔文粘弹性介质模型是地震学中一种重要的模型, 侧重于固相的特征, 对它的研究和数值模拟受到广大学者的重视。CARCIONE等[27-28]对粘弹地层中传播的声波进行了数值模拟。ROBERTSSON等[29]利用速度-应力方程组, 采用交错网格有限差分法对二维粘弹性介质中的弹性波进行了数值模拟研究, 并且将该算法推广到三维介质中。杜启振[30]利用伪谱法对各向异性粘弹介质中的波场进行了数值模拟。奚先等[31]利用波动方程交错网格有限差分数值模拟方法, 对地震波在二维粘弹性随机介质中的传播进行了模拟并研究了其波场特征。宋常瑜等[32]采用交错网格高阶有限差分数值模拟方法进行了井间地震粘弹性波场数值模拟。唐启军等[33]将Von Karman型的随机各向同性背景引入粘弹性单斜各向异性波动方程, 并应用交错网格技术进行模拟。
本文以一维开尔文粘弹模型为例, 首先讨论4种近似解析离散化方法的基本思想, 推导了差分方程的建立过程, 介绍了空间导数的求取和方程稳定性, 然后进行数值模拟, 依据数值模拟精度和计算效率, 确定了适合粘弹性声波方程数值模拟的方法。并首次将近似解析离散化方法应用到二维粘弹声波方程的数值模拟中, 通过对波场快照和地面地震记录的分析, 讨论了粘弹介质中声波的衰减规律。
1 方法原理地震勘探的非完全弹性介质的研究中, 经常使用一种称为粘弹性体或开尔文-佛各特(Kelvin-Voigt)体的模型。这种模型假定, 介质的应力包括两个部分, 一部分是弹性应力, 另一部分是粘滞应力, 其中弹性应力和应变成正比, 粘滞应力和应变的时间变化率成正比。也就是说, 应力与应变不再是简单的瞬时关系, 而与应变的历史有关, 其位移满足的矢量波动方程表示为:
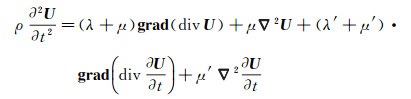
|
(1) |
式中:ρ为介质密度; U=(u, v, w)T为介质质点x, y和z方向的位移; grad表示梯度算子; div表示散度算子; ∇2为拉普拉斯算子; λ和μ为介质的拉梅系数; λ′和μ′为描述粘滞性质的两个参数, 称为粘滞系数。
1.1 4种NAD方法近似解析离散化是一种新的数值模拟方法, 下面以一维粘弹介质声波方程为例, 讨论该类方法的基本思想及4种NAD差分方程建立过程。
由公式(1) 可以得到一维粘弹介质声波波动方程:
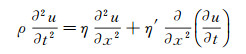
|
(2) |
其中, u表示质点x方向的位移, η=λ+2μ, η′=λ′+2μ′。
设满足声波方程的解为U, 有如下定义:
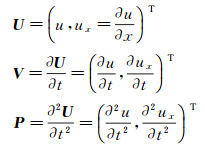
|
(3) |
式中:u表示质点位移大小; ux表示位移u在x方向的梯度; V表示U对时间的一阶偏导数; P表示U对时间的二阶偏导数。U, V和P之间满足:
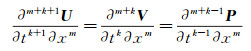
|
(4) |
式中:m, k分别表示U对x和t的偏导阶数。
时间上利用截断的泰勒公式对U和V展开可以得到:
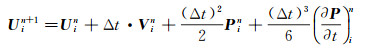
|
(5) |
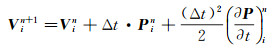
|
(6) |
式中:i表示U和V的空间网格点坐标; n和n+1表示U和V的时间网格坐标。P和P对时间的一阶偏导数可以由波动方程(2) 转化为U和V对空间的高阶偏导, 即:
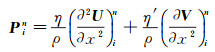
|
(7) |
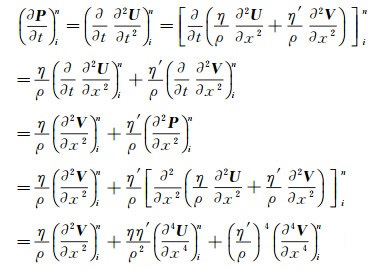
|
(8) |
由公式(5) 至公式(8) 可知, 只需要知道U和V及它们的空间偏导数在第n时间层的值, 即可计算第n+1时间层的值Uin+1, 其中, i表示空间网格坐标。在公式(7) 和公式(8) 中, 有位移U和V的空间高阶偏导数, 如∂2U/∂x2, ∂2V/∂x2, ∂4U/∂x4和∂4V/∂x4。根据NAD类方法的思想, 这些空间导数是利用待求空间网格点周围的27个点的位移及梯度共同逼近, 而不是仅仅采用位移近似, 这里只列举其中两个u对x的高阶导数((9) 式, (10) 式)进行说明, 其余高阶偏导数的近似函数见文献[19]。
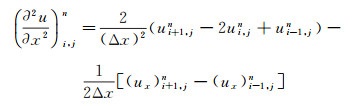
|
(9) |
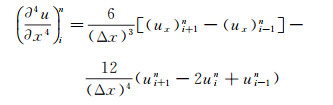
|
(10) |
从公式(9) 和公式(10) 可以看出, 要计算u对空间x的高阶导数, 不仅需要x方向左右两个点的位移, 还需要这两个点的位移梯度ux, 这正是NAD类方法与其它方法的不同之处。由于加上了梯度值, 使得近似精度更高, 更适合大尺度模型下粗网格的数值模拟[19]。
在公式(7) 和公式(8) 中, 有V对空间的高阶导数, 如果采用公式(11) 表示的一阶向后差分近似, 则称为近似解析离散化方法(NADM)[19]。
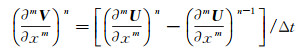
|
(11) |
式中:m表示空间偏导阶数。如果质点速度V也采用类似(9) 式和(10) 式的展开式, 则称为改进的近似解析离散化(Improving Nearly-Analytic Discrete, 简称INAD)方法[22]。如果将公式(5) 改为公式(12), 则称为精化的近似解析离散化方法(Refined Nearly-Analytic Discrete, 简称RNAD)[24], 仅仅是将公式(5) 中上一时刻的速度场替换为当前速度场, 用来计算新时间层的位移。
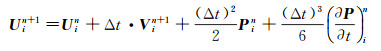
|
(12) |
如果计算位移场U时的速度项V由n和n+1时刻速度场的加权组合来代替, 则称为加权近似解析离散化方法(Weighted Nearly Analytic Discrete, 简称WNAD)[25], 即采用公式(13) 对位移场进行时间层推进。
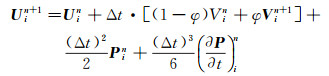
|
(13) |
式中:φ为加权系数, 取值范围为0~1。
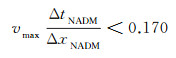
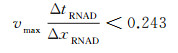
1.2 算法稳定性稳定性条件是有限差分数值模拟中一个非常重要的问题, 如果不满足稳定性条件, 则前面各层的舍入误差将会影响到后面各层的值, 如果误差的影响越来越大, 会使得有限差分的结果完全错误。文献[19, 22, 24, 25]利用Fourier方法研究了以上4种方法的稳定性, 并给出了稳定性条件。假设Δt为时间步长, Δx为空间网格间距, 最大的速度值为vmax, 稳定性条件为:
|
(14a) |
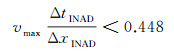
|
(14b) |
|
(14c) |
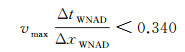
|
(14d) |
稳定性条件方面, NADM方法最为严格, 空间步长相同时, 所需的时间网格最小。INAD方法最为宽松, 所需要满足稳定性条件的时间网格最大, 更有利于进行长采样时间的数值模拟。
1.3 算法精度和效率分析为了比较NADM, RNAD, INAD和WNAD 4种近似解析离散化方法的数值模拟精度, 设置了一维粘弹介质模型, 模型长度16km, 声波速度4000m/s。模型品质因子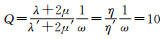
公式(2) 表示的一维粘弹介质声波方程, 其解析解可以表示为:
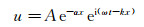
|
(15) |
式中:A为振幅; 波数k和吸收系数α都与频率ω有关。
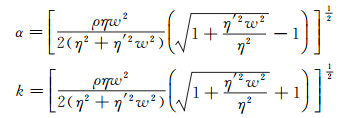
|
(16) |
数值模拟中, 取dt=0.8ms, dx=20m。在模型的8km处加载公式(15) 表示的震源, 可得图 1所示的2s时刻的波场快照和相对误差曲线, 相对误差定义如下:
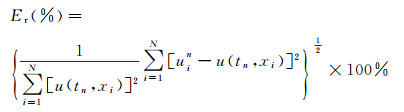
|
(17) |
|
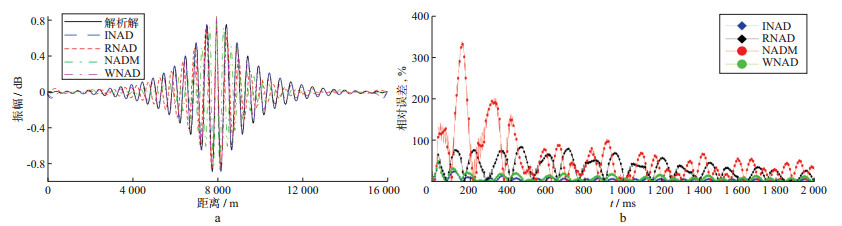
图 1 一维粘弹声波方程数值模拟波场快照(a)和相对误差(b) |
式中:u(tn, xi)表示精确解析解; uin表示数值解。采用WNAD方法时, 公式(13) 中的加权系数φ取0.5[25]。
从图 1可以看出:① INAD和WNAD两种方法数值模拟的结果与解析解的波剖面基本重合, 模拟精度较高, 而NADM和RNAD的相对误差较大; ② 数值模拟结果显示, 随着传播距离的增加, 振幅随之发生衰减, 而波长随之增加。采用同样的方法, 分析不同模型参数下的相对误差, 结果如表 1所示。
| 表 1 采用不同计算方法和模型时位移的平均相对误差 |
从表 1可以看出, 4种方法的相对误差都随时间步长或空间步长的增加而增大。整体而言, INAD结果的相对误差最小, 在空间步长为50m时, 平均相对误差为10.31%, 说明了该方法的可靠性和实用性。
下面从所需存储空间和计算时间两方面分析以上4种方法的计算效率。由于RNAD, WNAD和INAD 3种方法在速度场V的时间层推进上没有区别, 只是在计算位移场U时采用的速度场不同, RNAD用的是n+1时刻的速度场, INAD用的是n时刻的速度场, WNAD用的是加权的速度场, 所以这3种方法存储数组的数量没有差别。而NADM方法由于不需要按公式(6) 进行速度场时间层推进, 而是用位移场的向后差分进行计算, 所以存储数组个数减少了2个。从计算时间来看, 由于INAD具有最大的库郎数, 在取同样空间步长时, 它可采用较大的时间步长, 所以在同样的采样时间内, 其计算次数和时间最少。例如计算上述模型1时, NADM, RNAD, WNAD和INAD可取的时间步长分别为0.8, 1.2, 1.7, 2.2ms, 它们的时间推进层数分别约为2500, 1667, 1176和909次, INAD计算时间约是NADM, RNAD和WNAD的36%, 54%和77%。
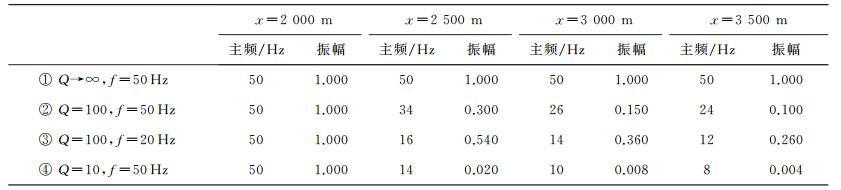
综合来看, 对粘弹声波方程进行数值模拟时, INAD方法具有较高的精度和计算效率, 所以本文利用该方法进行数值模拟, 并进一步分析一维粘弹介质中声波的传播规律。模型长度设置为4km, 声波速度4000m/s, 空间步长dx=10m, 时间步长dt=0.5ms。数值模拟时, 改变品质因子和信号频率:① Q→∞, f=50Hz; ② Q=100, f=50Hz; ③ Q=100, f=20Hz; ④ Q=10, f=50Hz。在x=2km处加载雷克子波震源信号, 得到2000, 2500, 3000, 3500m处质点的振动曲线和振幅谱如图 2所示, 振动曲线的主频及振幅见表 2。

|
图 2 一维粘弹声波方程数值模拟振动曲线(a, b, c, d)及其对应的频谱(e, f, g, h) |
| 表 2 不同Q及f时的信号主频及振幅 |
一维模型中传播的声波为平面波, 不存在波前扩散, 振幅和频率的衰减都是由介质的粘弹性导致的, 分析图 2和表 2, 结论如下。
1) 当Q→∞时, 随传播距离和时间的增加, 振幅和频率没有衰减, 粘弹声波方程等价于完全弹性声波方程, 同时也证明了INAD方法模拟结果的可靠性。
2) 比较② 和④ 说明, 当震源主频不变时, Q的大小决定了振幅和频率的衰减速度, 当Q=10时, 振幅发生最大的衰减, 衰减至0.004;频率也降低得最快, 降至8Hz。
3) 比较② 和③ 可以看出, 当Q一定时, 衰减系数近似地与频率的平方成正比, 高频信号衰减得快, 低频衰减得慢。② 中的频率降低了26Hz, 振幅降低了90%, 而③ 中的频率降低了8Hz, 振幅降低了74%。所以在地震勘探中, 地震波随着传播距离的增大, 高频成分很快被衰减, 深部地震信号只保留较低的频率成分。
4) 同公式(14) 表示的含义相同, 振幅随传播距离呈指数衰减, 开始衰减速度快, 随传播距离的增大, 衰减速率降低。频率的衰减也是如此。如模型④ 中的最初500m, 频率降低了36Hz, 振幅降低了98%, 而最后500m, 频率只降低了2Hz, 振幅降低50%。
2 二维模型试算二维粘弹介质声波波动方程为:
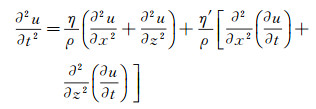
|
(18) |
与一维情况相同, 二维粘弹介质声波方程INAD方法的差分公式依然为公式(5) 和公式(6), 只是公式中P和∂P/∂t有所变化, 如下式所示:
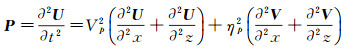
|
(19) |
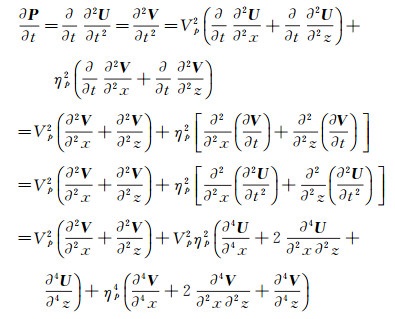
|
(20) |
其中,
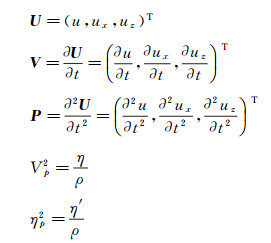
|
(21) |
且品质因子Q与λ, μ, λ′和μ′有关, 其大小由1.3节中公式给出。
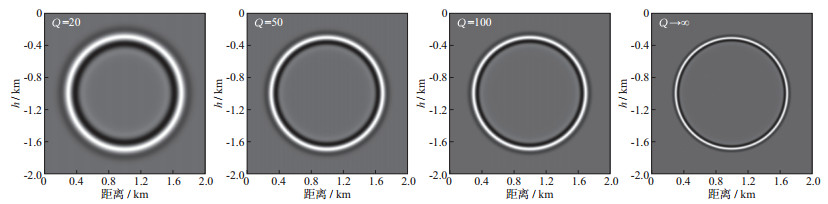
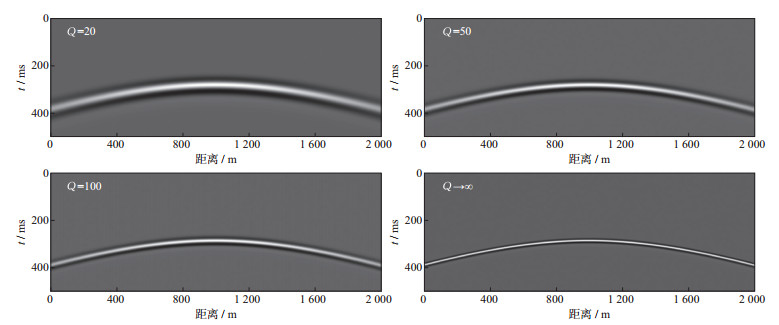
2.1 均匀粘弹声波方程模拟设置模型长度和深度均为2000m, vP=4000m/s。为了比较, 计算Q=20, 50, 100和趋近于∞(即完全弹性声波模拟)4种情况。时间步长Δt=0.5ms, 空间网格Δx=Δz=10m, 模型中间(x=1000m, z=1000m)位置激发主频50Hz雷克子波, 获得的200ms波场快照如图 3所示, 图 4为地表接收到的地震记录, 记录长度500ms。
|
图 3 200ms时刻波场快照 |
|
图 4 z=0处地震记录 |
从图 3和图 4所示的波场快照和地震记录可以看出:① 模拟波场非常清晰, 没有数值频散; ② 同一时刻, 粘弹声波模拟和完全弹性(Q→∞)声波模拟的波前位置相同, 证实了方法的可靠性; ③ 随着Q的减小, 地震波波长增加, 波数降低; 频率降低, 同相轴变宽, 子波延续时间增加; ④ 粘弹性介质中, 地震波随传播距离的增加, 振幅呈指数衰减, 地震记录中远道的振幅要明显小于近道。
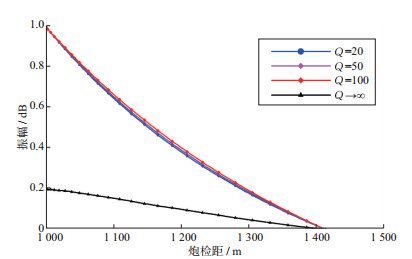
为了分析地震波衰减规律, 将图 4中的4个反射波的振幅归一化到0~1, 得到炮检距-振幅曲线(图 5)。从图 5可以看出:① 当采用完全弹性声波模拟时(Q→∞), 与一维情况不同, 振幅随地震波的传播发生波前扩散, 振幅与传播距离呈反比关系; ② 当采用粘弹声波模拟时, 除存在波前扩散外, 还存在粘弹介质对地震波的吸收衰减, 使得衰减加剧; ③ 衰减速度由Q决定, Q越小, 衰减越快。
|
图 5 炮检距-振幅曲线 |
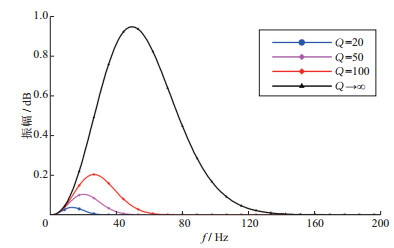
对图 4所示的地震记录, 提取x=1000m位置处质点的单道记录并进行频谱分析, 得到不同Q情况下的振动曲线的振幅谱(图 6)。图 6显示了不同Q时频率衰减大小, 完全弹性声波模拟时记录信号的主频依然为50Hz, 频带范围为32~70Hz。随着Q的减小, 粘弹声波信号的高频成分减少得越多, Q=20时的频率降低至14Hz, 频带范围减小为8~19Hz, 这与实际地震记录中的频谱特征一致。
|
图 6 振幅谱曲线(x=1000m, z=0) |
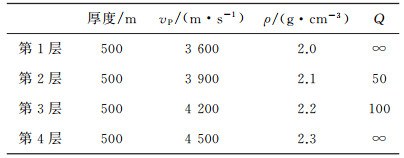
利用INAD方法对4层层状模型分别进行粘弹和完全弹性声波方程模拟试算, 模型长度和深度均为2000m, 各层岩石物理参数如表 3所示。
| 表 3 4层水平层状介质模型参数 |
为了比较粘弹性和完全弹性介质中地震波场的差异, 第2层和第3层的Q分别取50, 100。时间步长Δt=0.5ms, 空间网格Δx=Δz=10m, 模型地表中间(x=1000m, z=0) 位置激发主频为40Hz的雷克子波, 获得不同时刻的波场快照(图 7, 图 8, 图 9)和地表接收的单炮记录(图 10), 记录长度600ms。在数值模拟中, 采用PML吸收边界处理, 算法见文献[33]和文献[34], 这里不再赘述。
|
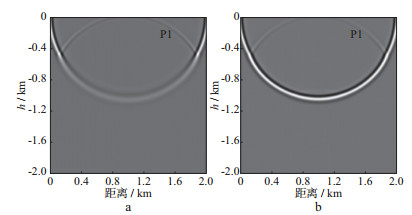
图 7 t=300ms波场快照 a粘弹声波模拟; b完全弹性声波模拟 |
|
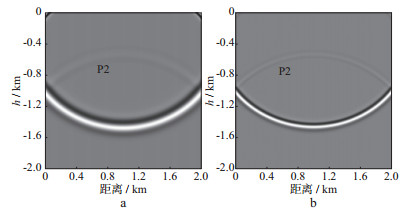
图 8 t=400ms波场快照 a粘弹声波模拟; b完全弹性声波模拟 |
|
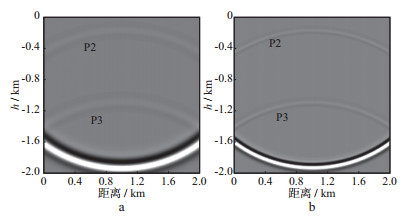
图 9 t=500ms波场快照 a粘弹声波模拟; b完全弹性声波模拟 |
|
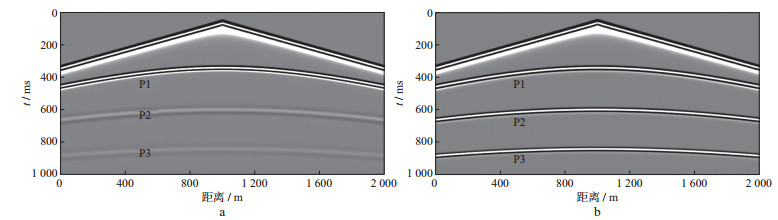
图 10 地震记录 a粘弹声波模拟; b完全弹性声波模拟 |
图 7至图 10中, P1, P2和P3代表来自3个反射界面的反射P波。图 7中, 因为第1层设置为完全弹性介质, 所以粘弹声波和弹性声波模拟快照中的P1相同。而透射进入第2层、第3层地层的P波则出现了差异, 正是由于粘弹介质对地震波的吸收衰减, 导致了粘弹声波模拟结果中的P2和P3反射波振幅明显衰减, 同相轴变宽, 子波延续时间增加, 波长增大。
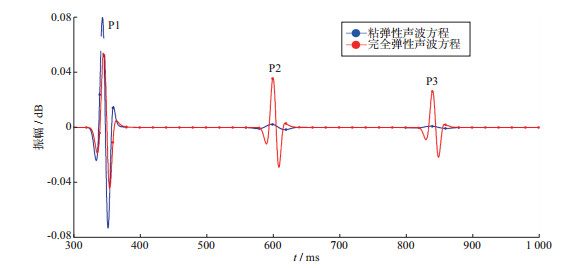
图 11是从上述两次模拟地面记录中抽取的单道地震记录(x=1500m), 由于直达波能量太强, 所以显示时间从300ms开始。波前扩散导致弹性声波记录的振幅随传播时间和距离逐步减弱, 而粘弹声波记录的振幅衰减速度增大, 这与波场快照中的规律一致。图 11显示了第1层反射波(350ms左右)振幅, 可以看出, 弹性声波的振幅要略小于粘弹声波的振幅, 这是由于第2层变为粘弹介质后, 导致P波的垂直反射系数增大。为了进一步分析两次模拟记录在频谱上的差别, 利用广义S变换, 对这两道地震记录进行时频分析, 结果如图 12和图 13所示。
|
图 11 x=1500m处单道地震记录 |
|
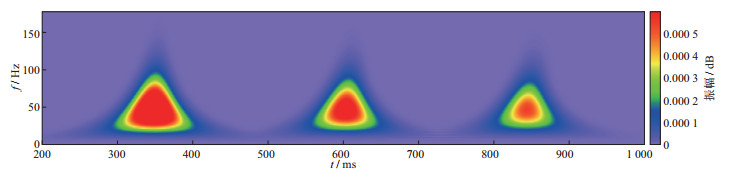
图 12 x=1500m处单道地震记录时频分析结果(完全弹性声波模拟) |
|
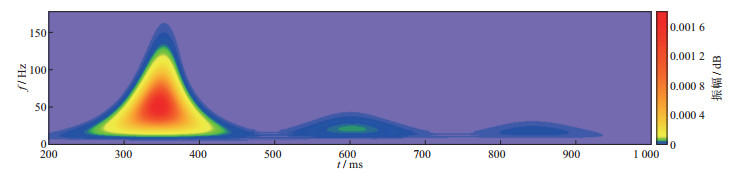
图 13 x=1500m处单道地震记录时频分析结果(粘弹声波模拟) |
从时频分析结果中提取3层反射波主频和振幅,结果如表 4所示。表 4中数据表明:① 当采用弹性声波模拟时, 子波信号的主频和频带范围基本不变, 实际上这并不能准确地描述地震波在地下的传播规律。在传播过程中发生的振幅衰减是由波前扩散导致的, 在2000m厚度模型中, 振幅衰减了约50%。② 采用粘弹声波模拟能更加精确地描述地震波在粘弹介质中的传播特征, 子波主频和频带宽度均随传播深度的增加而减小, 衰减速度与介质的品质因子和子波频率有关。振幅除了波前扩散外, 衰减会变得更剧烈, 本模型中, 振幅衰减了约98%。③ 虽然子波频率降低和频带变窄会导致地震资料纵向分辨率降低, 但这些频率衰减特征正好可以指导含油气储层的预测工作(因为岩石含流体后, 会使其粘弹性质更加明显)。
| 表 4 弹性和粘弹性声波模拟的3层反射波主频及振幅 |
粘弹介质地震波场的数值模拟研究对地震勘探具有重要的意义, 有助于人们更清楚地认识地震波在岩石和油气储集区的传播规律, 具有较强的理论和现实意义。本文将一种新的数值模拟方法应用到粘弹介质声波方程的数值模拟中, 研究结果表明:① 改进的近似解析离散化(INAD)有限差分算法在粗网格下具有较高的精度, 更有利于大尺度模型的数值模拟, 为粘弹介质的地震波场数值模拟提供了新的思路和方法; ② 采用完全弹性声波模拟时, 振幅只随波前扩散发生衰减, 而子波信号的频率和频带范围基本不变; ③ 采用粘弹声波模拟时, 振幅在波前扩散的基础上, 衰减幅度增加; 同时, 子波主频和频带宽度随传播深度的增加而减小, 衰减速度与介质的品质因子和子波频率有关。
由于近似解析离散化方法在空间上可求得位移的最高5阶空间导数, 且粘弹介质波动方程中存在速度项, 使得本文中采用的INAD方法的差分精度为时间二阶和空间四阶, 在下一步研究中, 需要进一步研究时间差分精度更高的近似解析离散化方法, 提高粘弹介质的模拟精度。其次, 可将该类方法在其它粘弹介质模型的全波场数值模拟中进一步推广, 扩大该类方法的适用范围。
| [1] | CERVENY V. Seismic rays and ray intensities in inhomogeneous anisotropic media[J]. Geophysical Journal International, 1972, 29(1): 1-33DOI:10.1111/j.1365-246X.1972.tb06147.x |
| [2] | KOSLOFF D D, BAYSAL E. Forward modeling by a Fourier method[J]. Geophysics, 1982, 47(10): 1402-1412DOI:10.1190/1.1441288 |
| [3] | RESHEF M, KOSLOFF D D, EDWARDS M, et al. Three dimensional elastic modeling by the Fourier method[J]. Geophysics, 1988, 53(9): 1184-1193DOI:10.1190/1.1442558 |
| [4] | DRAKE L A. Rayleigh waves at a continental boundary by the finite element method[J]. Bulletin of the Seismological Society of America, 1972, 62(5): 1259-1268 |
| [5] | BOUCHON M, COUTANT O. Calculation of synthetic seismograms in a laterally varying medium by the boundary element-discrete wavenumber method[J]. Bulletin of the Seismological Society of America, 1994, 84(6): 1869-1881 |
| [6] | KOMATISSCH D, BARNES C, TROMP J. Simulation of anisotropic wave propagation based upon a spectral element method[J]. Geophysics, 2000, 65(4): 1251-1260DOI:10.1190/1.1444816 |
| [7] | ALTERMAN Z, KARAL F C. Propagation of seismic wave in layered media by finite difference methods[J]. Bulletin of the Seismological Society of America, 1968, 58(1): 367-398 |
| [8] | KELLY K R, WARD R W, TREITEL S, et al. Synthetic seismograms:a finite-difference approach[J]. Geophysics, 1976, 41(1): 2-27DOI:10.1190/1.1440605 |
| [9] | VIRIEUX J. P-SV wave propagation in heterogeneous media:velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4): 889-901DOI:10.1190/1.1442147 |
| [10] | GRAVES R W. Simulation seismic wave propagation in 3D elastic media using staggered-grid finite differences[J]. Bulletin of the Seismological Society of America, 1996, 86(4): 1091-1106 |
| [11] |
董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J].
地球物理学报, 2000, 43(3): 411-419 DONG L G, MA Z T, CAO J Z, et al. The staggered-grid high-order difference method of first-order elastic equation[J]. Chinese Journal of Geophysics, 2000, 43(3): 411-419 |
| [12] |
董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J].
地球物理学报, 2000, 43(6): 856-864 DONG L G, MA Z T, CAO J Z. The stability study of the staggered-grid high-order difference method of first-order elastic equation,[J]. Chinese Journal of Geophysics, 2000, 43(6): 856-864 |
| [13] |
董良国. 弹性波数值模拟中的吸收边界条件[J].
石油地球物理勘探, 1999, 34(1): 46-56 DONG L G. Absorptive boundary condition in elastic-wave numerical modeling[J]. Oil Geophysical Prospecting, 1999, 34(1): 46-56 |
| [14] |
王书强, 杨顶辉, 杨宽德. 弹性波方程的紧致差分方法[J].
清华大学学报(自然科学版), 2002, 42(8): 1128-1131 WANG S Q, YANG D H, YANG K D. Compact finite difference scheme for elastic equations[J]. Journal of Tsinghua University(Science and Technology), 2002, 42(8): 1128-1131 |
| [15] | SAENGER E H, GOLD N, SHAPIRO S A. Modeling the propagation of elastic waves using a modified finite-difference grid[J]. Wave Motion, 2000, 31(1): 77-92DOI:10.1016/S0165-2125(99)00023-2 |
| [16] | SAENGER E H, BOHLEN T. Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid[J]. Geophysics, 2004, 69(2): 583-591DOI:10.1190/1.1707078 |
| [17] | KONDOH Y, HOSAKA Y, ISHⅡ K. Kernel optimum nearly-analytical discrimination algorithm applied to parabolic and hyperbolic equations[J]. Computers & Mathematics with Applications, 1994, 27(3): 59-90 |
| [18] |
杨顶辉, 滕吉文, 张中杰. 三分量地震波场的近似解析离散模拟技术[J].
地球物理学报, 1996, 39(S1): 283-291 YANG D H, TENG G W, ZHANG Z J. Nearly-analytical discretization modeling technique of 3-component seismic wave-fields[J]. Chinese Journal of Geophysics, 1996, 39(S1): 283-291 |
| [19] | YANG D H, TENG J W, ZHANG Z J, et al. A nearly-analytic discrete method for acoustic and elastic wave equation[J]. Bulletin of the Seismological Society of America, 2003, 93(2): 882-890DOI:10.1785/0120020125 |
| [20] | YANG D H, LU M, WU R S, et al. An optimal nearly-analytic discrete method for 2D acoustic and elastic wave equations[J]. Bulletin of the Seismological Society of America, 2004, 94(5): 1982-1991DOI:10.1785/012003155 |
| [21] | YANG D H, SONG G J, LU M. Optimally accurate nearly-analytic discrete scheme for wave-filed simulation in 3D anisotropic media[J]. Bulletin of the Seismological Society of America, 2007, 97(5): 1557-1569DOI:10.1785/0120060209 |
| [22] | YANG D H, SONG G J, CHEN S, et al. An improved nearly analytical discrete method:an efficient tool to simulate the seismic response of 2-D porous structures[J]. Journal of Geophysics & Engineering, 2007, 4(1): 40-52 |
| [23] |
卢明. 改进的近似解析离散化方法及弹性波波场模拟[D]. 北京: 清华大学, 2004
LU M.The optimum nearly analytic discrete method and elastic wave numerical simulations[D]. Beijing:Tsinghua University, 2004 http://cdmd.cnki.com.cn/Article/CDMD-10003-2005036250.htm |
| [24] |
宋国杰. 三维弹性波方程的改进近似解析离散化方法及波场模拟[D]. 北京: 清华大学, 2008
SONG G J.The improved nearly analytic discrete method for 3D elastic equations and its numerical simulation[D]. Beijing:Tsinghua University, 2008 http://cdmd.cnki.com.cn/Article/CDMD-10003-2009083304.htm |
| [25] |
宋国杰. 基于WNAD方法的非一致网格算法及其弹性波场模拟[J].
地球物理学报, 2010, 53(8): 1985-1992 SONG G J. Non-uniform grid algorithm based on the WNAD method and elastic wave-field simulations[J]. Chinese Journal of Geophysics, 2010, 53(8): 1985-1992 |
| [26] | TONG P, YANG D H, HUA B L. High accuracy wave simulation-Revised derivation, numerical analysis and testing of a nearly analytic integration discrete method for solving acoustic equation[J]. International Journal of Solids & Structures, 2011, 48(1): 56-70 |
| [27] | CARCIONE J M, KOSLOFF D, KOSLOFF R. Wave propagation simulation in a linear viscoacoustic medium[J]. Geophysical Journal International, 1988, 93(2): 393-401DOI:10.1111/j.1365-246X.1988.tb02010.x |
| [28] | CARCIONE J M, KOSLOFF D, KOSLOFF R. Viscoacoustic wave propagation simulation in the Earth[J]. Geophysics, 1988, 53(6): 769-777DOI:10.1190/1.1442512 |
| [29] | ROBERTSSON J O A, BLANCH J O. Viscoelastic finite-difference modeling[J]. Geophysics, 1994, 59(9): 1444-1456DOI:10.1190/1.1443701 |
| [30] |
杜启振. 各向异性黏弹性介质伪谱法波场模拟[J].
物理学报, 2004, 53(12): 4428-4434 DU Q Z. Wavefield forward modeling with the pseudo-spectral method in viscoelastic and azimuthally anisotropic media[J]. Acta Physica Sinica, 2004, 53(12): 4428-4434DOI:10.3321/j.issn:1000-3290.2004.12.069 |
| [31] |
奚先, 姚姚. 二维粘弹性随机介质中的波场特征分析[J].
地球物理学进展, 2004, 19(3): 608-615 XI X, YAO Y. The analysis of the wave field characteristics in 2-D viscoelastic random medium[J]. Progress in Geophysics, 2004, 19(3): 608-615 |
| [32] |
宋常瑜, 裴正林. 井间地震粘弹性波场特征的数值模拟研究[J].
石油物探, 2006, 45(5): 508-513 SONG C Y, PEI Z L. Numerical simulation of viscoelastic wevefield exploration[J]. Geophysical Prospecting for Petroleum, 2006, 45(5): 508-513 |
| [33] |
唐启军, 韩立国, 王恩利, 等. 基于随机各向异性背景的粘弹性单斜介质二维三分量正演模拟[J].
西北地震学报, 2009, 30(1): 35-39 TANG Q J, HAN L G, WANG E L. 2-D three-component seismic modeling for viscoelastic monoclinic media based on background of random isotropic media[J]. Northwestern Seismological Journal, 2009, 30(1): 35-39 |
| [34] |
单启铜, 乐友喜. PML边界条件下二维粘弹性介质波场模拟[J].
石油物探, 2007, 46(2): 126-130 SHAN Q T, YUE Y X. Wavefield simulation of 2-D viscoelastic medium in perfectly matched layer boundary[J]. Geophysical Prospecting for Petroleum, 2007, 46(2): 126-130 |