2. 中国科学院地质与地球物理研究所, 中国科学院油气资源研究重点实验室, 北京100029;
3. 中国石油化工股份有限公司石油物探技术研究院, 江苏南京211103;
4. 山东科技大学地球科学与工程学院, 山东青岛266590
2. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. Sinopec Geophysical Research Institute, Nanjing 211103, China;
4. .College of Earth Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China
各向异性正演数值模拟是各向异性逆时偏移和各向异性全波形反演的基础[1]。1986年, THOMSEN[2]提出了在大多数情况下地球介质为弱各向异性(各向异性参数为10%~20%)的观点, 并在弱各向异性假设下提出弱各向异性横向各向同性(TI)理论, 即用3个各向异性参数——Thomsen各向异性参数ε(纵波各向异性参数)、δ(变异系数)和γ(横波各向异性参数)表述P波、SV波及SH波特征。此后30年, 关于各向异性介质的研究基本都是基于弱各向异性理论。
1996年, TSVANKIN[3]基于THOMSEN的弱各向异性理论推导得到P-SV波VTI介质精确相速度频散方程。2006年, ZHOU等[4]从TSVANKIN相速度频散方程出发, 推导得到TTI介质qP波波动方程, 该方程虽然采用了令横波速度为0的TTI声波近似, 但仍然是一个P-SV波耦合的波动方程, 因为各向异性波场传播过程中伪SV波仍然存在[5], 而且在角度剧变(即各向异性的对称轴在空间变化较快)情况下波场传播存在严重的不稳定性问题[6]。为了解决TTI介质声波近似各向异性波场传播存在的不稳定性问题, FLETCHER等[7]引入适当的横波分量来减小角度剧变时产生的不稳定性, 但是同时也带来了较强的伪SV波假象。DUVENECK等[8-9]从Hooke定律和运动学方程出发推导得到新的TTI介质方程; ZHANG等[10-11]从VTI介质弹性波方程出发采用自共轭旋转方式推导出一个自共轭3D TTI波动方程。但上述方程仍然存在伪SV波假象且在角度剧变时不稳定。FOWLER等[12]从特征值矩阵分析的角度对各种TTI介质耦合方程的精度和稳定性进行了综合分析。BUBE等[13-14]讨论了二阶TI介质波动方程在TTI介质声波近似情况下不稳定性产生的原因并推导了新的声波和弹性波TI介质一阶波动方程。
TTI介质正演时, 吸收边界条件至关重要, 因为吸收边界条件极大地影响正演模拟效果。地下介质被视为无限半空间, 而计算区域有限, 因此在人为截取的有限空间内求解波动方程会导致很强的人工边界反射, 必须采用吸收边界条件对人工边界反射进行有效吸收。目前常用的吸收边界条件包括单程波旁轴近似吸收边界条件[15]和衰减吸收边界条件[16-17]两大类。CLAYTON等[15]提出的单程波旁轴近似吸收边界条件应用广泛, 在小角度反射时吸收效果较好, 但对大角度入射的波吸收效果较差。CERJAN等[16]提出了添加阻尼层的海绵吸收边界条件, 该边界条件不受波动方程形式的限制, 很容易实现, 但是边界吸收的效果仍较差。BORDING[18]对CERJAN等[16]提出的阻尼系数进行了优化, 计算得到优化的海绵吸收系数, 但是计算效率相对CERJAN等的方法有所降低。BERENGER[17]最早在电磁学领域提出了完全匹配层(PML)吸收边界条件, 能达到完美的边界吸收效果。CHEW等[19]将PML吸收边界条件用于地震波数值模拟中, 取得了很好的应用效果。BÉCACHE等[20]对各向异性介质的PML吸收边界条件进行了深入研究, 指出各向异性介质应用PML吸收边界条件时存在不稳定性。PML吸收边界条件是目前应用效果最好的吸收边界条件, 代表吸收边界技术研究的前沿发展方向, 但是其公式推导和编程实现复杂, 需要对不同的波动方程推导不同的PML方程形式。
作为PML吸收边界条件技术研究的一个重要方面, 分裂式PML(SPML)吸收边界条件已经得到广泛应用。COLLINO等[21]提出二维弹性波介质一阶速度-应力方程的SPML算法; 裴正林[22-23]将该算法推广到三维弹性波介质, 实现了基于SPML吸收边界条件的三维弹性波介质波动方程交错网格高阶有限差分法数值模拟。
本文研究的TTI介质时间域SPML吸收边界条件能很好地吸收边界反射, 实现TTI介质高精度数值模拟。
1 方法原理 1.1 TTI介质耦合qP波波动方程P-SV波VTI介质精确相速度频散方程为[3]:
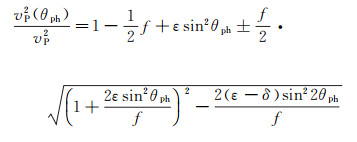
|
(1) |
式中:f=1-vSZ2/vPZ2, vSZ表示横波速度, vPZ表示纵波速度; vP(θph)表示相速度, θph表示相速度传播角度; ε和δ表示Thomsen各向异性参数[2]。
在推导过程中直接引入TTI介质声波近似(TTI介质声波近似情况下直接令横波速度vSZ=0)[24], 此时推导得到的2D TTI介质方程为[4]:
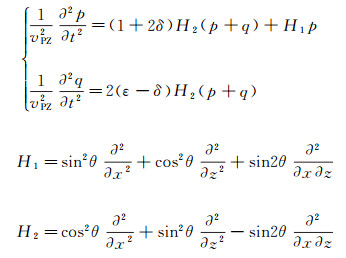
|
(2) |
式中:θ为对称轴倾角; p为地震波场; q为辅助波场; H1和H2为辅助变量, 其3D TTI方程形式为:
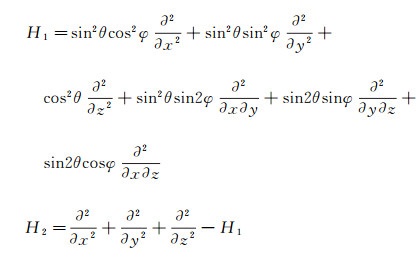
|
(3) |
式中:φ为三维方位角。当θ=0时, (3) 式退化为3D VTI方程(垂直对称轴的TI方程); 当θ=90°时, (3) 式退化为3D HTI方程(水平对称轴的TI方程); 当三维方位角φ=0时, (3) 式简化为2D TTI方程。VTI介质和HTI介质都可以看作是TTI介质的某种特殊情形。
本文将ZHOU等[4]、DUVENECK等[8-9]和ZHANG等[10-11]直接采用vSZ=0的TTI介质声波近似思想推导得到的TTI介质方程归纳为基于TTI介质声波近似的TTI介质方程。但是这种方程在实际计算中往往会产生数值不稳定问题, 尤其是在角度剧变的情况下[6]。FLETCHER等[7]完全放弃了采用TTI介质声波近似的思路, 提出在方程推导中保留横波分量。引入横波分量的方式能有效消除TTI介质声波近似产生的不稳定问题, FLETCHER等[7]引入横波分量推导得到的2D TTI介质纵横波耦合qP波波动方程为:
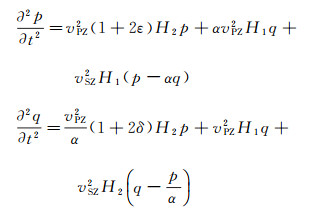
|
(4) |
式中:vSZ2=vPZ2(ε-δ)/σ, σ表征引入的横波分量vSZ的大小, 本文σ取经验常数0.75[7]; α为非零常量参数, 一般取α=1[7]。其辅助变量H1和H2的三维TTI方程形式与ZHOU等[4]相同。本文将FLETCHER等[7]和李博等[25]引入横波分量推导得到的TTI介质方程归纳为TTI介质纵横波耦合方程。
TTI介质波场模拟首先要满足物理稳定性条件, 即P-SV波VTI介质精确相速度频散方程((1) 式)中的相速度的平方不能小于0[26]:
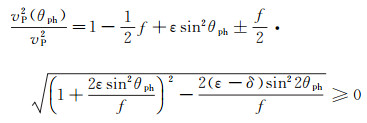
|
(5) |
由(5) 式推导得到TI介质波场模拟中的物理稳定性条件为:

|
(6) |
在TTI介质声波近似情况下, vSZ=0, 则f=1, 由(6) 式推导得到TTI介质声波近似情况下的物理稳定性条件为:
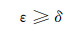
|
(7) |
在变速介质情况下, 由于对变系数求导会带来微分算子的附加项, 影响算子的稳定性,因此,我们借助对称算子理论, 将原始偏微分方程适当对称化, 得到与常系数偏微分方程一样稳定的微分算子[11, 27-28]。
经实际测试, TTI介质波场传播不稳定的情况主要由角度剧变产生, 包括对称轴倾角θ或者三维方位角φ快速变化的区域[6]。本文设计了一个楔形2D TTI介质模型用于算法稳定性测试(图 1), 模型的主要特点是角度剧变(图 1d), 因此能很好地测试各向异性波动方程算法的稳定性。模型横向网格数和纵向网格数都为300, 横向网格间距和纵向网格间距都为10m。
|
图 1 楔形2D TTI介质模型各向异性参数变化情况 a纵波速度vPZ; b纵波各向异性参数ε; c变异系数δ; d对称轴角度θ |
数值模拟时, 雷克震源子波主频取25Hz, 传播时间为3s, 时间采样间隔为0.0005s, 吸收边界条件采用优化海绵吸收边界条件[18], 分别采用TTI介质声波近似方程(ZHOU等[4]方程)和引入横波分量的TTI介质纵横波耦合方程(FLETCHER等[7]方程)来进行数值模拟。
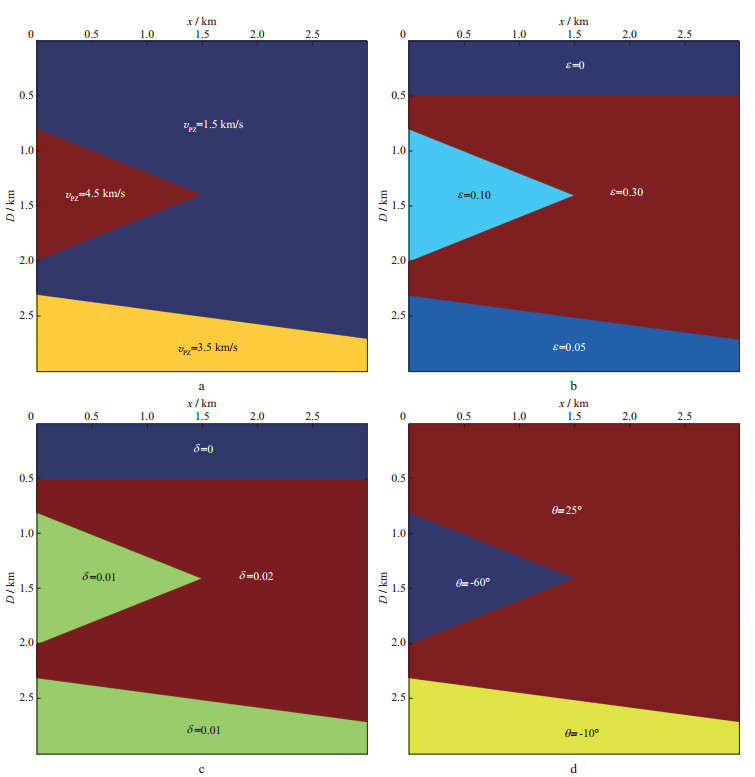
从t=1s时刻的波场快照(图 2a, 图 2b)可以看出, ZHOU等[4]方程基本上还能保持稳定传播, FLETCHER等[7]方程由于引入了横波分量, 产生了伪横波(SV波)噪声(图 2b中红色箭头所示)。而从t=1.5s时刻的波场快照(图 2c, 图 2d)可以看出, ZHOU等[4]方程由于楔形界面处角度剧变已经产生不稳定现象, FLETCHER等[7]方程由于引入了横波分量, 能减小不稳定情况的产生, 仍然能保持稳定传播。因此FLETCHER等[7]各向异性波动方程是一种稳定的TTI介质波动方程, 我们讨论的二维和三维TTI介质正演模拟将采用该方程。
|
图 2 楔形2D TTI介质模型波场快照 a t=1s时采用ZHOU等[4]方程得到的波场快照; b t=1s时采用FLETCHER等[7]方程得到的波场快照; c t=1.5s时采用ZHOU等[4]方程得到的波场快照; d t=1.5s时采用FLETCHER等[7]方程得到的波场快照 |
本文对常见的TTI介质波动方程进行了归纳, 认为基于TTI介质精确相速度频散方程推导得到的TTI介质波动方程可以分为两类:一类为TTI介质声波近似方程; 另一类为TTI介质纵横波耦合方程。其中TTI介质声波近似方程可以视为TTI介质纵横波耦合方程在横波速度为0时的某种特例。从TTI介质波场传播稳定性的角度对这两类方程进行对比分析可知, 引入横波分量的TTI介质纵横波耦合方程适用于TTI介质。
1.2 2D TTI介质时间域分裂式完全匹配层(SPML)波动方程推导基于FLETCHER等[7]的二阶2D TTI介质纵横波耦合波动方程((4) 式)来推导2D TTI介质时间域SPML波动方程。TTI介质波动方程的特点是含有比较复杂的交叉导数项, 如何有效处理TTI介质方程中的交叉导数项是PML吸收边界条件研究的难点。本文的思路是针对TTI介质波动方程的特点对二阶方程中的交叉导数项进行分裂, 得到其一阶方程的形式, 进而推导得到TTI介质一阶SPML波动方程。
引入4个辅助波场项ψx, ψz, Ωx, Ωz, 从FLETCHER等[7]的二阶2D TTI介质波动方程出发, 推导得到一阶2D TTI介质波动方程的形式, 对方程进行傅里叶变换并引入X和Z方向的频率域PML拉伸函数, 推导得到2D TTI介质频率域SPML波动方程, 将此方程反傅里叶变换到时间域, 即可得到2D TTI介质时间域SPML波动方程:

|
(8) |
其中, 辅助变量形式为:
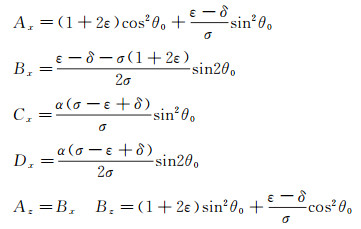
|
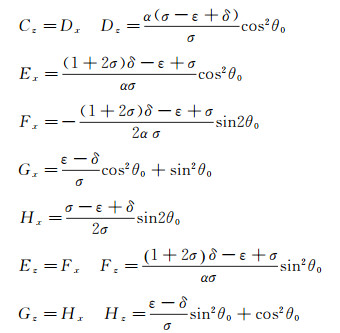
|
PML波动方程推导过程中引入的频率域PML拉伸函数ξx, ξz表示为:
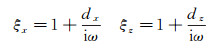
|
(9) |
其中, 引入了PML衰减因子dx, dz。本文采用的PML衰减因子表达式为[21]:
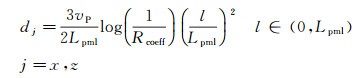
|
(10) |
式中:Lpml为PML边界层的厚度; l为计算点距PML边界的距离; Rcoeff为理论反射系数, 本文取Rcoeff=0.0001。
一系列公式推导研究可以发现, 所有2D TTI介质的SPML方程都具有相同的形式, 差分离散形式也相同, 只是PML辅助变量表达形式不一致, 其具体形式根据不同的TTI方程形式而定。本文只讨论二维TTI介质情形, 但是这种方法也可以扩展到三维TTI介质(详细推导见附录A), 在此不再展开讨论。
1.3 2D TTI介质SPML波动方程数值实现采用高阶交错网格有限差分法来实现1.2节推导的2D TTI介质SPML波动方程。对(8) 式进行高阶交错网格有限差分离散, 具体实现公式如下:
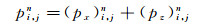
|
(11a) |
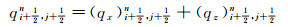
|
(11b) |
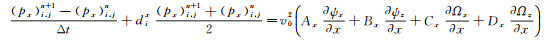
|
(11c) |
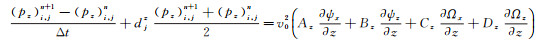
|
(11d) |
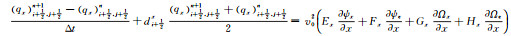
|
(11e) |
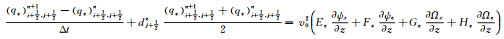
|
(11f) |
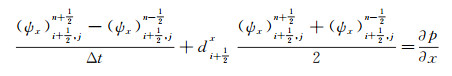
|
(11g) |
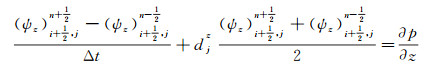
|
(11h) |
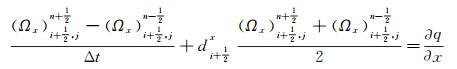
|
(11i) |
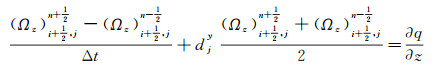
|
(11j) |
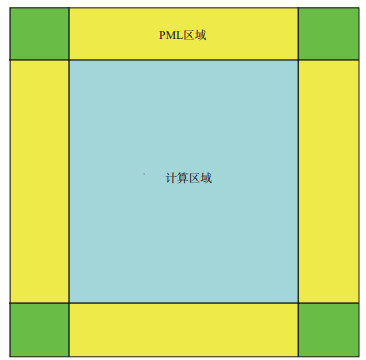
从二维SPML数值实现示意图(图 3)可以看出, 二维PML区域分为4个边和4个角共8块区域, 具体实现时, 我们需要分别考虑各PML区域波场的衰减。理论上, 无吸收边界条件具有最强的边界反射, 而PML吸收层数越多, 边界反射吸收效果越好。但是增加的PML吸收层数也带来了更多的计算量, 从而在一定程度上降低了计算效率, 因此在实际应用中需要在PML吸收层数与计算效率之间寻求平衡。
|
图 3 二维SPML数值实现示意图解 |
为了验证本文提出的TTI介质SPML吸收边界条件的有效性, 首先采用简单均匀2D TTI介质模型进行SPML点源响应测试。模型横向网格数和纵向网格数都为256, 横向网格间距和纵向网格间距都为10m, 速度为3000m/s。TTI介质的各向异性参数ε=0.3, δ=0.1, 对称轴倾角为45°。
均匀TTI介质模型的单道记录能很好地测试不同PML边界层条件下的边界反射吸收效果。数值模拟时, 雷克震源子波主频取25Hz, 震源位置设置在模型的中心, 单检波点取在震源位置左侧50个网格点处, 传播时间为1.5s, 时间采样间隔为0.0015s, 采用12阶高阶交错网格有限差分格式进行模拟。采用SPML吸收边界条件, PML边界吸收层数分别设为10层、20层和30层。取3种情形的单道记录进行对比(图 4)。由图 4可见, PML吸收层数为10层时边界反射吸收效果不理想; 而PML吸收层数为20层时已经取得了比较好的边界反射吸收效果(图 4a), 但从局部放大图可以看出, 仍然存在着微弱的边界反射; 而PML吸收层数为30层时边界反射导致的波场误差降到仅为10-5, 此时边界反射基本被消除(图 4b)。从PML吸收层数为20层时SPML波动方程在t=0.72s和t=0.90s的波场快照(图 5)也可以看到微弱的边界反射。因此本例选定PML边界吸收层数为30层。图 6a到图 6f分别给出了SPML波动方程在PML吸收层数为30层时各个时刻的波场快照。由图 6可见, SPML对边界反射吸收效果明显。

|
图 4 均匀2D TTI介质模型不同PML吸收层数单道记录 a PML吸收层数分别为10层、20层和30层; b PML吸收层数分别为20层和30层时的局部放大显示结果 |
|
图 5 均匀2D TTI介质模型采用2D TTI介质SPML波动方程在PML吸收层数为20层时不同时刻的正演波场快照 a t=0.72s; b t=0.90s |

|
图 6 均匀2D TTI介质模型采用2D TTI介质SPML波动方程在PML吸收层数为30层时不同时刻的正演波场快照 a t=0.39s; b t=0.45s; c t=0.51s; d t=0.57s; e t=0.72s; f t=0.90s |
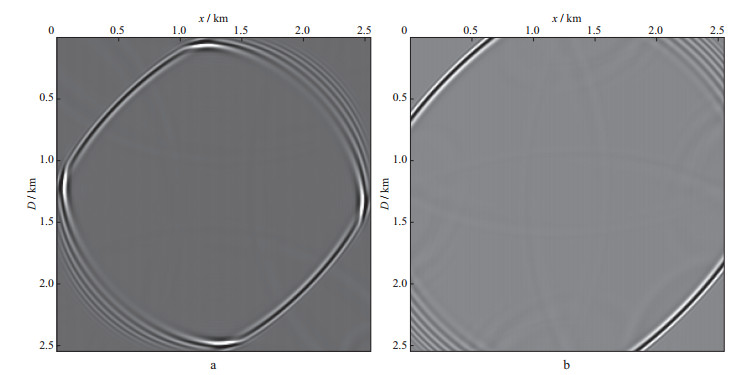
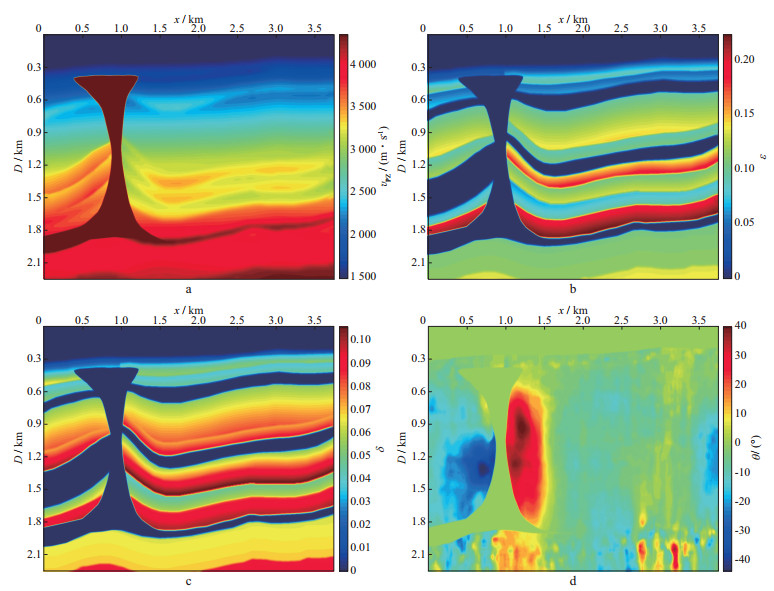
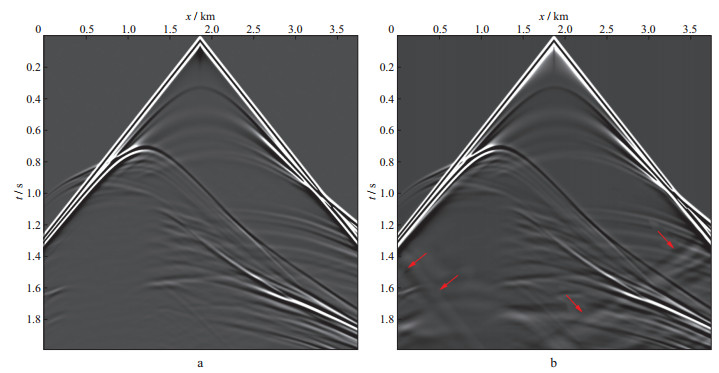
以复杂BP2007 2D TTI介质海洋标准模型为例, 对比TTI介质SPML吸收边界条件与优化海绵吸收边界条件对边界反射的吸收效果[18]。本文数值模拟时采用截取的部分BP2007 2D TTI介质海洋标准模型(图 7), 该模型主要模拟了近海岸的地质构造, 特点是左部有一个被TTI各向异性地层包围的高速各向同性盐丘, 模型参数包括纵波速度vPZ, Thomsen纵波各向异性参数ε, Thomsen变异系数δ, 对称轴角度θ, 模型横向网格数nx=601, 纵向网格数nz=361, 横向网格间距和纵向网格间距都为6.25m, 其中海水层为各向同性介质。数值模拟时, 雷克震源子波主频取25Hz, 采用SPML吸收边界条件, PML边界设为30层, 传播时间为2s, 时间采样间隔为0.0004s, 采用12阶高阶交错网格有限差分格式进行模拟。因为震源置于各向同性的海水层中, TTI数值模拟时不会出现影响qP波场传播的伪横波(SV波)噪声, 此种情况下不需要采取在震源处添加各向同性薄层消除伪SV波噪声的策略[5, 29]。从BP2007 2D TTI介质海洋标准模型的正演单炮记录(图 8)来看, SPML消除边界反射效果良好(图 8a), 而优化海绵吸收边界条件仍然有着比较强的边界反射(图 8b中红色箭头标示), SPML吸收边界条件明显优于优化海绵吸收边界条件的边界反射吸收效果。
|
图 7 截取的部分BP2007 2D TTI介质海洋标准模型各向异性参数变化情况 a纵波速度vPZ; b纵波各向异性参数ε; c变异系数δ; d对称轴角度θ |
|
图 8 BP2007 2D TTI介质海洋标准模型采用不同边界条件正演的单炮记录 a SPML吸收边界条件; b优化海绵吸收边界条件 |
本文对常见的几种TTI介质波动方程进行了归纳, 并从波场传播稳定性的角度进行分析, 结果表明引入横波分量的TTI介质纵横波耦合波动方程适用于TTI介质。基于TTI介质纵横波耦合二阶波动方程, 推导得到一阶方程形式的TTI介质SPML波动方程, 研究发现, 所有2D TTI介质的SPML方程都具有相同的形式, 差分离散形式也相同, 只是PML辅助变量表达形式不一致, 其根据不同的TTI方程形式而定。数值模拟结果表明, 本文研究的SPML吸收边界条件能达到很好的人工边界反射吸收效果。本文方法可以进一步推广到三维TTI介质的高精度模拟中。至于2D VTI或3D VTI介质情形, 由于对称轴角度为0, 波场传播较稳定, 此时适合采用噪声相对较少的VTI介质声波近似方程, 因为TTI介质纵横波耦合方程虽然由于引入了横波分量解决了地震波在各向异性介质中传播的不稳定性问题, 但是也带来了更多的横波噪声。VTI介质波动方程的特点是不含比较复杂的交叉导数项, 可以采用计算效率更高的非SPML吸收边界条件来实现。
附录A 3D TTI介质时间域SPML波动方程3D TTI介质时间域SPML波动方程的推导基于FLETCHER等[7]的二阶3D TTI介质纵横波耦合波动方程((4)式)。与二维TTI介质相比, 三维TTI介质时间域SPML波动方程的推导首先需要从FLETCHER等[7]的二阶3D TTI介质波动方程出发, 推导得到一阶3D TTI介质波动方程的形式, 然后对方程进行傅里叶变换并引入x, y和z3个方向的频率域PML拉伸函数, 将推导得到的3D TTI介质频率域SPML波动方程反傅里叶变换, 即可得到3D TTI介质时间域SPML波动方程:
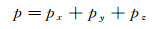
|
(A1a) |
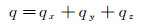
|
(A1b) |
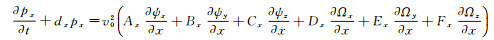
|
(A1c) |
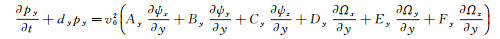
|
(A1d) |
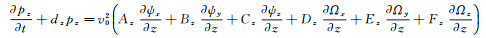
|
(A1e) |
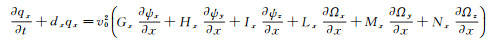
|
(A1f) |
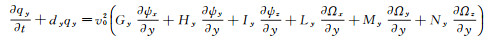
|
(A1g) |
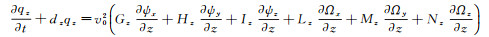
|
(A1h) |
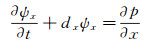
|
(A1i) |
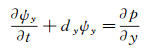
|
(A1j) |

|
(A1k) |
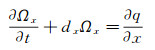
|
(A1l) |
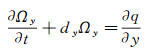
|
(A1m) |
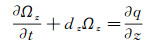
|
(A1n) |
推导的辅助变量形式为:
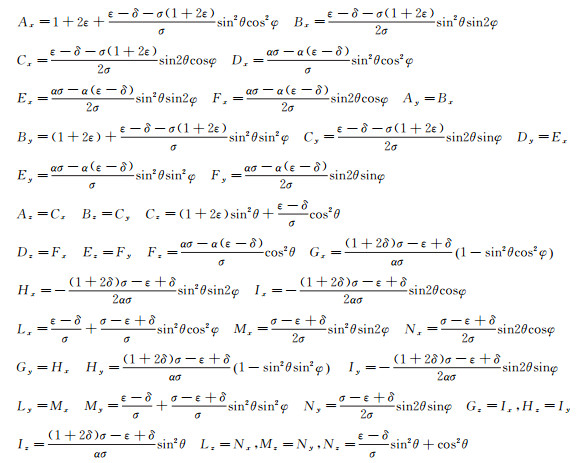
|
PML波动方程推导过程中引入的频率域PML拉伸函数ξx, ξy, ξz表示为:
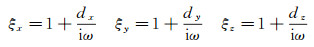
|
(A2) |
引入的PML衰减因子dx, dy, dz表达式为:
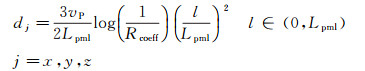
|
(A3) |
式中:Lpml是PML边界层的厚度;l是计算点距PML边界的距离;Rcoeff是理论反射系数值, 取0.0001。
对一系列公式推导研究可以发现, 所有3D TTI介质方程的SPML方程都具有相同的形式, 差分离散形式也相同, 只是PML辅助变量表达形式不一致, 其具体形式根据不同的TTI方程形式而定。
| [1] | WARNER M, RATCLIFE A, NANGOO T, et al. Anisotropic 3D full-waveform inversion[J]. Geophysics, 2013, 78(2): R59-R80DOI:10.1190/geo2012-0338.1 |
| [2] | THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966DOI:10.1190/1.1442051 |
| [3] | TSVANKIN I. P-wave signatures and notation for transversely isotropic media:an overview[J]. Geophysics, 1996, 61(2): 467-483DOI:10.1190/1.1443974 |
| [4] | ZHOU H B, ZHANG G Q, BLOOR R. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media[J]. Expanded Abstracts of 76th Annual Internat SEG Mtg, 2006: 194-198 |
| [5] | GRECHKA V, ZHANG L, RECTOR J W. Shear waves in acoustic anisotropic media[J]. Geophysics, 2004, 69(2): 576-582DOI:10.1190/1.1707077 |
| [6] | BAKKER P M, DUVENECK E. Stability analysis for acoustic wave propagation in tilted TI media by finite differences[J]. Geophysical Journal International, 2011, 185(2): 911-921DOI:10.1111/gji.2011.185.issue-2 |
| [7] | FLETCHER R P, DU X, FOWLER P J. Reverse time migration in tilted transversely isotropic (TTI) media[J]. Geophysics, 2009, 74(6): 179-187DOI:10.1190/1.3269902 |
| [8] | DUVENECK E, MILCIK P, BAKKER P M. Acoustic VTI wave equations and their application for anisotropic reverse-time migration[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008: 2186-2190 |
| [9] | DUVENECK E, BAKKER P M. Stable P-wave modeling for reverse-time migration in tilted TI media[J]. Geophysics, 2011, 76(2): 65-75DOI:10.1190/1.3533964 |
| [10] | ZHANG Y, ZHANG H Z. A stable TTI reverse time migration and its implementation[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009: 2794-2798 |
| [11] | ZHANG Y, ZHANG H Z, ZHANG G Q. A stable TTI reverse time migration and its implementation[J]. Geophysics, 2011, 76(3): WA3-WA11DOI:10.1190/1.3554411 |
| [12] | FOWLER P J, DU X, FLETCHER R P. Coupled equations for reverse time migration in transversely isotropic media[J]. Geophysics, 2010, 75(1): S11-S22DOI:10.1190/1.3294572 |
| [13] | BUBE K P, NEMETH T, STEFANI J P, et al. First-order systems for elastic and acoustic variable-tilt TI media[J]. Geophysics, 2012, 77(5): T157-T170DOI:10.1190/geo2011-0249.1 |
| [14] | BUBE K P, NEMETH T, STEFANI J P, et al. On the instability in second-order systems for acoustic VTI and TTI media[J]. Geophysics, 2012, 77(5): T171-T186DOI:10.1190/geo2011-0250.1 |
| [15] | CLAYTON R, ENQUIST B. Absorbing boundary conditions for acoustic and elastic wave equations[J]. Bulletin of the Seismological Society of America, 1977, 67(6): 1529-1540 |
| [16] | CERJAN C, KOSLOFF D, KOSLOFF R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J]. Geophysics, 1985, 50(4): 705-708DOI:10.1190/1.1441945 |
| [17] | BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200DOI:10.1006/jcph.1994.1159 |
| [18] | BORDING R P. Finite difference modeling-nearly optimal sponge boundary conditions[J]. Expanded Abstracts of 74th Annual Internat SEG Mtg, 2004: 1921-1924 |
| [19] | CHEW W C, LIU Q H. Perfectly matched layers for elastodynamics:a new absorbing boundary condition[J]. Journal of Computational Acoustics, 1996, 4(4): 341-359DOI:10.1142/S0218396X96000118 |
| [20] | BÉCACHE E, FAUQUEUX S, JOLY P. Stability of perfectly matched layers, group velocities and anisotropic waves[J]. Journal of Computational Physics, 2003, 188(2): 399-433DOI:10.1016/S0021-9991(03)00184-0 |
| [21] | COLLINO F, TSOGKA C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294-307DOI:10.1190/1.1444908 |
| [22] |
裴正林. 三维各向异性介质中弹性波方程交错网格高阶有限差分法数值模拟[J].
石油大学学报(自然科学版), 2004, 28(5): 23-29 PEI Z L. Three-dimensional numerical simulation of elastic wave propagation in 3-D anisotropic media with staggered-grid high-order difference method[J]. Journal of the University of Petroleum, 2004, 28(5): 23-29 |
| [23] |
裴正林. 三维各向同性介质弹性波方程交错网格高阶有限差分法模拟[J].
石油物探, 2005, 44(4): 308-315 PEI Z L. Numerical simulation of elastic wave equation in 3-D isotropic media with staggered-grid high-order difference method[J]. Geophysical Prospecting for Petroleum, 2005, 44(4): 308-315 |
| [24] | ALKHALIFAH T. Acoustic approximations for processing in transversely isotropic media[J]. Geophysics, 1998, 63(2): 623-631DOI:10.1190/1.1444361 |
| [25] |
李博, 李敏, 刘红伟, 等. TTI介质有限差分逆时偏移的稳定性探讨[J].
地球物理学报, 2012, 55(4): 1366-1375 LI B, LI M, LIU H W, et al. Stability of reverse time migration in TTI media[J]. Chinese Journal of Geophysics, 2012, 55(4): 1366-1375 |
| [26] |
李博. 地震偏移成像和GPU超算技术[D]. 北京: 中国科学院大学, 2011
LI B.Seismic migration and GPU supercomputing technology[D]. Beijing:University of Chinese Academy of Sciences, 2011 |
| [27] | CLAERBOUT J F. Imaging the earth's interior[M]. Palo Alto, California: Blackwell Scientific Publications, 1985: 1-398. |
| [28] |
刘洪, 王秀闽, 曾锐, 等. 单程波算子积分解的象征表示[J].
地球物理学进展, 2007, 22(2): 463-471 LIU H, WANG X M, ZENG R, et al. Symbol description to integral solution of one-way wave operator[J]. Progress in Geophysics, 2007, 22(2): 463-471 |
| [29] |
张衡, 刘洪, 唐祥德, 等. 基于平均导数优化方法的VTI介质频率空间域正演[J].
地球物理学报, 2015, 58(9): 3306-3316 ZHANG H, LIU H, TANG X D, et al. Forward modeling of VTI media in the frequency-space domain based on an average-derivative optimal method[J]. Chinese Journal of Geophysics, 2015, 58(9): 3306-3316DOI:10.6038/cjg20150924 |


