2. 中国石油化工股份有限公司石油勘探开发研究院, 北京100083;
3. 西北有色工程有限责任公司, 陕西西安710000
2. Research Institute of Petroleum Exploration and Development, SINOPEC, Beijing 100083, China;
3. Northwest Nonferrous Engineering Co., Ltd, Xi'an 710000, China
横波速度是地震波正演模拟、AVO分析、叠前地震资料反演、储层预测等研究的基础数据[1-18]。由于横波测井成本昂贵, 实际储层预测研究中经常缺少横波速度数据, 因此, 采用一定的方法精确预测横波速度是地球物理的重要研究内容之一。
预测横波速度的方法主要包括经验公式法[17-18]、岩石物理模型法[1-16]以及神经网络法[6], 其中经验公式法和神经网络法严格受制于拟合公式和训练网络时所使用的数据样点, 可推广性差且物理意义常常不够明确。岩石物理模型的本质是表征岩石微观特征参数与速度之间关系的数学公式, 具有明确的物理意义且可以被广泛地推广应用, 针对某种岩石特征提出的岩石物理模型可应用于其它具有类似岩石特征的区域。目前, 基于岩石物理模型的横波速度预测方法已经成为石油工业界的主流方法, 但针对碎屑岩的方法研究较多[7-16], 针对碳酸盐岩的方法研究相对较少。
与碎屑岩相比, 碳酸盐岩的孔隙结构更加复杂, 因而在碎屑岩中应用效果较好的方法不能很好地应用于碳酸盐岩[1-6]。针对这个问题, XU等[1]在Xu-White岩石物理模型的基础上结合Kuster-Toksöz(KT)[7-9]岩石物理模型和微分等效介质理论[19], 通过分析黏土孔隙、粒间孔隙、刚性孔隙和微裂缝等4种孔隙类型对弹性波的影响, 建立了Xu-Payne模型。陈启艳等[6]用实例证明了Xu-Payne模型的碳酸盐岩横波速度预测效果优于Xu-White模型。目前Xu-Payne模型算法已经被编入多个软件, 成为应用最为广泛的碳酸盐岩横波速度预测方法。然而, Xu-Payne模型有如下缺点:① 仅考虑白云石、方解石、黏土3种矿物, 当岩石中还有其它矿物时该模型的应用受到限制; ② 假设黏土孔隙在总孔隙度中的体积分数与黏土在总矿物中的体积分数一致, 当岩石中黏土含量较高时, 会过高估计黏土孔隙的体积分数; ③ 考虑了4种孔隙类型, 便于正演研究不同类型孔隙对弹性参数的影响, 但是利用该模型进行横波速度预测时无法精确获取每种类型的孔隙体积分数。张广智等[4]也基于Xu-White模型提出一种碳酸盐岩模型, 他们将岩石等效为方解石、白云石两种矿物及饱和流体3种孔隙(粒间空隙、溶洞和裂缝)构成的混合物, 利用KT理论和微分等效介质模型(differential equivalent medium model, DEM)求取3种孔隙类型的体积分数, 进而计算横波速度。该模型克服了Xu-Payne模型的②, ③ 项缺点, 但是不适合具有复杂岩性的碳酸盐岩。SUN等[2]利用DEM模型构建了一种针对复杂孔隙类型碳酸盐岩的速度预测方法, 但该方法没有克服Xu-Payne模型的①, ② 项缺点。
鄂尔多斯盆地奥陶系马家沟组马五段发育了一套以碳酸盐岩为主夹蒸发岩的储层, 已经发现了靖边整装风化壳气田[20]、大牛地气田等一系列气田。马五段岩性以白云岩为主, 夹石灰岩及蒸发岩, 具体包括微晶-粗粉晶白云岩、泥云岩、膏云岩、含膏泥云岩、含膏云岩、微晶灰岩、砂屑灰岩、叠层石灰岩等。马家沟组顶部经历了长期的风化剥蚀及淋滤作用, 导致地层溶蚀孔、缝发育, 且长期的淋滤作用造成地层垮塌, 大量的溶孔、溶缝被泥质充填。复杂的岩性及次生孔隙导致该区横波速度预测困难, 尤其是碳酸盐岩中夹杂的石英、硬石膏矿物及部分层段较高含量的黏土, 使得当前工业界广泛使用的碳酸盐岩速度预测技术——Xu-Payne岩石物理模型[1]不再适用, 其它碳酸盐岩岩石物理模型[2, 4]也不能有效解决该区碳酸盐岩的横波速度预测问题。本文针对Xu-Payne岩石物理模型的不足, 基于多孔隙类型微分Kuster-Toksöz(DKT)岩石物理模型[9]、VRH平均公式、Wood方程[21]、Gassmann方程[22], 提出了一种新的碳酸盐岩岩石物理模型, 在纵波速度的约束下计算碳酸盐岩横波速度。
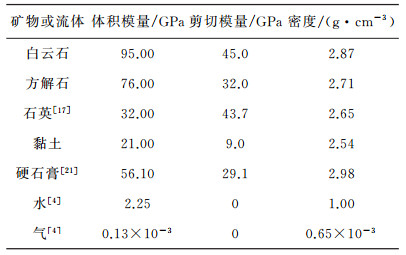
1 方法原理 1.1 Xu-Payne岩石物理模型及其存在的问题Xu-Payne模型是目前应用最为广泛的碳酸盐岩岩石物理模型[1]。该模型将碳酸盐岩等效为由白云石、方解石、黏土、总孔隙度及其中流体组成的混合物, 如图 1a所示。总孔隙度φt被分为4个部分:① 和泥质有关的黏土孔隙(实际为黏土裂缝)φcl; ② 粒间孔隙φip; ③ 刚性孔隙(孔洞、洞穴等)φst; ④ 微裂缝(裂隙)φcr, φt=φcl+φcr+φst+φip。其中, 粒间孔隙、刚性孔隙、微裂缝是有效孔隙, 黏土孔隙是无效孔隙。该模型假定黏土孔隙(φcl)在总孔隙度(φt)中的体积分数与黏土在总矿物中的体积分数(fcl)成正比, 即由公式φcl=fcl×φt计算得到; 微裂缝的体积分数由公式φcr=φine-βσe计算得到, 其中φin是在上覆有效地层压力为0时的初始裂缝孔隙度, β是常数, σe是有效压力。各种孔隙的形状为理想椭球体, 不同的椭球体由孔隙纵横比(孔隙的短轴与长轴之比)描述。孔洞、溶洞等刚性孔隙的椭球体较圆, 设置其纵横比为0.80;粒间孔隙纵横比设置为0.15;裂缝孔隙纵横比设置为0.02。Xu-Payne模型的计算过程为:① 利用VRH平均公式将岩石矿物成分(此处指白云石、方解石、黏土3种)混合起来得到岩石基质的弹性参数; ② 利用微分等效介质模型[19]与KT模型[8]将干孔隙加入岩石基质中, 得到干岩石的弹性参数; ③ 利用Wood公式计算混合流体的体积模量; ④ 利用Gassmann方程计算饱和流体岩石的弹性参数。Xu-Payne模型在矿物简单、黏土含量较低的碳酸盐岩中应用效果较好, 但在研究区目的层应用Xu-Payne模型进行横波速度预测时, 部分层段应用效果不好。分析认为原因在于:① Xu-Payne模型假设岩石中仅存在白云石、方解石、黏土3种矿物, 而实际岩石中还含有其它矿物, 例如石英、硬石膏等, Xu-Payne模型中的白云石、方解石、黏土的纵横波速度关系不能够表征其它矿物的纵横波速度关系; ② Xu-Payne模型假设黏土孔隙为裂缝, 且黏土孔隙在总孔隙度中的体积分数与黏土矿物在总矿物中的体积分数一致, 在实际岩石中黏土含量较高的情况下, Xu-Payne模型计算的黏土裂缝体积分数较大, 从而导致计算的速度偏小; ③ 利用Xu-Payne模型进行速度预测时, 需输入刚性孔隙、粒间孔隙、微裂缝3种孔隙类型的体积分数, 而这些参数的精确值很难获取, 直接降低了Xu-Payne模型的应用效果。
|
图 1 Xu-Payne岩石物理模型(a)及改进的Xu-Payne岩石物理模型(b)的物质组成 |
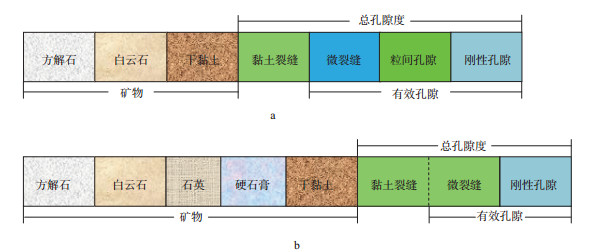
本文对Xu-Payne模型进行了改进, 使其能适用于黏土含量高且矿物类型多的碳酸盐岩(图 1b)。改进的Xu-Payne模型将岩石矿物等效为方解石、白云石、干黏土、石英、硬石膏5种矿物构成的混合物, 将总孔隙度笼统地划分为柔性孔隙(或称为柔性裂缝, 是黏土孔隙和有效孔隙中的微裂缝之和)和刚性孔隙两种, 通过刚性孔隙与柔性孔隙体积分数的自适应变化来描述岩石中复杂的孔隙类型, 避免了黏土孔隙与黏土含量挂钩的问题, 同时, 因减少了孔隙类型种类而增强了模型的可应用性(不需要输入孔隙类型数据)。与Xu-Payne模型一样, 改进的Xu-Payne模型通过多个岩石物理模型的组合来构建, 流程如图 2所示。
|
图 2 改进的Xu-Payne岩石物理模型构建流程 |
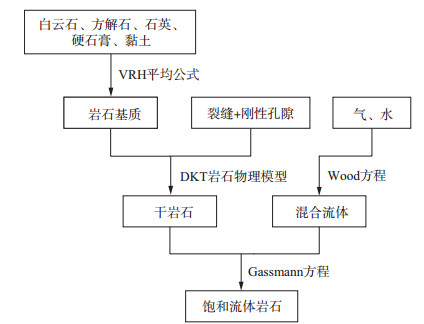
1) 使用VRH平均公式[21]估算岩石基质的体积模量和剪切模量:
|
(1) |
式中:MVR指弹性模量, 本文指体积模量和剪切模量; 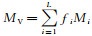
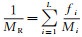
| 表 1 岩石组分的物理参数 |
2) 使用DKT岩石物理模型[9]计算含孔隙干岩石的体积模量和剪切模量。DKT岩石物理模型的实质是多次迭代使用KT岩石物理模型, 每次使用时都向基质中加入微量的孔隙度, 直到所加入的孔隙与实际值一致为止。该模型克服了KT岩石物理模型受φ/α«1(φ指孔隙度, α指孔隙纵横比)的限制, 能有效预测多孔隙类型岩石的速度。
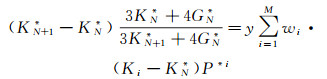
|
(2) |
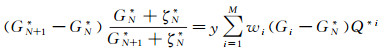
|
(3) |
式中:KN*, GN*指N次迭代后等效岩石基质的体积模量和剪切模量; KN+1*, GN+1*指N次迭代后未知的体积模量和剪切模量, 即所要求取的干岩石的体积模量和剪切模量; 等式右边的求和代表了M种孔隙类型(每种孔隙类型在总孔隙度φt中的体积分数为wi, 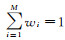
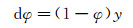
|
(4) |
如果迭代次数是N, 则公式(4) 变为:
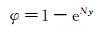
|
(5) |
3) 使用Wood方程[21]计算流体的体积模量:
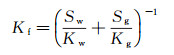
|
(6) |
式中:Kf指混合流体的体积模量; Kw, Kg分别指水、气的体积模量; Sw, Sg分别指含水、含气饱和度(Sw+Sg=1)。
4) 使用Gassmann方程[21]计算饱和流体岩石的体积模量和剪切模量:
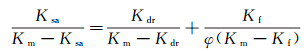
|
(7) |
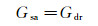
|
(8) |
式中:Ksa, Kdr, Km, Kf分别指饱和流体岩石、干岩石、岩石基质、流体的体积模量; Gsa, Gdr分别指饱和流体岩石、干岩石的剪切模量; φ指孔隙度。
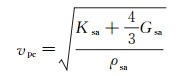
5) 利用弹性参数与纵、横波速度之间的关系计算饱和流体岩石的纵波速度和横波速度, 公式为:
|
(9) |
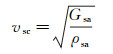
|
(10) |
式中:vpc, vsc分别指饱和流体岩石的纵、横波速度; ρsa为饱和流体岩石的密度, 由ρsa=ρm(1-φ)+ρfφ计算得到。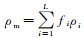
根据上述流程建立纵、横波速度与可变的孔隙参数(ws和wc)之间的关系, 通过使计算的纵波速度vpc与实测纵波速度vpm之差的绝对值达到极小值ε来建立目标函数:
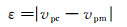
|
(11) |
采用迭代算法求解该目标函数, 反演得到孔隙参数ws和wc, 将其代入公式(2)~公式(10) 计算横波速度vsc。
1.3 模型参数与速度正演利用改进的Xu-Payne模型正演纵、横波速度随孔隙度、孔隙类型的变化规律, 通过与测井数据进行对比, 定性观察岩石物理模型能否表征测井数据的矿物-孔隙度-速度关系, 以验证本文改进的Xu-Payne模型的有效性。以研究区目的层实际矿物含量为例, 设计两组基质模型:① 低黏土含量矿物组合模型, 矿物体积分数为[fdo, fli, fqu, fcl, fan]=[0.95, 0.04, 0, 0.01, 0], 下标“do”, “li”, “qu”, “cl”, “an”分别指白云石、方解石、石英、黏土、硬石膏; ② 高黏土含量矿物组合模型, 矿物体积分数为[fdo, fli, fqu, fcl, fan]=[0.100, 0.600, 0.025, 0.250, 0.025]。假设孔隙度在[0, 0.15]范围内变化, 刚性孔隙的体积分数ws在[1 0]之间按照-0.2步长变化, 相对地, 柔性孔隙的体积分数wc在[0, 1]之间按照0.2的步长变化, 含气饱和度为50%。岩石组分的弹性参数和密度如表 1所示, 其中白云石、方解石、黏土的参数在文献[21]的基础上进行了微调。理论上, 流体的体积模量和密度应该用Baztle-Wang公式[21]来计算, 本文研究过程中由于缺乏准确的流体矿化度等参数, 测试了已发表的碳酸盐岩模型研究文献[2, 4, 6, 11]中的参数, 选择了速度预测效果最好的一组参数[4]。
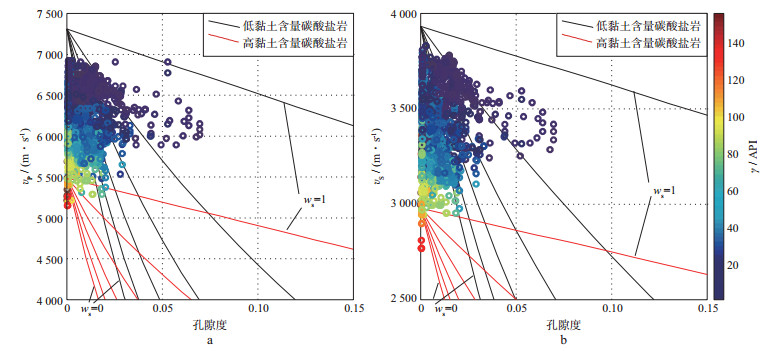
本文方法正演计算的纵、横波速度随孔隙度、孔隙类型的变化规律如图 3所示。其中, 红色线和黑色线分别表示高黏土含量矿物组合模型和低黏土含量矿物组合模型情况下岩石速度随孔隙度、孔隙类型的变化规律。自上而下的6条红色线和黑色线分别表征刚性孔隙ws为1.0, 0.8, 0.6, 0.4, 0.2, 0, 对应的柔性孔隙wc分别为0, 0.2, 0.4, 0.6, 0.8, 1.0。彩色圆点表示研究区A井目的层段的测井数据, 不同颜色表征不同的伽马数值(这里用伽马数值指示黏土含量, 通常伽马数值升高表示黏土含量升高)。图 3显示, 当孔隙度不变、柔性孔隙增加时, 岩石的速度降低; 当孔隙类型不变、孔隙度增加时, 岩石的速度降低; 黏土含量增加时, 岩石速度显著降低。由图 3可见, 在取表 1所示参数的情况下, 通过矿物-孔隙度-孔隙类型的组合变化, 可以覆盖几乎所有的测井数据点, 定性表明改进的Xu-Payne模型可以解释测井数据矿物-孔隙度-速度之间的关系。
|
图 3 基于本文方法正演计算的纵波速度(a)和横波速度(b) |
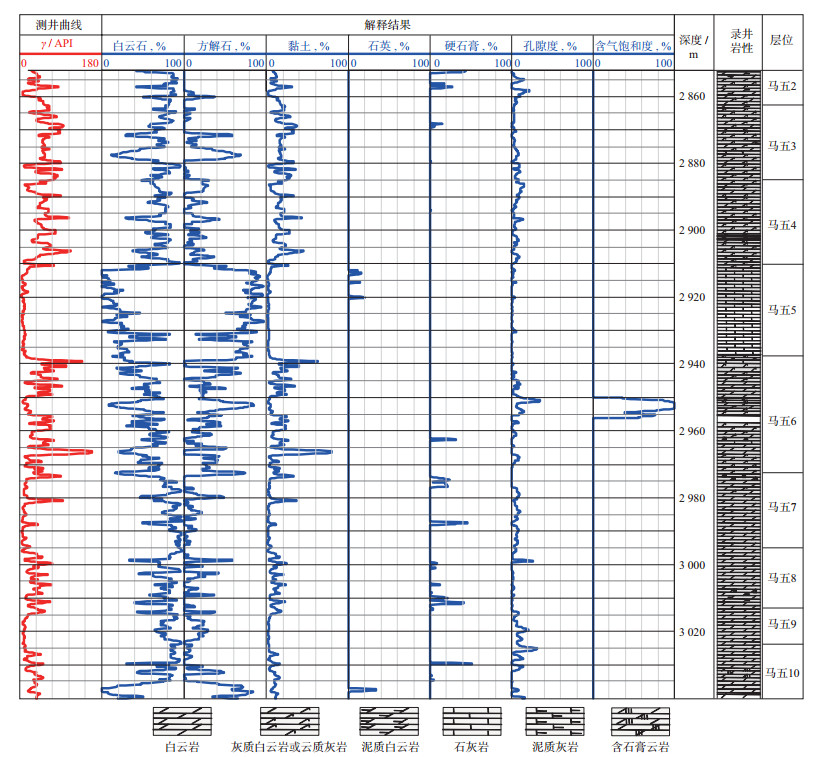
应用本文改进的Xu-Payne模型速度预测方法对鄂尔多斯盆地北部D气田A井马五段进行了横波速度预测。图 4展示了该井目的层段的层位、录井岩性、伽马曲线以及测井解释结果。录井资料显示, 该井马五段主要发育的岩性包括白云岩、石灰岩、灰质白云岩、云质灰岩、泥质白云岩、泥质灰岩、含石膏云岩; 马五5段、马五7段、马五9段测井伽马数值小于20API, 表明这几个层段黏土含量低; 部分层段伽马数值较高, 最高达到150API, 表明这些层段的黏土含量较高; 岩石孔隙流体主要是水, 在马六段发育一个含气层段。根据多矿物测井解释估算矿物含量[23]、孔隙度、含气饱和度, 其中测井解释矿物主要包括白云石、方解石、黏土, 部分层段含石英和硬石膏。将这些数据代入岩石物理模型, 在纵波速度的约束下求取刚性孔隙与柔性裂缝的体积分数ws, wc, 再将所得的孔隙体积分数代入岩石物理模型, 计算横波速度。
|
图 4 鄂尔多斯盆地D气田A井测井解释结果与录井资料对比 |
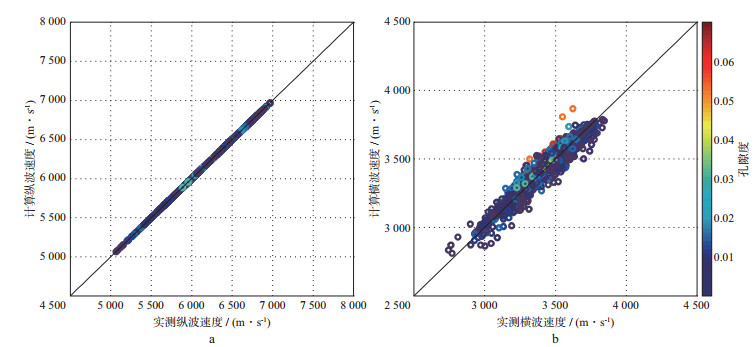
图 5对比了本文方法计算的纵波速度、横波速度与实测数据, 图中黑色的对角线表示预测速度与实测速度完全一致。由图 5a可见, 作为约束的纵波速度与实测速度基本一致, 其线性拟合相关系数为0.995;而在横波速度交会图上(图 5b), 样点均匀分散在黑色线上及黑色线两边, 表明预测横波速度与实测横波速度也基本吻合。
|
图 5 本文方法计算的纵波速度(a)、横波速度(b)与实测数据交会分析 |
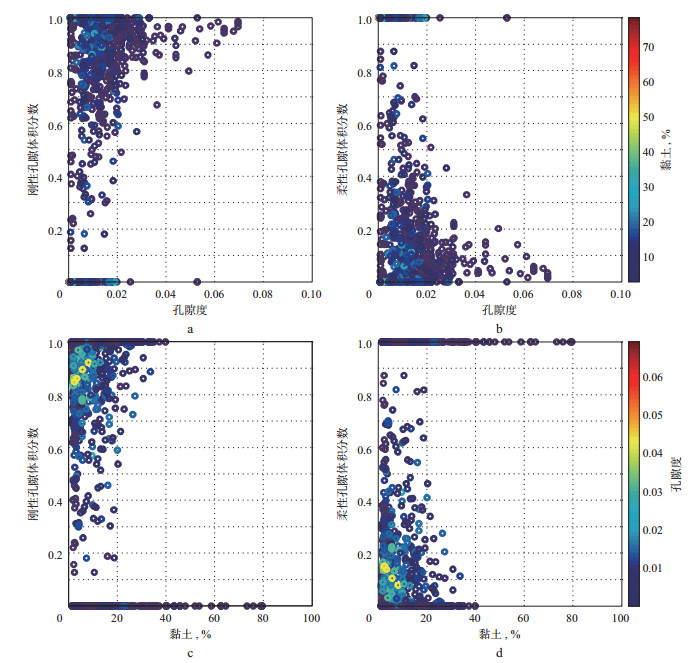
图 6a和图 6b是利用本文方法计算的刚性孔隙及柔性裂缝的体积分数与孔隙度交会图, 彩色圆点表征黏土含量(由伽马测井曲线计算得到, 如图 4所示); 图 6c和图 6d是计算的刚性孔隙及柔性孔隙的体积分数与黏土含量的交会图, 彩色圆点表征孔隙度。由图 6a和图 6b可见, 随着孔隙度的增加, 刚性孔隙的体积分数有增加的趋势, 柔性裂缝的体积分数有降低的趋势。由图 6c和图 6d可见, 所求得的刚性孔隙和柔性裂缝的体积分数与黏土并无特别的关系, 这点与Xu-Payne模型不同。
|
图 6 由本文方法计算得到的刚性孔隙和柔性孔隙体积分数与孔隙度、黏土关系 a刚性孔隙体积分数与孔隙度交会; b柔性孔隙体积分数与孔隙度交会; c刚性孔隙体积分数与黏土交会; d柔性孔隙体积分数与黏土交会 |
作为对比, 本文利用多矿物扩展的Xu-Payne模型及原始的Xu-Payne模型求取了横波速度。多矿物扩展的Xu-Payne模型是指:将1.1节所述Xu-Payne模型计算过程中的步骤① 改为利用VRH公式计算白云石、方解石、石英、黏土、硬石膏5种矿物混合的体积模量和剪切模量并将其作为基质模量, 其它计算步骤不变。为了利用原始的Xu-Payne岩石物理模型, 假设岩石中仅含有白云石、方解石、黏土3种矿物并进行测井解释, 得到一套含3种矿物体积分数及对应孔隙度、含气饱和度数据的解释结果, 该解释结果仅用于利用Xu-Payne模型计算速度。
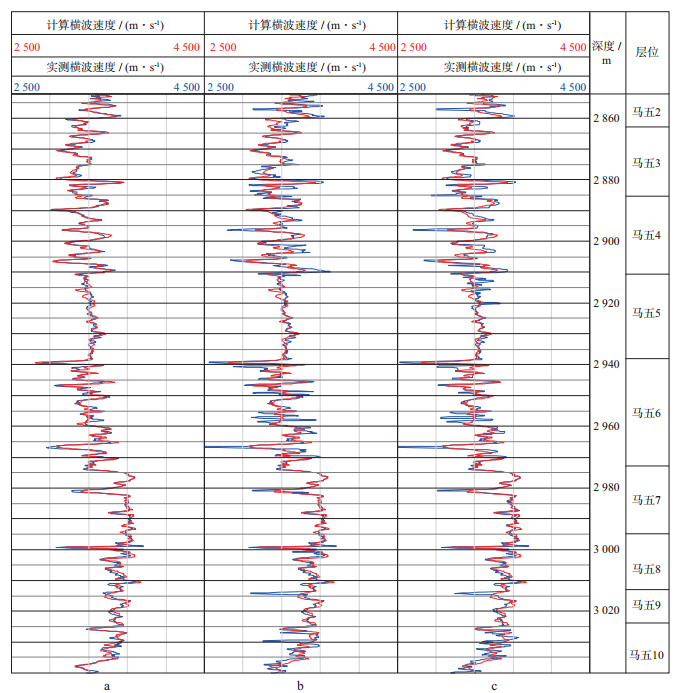
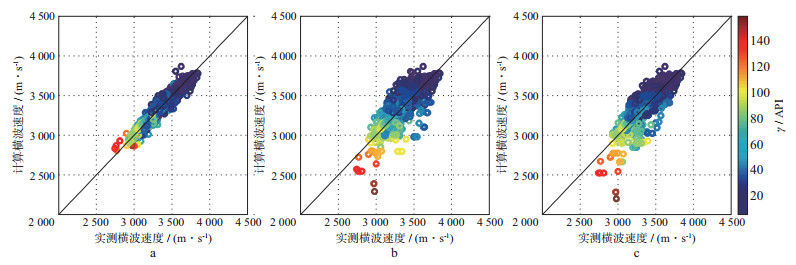
图 7和图 8分别是本文方法、多矿物扩展的Xu-Payne模型、原始Xu-Payne模型预测的横波速度与实测横波速度对比剖面和交会结果。结合图 7和图 8可以看到:本文方法预测的横波速度与实测速度吻合度最高, 趋势一致且速度数值差别较小; 多矿物扩展的Xu-Payne模型、原始Xu-Payne模型所预测的速度与实测速度基本一致, 但在部分层段有不吻合的现象。将图 7与图 4进行对比分析发现, 多矿物扩展的Xu-Payne模型与原始Xu-Payne模型在黏土含量较低的层段所得预测速度与实测速度吻合度较高(例如在马五段), 在黏土含量较高的层段预测速度与实测速度相比偏小, 尤其是在孔隙度和黏土含量都较高的层段; 而本文方法在低黏土含量和高黏土含量层段都能得到较好的速度预测结果, 说明本文对Xu-Payne模型的改进是有效的。
|
图 7 3种岩石物理模型速度预测结果对比 a本文方法; b多矿物扩展的Xu-Payne模型; c原始Xu-Payne模型 |
|
图 8 3种岩石物理模型的预测速度与实测速度交会结果 a本文方法; b多矿物扩展的Xu-Payne模型; c原始Xu-Payne模型 |
为了定量对比3种速度预测方法的差别, 分别计算了实测数值与预测数值之间的均方根误差(RMSE)、线性拟合的相关系数R2。RMSE计算公式如下:
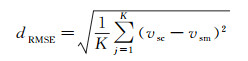
|
(12) |
式中:vsc, vsm分别指预测横波速度和实测横波速度; K指样点数, 本文K=1505。表 2是3种方法的误差统计结果, 由表 2可知:① 本文方法的RMSE低于多矿物扩展的Xu-Payne模型和Xu-Payne模型; ② 本文方法的R2高于多矿物扩展的Xu-Payne模型及Xu-Payne模型; ③ 多矿物扩展的Xu-Payne模型统计参数略优于Xu-Payne模型的统计参数。
| 表 2 3种岩石物理模型横波速度预测误差统计 |
针对鄂尔多斯盆地北部D气田奥陶系马家沟组马五段发育的岩性和孔隙结构均复杂的碳酸盐岩储层, 构建了一个新的碳酸盐岩岩石物理模型——改进的Xu-Payne岩石物理模型。利用该模型在纵波速度的约束下求取刚性孔隙与柔性孔隙的体积分数, 将孔隙体积分数代入岩石物理模型可以预测横波速度。应用改进的Xu-Payne模型对D气田研究区A井进行了横波速度预测, 预测结果与实测横波速度基本吻合。目的层井段统计结果显示, 本文方法预测结果优于多矿物扩展的Xu-Payne模型和Xu-Payne模型。
| [1] | XU S, PAYNE M. Modeling elastic properties in carbonate rocks[J]. The Leading Edge, 2009, 28(1): 66-74DOI:10.1190/1.3064148 |
| [2] | SUN S Z, WANG H Y, LIU Z S, et al. The theory and application of DEM-Gassmann rock physics model for complex carbonate reservoirs[J]. The Leading Edge, 2012, 31(2): 152-158DOI:10.1190/1.3686912 |
| [3] | WANG H, SUN S Z, YANG H J, et al. The influence of pore structure on P-and S-wave velocities in complex carbonate reservoirs with secondary storage space[J]. Petroleum Science, 2011, 8(4): 394-405DOI:10.1007/s12182-011-0157-6 |
| [4] |
张广智, 李呈呈, 印兴耀, 等. 基于修正Xu-White模型的碳酸盐岩横波速度估算方法[J].
石油地球物理勘探, 2012, 47(5): 717-722 ZHANG G Z, LI C C, YIN X Y, et al. A shear velocity estimation method for carbonate rocks based on the improved Xu-Wthie model[J]. Oil Geophysical Prospecting, 2012, 47(5): 717-722 |
| [5] |
蔡涵鹏, 贺振华, 唐湘蓉, 等. 碳酸盐岩孔隙结构影响分析和等效孔隙结构参数计算[J].
石油物探, 2013, 52(6): 566-572 CAI H P, HE Z H, TANG X R, et al. Impact analysis of pore structure and calculation of equivalent pore structure parameters for carbonate[J]. Geophysical Prospecting for Petroleum, 2013, 52(6): 566-572 |
| [6] |
陈启艳, 高建虎, 董雪华, 等. 碳酸盐岩地层横波速度预测[J].
天然气地球科学, 2014, 25(6): 921-927 CHEN Q Y, GAO J H, DONG X H, et al. Shear velocity estimation in carbonate reservoir[J]. Natural Gas Geosciences, 2014, 25(6): 921-927DOI:10.11764/j.issn.1672-1926.2014.06.921 |
| [7] | XU S, WHITE R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118DOI:10.1111/gpr.1995.43.issue-1 |
| [8] | KUSTER G, TOKSÖZ M. Velocity and attenuation of seismic waves in two phase media[J]. Geophysics, 1974, 39(5): 587-618DOI:10.1190/1.1440450 |
| [9] | LIU Z S, SUN Z D. The differential Kuster-Toksöz rock physics model for predicting S-wave velocity[J]. Journal of Geophysics & Engineering, 2015, 12(5): 839-848 |
| [10] |
马中高, 解吉高. 岩石的纵、横波速度与密度的规律研究[J].
地球物理学进展, 2005, 20(4): 905-910 MA Z G, XIE J G. Relationship among compressional wave, shear wave velocities and density of rocks[J]. Progress in Geophysics, 2005, 20(4): 905-910 |
| [11] |
谢月芳, 张纪. 岩石物理模型在横波速度估算中的应用[J].
石油物探, 2012, 51(1): 65-70 XIE Y F, ZHANG J. The application of rock physics model in S-wave velocity prediction[J]. Geophysical Prospecting for Petroleum, 2012, 51(1): 65-70 |
| [12] |
郭栋, 印兴耀, 吴国忱. 横波速度计算方法与应用[J].
石油地球物理勘探, 2007, 42(5): 535-538 GUO D, YIN X Y, WU G C. Computational approach of S-wave velocity and application[J]. Oil Geophysical Prospecting, 2007, 42(5): 535-538 |
| [13] |
化世榜, 印兴耀, 宗兆云, 等. 一种改进的泥质砂岩岩石物理模型[J].
石油物探, 2016, 55(5): 649-656 HUA S B, YIN X Y, ZONG Z Y, et al. An improved rock physics model for shale sandstone[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 649-656 |
| [14] |
董宁, 霍志周, 孙赞东, 等. 泥页岩岩石物理建模研究[J].
地球物理学报, 2014, 57(6): 1990-1998 DONG N, HUO Z Z, SUN Z D, et al. An investigation of rock physics model for shale[J]. Chinese Journal of Geophysics, 2014, 57(6): 1990-1998DOI:10.6038/cjg20140629 |
| [15] |
刘喜武, 刘宇巍, 霍志周, 等. 页岩油气层地震岩石物理计算方法研究[J].
石油物探, 2016, 55(1): 10-17 LIU X W, LIU Y W, HUO Z Z, et al. Study on seismic rock physics computational method for shale reservoir[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 10-17 |
| [16] | HORNBY B E. Anisotropic effective-medium modeling of the elastic properties of shales[J]. Geophysics, 1994, 59(10): 1570-1583DOI:10.1190/1.1443546 |
| [17] | HAN D H, NUR A, MORGAN D. Effect of porosity and clay content on wave velocities in sandstones[J]. Geophysics, 1986, 51(11): 2093-2107DOI:10.1190/1.1442062 |
| [18] | CASTAGNA J P, BATZLE M I, EASTWOOD R I. Relationship between compressional wave and shear wave velocities in clastic silicate rocks[J]. Geophysics, 1985, 50(5): 571-581 |
| [19] | NORRIS A N. A differential scheme for the effective moduli of composites[J]. Mechanics of Materials, 1985, 4(1): 1-16DOI:10.1016/0167-6636(85)90002-X |
| [20] |
冉新权, 付金华, 魏新善, 等. 鄂尔多斯盆地奥陶系顶面形成演化与储集层发育[J].
石油勘探与开发, 2012, 39(2): 154-161 RAN X Q, FU J H, WEI X S, et al. Evolution of the Ordovician top boundary and its relationship to reservoirs' development, Ordos Basin[J]. Petroleum Exploration and Development, 2012, 39(2): 154-161 |
| [21] | MAVKO G, MUKERJI T, DVORIKIN J. The rock physics handbook:tools for seismic analysis in porous media[M]. Cambridge: Cambridge University Press, 1998: 95-98. |
| [22] | GASSMANN F. Elastic waves through a packing of spheres[J]. Geophysics, 1951, 16(4): 673-685DOI:10.1190/1.1437718 |
| [23] |
雍世和, 张超谟.
测井数据处理与综合解释[M]. 山东东营: 中国石油大学出版社, 2002: 313-320.
YONG S H, ZHANG C M. Logging data processing and comprehensive interpretation[M]. Dongying: China University of Petroleum Press, 2002: 313-320. |



 ,
,