2. 中国石油化工股份有限公司重庆涪陵页岩气勘探开发有限公司, 重庆 408000
2. Sinopec Fuling Chongqing Shale Gas Exploration and Development Co., Ltd, Chongqing 408000, China
随着水平井技术的不断突破与完善, 在页岩气、煤层气等非常规油气藏勘探开发中, 压裂技术被大量应用, 如水力压裂和裂缝发育增长[1]、监控断层[2]、跟踪注射液体或蒸汽生产的构造形态变化[3]、裂缝网络成像和岩石地层与储层的压实[4]等。
微地震是目前水力压裂监测技术的主要方式。水力压裂过程导致地下的微破裂事件活动非常复杂。随着压裂液的不断注入, 其在地层裂缝延伸过程中, 打破地层原有应力平衡, 应力状态发生改变。ITO等[5]的研究结果表明, 水力剪切作用使天然裂缝面发生剪切滑动, 产生微地震事件。BAIG等[6]研究指出, 地震事件频带范围从几赫兹到上千赫兹, 破裂半径(数十米) 较大的断层面产生一个波长较大和频率较低的信号, 而破裂半径小(几十厘米至几米) 的断层会产生更高的频率信号。压裂微地震事件震级一般为-3~0级, 产生的破裂面半径约为数十厘米至几米, 频率范围为50~500Hz。压裂液在地层延伸过程中产生张性破裂, 为低频信号, 受监测设备频带范围的限制, 这种张型形变无法被监测到[7]。地震b值理论表明, 微地震事件数量随震级减少而大幅增加(由b值确定), 大量的弱小事件受监测条件影响无法被监测到;监测到的微地震事件是地下应力状况受压裂影响而发生地质力学形变中的一部分[8], 主要以张剪型裂缝破裂为主。在我国西部, 压裂目标区域埋藏较深, 传播至地面的微地震事件能量较弱, 加之信噪比较低(地面监测方式), 被有效检测和识别出来的微地震事件较少。
本文研究在压裂目标区域布置地面接收检波器, 采用矩张量反演获得裂缝不同破裂类型对应的地震矩, 与岩石破裂力学分析相结合, 获得裂缝破裂面的尺寸、位移和微震事件的震级等参数, 实现裂缝规模的定量反演, 结合微震事件发生的时间顺序, 解释裂缝的几何形状和发育过程。
1 方法原理及技术流程微地震事件是伴随岩石破裂或错动而产生的强度较弱的地震波, 通常发生在裂缝断裂面上。微地震资料处理首先要有可有效识别的微地震事件, 并拾取其准确的到达时间, 用于微地震精确定位。地面微地震资料由于背景噪声大, 在压裂深度较深区域, 弱的微地震事件往往淹没在噪声中, 难以有效识别。在我国西部, 地表条件和表层速度结构复杂, 地表落差大, 导致校正量计算不准确, 微地震事件同相轴难以有效校平, 导致定位误差明显增大, 严重影响后续处理与解释。
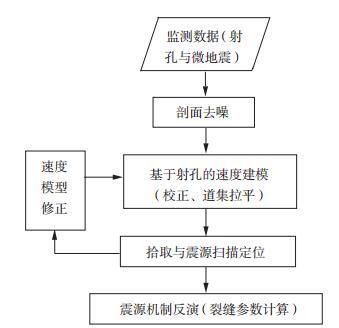
地面微地震资料的处理流程主要包括道集资料去噪、速度模型建立、震源定位和震源机制反演4个步骤(图 1), 本文重点阐述震源机制反演及结果的解释, 下面对处理的几个步骤进行简要介绍。
|
图 1 微地震资料处理流程 |
微地震资料去噪的目的是从噪声背景中准确识别出有效信号, 主要利用信号与噪声在传播方向(视速度)、频率特性、相关性等方面的差异来区分。常用的去噪方法有F-K滤波、拉东变换和互相关去噪等, 可有效去除噪声, 为后续处理奠定基础。
速度建模的主要目的是为震源定位提供高精度的速度模型。压裂施工通常产生多个射孔事件, 射孔资料能量较强, 射孔位置已知, 且震源为爆炸源(无方向性差异), 其到达各个检波器的波形具有很好的相似性和识别度, 易获得可靠的旅行时。采用声波测井曲线建立初始速度模型, 通过多个射孔事件的旅行时反演, 获得较为准确的地震波层速度模型, 合理的剩余校正量有利于消除微地震事件同相轴的不连续性。
震源定位的方法较多, 主要利用信号的旅行时与振幅信息。当信噪比不高时, 通常采用扫描定位方法。扫描定位的基本原理是通过多次覆盖叠加, 并对地下所有可能的震源位置进行扫描, 能量最大的点即为定位结果。即当两道数据的信号具有相同的到时(相位), 如果将它们叠加, 则信号得到加强; 在相位不同时进行叠加, 则信号减弱; 多道信号叠加也是如此。实际资料中, 非爆炸震源事件的相位变化可能导致扫描定位错误, 因此, 在叠加时需要先消除震源相位变化再进行叠加定位。
震源机制是描述地下裂缝破裂的重要参数, 是裂缝解释的重要依据。不同的观测方式一般采用不同的震源机制反演方法(表 1)。井中观测信噪比高、数据量小、观测角度偏窄, 通常采用矩张量反演方法; 而地面资料信噪比低、数据量大、观测范围大, 常采用P波初动反演方法[9]。震源机制的矩张量反演是采用观测到的地面位移推断震源属性, 震源属性用矩张量描述, 根据AKI等[10]的理论公式有:
| 表 1 P波初动与矩张量反演方法适用性对比 |
| $ U = \mathit{\boldsymbol{M}}*G $ | (1) |
式中:U为地面观测到的地震数据; M为描述震源的二阶矩张量; G为地震波传播过程的格林函数。已知地震数据和格林函数的情况下, 通过求解线性方程组反演得到矩张量[11]。采用地面资料进行矩张量反演存在两个主要问题:①资料品质较低, 噪声干扰大; ②传播函数计算成本高, 反演对内存需求非常大。通过对地面微地震数据的有效处理, 对于信噪比较高的资料, 矩张量反演也可以获得较理想的结果, 主要包括以下4个方面。
1) 数据优选。地面观测数据通常在千道以上, 为了保证矩张量反演的可靠性, 同时有效降低内存需求和计算量, 需要剔除噪声污染较大的地震道数据。其优选原则是, 所选道既具有高信噪比, 又能有效反映微地震事件相位与振幅变化。另外由于微地震震源在节面上辐射的能量非常弱, 因此, 优先选取在观测系统上极性变化的道数据。
2) 多道叠加。由于地面微地震资料信噪比相对于井中资料低得多, 采用多道叠加能够有效压制噪声, 提高波形质量, 保证波形反演结果的稳定、可靠。
3) 时差校正。时差校正包括两部分, 即微地震事件的动校正和剩余校正。常规处理流程中建立的速度模型能够有效地校平射孔事件同相轴, 而离射孔点位置较远的微地震事件同相轴存在较大低频的动校正量。根据扫描定位结果可以计算其低频校正量, 使微地震事件同相轴拉平。但是通常不同事件的剩余校正量存在差异, 根据林伯香等[12]提出的高频静校正计算思想, 以叠加能量为目标函数, 求取其剩余校正量, 最终获得校平后的微地震事件同相轴。
4) 子波选取。矩张量反演中需要选取合适的地震子波与实际数据进行匹配, 通常采用经过时差校正叠加后的数据作为输入子波。由于叠加会降低子波的频率, 因此, 在实际反演中需要进行频率匹配处理, 即反演的子波主频参数要与叠加后的数据主频一致。
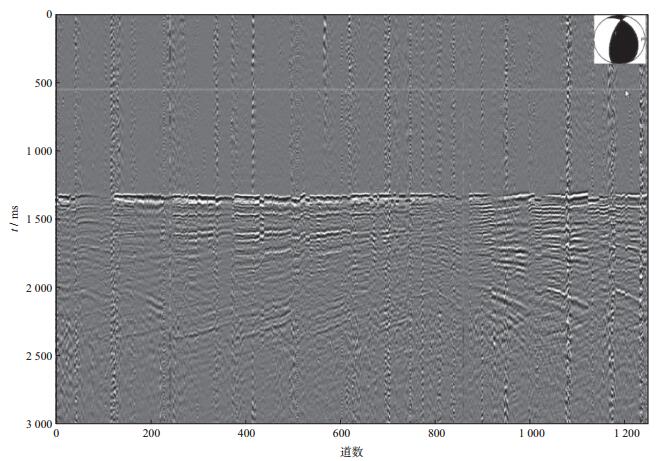
下面通过一个应用实例进行说明。所选资料为地面观测的一个微地震事件, 共1250道接收。经过常规的微地震前期处理(如去噪、校正等) 后, 微地震信号具有较高的信噪比, 见图 2(约1300ms处)。图 2右上角为反演该微地震事件得到的震源机制解。考虑到计算成本, 我们从1250道微地震数据中选取了173道, 经过校正、多道叠加和时差校正后, 获得反演的输入数据如图 3a所示。从图 3a中可以看出, 处理后的数据有效反映原始微地震数据振幅与相位变化, 同时在波形上具有很好的一致性。为了检验反演结果的可靠性, 应用反演结果进行正演模拟, 正演合成记录结果如图 3b所示。对比图 3a和图 3b发现, 除了正演合成数据频率略低外, 两者在振幅和相位上具有非常好的相似性。因此, 反演结果是可靠的。
|
图 2 地面观测的微地震事件与震源机制解 |

|
图 3 处理后的微地震数据(a) 与矩张量反演结果的正演合成记录(b) |
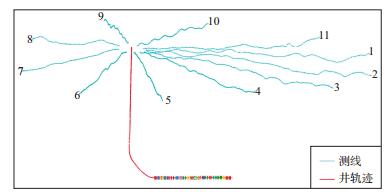
选取的压裂井位于四川盆地和盆边山地过渡地带, 研究区地势以低山、丘陵为主, 横跨长江南、北两岸, 地势大致东南高、西北低, 西北-东南断面呈向中部长江河谷倾斜的对称马鞍状。海拔最高1977m, 最低138m, 多在200~800m, 采用水平井压裂, 观测系统如图 4所示, 红色线为水平井轨迹(彩色部分为压裂段), 压裂垂直深度在2600m左右, 青色线为检波器分布, 呈放射状布设, 共11条测线, 测线总长度约37km; 道距为20m;观测道数共1864道, 每道24只检波器堆埋组合。
|
图 4 观测系统分布 |
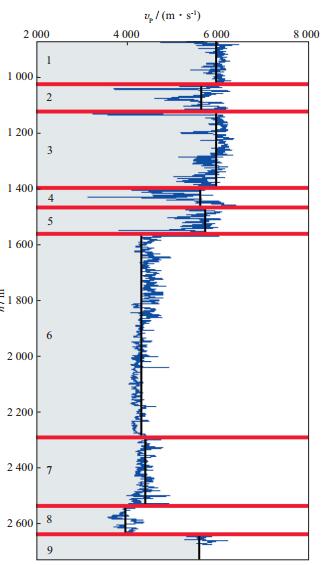
根据声波测井曲线建立初始速度模型, 结果如图 5所示。图 5中, 蓝线为声波测井曲线, 红线为划分的地层模型, 共9层, 页岩压裂段位于第8层, 可以看出, 页岩层位于两个高速层之间, 上层速度相对于页岩层差异不是特别大, 而下层速度则明显较高, 这样的速度结构容易引起层间多次波或底层的多次反射。微地震处理主要采用的是直达波信号, 对于井中观测而言, 容易产生直达波和多次反射的叠加(影响程度与实际微地震事件、观测井位置有关), 导致无法正确拾取初至旅行时, 而这对于地面观测影响则较小。
|
图 5 声波测井与层速度 |
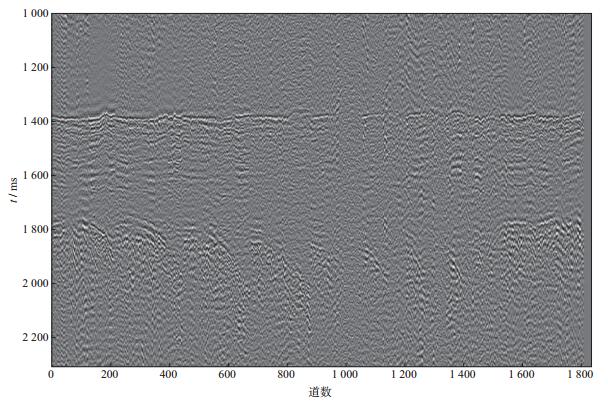
经过去噪、时差校正等处理获得微地震事件如图 6所示。从图 6中可以看出, 微地震事件位于剖面中1400ms处。同相轴存在着较大的道间时差, 分析其原因主要有两种:①地形高程变化大, 地表速度模型复杂; ②信噪比低, 射孔信号中有效识别旅行时的道数据少, 基于射孔数据的校正存在误差。这两个原因直接导致校正量计算存在一定误差, 微地震事件同相轴无法充分校平, 基于数据分析的认识, 采用文献[9]中的方法进行震源机制反演。水力压裂监测相对于天然地震其观测角度要小, 通常单边排列长度小于或约等于目标检测点垂直深度, 因此, 最大观测仰角角度小于45°。当震源断层面的地震波在地面出射的位置不能有效被观测系统所覆盖时, 采用P波极性的反演难以获得准确的震源机制, 没有足够的极性变化数据进行控制。因此, 杨心超等[13]在文献[9]的基础上进行了改进, 主要在反演中引入震源振幅信息, 以极性与振幅同时与实际资料匹配为目标函数, 消除反演中由于观测系统的不充分引起的多解性问题, 增强了反演结果的可靠性。图 6所示的微地震事件反演的结果如图 7所示。从图 7可以看出, 除了在节面上由于能量较弱, 存在一定误差(图中由蓝变红的过渡带), 其它道数据的振幅与极性均匹配很好, 这说明反演结果是可靠的。
|
图 6 微地震事件 |
|
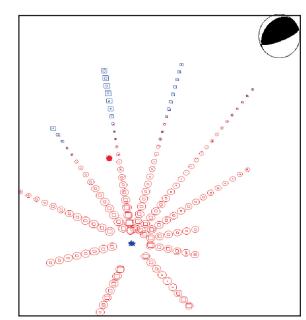
图 7 震源机制解 |
图中, 方形代表实际数据, 圆形为理论计算结果, 红色表示正极性, 蓝色表示负极性, 方形与圆形的大小代表振幅值。
根据BAIG公式[6]计算微地震事件的震级:
| $ {M_w} = \frac{2}{3}{\rm{lg}}{M_0}-6 $ | (2) |
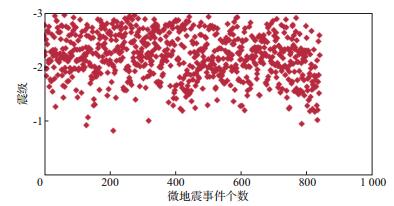
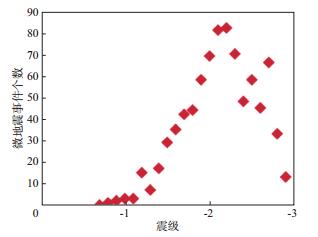
式中:Mw为矩震级; M0为反演的标量地震矩, 单位为N·m。图 8为整个压裂中所有事件的矩震级, 可以看出, 微地震事件主要分布在-3~0级。图 9展示了不同震级段的微地震事件个数分布, 由于地面监测中微地震事件样本个数相对少, 从统计角度考虑, 采用0.1级作为震级的变化, 随着震级减少, 微地震事件个数增加, 在震级为-2.2级处, 微地震事件个数达到最大, 随微地震事件个数减少, 这是由于微地震信号变弱, 能有效检测出的微地震信号变少, 小于-3级的微地震数据已经无法被监测到。因此, 结合本次压裂的实际情况认为, 在埋深约为2600m处, -2.2级微地震为地面观测的主要监测事件。
|
图 8 微地震事件矩震级 |
|
图 9 震级与数量的分布 |
利用反演的标量地震矩M0与页岩剪切模量μ, 根据公式(3) 计算微地震事件体积:
| $ V = \sum \frac{{{M_0}}}{\mu } = Ad $ | (3) |
式中:A为断层滑移面积; d为滑移位移。
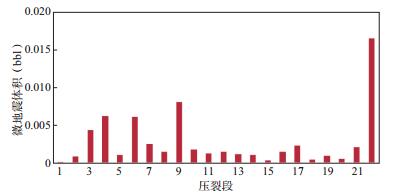
图 10显示不同压裂段计算的微地震事件体积统计结果, 微地震事件体积与微地震事件能量成正比, 与实际注入地下压裂液相比(数千方), 其数值非常小, 可能的解释是压裂液在地层中的渗透和耐震(aseismic) 现象[14], 即水力压裂中大量的裂缝张开和裂缝延伸过程所辐射的能量为低频信号, 而不是所监测到的微地震事件。
|
图 10 不同压裂段的微地震事件体积(1bbl≈158.987×10-3m3) |
水力压裂中, 地层岩石在应力作用下发生的形变主要为张形变和剪切形变, 产生张开型裂缝、剪切型裂缝或两者混合型裂缝。其中, 纯张开型裂缝由于作用时间长(相对于微地震监测而言), 辐射的波场较强, 还有仪器参数因素的影响, 在地面观测中无法监测接收[6], 且不产生极性的变化。大量的实际压裂监测显示, 微地震事件中大部分都存在极性变化, 由此说明, 微地震事件主要是剪切为主的裂缝破裂产生, P波初动反演正是基于断层面错动在地面不同接收点的P波初动极性不同[9]来求解的。
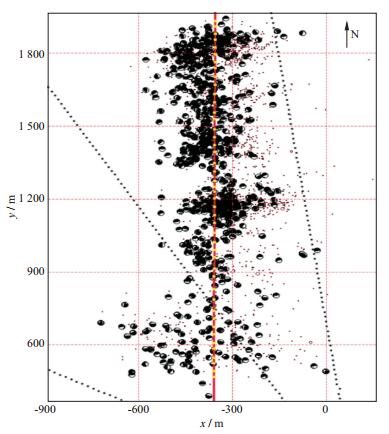
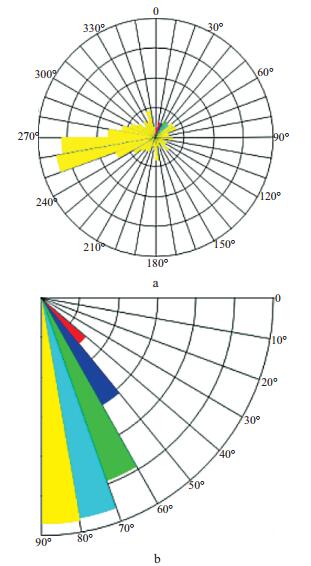
根据反演出的剪切裂缝走向, 并基于剪切形变的应力分析, 解释区域最大、最小应力场分布, 为井位部署提供建议。对整个压裂段(共800多个微地震事件) 进行反演, 结果如图 11所示。震源机制确定结果是两个相互垂直的平面, 理论上, 这两个平面均有可能是裂缝面, 因此, 如何确定其中的一个面为裂缝破裂面非常重要。目前采取的主要方法是结合实际压裂情况与地质认识进行判定。FISHER等[14]对大量实际的微地震压裂进行了统计, 结果显示, 在深度大于4000ft (1ft≈0.3048m), 主要发育高角度裂缝。基于产生垂直裂缝的解释, 对反演结果的方位角和倾角进行了统计, 结果如图 12所示, 方位角主要集中在250°~270°, 裂缝倾角大部分为大于60°的高角度裂缝。
|
图 11 微地震事件与震源机制解 |
|
图 12 微地震事件方位角(a) 与倾角(b) 分布 |
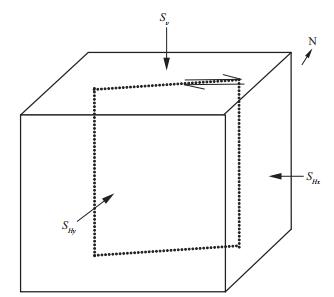
根据文献[15]描述, 该地区目标层的垂向应力在49.2~53.7MPa, 最大水平应力在52.2~55.5MPa, 最小水平主应力在48.6~49.9MPa, 水平应力差系数为0.06~0.14。根据应力系数小于0.30的标准, 在该区域可压裂形成充分的裂缝网络。区域内垂向应力介于最大水平主应力和最小水平主应力之间, 基于此认识建立该区域裂缝发育模型如图 13所示, 其中SHx为东西方向应力, SHy为南北方向应力, Sv为垂直方向应力, 图中虚框为剪切破裂的裂缝面。根据反演的剪切裂缝方位角统计(图 12), 其剪切方位集中于260°左右, 即裂缝沿近似东西方向发育, 裂缝首先沿最小水平主应力方向张开, 随着压裂液注入和应力状况的改变, 裂缝在张开面发生剪切错动, 裂缝断层为走滑型。
|
图 13 裂缝模型与应力分布 |
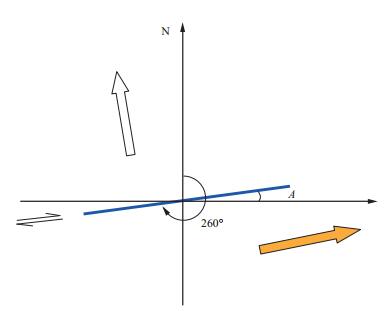
基于图 13的裂缝模型分析与解释, 产生260°的剪切裂缝的最大水平主应力为图 14中黄色箭头所示, 最小水平主应力为白色箭头(北偏西10°), 蓝色线为剪切裂缝, 角度A为10°。通常, 水力压裂设计中压裂井沿最小水平主应力方向(即垂直于最大水平主应力方向) 布置, 基于上述分析与认识, 建议水平井在现有方位(正北向) 调整为北偏西10°, 更有利于压裂与造缝。
|
图 14 剪切裂缝与应力分析 |
对我国四川盆地某压裂井的页岩气水力压裂地面观测数据开展了地面微地震震源机制反演及裂缝解释技术应用研究, 通过震源机制反演获得裂缝破裂震级、剪切裂缝发育的地质参数; 基于地质应力场分析, 解释该区域破裂裂缝为走滑型高角度裂缝, 以此建立剪切裂缝破裂模型, 解释了局部最大、最小水平主应力方向和裂缝延展方向, 最终给出了压裂井方位调整为北偏西10°的建议。
采用震源机制反演区域应力张量, 获得地下网格点上的应力变化情况, 对于压裂解释更为直观, 建议在微地震事件较丰富的压裂工区进行应力张量反演。
| [1] | CALEY A J, KENDALL J M, JONES R H, et al. Monitoring fractures in 4D using microseismic data[J]. Expanded Abstracts of 63rd EAGE Annual Conference, 2001: 1-15 |
| [2] | BOONE T J, NECHTSCHEIN S J, SMITH R J, et al. Microseismic monitoring for fracturing in the Colorado Shales above a thermal oil recovery operation[J]. The 37th US Symposium on Rock Mechanics (USRMS), 1999: 1069-1076 |
| [3] | MAXWELL S C, URBANCIC T I, PRINCE M, et al. Passive imaging of seismic deformation associated with steam injection in Western Canada[J]. Expanded Abstracts of 78th SPE Annual Conference, 2003: 5-8 |
| [4] | MAXWELL S C, URBANCIC T I, STEINSBERGER N, et al. Microseismic imaging of hydraulic fracture complexity in the Barnett shale[J]. Expanded Abstracts of 77th SPE Annual Conference, 2002: 440-447 |
| [5] | ITO Y, OBARA K. Very low frequency earthquakes within accretionary prisms are very low stress-drop earthquakes[J]. Geophysical Research Letters, 2006, 33(9): 72-88 |
| [6] | BAIG A, URBANCIC T. Magnitude determination, event detectability, and assessing the effectiveness of microseismic monitoring programs in petroleum applications[J]. CSEG Recorder, 2010, 35(2): 22-26 |
| [7] | DERSHOWITZ W S, COTTRELL M G, LIM D H, et al.A discrete fracture network approach for evaluation of hydraulic fracture stimulation of naturally fractured reservoirs[C]//44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium.Salt Lake City:American Rock Mechanics Association, 2010:55-61 |
| [8] | MAXWELL S C. What does microseismic tell us about hydraulic fracture deformation[J]. CSEG Recorder, 2011, 36(8): 31-45 |
| [9] |
杨心超, 朱海波, 崔树果, 等. P波初动震源机制解在水力压裂微地震监测中的应用[J].
石油物探, 2015, 54(1): 43-50 YANG X C, ZHU H B, CUI S G, et al. Application of Pwave first-motion focal mechanism solutions in microseismic monitoring for hydraulic fracturing[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 43-50 |
| [10] | AKI K, RICHARDS P G. Quantitative Seismology[M]. USA: University Science Books, 2002: 1-700. |
| [11] |
朱海波, 杨心超, 王瑜, 等. 水力压裂微地震监测的震源机制反演方法应用研究[J].
石油物探, 2014, 53(5): 556-561 ZHU H B, YANG X C, WANG Y, et al. The application of microseismic source mechanism inversion in hydraulic fracturing monitoring[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 556-561 |
| [12] |
林伯香, 朱海波, 徐颖. 关于起伏地表偏移表层高频校正量计算方法的讨论[J].
石油物探, 2014, 53(4): 391-396 LIN B X, ZHU H B, XU Y. Discussion on the calculation methods of high frequency statics for the migration from rugged topography[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 391-396 |
| [13] |
杨心超, 朱海波, 李弘, 等. 基于P波辐射花样的压裂微地震震源机制反演方法研究及应用[J].
石油物探, 2016, 55(5): 640-648 YANG X C, ZHU H B, LI H, et al. Micro-seismic focal mechanisminversion based on P wave radiation pattern and application[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 640-648 |
| [14] | FISHER M K, WARPINSKI N R. Hydraulic-fracture-height growth:real data[J]. SPE Production & Operations, 2012, 27(1): 8-19 |
| [15] |
郭旭升.
涪陵页岩气田焦石坝区块富集区机理与勘探技术[M]. 北京: 科学出版社, 2014: 214-220.
GUO X S. Mechanism and exploration technology at enrichment of Jiao Shiba in Fuling shale gas field[M]. Beijing: Science Press, 2014: 214-220. |


