在地震勘探领域, 转换波静校正需要准确的近地表横波速度[1-4]。在地震工程领域, 一般需要地表到地下30m的平均横波速度进行场地分类[5]。但长期以来获得近地表横波速度的手段并不多, 主要有基于浅层SH折射波的旅行时解释或层析反演和钻井资料分析两种, 当存在下伏低速层等复杂情况时, 前者会导致错误的解释结果, 后者由于施工成本较高, 井的分布密度十分有限。虽然在地震勘探领域一般将面波视为噪声将其去除[6-7], 但这种做法正在改变, 因为面波特有的频散特征可以用来获得近地表信息[1]。多道面波分析技术(multichannel analysis of surface waves, MASW) 是20世纪90年代发展起来的一种基于面波的近地表无损探测技术, 它通过反演面波相速度频散曲线来获得近地表横波速度甚至品质因子。由于施工方便, 不受常规折射波中存在的隐蔽层问题困扰, 这项技术目前发展十分迅速[8-10]。
MASW技术的关键步骤在于获得准确的面波相速度频散图像, 进而根据能量峰值拾取频散曲线和反演。F-K变换法是最早用于主动源面波频散曲线成像的方法。将时-空域面波记录进行二维傅里叶变换得到频率-波数谱, 通过拾取能量峰值和简单的变换关系可得到相速度频散曲线[11-14]。MCMECHAN等[15]最早提出了频率-慢度变换法(ω-p变换法), 并用其对勘探地震记录中的面波进行了频散成像。相移法是目前提取主动源面波频散曲线应用最为广泛的一项技术, 已经成为许多面波处理商业软件的标准模块[16-18]。DAL等[19]曾对F-K变换法、ω-p变换法和相移法进行比较, 结果显示相移法的总体性能优于前二者。LUO等[20]将高分辨率线性拉东变换(high-resolution linear Radon transform, HR-LRT) 用于面波相速度频散成像, 其相速度分辨率远高于F-K变换法、ω-p变换法以及相移法。
多重信号分类(MUSIC) 是一种基于矩阵特征结构分解的超高分辨率空间谱估计方法[21], 用于估计信号到达方向。该方法于20世纪90代末即被引入地震勘探领域, 用于获得高分辨率叠加速度谱[22-24]。相对于F-K等变换类方法, MUSIC方法在主动源面波频散成像方面的应用研究还较少。IRANPOUR等[25]率先用MUSIC方法获得Scholte波的高分辨率频率-波数谱。随后, WINSBORROW等[26]将其应用于海底Love波的频散成像。BOIERO等[27]进一步将该方法应用于小尺度三维地震工程面波的频散特征分析。MISBAH等[28]则将该方法应用于面波衰减系数的提取。但是上述研究均在频率-波数域内进行, 需要进行插值才能获得对应的频率-相速度频散图像。尤其需要指出的是, 同为高分辨率方法, MUSIC法与HR-LRT法在获取高分辨率面波频散图像方面存在哪些差异尚未见报道。本文提出了一种直接在频率-速度域进行多重信号分类的高分辨率面波频散成像方法(fv-MUSIC法), 该方法无需额外的插值转换即可获得高分辨率的频率-相速度图像。此外, 通过理论面波数据、工程面波数据和地震勘探中的含面波数据对比了fv-MUSIC法、相移法和HR-LRT法的频散成像效果, 验证了fv-MUSIC方法的有效性和独特优势。
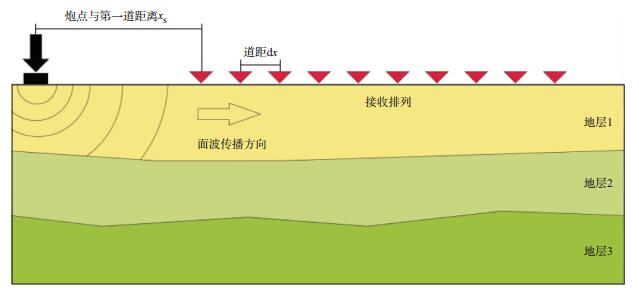
1 fv-MUSIC方法原理根据典型的主动源面波采集方式(图 1), 在地表采用锤击或落重法激发主动源面波(地震勘探中多采用爆炸震源), 假设共有N个检波器等间距均匀分布接收(也可以采用不等距分布), 道距为dx, 炮点与第一道距离为xS, 则第i道的炮检距为xi=xS+(i-1) dx。传统的频率域波束形成器形式为[29]:
|
图 1 MASW面波采集 |
| $ {\mathit{\boldsymbol{P}}_{{\rm{FDBF}}}}(k, \omega ) = {\mathit{\boldsymbol{e}}^H}\left( k \right)\mathit{\boldsymbol{R}}(\omega )\mathit{\boldsymbol{e}}\left( k \right) $ | (1) |
式中:
| $ \mathit{\boldsymbol{e}}\left( k \right) = {[{\rm{exp}}(-jk{x_1}){\rm{exp}}(-jk{x_2}){\rm{ }} \cdots {\rm{exp}}(-jk{x_N})]^{\rm{T}}} $ | (2) |
为水平波数形式的平面波导向矢量(steering vector), H代表复共轭转置; R(ω) 为空间谱相关矩阵,
| $ \mathit{\boldsymbol{R}}(\omega ) = \left[{\begin{array}{*{20}{c}} {{R_{11}}(\omega )}&{{R_{12}}(\omega )}& \cdots &{{R_{1N}}(\omega )}\\ {{R_{21}}(\omega )}&{{R_{22}}(\omega )}& \cdots &{{R_{2N}}(\omega )}\\ \vdots & \vdots &{}& \vdots \\ {{R_{N1}}(\omega )}&{{R_{N2}}(\omega )}& \cdots &{{R_{NN}}(\omega )} \end{array}} \right] $ | (3) |
其中,
为了直接得到频率-速度域高分辨率面波频散图像, 利用水平波数与相速度之间的关系k=ω/v, 我们将波束形成器形式改写为:
| $ {\mathit{\boldsymbol{P}}_{{\rm{FDBF}}}}(v, \omega ) = {\mathit{\boldsymbol{e}}^{\rm{H}}}\left( v \right)\mathit{\boldsymbol{R}}(\omega )\mathit{\boldsymbol{e}}\left( v \right) $ | (4) |
其中,
| $ \mathit{\boldsymbol{e}}\left( v \right)={{\left[\rm{exp}\left( \frac{-j\omega {{x}_{1}}}{v} \right)\ \ ~\rm{exp}\left( \frac{-j\omega {{x}_{2}}}{v} \right)\rm{ }\cdots \rm{exp}\left( \frac{-j\omega {{x}_{N}}}{v} \right) \right]}^{\rm{T}}} $ | (5) |
为对应相速度v和角频率ω的平面波导向矢量。
因为空间谱相关矩阵R (ω) 是一艾尔米特对称正定矩阵, 所以它的特征向量通常与R(ω) 正交, 特征值一般都为正值[21]。将其逆矩阵进行特征分解, 有:
| $ {\mathit{\boldsymbol{R}}^{-1}}(\omega ) = \sum\limits_{i = 1}^N {\lambda _i^{-1}(\omega ){\mathit{\boldsymbol{v}}_i}(\omega )\mathit{\boldsymbol{v}}_{_i}^{\rm{H}}(\omega )} $ | (6) |
式中:N为特征值个数, 等于接收道数; λi为第i个特征值; vi为对应λi的特征向量。这些特征值与特征向量可以进一步分为对应信号和噪声的两个子空间部分, 即:
| $ \begin{array}{l} {\mathit{\boldsymbol{R}}^{-1}}(\omega ) = \sum\limits_{i = 1}^{{N_{\rm{s}}}} {\lambda _i^{-1}(\omega ){\mathit{\boldsymbol{v}}_i}(\omega )\mathit{\boldsymbol{v}}_{_i}^{\rm{H}}(\omega )} + \\ \sum\limits_{i = {N_{\rm{s}}} + 1}^N {} \lambda _i^{-1}(\omega ){\mathit{\boldsymbol{v}}_i}(\omega )\mathit{\boldsymbol{v}}_i^H(\omega ) \end{array} $ | (7) |
其中较大的Ns个特征值对应信号子空间, 其余特征值对应噪声子空间。MUSIC方法只利用其中的噪声子空间部分进行最大分辨率空间谱估计, 即:
| $ \mathit{\boldsymbol{R}}_{{\rm{MUSIC}}}^{-1}(\omega ) = \sum\limits_{i = {N_{\rm{s}}} + 1}^N {} {\mathit{\boldsymbol{v}}_i}(\omega )\mathit{\boldsymbol{v}}_{_i}^{\rm{H}}(\omega ) $ | (8) |
将(8) 式与平面波导向矢量(公式(5)) 相结合, 得到最终的fv-MUSIC谱估计结果:
| $ {\mathit{\boldsymbol{P}}_{{\rm{MUSIC}}}}({v_{\rm{T}}}, \omega ) = \frac{1}{{{\mathit{\boldsymbol{e}}^{\rm{H}}}({v_{\rm{T}}})\mathit{\boldsymbol{R}}_{{\rm{MUSIC}}}^{-1}(\omega )\mathit{\boldsymbol{e}}({v_{\rm{T}}})}} $ | (9) |
这里的vT表示角频率ω的扫描相速度或实验相速度。对每个频率都采用一系列的相速度vT代入(9) 式, 即可获得最终的频散相速度图像。
2 理论模型测试首先合成一个简单的频散波记录, 用于检验在理想条件下fv-MUSIC方法的频散成像效果, 并将其与相移法、HR-LRT法进行对比。震源函数为主频20Hz的雷克子波, 假设理论相速度频散关系为:
| $ v\left( f \right) = {v_0} + \Delta v{\rm{exp}}\left( {\frac{{-{f^2}}}{{{\sigma ^2}}}} \right) $ | (10) |
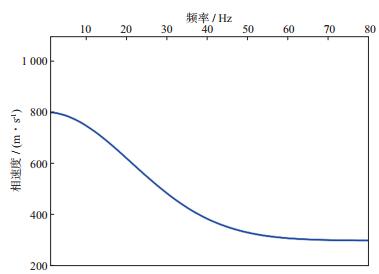
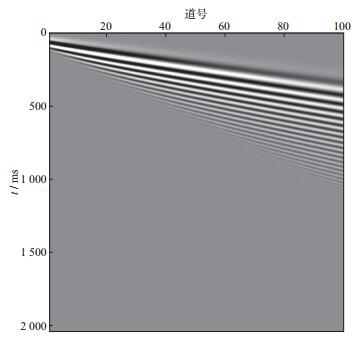
式中:v0代表高频极限时的相速度, 取300m/s; Δv为速度变化梯度, 取500m/s; σ=30。由(10) 式得到的理论相速度频散曲线见图 2, 通过(10) 式和炮检距xi可以得到每道的相位延迟, 经过傅里叶反变换即得到最终的理论频散波地震记录(图 3)。该记录接收道数100, 道距2m, 炮点与第一道距离10m, 时间采样间隔2ms。记录中只有单纯的频散波, 可以近似看成基阶模式瑞雷波或勒夫波, 代表横波速度随深度增加而递增的典型地层条件下接收到的面波记录。
|
图 2 理论频散曲线 |
|
图 3 简单频散波地震记录 |
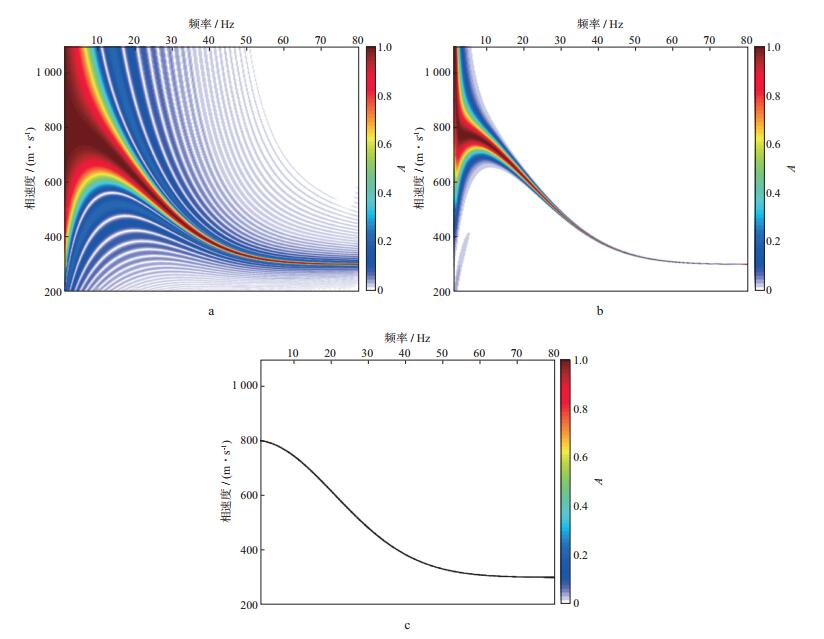
分别采用相移法、fv-MUSIC法和HR-LRT法获得的频散图像见图 4。对比发现, fv-MUSIC法分辨率最高, 几乎达到和理论频散曲线相同的效果; HR-LRT法效果次之; 相移法效果不够理想, 除了相速度能量轴最粗之外, 还存在许多能量较弱的虚假相速度。在处理实际面波资料时, 有可能将这些虚假相速度能量轴误判为某阶面波模式, 得到错误的反演结果。一种好的频散成像方法应该在突出真实面波相速度的同时尽可能压制上述假象。在计算效率方面, 由于相移法是在频率域进行简单的倾斜叠加, 所以速度最快, 用时约7s。fv-MUSIC法由于对每个频率都进行矩阵特征分解, 所以计算量增加, 用时约35s。HR-LRT法由于在每个频率都需要进行反演问题的求解, 计算效率最低, 用时约338s, 并且正则化参数的选择直接影响HR-LRT法频散成像的效果和计算效率, 需要通过多次试验来获得满意的频散图像。
|
图 4 理论模型3种方法频散成像效果 a 相移法; b HR-LRT法; c fv-MUSIC法 |
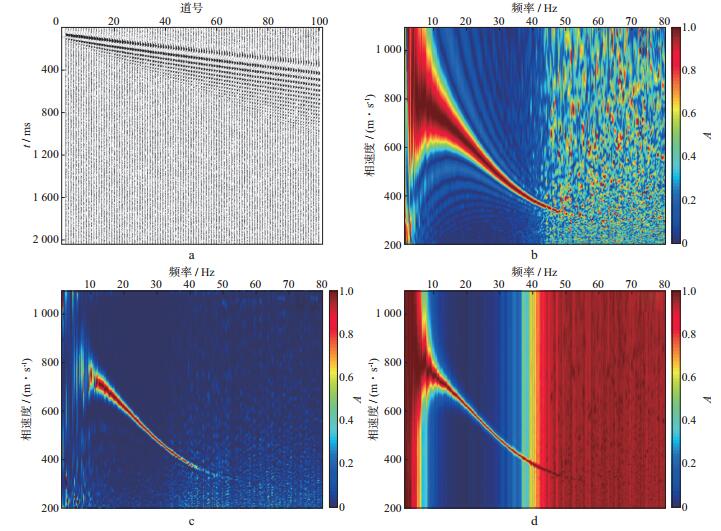
将图 3所示频散波地震记录加入一定程度的均匀分布随机噪声, 使其信噪比为1, 得到如图 5a所示含噪记录, 用以考察3种频散成像方法的抗噪性。图 5b到图 5d为3种方法频散成像结果, 可见由于噪声的影响, 3种方法高频部分(>50Hz) 的相速度聚焦都不成功, 低频部分( < 10Hz) 也出现了明显的抖动。也就是说, 从成像频带宽度来看, 3种方法的抗噪性基本一致。因为MASW方法基于地层横向速度不变或缓变这一假设条件, 所以得到的相速度频散曲线反映的是接收排列范围内地下的平均效应。为了得到二维近地表横波速度剖面, 一般采用滚动式面波激发采集方式得到一系列频散图像, 提取频散曲线, 反演得到一组一维横波速度, 通过横向插值构建出二维横波速度分布图。所以, 如果能用更少的接收道数得到合理的频散图像, 将有利于提高MASW方法的横向分辨能力。以下选择图 5a中第41至第50道(共10道) 记录进行频散分析, 比较3种方法的成像效果(图 6)。
|
图 5 频散波记录信噪比为1时3种方法频散成像效果 a 含噪声频散波记录; b 相移法频散成像效果; c HR-LRT法频散成像效果; d fv-MUSIC法频散成像效果 |
|
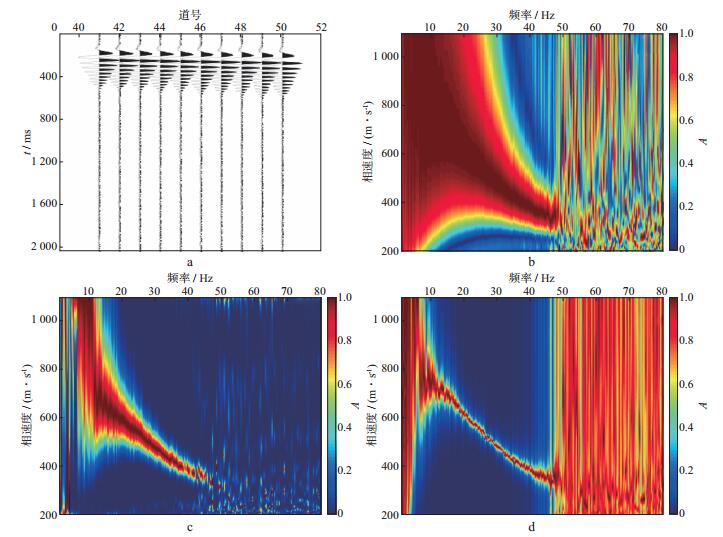
图 6 中间10道记录及3种方法频散成像效果 a 第41至第50道信号; b 相移法频散成像效果; c HR-LRT法频散成像效果; d fv-MUSIC法频散成像效果 |
对比图 6b至图 6d可见, 记录道数减少后, 相移法得到的频散图像的相速度分辨率大幅下降, HR-LRT法得到的频散图像的相速度分辨率下降也十分明显。这是因为, 作为倾斜叠加类算法, 相移法和HR-LRT法的分辨率直接受接收排列长度影响, 接收排列越长, 分辨率越高, 反之越低。fv-MUSIC法的相速度分辨能力依然很高(图 6d), 只是由于记录道数减少, 其相速度能量轴的光滑度相比图 5d有所下降, 速度能量轴出现了抖动。对比图 6b, 图 6c和图 6d可见, fv-MUSIC法成像效果优于相移法和HR-LRT法。
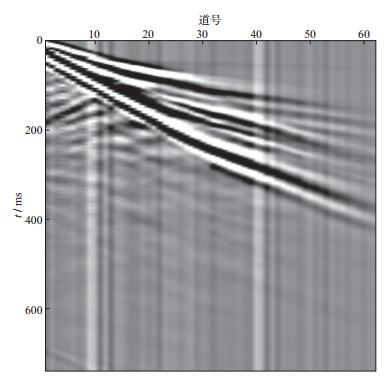
3 实际资料应用试验 3.1 工程面波记录选择一炮采集于美国Texas A & M大学(TAMU) 国家地学技术试验场的MASW工程面波记录(图 7), 62道接收, 道距0.6096m, 时间采样间隔0.7813ms, 炮点与第一接收道距离3.048m。该数据由美国工程地球物理协会于2011年公开向外界发布, 用于近地表面波科研人员测试处理与反演算法的研究[30]。
|
图 7 MASW工程面波记录 |
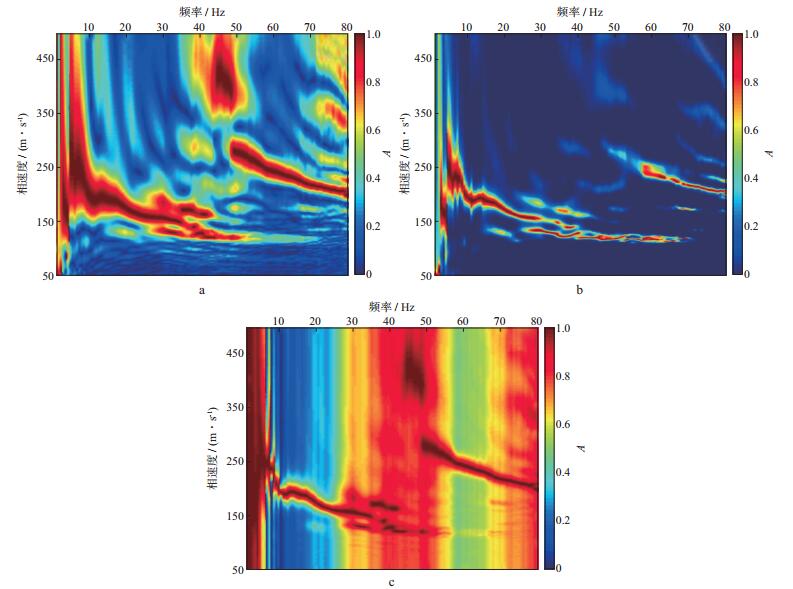
由图 7可见, 该试验场浅地表存在横向速度变化, 记录第10道、第22道附近都能看到明显的背向散射面波, 这会对后续频散曲线的提取产生一定影响。图 8为3种频散成像方法处理得到的频散图像, 可以看到基阶模式与第一高阶模式瑞雷波能量很强, 特别是第一高阶模式瑞雷波从50Hz一直延续到80Hz, 非常适合于后续基阶与高阶模式的瑞雷波联合反演。从3种方法的成像品质来看, 相移法分辨率最低, 并且频散图像中存在大量背景噪声干扰; fv-MUSIC法和HR-LRT法得到的频散图像分辨率不相上下, 都明显高于相移法, 并且背景噪声得到了较好压制, 主要瑞雷波模式得以很好凸显。HR-LRT法得到的频散图像虽然分辨率很高, 但对有效面波模式造成了压制(图 8b), 第一高阶模式瑞雷波的能量强度与连续性明显不如相移法和fv-MUSIC法。
|
图 8 工程面波记录3种方法频散成像效果 a 相移法; b HR-LRT法; c fv-MUSIC法 |
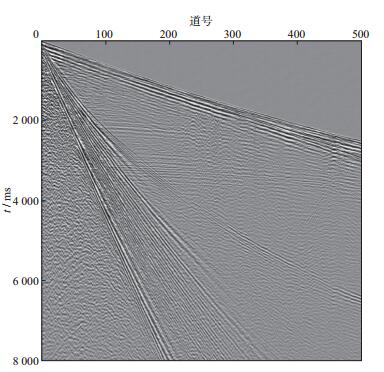
选择中国西部某工区一个含面波地震勘探反射波记录进一步对比了3种频散成像方法的效果(图 9)。该记录接收道距不均匀, 但总体保持在10m左右。记录中面波十分发育, 线性同相轴连续并清晰可辨, 没有空间假频现象, 多模式特征十分明显, 在2.2s和3.1s附近能看到明显的反射波同相轴。记录中面波的线性同相轴特征和反射波同相轴的双曲线特征都表明, 该工区地表比较平坦, 地下无明显倾斜构造, 可以看作水平层状介质,适合采用面波法进行处理。
|
图 9 含面波地震勘探反射波记录 |
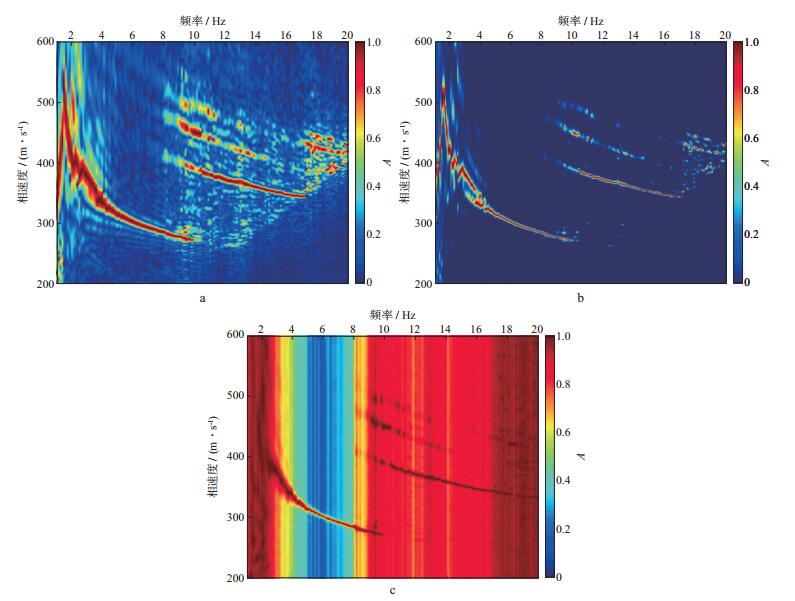
图 10给出了3种频散成像方法得到的面波频散图像。通过比较可以发现, 相移法得到的图像中背景噪声比较严重, 但可以清晰识别3~10Hz之间的基阶模式瑞雷波和8~17Hz之间的第一高阶模式瑞雷波。实际上, 第二高阶模式与第三高阶模式瑞雷波也能识别, 但是能量较弱, 受噪声污染比较严重。fv-MUSIC法得到的频散图像在低于3Hz的部分成像效果看起来不如其它两种方法, 但是理论模型测试(参见第2节) 表明, 频率太低的部分因为噪声的影响相速度可靠性较低, 不应该进行提取并参与到反演中。因此, 3种方法都能够可靠拾取的基阶模式相速度频率范围是3~10Hz。在图 10c中, fv-MUSIC方法对第一高阶模式可以识别到20Hz, 而其它两种方法只能识别到17Hz左右(图 10a, 图 10b), 这进一步说明3种方法中fv-MUSIC方法存在优势。
|
图 10 实际资料3种方法频散成像效果 a 相移法; b HR-LRT法; c fv-MUSIC法 |
本文基于多重信号分类算法提出了一种直接在频率-速度域进行面波高分辨率频散成像的方法, 即fv-MUSIC方法。通过与目前广泛使用的相移法和HR-LRT法进行比较, 获得以下认识:
1) 对于不含噪声的理论面波数据, fv-MUSIC方法的频散成像分辨率可以接近理论频散曲线的程度;
2) 存在随机噪声干扰时, fv-MUSIC方法的成像频带范围和相移法、HR-LRT法基本一致, 所以, fv-MUSIC方法的抗噪性与相移法和HR-LRT法相当;
3) 采用短排列接收时, 相移法和HR-LRT法的相速度分辨率显著下降, 而fv-MUSIC法依然能保持较高分辨率;
4) 在对实际面波资料进行频散成像时, fv-MUSIC方法能在压制背景干扰的同时不降低高阶模式面波的成像质量。
需要指出的是, F-K变换法和HR-LRT法由于存在正反变换, 在面波提取和模式分离方面依然具有很重要的作用。而fv-MUSIC法属于单纯的空间谱估计技术, 在这些方面的作用有限。
| [1] |
孟小红, 郭良辉. 利用地震瑞利波速度反演求取P-SV波横波静校正量[J].
石油地球物理勘探, 2007, 42(4): 448-453 MENG X H, GUO L H. Using velocity inversion of seismic Rayleigh wave to compute s-wave statics of P-SV wave[J]. Oil Geophysical Prospecting, 2007, 42(4): 448-453 |
| [2] | MARI J L. Estimation of static corrections for shear-wave profiling using the dispersion properties of Love waves[J]. Geophysics, 1984, 49(8): 1169-1179 DOI:10.1190/1.1441746 |
| [3] | BOIERO D, MARSDEN P, ESAULOV V, et al. Building a near-surface velocity model in the South Ghadames basin:surface-wave inversion to solve complex statics[J]. Expanded Abstracts of 83rd Annual Internat SEG Mtg, 2013: 1811-1815 |
| [4] | PIATTI C, SOCCO L V, BOIERO D, et al. Constrained 1D joint inversion of seismic surface waves and P-refraction travel times[J]. Geophysical Prospecting, 2013, 61(S1): 77-93 |
| [5] |
夏江海, 高玲利, 潘雨迪, 等. 高频面波方法的若干新进展[J].
地球物理学报, 2015, 58(8): 2591-2605 XIA J H, GAO L L, PAN Y D, et al. New findings in high-frequency surface wave method[J]. Chinese Journal of Geophysics, 2015, 58(8): 2591-2605 |
| [6] |
徐颖, 刘晨, 吕秋玲, 等. 多域组合去噪技术在塔中奥陶系低信噪比资料处理中的应用[J].
石油物探, 2015, 54(2): 172-179 XU Y, LIU C, LV Q L, et al. Application of multi-domain composite denoising technology for the processing of Ordo-vician low SNR seismic data in Tazhong area[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 172-179 |
| [7] |
王德营, 李振春, 王姣. S域时频滤波分析与改进[J].
石油物探, 2015, 54(4): 396-403 WANG D Y, LI Z C, WANG J. The analysis and improvement on time-frequency filtering in S-transform domain[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 396-403 |
| [8] | PARK C B, MILLER R D, XIA J. Multichannel analysis of surface waves[J]. Geophysics, 1999, 64(3): 800-808 DOI:10.1190/1.1444590 |
| [9] | SOCCO L V, FOTI S, BOIERO D. Surface-wave analysis for building near-surface velocity models-established approaches and new perspectives[J]. Geophysics, 2010, 75(5): A83-A102 |
| [10] | FOTI S, PAROLAI S, ALBARELLO D, et al. Application of surface-wave methods for seismic site characterization[J]. Surveys in Geophysics, 2011, 32(6): 777-825 DOI:10.1007/s10712-011-9134-2 |
| [11] | GABRIELS P, SNIEDER R, NOLET G. In situ measurements of shear-wave velocity in sediments with higher-mode Rayleigh waves[J]. Geophysical Prospecting, 1987, 35(2): 187-196 DOI:10.1111/gpr.1987.35.issue-2 |
| [12] | TSELENTIS G, DELIS G. Rapid assessment of S-wave profiles from the inversion of multichannel surface wave dispersion data[J]. Annali Di Geofisica, 1998, 41(1): 1-15 |
| [13] | FOTI S, LANCELLOTTA R, SAMBUELLI L, et al. Notes on f-k analysis of surface waves[J]. Annali Di Geofisica, 2000, 43(6): 1199-1209 |
| [14] |
李子伟, 刘学伟. 空间假频对频率-波数域瑞利面波频散曲线反演的影响[J].
石油地球物理勘探, 2013, 48(3): 395-402 LI Z W, LIU X W. Effects of spatial aliasing on frequency-wave number domain inversion of Rayleigh-wave dispersion curve[J]. Oil Geophysical Prospecting, 2013, 48(3): 395-402 |
| [15] | MCMECHAN G A, YEDLIN M J. Analysis of dispersive waves by wave field transformation[J]. Geophysics, 1981, 46(6): 869-874 DOI:10.1190/1.1441225 |
| [16] | PARK C B, MILLER R D, XIA J. Imaging dispersion curves of surface waves on multi-channel records[J]. Expanded Abstracts of 68th Annual Internat SEG Mtg, 1998: 1377-1380 |
| [17] | RYDEN N, PARK C B, ULRIKSEN P, et al. Multimodal approach to seismic pavement testing[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(6): 636-645 DOI:10.1061/(ASCE)1090-0241(2004)130:6(636) |
| [18] | OBANDO E A, PARK C B, RYDEN N, et al. Phase-scanning approach to correct time-shift inaccuracies in the surface-wave walk-away method[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(12): 1528-1539 DOI:10.1016/j.soildyn.2010.07.006 |
| [19] | DAL M G, PIPAN M, FORTE E, et al. Determination of Rayleigh-wave dispersion curves for near surface applications in unconsolidated sediments[J]. Expanded Abstracts of 73rd Annual Internat SEG Mtg, 2003: 1247-1250 |
| [20] | LUO Y, XIA J, MILLER R D, et al. Rayleigh-wave dispersive energy imaging using a high-resolution linear Radon transform[J]. Pure and Applied Geophysics, 2008, 165(5): 903-922 DOI:10.1007/s00024-008-0338-4 |
| [21] | SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280 DOI:10.1109/TAP.1986.1143830 |
| [22] | BIONDI B L, KOSTOV C. High-resolution velocity spectra using eigenstructure methods[J]. Geophysics, 1989, 54(7): 832-342 DOI:10.1190/1.1442712 |
| [23] | KIRLIN R L. The relationship between semblance and eigenstructure velocity estimators[J]. Geophysics, 1992, 57(8): 1027-1033 DOI:10.1190/1.1443314 |
| [24] | BARROS T, LOPES R, TYGEL M. Implementation aspects of eigendecomposition-based high-resolution velocity spectra[J]. Geophysical Prospecting, 2015, 63(1): 99-115 DOI:10.1111/gpr.2015.63.issue-1 |
| [25] | IRANPOUR K E, MUYZERT E, GRION S. Local velocity analysis by parametric wavenumber estimation in seismic (fk-MUSIC)[J]. Expanded Abstracts of 64th EAGE Annual International Conference and Exhibition, 2002: 171-174 |
| [26] | WINSBORROW G, HUWS D G, MUYZERT E. Acquisition and inversion of Love wave data to measure the lateral variability of geoacoustic properties of marine sediments[J]. Journal of Applied Geophysics, 2003, 54(1/2): 71-84 |
| [27] | BOIERO D, BERGAMO P, REGE R B, et al. Estimating surface-wave dispersion curves from 3D seismic acquisition schemes:part 1, 1D models[J]. Geophysics, 2011, 76(6): G85-G93 DOI:10.1190/geo2011-0124.1 |
| [28] | MISBAH A S, STROBBIA C L. Joint estimation of modal attenuation and velocity from multichannel surface wave data[J]. Geophysics, 2014, 79(3): EN25-EN38 DOI:10.1190/geo2013-0028.1 |
| [29] | JOHNSON D H, DUDGEON D E. Array signal processing[M]. Upper Saddle River: PTRPrentice-Hall Inc, 1993: 349-392. |
| [30] | TRAN K T, HILTUNEN D R. One-dimensional inversion of full waveforms using a genetic algorithm[J]. Journal of Environmental & Engineering Geophysics, 2012, 17(4): 197-213 |


