2. 波现象与反演成像研究组WPI, 同济大学海洋与地球科学学院, 上海 200092
2. Wave Phenomena and Inversion Imaging Research Group (WPI), School of Ocean and Earth Science, Tongji University, Shanghai 200092, China
随着计算机技术的快速发展和“两宽一高”采集技术的进步, 地震全波形反演(FWI) 技术研究也得到快速发展, 有效促进了油气勘探的发展。在以估计“全/宽”波数带的弹性参数为目标的FWI中, 利用低频长偏移距透射波估计背景速度占有重要位置。但是, 在目前的陆上地震数据中, 缺乏有效的低频成分。有效的初始背景速度场对于透射波FWI和反射波FWI克服周期跳(Cycle-skipping) 现象、提高收敛效率非常重要。充分利用地震数据包含的信息, 根据散乱的速度和界面深度信息特点, 对不同来源、不同精度的散乱速度场插值产生有效背景速度模型是速度建模的核心环节之一。
勘探地震某种程度上属于信息处理的学科, 抽象地看, 地震数据处理中经常碰到的各种类型的数据基本上都是散乱采样(规则采样可以视为散乱数据采样的特殊形式)。对于来自不规则空间位置的测井数据, 有必要利用基于散乱数据插值的方法获得全空间的、规则的参数场数据体。尤其对速度反演和建模而言, 参数场(主要是速度场) 的描述也希望用尽可能少的特征点支撑起整个参数场。利用非规则(散乱) 的数据表达连续的函数或其一阶和二阶导数有着重要的应用。剖分方式和基函数的选择是其中最关键的两点。Haar条件保证了一维多项式基函数插值有唯一的解, 也发展了一套有效的插值方法, 但高维情况下解不唯一, 高维离散数据插值, 尤其是高维散乱数据插值, 是一个正在发展中的问题。
在不同的应用领域, 根据实际需要, 不同的学者提出了不同的插值方法。气象学及地质学家SHEPARD[1]在研究降水量和高程时提出了Shepard插值法; SIBSON[2]在研究自然邻近法的基础上发展了自然邻域插值法; HARDY[3]在处理飞机外形的曲面拟合问题时提出了以多二次曲面(Multiquadric) 函数为代表的径向基函数插值法; DUCHON[4]从样条弯曲能量最小出发推导出多元问题的薄板样条函数; 南非矿业工程师KRIGE[5]在矿产估计过程中首先提出了克里金插值技术; 后来MATHERON[6]提出地质统计学概念, 将克里金插值方法引入地质统计学, 使得克里金插值方法得到迅速发展; SCHUMAKER[7]在1976年提出了散乱数据的两步拟合方法。两步拟合法是指将一个复杂的问题分解为两个简单的问题来处理, 成为了目前应用较多的散乱数据拟合方法。
根据实际的地下介质特点, 描述速度场的方法一般用界面加层速度的方式, 界面的描述基于解释出的散乱点, 模型的描述需要对散乱数据连续化。更关键的是解波场方程的导函数也需要离散数据(散乱数据) 的逼近。非规则数据的插值和逼近表达连续函数以及任意点的导函数在地震勘探中成为一个广为关注的议题。高维叠前数据规则化方法已经有很多的文献进行了讨论[8-10], 速度场的特征描述也逐渐得到研究。HALE[11]对自然邻域法进行修改, 发展了一种混合邻域法, 并用成像剖面作为约束, 提出了一种成像指导的混合邻域插值法; DOUMA等[12]将混合邻域插值法应用到反演中的低频背景速度建模。我们认为, 速度场的特征描述与基于此特征描述的波传播方法研究可以为多尺度参数反演提供良好的基础。
本文首先对以下几种散乱数据插值方法进行了分析和总结, 主要包括三角剖分法、自然邻域法、反距离插值法、径向基函数插值法以及克里金插值法, 分析了上述各种方法的优缺点。在此基础上, 将三维克里金插值方法应用到不同信息来源的速度场融合中, 首先采用克里金插值方法将实际测井数据插值成三维速度场, 然后分别采用克里金方差融合策略和多尺度空间波数域Gabor变换2种方法融合速度场。融合后的速度场精度提高了, 偏移成像质量也得到明显改善。最后, 讨论了基于散乱数据支撑的特征速度场的描述问题, 提出了多尺度特征速度场的表达策略。
1 散乱数据插值方法根据Haar插值条件, 高维离散数据插值结果是不唯一的。散乱数据插值的核心包括两点:①网格体系; ②基函数空间。当然, 散乱数据插值也存在无网格、全局的插值。但是, 一般而言局部的、有网格的插值更符合函数变化的本质, 即相邻点的函数值之间有更强的关系。
1.1 散乱数据散乱数据插值的定义一般描述为:假设在d维欧式空间中, 存在n个散乱、无规则的数据点X={x1, x2, …, xn}⊂Rd, 每个数据点的值为:F={f1, f2…, fn}⊂R。散乱数据插值就是要构建一个函数f(x):Rd→R, 使得在每个已知的数据点上满足:
| $ f({{x}_{i}})={{f}_{i}}\ \ \ ~i=1, 2, \cdots, n $ | (1) |
根据基函数支撑的空间范围可将基函数分为局部支撑和全局支撑, 其中局部支撑是指基函数只受周围几个点的影响; 而全局支撑是指基函数受整个空间数据的影响。基函数为局部支撑的插值方法叫做局部插值法, 常见的局部插值方法有:三角剖分法、自然邻域法等; 基函数为全局支撑的插值方法叫做全局插值法, 常见的全局插值方法有:反距离加权法、径向基函数法以及克里金法等。
1.2.1 三角剖分插值法三角剖分插值法是一种局部插值方法, 该方法首先将整个区域分解成不同的三角形区域, 在每个小区域上进行插值, 然后将不同的区域拼接在一起, 得到整个区域的插值结果。三角剖分插值过程分为两步:①对区域进行三角剖分; ②构造插值基函数, 求取插值系数。
在步骤①中, 当数据点大于等于4时, 会出现几种不同的剖分形式, 在实际应用中为了满足特定的需要, 不同学者提出了不同的三角剖分判别准则[13]。其中一种比较常用的判别准则为最大外接圆最小的优化剖分, 又称德劳内(Delaunay) 三角剖分[14]。Delaunay三角剖分最早可追溯到1907年提出的沃罗诺伊(Voronoi) 图[15], 前人研究认为任何Delaunay三角剖分都是Voronoi图的对偶剖分。以20个数据点为例, 它们形成的Voronoi图和Delaunay三角剖分见图 1[16]。三角剖分是基于二维平面上的概念, 当数据扩展到三维时, 三角剖分就变成了四面体剖分。四面体的剖分思想和三角剖分一致, 只是在剖分的实现上比三角剖分复杂。
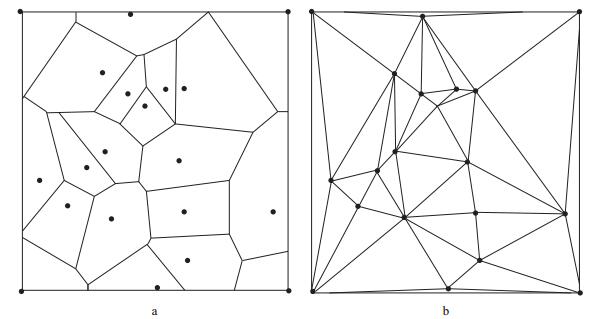
|
图 1 由20个点组成的Voronoi图(a) 和Delaunay三角剖分(b) |
在步骤②中, 可以直接选用三角剖分的3个顶点进行插值, 此时构造的插值函数可表示成:
| $ f\left( x \right) = \sum\limits_{i = 1}^3 {{\varphi _i}\left( x \right){f_i}} $ | (2) |
式中:i=1, 2, 3是三角形的顶点; fi是顶点的值; φi(x) 是构造的插值基函数, 它决定了输入数据fi的加权大小。但是此时的插值只能达到C0连续(函数连续), 在三角形的顶点和边上不连续。为了保证C1连续(一阶导数连续), 需要利用其它信息构造更高阶的插值方法。三次九参数法是改进插值连续性的一种重要方法, 该方法除了利用顶点上的值, 还利用了在三角形顶点的2个沿三角形边的方向导数值来保证连续性, 但是此时存在一个自由的参数, 在求解方程组时, 需添加C1的连续性条件来保证三角形拼接的连续性, 但是使C1连续性满足的条件非常难以达到, 有时会使得方程组无解, 此时通常采用最小二乘法获得一个与C1连续的类似曲面当做插值曲面[17]。Clough-Tocher法[18]给出了改进插值连续性的策略, 该策略在三角形片的边界上再增加一个穿越边界方向的方向导数, 从而满足C1的连续性条件。在Clough-Tocher法的基础上, Powell-Sabin方法[19]不仅构造出C1连续的曲面, 而且降低了分片多项式的次数。
三角剖分插值是一种局部插值方法, 不需要求解大型的线性方程组, 即使对大量的数据点, 插值效率也非常高; 当添加新的数据点时, 不需全部重新计算插值系数, 应用比较灵活。对于存在速度间断面、具有简单构造的地下速度场, 可以将速度场划分成一系列不规则的块体, 在块体内部, 速度变化光滑缓慢, 在块体边界上, 速度变化剧烈。此时可以依照块体的形状进行三角剖分, 剖分简单, 可得到比较好的插值效果, 但是在边界处可能会出现不连续现象。
三角剖分插值要求必须在插值之前完成剖分。对于简单的区域, 剖分比较方便, 但是当区域构造比较复杂时, 剖分就变得比较困难, 尤其是高维情况。三角剖分插值还要求散乱数据点为凸集, 且对散乱数据点的分布有一定的要求, 当散乱数据点共线(或接近共线) 时, 会形成狭长状的三角形(如图 1中的边界部分), 使得插值结果变差。此外, 三角剖分形式不唯一, 不同剖分可能会产生截然不同的结果, 无法确保最优的剖分。
1.2.2 自然邻域插值法自然邻域插值法又叫Sibson插值法, 由SIBSON[2]在1981年提出。Sibson插值法是一种局部插值方法, 是最近邻点插值法的一种改进。最近邻点插值法, 又称泰森多边形插值法, 其做法是首先将插值区域按照Voronoi图进行剖分, 生成邻近区域, 然后将邻近区域内的值等于区域内部插值数据点的值。所以最近邻点插值结果不连续, 是分段常量的。SIBSON[2]修改了最近邻点插值法, 对邻域区域赋予一个加权系数, 插值时使用邻点的加权平均来确定插值点的值。Sibson插值法可归纳为两步:①生成Voronoi图; ②构造插值函数。
在步骤①中, 首先将所有散乱数据点按照Voronoi图进行剖分, 如图 2a; 然后将待插值点x插入剖分网格中, 形成新的Voronoi图, 如图 2b。新加入的插值点x形成的区域(图 2b中灰色部分) 与已知的数据点形成的区域中会存在一条公共的边(点), 我们把与x形成的区域有公共边(点) 的已知散乱数据点称为自然邻域点。一般来说, 在一个区域中自然邻域点最少有d+1个(d是空间的维度), 最多有n-1个(n是已知点的个数)。对于二维情况, 自然邻域点的个数不超过6个。
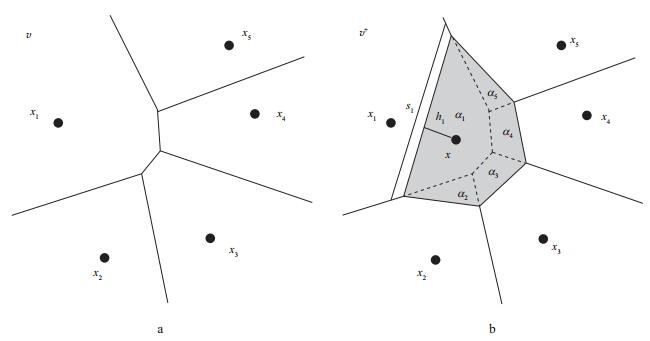
|
图 2 散乱数据点形成的Voronoi图 a 所有已知点; b 插值点x加入后 |
在步骤②中, 构造的插值函数写成:
| $ f\left( x \right) = \sum\limits_{i = 1}^N {{\varphi _i}\left( x \right){f_i}} $ | (3) |
式中:N代表自然邻域点个数; fi是已知散乱数据点值; φi(x) 是加权系数, 可由下式确定:
| $ {\varphi _i}\left( x \right) = \frac{{{\alpha _i}\left( x \right)}}{{\sum\limits_{i = 1}^N {{\alpha _i}\left( x \right)} }} $ | (4) |
式中:αi(x) 是在x区域中与自然邻域点相邻的面积, 如图 2b中αi所示。
我们对Sibson插值方法中的加权系数进行修改。在Sibson插值中, 公式(4) 中的αi(x) 由剖分形成的自然邻域面积决定, 采用一种新的加权系数定义方式, 可以将αi(x) 修改成:
| $ \alpha {\prime _i}\left( x \right) = \frac{{{s_i}\left( x \right)}}{{{h_i}\left( x \right)}} $ | (5) |
式中:si(x) 是插值点x与自然邻域点形成的区域边长; hi(x) 是插值点x到自然邻域点距离的一半, 如图 2b所示。
SIBSON[2]和FARIN等[20]指出:除了在已知点上, 自然邻域插值法在整个区域上连续。为了保持连续性, SIBSON在插值多项式中添加了导数约束项使得插值函数在每个点上也连续, 但此方法在实际数据应用中没有得到实用化发展, 主要原因是导数一般未知。WATSON[21]阐述了几个不同的估计梯度的计算方法。当插值点在点集外时, 自然邻域法无法计算, 此时可以添加一些鬼点来构造新的凸集。
自然邻域法是一种局部插值方法。一般来说, 与插值点x形成的区域有接触的自然邻域点非常少, 即使当n非常大时, 自然邻域点也远远小于n, 所以构建插值函数比较简单; 自然邻域法加权系数取决于周围散乱数据点与插值点形成的区域大小; 当散乱数据点的分布密度明显不均匀时, 基于区域插值的自然邻域法可以补偿数据密度的变化, 效果优于对数据敏感、基于距离插值的方法。可见, 自然邻域法是一种稳健的、有界的插值方法, 并且具有线性精度。但是, 自然邻域法需要预先进行Voronoi剖分, 在三角剖分中遇到的剖分问题在自然邻域法中同样会碰到。
1.2.3 反距离加权插值法反距离加权插值法又称Shepard法, 最早由SHEPARD[1]在1968年提出。其基本思想是利用散乱数据点与插值点距离不同进行插值, 加权系数大小与距离成反比。反距离加权插值法可归纳为两步:①构造插值函数; ②求取加权系数。
在步骤①中, 可以构建如下插值函数:
| $ f\left( x \right) = \sum\limits_{i = 1}^n {{w_i}\left( x \right){f_i}} $ | (6) |
式中:wi(x) 为加权系数; fi为已知的散乱数据点值; n为已知点个数。加权系数可写成:
| $ \begin{array}{l} {w_i}\left( x \right) = \frac{{{h_i}\left( x \right)}}{{\sum\limits_{i = 1}^n {{h_i}(x)} }}\\ {h_i}\left( x \right) = \frac{1}{{{{\left[{{d_i}\left( x \right)} \right]}^k}}} \end{array} $ | (7) |
式中:di(x) 是x和xi间的欧式距离, 可表示成di(x)=‖x-xi‖2; k为指数常量, 一般k≥1。当k=1, 2时, 插值函数变成SHEPARD[1]和GORDON等[22]给出的形式。
由公式(6) 和公式(7) 可看出, 当插值点x很靠近xi时, hi(x) 趋于无穷大, f(xi) 趋于fi, 为了保证插值函数的连续性, 在xi处可令f(xi)=fi, 此时虽然保证了插值函数连续, 但是插值函数却在散乱数据点附近的结果表现为平面(原因是其各阶导数为零)。一个相应的修改方案就是修改成带导数条件的Shepard插值, 把已知点的导数信息加进去。此时公式(6) 可修改成:
| $ f\left( x \right)=\sum\limits_{i=1}^{n}{{{w}_{i}}\left( x \right){{g}_{i}}}\ \ ~{{g}_{i}}={{f}_{i}}+{{\alpha }_{i}}\left( x-{{x}_{i}} \right) $ | (8) |
式中:αi为xi处的各阶导数, 但是由于在一般情况下散乱数据点的导数未知, 所以需要利用其它方法去获得导数信息。
Shepard插值是一种全局插值方法, 为了适应局部性, 可以对其进行修改。其中一种简单的修改就是限制hi(x) 的影响范围, 比如可以将公式(7) 中的hi(x) 修改成[17]:
| $ {{h}_{i}}\left( x \right)={{\left\{ \frac{{{\left[r-{{d}_{i}}\left( x \right) \right]}_{+}}}{r{{d}_{i}}\left( x \right)} \right\}}^{2}} $ | (9) |
式中:r是选取的影响范围半径。[r-di(x)]+满足条件:
| $ {{\left[r-{{d}_{i}}\left( x \right) \right]}_{+}}=\left\{ \begin{align} & r-{{d}_{i}}\left( x \right)\ \ \ {{d}_{i}}\left( x \right)~<r \\ & 0\ \ \ \ \ \ \ \ \ \ \ \ \ {{d}_{i}}\left( x \right)\ge r \\ \end{align} \right. $ | (10) |
这样就可以将全局的插值法修改成局部插值, 插值函数的影响也被控制在一定的范围内。
反距离加权插值是一种基于距离的插值方法, 对数据的分布比较敏感, 该方法会产生平滑效应, 在精度和效率上比一些基于三角剖分的插值方法差一点, 但是它不需要剖分, 很容易扩展到高维空间, 而且加权系数的选择比较灵活, 同时还可修改距离范数, 方便应用于各向异性情况。
1.2.4 径向基函数插值法径向基函数插值法[3-4]是一种全局插值方法, 其基本思想是首先确定一个随距离变化的基函数, 然后把各个散乱数据点进行线性加权求和, 得到插值点的值。径向基函数的插值过程可归纳为以下两步:
①选择基函数, 构造插值函数。一般情况下, 径向基函数插值可写成如下形式:
| $ f\left( x \right) = \sum\limits_{i = 1}^n {{\lambda _i}\varphi } \left( {||x-{x_i}||} \right) $ | (11) |
式中:n是已知散乱数据点个数; λi是插值系数; φ(‖x-xi‖) 是随距离变化的基函数, 基函数的选择有多种形式。
②构建插值线性方程组, 求取加权系数。将所有已知散乱点的值代入到构造的插值函数中, 形成的插值线性方程组为:
| $ \mathit{\boldsymbol{f}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \lambda }} $ | (12) |
式中:f为已知的散乱数据点的值形成的向量; Φ是基函数φ(‖x-xi‖) 展开形式的矩阵; λ是求取的插值系数向量。求解上述线性方程组, 可以得到系数向量:
| $ \mathit{\boldsymbol{\lambda }} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{-1}}\mathit{\boldsymbol{f}} $ | (13) |
插值过程中也可利用导数信息以获得更好的插值效果, 此时可在公式(11) 的基础上, 添加一个多项式约束, 构造的插值函数就变成:
| $ f\left( x \right) = \sum\limits_{i = 1}^n {{\lambda _i}\varphi } \left( {\left\| {x-{x_i}} \right\|} \right) + \sum\limits_{i = 1}^m {{\alpha _i}{x^i}} $ | (14) |
式中:αi为m阶多项式系数; m表示已知的插值曲面斜率为0的离散点个数。对公式(14) 求导并且令导数等于0, 可得到:
| $ \sum\limits_{i = 1}^n {{\lambda _i}\varphi '} \left( {\left\| {x-{x_i}} \right\|} \right) + \sum\limits_{i = 1}^m {i{\alpha _i}{x^{i-1}}} = 0 $ | (15) |
将已知的n个散乱数据点和m个导数值分别代入公式(14) 和公式(15), 可得到n+m个方程, 方程中未知数个数为n+m。
为了构造更一般地具有m阶多项式精度的插值函数, 导数的约束项可换成具有m阶的多项式基函数, 插值函数变成:
| $ f\left( x \right) = \sum\limits_{i = 1}^n {{\lambda _i}\varphi } \left( {\left\| {x-{x_i}} \right\|} \right) + \sum\limits_{i = 1}^m {{\alpha _i}q} \left( {\left\| {x-{x_i}} \right\|} \right) $ | (16) |
式中:q(‖x-xi‖) 为m阶多项式基函数; λi, αi为插值系数, 它们满足方程组:
| $ \left\{ \begin{array}{l} f\left( {{x_j}} \right) = \sum\limits_{i = 1}^n {{\lambda _i}\varphi } \left( {\left\| {{x_j}-{x_i}} \right\|} \right) + \sum\limits_{i = 1}^m {{\alpha _i}q} \left( {\left\| {{x_j}-{x_i}} \right\|} \right)\;\;\;j = 1, 2, \cdots, n\\ \sum\limits_{i = 1}^n {{\alpha _i}q} \left( {\left\| {{x_j}-{x_i}} \right\|} \right) = 0\;\;\;\;j = 1, 2, \cdots, m \end{array} \right. $ | (17) |
对于径向基函数插值方法而言, 基函数的选择至关重要, 目前有许多种不同形式的基函数, 几种常见的基函数形式如表 1所示[23-24]。这些径向基函数已经在不同的领域中得到广泛应用[25-26]。在数学上, FRANKE等[27]做了大量的各种散乱数据插值方法的实例对比[28], 结果发现径向基函数插值最让人满意。许多学者也曾利用径向基函数去求解各种偏微分方程问题。比如, POLLANDT[29]利用径向基函数近似求解非线性椭圆偏微分方程中的多维边界元方法; SONAR[30]利用薄板样条基函数去求解双曲型守恒律方程。
| 表 1 常见的径向基函数 |
从径向基函数插值过程中可以看出, 径向基函数插值可归结为一个求解线性方程组问题。但是该线性方程组的系数矩阵不是稀疏的, 并且由于径向基函数是一种全局插值方法, 从而随着数据点的增加, 矩阵的规模越来越大, 使得储存量和计算量显著增加, 而且在求解过程中还可能出现病态问题, 这都给计算带来了巨大的挑战。常规的解决方案是利用迭代法求解线性方程组, 可以从目前大量的迭代法中寻找一个合适的迭代方法进行求解; 另一个方法是引入紧支撑正定径向基函数[31]。紧支撑正定径向基函数对任何给定的连续性条件及任何给定维数的自变量空间, 可以找到一个截断多项式, 使得由其产生的径向函数在给定的维数空间正定且满足给定的连续性条件, 由此导出的线性方程组是一个稀疏矩阵。
1.2.5 克里金插值法克里金插值法是在地质统计学的基础上, 利用变差函数理论进行最小方差无偏估计(Best Linear Unbiased Evaluation, 又称BLUE估计) 的一种全局插值方法。克里金插值分为两步:①利用区域变差函数理论统计区域的变差函数; ②利用最小方差无偏估计建立并求解关于插值系数的方程组。
变差函数又称变异函数, 是地质统计学的基本理论。在一维情况下, 当空间点x变化时, 设区域化变量在x和x+h处的值为Z(x) 和Z(x+h), 则两值之差的方差之半定义为区域化变量在x轴方向上的变差函数, 记为:
| $ \gamma \left( {x, h} \right) = \frac{1}{2}{\rm{var}}[Z\left( x \right)-Z(x + h)] $ | (18) |
式中:Z(x) 和Z(x+h) 分别为变量在x和x+h处的值; γ(x, h) 为变差函数。
在克里金插值过程中, 要求区域变量符合内蕴假设和二阶平稳假设。内蕴假设是指随机变量Z(x) 要满足E[Z(x+h)-Z(x)]=0, x∈Ω, h, 并在整个区域内, 随机函数的增量Z(x+h)-Z(x) 的方差函数存在且只与h有关, 而与x的位置无关, 即:
| $ \gamma \left( h \right) = \gamma \left( {x, h} \right) = \frac{1}{2}{\rm{var}}\{ Z\left( {x + h} \right)- Z(x)\} = \frac{1}{2}E\{ {[Z\left( {x + h} \right)-Z\left( x \right)]^2}\} $ | (19) |
二阶平稳是指随机变量Z(x) 的数学期望是一个常数, 并且每一对随机变量Z(x) 和Z(x+h) 之间协方差函数仅依赖于两点之间的差向量h。即有:
| $ \begin{array}{l} C\left( h \right) = C\left( {x, x + h} \right) = E\{ \{ Z\left( {x + h} \right)- \\ E[Z\left( {x + h} \right)]\} \{ Z\left( x \right) - E[Z\left( x \right)]\} \} \\ = E\left[{Z\left( {x + h} \right)Z\left( x \right)} \right] -{m^2} \end{array} $ | (20) |
式中:C代表协方差函数。在满足上述假设条件下, 可得到变差函数与协方差函数的关系:
| $ \gamma \left( {{x_1}-{x_2}} \right) = \gamma \left( {{x_1}, {x_2}} \right) = C\left( 0 \right)-C({x_1}, {x_2}) $ | (21) |
变差函数存在不同的理论模型, 其中常见的有线性模型、指数模型、高斯模型以及球状模型等, 它们表征了区域变量的变化形式。在计算变差函数时, 无法直接计算理论的变差函数, 需要计算一个实验变差函数来拟合理论变差函数, 从而求出理论模型的系数。由于区域变量符合二阶平稳假设, 可以将一对数据[Z(x), Z(x+h)]看成是一对随机变量的实现, 所以实验变差函数可以写成:
| $ {\gamma ^*}\left( h \right) = \frac{1}{{2N\left( h \right)}}\sum\limits_{i = 1}^{N\left( h \right)} {{{\left[{Z\left( {{x_i}} \right)-Z\left( {{x_i} + h} \right)} \right]}^2}} $ | (22) |
式中:N(h) 为数据对[Z(x), Z(x+h)]的个数; γ*(h) 为实验变差函数。
得到区域变差函数后, 可构建插值函数:
| $ Z\left( x \right) = \sum\limits_{i = 1}^n {{\lambda _i}Z\left( {{x_i}} \right)} $ | (23) |
式中:xi为已知散乱数据点; Z(xi) 为散乱数据点上的值; n为已知点个数; λi为插值系数; Z(x) 为插值结果。克里金插值采用无偏性和最小方差来保证插值的效果, 得到:
| $ \left\{ \begin{array}{l} E{Z^*}\left( x \right) = \sum {\lambda _j}EZ\left( {{x_j}} \right) = 0 = EZ\left( x \right)\\ \mathop {\min }\limits_\lambda D\left[{{Z^*}\left( x \right)-Z\left( x \right)} \right] = E{\left[{{Z^*}\left( x \right)-Z\left( x \right)} \right]^2} \end{array} \right. $ | (24) |
式中:Z(x) 为期望理论结果; Z*(x) 为实际插值得到的结果。利用拉格朗日乘数法可构造目标函数F:
| $ F = E\left\{ {{{\left[{Z\left( x \right)-{Z^*}\left( x \right)} \right]}^2}} \right\} -2\mu \sum\limits_{i = 1}^n {{\lambda _i} -1} $ | (25) |
式中:μ为拉格朗日乘数。为了满足无偏性和最小方差, 对目标函数求导, 并使其导数等于零, 得到:
| $ \left\{ \begin{array}{l} \frac{1}{2}\frac{{\partial F}}{{\partial {\lambda _J}}} = \sum\limits_{i = 1}^n {{\lambda _i}C\left( {{x_i}, {x_j}} \right)-\mu-} C\left( {{x_0}, {x_j}} \right) = 0\;\;j = 1, 2, \cdots, n\\ \frac{1}{2}\frac{{\partial F}}{{\partial \mu }} =-(\sum\limits_{i = 1}^n {{\lambda _i} - 1} ) = 0 \end{array} \right. $ | (26) |
再利用协方差与变差函数的关系, 得到克里金插值方程组为:
| $ \left\{ \begin{array}{l} \sum\limits_{i = 1}^n {{\lambda _i}\gamma \left( {{x_i}-{x_j}} \right) + \mu = \gamma (x-{x_j})\;\;j = 1, 2, \cdots, n} \\ \sum\limits_{i = 1}^n {{\lambda _i} = 1} \end{array} \right. $ | (27) |
利用计算所得到的插值系数和拉格朗日乘数, 可得到插值点的克里金估计方差:
| $ \sigma _{{\rm{ok}}}^2\left( x \right) = {\rm{var}}[{Z^*}\left( x \right)-Z(x)] = \sum\limits_{i = 1}^n {{\lambda _i}\gamma \left( {{x_i} -x} \right) + \mu } $ | (28) |
式中:σok2(x) 为插值后得到的估计值与期望理论值的方差。
对比克里金插值和径向基函数插值过程可以看出, 两者可归纳到一个框架中, 都是选择一个基函数, 构造插值函数, 然后形成插值线性方程组, 求解插值系数。不同之处在于:在选择基函数时, 克里金插值采用的是变差函数, 变差函数的形式由实际数据驱动拟合得到, 而径向基函数插值中基函数的选择可以看作是不同形式的协方差函数, 根据前述的协方差函数和变差函数的关系可以看出, 两者是等价的; 在求取插值系数时, 克里金插值额外添加了2个约束条件, 本质上还是一种线性加权方法。STEIN[32]曾证明了克里金插值过程与高斯随机过程的等价性。
当已知数据点比较多时, 克里金方程组比较庞大, 求解就变得较困难, 此时需要考虑用局部的少量点进行插值。为了提高计算效率, 许多学者对如何高效选点进行过研究, 比如:在二维情况下, HESSAMI等[33]利用Delaunay三角剖分加快选点; 在三维情况下, YAO等[34]利用Delaunay四面体剖分加快选点, 并在GPU上并行运算提高了效率。
克里金插值存在诸多变种, 比如:泛克里金法、协克里金法以及贝叶斯克里金法等等。虽然克里金插值用到了统计特性, 但是克里金插值是一种确定性的地质统计学方法, 它只得到一个确定性的模型。后来也有学者发展出了一系列随机地质统计学方法[35-36]。
1.3 小结散乱数据插值包括局部插值方法和全局插值方法。常见的局部插值方法有三角剖分法、自然邻域法等; 全局插值方法有反距离加权法、径向基函数法和克里金插值法等。所有的散乱数据插值方法实现过程都可归结为以下2个步骤, 其中局部插值法包括:①对区域进行剖分; ②构造插值基函数, 求取插值系数, 进行插值。全局的插值法包括:①选择或构造合适的基函数; ②求取加权系数, 利用插值函数进行插值。
局部插值方法计算简单, 插值效率高, 应用灵活, 需事先对区域进行剖分, 剖分结果的好坏直接影响插值结果, 插值结果连续性差, 边界性保存效果好, 比较适合存在断层、尖灭等具有速度间断面的速度场建模, 所以对于三角剖分、自然邻域插值这类局部插值方法可以比较方便地应用到层析成像或FWI中模型构造约束的正则化过程中, 以及用于提取构造、岩体刻画、地震解释等诸多方面。另外局部插值方法可以考虑局部的特征, 在精细化建模、成像等方面有非常大的应用潜力。
全局插值方法不需要剖分, 对数据的分布要求比局部插值要求低, 很容易扩展到高维, 插值精度高, 可以根据实际数据特点灵活选择基函数, 物理含义明确, 而且构建的插值函数具有平滑效应, 比较适合在低波数的大尺度背景速度建模中应用。
在全波形反演中, 由于初始模型距离反演的真实的参数模型太远, 使得FWI无法得到预计的理论目标, 甚至在实际应用中无法收敛。有效的背景速度建模对于透射波FWI和反射波FWI克服周期跳现象、提高收敛效率显得异常重要。结合局部和全局散乱数据插值方法特点和低波数的背景速度建模需求, 限于篇幅原因, 本文仅以克里金插值方法为例论述其在低波数背景速度建模中的应用。
2 克里金插值在背景速度建模中的应用在地震速度建模过程中, 经常会遇到少量高精度的测井数据, 如何利用这些少量高精度数据指导速度建模是一个值得研究的课题。本文利用时移加窗的三维各向异性克里金插值方法插值离散(散乱) 的测井数据, 在此基础上采用2种融合策略对多源速度进行融合, 获得更高精度的速度建模结果。
本次克里金插值采用的数据是某工区实测得到的58口井的声波时差(AC) 测井数据, 测井数据的二维平面和三维立体展示如图 3所示。对AC测井数据做滤波、平滑等处理后进行三维克里金插值。考虑到地下速度场的分层构造, 速度在水平方向上变化比较缓慢, 而在垂直方向上变化比较剧烈, 在计算区域变差函数时, 在垂直方向上乘以一个各向异性系数, 拉伸z轴, 然后分方向计算实验变差函数, 采用加权最小二乘法将实验变差函数与理论变差函数拟合。实际处理过程中, 在垂向上进行加窗时移处理, 既保证了所需要的精度, 又提高了效率。
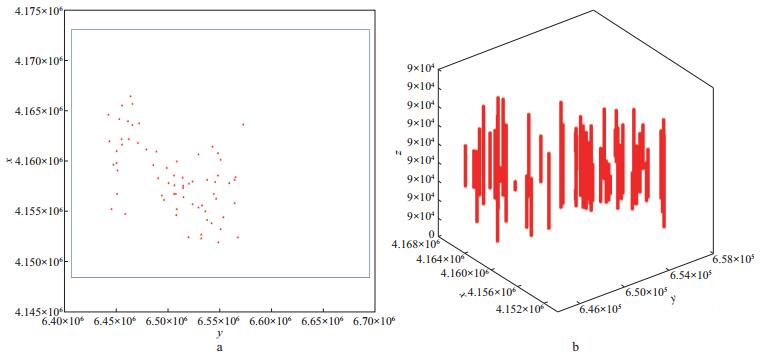
|
图 3 实际测井数据分布展示 a平面分布; b立体分布 |
插值后得到一个三维速度场和一个三维速度误差数据。同时, 对工区内采集到的地震数据做常规偏移速度分析(Migration Velocity Analysis, MVA) 处理, 得到一个低波数带的三维速度场。分别从克里金插值速度场和偏移速度分析得到的速度场中随机抽取x, y, z 3个方向的二维剖面, 如图 4, 图 5, 图 6所示。在图 4所示的方向上, 从克里金速度误差数据中抽取一个二维剖面, 如图 7所示。从图 4至图 6中可看出, 克里金插值速度场的大体趋势和偏移速度分析得到的速度一致, 此外, 克里金插值结果中包含很多偏移速度分析中没有的高波数成分, 这是因为测井数据本身就包含精度较高的高波数成分。
|
图 4 沿x轴抽取三维克里金插值结果显示 a 抽取剖面位置; b 偏移速度分析结果; c 克里金插值结果 |
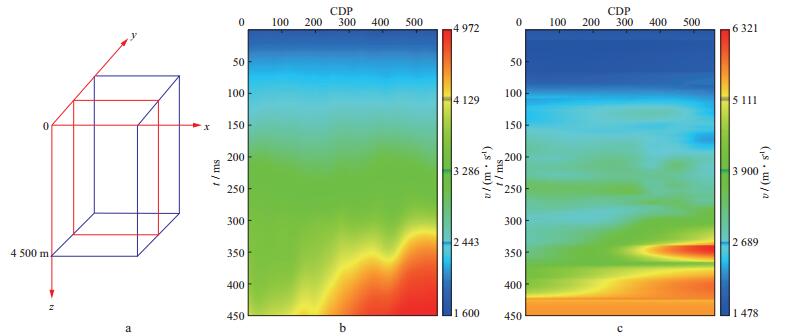
|
图 5 沿y轴抽取三维克里金插值结果显示 a 抽取剖面位置; b 偏移速度分析结果; c 克里金插值结果 |
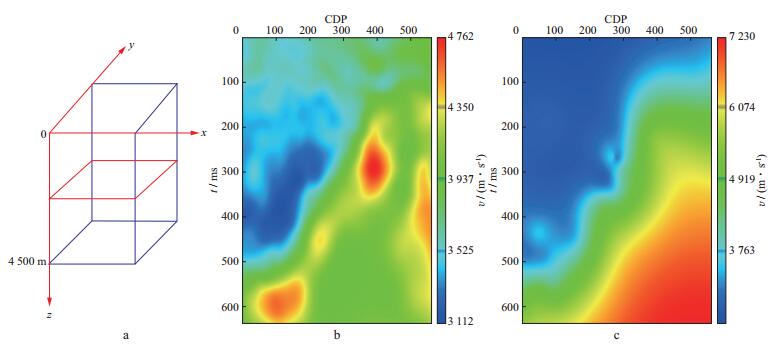
|
图 6 沿z轴抽取三维克里金插值结果显示 a 抽取剖面位置; b 偏移速度分析结果; c 克里金插值结果 |
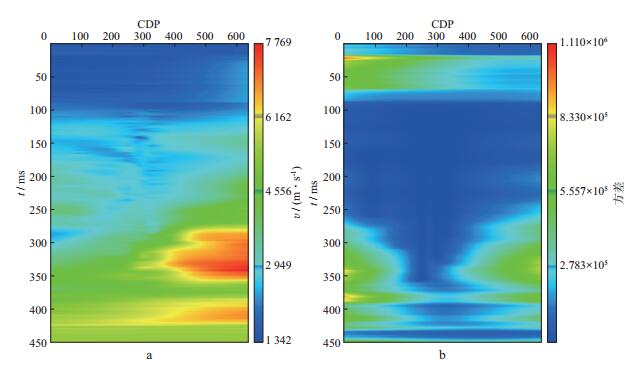
|
图 7 图 4a所示位置抽取的二维剖面 a 克里金插值结果; b 克里金方差结果 |
分析图 3和图 7, 可以看出有测井数据的地方方差比较小, 而没有测井数据的地方方差比较大。方差大表示该区域插值结果可信度低。从图 4中也可看出, 方差大的地方, 插值结果偏离速度分析结果也比较大。可见克里金方差可以作为评定插值结果的一个准则, 它表征了插值结果偏离理论结果的程度。
由于地下0~1000m段基本上没有测井数据, 所以克里金插值结果浅层数据不可靠。为了进一步提高速度建模的质量, 我们提出了2种速度场融合方法。
1) 基于克里金方差融合速度场。
根据上文可知, 克里金方差可以作为评定插值结果的一个准则, 克里金方差小的区域, 速度精度高; 克里金方差大的区域, 速度精度低。我们利用偏移速度分析得到的速度来改善克里金方差大的区域的速度, 提高速度场的精度。克里金方差融合可写成:
| $ v\left( {x, y, z} \right) = \alpha \left( {x, y, z, \sigma } \right){v_{{\rm{ok}}}}\left( {x, y, z} \right) + \beta \left( {x, y, z, \sigma } \right){v_{{\rm{mva}}}}(x, y, z) $ | (29) |
式中:v(x, y, z) 为融合后速度场; vok(x, y, z) 为克里金插值速度; vmva(x, y, z) 为偏移速度分析得到的速度; α(x, y, z, σ) 和β(x, y, z, σ) 分别为关于位置和方差的融合系数。
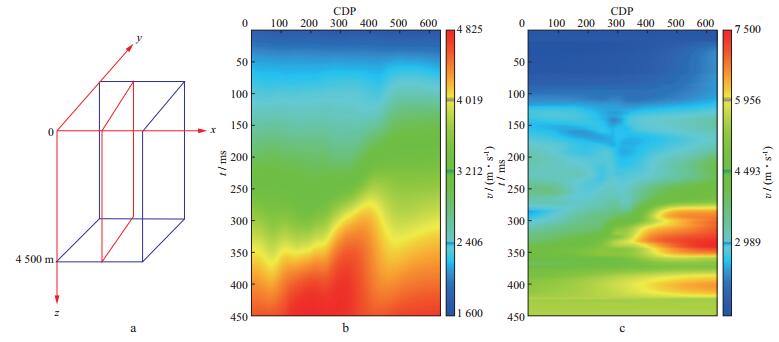
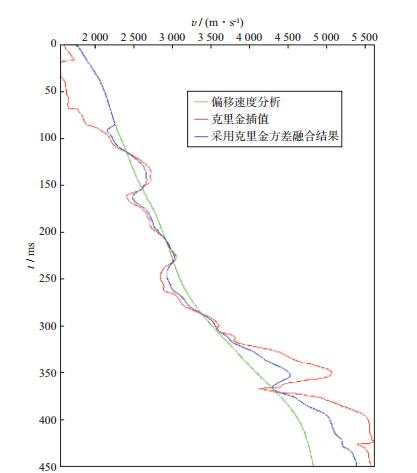
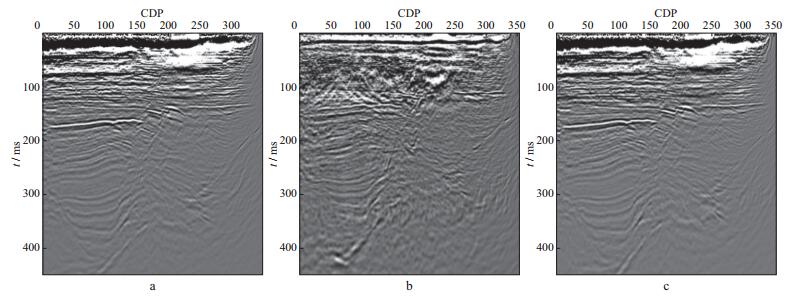
分别从克里金插值、偏移速度分析和基于克里金方差融合的速度场中抽取一剖面(剖面选取的方向和位置如图 4a所示), 结果如图 8所示。然后从图 8中的红线位置抽取一条线, 结果如图 9所示。对图 8所示的速度场进行二维克希霍夫偏移, 得到的叠加剖面如图 10所示。
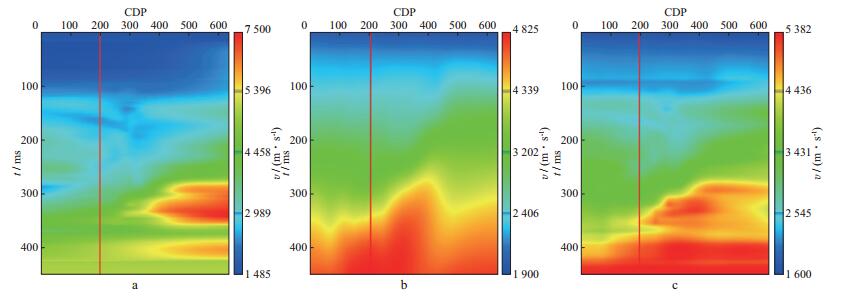
|
图 8 从图 4a所示位置抽取的速度剖面 a 克里金插值结果; b 偏移速度分析结果; c 采用克里金方差融合结果 |
|
图 9 从图 8红线位置抽取的速度场对比 |
|
图 10 对图 8的速度场采用克希霍夫偏移得到的叠加剖面 a 偏移速度分析结果; b 克里金插值结果; c 采用克里金方差融合结果 |
2) 空间波数域多尺度数据融合。
偏移速度分析中含有高精度的低波数成分, 测井速度中含有中、高波数成分。一般来说, 在某些未测量深度范围得不到可靠的速度。我们将偏移速度分析和克里金插值两个速度场进行多尺度Gabor变换, 转换到空间波数域, 对不同的空间和波数进行融合, 提高速度场精度。频率域和时间域多尺度Gabor函数公式[37]表示为:
| $ \begin{align} & {{_{{\hat{\varphi }}}}_{_{l,i,k}}}\left( \xi \right)=\frac{1}{L_{l}^{d/2}}{{\text{e}}^{\text{-2}\pi j\frac{k\cdot \xi }{{{L}_{l}}}}}{{\text{e}}^{{{(\frac{-\xi -{{\xi }_{_{l,i}}}}{{{\sigma }_{l}}})}^{2}}}} \\ & _{{{\varphi }_{l,i,k}}}\left( x \right)\approx {{\left( \sqrt{\frac{\pi }{{{L}_{l}}}{{\sigma }_{l}}} \right)}^{d}}\cdot {{e}^{2\pi j(x-\frac{k}{{{L}_{l}}})\cdot {{\xi }_{l,i}}}}\cdot {{e}^{-\sigma _{l}^{2}{{\pi }^{2}}{{(x-\frac{k}{{{L}_{l}}})}^{2}}}} \\ \end{align} $ | (30) |
式中:
| $ v\left( {x, y, z, {k_z}} \right) = \alpha \left( {x, y, z} \right){v_{{\rm{ok}}}}\left( {x, y, z, {k_z}} \right) + \beta \left( {x, y, z} \right){v_{{\rm{mva}}}}(x, y, z, {k_z}) $ | (31) |
式中:v(x, y, z, kz) 为波数域融合速度; vok(x, y, z, kz) 为波数域克里金插值速度; vmva(x, y, z, kz) 为波数域偏移速度分析速度; α(x, y, z) 和β(x, y, z) 为融合系数。然后利用Gabor反变换将波数域融合的速度变换到空间域。
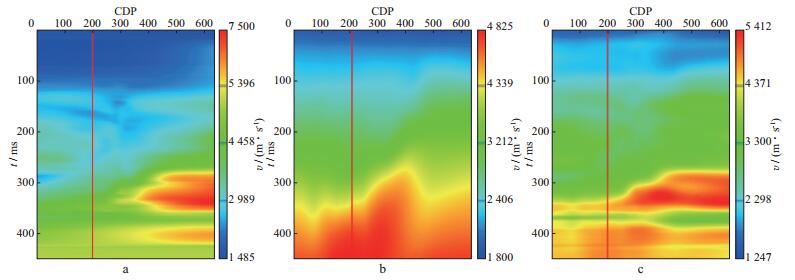
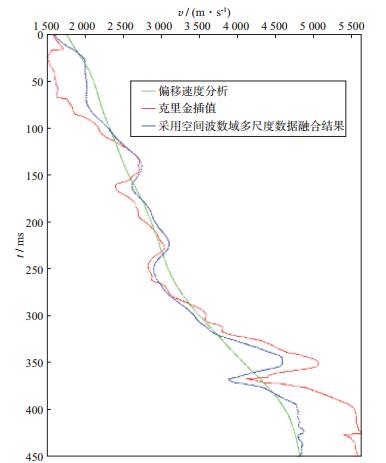
分别从克里金插值、偏移速度分析和基于空间波数域多尺度数据融合的速度场中抽取一剖面(剖面选取的方向和位置如图 4a所示), 结果如图 11所示。然后从图 11中的红线位置抽取一条线, 结果如图 12所示。分别对图 11所示的速度场进行二维克希霍夫偏移, 得到的叠加剖面如图 13所示。
|
图 11 从图 4a所示位置抽取的速度剖面 a 克里金插值结果; b 偏移速度分析结果; c 采用空间波数域多尺度数据融合的结果 |
|
图 12 从图 11红线位置抽取的速度场对比 |
|
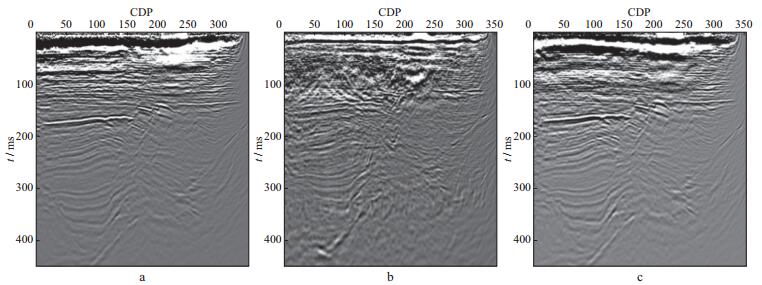
图 13 对图 11速度场采用克希霍夫偏移得到的叠加剖面 a 偏移速度分析结果; b 克里金插值结果; c 采用空间波数域多尺度数据融合的结果 |
上述处理表明, 克里金插值结果和偏移速度分析结果可融合在一起得到更高精度的速度场, 并且偏移成像结果得到明显改善。本文提出的速度融合方法为提高速度建模精度提供了一条实用的方法。
3 速度场的特征表达及多尺度反演我们把地下介质的分布特征抽象为:空间上广泛分布的层状沉积层, 加上火山活动, 构造运动等引起的大、小尺度的速度异常体(或波阻抗变化的异常体)。
此介质分布特征基本上可以用反射界面+层速度来描述。更进一步地, 可以用空间散乱分布的特征点支撑起速度场的背景变化。这样的表达对速度场的反演具有十分重要的作用, 可以大大减少要反演的模型空间, 提高速度反演的稳定性。该思想也可以推广到诸如密度、各向异性参数和Q值的反演中。
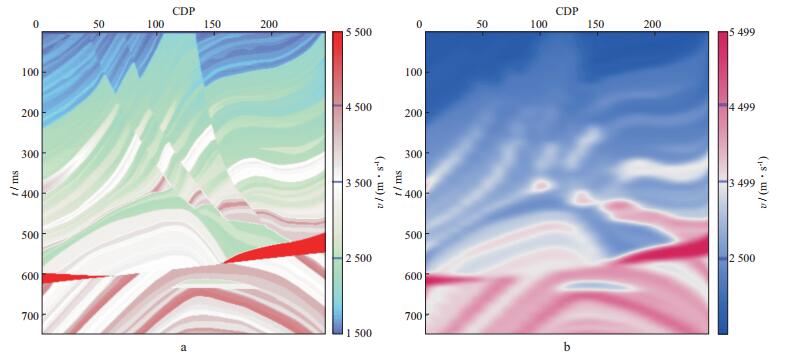
利用B样条函数基于离散的解释数据描述反射界面, 然后在反射界面间充填层速度值是目前基本的速度模型描述方法[38]。图 14a为原始的Marmousi模型, 共750×248个点。图 14b是利用等间隔的30道每道90个点进行B样条插值, 然后再横向线性插值得到的结果。可见该结果基本表达了Marmousi模型的背景速度变化。
|
图 14 速度模型描述结果 a 原始的Marmousi模型(采用750×248个点描述); b 利用B样条插值结果表达的Marmousi模型(采用30×90个点描述) |
事实上, 与地震波场数据一样, 速度参数场也是有特征的, 其特征就是反射界面的几何形状。在成像剖面上进行地震解释(可以是自动的), 得到特征散乱点的位置和速度值, 利用合适的散乱数据插值方法可以用更少的特征点很好地描述速度场的背景变化。这样的描述方法可以很方便地与Monte Carlo类的速度反演方法结合。更进一步地, 若特征散乱点的剖分与波动方程的数值模拟结合在一起, 可以发展一套多尺度的速度场反演方法。
4 结论散乱数据插值(与拟合) 目前已经在地震勘探中得到广泛应用, 特别是在速度(或其它参数) 建模中的作用越来越重要。散乱数据插值包括局部(有网格) 插值方法和全局(无网格) 插值方法。前者的代表方法有三角剖分法、自然邻域法以及样条函数法等; 后者有反距离加权法、径向基函数法(克里金插值法也属于径向基函数方法)。前者计算简单, 需事先对区域进行剖分, 插值结果连续性差, 扩展到高维困难; 后者不需剖分, 容易扩展到高维, 但有过强的平滑效应, 插值系数求解计算量大。
利用三维克里金插值方法将各种信息来源的速度值融合在一起, 是信息融合的主要方法。本文将实际测井数据插值成三维速度场, 在实现三维克里金插值过程中, 考虑到地下速度场在水平方向上变化比较缓慢, 而在垂直方向上变化比较剧烈的情况, 采用在垂向上乘以各向异性系数、分方向计算实验变差函数方法来适应地下速度场的变化特点。在计算过程中, 采用加窗时移处理, 提高了三维插值效率。然后采用克里金方差融合和频率空间域融合方法将来自测井的速度场和来自偏移速度分析的速度场融合在一起。实验结果表明融合后的速度场有更好的成像质量, 可以为后续的速度反演提供更好的初始模型。
散乱数据插值(或拟合) 是一个反问题, 如何根据信号或图像的特征来约束插值结果是目前关注的重点。另一个关键的问题是在地震参数反演过程中, 将要反演的速度场的特征表达(一般地, 可以提为基于散乱点的表达)、基于特征表达的地震波正演模拟和地震波反演方法融合在一起, 形成多尺度的速度反演方法。我们认为这是散乱数据插值(拟合) 在地震勘探中最有意义的发展方向。
| [1] | SHEPARD D. A two-dimensional interpolation function for irregularly-spaced data[J]. Proceedings of the 23rd ACM National Conference, 1968: 517-524 |
| [2] | SIBSON R.A brief description of natural neighbour interpolation[C]//BARNETT V.Interpreting multivariate data.New York:John Wiley & Sons, 1981:21-36 |
| [3] | HARDY R L. Multiquadric equations of topography and other irregular surfaces[J]. Journal of Geophysical Research, 1971, 76(8): 1905-1915 DOI:10.1029/JB076i008p01905 |
| [4] | DUCHON J. Splines minimizing rotation-invariant semi-norms in Sobolev spaces[M]. Berlin: Springer, 1977: 85-100. |
| [5] | KRIGE D G.A statistical approach to some mine valuations and allied problem on the Witwatersrand[D].Johannesburg:University of Witwaterskand, 1951 |
| [6] | MATHERON G. Principles of geostatistics[J]. Economic Geology, 1963, 58(8): 1246-1266 DOI:10.2113/gsecongeo.58.8.1246 |
| [7] | SCHUMAKER L L. Fitting surfaces to scattered data[M]. NewYork: Academic Press, 1976: 203-268. |
| [8] | ABMA R, KABIR N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91-E97 DOI:10.1190/1.2356088 |
| [9] | GAO J, STANTON A, SACCHI M D. Parallel matrix factorization algorithm and its application to 5D seismic reconstruction and denoising[J]. Geophysics, 2015, 80(6): V173-V187 DOI:10.1190/geo2014-0594.1 |
| [10] | ELY G, AERON S, HAO N, et al. 5D seismic data completion and denoising using a novel class of tensor decompositions[J]. Geophysics, 2015, 80(4): V83-V95 DOI:10.1190/geo2014-0467.1 |
| [11] | HALE D. Image-guided blended neighbor interpolation of scattered data[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009: 1127-1131 |
| [12] | DOUMA J, NAEINI E Z.Application of image-guided interpolation to build low frequency background model prior to inversion[J].Expanded Abstracts of 76th EAGE Annual Conference, 2014:We G106 05 |
| [13] |
周晓云, 朱心雄. 散乱数据点三角剖分方法综述[J].
工程图学学报, 1993, 14(1): 48-54 ZHOU X Y, ZHU X X. A survey of triangulation methods for seattered data points[J]. Journal of Engineering Graphics, 1993, 14(1): 48-54 |
| [14] | DELAUNAY B. Neue darstellung der geometrischen kristallographie[J]. Zeitschrift für Kristallographie-Crystalline Materials, 1933, 84(1): 109-149 |
| [15] | VORONOI G M. Nouvelles applications des parameters continues a la theorie des formes quadratiques.deuxieme memoire:recherches sur les parallelloedres primitives[J]. Journal fur die Reine und Angewandte Mathematik, 1908(134): 198-287 |
| [16] | ISKE A. Multiresolution methods in scattered data modelling[M]. Berlin: Springer Science & Business Media, 2004: 1-182. |
| [17] |
吴宗敏.
散乱数据拟合的模型、方法和理论[M]. 北京: 科学出版社, 2007: 1-166.
WU Z M. Scattered data fitting model, method and theory[M]. Beijing: Science Press, 2007: 1-166. |
| [18] | CLOUGH R W, TOCHER J L. Finite element stiffness matrices for analysis of plates in bending[J]. Proceedings of Conference on Matrix Methods in Structural Analysis, 1965: 515-545 |
| [19] | POWELL M J D, SABIN M A. Piecewise quadratic approximations on triangles[J]. ACM Transactions on Mathematical Software (TOMS), 1977, 3(4): 316-325 DOI:10.1145/355759.355761 |
| [20] | FARIN G. Surfaces over Dirichlet tessellations[J]. Computer Aided Geometric Design, 1990, 7(1/2/3/4): 281-292 |
| [21] | WATSON D F. Contouring:a guide to the analysis and display of spatial data[M]. New York: Pergamon Press, 1992: 1-321. |
| [22] | GORDON W J, WIXOM J A. Shepard's method of "metric interpolation" to bivariate and multivariate interpolation[J]. Mathematics of Computation, 1978, 32(141): 253-264 |
| [23] | POWELL M J D.The theory of radial basis function approximation in 1990[C]//LIGHT W A.Advances in numerical analysis.Oxford:Clarendon Press, 1992:105-203 |
| [24] | LIGHT W A.Some aspects of radial basis function approximation[C]//SINGH S P.Approximation theory, spline functions and applications.Dordrecht:Springer Science+Business Media.1992:163-190 |
| [25] | ZALA C A, BARRODALE I. Warping aerial photographs to orthomaps using thin plate splines[J]. Advances in Computational Mathematics, 1999, 11(2/3): 211-227 DOI:10.1023/A:1018928026708 |
| [26] | HARDY R L. Theory and applications of the multiquadrics-biharmonic method[J]. Computers & Mathematics with Application, 1990, 19(8/9): 163-208 |
| [27] | FRANKE R, NIELSON G M.Scattered data interpolation and applications:a tutorial and survey[C]//HAGEN H, ROLLER D.Geometric Modeling.Berlin:Springer Berlin Heidelberg, 1991:131-160 |
| [28] | FRANKE R. Scattered data interpolation:test of some methods[J]. Mathematics of Computation, 1982, 38(157): 181-200 |
| [29] | POLLANDT R. Solving nonlinear differential equations of mechanics with the boundary element method and radial basis functions[J]. International Journal for Numerical Methods in Engineering, 1997, 40(1): 61-73 DOI:10.1002/(ISSN)1097-0207 |
| [30] | SONAR T. Optimal recovery using thin plate splines in finite volume methods for the numerical solution of hyperbolic conservation laws[J]. IMA Journal of Numerical Analysis, 1996, 16(4): 549-581 DOI:10.1093/imanum/16.4.549 |
| [31] | WENDLAND H. Piecewise polynomial, positive definite and compactly supported radial basis functions of minimal degree[J]. Advances in Computational Mathematics, 1995, 4(1): 389-396 DOI:10.1007/BF02123482 |
| [32] | STEIN M L. Interpolation of spatial data:some theory for Kriging[M]. New York: Springer Science & Business Media, 1999: 1-249. |
| [33] | HESSAMI M, ANCTIL F, VIAU A A. Delaunay implementation to improve Kriging computing efficiency[J]. Computers & Geosciences, 2001, 27(2): 237-240 |
| [34] | YAO X M, WANG Q, LIU Z N, et al. Fast 3D Kriging interpolation using Delaunay tetrahedron with CUDA-enabled GPU[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015: 1739-1743 |
| [35] | DEUTSCH C V. A sequential indicator simulation program for categorical variables with point and block data:BlockSIS[J]. Computers & Geosciences, 2006, 32(10): 1669-1681 |
| [36] | DELBARI M, AFRASIAB P, LOISKANDL W. Using sequential Gaussian simulation to assess the field-scale spatial uncertainty of soil water content[J]. Catena, 2009, 79(2): 163-169 DOI:10.1016/j.catena.2009.08.001 |
| [37] | QIAN J L, YING L X. Fast Gaussian wavepacket transforms and Gaussian beams for the Schrödinger equation[J]. Journal of Computational Physics, 2010, 229(20): 7848-7873 DOI:10.1016/j.jcp.2010.06.043 |
| [38] | LING Y, WANG H Z, LIU S Y. Monte Carlo background velocity inversion method[J]. Expanded Abstracts of 84th Annual Internat SEG Mtg, 2014: 735-738 |


