2. 同济大学波现象与反演成像研究组, 上海 200092;
3. 上海青凤致远地球物理地质勘探科技有限公司, 上海 200093
2. Wave phenomena and inversion imaging group (WPI), Tongji University, Shanghai 200092, China;
3. Shanghai Qingfeng Zhiyuan Geophysics & Geology Technology Co.Ltd., Shanghai 200093, China
叠前深度偏移成功与否最重要的前提之一是速度的准确程度。层析反演是一种广泛应用的速度估算方法, 一般可分为射线层析[1-2]、胖射线层析[3-4]、波动方程层析[5-8]以及全波形反演[9-10]等。从层析分类中可以看出, 射线理论和波动理论是层析的两个极端理论基础。基于这两种理论的层析方法显示出了不同的特点。射线层析所需的计算量远远小于波动层析, 但射线理论受限于焦散和阴影区等问题。从数学角度看, 射线层析是一个十分病态的反演问题, 所以实际应用时需要加入正则化[11], 而波动方程层析对正则化的需求则低得多。针对上述射线理论与波动理论的极端特点, 寻找一种介于两者之间的层析方法很有必要。胖射线层析综合了对波动理论的感性认识, 定性地将层析核函数中的射线修改成射线束, 缺少严格的理论支持。本文提出的高斯束层析在建立核函数时利用了高斯束正演理论, 可认为是一种介于胖射线层析和波动层析之间的方法。
高斯束[12-13]正演理论可用于描述局部方向的波束传播, 作为模拟方法, 实际上是射线理论与波动理论的折中。高斯束的优势之一是可以解决焦散问题, 而焦散问题是射线理论面临的重大难题之一。高斯束方法已被广泛应用于偏移成像中[14-16], 但很少用于层析中。SEMTCHENOK等[17]提出了一种利用高斯束建立层析核函数的方法, 一个炮检对的一个震相在常规射线层析中只能建立一个层析方程, 而SEMTCHENOK利用高斯束对波场的贡献大小建立了多个射线积分方程。VERDEL等[18]利用SEMTCHENOK的思想展示了一种层析偏移速度分析策略, 并取得了很好的效果, 但他们建立高斯束层析矩阵的正演工具仍然是射线。LI等[19]给出了一种利用高斯束建立的核函数, 核函数的形态类似于胖射线层析, 是一个波束体。邵荣峰等[20]在此基础上实现了成像域层析偏移速度分析。本文以高斯束作为正演工具, 提出一种层析方法, 类似于LI等[19]的工作, 建立了形态为波束体的层析核函数, 并给出了详细的计算公式以及实际应用中的算法策略。我们将高斯束层析应用于偏移速度分析并得到了理想的速度更新结果。
本文首先从理论上推导出了高斯束层析核函数的表达方式, 并给出了该表达方式的详细计算方法, 提出了高斯束初值选取原则以及确定核函数边界的方法建议, 最后将高斯束层析应用于角度域共成像点道集偏移速度分析中, 并应用理论模型和实际资料测试了本文方法的应用效果。
1 高斯束层析理论利用高斯束积分方法可以实现观测波场的模拟, 旅行时可看作是来自不同高斯束共同贡献的结果。基于此, 根据不同高斯束对旅行时差的贡献, 推导出旅行时高斯束层析的核函数表达式。
在Rytov近似和Born近似下, 旅行时扰动Δτ, 频率ω, 初始模型中的背景波场u0和扰动波场us之间存在如下关系[21]:
| $ \Delta \tau = \frac{{{\rm{Im}}\left( {{u^s}/{u^0}} \right)}}{\omega } $ | (1) |
进一步在Born近似下(1) 式可写成:
| $ \Delta \tau = \frac{{{\rm{Im}}\left( {{u^s}/u} \right)}}{\omega } $ | (2) |
这里, u是观测波场, 可看作是背景波场和扰动波场之和。
| $ u = {u^0} + {u^s} $ | (3) |
零阶WKBJ近似下观测波场写成振幅A和旅行时τ的表达形式, 有:
| $ u = A{{\rm{e}}^{i\omega \tau }} $ | (4) |
| $ {u^0} = \psi {\smallint _\varphi }A(\varphi ){{\rm{e}}^{i\omega \tau }}\left( \varphi \right){\rm{d}}\varphi $ | (5) |
其中, ψ是调节高斯束积分结果的常数, 以保证高斯束积分与真实波场的振幅相等。
把(4) 式和(5) 式代入(2) 式, 经过简单推导得到旅行时差的表达式:
| $ \Delta \tau = \frac{{\psi {\smallint _\varphi }A\left( \varphi \right){\rm{sin}}[\tau \left( \varphi \right)-\tau]{\rm{d}}\varphi }}{{A\omega }} $ | (6) |
从上述高斯束计算波场的过程可知, 公式(5) 和公式(6) 中的φ是高斯束中心射线的标记, 由于高斯束与中心射线一一对应, 则高斯束也可以用φ标记。(6) 式中的旅行时残差是利用所有对观测波场有贡献的高斯束计算得到的。下面考察一个单独高斯束对旅行时残差的贡献。计算(2) 式中背景波场时只考虑利用一个高斯束, 而非高斯束积分, 此时背景波场为:
| $ {u^0} = \psi A({\varphi _0}){{\rm{e}}^{i\omega \tau }}\left( {{\varphi _0}} \right) $ | (7) |
同时(6) 式变成一个高斯束计算出的旅行时差:
| $ \Delta \tau \left( {{\varphi _0}} \right) = \frac{{\psi A\left( {{\varphi _0}} \right){\rm{sin[}}\tau \left( {{\varphi _0}} \right)-\tau]}}{{A\omega }} $ | (8) |
结合(6) 式和(8) 式可知, 以φ0为中心射线的高斯束对旅行时差的相对贡献为:
| $ c\left( {{\varphi _0}} \right) = \frac{{\Delta \tau \left( {{\varphi _0}} \right)}}{{\Delta \tau }} = \frac{{A\left( {{\varphi _0}} \right){\rm{sin}}[\tau \left( {{\varphi _0}} \right)-\tau]}}{{{\smallint _\varphi }A\left( \varphi \right){\rm{sin}}[\tau \left( \varphi \right)-\tau]{\rm{d}}\varphi }} $ | (9) |
由高斯束初值与高斯束几何扩散的关系可知, 选择适当的初值可以使得高斯束在接收点附近为平面波, 此时不同的φ对应的高斯束在观测点处的相位函数相同, 即(9) 式中的所有τ(φ) 均相等, 此时(9) 式等价于:
| $ c\left( {{\varphi _0}} \right) = \frac{{A\left( {{\varphi _0}} \right)}}{{{\smallint _\varphi }A(\varphi ){\rm{d}}\varphi }} $ | (10) |
对观测数据有贡献的高斯束中心射线均可利用观测点旅行时差建立如下层析方程:
| $ {\smallint _{{\mathit{\Gamma} ^\varphi }({\varphi _0})}}\Delta p{\rm{d}}l = \Delta \tau $ | (11) |
式中:Δp是慢度修正量; Γφ是中心射线路径; dl是沿射线路径长度的微分变量。
方程(11) 等号两边同时对φ加权积分, 权系数为c(φ), 得到:
| $ {\smallint _V}K\left( \mathit{\boldsymbol{x}} \right)\Delta p\left( \mathit{\boldsymbol{x}} \right){d}\mathit{\boldsymbol{x}} = \Delta \tau $ | (12) |
式中:积分范围V是对当前旅行时有贡献的高斯束中心射线覆盖的区域。其中, 核函数K(x) 为:
| $ K\left( \mathit{\boldsymbol{x}} \right) = \frac{{A\left( \varphi \right)}}{{\smallint A\left( \varphi \right)d\varphi }} $ | (13) |
至此, 我们得到了高斯束层析核函数的表达式((13) 式)。从(13) 式中可以看出, 核函数不只与连接炮检点的射线有关, 也与临近的高斯束有关。相对于射线层析, 高斯束层析更加符合波传播的物理事实, 即波传播是沿着波路径[6]而非射线路径传播。
2 高斯束层析核函数计算方法前文已经详细推导了高斯束层析的基础理论, 并给出了核函数的表达形式。公式(13) 所示的核函数计算不易实现, 本节在一定近似下探讨高斯束层析核函数的计算方法。
高斯束振幅的计算公式为[12]:
| $ A\left[{{\mathit{\boldsymbol{x}}^g}, {\mathit{\boldsymbol{x}}^s}, \varphi } \right] = \sqrt {\frac{{v\left( \varphi \right)}}{{Q(\varphi )}}} {\rm{exp}}\left\{ { - \frac{\omega }{2}q_0^2{\rm{Im[}}M(\varphi )]} \right\} $ | (14) |
式中:v(φ) 是观测点xg在中心射线上投影点x0处的速度; Q(φ) 是x0处的动力学射线追踪参数; q0是xg到x0的距离; M(φ) 是x0处相位函数的二阶导数。利用傍轴射线近似(Paraxial ray approximation, PRA) 对旅行时二阶导数近似[22], 有:
| $ M\left( \varphi \right) \approx M(\varphi + \Delta \varphi ) $ | (15) |
| $ Q\left( \varphi \right) \approx Q(\varphi + \Delta \varphi ) $ | (16) |
根据旅行时一阶扰动近似[23], 射线φ和连接炮检点的射线φ0路径差是φ-φ0的一阶扰动量, 此时有:
| $ v\left( \varphi \right) \approx v(\varphi + \Delta \varphi ) $ | (17) |
结合(15) 式、(16) 式和(17) 式, (14) 式近似为:
| $ A\left[{{\mathit{\boldsymbol{x}}^g}, {\mathit{\boldsymbol{x}}^s}, \varphi } \right] \approx \sqrt {\frac{{v\left( {{\varphi _0}} \right)}}{{Q({\varphi _0})}}} {\rm{exp}}\left\{ { - \frac{\omega }{2}q_0^2{\rm{Im[}}M({\varphi _0})]} \right\} $ | (18) |
至此, 只要知道观测点到中心射线的距离q0, 即可计算出(14) 式中高斯束的振幅。高斯束的振幅随着到中心射线的距离呈高斯型衰减, 如果接收点距离射线比较远则振幅衰减到一定程度时可以忽略该射线对观测点的振幅贡献, 因为核函数K(x) 已经相对很小以至于可以忽略。对于给定的一点x, 如果在核函数的范围之内(核函数边界的具体计算方法在下一节中详细讨论), 可以利用下面给出的策略计算。对观测点振幅有贡献的高斯束中, 距离观测点最远的中心射线标记为φmax, 观测点到此射线的距离为qmax, 即图 1中点R和A的距离:
|
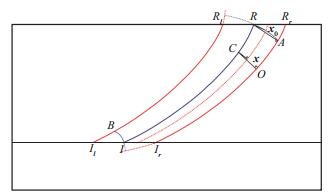
图 1 高斯束层析核函数边界示意 |
| $ {q_{{\rm{max}}}} = |RA| $ | (19) |
图 1中红色虚线是假想的经过点x的射线, 观测点R在假想射线上的投影点为x0, 现在需要计算点R到假想射线的距离用于计算高斯束振幅, 即:
| $ {q_0} = |R{\mathit{\boldsymbol{x}}_0}| $ | (20) |
令假想射线上垂足为x, 中心射线上存在一点C垂直于假想射线。经过点C作射线φmax的垂线, 垂足为O。将点C到上述两条中心射线的距离写成:
| $ r = |C\mathit{\boldsymbol{x}}| $ | (21) |
| $ {r_{{\rm{max}}}} = |CO| $ | (22) |
结合(19) 式至(22) 式即可近似计算出观测点到当前中心射线的距离q0:
| $ {q_0} \approx \frac{{{q_{{\rm{max}}}}r}}{{{r_{{\rm{max}}}}}} $ | (23) |
将(23) 式代入(18) 式, 中心射线经过点x的高斯束在观测点处的振幅可用下式近似计算:
| $ A\left[{{\mathit{\boldsymbol{x}}^g}, {\mathit{\boldsymbol{x}}^s}, \varphi } \right] \approx \sqrt {\frac{{v\left( {{\varphi _0}} \right)}}{{Q({\varphi _0})}}} {\rm{exp}}\cdot\left\{ { - \frac{\omega }{2}{{\left( {\frac{{{q_{{\rm{max}}}}r\left( \mathit{\boldsymbol{x}} \right)}}{{{r_{{\rm{max}}}}{{\left( \mathit{\boldsymbol{x}} \right)}^2}}}} \right)}^{\rm{2}}}{\rm{Im[}}M({\varphi _0})]} \right\} $ | (24) |
这样就得到了高斯束层析核函数(13) 式中的分子项, 下面推导分母项的计算公式。
经过观测点中心射线的垂直线段(三维时是截面) 上点与射线φ一一对应, 此时对射线的积分可以转换成对此线段上点的积分, 即
| $ {\smallint _\Psi }A({\mathit{\boldsymbol{x}}^g}, {\mathit{\boldsymbol{x}}^s}, \varphi ){\rm{d}}\varphi = \int_{-{q_{\max }}}^{{q_{\max }}} {A({\mathit{\boldsymbol{x}}^g}, {\mathit{\boldsymbol{x}}^s}, \varphi ){\rm{d}}q} $ | (25) |
式中:积分范围Ψ是对当前旅行时有贡献的高斯束中心射线的集合。将振幅计算公式((18) 式) 代入(25) 式, 有:
| $ \begin{array}{l} \int_{ - {q_{\max }}}^{{q_{\max }}} {\sqrt {\frac{{v\left( {{\varphi _0}} \right)}}{{Q({\varphi _0})}}} } {\rm{exp}}\left\{ { - \frac{\omega }{2}{q^2}{\rm{Im}}[M({\varphi _0})]} \right\}{\rm{d}}q\\ = C\sqrt {\frac{{2\pi v\left( {{\varphi _0}} \right)}}{{\omega {\rm{Im}}[M\left( {{\varphi _0}} \right)]Q({\varphi _0})}}} \end{array} $ | (26) |
高斯束的截断效应使得高斯束振幅积分出现误差, (26) 式中系数C补偿了忽略核函数边界之外高斯束对核函数的贡献带来的误差, 虽然这些贡献值相对很小。系数C的大小由高斯束宽度标准决定, 具体计算公式为:
| $ C = \frac{{\int_{- {q_{\max }}}^{{q_{\max }}} {{\rm{exp}}} \left\{ {- \frac{\omega }{2}{q^2}{\rm{Im}}[M({\varphi _0})]} \right\}{\rm{d}}q}}{{\int_{ - \infty }^{ + \infty } {{\rm{exp}}\left\{ { - \frac{\omega }{2}{q^2}{\rm{Im}}[M({\varphi _0})]} \right\}{\rm{d}}q} }} $ | (27) |
根据(13) 式, (24) 式和(26) 式, 可计算得到直接用作计算的高斯束层析核函数表达式:
| $ K\left( \mathit{\boldsymbol{x}} \right) = \frac{1}{C}\sqrt {\frac{{\frac{\omega }{2}{\rm{Im[}}M({\varphi _0})]}}{\pi }} {\rm{exp}}\left\{ { - \frac{\omega }{2}{{\left[{\frac{{{q_{{\rm{max}}}}r\left( \mathit{\boldsymbol{x}} \right)}}{{{r_{{\rm{max}}}}\left( \mathit{\boldsymbol{x}} \right)}}} \right]}^2}\cdot{\rm{Im[}}M({\varphi _0})]} \right\} $ | (28) |
高斯束层析应用于层析偏移速度分析时, 高斯束初值的选取原则以及层析核函数边界的计算方式是两个重要因素。本节首先确定层析核函数的边界, 在此基础上以核函数边界之外的中心射线对应的高斯束对观测点振幅贡献值可以忽略为原则, 确定高斯束的初值。
高斯束层析核函数的边界由6部分组成(图 1), 分别为曲线RlR, RA, AIr, IrI, IB和BRl。图 1中, IlIr是反射面上的Fresnel带, RlRr是地表处的角度道集投影Fresnel带(Projected Fresnel zone, PFZ)[24-25], IR是连接反射点和接收点的射线, IlRl和IrRr是把反射面上Fresnel带投影到地表面的射线, 根据投影Fresnel带的定义, 射线IR, IlRl和IrRr的出射角度相等。令射线IR的标记为φ0, IlRl和IrRr的标记分别为φmin和φmax。满足φ0≤φ≤φmax的射线记为φ, 接收点在所有射线φ上的投影点组成了曲线RA。同样, 满足φmin≤φ≤φ0的射线记为φ, 反射点在所有射线φ上的投影组成了曲线IB。至此, 高斯束层析核函数的边界被确定。反射面上Fresnel带可利用傍轴射线近似计算得到[26]。
接下来讨论高斯束宽度的选取准则。高斯束振幅随着距离射线的大小呈高斯型衰减, 某处振幅衰减至中心射线振幅的1/e时(e是自然常数), 可以将此处到射线的距离定义为高斯束的半宽度[12-13]。振幅衰减公式为:
| $ L\left( {s, q} \right) = {\rm{exp}}\left\{ {- \frac{\omega }{2}{\rm{Im[}}MP(s)]{q^2}} \right\} $ | (29) |
令(29) 式中的高斯束振幅衰减量为1/e, 得到:
| $ q = \frac{1}{{\sqrt {\frac{\omega }{2}{\rm{Im[}}M(s)]} }} $ | (30) |
即高斯束的宽度。高斯束初值选择遵循的原则为:连接反射点和接收点射线(中心射线) 对应的高斯束传播至地表时其宽度与投影Fresnel带的宽度相等。通过傍轴射线近似可导出, 高斯束层析核函数边界射线对应的高斯束对接收点振幅贡献大小为中心射线对应高斯束对观测点振幅贡献大小的1/e。在上述高斯束宽度标准下, (27) 式中的系数可以利用高斯函数的性质计算得到:
| $ C \approx 0.843 $ | (31) |
根据高斯束初值选取原则和高斯束层析核函数的计算公式, 我们计算了一个理论模型中层析偏移速度分析的核函数, 其分布形态如图 2所示。从图 2中可以看出, 高斯束层析中的核函数是有一定宽度的波路径, 相对于射线层析, 高斯束层析在理论上更加靠近波动理论, 与客观的物理现象更吻合。

|
图 2 高斯束层析核函数示意 |
图中, 背景是速度场, 蓝线是反射射线路径, 由红渐变白的波束是高斯束层析核函数。
4 数值实验 4.1 高斯束层析偏移速度分析高斯束层析方法可以应用在不同种类的层析成像中, 例如初至层析、透射层析、斜率层析以及反射层析等。我们基于角度域共成像点道集在成像域实现高斯束层析, 即角度域高斯束层析偏移速度分析。在层析偏移速度分析[2, 27]的框架下, 利用高斯束而非射线更新偏移速度场。相较于偏移距域层析偏移速度分析, 角度域共成像点道集更加符合物理规律, 如角度域共成像点道集可描述波传播的多路径问题; 并且, 利用角度域共成像点道集层析反演速度时, 层析核函数的构建只需进行初值射线追踪(射线追踪是计算高斯束的一步), 而利用偏移距域共成像点道集构建层析核函数必须进行费时且不稳定的两点射线追踪。
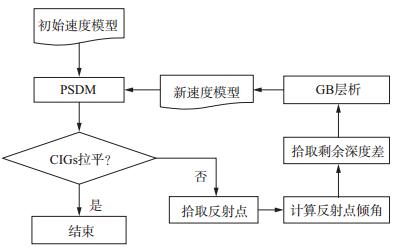
高斯束层析偏移速度分析的实现流程如图 3所示。基于给定的初始速度模型进行叠前深度偏移并生成角度域共成像点道集, 以道集是否拉平为判断准则考察速度场的优劣。角度域共成像点道集同相轴不平的情况下在偏移剖面中拾取反射点用于反射层析, 并计算反射点处的构造倾角。对应地在角度域共成像点道集上拾取出不同角度的成像深度, 并近似计算出“真深度”。将不同角度的成像深度差转化为旅行时差, 即得到了反射射线的旅行时差。根据角度域共成像点道集中的反射角度、地下反射点位置以及界面倾角, 利用初值射线追踪模拟出反射射线及其对应的高斯束, 建立高斯束层析矩阵。利用LSQR[28]求解层析方程组得到慢度更新量, 进而实现对速度模型的更新。
|
图 3 高斯束层析偏移速度分析流程 |
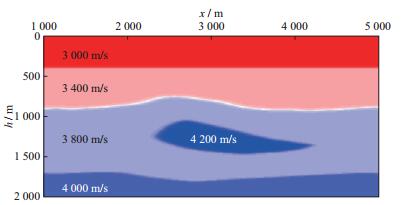
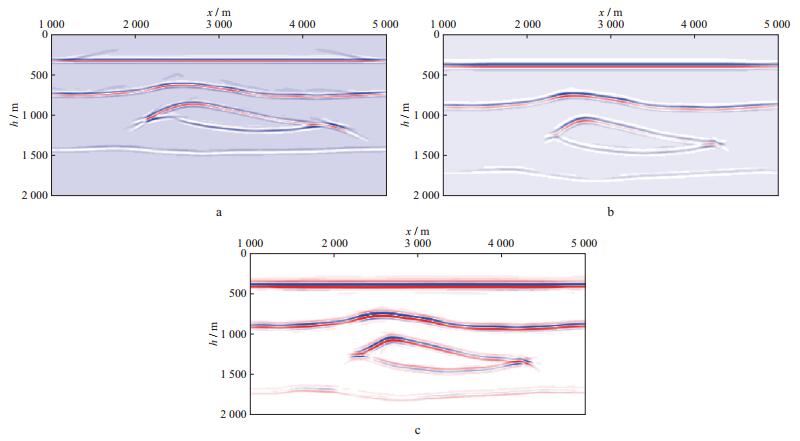
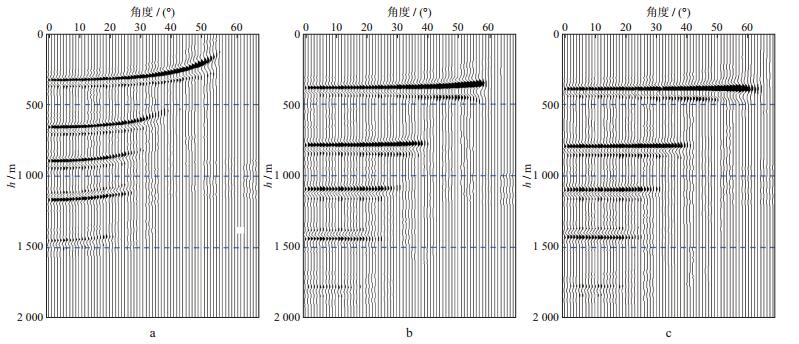
我们利用二维理论模型(图 4) 测试本文提出的高斯束层析偏移速度分析方法。理论模型中有4个沉积层, 其中第3层内有一个高速体, 具体的速度如图 4所示。理论模型大小为601×201, x和z方向的空间样点间隔均为10m。令201个震源点等间隔分布在1000~5000m, 震源间隔为20m, 每一炮均有101个检波点, 偏移距范围为-1000~1000m, 检波点间距为20m。由于理论模型比较简单, 实验中我们只做一次迭代就得到了理想的成像道集。初始速度模型和更新速度模型如图 5所示。图 6和图 7为初始模型、理论模型和更新模型对应的偏移剖面及成像道集。直接对比标准速度场、初始速度场和反演速度场, 层析明显修正了原始速度模型, 并反演出了层内的高速体。反演结果在成像剖面和成像道集中体现得更明显。初始速度对应的成像剖面明显不收敛且反射层位偏浅, 更新速度场的剖面同相轴聚焦更好, 与真实速度的成像剖面相比两者几乎没有差异。由于初始速度偏小, 因此偏移出的成像道集上翘严重, 高斯束层析反演更新后的速度与真实速度的角道集同相轴均被拉平。
|
图 4 理论速度模型 |
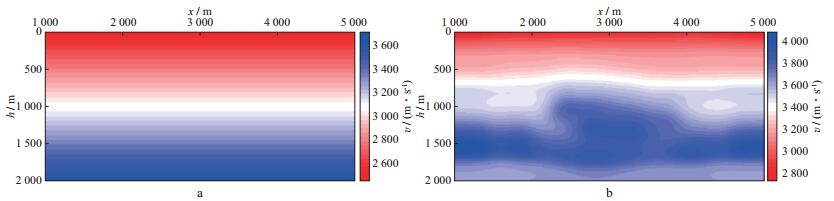
|
图 5 初始速度场(常梯度模型, 速度由2500m/s渐变至3700m/s)(a) 和高斯束层析得到的速度模型(b) |
|
图 6 采用不同速度模型偏移的成像剖面 a初始速度模型; b理论模型; c高斯束层析反演速度模型 |
|
图 7 采用不同速度模型偏移的角度域成像道集(CDP=300) a初始速度模型; b理论模型; c高斯束层析一次迭代反演速度模型 |
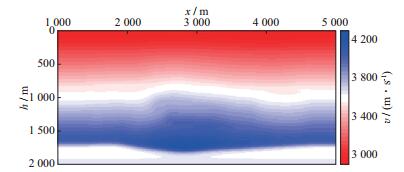
射线层析的核函数是射线长度, 所以其非零值仅存在于射线路径上, 层析过程中需要加入光滑正则化, 而光滑正则化降低了反演模型的分辨率。高斯束层析的核函数是有一定宽度的波束体, 本文实验中不需加入光滑正则化, 反演分辨率显著高于射线层析。对比高斯束层析的反演模型(图 5b) 和图 8所示射线层析反演模型可证实上述分析。
|
图 8 射线层析反演的速度模型 |
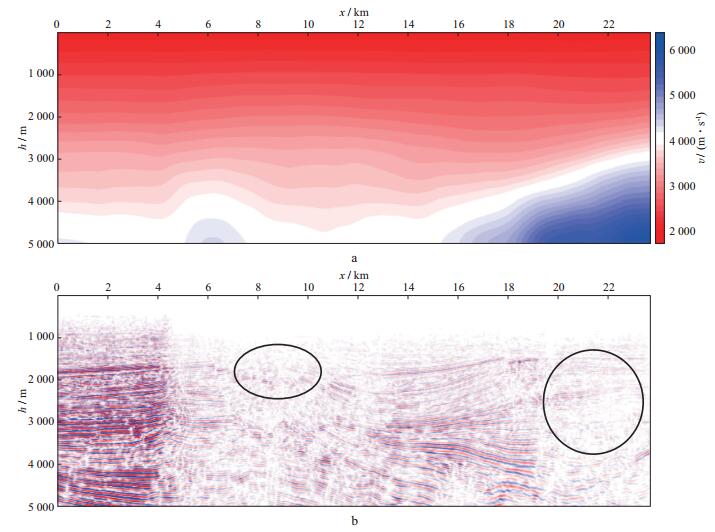
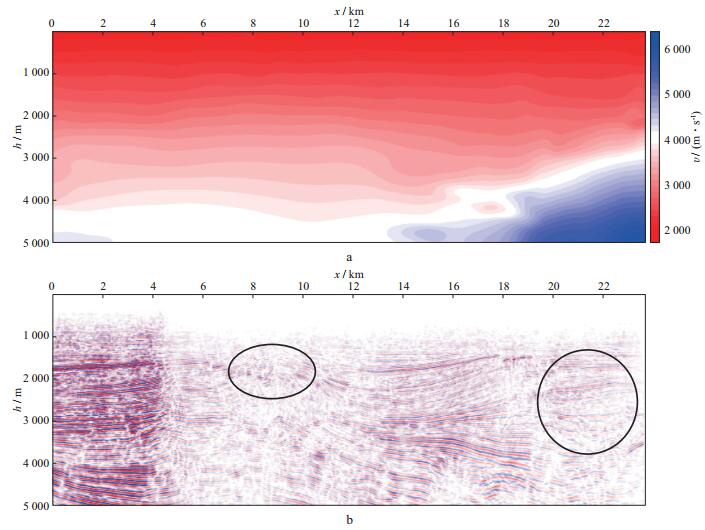
用于测试高斯束层析的实际数据来源于中国某探区的一条二维测线。该测线共232炮, 每炮最大偏移距3200m, 最小偏移距100m, 左侧单边接收; 道间距50m;炮间距大部分为100m, 小部分为50m。初始速度模型由时间域速度分析获得。该数据共952个CDP点, CDP间隔25m, 深度采样点数为501, 深度采样间隔为10m。初始速度模型和相应偏移剖面如图 9a和图 9b所示。在横向位置为1000, 3000, 9000m的3个CDP点抽取出3个角度域成像道集, 分别如图 10a, 图 10b和图 10c所示。从成像道集中可看出, x=1000m附近的初始速度比较准确, 同相轴基本水平; x=3000m附近同相轴有微小的下拉现象, 初始速度略微偏大; x=9000m附近的同相轴下拉现象明显, 初始速度显著偏大。高斯束层析偏移速度分析利用初始速度偏移得到的剖面和成像道集对初始速度进行更新, 图 11a和图 11b分别给出了反演后的速度模型和成像剖面。对比初始速度模型和反演速度模型可以看出, 模型左侧速度场更新量很小, 中部和右侧更新量相对较大。反演速度偏移剖面相对于原始剖面有明显改善, 例如图 11b中部小断块区域成像更清楚, 同时右侧的反射同相轴更加连续。从层析速度的偏移结果中抽取3个角度域成像道集如图 12a, 图 12b和图 12c所示, 与图 10对比可以看出, 同相轴有显著改善, 尤其是数据中部和右侧区域, 原始成像道集中同相轴的下拉现象已经被完全校正。
|
图 9 实际数据初始速度模型(a) 和相应的偏移剖面(b) |

|
图 10 实际数据初始速度模型偏移的3个角度域成像道集 a x=1000m; b x=3000m; c x=9000m |
|
图 11 反演速度模型(a) 和相应的偏移剖面(b) |

|
图 12 反演速度模型偏移的3个角度域成像道集 a x=1000m; b x=3000m; c x=9000m |
高斯束层析是介于射线层析与波动层析之间的一种层析方法, 该方法克服了射线层析的一些缺点, 同时保留了波动层析和射线层析的优点。与前人将高斯束应用于层析中的思路不同, 我们提出了一种利用高斯束建立有一定宽度的波束体层析核函数的层析方法, 更加符合客观的物理规律。高斯束层析核函数的计算公式由模拟出的高斯束中心射线和高斯束振幅组成, 具体计算时在一定近似下将多个高斯束模拟转换成模拟一个高斯束的计算, 从而提高计算效率。确定核函数边界有利于省略对核函数贡献较小的高斯束的计算, 可进一步提高计算效率。理论分析结果表明, 本方法在保持射线类方法高效特点的同时, 增强了层析过程的稳定性。高斯束层析方法可以应用在不同种类的层析反演中, 我们将高斯束层析应用于角度域共成像点道集层析偏移速度分析, 用理论模型和实际数据对方法进行了测试。数值实验结果证明了本文方法的有效性。层析中高斯束初值的选取原则应用于角度成像道集中更为合理, 并且角度成像道集层析偏移速度分析中不需两点射线追踪, 大大提高了层析效率。本文从正演算子的角度提高层析反演的稳定性和精度是提高反演质量的重点研究对象之一, 加入地质构造约束的先验信息以实现对反演过程的正则化是另一个工作重点, 这也是今后的研究方向之一。
致谢: 感谢中国石油化工股份有限公司石油物探技术研究院对WPI研究组及本项研究的支持。| [1] | BISHOP T N, BUBE K P, CUTLER R T, et al. Tomographic determination of velocity and depth in laterally varying media[J]. Geophysics, 1985, 50(6): 903-923 DOI:10.1190/1.1441970 |
| [2] | LIU Z, BLEISTEIN N. Migration velocity analysis:theory and an iterative algorithm[J]. Geophysics, 1995, 60(1): 142-153 DOI:10.1190/1.1443741 |
| [3] | VASCO D W, PETERSON J E, MAJER E L. Beyond ray tomography:wavepaths and Fresnel volumes[J]. Geophysics, 1995, 60(6): 1790-1804 DOI:10.1190/1.1443912 |
| [4] | XU S, ZHANG Y, HUANG T. Enhanced tomography resolution by a fat ray technique[J]. Expanded Abstracts of 76th Annual Internat SEG Mtg, 2006: 3354-3358 |
| [5] | LUO Y, SCHUSTER G T. Wave-equation traveltime inversion[J]. Geophysics, 1991, 56(5): 645-653 DOI:10.1190/1.1443081 |
| [6] | WOODWARD M J. Wave-equation tomography[J]. Geophysics, 1992, 57(1): 15-26 DOI:10.1190/1.1443179 |
| [7] | MARQUERING H, DAHLEN F A, NOLET G. Three-dimensional sensitivity kernels for finite-frequency traveltimes:the banana-doughnut paradox[J]. Geophysical Journal International, 1999, 137(3): 805-815 DOI:10.1046/j.1365-246x.1999.00837.x |
| [8] | SAVA P, BIONDI B. Wave-equation migration velocity analysis-I:theory[J]. Geophysical Prospecting, 2004, 52(6): 593-606 DOI:10.1111/gpr.2004.52.issue-6 |
| [9] | PRATT R G. Seismic waveform inversion in the frequency domain, Part 1:theory and verification in a physical scale model[J]. Geophysics, 1999, 64(3): 888-901 DOI:10.1190/1.1444597 |
| [10] | TARANTOLA A. Inversion of reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266 DOI:10.1190/1.1441754 |
| [11] |
李辉, 王华忠, 张兵. 层析反演中的正则化方法研究[J].
石油物探, 2015, 54(5): 569-581 LI H, WANG H Z, ZHANG B. The study of regularization in tomography[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 569-581 |
| [12] | ČERVENÝV, POPOVM M, PSENCIKI. Computation of wave fields in inhomogeneous media-Gaussian beam approach[J]. Geophysical Journal Royal Astronomical Society, 1982, 70(1): 109-128 |
| [13] | POPOV M M. A new method of computation of wave fields using Gaussian beams[J]. Wave Motion, 1982, 4(1): 85-97 DOI:10.1016/0165-2125(82)90016-6 |
| [14] | HILL R N. Gaussian beam migration[J]. Geophysics, 1990, 55(11): 1416-1428 DOI:10.1190/1.1442788 |
| [15] | HALE D.Migration by the Kirchhoff, slant stack and Gaussian beam methods[J].CWP Annual Report, 1992, http://www.cwp.mines.edu/documents/cwpreports/cwp-126.pdf. |
| [16] | POPOV M M, SEMTCHENOK N M, POPOV P M, et al. Depth migration by the Gaussian beam summation method[J]. Geophysics, 2010, 75(2): S81-S93 DOI:10.1190/1.3361651 |
| [17] | SEMTCHENOK N M, POPOV M M, VERDEL A R. Gaussian beam tomography[J]. Expanded Abstracts of 71st EAGE Annual Conference, 2009: U032 |
| [18] | VERDEL A R, SEMTCHENOK N M, POPOV M M, et al. Non-linear Gaussian beam tomography-a new method capable of determining highly complex velocity models[J]. Expanded Abstracts of 73rd EAGE Annual Conference, 2011: P141 |
| [19] | LI H, WANG H Z. An effective tomography algorithm with Gaussian beam[J]. CPS/SEG International Conference, 2014: 701-704 |
| [20] |
邵荣峰, 方伍宝, 蔡杰雄, 等. 高斯束层析偏移速度建模方法及应用[J].
石油物探, 2016, 55(1): 91-99 SHAO R F, FANG W B, CAI J X, et al. A method of migration velocity analysis based on Gaussian beam tomography and its application[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 91-99 |
| [21] |
刘玉柱, 董良国, 李培明, 等. 初至波菲涅尔体地震层析成像[J].
地球物理学报, 2009, 52(9): 2310-2320 LIU Y Z, DONG L G, LI P M, et al. Fresnel volume tomography based on the first arrival of the seismic wave[J]. Chinese Journal of Geophysics, 2009, 52(9): 2310-2320 |
| [22] | ČERVENÝV, KLIMESL. Paraxial ray approximations in the computation of seismic wavefields in inhomogeneous media[J]. Geophysical Journal Royal Astronomical Society, 1984, 79(1): 89-104 |
| [23] | ČERVENÝV. Seismic ray theory[M]. Cambridge: Cambridge University Press, 2001: 189-192. |
| [24] | HUBRAL P, SCHLEICHER J, TYGEL M, et al. Determination of Fresnel zones from traveltime measurements[J]. Geophysics, 1993, 58(5): 703-712 DOI:10.1190/1.1443454 |
| [25] | SCHLEICHER J, HUBRAL P, TYGEL M, et al. Minimum apertures and Fresnel zones in migration and demigration[J]. Geophysics, 1997, 62(1): 183-194 DOI:10.1190/1.1444118 |
| [26] | ČERVENÝV, SOARESJ E P. Fresnel volume ray tracing[J]. Geophysics, 1992, 57(7): 902-915 |
| [27] | WOODWARD M J, NICHOLS D, ZDRAVEVA O, et al. A decade of tomography[J]. Geophysics, 2008, 73(3): E5-E11 |
| [28] | PAIGE C C, SAUNDERS M A. LSQR:an algorithm for sparse linear equations and least squares problems[J]. Association for Computing Machinery Transactions on Mathematical Software, 1982, 8(1): 43-71 DOI:10.1145/355984.355989 |



 ,
,