2. 中国科学院油气资源研究重点实验室, 北京 100029
2. Key Laboratory of Petroleum Resources Research, Chinese Academy of Sciences, Beijing 100029, China
全波形反演最初由LAILLY[1]和TARANTOLA[2]等人提出, 他们以波动方程为基础, 建立模拟数据和观测数据差值的目标函数, 通过使其最小化来获得模型的更新量, 其模型更新量由梯度和搜索步长决定, 梯度可由入射波场和残差反传的波场计算得到。目前已经发展出了多种全波形反演(FWI) 方法, 按照不同求解波动方程的计算域, 大致可分为时间域反演[3-8]、频率域反演[9-11]和Laplace域反演[12-13]。按照求解方式不同又可分为局部梯度类迭代反演[2-3, 14-15]和全局优化搜索反演[16-19]等。
无论是时间域、频率域还是Laplace域, 巨大的计算量是FWI瓶颈之一。近年来高性能计算技术的发展使这一问题得以缓解。高性能计算的主要发展思路是并行计算。相对于CPU而言, GPU的多线程、多处理器的并行结构更能够满足高性能计算的发展需要[20], 而且在相同计算能力的情况下, GPU具有功耗小、价格低等特点。在GPU中, 用来进行数据处理的晶体管占据大部分空间, 只有少量晶体管用来进行指令流控制和数据缓存[21]。利用GPU进行密集型科学计算是一种潜力巨大且性价比高的解决方案[22]。
由于GPU具有对密集型计算任务加速的优势, 因此GPU技术被广泛应用于正演模拟、叠前偏移、逆时偏移、多次波压制以及全波形反演等地震数据处理。MICIKEVICIUS[23]用GPU实现了三维有限差分法计算, 并提出了单通法和双通法两种优化策略, 也是目前常用的程序优化方法。WANG等[24]研究了基于随机边界条件的GPU加速时间域全波形反演算法, LUO等[25]实现了多GPU的两级并行的全波形反演, MAO等[26]利用GPU加速实现了二维多尺度时间域全波形反演。KIM等[27-28]利用GPU加速实现了三维声波混合域全波形反演的快速计算。SHIN等[29]实现了单GPU的三维Laplace域的全波形反演, GOKHBERG等[30]用谱元法在CPU/GPU异构集群实现了全波形反演, 张猛[31]对CPU/GPU平台上全波形反演的各种实用问题进行了分析。LIU等[32]实现了三维混合域全波形反演, 但其宽度较窄。YANG等[33]在GPU平台上实现了二维时间域的全波形反演。由于GPU的显存限制, 以往的研究多是针对二维或者小规模的三维全波形反演, 为克服这一限制, 本文采用多GPU动态加载并行方案, 针对不同大小的数据采用不同的并行方案, 当计算数据过大时, 采用区域分解的方法, 从而可以实现大规模三维全波形反演; 采用简化的混合域全波形反演, 能够更快速的计算从以往的单GPU加速到现在的多GPU加速; 最后利用Overthrust模型测试了本文方法的可行性和有效性。
1 GPU架构及程序优化 1.1 GPU架构GPU体系架构如图 1所示。
|
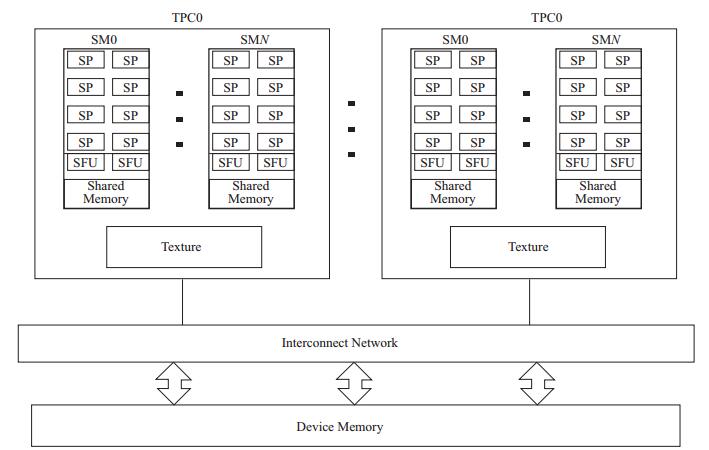
图 1 GPU运算单元结构[21] |
首先从硬件架构上对GPU进行并行层次分析。GPU主要由两部分组成, 一部分是流处理器阵列, 另一部分是存储器系统, 两部分连接在同一片板卡上。如图 1所示, 其中多个线程处理器群(Thread Processing Cluster, TPC) 组成了一个流处理器阵列, 其中每个TPC中有2~3个流多处理器(Streaming Multiprocessor, SM), 每个流多处理器中包含8个流处理器(Streaming Processor, SP)[34]。在GPU中最基本单元是SP, SP是由算术逻辑运算器、加法器、乘法器以及寄存控制器组成。SP可以在一个时钟周期内完成一次逻辑运算, 或一次32位浮点数加法或乘法运算等。从硬件架构上看, 一个流多处理器相当于一个8路单指令多数据流(Single Instruction Multiple Data) 处理器, 称之为单指令流多线程(Single Instruction Multiple Thread, SIMT)[21]。
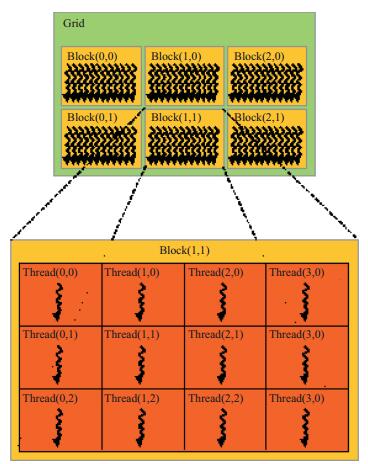
图 2为统一计算设备架构(Compute Unified Device Architecture, CUDA) 编程模式示意图, 可以看出, 核函数将线程划分为网格(Grid) 形式, 每个网格又被分成无数个线程块(Block), 一定数量的线程(Thread) 组成(一般不超过1024个线程) 一个线程块。ThreadIdx和BlockIdx是用来标明线程号和线程块号的CUDA内置变量。在核函数中每个线程都有一个唯一的偏移量, 偏移量可以通过线程号、线程块号以及线程维度信息计算得到。在一维情况下偏移量等于线程号即为ThreadIdx.x; 在二维情况下且Block大小为(Bx, By) 的时, 计算线程偏移量公式为ThreadIdx.x+ThreadIdx.y×Bx; 而在Block大小为(Bx, By, Bz) 的三维情况下, 线程偏移量计算公式为ThreadIdx.x+ThreadIdx.y×Bx+ThreadIdz.z×By×Bz。在同一个网格下的不同线程块中线程不能进行通讯, 意味着不同线程块中线程无法进行数据传输, 它们完全并行且独立执行。
|
图 2 CUDA编程模式[21] |
与CPU相比, GPU在计算能力和存储器带宽上有显著优势, 面对相同量计算任务, GPU所需要的硬件成本和计算功耗都低于CPU, 因此, GPU是大规模高性能计算的明智选择。
CUDA的出现使得基于GPU的通用计算(GeneralPurpose GPU, GPGPU) 得到了高速发展。现阶段GPU的浮点运算能力已经达到每秒数十万亿次级别, 是X86处理器计算能力的数十倍。但是要发挥GPU巨大的计算优势, 就需要对程序进行一定的优化, 未经优化的程序反而会降低程序的计算效率。
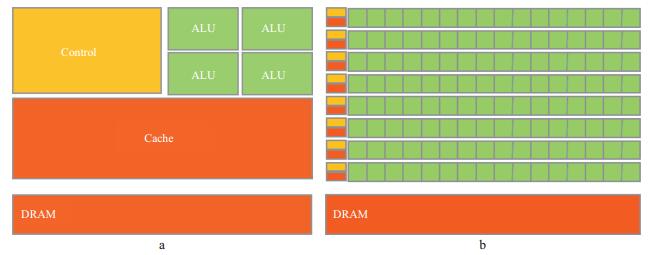
图 3对比了CPU和GPU的微观硬件架构, 可以看出CPU和GPU计算能力差异巨大的原因。图中ALU (Arithmetic Logic Unit, 算术逻辑单元) 是计算单元, CPU只具有很少的ALU, 而GPU则具有大量的ALU; CPU具有大量的数据缓存和逻辑控制单元, 而GPU的数据缓存和逻辑控制单元较少, 这就导致GPU的计算能力要远远高于CPU的计算能力, 但数据读取以及逻辑运算能力较差, 因此GPU非常适合处理计算密集型和并行度较高的计算问题。在FWI中, 波场的正传、反传以及梯度计算的计算量所占比例最大。本文的波场正传和反传均采用时间域有限差分算法, 有限差分算法中, 每个点都是离散的, 其计算是独立的, 可以同时进行, 因此GPU非常适合这种细粒度并行计算。根据计算阶数的不同需要不同个数的邻近网格点上一个时刻的值, 因此在计算时需要采用共享内存方式存储邻近网格点的数值, 隐藏访存延迟。GPU高性能计算用于地震波有限差分数值模拟能大大提高计算速度, 并且具有更小的能耗。梯度的计算也每个点独立计算, 不涉及和其它网格点的数据交换, 属于细粒度的并行, 因此采用GPU同样能提高梯度的计算效率。如何根据FWI的求解区域分配计算任务、如何传输数据以及如何发挥GPU的最优计算性能都需要根据硬件信息以及算法进行优化, 其中包括线程块的大小、多GPU之间的数据传输、共享内存的使用等。
|
图 3 CPU的微观架构(a) 和GPU的微观架构(b) 对比 |
在GPU中最基本的执行单元是线程, 其次是线程块, 每个线程块的大小影响着计算性能, 线程块中的每一个线程被发送到一个SP上。每个SM上有8个SP, 每个SM最多可以同时执行8个线程块。SM最多能执行的线程数量和线程能使用的资源相互矛盾, 一个SM里同时执行的线程越多, 就越能隐藏线程访存延迟, 这样每个线程能使用的资源相对就越少, 因此需要选取适当的线程块大小, 使两者平衡, 从而得到最优的执行效率。不同的硬件拥有的计算资源不一样, 为充分利用硬件资源需要进行测试分析。
本文采用12阶规则网格有限差分法进行波场正传和反传计算。为此, 我们使用NVIDIA Tesla K20m GPU对此算法进行了测试分析。三维模型大小256×256×256, 网格间距10m。
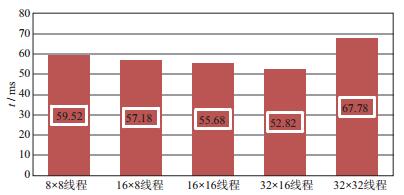
图 4中横坐标表示线程块大小, 纵坐标表示某一个时刻的计算时间(ms), 从图中可以看出, 刚开始随着线程块大小的增加, 计算时间逐渐减少, 这是因为每个SM上执行的线程数量随着线程块大小的增加而增加; 当线程块中的线程数量增加到32×32时, 计算时间反而急剧增加, 这是因为过大的线程块增加了寄存器的使用数量, 使得能同时计算的线程块数量减少, 同时执行的线程数量也减少所致。综合考虑线程块大小及其使用资源数量, 我们进行12阶交错网格有限差分计算时采用的线程块大小为32×16。
|
图 4 不同线程块计算时间对比 |
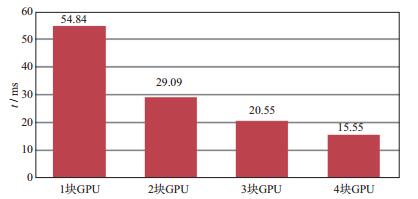
当计算的数据体十分巨大时, 单个GPU显存无法满足计算需求, 需采用多GPU并行方案将数据进行区域分解, 每个GPU运算一个区域。这样不仅能克服单个GPU显存较小的问题, 同时由于多个GPU并行计算, 提高了计算效率, 减少了计算耗时。我们以规则网格12阶有限差分进行测试, 网格大小256×256×256, 网格间距10m。
图 5中横坐标代表GPU数量, 纵坐标代表计算一个时刻波场的计算耗时, 从图中可以看出, 随着GPU的增多, 计算时间成线性减少, 理想情况下应该成倍数减少, 但是由于区域分解后需要对分解后的数据进行扩边用来交换数据, 保证数据的一致性; 同时由于各个GPU之间也需要进行数据交换, 增加了计算耗时, 因此无法达到理想的情况。
|
图 5 多GPU计算性能对比 |
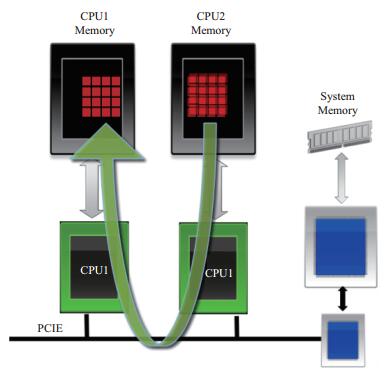
利用多GPU进行有限差分计算时, 计算边界处需要进行数据交换, 数据交换分为两种:一种是数据传输到CPU端, 再从CPU端传输到另一块GPU端; 第二种是2块GPU在一条PCIE线上时, 可以直接利用对等网络(peer-to-peer, P2P) 技术进行数据交换(图 6), 不需要经过CPU, 大大减少了传输时间。利用P2P技术传输4GB大小数据, 所耗时间为0.11s, 不使用P2P技术时的传输时间为0.28s, 可以看出P2P技术大大提高了传输速度, 特别是针对多GPU全波形反演时频繁的数据交换情况。
|
图 6 P2P技术原理 |
在使用GPU时, 需要将数据传输到GPU上, 有两种方法提高传输效率, 一是使用锁页内存(其存放的数据传输到GPU不需要CPU干涉) 提高传输速度; 第二种方法是改进硬件条件, 如最新Nvlink技术的传输速度达到80GB/s, 是现有PCIE3.0技术传输速度的4倍以上。本文主要是在程序上进行方法的改进, 因此采用锁页内存方式提高数据的传输效率。经过测试, 使用锁页内存传输4GB大小的数据用时0.13s, 而不使用锁页内存传输同样大小的数据, 则需要0.17s。
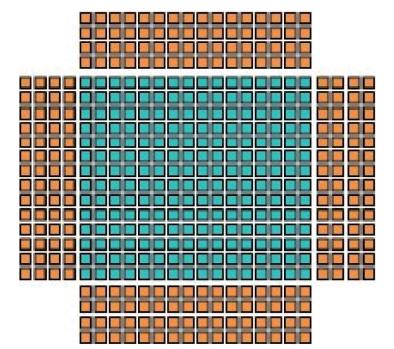
前文谈到, 在进行12阶规则网格的有限差分计算时, 需要读取网格点邻近点上一时刻的波场, 而且需要重复读取。为了避免每次计算都需要单独读取波场值, 我们采用共享内存的方式加以解决。计算时, 直接在开辟的共享内存区域重复进行高速访存, 这样很大程度上提高了有限差分法的计算效率。图 7为共享内存示意图, 其中蓝色部分是需要计算的点, 黄色部分是边界上需要多余读取的数据点。由图可知共享内存实际存储的数据要比计算数据大, 以12阶规则网格为例, 实际存储的数据大小为12nx+12ny+ny×nx, 其中nx为计算区域x方向的网格点数, ny为y方向的网格点数。测试发现, 使用共享内存比未使用共享内存的程序加速比高2.6倍。
|
图 7 共享内存示意 |
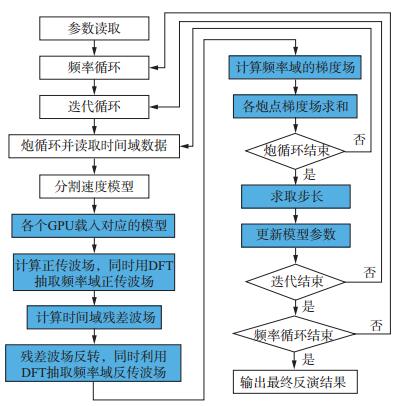
对于三维全波形反演, 频率域FWI的正传和反传均需要存储巨大的阻抗矩阵, 而时间域FWI梯度计算太复杂[35]。因此, 本文基于混合域思想对其进行简化。简化的方法是将波场的正传和反传都放到时间域求取, 利用离散傅里叶变换(DFT) 抽取相应波场的频率成分, 在频率域求取残差, 再用离散傅里叶反变换(IDFT) 将频率域残差返回时间域进行反传; 然后将反传时间域波场再次用DFT转换到频率域波场, 在频率域求取梯度场。为了方便GPU实现, 简化的频率域方法直接在时间域进行残差计算, 然后将残差波场反传并用DFT转换到频率域, 在频率域求取梯度。简化的混合域全波形反演流程如图 8所示。
|
图 8 简化的混合域全波形反演流程 |
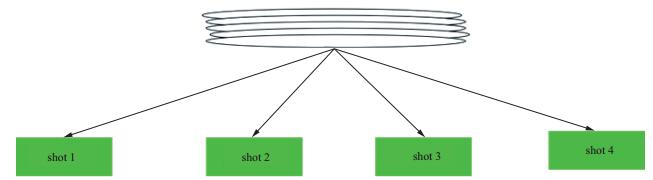
图 8中蓝色部分是利用GPU实现的, 需要注意的是对于单个节点来说数据加载是动态的, 根据计算数据的大小和现有计算资源动态选取并行方案。在炮循环之前, 程序会读取各个节点的硬件信息, 主要是GPU的个数和单个GPU的显存大小, 当需要计算的数据小于GPU的显存时, 采用一个GPU计算一炮地震数据, 如图 9所示。
|
图 9 单GPU未进行区域分解 |
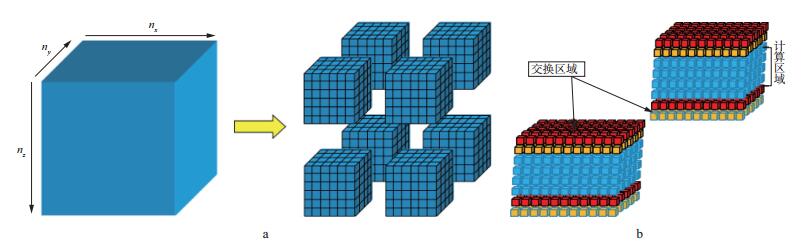
当需要计算的数据大于单个GPU的显存时, 系统会根据实际需要的显存数量以及GPU个数动态地将数据进行区域分解, 以获得最佳的计算性能, 这时每个GPU将计算一小块反演区域的数据, 如图 10a所示(本文指定z方向划分)。
|
图 10 多GPU区域分解(a) 和交换区域增加(b) |
同时由于整个反演区域分解成数个小的反演区域, 那么区域边界处就需要进行数据交换, 以保证数据的一致性, 这样在小数据的边界处增加了交换区域, 见图 10b。
GPU实现程序伪代码如下:
读取各个节点的硬件信息;
if (小于单个GPU内存)
{for (炮循环)
根据节点数以及GPU个数信息MPI向各节点发送多少炮数据;
for (单GPU需要计算的炮数循环)
为每个GPU动态发送炮数据
for (时间循环)
每个GPU同时计算一炮数据
}
else (大于单个GPU内存)
{for (炮循环){
根据节点数以及GPU个数信息MPI向各节点发送多少炮数据;
并将每个节点上单炮数据进行区域分解, 载入对应的GPU
for (时间循环)
每个GPU计算一小块炮数据
}}
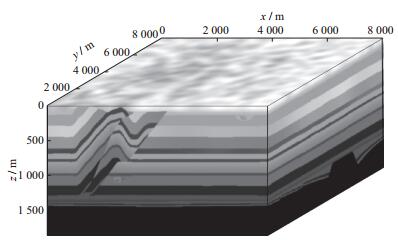
3 模型测试我们利用SEG的Overthrust模型(图 11) 对本文方法进行了测试, 网格大小801×801×187, 网格间距均为10m。地表放炮, 共100炮, 炮间距40m, x方向和y方向各10炮, 第一炮位置位于x=3800m, y=380m处。使用主频为35Hz的零相位雷克子波, 采集系统是地表全接收。时间采样率2ms, 采样点数为2000。共正演地震数据478GB。反演频率从1.5Hz开始, 每次增加1.5Hz, 2个频率组成一个频率组, 最大频率60Hz。由于计算数据太大, 这里动态分配为4个GPU进行处理。
|
图 11 Overthrust真实模型 |
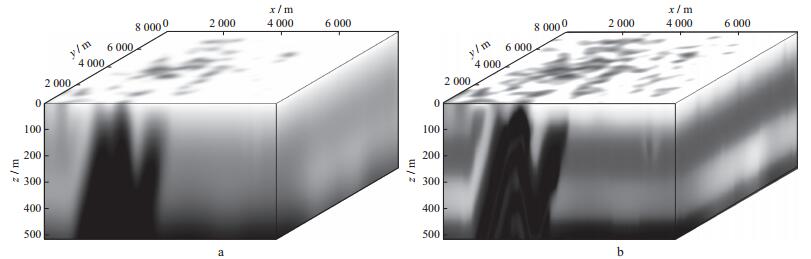
根据节点信息, 程序首先将初始模型数据分解成4个小数据体, 每个数据体大小如图 12a所示, 每个GPU负责一个小数据体的计算, 其反演结果见图 12b, 可以看出反演结果和真实模型(图 11) 能相互对应, 在反演结果中能清楚地识别断层之间褶皱成因的背斜。图 13a和图 13b分别为初始模型和反演结果在x=4000m, y=4000m, z=400m处的切片。由图 13a可以看出, 河道信息比较模糊, 无法识别; 由图 13b可看出, 反演结果很好恢复出了河道信息, 能有效识别出逆断层, 虽然局部信息有差别, 但大体都恢复得很好。
|
图 12 使用4块GPU时, 初始模型数据分解成的小数据体(a) 及小数据体反演结果(b)(z方向上分解成的4个小数据体之一) |

|
图 13 使用4块GPU时, 初始模型(a) 和反演结果(b) 在x, y, z方向上的切片及其连片显示 |
采用4节点8核CPU与同样数量的GPU进行对比。在相同任务量(一次迭代计算) 的情况下, GPU耗时996s, 而CPU耗时14458s, 同样数量的GPU相对于CPU其程序加速比达到了14.5倍, 可见GPU在FWI的快速计算中具有明显优势。
4 结论简化混合域方法直接利用时间域数据来实现多尺度反演, 与以前的混合域方法相比, 流程每次迭代少了一次DFT和IDFT, 并且可以获得良好的反演效果。
GPU显存有限, 所以针对大规模三维混合域波形反演, 特别是叠前大数据的计算, 多GPU成为必然选择。在使用多GPU计算时需要对程序进一步优化, 才能发挥GPU的最优性能, 本文提出的多GPU动态并行方案具有良好的全波形反演结果并具有较好的加速性能, 为实现大规模FWI的实际应用提供一种可选择的计算方法和计算框架。
| [1] | LAILLY P.The seismic inverse problem as a sequence of before stack migrations[C]//BEDNAR J B.Conference on inverse scattering:theory and application.Philadelphia:SIAM, 1983:206-220 |
| [2] | TARANTOLA A, NERCESSIAN A, GAUTHIER O. Nonlinear inversion of seismic reflection data[J]. Geophysics, 1984, 49(2): 645-649 |
| [3] | BLEISTEIN N, COHEN J K, HAGIN F G. Two and one-half dimensional Born inversion with an arbitrary reference[J]. Geophysics, 1987, 52(1): 26-36 DOI:10.1190/1.1442238 |
| [4] | CRASE E, PICA A, NOBLE M, et al. Robust elastic nonlinear waveform inversion:application to real data[J]. Geophysics, 1990, 55(5): 527-538 DOI:10.1190/1.1442864 |
| [5] | KOLB P, COLLINO F, LAILLY P. Pre-stack inversion of a 1-D medium[J]. Proceedings of the IEEE, 1986, 74(3): 498-508 DOI:10.1109/PROC.1986.13490 |
| [6] | MARFURT K J. Accuracy of finite difference and finite element modeling of the scalar and elastic wave equation[J]. Geophysics, 1984, 49(5): 533-549 DOI:10.1190/1.1441689 |
| [7] | PICA A, DIET J P, TARANTOLA A. Nonlinear inversion of seismic reflection data in a laterally invariant medium[J]. International Journal of Science Education, 1990, 55(3): 284-292 |
| [8] | WANG B L, GAO J H. Fast full waveform inversion of multi-shot seismic data[J]. Expanded Abstracts of 80thAnnual Internat SEG Mtg, 2010: 4453-4459 |
| [9] | PRATT G, SHIN C, HICKS. Gauss-Newton and full Newton methods in frequency space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362 DOI:10.1046/j.1365-246X.1998.00498.x |
| [10] | SIRGUE L, PRATT R G. Efficient waveform inversion and imaging:a strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(1): 231-248 DOI:10.1190/1.1649391 |
| [11] | SONG Z M, WILLIAMSON P R, PRATT R G. Frequency-domain acoustic-wave modeling and inversion of crosshole data:part Ⅱ:inversion method, synthetic experiments and real-data results[J]. Geophysics, 1995, 60(S1): 796-809 |
| [12] | CHANGSOO S, HO C Y. Waveform inversion in the Laplace domain[J]. Geophysical Journal International, 2008, 173(3): 922-931 DOI:10.1111/gji.2008.173.issue-3 |
| [13] | HA W, SHIN C. Laplace-domain full-waveform inversion of seismic data lacking low-frequency information[J]. Geophysics, 2012, 77(5): R199-R206 DOI:10.1190/geo2011-0411.1 |
| [14] | GAUTHIER O, VIRIEUX J, TARANTOLA A. Two-dimensional nonlinear inversion of seismic waveforms:numerical results[J]. Geophysics, 1986, 51(7): 1387-1403 DOI:10.1190/1.1442188 |
| [15] | MORA P. Nonlinear two-dimensional elastic inversion of multioffset seismic data[J]. Geophysics, 1987, 52(9): 1211-1228 DOI:10.1190/1.1442384 |
| [16] | SEN M K, STOFFA P L. Global optimization methods in geophysical inversion[J]. Advances in Exploration Geophysics, 1995, 4: 269-277 DOI:10.1016/S0921-9366(06)80009-5 |
| [17] | SAMBRIDGE M, DRIJKONINGEN G. Genetic algorithms in seismic waveform inversion[J]. Geophysical Journal International, 1992, 109(2): 323-342 DOI:10.1111/gji.1992.109.issue-2 |
| [18] | JIN S, MADARIAGA R. Nonlinear velocity inversion by a two-step Monte Carlo method[J]. Geophysics, 1994, 59(4): 577-590 DOI:10.1190/1.1443618 |
| [19] | SEN M K, STOFFA P L. Nonlinear one-dimensional seismic waveform inversion using simulated annealing[J]. Geophysics, 1991, 56(10): 1624-1638 DOI:10.1190/1.1442973 |
| [20] |
赵改善. 地球物理高性能计算的新选择:GPU计算技术[J].
勘探地球物理进展, 2007, 30(5): 399-404 ZHAO G S. New alternative to geophysical high performance computing:GPU computing[J]. Progress in Exploration Geophysics, 2007, 30(5): 399-404 |
| [21] | KIRK D.NVIDIA CUDA software and GPU parallel computing architecture[OB/EL].http://kr.nvidia.com/content/cudazone/download/showcase/kr/Tutorial-DKIRK.pdf, 2007:103-104 |
| [22] |
李博, 刘国峰, 刘洪. 地震叠前时间偏移的一种图形处理器提速实现方法[J].
地球物理学报, 2009, 52(1): 245-252 LI B, LIU G F, LIU H. A method of using GPU to accelerate seismic pre-stack time migration[J]. Chinese Journal of Geophysics, 2009, 52(1): 245-252 |
| [23] | MICIKEVICIUS P. 3D finite difference computation on GPUs using CUDA[J]. The Workshop on General Purpose Processing on Graphics Processing Units, 2009: 79-84 |
| [24] | WANG B L, GAO J H, ZHANG H L, et al. CUDA-based acceleration of full waveform inversion on GPU[J]. Expanded Abstracts of 81stAnnual Internat SEG Mtg, 2011: 2528-2533 |
| [25] | LUO J R, GAO J H, WANG B L. Multi-GPU based two-level acceleration of full waveform inversion[J]. Journal of Seismic Exploration, 2012, 21(4): 377-394 |
| [26] | MAO J, WU R S, WANG B L. Multiscale full waveform inversion using GPU[J]. Expanded Abstracts of 82ndAnnual Internat SEG Mtg, 2012: 7-13 |
| [27] | KIM Y, SHIN C, CALANDRA H. 3D hybrid waveform inversion with GPU devices[J]. Expanded Abstracts of 82ndAnnual Internat SEG Mtg, 2012: 1-5 |
| [28] | KIM Y, SHIN C, CALANDRA H, et al. An algorithm for 3D acoustic time-Laplace-Fourier-domain hybrid full waveform inversion[J]. Geophysics, 2013, 78(4): R151-R166 DOI:10.1190/geo2012-0155.1 |
| [29] | SHIN J, HA W, JUN H, et al. 3D Laplace-domain full waveform inversion using a single GPU card[J]. Computers & Geosciences, 2014, 67(1): 1-13 |
| [30] | GOKHBERG A, FICHTNER A. Full-waveform inversion on heterogeneous HPC systems[J]. Computers & Geosciences, 2016, 89(3): 260-268 |
| [31] |
张猛, 王华忠, 任浩然, 等. 基于CPU/GPU异构平台的全波形反演及其实用化分析[J].
石油物探, 2014, 53(4): 461-467 ZHANG M, WANG H Z, REN H R, et al. Full waveform inversion on the CPU/GPU heterogeneous platform and its application analysis[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 461-467 |
| [32] | LIU L, DING R, LIU H, et al. 3D hybrid-domain full waveform inversion on GPU[J]. Computers & Geosciences, 2015, 83(1): 27-36 |
| [33] | YANG P L, GAO J H, WANG B L. A graphics processing unit implementation of time-domain full-waveform inversion[J]. Geophysics, 2015, 80(3): F31-F39 DOI:10.1190/geo2014-0283.1 |
| [34] |
王泽寰, 王鹏. GPU并行计算编程技术介绍[J].
科研信息化技术与应用, 2013, 4(1): 81-87 WANG Z H, WANG P. Introduction to GPU parallel programming technology[J]. E-Scinence Technology & Application, 2013, 4(1): 81-87 |
| [35] | VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26 DOI:10.1190/1.3238367 |



 ,
,