全波形反演(FWI) 直接基于波动方程, 以模型正演与观测地震波形一致为依据, 可高精度反演速度、密度、波阻抗和Q值等岩性参数[1-2]。目前, 全波形反演精细速度建模已开始应用于油气勘探地震资料成像中[3-5], 但大规模工业化应用仍面临诸多挑战。
局部极小值是FWI这类非线性反演的固有难题, 为此, 学者们提出了许多提高FWI目标函数线性度的方法[6-9]。海量计算是FWI的另一个难题, 尤其是3D FWI, 其计算开销是常规逆时偏移的数倍乃至数十倍, 因此基于GPU集群的高性能计算技术受到广泛的重视[10-11]。
3D FWI高性能计算方案的核心是实现单炮反演梯度的高效计算和多炮作业间的稳健并行管理。FWI的梯度计算需要震源波场和检波点波场同时刻相关, 类似于完成一次逆时偏移(RTM)[12-13], 因此可借鉴RTM的不同实现方法, 包括:完全保存震源波场的完全存储法; 优选有限波场时间切片用于反传重建震源波场的监测点方法[14-15]; 保存所有时刻边界波场值以反传重建震源波场的有效边界法[16]; 引入随机边界, 保存最后两个时刻的随机波场以实现震源波场重建的随机边界法[17]。一般来说, GPU存储空间相对有限, 难以满足完全存储法和监测点方法对波场存储的要求, 如果借助主机端内存或硬盘来保存, 则会增加GPU端与CPU端的数据交换, 极大地牺牲GPU计算时间。有效边界方法在进行边界赋值时难以满足GPU合并访存要求, 会带来高延迟, 降低GPU计算效率。随机边界法只需要保存最后两个时刻的随机波场, 存储量小(当前的主流GPU显存已能满足存储需要), 且随机波场的载入很容易满足GPU合并访存要求, 能充分发挥GPU的高效计算能力。
FWI多炮并行作业管理的常用方案是消息传递接口(message passing interface, MPI)[10], 利用MPI提供的消息通信接口, 将并行集群中参与计算的诸多节点纳入统一的通信域中, 节点间通过消息传递实现数据交换、同步、互斥等协同工作。基于MPI的节点间并行实现在编程上更简洁直观, 有助于减轻开发人员的工作强度, 但是其缺点是[18]:对于大规模节点共同参与的并行作业一旦某一个节点宕机则会导致整个作业终止。此外, 由于节点间通信会导致网络阻塞, 并行节点规模越大, MPI并行加速比越低。
本文首先简单回顾时间域FWI的基本理论; 然后介绍为提高梯度计算效率, 采用随机边界实现震源波场高效重建的方法; 接着重点介绍为克服MPI多节点并行作业管理的缺点, 基于共享存储空间和文件锁技术的“作业池”机制的设计与实现; 最后用三维SEG/EAGE推覆体模型进行数值测试, 验证所提出的方法技术的正确性。
1 方法原理全波形反演每次迭代都需要若干次地震波场模拟, 为便于处理介质的非均匀性, 使用如下声波方程[19]:
| $ \frac{1}{{\rho \left( x \right){v^2}\left( x \right)}}\frac{{{\partial ^2}p\left( {x, t} \right)}}{{\partial {t^2}}} = \nabla \cdot[\frac{1}{{\rho \left( x \right)}}\nabla p\left( {x, t} \right)] + s\left( {{x_s}, t} \right){\rm{ }}\;\;x \in {R^3} $ | (1) |
式中:R3表示三维实空间; p(x, t) 为波场值; ρ(x) 和v(x) 分别为地下介质密度和速度; xs为炮点坐标; s(xs, t) 为震源函数。定义p(xr, t; xs) 为给定模型的数值模拟波场值, d(xr, t; xs) 为实际地震记录, 波场残差δp(xr, t; xs)=p(xr, t; xs)-d(xr, t; xs), 其中, xr为检波点坐标。则反演的目标函数可表示为:
| $ S\left( v \right) = \frac{1}{2}\sum\limits_s {\sum\limits_t {\sum\limits_t {\delta {p^2}} } } ({x_{\rm{r}}}, t;{x_{\rm{s}}}) $ | (2) |
全波形反演就是寻求目标函数S(v) 的极小值, 满足目标函数极小值的速度即为反演的最终速度。由Born近似理论及伴随方法[4-5]可推导出目标函数S(v) 对速度v的导数为:
| $ g(x) = \frac{2}{{{v^3}(x)}}\sum\limits_s {\sum\limits_t {\sum\limits_t \lambda } } (x, t;{x_{\rm{r}}})\frac{{{\partial ^2}p\left( {x, t;{x_{\rm{s}}}} \right)}}{{\partial {t^2}}} $ | (3) |
其中, λ(x, t; xr) 为波场残差反传波场, 满足:
| $ \frac{1}{{\rho \left( x \right){v^2}\left( x \right)}}\frac{{{\partial ^2}\lambda \left( {x, t;{x_{\rm{r}}}} \right)}}{{\partial {t^2}}} = \nabla \cdot[\frac{1}{{\rho \left( x \right)}}\nabla \lambda \left( {x, t;{x_r}} \right)] + \delta p({x_r}, t;{x_s}) $ | (4) |
此反传波场方程称为伴随方程, 它以波场残差作为震源。
1.1 反演梯度的高效计算为了在GPU/CPU异构的高性能计算平台上实现3D FWI梯度计算并得到很高的计算效率, 我们将CLAPP提出的随机边界条件[17]与GPU加速相结合, 高效重建震源波场。随机边界能够保存波场能量, 同时又打破波前面的相干性, 利用该特性可以重建震源波场, 并且进一步将其与检波点波场同时刻相关, 得到反演梯度。与有效边界存储法和监测点方法相比, 这种方法存储量小、计算效率高。
在边界区域设置随机变化的速度场构成随机边界条件:
| $ v({x_{\rm{b}}}) = {v_0}({x_{\rm{b}}}) + [{\rm{Ran}}({S_{{\rm{seed}}}})-0.5] \times {F_{{\rm{taperr}}}}\left( {\frac{r}{R}} \right) \times \alpha $ | (5) |
式中:α为与速度有关的量, 与速度有相同的量纲; R代表随机边界区域的厚度; r代表随机边界区域中的点距边界的距离; Ftaper∈(0, 1) 为一平滑窗函数; Ran (Sseed) 代表由种子数Sseed产生的随机数, Ran (Sseed)∈(0, 1);xb代表随机边界中的点; v(xb) 代表随机边界中的点xb处的随机速度值; v0(xb) 代表随机边界上r=0处的速度值, 由它产生随机边界中各点的随机速度值。通过调节α和R可以得到合适的随机边界。
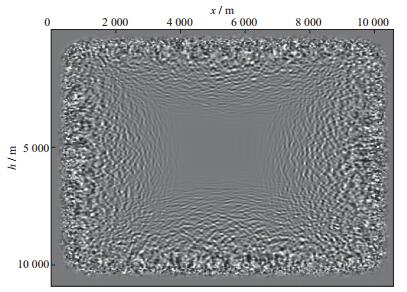
以速度为2500m/s的均匀介质为例, 如图 1所示, 在模型边界处设置50个网格层的随机边界(网格间隔为20m), R=50, v0=2500m/s, α=1000m/s。设置震源在介质中心位置, 先正传波场到随机边界上, 波场会被边界处的随机介质散射打乱, 再将打散的地震波场反传, 即可重建任一过去时刻的震源波场。图 2给出了某一时刻的反传重建波场快照, 可见波场呈现散乱的随机状, 说明边界处介质的随机性设置得较适当。

|
图 1 随机边界 |
|
图 2 利用随机边界重建震源波场 |
随机边界反传重建波场在效率和存储方面具有明显优势, 但也有不足之处:重建波场中的低频成分会有损失, 不过仍能满足成像精度的需要, 前人的工作证明了这一点[17]。
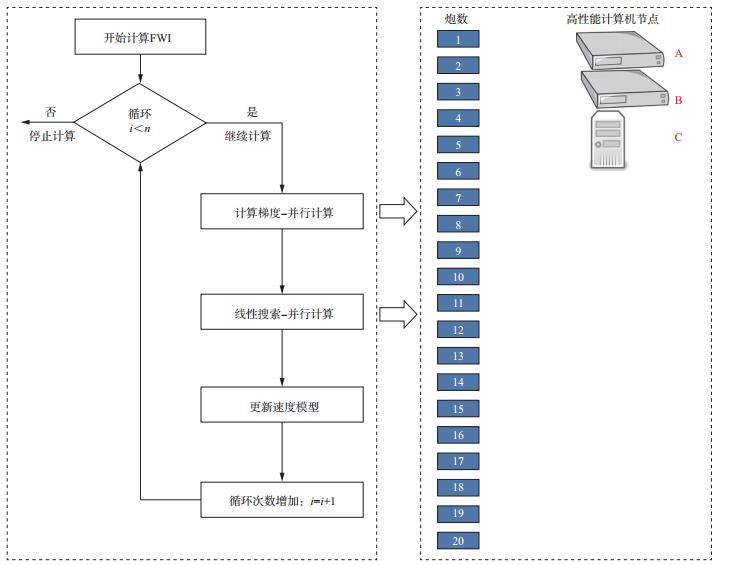
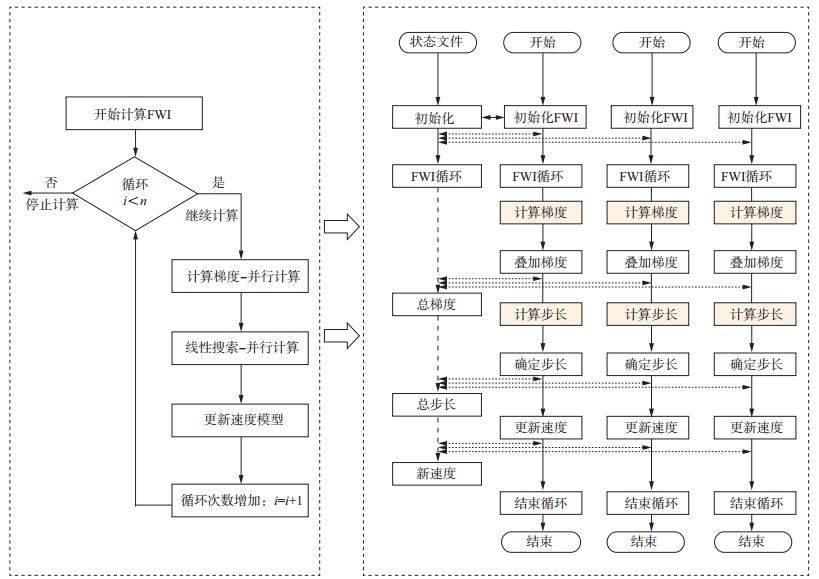
1.2 大规模并行作业管理机制全波形反演的每次迭代计算包含计算梯度、线性搜索、更新速度模型等步骤, 而计算梯度、线性搜索等过程的实现(图 3), 需要进行大量炮点的地震波场模拟[20]。3D FWI需要大型计算机集群并行运算, 如何实现灵活、稳健和高效的全波形反演的大规模并行作业管理, 是实现产业化全波形反演技术的一大难点。
|
图 3 全波形反演流程 |
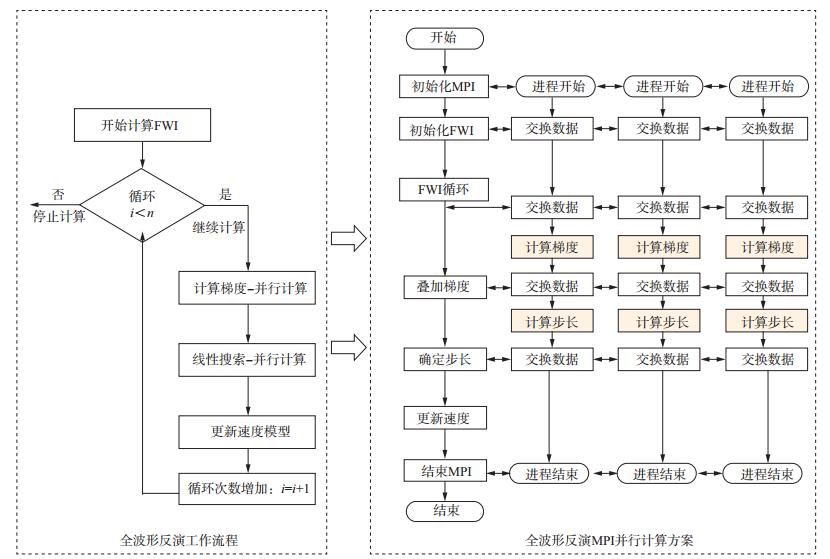
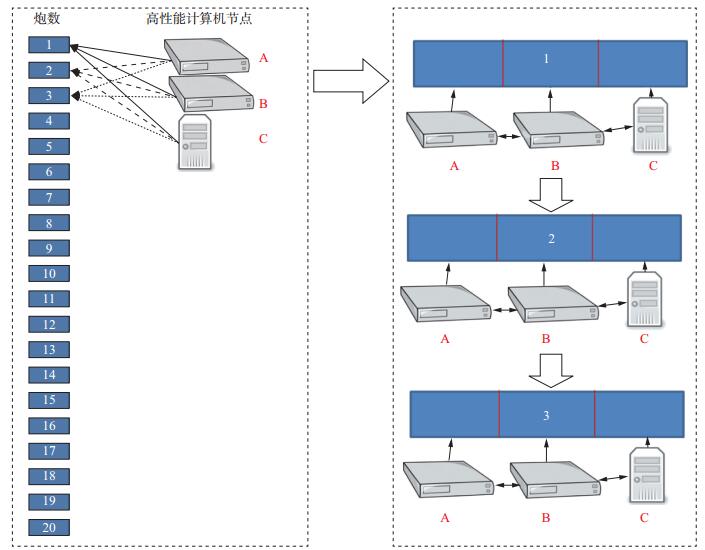
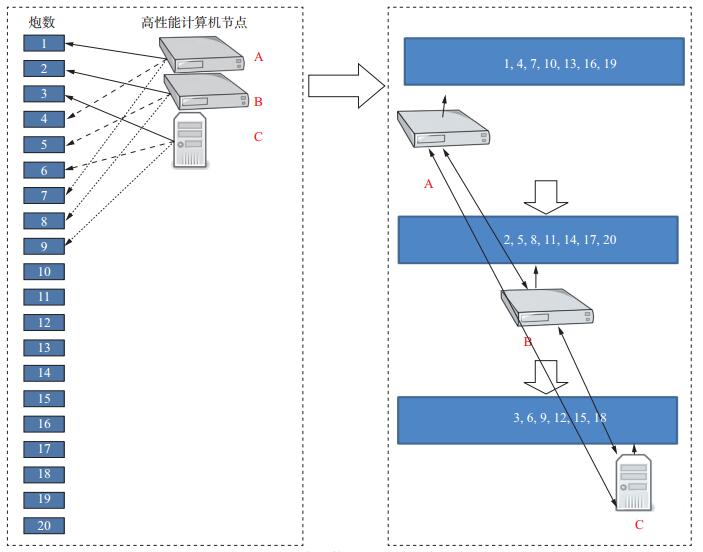
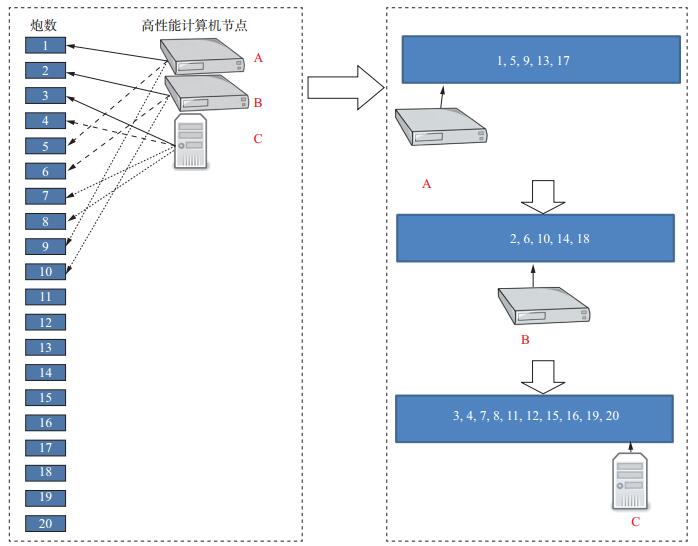
目前已公开的全波形反演并行作业管理方案, 都是采用MPI技术实现(图 4), 参与计算的节点之间通过MPI互相关联在一个通信域中, 节点之间通过网络通讯交换数据。MPI编程有两个固有缺点:①不支持计算节点的动态增减; ②任何一个计算节点如出现故障, 则整个通信域中的节点都会停止作业。基于MPI的FWI并行计算实现方法通常有3种(为便于说明, 这里以20炮为例, 数字1~20分别表示1~20炮地震数据, A, B, C分别表示参与计算的GPU/CPU异构集群节点, 假定A和B的计算效率相同, C的计算效率是A或B的两倍, 以下讨论的并行作业管理是关于节点间或进程间的, 因此, 对于单纯的CPU集群同样适用)。第1种是基于单炮区域分解的MPI并行实现方法。如图 5所示(图中编号1~20表示炮号, 大箭头仅表示计算顺序, 无输入、输出的依赖关系), 该方法依次计算炮1, 2, 3, …, 20, 并在计算每一炮的过程中, 把该炮计算区域按参与计算的节点数(或进程数) 分解, 所有节点都将参与每一炮的计算, 在计算过程中, 所有计算节点(或进程) 需要在每一个计算时刻点同步, 并相互交换边界重叠区域的计算结果。其优点是:多节点协作能够克服单个计算节点内存不足的问题。其缺点是:①计算效率高的节点(或进程) 总是在每一个时刻点等待计算效率低的节点, 导致整体并行计算效率下降; ②节点之间需要在每个时刻交换数据, 因而该方法受计算节点之间网络带宽限制。第2种是基于均分炮数的MPI并行实现方法。如图 6所示, 20炮被尽可能均匀地分配到每一个计算节点上, 每一个计算节点负责一部分炮的计算。其优点是:计算节点之间无需交换数据, 不受网络带宽的限制。其缺点是:计算效率高的节点要等待计算效率最低的节点, 导致整体并行计算效率下降。第3种方法是基于主从编程模型, 存在一个主节点负责并行作业的调度和管理, 从节点通过与主节点通信来获取计算任务。其优点是:可以充分利用计算节点的计算能力, 保证能者多劳。其缺点是:海量节点的大规模并行计算会出现通信拥堵, 因为太多的从节点会在同一时刻要求与主节点通信, 会对网络带来极大压力, 使得通信成本太高, 计算效率无法随着节点数的增加而线性提高。除了3种基本实现方法, 还可以将3种方法相互组合形成混合式的并行作业管理方案, 在此不再一一赘述。
|
图 4 全波形反演MPI并行计算实现过程 |
|
图 5 基于单炮区域分解的MPI并行实现方法 |
|
图 6 基于均分炮数的MPI并行实现方法 |
综上所述, 在FWI技术实现中, 采用基于MPI的并行作业管理方案存在诸多不足:①不支持计算节点的动态增加和减少, 缺乏灵活性, 难以适应实际生产作业中的需求变动; ②稳定性差, 采用MPI技术时, 即使节点之间不发生数据交换, 也相互关联, 一旦某个节点出现硬件故障, 整个计算立即失败; ③对异构设备适应性差, 异构的计算机集群各节点间效率不一致, 采用MPI并行实现会导致整体计算效率将被最慢的节点拖累; ④硬件成本高, MPI并行实现对计算机集群节点之间的网络速度和稳定性要求很高, 迫使人们采用Infiniband以及其它较昂贵的设备来提高网络通信效率和稳定性; ⑤大规模并行计算效率低下, MPI技术的并行效率随计算机节点数增加而降低(尤其当节点数达到几十个以上时), 无法达到近似线性的加速比, MPI对计算效率提升的瓶颈作用就有体现。
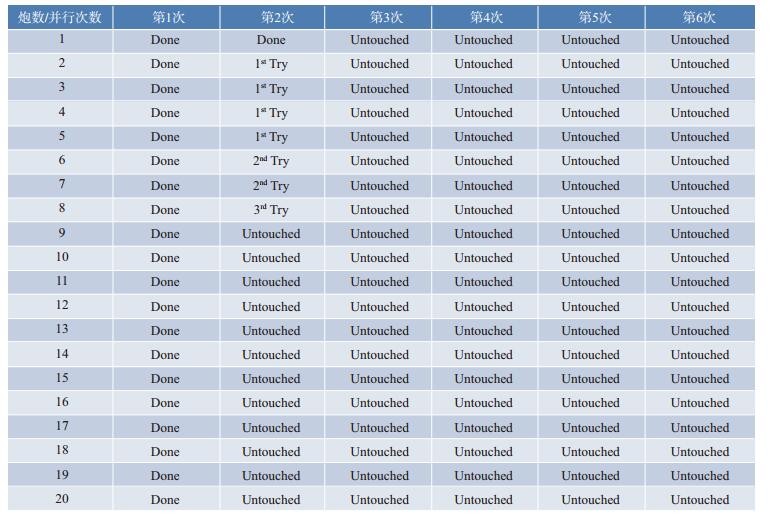
为克服全波形反演技术采用MPI并行实现中存在的以上不足, 我们研发了基于“作业池”的并行作业管理机制, 具有如下技术优势:并行计算节点的动态增减, 具备硬件容错能力, 支持异构设备, 对网络等硬件设施要求低, 并行计算效率随计算节点近似线性增加(这里“节点”可以是物理上的计算节点, 也可以是并行计算中的进程, 下同)。该方法对每一个全波形反演项目, 首先根据项目的具体情况产生一个作业状态文件, 如图 7所示, 用来记录每一次并行计算过程中每一炮的计算状态。这些计算状态分为:已经完成(Done)、没有被计算(Untouched)、有一个节点在计算(1st Try)、有两个节点在计算(2nd Try)、有3个节点在计算(3rd Try)……。在每一次并行计算过程中, 采用自动作业控制方法来实现“按需分配”计算机资源, 如图 8所示, 计算节点A, B, C在每次并行计算时, 会依次查看所有的炮(1~20), 如果本次并行中某炮还是Untouched状态, 该节点就启动对该炮的计算, 并把本次并行中该炮的状态更改为1st Try状态, 并且一旦计算完成, 就把该炮状态更改为Done状态。如果一个计算节点发现本次并行计算中没有任何一炮在Untouched状态, 就依次查看是否有1st Try状态的炮, 如果有, 该节点立即启动对该炮的计算, 并把本次并行中该炮的状态更改为2nd Try状态。依次类推, 直到所有炮都被计算完而且状态都为Done状态, 本次并行完成。在具体编程实现上, 为使不同节点对作业状态文件的操作不出现竞态条件问题(race condition), 我们需要对作业状态文件进行加锁处理(例如, 利用fcntl来锁文件)。基于自动作业控制的并行实现方法能够充分实现异构计算机集群的高效并行, 并且任何节点如果出现硬件故障(如死机), 都不会导致整个全波形反演项目中断。
|
图 7 并行作业状态控制文件 |
|
图 8 基于自动作业控制的并行实现方法 |
每个计算节点都是独立的主节点(主进程), 共用一个共享盘, 节点和节点之间没有直接通信, 节点与共享盘之间只有在控制点上有数据交换。在全波形反演计算过程中, 每个计算节点上都独立启动一个作业(主进程), 这些主进程会通过竞争的方式读写位于共享盘中的状态文件和共享数据体, 如图 9右边所示。所有主进程都能通过作业状态文件找到参与全波形反演计算的切入点, 修改作业状态文件。这种分布式并行计算节点之间没有紧密的依存关系, 因此在实际应用中具有如下优点:①支持硬件设备的动态增加和减少, 参与计算的节点可以动态增加和减少, 每个节点/进程都可以通过共享状态文件/数据来调节工作切入点; ②稳定性好, 由于计算机节点无相互关联, 在长时间的全波形反演计算中, 即使部分节点出现故障中断, 整个计算作业仍会继续; ③支持异构设备, 不同计算效率的节点能够根据状态文件自己调整计算量, 不会干预其它节点的计算; ④硬件成本低, 并行计算对系统的稳定性、网络通信等要求比较低, 因此可以使用低成本的硬件设备; ⑤并行计算效率不受节点数目影响, 由于没有节点间的网络通讯瓶颈, 增加节点不会带来额外的计算效率损失。
|
图 9 全波形反演分布式并行计算实现方法 |
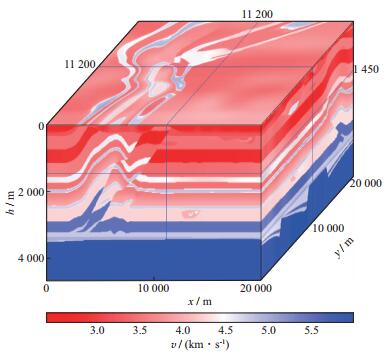
三维SEG/EAGE推覆体模型是检验三维全波形反演方法正确性的通用模型, 模型大小为20.00km×20.00km×4.65km, 速度范围为2200~6000m/s (图 10)。该模型模仿野外复杂地质构造, 主要由受构造运动影响拉张分裂的基岩和推覆于其上的沉积岩序列两部分构成。其顶界面为一不整合面。在此不整合面之上, 发育有12层连续沉积层序, 每层厚度设计尺度与野外实际观测相同, 沉积序列被其底部发育的岩体分开。推覆体模型的岩相及地层学特征模拟了区域张应力作用下的海相与构造混合沉积分布于某些沉积层位中的河道及裂缝。在此区域中, 所有封闭的圈闭均含有油气。
|
图 10 三维SEG/EAGE推覆体模型 |
推覆体模型构造复杂, 纵向层位多变并具有强烈的横向速度变化, 可以用来检验全波形反演方法的适应性和其对复杂构造的成像能力。断层的平面分布等构造现象可以考察全波形反演对构造细节刻画的能力。尤为重要的是, 中深层较小的含油气圈闭, 可以有效地反映全波形反演的高分辨能力以及储层刻画能力。
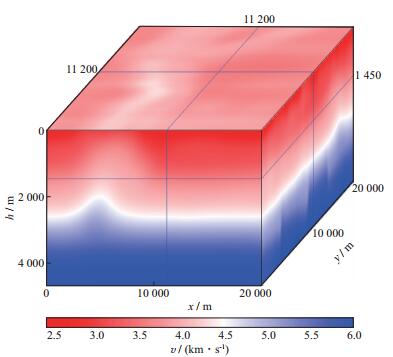
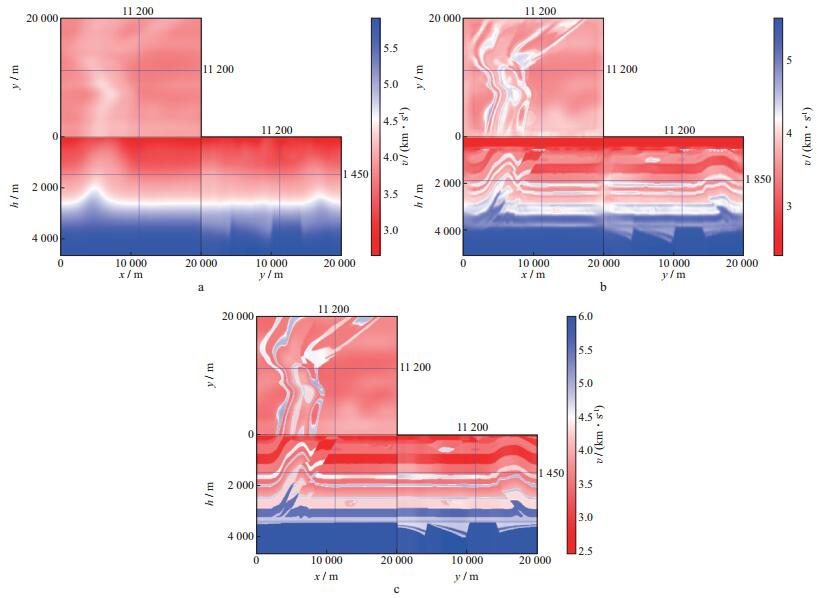
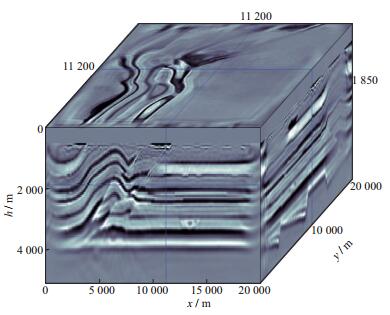
采用图 11所示的平滑模型作为反演的初始速度模型, 设置10000炮用于反演测试, 沿inline和xline等间隔分别布设100炮, 双边放炮, 最大偏移距8000m, 道间距40m, 反演前先对数据进行带通滤波, 滤波后主频为8Hz。计算平台是20个配有GPU M2090节点和28个配有GPU K20节点组成的GPU/CPU异构高性能计算机集群, 且集群节点的计算能力不同(主要体现在GPU卡M2090和K20之间的计算效率有差异), 集群节点的资源配置见表 1和表 2, 反演的计算规模和效率见表 3。作业池并行机制实现了节点间的解耦, 整个作业调度过程采用了竞争机制, 所有计算节点到“作业池”中抢任务, 直到所有任务完成为止, 相比传统MPI并行机制既减少了通信开销, 又不会被效率低的节点所拖累。另外, 为了测试作业池并行机制的稳健性, 我们在反演过程中会每隔若干小时人为停止某些进程, 并相应地加入一些新节点, 以模拟硬件故障情况下程序并行机制的稳健性。经过40次反演, 程序运行稳健, 由不同配置节点组成的集群在动态增减节点的情况下顺利完成反演, 运算中各节点根据各自的计算能力自动实现均衡负载, 总用时约67h。图 12a, 图 12b和图 12c分别为深度在1450m处, inline和xline均位于11200m处的初始速度模型、迭代40次的反演速度模型和真实速度模型切片。与初始模型相比, 反演模型河道识别清晰, 小的速度异常体也得到呈现, 断层断面刻画清楚。图 13是迭代40次对应的反演梯度, 其对应了此次迭代速度模型的更新量。可见, 基于作业池并行机制的FWI技术实用、可靠, 并行节点间的解耦使得节点间互不干扰, 既灵活又稳健, 竞争式的作业调度提高了并行效率。
|
图 11 三维SEG/EAGE推覆体初始平滑模型 |
| 表 1 集群节点的资源参数 |
| 表 2 GPU设备的参数 |
| 表 3 反演测试的规模和效率 |
|
图 12 深度在1450m处, inline和xline均位于11200m处的速度模型切片 a 初始速度模型; b 迭代40次的反演速度模型; c 真实速度模型 |
|
图 13 迭代40次的反演梯度 |
本文分析了三维全波形反演中面临的梯度计算效率及并行稳定性难题, 提出将GPU加速技术与随机边界相结合以构建梯度计算引擎, 弥补了GPU在数据存储和交换方面的不足, 充分发挥了GPU加速技术的优势; 研发的作业池机制, 利用共享的作业状态文件控制并行作业的进程, 避免了计算节点间的直接通信和相互影响, 提高了大规模并行计算的稳健性。
三维SEG/EAGE推覆体模型算例验证了本文并行计算技术的高效性和稳健性, 作业池机制带来的计算节点动态增减功能, 增强了FWI对不同硬件条件和计算资源变动的适应性, 有助于全波形反演技术的大规模工业化应用。
| [1] | LAILLY P. The seismic inverse problem as a sequence of before stack migrations[J]. Expanded Abstracts of conference on inverse scattering, theory and application, society for industrial and applied mathematics, 1983: 206-220 |
| [2] | TARANTOLA A. Inversion of seismic-reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266 DOI:10.1190/1.1441754 |
| [3] | KAPOOR S, VIGH D, WIARDA E, et al.Full waveform inversion around the world[J].Expanded Abstracts of 75th EAGE Conference & Exhibition incorporating SPE, 2013:We-11-03 |
| [4] | JOSEPH M, TIMOTHY K, THIERRY T, et al. 3D acoustic waveform inversion of land data:a case study from Saudi Arabia[J]. Expanded Abstracts of 82ndAnnual Internat SEG Mtg, 2012: 1-5 |
| [5] | PLESSIX R, BAETEN G, DEMAAG J W, et al. Full waveform inversion and distance separated simultaneous sweeping:a study with a land seismic data set[J]. Geophysical Prospecting, 2012, 60(4): 733-747 DOI:10.1111/gpr.2012.60.issue-4 |
| [6] | LUO Y, SCHUSTER G T. Wave-equation traveltime inversion[J]. Geophysics, 1991, 56(5): 645-653 DOI:10.1190/1.1443081 |
| [7] | SHIN C, CHA Y H. Waveform inversion in the Laplace domain[J]. Geophysical Journal International, 2008, 173(3): 922-931 DOI:10.1111/gji.2008.173.issue-3 |
| [8] | XU S, WANG D L, CHEN F, et al. Full waveform inversion for reflected seismic data[J]. Expanded Abstracts of 74th EAGE Conference & Exhibition incorporating SPE EUROPEC, 2012: W024 |
| [9] | MIKE W, LLUÍS G. Robust adaptive waveform inversion[J]. Expanded Abstracts of 85thAnnual Internat SEG Mtg, 2015: 1059-1063 |
| [10] | YOUNGSEO K, CHANGSOO S, HENRI C, et al. An algorithm for 3D acoustic time-Laplace-Fourier-domain hybrid full waveform inversion[J]. Geophysics, 2013, 78(4): R151-R166 DOI:10.1190/geo2012-0155.1 |
| [11] | YANG P L, GAO J H, WANG B L. A graphics processing unit implementation of time-domain full-waveform inversion[J]. Geophysics, 2015, 80(3): F31-F39 DOI:10.1190/geo2014-0283.1 |
| [12] | CHAVENT G, PLESSIX R E. An optimal true amplitude least-squares prestack depth-migration operator[J]. Geophysics, 1999, 64(2): 508-515 DOI:10.1190/1.1444557 |
| [13] | SHIN C, MIN D J, YANG D, et al. Evaluation of poststack migration in terms of virtual source and partial de-rivative wavefields[J]. Journal of Seismic Exploration, 2003, 12(1): 17-37 |
| [14] | SYMES W. Reverse time migration with optimal check pointing[J]. Geophysics, 2007, 72(5): SM213-SM221 DOI:10.1190/1.2742686 |
| [15] | ANDERSON J E, TAN L J, WANG D. Time-reversal checkpointing methods for RTM and FWI[J]. Geophysics, 2012, 77(4): S93-S103 DOI:10.1190/geo2011-0114.1 |
| [16] | GAO J H, YANG P L, WANG B L. Using the effective boundary saving strategy in GPU-based RTM programming[J]. Expanded Abstracts of 84thAnnual Internat SEG Mtg, 2014: 4014-4021 |
| [17] | CLAPP R G. Reverse time migration with random boundaries[J]. Expanded Abstracts of 79thAnnual Internat SEG Mtg, 2009: 2809-2813 |
| [18] | SUH Y, YEH A, WANG B, et al. Cluster programming for reverse time migration[J]. The Leading Edge, 2010, 29(1): 94-97 DOI:10.1190/1.3284058 |
| [19] |
徐义, 张剑锋. 地震波数值模拟的非规则网格PML吸收边界[J].
地球物理学报, 2008, 51(5): 1520-1526 XU Y, ZHANG J F. An irregular-grid perfectly matched layer absorbing boundary for seismic wave modeling[J]. Chinese Journal of Geophysics, 2008, 51(5): 1520-1526 |
| [20] |
胡光辉, 贾春梅, 夏洪瑞, 等. 三维声波全波形反演的实现与验证[J].
石油物探, 2013, 52(4): 417-425 HU G H, JIA C M, XIA H R, et al. Implementation and validation of 3D acoustic full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2013, 52(4): 417-425 |


