全波形反演(FWI) 具有求取高分辨率、高精度地下物性参数的能力。TARANTOLA[1]于20世纪80年代首次提出了基于广义最小二乘的时间域全波形反演技术。近10年来, 随着计算机技术的发展, 全波形反演成为国内外地震勘探领域研究的热点之一。目前全波形反演理论研究日臻成熟, 但相较于线性射线层析, 全波形反演由于匹配走时、振幅和相位等信息, 非线性程度高, 极易陷入局部极值产生周期跳问题, 此外, 所需计算资源巨大, 因此, 全波形反演的工业化应用面临诸多挑战。
传统全波形反演是一高度非线性反问题, 数据缺失低频信息或初始模型不准时, 模型在迭代更新过程中容易陷入局部极小值[2]。为降低反演的非线性性, BUNKS等[3]、SIRGUE等[4]分别从时间空间域和频率空间域给出从低频到高频的多尺度反演策略。BROSSIER等[5]采用凸性更好、性态更优的互相关目标泛函完成全波形反演, 相较常规L2范数而言, 其局部极小值更少。WU等[6]从原始地震数据中提取包含丰富低频信息的信号包络反演宏观背景速度以解决低频缺失造成的局部极小值问题。LI等[7]采用相位追踪和频率外推方法从地震波高频数据中人工模拟出低频信息并完成了低波数背景速度重构, 削弱了传统全波形反演的非凸性。
巨大的计算成本是全波形反演在实际应用中的重要制约因素。为提高全波形反演计算效率, KREBS等[8]和BEN-HADJ-ALI等[9]分别在时间域和频率域采用超级震源技术显著减少每次迭代正演模拟的计算时间, 并采用随机相位编码有效压制反演结果中的串扰噪声, 在保证反演质量的前提下大大提高了全波形反演计算效率。
目前国际上海洋地震资料全波形反演成功应用实例越来越多。在SIRGUE等[10]采用三维宽方位海底电缆数据对北海油田成功构建全波形反演高精度速度模型之后, 大偏移距、宽方位、宽频海上拖缆数据、海底电缆数据、常规拖缆采集数据及宽频数据、窄方位海底电缆数据等浅水环境和深水环境全波形反演成功应用案例越来越多。
相较海上资料, 陆上地震资料全波形反演的成功应用还存在不小的挑战[11]。在陆上地震数据采集过程中, 受震源强度、震源激发响应、表层吸收衰减、各种干扰噪声、复杂近地表传播机制及检波器耦合效应等影响, 不同震源、不同检波点地震信号振幅能量严重不均衡, 局部地区存在震源稀疏, 数据不完备现象, 且受采集仪器限制, 地震信号往往缺失低频及大偏移距数据信息。PLESSIX等[12-13]采用专门为全波形反演采集的低频、大偏移距、高密度陆地可控震源数据完成了内蒙古地区二维高精度速度模型建模, 并取得较好应用效果。HE等[14]指出, 当陆上地震资料数据不完备时, 反演结果中存在较强噪声, 迭代收敛性和稳健性都有一定程度影响, 为此他们给出了一种有效的噪声算子滤波方法, 然而当地质条件较为复杂、构造起伏剧烈时, 该方法仍存在一定的局限性。我国以陆上探区为主, 研发适合于陆上地震资料的全波形反演技术迫在眉睫。
本文给出适用于不完备陆上地震资料的稳健的全波形反演策略:采用相位匹配的非零延迟归一化互相关目标泛函提高反演问题的凸性和稳健性, 降低不同震源和检波器振幅能量不均衡对反演造成的影响; 基于已知工区构造先验信息将反演工区分块并对不同区块在波数域完成反演噪声压制; 对整体模型更新量采用自适应高斯平滑技术减弱不同区块模型更新量的耦合效应, 从而使该反演策略适用于任意地质构造条件下陆上地震资料的高精度速度建模。最后采用东北某探区实际二维地震资料进行了应用测试。
1 方法原理 1.1 互相关目标泛函反演框架L2范数全波形反演在迭代过程中需要与地震数据的振幅、波形、相位信息匹配, 其对数据振幅信息非常敏感。由于陆上地震资料激发和接收条件等因素的限制, 原始采集的地震记录存在炮间、道间能量不均衡, 在局部区域非常稀疏。当采用此类数据进行凸性相对较差的L2范数全波形反演时, 不均衡的残差能量会引起模型更新量在不同地区存在较大差异, 从而导致反演不收敛或不稳定, 使反演结果陷入局部极值。为提高反演的稳健性, 在进行陆上地震资料反演时需要给旅行时更多的权重, 以降低振幅的影响。基于相位拟合的互相关目标泛函更强调匹配数据的相位信息, 凸性更优, 且相对于L2范数具有更广的波谷, 因而反演结果更加稳健[5, 15]。本文采用BROSSIER等[5]给出的非零延迟归一化互相关目标泛函理论框架实现陆上地震资料的全波形反演。非零延迟归一化互相关目标泛函为:
| $ \begin{array}{l} {\chi _{{\rm{XcorN}}}}(m) =- \frac{1}{2}\sum\limits_{{x_{\rm{s}}}} {\sum\limits_{{x_{\rm{r}}}} {\sum\limits_\tau \bullet } } {\left[{W\left( \tau \right)\frac{{\sum\limits_t {{d_{{\rm{cal}}}}} (t, {x_{\rm{r}}};{x_{\rm{s}}}){d_{{\rm{obs}}}}(t + \tau, {x_{\rm{r}}};{x_{\rm{s}}})}}{{\left\| {{d_{{\rm{cal}}}}({x_{\rm{r}}};{x_{\rm{s}}})} \right\|\left\| {{d_{{\rm{obs}}}}({x_{\rm{r}}};{x_{\rm{s}}})} \right\|}}} \right]^2} \end{array} $ | (1) |
式中:m为要反演的模型参数; τ为延迟时间; xr为检波器坐标; xs为震源坐标; W(τ) 为惩罚函数; dcal(t, xr; xs) 为人工合成地震记录; dobs(t+τ, xr; xs) 为时延观测地震记录。
即使观测地震记录和模拟地震记录相位差大于半个地震波波长, 该目标泛函亦可稳定收敛, 而且归一化的引入也减小了不同震源和检波器振幅能量不均衡引起的噪声干扰问题。梯度表达式可用伴随状态法求解, 但与L2范数不同, 非零延迟归一化互相关目标泛函需修改反传震源项[5]。采用目标泛函对模型参数的导数可求解梯度表达式:
| $ \begin{array}{l} \frac{{\partial {\chi _{{\rm{XcorN}}}}(m)}}{{\partial m}} =- \sum\limits_{{x_{\rm{s}}}} {\sum\limits_{{x_{\rm{r}}}} {\sum\limits_t {\frac{{\partial \sum\limits_t {{d_{{\rm{cal}}}}} (t, {x_{\rm{r}}};{x_{\rm{s}}})}}{{\partial m}}} } } \bullet \\ \sum\limits_\tau {{W^2}\tau } \frac{{\sum\limits_t {{d_{{\rm{cal}}}}} (t, {x_{\rm{r}}};{x_{\rm{s}}}){d_{{\rm{obs}}}}(t + \tau, {x_{\rm{r}}};{x_{\rm{s}}})}}{{\left\| {{d_{{\rm{cal}}}}({x_{\rm{r}}};{x_{\rm{s}}})} \right\|\left\| {{d_{{\rm{obs}}}}({x_{\rm{r}}};{x_{\rm{s}}})} \right\|}} \bullet \\ \left[{\frac{{{d_{{\rm{obs}}}}(t + \tau, {x_{\rm{r}}};{x_{\rm{s}}})}}{{\left\| {{d_{{\rm{cal}}}}({x_{\rm{r}}};{x_{\rm{s}}})} \right\|\left\| {{d_{{\rm{obs}}}}({x_{\rm{r}}};{x_{\rm{s}}})} \right\|}}} \right.-\\ \left. {\frac{{{d_{{\rm{cal}}}}(t, {x_{\rm{r}}};{x_{\rm{s}}})\sum\limits_t {{d_{{\rm{cal}}}}} (t, {x_{\rm{r}}};{x_{\rm{s}}}){d_{{\rm{obs}}}}(t + \tau, {x_{\rm{r}}};{x_{\rm{s}}})}}{{{{\left\| {{d_{{\rm{cal}}}}({x_{\rm{r}}};{x_{\rm{s}}})} \right\|}^3}\left\| {{d_{{\rm{obs}}}}({x_{\rm{r}}};{x_{\rm{s}}})} \right\|}}} \right] \end{array} $ | (2) |
NANGO[16]采用稀疏震源子集对常规缺乏低频和大偏移距的窄方位海上拖缆数据进行了全波形反演研究, 采用水平光滑预处理技术压制梯度大倾角噪声, 保留反演速度中的地质构造信息。当工区地质背景较为复杂时, 水平光滑预处理技术不再适用。相对海上拖缆数据, 陆上资料的稀疏性更强, 而且信噪比低, 数据质量相对更差。当工区震源较为稀疏, 且覆盖次数较低时, 全波形反演会在梯度中引入强烈的反演噪声[14, 16]。为得到较为准确的、符合地质构造背景的速度模型, 需要压制迭代过程中产生的反演噪声。HE等[14]提出了在波数域压制噪声的方法, 但该方法的不足之处在于若选择的构造倾角较小, 则高陡构造也被压制; 若选择的构造倾角过大, 虽然在滤波后的反演结果中保留了高陡构造特征, 但会带来保留较强噪声干扰的结果。本文为突破上述单角度波数域滤波的限制, 基于已有地质构造信息, 对地下介质分区, 采用分而治之思想, 对不同区块选取相应角度的波数域滤波算子压制噪声, 在有效压制噪声的前提下, 尽可能保留地质构造特征信息。继而采用整体自适应高斯平滑滤波技术减小不同区块梯度波数域滤波后的不一致性。
分区波数域滤波需要在每次迭代过程中按照成像剖面沿地质构造倾角分区。局部构造倾角场可采用局部平面波解构滤波法[17]或图像梯度结构张量算法[18]求解, 本文采用局部平面波解构法求解构造倾角场。平面波解构滤波器利用局部平面波的叠加表征地震数据, 可以较好地估计平滑连续同相轴的局部倾角信息。根据局部平面波的物理模型, 用局部有限差分方程定义平面波解构滤波器为:
| $ \frac{{\partial P\left( {x, t} \right)}}{{\partial x}} + \sigma \left( {x, t} \right)\frac{{\partial P\left( {x, t} \right)}}{{\partial t}} = 0 $ | (3) |
式中:P(x, t) 为局部平面波波场; σ(x, t) 为平面波局部斜率场。(3) 式可化简为基于最小二乘的倾角估计问题:
| $ \mathit{\boldsymbol{C'}}({\sigma _0})\Delta \sigma \mathit{\boldsymbol{d}} + \mathit{\boldsymbol{C}}\left( {{\sigma _0}} \right)\mathit{\boldsymbol{d}} \approx 0 $ | (4) |
式中:σ0为斜率初始值; Δσ为斜率增量; C为局部倾角的函数; d为原始数据。利用(4) 式可构建局部倾角场。根据构造的局部倾角场将整个地质工区分为不同区块, 每个区块对应不同的主要构造倾角。利用不同区块的主要构造倾角和各自相应的波数域滤波算子对不同区块梯度压制噪声。各区块采用的噪声压制算子公式为:
| $ \mathit{\boldsymbol{s}}_n^i = {\left( {{\mathit{\boldsymbol{P}}^{-1}}} \right)^i}{\mathit{\boldsymbol{T}}^i}{\mathit{\boldsymbol{P}}^i}\mathit{\boldsymbol{g}}_n^i $ | (5) |
式中:gni表示第i区块梯度场; Pi为傅里叶正变换; Ti表示波数选择算子, 为不同区块构造倾角θi的函数; (P-1)i为傅里叶反变换; sni为第i区块噪声压制后的梯度场。
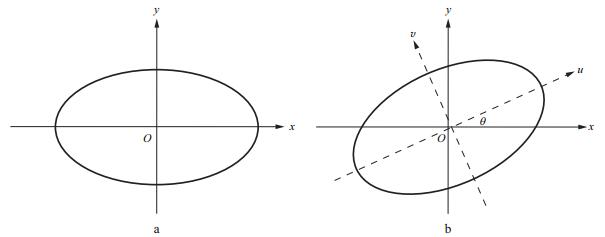
1.3 自适应各向异性高斯平滑算子分区滤波梯度场在整合为整体梯度时不同区块交界处存在边界效应, 这将在反演结果中引入明显的区块边界。为削弱这种边界效应, 本文对整体梯度场采用自适应各向异性高斯平滑滤波算子[19]沿倾角方向滤波。各向异性高斯滤波算子在x, y平面上的投影为椭圆(如图 1a所示), 该滤波算子表达式为:
|
图 1 各向异性高斯平滑算子无旋转(a) 和旋转θ(b) 在x-y平面上的投影 |
| $ G\left( {x, y, {\sigma _x}, {\sigma _y}} \right) = \frac{1}{{2\pi {\sigma _x}{\sigma _y}}}{\rm{exp}}\left[{-\frac{1}{2}\left( {\frac{{{x^2}}}{{{\sigma ^2}_x}} + \frac{{{x^2}}}{{{\sigma ^2}_y}}} \right)} \right] $ | (6) |
针对不同的构造倾角θ, 采用旋转的方式得到如图 1b所示的投影, 由坐标变换可得旋转后的坐标u-v和x-y坐标的关系为:
| $ \left( \begin{array}{l} u\\ v \end{array} \right) = \left( {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }\\ {-\sin \theta }&{\cos \theta } \end{array}} \right)\left( \begin{array}{l} x\\ y \end{array} \right) $ | (7) |
旋转后的高斯滤波算子为:
| $ \begin{array}{l} \left( {x, y, {\sigma _u}, {\sigma _v}, \theta } \right) = \frac{1}{{2\pi {\sigma _u}{\sigma _v}}}{\rm{exp}}\left\{ {- \frac{1}{2} \bullet } \right.\\ \left[{\frac{{{{(x{\rm{cos}}\theta + y{\rm{sin}}\theta )}^2}}}{{\sigma _u^2}} + {{\frac{{(-x{\rm{sin}}\theta + y{\rm{cos}}\theta )}}{{\sigma _v^2}}}^2}} \right] \end{array} $ | (8) |
采用构建的自适应各向异性高斯滤波算子可对整合后的梯度场沿着构造倾角平滑:
| $ {\mathit{\boldsymbol{d}}_n} = \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{s}}_n} $ | (9) |
式中:sn为整合梯度场; dn表示高斯滤波梯度场; G为自适应各向异性高斯滤波算子。
在构建出构造较为连续、噪声污染较少的梯度场后, 采用预条件拟牛顿(L-BFGS) 迭代最优化算法对速度模型迭代更新, 迭代步长采用非精确线性搜索技术求取。
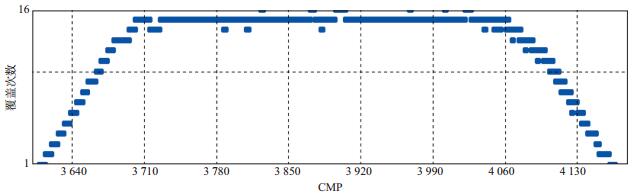
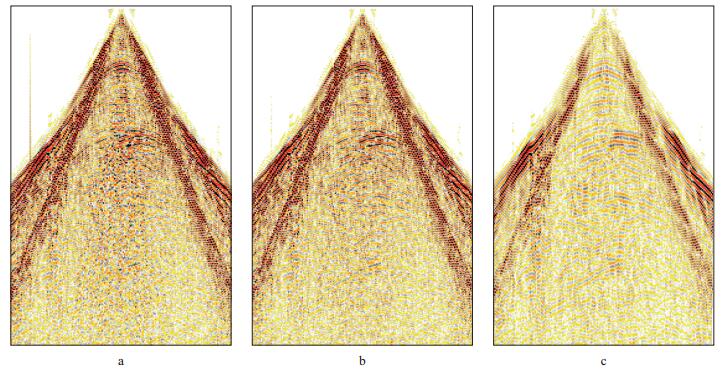
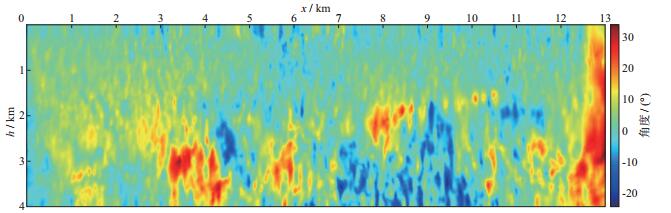
2 实际资料应用为验证本文方法的有效性, 选取东北某探区一条二维线进行全波形反演。沿探区东西方向抽取44炮单炮地震记录, 每炮180道左右。震源在x方向的分布范围为13000m, 炮点距350m左右, 相对稀疏。图 2为该二维线覆盖次数图。其中, 最大覆盖次数为16次。图 3a为去除面波、线性噪声、异常振幅, 并进行地表一致性振幅补偿、球面扩散补偿后的原始单炮地震记录。图 3b为6Hz以上频率段观测地震记录。该记录中面波得到了有效压制, 信噪比得以提高。图 3c为图 3b的低频段信息, 频率范围为6~20Hz。本文采用6~20Hz频率段数据进行反演测试。图 4为二维深度域克希霍夫叠前偏移剖面。对偏移剖面采用局部平面波解构滤波可获取地质构造倾角信息(图 5)。从构造倾角场中可以看出, 浅层的主要反射层构造倾角较小, 大部分集中在10°之内, 中、深层构造倾角较大, 为-25°~35°。
|
图 2 研究区某二维线覆盖次数分布 |
|
图 3 研究区某二维线单炮地震记录 a 去噪和振幅补偿后的观测地震记录; b 消除面波后的观测地震记录; c 6~20Hz观测地震记录 |

|
图 4 深度域克希霍夫叠前偏移剖面 |
|
图 5 叠前偏移剖面构造倾角场 |
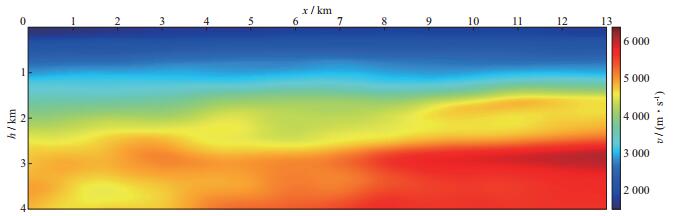
地震子波是传统基于L2范数实际资料全波形反演成败的一个关键因素[11]。由于实际资料的地震子波是时变和空变的, 而且在相同条件下, 不同子波正演模拟出的人工合成地震记录在振幅、相位和波形上均存在较大差别, 因而如何做好地震子波估计是全波形反演的重要环节。本文采用基于相位拟合的非零延迟归一化互相关目标反演理论框架完成速度场的重构, 在反演迭代过程中削弱了原始地震记录和观测地震记录振幅和波形的影响, 更加强调相位的作用, 在一定程度上减小了对地震子波估计的要求, 因此本文采用合适主频的雷克子波完成正演模拟及速度重构, 非零延迟的引入在一定程度上允许地震子波具有一定的相位延迟。本文采用的初始速度模型为反射波旅行时层析速度反演模型(图 6), 该模型具有较为充分的低波数信息及宏观地质构造背景信息。
|
图 6 反射波旅行时层析速度模型 |
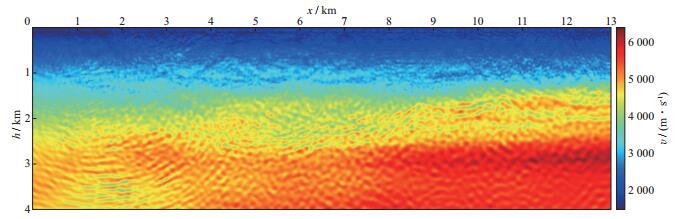
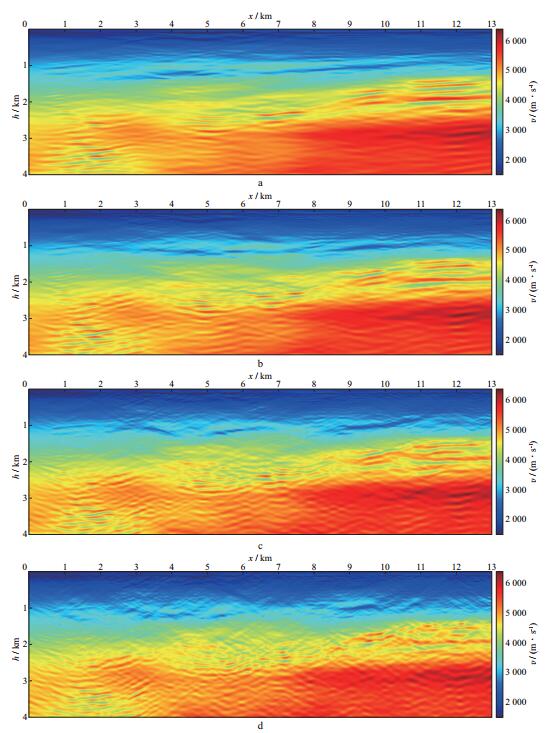
采用原始稀疏观测地震记录进行互相关全波形反演时, 由于覆盖次数较少, 反演的非线性程度较高, 反演结果存在较强的噪声。图 7显示了6~20Hz数据迭代20次的全波形反演结果。由图 7可见, 反演结果信噪比较低, 有效地质构造信息被反演噪声湮没。图 8给出了在每次迭代过程中采用单一角度(10°, 15°, 25°, 35°) 波数域滤波迭代20次得到的反演结果。相较于原始资料直接重构的速度模型, 采用单一角度波数域滤波后构建的反演速度有效压制了串扰噪声, 增强了有效地质构造的连续性。然而单一角度波数域滤波本身存在缺陷, 当采用的滤波算子角度过小时, 虽然反演结果信噪比显著提高, 但滤波算子消除了大角度的地质构造信息(图 8a, 图 8b)。由于该工区的构造倾角范围为-25°~35°, 当采用大角度波数域滤波算子时, 虽然大倾角的地质构造信息得以保留, 但是反演结果中也相应引入了较为严重的大角度线性噪声(图 8c, 图 8d)。
|
图 7 互相关目标泛函全波形反演结果 |
|
图 8 采用单一角度波数域滤波后互相关目标泛函全波形反演结果 a 滤波角度10°; b 滤波角度15°; c 滤波角度25°; d滤波角度35° |
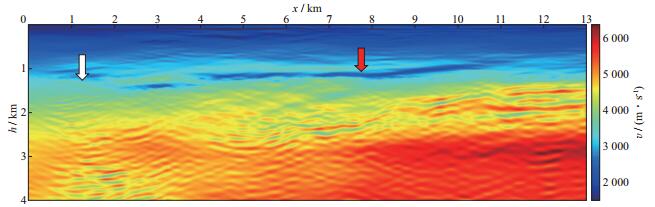
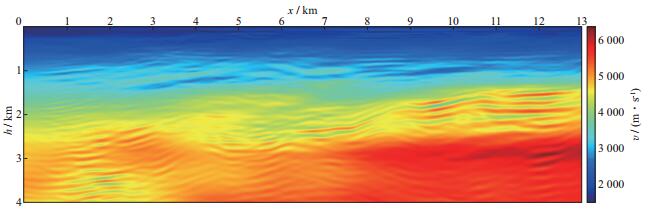
该工区构造倾角在浅层集中在10°以下, 深层主要集中在25°左右, 因此本文采用浅、深层分区波数域滤波算子完成全波形反演建模。图 9给出了分区波数域滤波建模结果。由图 9可见, 浅层和深层都保留了有效地质构造信息, 与单一大角度波数域滤波反演结果(图 8c, 图 8d) 相比, 分辨率有一定改善, 但是在红色箭头处, 出现低速异常体, 反演结果陷入局部极值, 且白色箭头的位置速度出现不耦合现象。为此, 每次迭代在分区波数域滤波的基础上引入各向异性自适应高斯平滑算子。图 10显示了最终的重构模型, 该重构结果不仅信噪比提高而且构造更加连续, 局部极值问题得到削弱。
|
图 9 分区波数域滤波互相关全波形反演结果(浅层10°, 深层15°) |
|
图 10 分区波数域滤波后采用各向异性自适应高斯平滑处理得到的互相关全波形反演结果 |
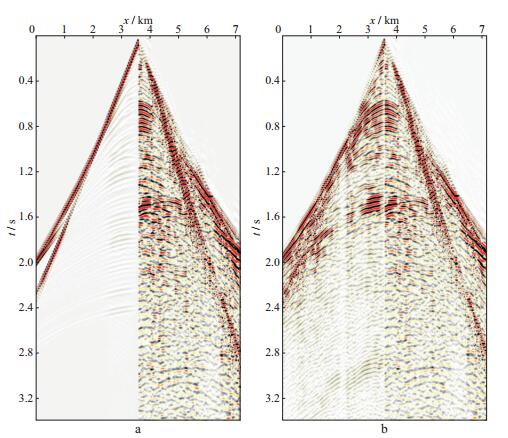
图 11给出了初始模型、反演速度模型正演模拟归一化地震记录和归一化观测地震记录的对比结果。与初始模型正演模拟地震记录相比, 反演模型的模拟地震记录主要反射层的相位与观测地震记录匹配得更好, 从相位拟合的角度验证了反演的准确性与稳健性。
|
图 11 观测地震记录与模拟地震记录结果对比 a 初始模型正演模拟地震记录(左) 与观测地震记录(右); b 反演模型正演模拟地震记录(左) 与观测地震记录(右) |
本文给出陆上地震资料不完备条件下采用全波形反演进行高精度速度建模的方案。采用基于相位拟合的非零延迟归一化互相关目标泛函取代传统的基于数据波形、振幅、相位匹配的L2范数目标泛函, 提高了反演的稳健性, 且降低了对地震子波精度和原始地震资料振幅能量均衡的要求。采用分区波数域滤波算子和各向异性自适应高斯平滑技术有效减少了原始地震资料稀疏时反演结果中较强的反演噪声并保留了有效地质构造信息, 反演结果更加合理、准确, 而且反演过程较为稳健。二维陆上地震资料反演测试结果表明本文给出的陆上地震资料反演策略不仅有效消除了反演结果中强烈的噪声, 而且构建了具有地质意义的高分辨率速度模型, 波形的匹配表明本文反演方法相对层析反演结果更优。
| [1] | TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266 DOI:10.1190/1.1441754 |
| [2] | VIRIUEX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26 DOI:10.1190/1.3238367 |
| [3] | BUNKS C, SALECK F. Multi-scale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473 DOI:10.1190/1.1443880 |
| [4] | SIRGUE L, PRATT R G. Efficient waveform inversion and imaging:a strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(1): 231-248 DOI:10.1190/1.1649391 |
| [5] | BROSSIER R, OPERTO S. Velocity model building from seismic reflection data by full-waveform inversion[J]. Geophysical Prospecting, 2015, 63(2): 354-367 DOI:10.1111/gpr.2015.63.issue-2 |
| [6] | WU R S, LUO J, WU B. Seismic envelope inversion and modulation signal model[J]. Geophysics, 2014, 79(3): WA13-WA24 DOI:10.1190/geo2013-0294.1 |
| [7] | LI Y Y, DEMANET L. Full-waveform inversion with extrapolated low-frequency data[J]. Geophysics, 2016, 81(6): R339-R348 DOI:10.1190/geo2016-0038.1 |
| [8] | KREBS J R, ANDERSON J E, HINKLEY D, et al. Fast full-wavefield seismic inversion using encoded sources[J]. Geophysics, 2009, 74(6): WCC177-WCC188 DOI:10.1190/1.3230502 |
| [9] | BEN-HADJ-ALI H, OPERTO S, VIRIEUX J. An efficient frequency-domain full waveform inversion method using simultaneous encoded sources[J]. Geophysics, 2011, 76(4): R109-R124 DOI:10.1190/1.3581357 |
| [10] | SIRGUE L, BARKVEL O. 3D waveform inversion in Valhall wide-azimuth OBC[J]. Expanded Abstracts of 71st Annual Internat EAGE Mtg, 2009: U038 |
| [11] |
杨勤勇, 胡光辉, 王立歆. 全波形反演研究现状及发展趋势[J].
石油物探, 2014, 53(1): 77-83 YANG Q Y, HU G H, WANG L X. Research status and development trend of full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(1): 77-83 |
| [12] | PLESSIX R E, BAETEN G. Application of acoustic full waveform inversion to a low-frequency large-offset land dataset[J]. Expanded Abstracts of 80thAnnual Internat SEG Mtg, 2010: 930-934 |
| [13] | PLESSIX R E, BAETEN G. Full waveform inversion and distance separated simultaneous sweeping:a study with a land seismic data set[J]. Geophysical Prospecting, 2012, 60(4): 733-747 DOI:10.1111/gpr.2012.60.issue-4 |
| [14] | HE B H, WU G C. Robust full-waveform inversion with incomplete refraction[J]. Expanded Abstracts of 84th Annual Internat SEG Mtg, 2014: 150-153 |
| [15] | MASONI I, BROSSIER R.Alternative misfit functions for FWI applied to surface wave[J].Expanded Abstracts of 75th Annual Internat EAGE Mtg, 2013:Th P10 13 |
| [16] | NANGOO T P.Seismic full-waveform inversion of 3D field data--from the near surface to the reservoir [D].London:University of Imperial College, 2013 |
| [17] | FOMEL S. Applications of plane-wave destruction filters[J]. Geophysics, 2002, 67(10): 1946-1960 |
| [18] | HALE D.Local dip filtering with directional Laplacians[R].CWP report, 2007 |
| [19] |
王怀野, 张科, 李言俊. 一种自适应各向异性高斯滤波方法[J].
计算机工程与应用, 2004, 40(10): 18-19 WANG H Y, ZHANG K, LI Y J. An adaptive anisotropic Gaussian filter for noise reduction[J]. Computer Engineering and Applications, 2004, 40(10): 18-19 |


