岩性油气藏的精确描述是勘探地震学的重要目标。小尺度地质体的精确构造成像、振幅保真成像、反射系数甚至其它弹性参数的精确估计是勘探地震学的核心问题。随着高性能计算机技术的快速进步以及全方位、高密度、宽频带的地震数据采集技术的飞速发展, 以估计全或宽波数带的弹性参数为目标的全波形反演(FWI) 方法再次成为勘探地震学的研究热点。(各向异性) 逆时偏移(RTM) 方法的成功实用化则进一步推动了对FWI技术的研究。然而, 由于叠前地震数据的不完备(如有限观测孔径、有限带宽(尤其是缺失低频) 和空间不规则的观测以及地表不一致的观测, 也包括强噪声环境下的观测)、正演模型的不完善(正演算子无法很好地预测实际波场中的各种波现象)、初始模型距离反演的“真”参数模型太远、地震子波的未知且空变等多种因素制约, 使得经典FWI难以达到其理论预计的目标, 甚至在实际应用中根本不收敛。
本质上, 经典FWI是一个非线性性很强的反演问题, 根本原因在于实际观测的地震波场的变化与要反演参数的变化之间关系很弱。另外, 包含要反演参数的控制方程不能很好地预测实测数据也是一个重要因素。而地震波反演成像的核心问题是将解一个非线性(较) 强的反问题转化为提一个更凸的反问题并进行求解。如何将一个非线性强的反问题转化为凸性更好的反问题并进行求解, 一直是地球物理反问题研究人员关注的焦点。典型地, 包括引入波场的Laplace变换[1]、引入波场的对数变换[2]、引入波场的Hilbert变换[3-4], 还有不进行数据逼近而利用像域中成像道集的拉平或聚焦建立目标泛函的反演方法[5]。更为全面地讨论如何构建较凸反问题的, 应该是波场重构反演(wavefield reconstruction inversion, WRI) 方法[6-7], 其基本思想是通过引入增广的状态变量解决正问题不能很好地预测实际地震数据中波现象的问题。但是, 引入增广的状态变量并没有明确地指出仅仅特征波场和特征参数之间才存在更为密切、更为线性的联系。而勘探地震中地下介质参数的分布和叠前数据本身都是具有特征的, 特征波场和特征参数之间才存在更为密切的关系[8-9]。
本文提出仅仅用与特征参数关系密切的特征波场进行反演的思想与方法。特征波场与反演参数之间的关系更紧密, 基于特征波场的反问题凸性更好。特征波反演成像由四个基本步骤组成:特征波场的提取、波动理论的透射波层析成像、波动理论的一次反射波层析成像、最小二乘叠前深度偏移成像。特征波反演成像的中心工作在于特征波场的提取。特征波反演成像中梯度的预条件要相对简单, 因为此时特征波对应的梯度干扰大大减弱。另外, 反射子波特征对于估计反射系数或波阻抗一类的反演成像十分重要[10]。特征波成像是基于对实测炮集中所包含的波现象认识的一种反演框架。我们认为, 只有经过相当长时间的特征波反演成像方法研究, 经典FWI中所蕴含的问题才能逐步得到认识和解决, 进而发展出工业界实用化的反演成像技术。
1 求解强非线性反问题或提出更凸的反问题地震波反演成像是勘探地震的核心问题, 它是一个标准的非线性反演问题, 其非线性程度随着地下介质的复杂程度提高(譬如小尺度速度异常体存在、横向变速剧烈等) 而提高。实测波场变化与地下介质变化之间的非线性程度决定了地震波反演问题的非线性程度。针对勘探地震中的参数反演问题, 我们是专注于寻找解决较强非线性反演问题的方法, 还是专注于提一个凸性更强的反演问题来求解?
ROCKAFELLAR[11]指出, 优化问题的核心不在于问题的线性与非线性, 而是问题的凸性与非凸性。显然, 提一个更凸的反问题比奋力解一个强非线性反问题更合理。
自TARANTOLA[12]建立以波动方程为基础的地震反演理论近30年(尤其是最近几年) 来, 随着以“两宽一高”为代表的地震数据采集技术以及以GPU为代表的高性能计算机技术的进步, FWI方法和技术取得了长足的进步。专家学者在降低反演问题非线性性方面做了很多有益的探索, 提出了很多有效的方法。基本思想是从数据或波场入手来改进反演成像方法, 典型的做法包括:从低频数据到高频数据的多尺度反演[13-14]; 从近偏移距数据到远偏移距数据的反演[15]; 从小到大调节Laplace阻尼参数进行的由初至时刻不断放大时窗的反演[1]; 定义不同误差泛函的反演[3, 16-22]。另一类方法则是将传统的数据域反演扩展到成像域的反演[5, 23-24]。
上述反演方法并没有从更为抽象的角度主动地将地震波反演问题提成一个更凸的问题。本文希望在数据的特征表达和参数的特征表达概念下, 将经典FWI转化为一个临近的、更凸的反问题进行求解。
2 Bayes反演理论的缺陷Bayes反演理论是地震波反演成像的基础[25]。Bayes估计的思想可以简单概括为:参数估计的结果是由后验概率密度函数P(m/d) 所决定的均值E{m/d}:
| $\boldsymbol{\hat m} = E\left\{ {\boldsymbol{m}/\boldsymbol{d}} \right\} = \int {\boldsymbol{m}P\left( {\boldsymbol{m}/\boldsymbol{d}} \right){\rm{d}}\boldsymbol{m}} $ | (1) |
式中: d代表观测数据, m为系统(或模型) 参数。公式(1) 表示参数估计的结果是由观测数据所对应的模型参数出现的概率所决定的。
由于后验概率密度P(m/d) 很难估计, 所以将其转化为较容易估计的模型空间的先验概率密度函数P(m)、数据空间的概率密度函数P(d) 和条件概率密度函数P(d/m) 来表示, 其中P(d/m) 体现了正算子的不确定性。计算后验概率密度函数P(m/d) 的Bayes公式为:
| $P\left( {\boldsymbol{m}/\boldsymbol{d}} \right) = \frac{{P\left( {\boldsymbol{d}/\boldsymbol{m}} \right)P\left( \boldsymbol{m} \right)}}{{P\left( \boldsymbol{d} \right)}}$ | (2) |
Bayes估计的基本思想是后验概率密度P(m/d) 最大时(即MAP方法) 得到最好的反演解。反演解由期望值
| $\begin{array}{c} S\left( \boldsymbol{m} \right) = \frac{1}{2}\{ {\left( {g\left( \boldsymbol{m} \right)- {\boldsymbol{d}_{{\rm{obs}}}}} \right)^{\rm{H}}}\boldsymbol{C}_{\rm{D}}^{- 1}\left[{g\left( \boldsymbol{m} \right)-{\boldsymbol{d}_{{\rm{obs}}}}} \right] + \\ \left. {{{\left( {\boldsymbol{m} -{\boldsymbol{m}_{{\rm{Prior}}}}} \right)}^{\rm{H}}}\boldsymbol{C}_{\rm{M}}^{ -1}\left( {\boldsymbol{m} -{\boldsymbol{m}_{{\rm{Porio}}}}} \right)} \right\} \end{array}$ | (3) |
式中: CD为数据协方差矩阵; CM为模型协方差矩阵; dobs代表实测数据; dcal=g(m) 代表正问题; mprior代表参数的先验值。
(3) 式存在的问题是隐含了一个很基本的假设:正问题g(m) 是可以解释实测数据dobs的, 不能解释的残差是符合高斯或某种广义高斯分布的。这种假设与勘探地震的实际情况很不相符, 必须进行修改。
TARANTOLA[25]指出:正问题不能很好地解释实测地震数据, 其引入的数据残差与观测噪声(非信号部分) 引入的数据残差可能是同一水平的。
我们认为, 考虑到正演模型选择过于简单(譬如仅考虑单参数) 及震源函数未知等因素的影响, 正问题的表达不合适引起的数据逼近误差很可能超过观测噪声引起的数据逼近误差。这就使经典的FWI完全失去了意义。Bayes估计理论似乎蕴含了正问题不准确引起的问题, 但要么忽视它, 要么没有具体的解决方案。
以下我们引入正问题的计算结果--状态变量, 并将状态变量作为与模型参数同等地位的待反演参数看待。这是深化对地震波反演问题的认识、将非线性的地震波反演成像问题提成一个更凸的反演问题的关键。
3 对状态变量独立的地震波反演问题的认识状态变量是最优控制理论[26]描述系统状态的变量, 与系统参数具有同等地位, 共同满足控制方程。
勘探地震中, 引入状态变量和系统参数的正问题的描述方法如下:将激励、探区介质分布、响应视为一个系统, 对应该系统的非线性正问题的数学描述可以抽象为:
| $A\left( \boldsymbol{m} \right)\boldsymbol{u = }\delta \left( {\boldsymbol{x}-{\boldsymbol{x}_{\rm{s}}}} \right)f\left( {\boldsymbol{x}, t} \right) =-f\left( {{\boldsymbol{x}_{\rm{s}}}, t} \right)$ | (4) |
式中:A为正演算子; u为要正演合成的波场, 即状态变量(系统响应); f为震源函数(激励函数)。
在地震波反演中, A的一般形式为:
| $A = \frac{1}{{{v^2}}}\frac{{{\partial ^2}}}{{{\partial ^2}t}}-\left( {\frac{{{\partial ^2}}}{{{\partial ^2}x}} + \frac{{{\partial ^2}}}{{{\partial ^2}y}} + \frac{{{\partial ^2}}}{{{\partial ^2}z}}} \right) = \frac{1}{{{v^2}}}\frac{{{\partial ^2}}}{{{\partial ^2}t}}-\nabla $ | (5) |
A的形式受所选择的波动方程的影响, 如常密度声波/变密度声波方程、各种拟声波方程、弹性波方程等。
野外观测到的地震数据可以表述为:
| $P\left( {{\boldsymbol{d}^{{\rm{obs}}}}} \right) = P\left( \boldsymbol{u} \right) + \boldsymbol{\eta }$ | (6) |
此处, P(·) 表示针对实测数据和状态变量的变换算子; η表示随机噪声函数, 在大部分情况下假设它是高斯白噪的。
由(6) 式定义实测数据和状态变量之间的关系, 蕴含了引入变换算子使得实测数据和状态变量进行匹配的思想, 也可以说引入了让状态变量独立出来作为一个待处理的参量看待的思想, 不再认为状态变量完全由系统参数、控制方程和激励函数决定(理论上的确由它们确定)。这样的观点对后续的反演成像非常有意义。
地震数据反演成像主要包括相互有紧密联系的两条途径:一是Bayes估计理论; 二是约束最优化理论。广义高斯分布假设下代价函数最小反问题优化求解方法与约束最优化理论基本上是等价的。下面我们从约束优化理论展开状态变量独立的地震波反演成像问题的讨论。
最简单的FWI成像目标函数定义为:
| $\mathop {\min }\limits_{\boldsymbol{m} \in {\bf{M}}} J\left( \boldsymbol{m} \right) = \frac{1}{2}{\left\| {{\boldsymbol{d}^{{\rm{obs}}}}-{\boldsymbol{d}^{{\rm{cal}}}}\left( \boldsymbol{m} \right)} \right\|^2}$ | (7) |
式中: dobs为野外观测数据, dcal(m) 为正演模拟数据; M是系统(模型) 参数空间。(7) 式就是数据残差为高斯分布假设下的最大似然估计方法。另一个蕴含的假设是正问题的解能够解释实测地震数据, 并使二者的残差满足高斯分布。这与地震波反演成像的实际情况相差甚远, 反演结果有很强的多解性, 完全不能满足实际应用的要求。因此, 人们对(7) 式进行了各种各样的修改, 发展了很多经典的FWI变种形式。一般地, 是沿着Bayes估计的路线提出各种修改方法。概念上, 各种典型的修改方法可以抽象为:
| $\begin{array}{l} \mathop {\min }\limits_{\boldsymbol{m} \in {\bf{M}}} J\left( \boldsymbol{m} \right) = \frac{1}{2}{\left\| {T\left( {{\boldsymbol{d}^{{\rm{obs}}}}} \right)- T\left[{\boldsymbol{u}\left( \boldsymbol{m} \right)} \right]} \right\|^2} + \\ \alpha {\left\| {D\boldsymbol{m}} \right\|_p}\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\boldsymbol{u}\left( \boldsymbol{m} \right) = {\left[{A\left( \boldsymbol{m} \right)} \right]^{ -1}}\boldsymbol{f} \end{array}$ | (8) |
式中:算子T(·) 可以选择各种各样的形式。譬如, 可以对波场取对数, 分别利用相位项的逼近和振幅项的逼近进行反演[T(u)=ln u[2], T(u)=Re (ln u) 和T(u)=Im (ln u)[27-28]]; 可以对波场进行Laplace变换, 利用从初至到达时开始不断扩大的窗函数截取不断增加的波场进行反演[T(u)=∫Wu(t) e-stdt[1]]; 还可以对波场取包络, 减轻FWI的Cycle-Skipping现象[
状态变量独立的地震波反演问题可以提成如下控制方程约束下的优化问题, 即:
| $\begin{array}{l} \mathop {\min }\limits_{\boldsymbol{m} \in {\bf{M}}, \boldsymbol{u} \in {\bf{U}}} \frac{1}{2}\left\| {{P^{{\rm{cal}}}}\left( \boldsymbol{u} \right)-{P^{{\rm{obs}}}}\left( {{\boldsymbol{d}^{{\rm{obs}}}}} \right)} \right\|_2^2\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;A\left( \boldsymbol{m} \right)\boldsymbol{u} = \boldsymbol{q} \end{array}$ | (9) |
式中:Pcal(·) 为施加在正演波场上的变换函数; Pobs(·) 为施加在观测数据上的变换算子, 它可以是非线性算子, 一般定义为线性算子; U是状态变量空间; A(m) u=q为控制(或状态) 方程, q为激励(震源) 函数。状态变量空间U和模型参数空间M构成了满足控制方程A(m) u=q的联合空间, 地震波反演成像就是在此联合空间中寻找最优解。事实上, 激励函数q ∈ Q也是需要反演的, 但是在勘探地震中, 一般假定激励函数是已知的。关于模型参数和状态变量的罚函数(约束函数), 为了讨论简单计, 没有包括在上式中, 但这不会影响下述问题的讨论。
5 特征波反演方法我们认为, 无论如何选择控制方程、如何描述相应的定解问题, 都不可能完全解释实测地震数据。既然如此, 我们从实测数据中筛选出能被控制方程较准确预测的波场, 将这部分波场称为特征波场(CWF), 基于CWF发展一套特征波反演理论。特征地震波反演成像问题的凸性有明显的改善, 为简洁计, 下面的讨论没有考虑正则化问题。
基于CWF的特征波反演成像方法技术的核心在于特征波场数据的提取。实质上, 特征波场也对应模型参数的特征成分。
压缩感知框架下的特征波场提取问题可以提为:
| $\min {\left\| {\boldsymbol{d}_{\rm{C}}^{{\rm{obs}}}} \right\|_p}\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\left\| {\boldsymbol{d}_{\rm{C}}^{{\rm{obs}}}-{\boldsymbol{d}^{{\rm{obs}}}}} \right\| \le \varepsilon $ | (10) |
式中: dCobs为提取的特征波场。一般地, 从高维地震数据体中提取的dCobs表现为线性相位变化的局部平面波场。因此, 我们给出的特征波场的定义为:时空局部的、单震相的、带方向的带限波场。
在提取特征波场的基础上, 特征波场反演问题提为:
| $\begin{array}{l} \mathop {\min }\limits_{\boldsymbol{m} \in {\bf{M}}, \boldsymbol{u} \in {\bf{U}}} \frac{1}{2}\left\| {R{\boldsymbol{u}^C}-\boldsymbol{d}_{\rm{C}}^{{\rm{obs}}}} \right\|_2^2\\ {\rm{s}}{\rm{.t}}{\rm{. }}{A^{\rm{C}}}\left( {{\boldsymbol{m}^{\rm{C}}}} \right){\boldsymbol{u}^{\rm{C}}} = \boldsymbol{q} \end{array}$ | (11) |
式中:R是采样算子, AC为描述特征波传播的波场正传算子, uC为正演计算的特征波场, mC为与特征波场对应的特征参数。它们共同满足控制方程AC(mC) uC=q。由于我们仅仅考虑特征波场, 因此, 可以比较完整地进行特征波场的预测, (11) 式可以重写为:
| $\mathop {\min }\limits_{\boldsymbol{m} \in {\bf{M}}} \frac{1}{2}\left\| {R\left[{{A^{\rm{C}}}{{\left( {{\boldsymbol{m}^{\rm{C}}}} \right)}^{-1}}\boldsymbol{q}} \right] -\boldsymbol{d}_{\rm{C}}^{{\rm{obs}}}} \right\|_2^2$ | (12) |
VAN LEEUWEN等[7]提出如下波动方程约束的优化反演问题(波场重构反演方法):
| $\mathop {\min }\limits_{\boldsymbol{m} \in {\bf{M}}, \boldsymbol{u} \in {\bf{U}}} {\lambda ^2}\left\| {A\left( \boldsymbol{m} \right)\boldsymbol{u}-\boldsymbol{q}} \right\|_2^2 + \frac{1}{2}\left\| {P\boldsymbol{u}-{\boldsymbol{d}^{{\rm{obs}}}}} \right\|_2^2$ | (13) |
上式也可以写为:
| $\mathop {\min }\limits_{\boldsymbol{m} \in {\bf{M}}, \boldsymbol{u} \in {\bf{U}}} \left\| {A\left( \boldsymbol{m} \right){P^{-1}}{\boldsymbol{d}^{{\rm{obs}}}}-\boldsymbol{q}} \right\|_2^2$ | (14) |
可见波场重构反演方法的思想也是提取实测波场中满足控制方程的部分参与反演, 即认为u=P-1 dobs, 并利用(13) 式定义了如下的增广状态变量:
| $\begin{array}{l} {\boldsymbol{u}_\lambda } = {\left[{{\lambda ^2}A{{\left( \boldsymbol{m} \right)}^*}A\left( \boldsymbol{m} \right) + {P^*}P} \right]^{ - 1}} \cdot \\ \left[{{\lambda ^2}A{{\left( \boldsymbol{m} \right)}^*}\boldsymbol{q} + {\boldsymbol{P}^*}{\boldsymbol{d}^{{\rm{obs}}}}} \right] \end{array}$ | (15) |
但是, VAN LEEUWEN等没有提出可行的计算重构波场(或计算增广状态变量) 的方法。
我们坚持用特征波场进行地震波反演的理念受到如下线性问题求解方式的启发:
| $A\boldsymbol{m} = {\boldsymbol{d}^{{\rm{obs}}}} \Rightarrow \boldsymbol{U}\sum {{\boldsymbol{V}^{\rm{T}}}\boldsymbol{m}} = {\boldsymbol{d}^{{\rm{obs}}}} \Rightarrow {\boldsymbol{m}_{\rm{C}}} = \sum\nolimits_{}^{-1} {\boldsymbol{d}_{\rm{C}}^{{\rm{obs}}}} $ | (16) |
式中: mC=VTm可以视为模型参数的特征表达; dCobs=UTdobs可以视为实测数据的特征表达。若∑是非零元素形成的对角阵, 则mC和dCobs之间就建立起了一对一的投影关系。据此可以认为, 特征波场和特征模型参数之间的关系要比一般性的实测波场和模型参数之间的关系更密切, 对应的正演问题预测的可靠性要提高很多, 对应的反问题的凸性也会高很多。
特征波反演的核心问题之一在于解问题(10) 式。相比于波场重构反演方法[6], 特征波场反演的物理意义十分明确, 可操作性很强, 据此可以构建出有效的反演技术路线。尤其是, 公式(10) 的求解一般在压缩感知框架下进行, 可以将先进的信号处理理论运用于特征波提取及反演成像中。更重要的是, 特征波的提取不仅仅是现代信号框架(或压缩感知框架) 下的操作, 而是按照波动理论的物理意义进行操作(譬如仅仅提出透射波场和一次反射波场), 尽可能建立起特征波场与特征参数之间的联系, 使得提出的特征波反演成像问题更凸。
特征波反演成像的基本过程可以描述如下。首先, 我们将一般的地震数据表达成特征数据, 提取特征数据的过程可用下式抽象地表示:
| $\boldsymbol{d}_{\rm{C}}^{{\rm{obs}}}\left( {{\boldsymbol{x}_{\rm{s}}}, {\boldsymbol{p}_{\rm{s}}}, {\boldsymbol{x}_{\rm{r}}}, {\boldsymbol{p}_{\rm{r}}}, t} \right) = P\left[{{\boldsymbol{d}^{{\rm{obs}}}}\left( {{\boldsymbol{x}_{\rm{s}}}, {\boldsymbol{x}_{\rm{r}}}, t} \right)} \right]$ | (17) |
式中: xs代表炮点的位置, xr代表检波点的位置, ps代表炮点端的射线参数, pr代表检波点端的射线参数, t是到达时, dCobs(xs, ps, xr, pr, t) 表示特征地震数据, dobs(xs, xr, t) 代表常规地震数据, P(·) 代表某种变换算子。变换算子P(·) 的选择可以非常灵活, 代表我们希望用什么样的波场成分进行反演成像。
在特征波场的概念下, 一般的正问题可写成如下积分形式:
| $\begin{array}{l} {\boldsymbol{u}^{\rm{C}}}\left( {{\boldsymbol{x}_{\rm{s}}}, {\boldsymbol{p}_{\rm{s}}}, {\boldsymbol{x}_{\rm{r}}}, {\boldsymbol{p}_{\rm{r}}}, t} \right) = \int {K\left[{{\boldsymbol{v}_{\rm{b}}}\left( \boldsymbol{x} \right) + } \right.} \\ \left. {\delta {\boldsymbol{v}_{\rm{b}}}\left( \boldsymbol{x} \right);{\boldsymbol{x}_{\rm{s}}}, {\boldsymbol{x}_{\rm{r}}}, \boldsymbol{x}, t} \right]{\boldsymbol{m}^{\rm{C}}}\left( \boldsymbol{x} \right){\rm{d}}\boldsymbol{x} \end{array}$ | (18) |
式中: u C(x s, p s, x r, p r, t) 是特征波场数据, K代表灵敏度核函数, m C(x) 是特征模型参数(即反射界面的反射系数); v b(x) 是背景速度。在K的性质比较好(譬如其逆算子存在) 的情况下, 特征波场数据与特征模型参数之间建立起了一对一的映射关系, 此时的反演成像问题凸性一定是好的。
在上述正问题的基础上, 可以建立如下地震波反演成像问题:
| $\begin{array}{c} J\left[{\delta {\boldsymbol{v}_{\rm{b}}}\left( \boldsymbol{x} \right), {\boldsymbol{m}^{\rm{C}}}\left( \boldsymbol{x} \right)} \right] = \left\| {{\boldsymbol{u}^{\rm{C}}}\left[{{\boldsymbol{v}_{\rm{b}}}\left( \boldsymbol{x} \right) + } \right.} \right.\\ {\left. {\left. {\delta {\boldsymbol{v}_{\rm{b}}}\left( \boldsymbol{x} \right), {\boldsymbol{m}^{\rm{C}}}\left( \boldsymbol{x} \right)} \right] -\boldsymbol{d}_{\rm{C}}^{{\rm{obs}}}} \right\|^2} \end{array}$ | (19) |
式中: u C[v b(x)+δv b(x), m C(x)]为计算的特征波场, δv b(x) 是背景速度的低波数扰动; m C(x) 则为速度场的高波数扰动(反射系数), 它代表了速度模型的几何特征(即反射界面的几何形态信息)。假定背景速度v b(x) 是已知的, δ v b(x) 和m C(x) 是要反演的模型参数。事实上, 背景速度v b(x) 也要通过透射波层析反演来确定。
用(18) 式和(19) 式可以进行各种特征波现象的反演。关键是特征波场对应什么样的波现象, 以及对应波现象的正问题如何描述。若将d Cobs和u C界定为一次反射波场, 则可以进行一次反射波的反演。同样, 也可以进行透射波的反演和多次波的反演。
一般地, 人们常用(19) 式进行一次反射波层析成像和最小二乘PSDM, 它们对应的梯度分别为∂J/∂δvb和∂J/∂mC。在数据域波动方程反射波层析反演中, 关键的问题在于如何将来自于同一反射层的同震相的d Cobs和u C对应起来, 不发生“串层”的情况, 这是数据域反射波层析成像的关键所在。同样, 在FWI (它不仅仅用了一次反射波和绕射波, 还用了多次反射和绕射波) 中也存在相应的问题, 这就是Cycle-Skipping (周期跳跃) 现象。在周期跳跃现象中, 数据的匹配要求更严格, 不能超过半个子波周期。这也是FWI中初始模型参数要非常接近真实模型参数的原因, 在这样的条件下, FWI反演问题才比较凸, 比较满足线性性要求。
为了避免上述数据匹配存在的困难, 可以将波动方程的反射波层析退化为反射波旅行时层析(reflection travel-time tomography, RT_Tomo)。此时反射波层析的要求变成测出(自动测出) 同一反射层的d Cobs和u C的旅行时差Δt。这也是RT_Tomo的核心工作, 其它按照一般的反射波层析框架操作即可。
成像域的反射波层析也可以基于特征波反演框架进行描述。事实上, 在特征波场情形下, 成像域的模型参数层析反演应该与数据域的模型参数层析反演等价。
如果进行旅行时层析, 无论是数据域还是成像域, 基本的问题都是时差测量问题。数据域中, 实测数据同相轴到达时是确定的, 实测数据和合成数据对应同相轴的时差测量结果可以认为是绝对的; 成像域中, 反射界面真深度是未知的, 基于成像道集的剩余深度差(residual moveout, RMO) 测量是相对的。这也是为什么需要在时间域进行层析速度反演的重要原因。实测数据和合成数据对应同相轴的时差测量是当前层析速度反演的一个核心问题, 解决了此问题, FWI中的周期跳跃问题就不存在了。AWI (Adaptive Waveform Inversion) 方法[22, 29]的本质也是试图解决这个问题。
6 特征波场提取的思想与方法从实测地震数据中根据反演成像的要求提取出特征波场的问题可以抽象为如下变换:
| $\boldsymbol{d}_{\rm{C}}^{{\rm{obs}}} = P\left( {{\boldsymbol{d}^{{\rm{obs}}}}} \right)$ | (20) |
其中, 变换算子P(·) 可以根据反演成像方法的需要选择各种形式, 关键是构建特定的反演方法时想利用什么样的波现象、想利用该波现象的什么特征。譬如, 对波场的Laplace变换[1]、对波场的Hilbert变换[3]、对波场的对数变换[27, 30]等。这些变换算子都侧重于提取反射子波的特征。
我们提取的特征波场首先考虑的是区别利用不同的波现象, 然后再进一步考虑利用特定波现象的更进一步的特征。我们认为, 特定波现象的方向传播特征是很基本的波场特征, 因此, 特征波场变换算子至少包含三重含义:①区分波现象; ②提取时空局部的方向波场; ③更进一步的子波波形特征的提取。
区分波现象主要是分开纵横波、透射波和反射波, 绕射波和反射波, 还包括分开一次波和多次波。提取时空局部的方向波场主要有基于基函数族和基于数据驱动的两种线性局部平面波提取方法。子波特征的提取主要是提取带限子波的到达时和相位。
这三个方面目前都存在问题, 尤其是在实测地震数据有较强噪声的情况下。带限子波的到达时和相位因为与振幅搅在一起, 其估计从概念上就存在问题。因此, 带限子波波形特征的表达和提取对于反演成像而言是更为重要的研究内容, 否则可能连到达时的含义都说不清楚, 速度层析反演的精度完全无法评价。子波振幅的影响因素就更复杂了。
本文主要关注的是在压缩感知框架下如何提取时空局部的方向波场。这个问题被提为如下变换域的反问题:
| $\begin{array}{l} {{\boldsymbol{\hat d}}_{\rm{C}}} = {\rm{arg}}\;\mathop {{\rm{min}}}\limits_{{\boldsymbol{d}_{\rm{C}}}} {\left\| {{\boldsymbol{d}_{\rm{C}}}} \right\|_1}\\ {\rm{s}}{\rm{.t}}{\rm{. }}{\left\| {\boldsymbol{A}{\boldsymbol{d}_{\rm{C}}}-{\boldsymbol{d}^{{\rm{obs}}}}} \right\|_2} \le \varepsilon \end{array}$ | (21a) |
式中: A是变换矩阵, 列向量构成基函数族。数据的特征表达原则上也可以用如下数据驱动的方式:
| $\mathop {\min }\limits_\boldsymbol{X} {\left\| \boldsymbol{X} \right\|_*}{\rm{s}}{\rm{.t}}{\rm{. }}{\left\| {\boldsymbol{A}\left( \boldsymbol{X} \right)-{\boldsymbol{d}^{{\rm{obs}}}}} \right\|_2} \le \varepsilon $ | (21b) |
式中:‖ X ‖ *代表核范数, 是矩阵X SVD分解后的奇异值的和;
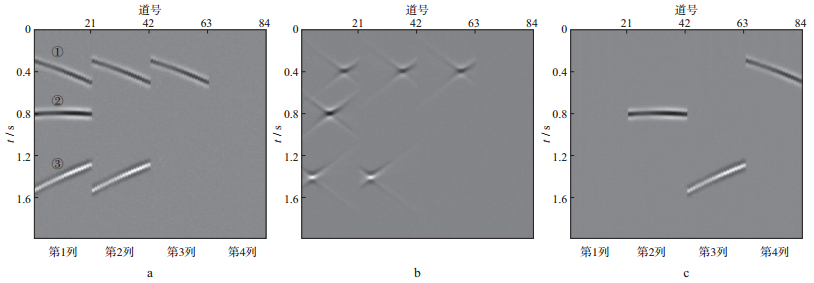
图 1展示了抽取特征波场的基本思想和做法。其中图 1a为匹配追踪方法抽取特征波场的示意图,从左到右包含4列:第1列为包含3个同相轴(①~③) 的局部波场;第2列为匹配追踪方法抽取水平同相轴②后的结果;第3列为再抽取斜同相轴③后的结果;第4列为3个同相轴全部抽取后的结果。图 1b为图 1a对应的τ-p谱。图 1c展示了数据恢复情况:第1列为原数据(图 1a第1列所示) 与反变换数据的差;第2列展示了恢复出的水平同相轴②;第3列展示了恢复的斜同相轴③;第4列展示了恢复的斜同相轴①。至此,比较完整地恢复出了原数据,实现了抽取和恢复的全过程。发展该方法的另一个目的是解决层析反演中实测数据同相轴和合成数据同相轴对应的时差测量问题,试图通过这样的方法避开周期跳跃现象。
|
图 1 特征波场的抽取 a 匹配追踪方法抽取特征波场方法的示意; b 与抽取的特征波场相对应的τ-p谱; c 数据恢复 |
数据域地震波反演的经典方法自然是FWI方法。经典FWI的目标是估计全或宽波数带的参数场。但是, 到目前为止的实践表明, 即使用经典FWI结合低频长偏移距数据估计低波数(背景) 的速度,也不是任何情形都能收敛的。这正是经典FWI衍生出很多变种的原因, 但这也造成了FWI概念的滥用。
此处我们要讨论的是基于CWF的特征波场反演(CWI), 包括四个关键步骤:①用压缩感知方法提取所要的特征波场(目前主要是初至波、早至波、一次反射波, 提取特征波场的目的主要是用来进行层析成像, 估计背景参数的变化); ②基于到达时(相位) 的透射波波动理论层析反演; ③基于到达时(相位) 的一次反射波波动理论层析反演; ④主要针对方位角度反射系数的最小二乘叠前深度偏移成像。
特征波场必须与要反演的参数之间有更紧密的关系才能使得构建的反演问题的凸性更好。我们提出如下的模型参数分解方法:
| $\boldsymbol{m}\left( \boldsymbol{x} \right) = {\boldsymbol{m}_0}\left( \boldsymbol{x} \right) + \Delta \boldsymbol{m}\left( \boldsymbol{x} \right) + R\left( {\boldsymbol{x, }\theta, \varphi } \right)$ | (22) |
式中:R(x, θ, φ) 代表方位角度反射系数, θ代表入射角度, φ代表方位角。
基于上述模型分解, 波场也可以分解为:
| $\begin{array}{l} G\left( {{\boldsymbol{x}_{\rm{r}}}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right) = {G_0}-{\omega ^2}{G_0}\delta \boldsymbol{m}{G_0} + {\omega ^4}{G_0}\delta \boldsymbol{m}{G_0}\delta \boldsymbol{m} \cdot \\ {G_0} + \cdots = {G_0}-{\omega ^2}\int {{G_0}\left( {{\boldsymbol{x}_{\rm{r}}}\left| \boldsymbol{\xi } \right.} \right){G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)} \delta \boldsymbol{m}\left( \boldsymbol{\xi } \right) \cdot \\ {\rm{d}}\boldsymbol{\xi + }{\omega ^4}\int {\int {{G_0}\left( {{\boldsymbol{x}_{\rm{r}}}\left| \boldsymbol{\eta } \right.} \right)\delta \boldsymbol{m}\left( \boldsymbol{\eta } \right){G_0}\left( {\boldsymbol{\eta }\left| \boldsymbol{\xi } \right.} \right)\delta \boldsymbol{m}\left( \boldsymbol{\xi } \right) \cdot } } \\ {G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right){\rm{d}}\boldsymbol{\xi }{\rm{d}}\boldsymbol{\eta + } \cdots \end{array}$ | (23) |
等式右端三项的具体含义分别为:第一项对应透射波; 第二项对应一次反射波; 第三项对应二次散射波。更高阶的散射波没有列出。地下存在散射点引起的场的扰动可以表示为:
| $\begin{array}{l} \delta G\left( {{\boldsymbol{x}_{\rm{r}}}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right) = G-{G_0} =-{\omega ^2}\int {{G_0}\left( {{\boldsymbol{x}_{\rm{r}}}\left| \xi \right.} \right) \cdot } \\ {G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)\delta \boldsymbol{m}\left( \xi \right){\rm{d}}\boldsymbol{\xi + }{\omega ^4}\int {{G_0}\left( {{\boldsymbol{x}_{\rm{r}}}\left| \boldsymbol{\eta } \right.} \right)\delta \boldsymbol{m}\left( \boldsymbol{\eta } \right) \cdot } \\ {G_0}\left( {\boldsymbol{\eta }\left| \boldsymbol{\xi } \right.} \right)\delta \boldsymbol{m}\left( \boldsymbol{\xi } \right){G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right){\rm{d}}\boldsymbol{\xi }{\rm{d}}\boldsymbol{\eta + } \cdots \\ = \delta {G_1}\left( {{\boldsymbol{x}_{\rm{r}}}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right) + \delta {G_2}\left( {{\boldsymbol{x}_r}\left| {{\boldsymbol{x}_s}} \right.} \right) + \cdots \end{array}$ | (24) |
式中:δG1(x r| x s) 代表一阶扰动场; δG2(x r| x s) 代表二阶扰动场; 更高阶的扰动场被忽略。当弱散射假设成立时, 更高阶的扰动场很弱, 忽略掉是合理的。
对应地, 零阶扰动波场(透射波场)、一阶扰动波场和二阶扰动波场的波场扰动相对于介质扰动的梯度分别定义如下。
| $\frac{{\partial {G_0}\left( {{\boldsymbol{x}_{\rm{r}}}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)}}{{\partial \boldsymbol{m}}} = \mathop {\lim }\limits_{\boldsymbol{m} \to {\boldsymbol{m}_0}} \frac{{{G_0}\left( \boldsymbol{m} \right)-{G_0}\left( {{\boldsymbol{m}_0}} \right)}}{{\boldsymbol{m}-{\boldsymbol{m}_0}}}$ | (25a) |
| $\begin{array}{l} \frac{{\partial \delta {G_1}\left( {{\boldsymbol{x}_{\rm{r}}}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)}}{{\partial \delta \boldsymbol{m}\left( \boldsymbol{x} \right)}} = \frac{\partial }{{\partial \delta \boldsymbol{m}\left( \boldsymbol{x} \right)}}\left[{-{\omega ^2}\int {{G_0}\left( {{\boldsymbol{x}_{\rm{r}}}\left| \boldsymbol{\xi } \right.} \right){G_0}\left( {\left. \boldsymbol{\xi } \right|} \right.} } \right.\\ \left. {\left. {{\boldsymbol{x}_{\rm{s}}}} \right)\delta \boldsymbol{m}\left( \boldsymbol{\xi } \right){\rm{d}}\boldsymbol{\xi }} \right] = -{\omega ^2}{G_0}\left( {{\boldsymbol{x}_{\rm{r}}}\left| \boldsymbol{x} \right.} \right){G_0}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right) \end{array}$ | (25b) |
| $\begin{array}{l} \frac{{\partial \delta {G_2}\left( {{\boldsymbol{x}_{\rm{r}}}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)}}{{\partial \delta \boldsymbol{m}\left( \boldsymbol{x} \right)}} = \frac{\partial }{{\partial \delta \boldsymbol{m}\left( \boldsymbol{x} \right)}}\left[ {{\omega ^4}\int {\int {{G_0}\left( {{\boldsymbol{x}_{\rm{r}}}\left| \boldsymbol{\eta } \right.} \right)\delta \boldsymbol{m}\left( \boldsymbol{\eta } \right)} } } \right. \cdot \\ \left. {{G_0}\left( {\boldsymbol{\eta }\left| \boldsymbol{\xi } \right.} \right)\delta \boldsymbol{m}\left( \boldsymbol{\xi } \right){G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right){\rm{d}}\boldsymbol{\xi }{\rm{d}}\boldsymbol{\eta }} \right]\\ = \frac{\partial }{{\partial \delta \boldsymbol{m}\left( \boldsymbol{x} \right)}}\left\{ { - {\omega ^2}\int {{G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_s}} \right.} \right)\delta \boldsymbol{m}\left( \boldsymbol{\xi } \right)\left[ { - {\omega ^2}\int {{G_0}\left( {\left. {{\boldsymbol{x}_{\rm{r}}}} \right|} \right.} } \right.} } \right.\\ \left. {\left. {\left. \boldsymbol{\eta } \right)\delta \boldsymbol{m}\left( \boldsymbol{\eta } \right){G_0}\left( {\boldsymbol{\eta }\left| \boldsymbol{\xi } \right.} \right){\rm{d}}\boldsymbol{\eta }} \right]{\rm{d}}\boldsymbol{\xi }} \right\}\\ = \frac{\partial }{{\partial \delta \boldsymbol{m}\left( \boldsymbol{x} \right)}}\left[ { - {\omega ^2}\int {{G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)\delta \boldsymbol{m}\left( \boldsymbol{\xi } \right)\delta {G_1}\left( {\xi \left| {{\boldsymbol{x}_{\rm{r}}}} \right.} \right){\rm{d}}\boldsymbol{\xi }} } \right]\\ = - {\omega ^2}{G_0}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)\delta {G_1}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{r}}}} \right.} \right) - {\omega ^2}\int {{G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right) \cdot } \\ \delta \boldsymbol{m}\left( \boldsymbol{\xi } \right)\frac{{\partial \delta {G_1}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{r}}}} \right.} \right)}}{{\partial \delta \boldsymbol{m}\left( \boldsymbol{x} \right)}}{\rm{d}}\boldsymbol{\xi }\\ = - {\omega ^2}{G_0}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)\delta {G_1}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{r}}}} \right.} \right) + {\omega ^4}\int {{G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right) \cdot } \\ \delta \boldsymbol{m}\left( \boldsymbol{\xi } \right){G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right){G_0}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{r}}}} \right.} \right){\rm{d}}\boldsymbol{\xi }\\ = - {\omega ^2}{G_0}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)\delta {G_1}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{r}}}} \right.} \right) + {G_0}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{r}}}} \right.} \right){\omega ^4} \cdot \\ \int {{G_0}\left( {\boldsymbol{\xi }\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)\delta \boldsymbol{m}\left( \boldsymbol{\xi } \right){G_0}\left( {\boldsymbol{\xi }\left| \boldsymbol{x} \right.} \right){\rm{d}}\boldsymbol{\xi }} \\ = - {\omega ^2}{G_0}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right)\delta {G_1}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{r}}}} \right.} \right) - {\omega ^2}{G_0}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{r}}}} \right.} \right) \cdot \\ \delta {G_1}\left( {\boldsymbol{x}\left| {{\boldsymbol{x}_{\rm{s}}}} \right.} \right) \end{array}$ | (25c) |
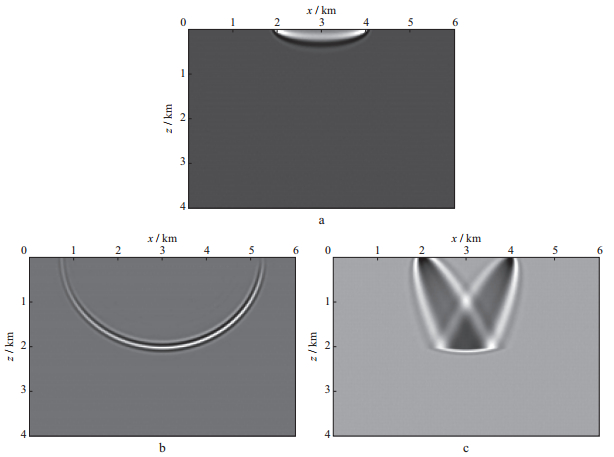
(25a) 至(25c) 式分别定义了联系波场扰动和介质参数扰动的积分核(Kernel)。波动理论下, 3个梯度项的示意图分别如图 2a, 图 2b和图 2c所示。
更进一步地, 对于一阶扰动和二阶扰动而言, 必须充分利用地下介质的既有特征。我们将油气地震勘探面对的地下介质的特征表述为:在空间上广泛分布的层状沉积层, 加上火山活动、构造运动等导致的大小尺度速度异常体(或波阻抗变化的异常体)。即地下介质的分层性是勘探地震所面对的介质的重要特征, 产生绕射和散射的介质特征是次要的。
因此, 二阶扰动波场的层析成像和一阶扰动波场的偏移成像都利用了这样的特征。只有对反射界面而言, 才会产生图 2c所示的“兔子耳朵”响应。对于层析成像而言, 可以利用反偏移计算图 2c所示的二阶扰动响应; 对于偏移成像而言, 可以针对方位角度反射系数进行成像。
|
图 2 透射波扰动响应(a)、一阶扰动场响应(b) 和二阶扰动场响应(c) |
实质上, FWI是一种假设地下介质为背景+散射体(点) 模式的反演成像方法。这样的成像方法应该对应封闭面上全方位激发接收的观测方式, 而不是勘探地震仅在地表面进行的观测方式。我们认为这也是FWI方法或逆散射成像方法不能很好地用于油气地震勘探领域的重要原因。
基于上述分析, 我们认为, 将FWI分为如CWI所阐述的三个线性反演步骤在数学物理上是合理的。更进一步地, 我们认为背景速度和各向异性参数与一阶扰动和二阶扰动场中的同相轴的到达时(相位) 关
系密切, 这些参数的估计不仅要利用到达时(相位), 还要尽可能剥离振幅对达到时(相位) 测量的影响。事实上, 层析反演的理论框架基本是定型的, 实际数据到达时(相位)、合成数据到达时(相位) 以及对应同相轴上二者之间的差的测量是层析成像方法与技术的核心问题。我们提出压缩感知框架下的CWF提取, 其中一个重要的目的就是发展出有效的对应同相轴上实际数据到达时(相位) 和合成数据到达时(相位) 之间的差的测量方法。
这是我们坚持的将FWI实用化的具体路线。鉴于篇幅, 具体数值结果见参考文献[10]。
8 成像域的特征波反演地震波反演也可以在成像域中进行, 基本思想是不同角度(或偏移距) 的数据产生的像理论上应出现在相同的空间位置上, 即所谓的正确的成像速度产生正确的像, 错误的成像速度产生错误的像。也可以说成像速度的扰动产生了像的扰动, 成像速度的扰动与像的扰动之间存在线性关系, 建立这样的线性关系就可以进行成像速度的反演。正确的像是对同一地下像点而言, 不同角度或偏移距的照明数据产生的像出现在该地下成像点上, 表现为成像道集拉平或聚焦在一起。我们认为, 这与Bayesian框架下的数据域的参数估计理论有着本质区别, 具体表现在:①在成像域仅仅能估计光滑的成像速度, 因为高波数的速度变化对产生拉平或聚焦的道集并无贡献, 而道集的拉平或聚焦正是建立像域反演目标泛函的基础; ②像域的成像速度估计缺乏概率统计意义下的解释。
特征数据体产生的像可以用下式表示:
| $\begin{array}{c} I\left( {{\boldsymbol{x}_I}, {z_I}\left| {\theta, \varphi } \right.} \right) = \sum\limits_S {\sum\limits_R {\int_t {u_{\rm{S}}^{\rm{C}}\left( {\boldsymbol{x}, t;{\boldsymbol{x}_{\rm{s}}}, {\boldsymbol{p}_{\rm{s}}}} \right) \cdot } } } \\ u_{\rm{R}}^{\rm{C}}\left( {\boldsymbol{x}, t;{\boldsymbol{x}_{\rm{r}}}, {\boldsymbol{p}_{\rm{r}}}} \right){\rm{d}}t \end{array}$ | (26) |
式中: xI=(xI, yI) 是像点的平面坐标; zI是像的深度; θ是张角; φ是方位角; uSC(x, t; x s, p s) 是外推到成像点处的源端特征波场; uRC(x, t; x r, p r) 是外推到成像点处的检波端特征波场。
构建像域的反问题有两条途径:一是通过检测成像道集的拉平或聚焦情况建立目标泛函, 通过对目标泛函的求导, 建立梯度导引类的优化反演方法, 估计成像速度[5, 34-37]; 二是直接建立像的扰动与成像速度扰动之间的线性关系[38-39], 基于此线性关系进行成像速度的层析反演。
首先讨论第一种方法。SHEN[35]给出了两类所谓的差异相似性优化(differential semblance optimization, DSO) 目标函数, 分别描述地下偏移距(h) 道集在零偏移距处的聚焦特性和角度(θ) 道集的拉平特性。目标函数分别为:
| $\begin{array}{l} \min {J_h}\left( \boldsymbol{m} \right) = \frac{1}{2}\left\| {P\left( h \right)I} \right\|_2^2 = \frac{1}{2}\sum\limits_x {\sum\limits_z {\sum\limits_h \cdot } } \\ {\left[{hI\left( {\boldsymbol{x}, z, h} \right)} \right]^2} \end{array}$ | (27) |
| $\begin{array}{c} {{\mathop{\rm minJ}\nolimits} _\theta }\left( \boldsymbol{m} \right) = \frac{1}{2}\left\| {P\left( \theta \right)I} \right\|_2^2 = \frac{1}{2}\sum\limits_x {\sum\limits_z {\sum\limits_\theta \cdot } } \\ {\left[{\frac{\partial }{{\partial \theta }}I\left( {\boldsymbol{x}, z, \theta } \right)} \right]^2} \end{array}$ | (28) |
式中:P(h)=h为零阶差分算子; P(θ)=∂/∂θ为一阶差分算子。
对于公式(27), 当速度正确时, 地下偏移距道集聚焦于h=0处, 目标函数取得极小值。该目标函数的凸性较好, 且不受周期跳跃问题制约, 但对中小尺度的速度扰动不敏感, 速度估计的精度低。SHAN等[40-41]指出, (27) 式的收敛受到成像道集振幅的影响。当地下照明能量较弱时, 需要引入照明补偿等, 否则强反射层的像会主导泛函能量, 影响泛函收敛。此外, (27) 式的梯度中含有一些近垂直的条带状假象, 影响反演的收敛。FEI等[42]通过修改成像差(用关于h的一阶差分算子作用于地下偏移距域的像) 的定义, 改善泛函梯度的性质并加速反演收敛。
根据成像原理, 当速度正确时, 角度道集的像是拉平的, 相邻角度像的差异较小。由此可以得出公式(28) 描述的角度道集DSO目标函数。由于(28) 式只需要对相邻角度的像进行差分运算, 所以弱化了周期跳跃问题的制约, 降低了对初始模型的精度要求。然而, 差分运算会放大角度道集中高频变化的影响, 对角度道集的质量也有一定的要求。
SOUBARAS等[28]提出了角度道集叠加能量最大化方法, 目标函数可以写为:
| $\max {J_{{\rm{SPM}}}}\left( \boldsymbol{m} \right) = \frac{1}{2}\sum\limits_x {\sum\limits_z {{{\left[{\sum\limits_\theta {I\left( {\boldsymbol{x}, z, \theta } \right)} } \right]}^2}} } $ | (29) |
式中:I(x, z, θ) 为角度域成像道集。该方法的精度高于上述DSO类的反演方法。然而, 当初始速度与真实速度的差异较大时, 角度道集的RMO较大, 甚至大于半个子波长度。此时, 若按照公式(29) 对所有角度叠加, 会遇到与FWI类似的周期跳跃问题。因此, 该方法对初始模型的要求较高。
值得提及的是, 地下偏移距成像道集是不区分反射和散射(绕射) 的, 都可以产生对应当前偏移速度的聚焦道集; 角度成像道集是针对反射波的, 只有反射界面才有对应的角度成像道集。因此, (27) 式定义的泛函和(28) 及(29) 式定义的泛函适用于不同的介质参数分布情形。我们认为, 反射界面的存在是勘探地震的特征, 应该充分利用这样的特征。
在上述目标泛函特性分析的基础上, 可以进入梯度导引的反演过程中。但是, 我们认为利用地下偏移距聚焦成像道集, 基于聚焦好坏建立目标泛函进行成像速度的反演理论上是存在问题的。不能用聚焦好坏(能量聚焦度) 作为目标函数进行优化反演、更新成像速度。原因之一是目标泛函的梯度不能指示速度修正量的正或负(这与数据逼近泛函不同); 原因之二是影响振幅的因素太多, 聚焦能量最小并不一定预示背景速度的修正是正确的。角度道集叠加能量最大化目标泛函同样存在不合适地利用振幅的问题。利用角度道集之间的像差建立目标泛函进行速度反演是合理的逻辑, 但是其中AVA关系的影响及像的振幅畸变的影响会导致方法不稳定。总之, 我们不认为在像域进行上述基于像的振幅构建泛函、进行背景速度反演的方式是正确的选择。DSO之类的像域背景速度估计概念20多年来始终无法在勘探地震中实际应用很能说明这一问题。
以下讨论构建像域反问题的第二种方法。首先建立像的扰动与成像速度扰动之间的关系。由(26) 式可见, 像的扰动必然是其中波场的扰动引起的, 而场的扰动又是由于成像速度的扰动(即成像速度与成像真速度之间的差) 引起的。因此, 引入像的扰动为:
| $\begin{array}{l} \delta I\left( {{\boldsymbol{x}_I}, {z_I}\left| {\gamma, \varphi } \right.} \right) = \sum\limits_S {\sum\limits_R {\int_t {\left[{\delta u_{\rm{S}}^C\left( {\boldsymbol{x}, t;{\boldsymbol{x}_{\rm{s}}}, {\boldsymbol{p}_{\rm{s}}}} \right) \cdot } \right.} } } \\ \left. {u_{\rm{R}}^{\rm{C}}\left( {\boldsymbol{x}, t;{\boldsymbol{x}_{\rm{r}}}, {\boldsymbol{p}_{\rm{r}}}} \right) + u_{\rm{S}}^{\rm{C}}\left( {\boldsymbol{x}, t;{\boldsymbol{x}_{\rm{s}}}, {\boldsymbol{p}_{\rm{s}}}\delta u_{\rm{R}}^{\rm{C}}\left( {\boldsymbol{x}, t;{\boldsymbol{x}_{\rm{r}}}, {\boldsymbol{p}_{\rm{r}}}} \right)} \right.} \right]{\rm{d}}t \end{array}$ | (30) |
很显然, 场的扰动与速度扰动之间的关系是由散射场的Born计算公式决定的, 即:
| $\begin{array}{c} \delta u_{\rm{S}}^{\rm{C}}\left( {\boldsymbol{x}, t;{\boldsymbol{x}_{\rm{s}}}, {\boldsymbol{p}_{\rm{s}}}} \right) = \int {{G_0}\left( {\boldsymbol{y}, t-\tau ;\boldsymbol{x}} \right) \cdot } \\ \frac{{2\delta {\boldsymbol{v}_I}\left( \boldsymbol{y} \right)}}{{\boldsymbol{v}_I^3\left( \boldsymbol{y} \right)}}\frac{{{\partial ^2}}}{{\partial {\tau ^2}}}S\left( {\boldsymbol{y}, \tau ;{\boldsymbol{x}_{\rm{s}}}} \right){\rm{d}}\tau {\rm{d}}\boldsymbol{y} \end{array}$ | (31a) |
| $\begin{array}{l} \delta u_{\rm{R}}^{\rm{C}}\left( {\boldsymbol{x}, t;{\boldsymbol{x}_{\rm{R}}}, {\boldsymbol{p}_{\rm{R}}}} \right) = \int {{G_0}\left( {\boldsymbol{y}, t-\tau ;\boldsymbol{x}} \right) \cdot } \\ \frac{{2\delta {\boldsymbol{v}_I}\left( \boldsymbol{y} \right)}}{{\boldsymbol{v}_I^3\left( \boldsymbol{y} \right)}}\frac{{{\partial ^2}}}{{\partial {\tau ^2}}}u\left( {\boldsymbol{y}, \tau ;{\boldsymbol{x}_{\rm{s}}}} \right){\rm{d}}\tau {\rm{d}}\boldsymbol{y} \end{array}$ | (31b) |
将(31) 式代入(30) 式可以导出像的扰动和成像速度扰动之间的线性关系:
| $A\Delta \boldsymbol{m} = \delta I$ | (32) |
用共轭梯度法求解上式可以得到更新的成像速度。公式(30) 至公式(32) 概念上是没有问题的, 抽象地讲, 这些公式可以用于不区分散射和反射的一般情形, 但是具体应用时要区分是用于反射情形还是用于散射情形。在实际应用中, (32) 式右端项表示的像的扰动很难有效获取, 因为真像是未知的!在针对反射情形的角度成像道集中, 像的扰动代表道集没有拉平, 本次偏移速度得到的像与真像之间有差异, 并且最主要的差异就是成像深度差RMO!因此, 还是要利用特征波场(局部平面波场) 与特征像(角度成像道集) 的概念, 建立起它们之间的联系, 进行基于RMO的波动理论的角度成像道集层析成像。其中, 有效的RMO的检测是最为核心的问题。在此基础上, 有必要和有可能的话, 再基于公式(30) 至公式(32) 进行层析成像。这是我们一直坚持的像域中速度估计与建模的基本理念。鉴于篇幅, 具体数值结果不在此展示。
9 结论与讨论FWI是勘探地震中地震波反演成像的核心理念。它将地下介质视为背景+散射(点) 的模式, 并试图对实测炮集中所有波现象进行基于振幅的波形逼近基础上的反演, 其目标是估计全或宽波数带的速度场。但勘探地震中的实践表明, 仅有地表观测的地震数据, 不对勘探地震介质的特征和波场特征加以利用, 即使仅用透射波进行基于低频长偏移距数据的背景参数估计, FWI方法也不很稳定(视数据情况达到收敛或不收敛)。
我们认为, 一定假设下的地震波正演方法可以预测实际地震波场是地震波反演最基本的要求。既然无论如何选择地震波正演模拟方法都无法完全预测实测数据中的波场, 转而追求尽可能好地模拟其中的部分特征波场、进行基于特征波场的反演成像是合理的逻辑。特征表达参数模型和特征表达数据体得到二者之间联系更密切的关系, 可以将强非线性的经典FWI问题转化为一个较凸的反问题并进行求解。基于上述理念提出的特征波反演成像(CWI) 方法, 其中心工作在于特征波场的提取, 包括三方面的含义:①特征波型的提取(波型分解); ②压缩感知框架下特征波场的提取(时空局部的方向波场的分解); ③反射子波特征的提取(子波分解)。特征波场与反演参数之间的关系更紧密, 基于特征波场的反问题凸性更好。另外, 特征波成像中梯度的预条件要相对简单, 因为特征波对应的梯度干扰大大减弱。
CWI包括四个关键步骤:①用压缩感知方法提取所要的特征波场; ②基于到达时(相位) 的透射波波动理论层析反演; ③基于到达时(相位) 的一次反射波波动理论层析反演; ④主要针对方位角度反射系数的最小二乘叠前深度偏移成像。到目前为止, 参数的低波数成分估计方法基本确定, 就是透射层析和反射波层析, 其中的反演方法框架已较为成熟(具体计算中还会有一些问题), 但是对应的到达时(相位) 差测量是一个核心问题。实质上, FWI中的周期跳跃就是因为没有解决好对应同相轴的时差(相位) 测量问题, 否则, 周期跳跃问题是不存在的。时差(相位) 测量一定会受到振幅的影响, 这也是物理上不可避免的, 我们能做的只是减少这种影响。我们将时差测量问题作为CWI的核心问题来对待。
关于参数的高波数成分估计, 我们认为目前还没有什么公认的方法技术路线。FWI方法假设地下介质是背景+散射(体), 而且在一个迭代过程中, 从低波数成分到高波数成分全部估计出来。实践证明, FWI方法中高波数分量估计的收敛性是十分没有保障的。即便是经典的最小二乘RTM (LS_RTM) 方法, 也是这样假设介质的分布, 在Born近似下进行数据逼近的反演, 收敛性也没有什么保障。LS_RTM经过这么多年的研究始终不能大规模处理实际数据也说明了这种技术的局限性。在射线+Born近似下的角度反射系数最小二乘反演估计可以算是利用了勘探地震地下介质特征的高波数分量估计方法, 但是在小尺度散射(绕射) 体分布比较多的探区, 这样的成像方法显然是不合适的。兼顾反射波和散(绕) 射波成像的高波数成分估计方法目前是有必要发展的, 我们正试图沿这样的路线发展出比较实用的高波数分量估计方法。
| [1] | SHIN C, CHA Y H. Waveform inversion in the Laplace-Fourier domain[J]. Geophysical Journal International, 2009, 177(3): 1067-1079 DOI:10.1111/gji.2009.177.issue-3 |
| [2] | SHIN C, MIN D. Waveform inversion using a log arithmic wavefield[J]. Geophysics, 2006, 71(3): R31-R42 DOI:10.1190/1.2194523 |
| [3] | BOZDA E, TRAMPERT J, TROMP J. Misfit functions for full waveform inversion based on instantaneous phase and envelope measurements[J]. Geophysical Journal International, 2011, 185(2): 845-870 DOI:10.1111/gji.2011.185.issue-2 |
| [4] | WU R S, HU C, WANG B. Nonlinear sensitivity operator and inverse thin-slab propagator for tomographic waveform inversion[J]. Expanded Abstracts of 84th Annual Internat SEG Mtg, 2014: 928-933 |
| [5] | SHEN P, SYMES W W. Automatic velocity analysis via shot profile migration[J]. Geophysics, 2008, 73(5): 49-59 DOI:10.1190/1.2972021 |
| [6] | VAN LEEUWEN T, HERRMANN F J. Mitigating local minima in full-waveform inversion by expanding the search space[J]. Geophysical Journal International, 2013, 195(1): 661-667 DOI:10.1093/gji/ggt258 |
| [7] | VAN LEEUWEN T, HERRMANN F J, PETERS B.A new take on fwi-wavefield reconstruction inversion[R].Amsterdam, Netherlands:76th EAGE Conference and Exhibition, 2014 |
| [8] |
王华忠, 冯波, 刘少勇, 等. 叠前地震数据特征波场分解、偏移成像与层析反演[J].
地球物理学报, 2015, 58(6): 2024-2034 WANG H Z, FENG B, LIU S Y, et al. Characteristicwavefield decomposition, imaging and inversion with prestack seismic data[J]. Chinese Journal of Geophysics, 2015, 58(6): 2024-2034 |
| [9] |
王华忠, 冯波, 王雄文, 等. 压缩感知及其在勘探地震中的应用[J].
石油物探, 2016, 55(4): 467-474 WANG H Z, FENG B, WANG X W. Compressed sensing and its application in seismic exploration[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 467-474 |
| [10] |
冯波.数据域波动方程层析速度反演方法研究[D].上海:同济大学, 2015
FENG B.Data domain wave equation tomography for velocity inversion[D].Shanghai:Tongji University, 2015 |
| [11] | ROCKAFELLAR R T. Lagrange multipliers and optimality[J]. SIAM review, 1993, 35(2): 183-238 DOI:10.1137/1035044 |
| [12] | TARANTOLA A. Linearized inversion of seismic reflection data[J]. Geophysical Prospecting, 1984, 32(6): 998-1015 DOI:10.1111/gpr.1984.32.issue-6 |
| [13] | BUNKS C, SALECK F M, ZALESKI S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473 DOI:10.1190/1.1443880 |
| [14] | SIRGUE L, PRATT R G. Efficient waveform inversion and imaging:a strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(1): 231-248 DOI:10.1190/1.1649391 |
| [15] | VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26 DOI:10.1190/1.3238367 |
| [16] | CARA M, LÉVÊQUE J J. Waveform inversion using secondary observables[J]. Geophysical Research Letters, 1987, 14(10): 1046-1049 DOI:10.1029/GL014i010p01046 |
| [17] | LUO Y, SCHUSTER G T. Wave-equation traveltime inversion[J]. Geophysics, 1991, 56(5): 645-653 DOI:10.1190/1.1443081 |
| [18] | GEE L S, JORDAN T H. Generalized seismological data functionals[J]. Geophysical Journal International, 1992, 111(2): 363-390 DOI:10.1111/gji.1992.111.issue-2 |
| [19] | FICHTNER A, KENNETT B L N, IGEL H, et al. Theoretical background for continental-and global-scale full-waveform inversion in the time-frequency domain[J]. Geophysical Journal International, 2008, 175(2): 665-685 DOI:10.1111/gji.2008.175.issue-2 |
| [20] | VAN LEEUWEN T, MULDER W A. A correlation-based misfit criterion for wave-equation traveltime tomography[J]. Geophysical Journal International, 2010, 182(3): 1383-1394 DOI:10.1111/j.1365-246X.2010.04681.x |
| [21] | MOGHADDAM P P, MULDER W A. The diagonalator:inverse data space full waveform inversion[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg, 2012: 1-6 |
| [22] | WARNER M, GUASCH L.Adaptive waveform inversion:FWI without cycle skipping[R].Amsterdam, Netherlands:76th EAGE Conference & Exhibition, 2014 |
| [23] | DE HOOP M V, VAN DER HILST R D, SHEN P. Wave-equation reflection tomography:annihilators and sensitivity kernels[J]. Geophysical Journal International, 2006, 167(3): 1332-1352 DOI:10.1111/gji.2006.167.issue-3 |
| [24] | WEIBULL W, ARNTSEN B, NILSEN E. Initial velocity models for full waveform inversion[J]. Expanded Abstracts of 82ndAnnual Internat SEG Mtg, 2012: 1-4 |
| [25] | TARANTOLA A. Inverse problem theory and methods for model parameter estimation[M]. Paris, France: SIAM, 2005: 20-37. |
| [26] |
赫孝良, 葛照强编著.
最优化与最优控制[M]. 西安: 西安交通大学出版社, 2015: 135-155.
HE X L, GE Z Q. Optimization and optimal control[M]. Xi'an: Xi'an Jiaotong University Press, 2015: 135-155. |
| [27] | BEDNAR J B, SHIN C, PYUN S. Comparison of waveform inversion, part 2:phase approach[J]. Geophysical Prospecting, 2007, 55(4): 465-475 DOI:10.1111/gpr.2007.55.issue-4 |
| [28] | SOUBARAS R, GRATACOS B. Velocity model building by semblance maximization of modulated-shot gathers[J]. Geophysics, 2007, 72(5): U67-U73 DOI:10.1190/1.2743612 |
| [29] | WARNER M, GUASCH L. Robust adaptive waveform inversion[J]. Expanded Abstract of 85th Annual Internat SEG Mtg, 2015: 1059-1063 |
| [30] | SUKJOON P, SHIN C, BEDNAR J B. Comparison of waveform inversion:part 2:amplitude approach[J]. Geophysical Prospecting, 2007, 55(4): 477-485 DOI:10.1111/gpr.2007.55.issue-4 |
| [31] | KREIMER N, STANTON A, SACCHI M D. Tensor completion based on nuclear norm minimization for 5D seismic data reconstruction[J]. Geophysics, 2013, 78(6): V273-V284 DOI:10.1190/geo2013-0022.1 |
| [32] | OROPEZA V, SACCHI M D. Simultaneous seismic data denoising and reconstruction via multichannel analysis[J]. Geophysics, 2011, 76(3): V25-V32 DOI:10.1190/1.3552706 |
| [33] | RECHT B. A simpler approach to matrix completion[J]. Journal of Machine Learning Research, 2011, 12(4): 3413-3430 |
| [34] | SYMES W W, VERSTEEG R. Velocity model determination using differential semblance optimization[J]. Expanded Abstracts of 63rd Annual Internat SEG Mtg, 1993: 696-699 |
| [35] | SHEN P. Differential semblance velocity analysis via shot profile migration[J]. Expanded Abstracts of 75th Annual Internat SEG Mtg, 2005: 2249-2253 |
| [36] |
刘玉金.复杂介质条件下基于反演的地震成像方法研究[D].青岛:中国石油大学(华东), 2014
LIU Y J.Seismic imaging based on inversion in complex media[D].Qingdao:China University of Petroleum (East China), 2014 |
| [37] | LIU Y, SYMES W W, LI Z. Extended reflection waveform inversion via differential semblance optimization[J]. Expanded Abstracts of 84th Annual Internat SEG Mtg, 2014: 1149 |
| [38] | BAKER P M, GERRITSEN S, CAO Q, et al. 3D RTM-based wave-path tomography:theory and applications to synthetic and field data[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015: 5259-5264 |
| [39] | BAKER P M, GERRITSENS, CAO Q, et al.3D RTM-based wave-path tomography tested at a realistic scale[R].Madrid, Spain:77th EAGE Conference & Exhibition-Workshops, 2015 |
| [40] | SHAN G, WANG Y. RTM based wave equation migration velocity analysis[J]. Expanded Abstracts of 83rd Annual Internat SEG Mtg, 2013: 4726-4731 |
| [41] | YANG T, SHRAGGE J, SAVA P. Illumination compensation for image-domain wavefield tomography[J]. Geophysics, 2013, 78(5): U65-U76 DOI:10.1190/geo2012-0278.1 |
| [42] | FEI W, WILLIAMSON P. On the gradient artifacts in migration velocity analysis based on differential semblance optimization[J]. Expanded Abstracts of 80th Annual Internat SEG Mtg, 2010: 4071-4076 |


