全波形反演(FWI)[1-5]利用地表或井中观测的地震信号进行反演以获得地下介质的物理参数, 如速度或密度分布等。数学上, 全波形反演可以看作是一种基于偏微分方程约束的优化问题, 通过不断迭代更新模型参数来减小观测数据和模型数据之间的误差(又称目标函数, 通常用最小二乘误差表示), 当目标函数小于预定误差时, 就认为所获得的模型参数能够表征地下介质的物理参数分布[3, 6]。最近20年, 大多是研究一阶基于梯度法的优化算法在全波形反演问题中的应用, 如梯度法[3, 7]和非线性共轭梯度法[7-11]。然而正如PRATT等[3]和SHIN等[4]的文献所述, 一阶方法难以得到可靠的步长, 导致一阶方法应用于FWI问题时收敛较慢, 从而影响反演结果的分辨率。
根据优化理论[3, 7, 9], 当初始模型比较接近真实模型时, 二阶优化算法相对于一阶算法具有更好的收敛速度, 而且二阶算法求解的是包含二阶信息的海森(Hessian) 矩阵的逆, 并将其作用在模型更新项, 可以补偿与震源相关的模糊效应、孔径不足效应和其它与振幅相关的影响。对于大型反演问题, 因为真实海森矩阵不是正定的, 显式构建真实的海森矩阵非常困难, 求解真实海森矩阵的逆也相当困难, 故通常利用高斯-牛顿海森矩阵来近似真实的海森矩阵, 而高斯-牛顿海森矩阵的逆通常是对称正定(半正定) 的, 可以通过迭代法求解[10, 12]。因为每次计算海森矩阵作用在某个向量上需要求解多个波动方程, 所以求解波形反演中高斯-牛顿海森矩阵逆的计算量非常大。
为了解决求解高斯-牛顿海森矩阵逆计算量巨大的问题, 本文采用将模型的更新转入曲波域[13-14]并进行稀疏约束的办法, 对数据进行降维采样, 随机选取炮点及频率数[15-16], 以减小计算量和提高反演结果的分辨率。最后用北海模型数据测试了方法的可行性和有效性。
1 方法原理 1.1 高斯-牛顿法全波形反演全波形反演可表示为:
| $\mathop {\min }\limits_\boldsymbol{m} \frac{1}{2}\left\| {\boldsymbol{P}- \boldsymbol{F}\left[{\boldsymbol{m}, \boldsymbol{Q}} \right]} \right\|_{2, 2}^2$ | (1) |
式中: P为输入的实际观测地震数据, 非线性函数F [m, Q]=DH-1[m]Q为频率域波动方程正演模拟的地震数据。如(1) 式所示, 求解频率域波动方程需要对每一频率求解大型稀疏亥姆霍兹(Helmholtz) 矩阵H的逆, 其中m为模型参数, Q为震源矩阵。
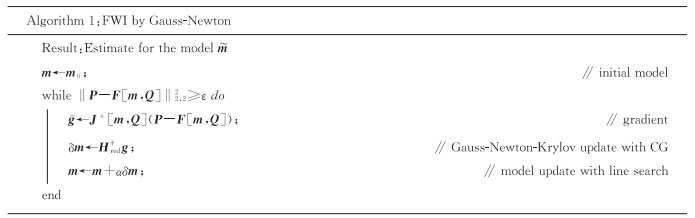
利用标准高斯-牛顿法实现公式(1) 需要求解高斯牛顿的子问题(算法1, 具体实现程序见图 1), 每一步迭代需要计算传统波形反演的梯度及海森矩阵的逆, 然后将海森矩阵的逆作用到梯度上, 最后通过线性搜索选择合适的步长。
|
图 1 高斯-牛顿子问题(算法1) 的实现程序 |
然而利用高斯-牛顿法求解上述波形反演问题时计算量非常大, 因为每一步迭代都需要求解一个线性的高斯-牛顿子问题(即求解海森矩阵的逆)。而求解子问题也需要多次进行子迭代(此迭代不同于波形反演模型迭代), 每次子问题的子迭代需要多次求解波动方程[17-18]。
为了解决计算量巨大的问题, 我们结合降维技术和压缩感知技术, 随机降低反演的炮集数据和随机减小频率数来减小数据量。目前有2种降低炮数据的方法, 第一种是同时激发震源技术, 该技术将传统的单炮震源随机加权相加, 形成一个超级炮集(一炮有多个震源同时激发); 第二种是随机抽取一部分子集。利用上述降维方法, 计算一个高斯-牛顿速度更新虽然需要多次子迭代, 但是其计算量可以控制在近似等于一个传统波形反演梯度迭代的计算量。频率域超级炮的表达式为:
| $\begin{array}{c} \left( {\mathit{\boldsymbol{R}}{M_i}} \right): = \left[{\mathit{\boldsymbol{R}}_i^\Sigma \mathit{\boldsymbol{F}}_\Sigma ^*{\rm{ding}}\left( {{e^{\hat i}}{\mathit{\boldsymbol{\theta }}_i}} \right){\mathit{\boldsymbol{F}}_\Sigma } \otimes \mathit{\boldsymbol{I}} \otimes \mathit{\boldsymbol{R}}_i^\mathit{\Omega }{\mathit{\boldsymbol{F}}_\mathit{\Omega }}} \right]\\ i = 1, 2, \cdots, N \end{array}$ | (2) |
式中: FΩ为傅里叶变换。将上述降维算子应用于全波形反演, 波形反演问题(公式(1)) 就变为:
| $\mathop {\min }\limits_{\boldsymbol{m}} \frac{1}{2}\left\| {\underline {\boldsymbol{P}} - \underline {\boldsymbol{F}} \left[ {{\boldsymbol{m}},{\boldsymbol{Q}}} \right]} \right\|_{2,2}^2$ | (3) |
式中, 下划线代表压缩降维后的数据和算子, 即[15, 19]:
| $\delta \underline {\boldsymbol{P}} : = {\boldsymbol{R}}M\left( {{\boldsymbol{P}} - {\boldsymbol{F}}\left[ {{\boldsymbol{m}},{\boldsymbol{Q}}} \right]} \right) = \underline {\boldsymbol{P}} - \underline {\boldsymbol{F}} \left[ {{\boldsymbol{m}},\underline {\boldsymbol{Q}} } \right]$ | (4) |
数据压缩降维后, 波形反演优化问题的高斯-牛顿迭代仅需要利用一部分频率和炮集数据。本文方法极大地减少了反演中求解波动方程的数量。波形反演中需要采用目标函数的梯度, 其梯度表达式为:
| $g = \boldsymbol{R}\left[{\sum\limits_\omega {{\omega ^2}\sum\limits_s {{{\left( {\boldsymbol{\bar u} \odot \boldsymbol{v}} \right)}_{s, \omega }}} } } \right] = {\boldsymbol{J}^*}\left[{\boldsymbol{m}, \boldsymbol{Q}} \right]\delta \boldsymbol{P}$ | (5) |
式中: u, v为震源正传波场和接收点反传波场。实际上(5) 式即为逆时偏移算子表达式, 逆时偏移算子的转置即为波动方程的线性近似算子, 又称为Born近似算子。
1.2 稀疏反演迭代波形反演梯度法利用梯度来更新模型, 但梯度并不等于速度更新量, 所以需要精确的步长, 在实施中寻找精确的步长非常困难[3, 5]。二阶高斯-牛顿法用海森矩阵的逆来标度梯度, 使其拥有相对正确的振幅信息。采用压缩降维技术后, 波形反演的计算量可以得到极大的减小, 然而数据量的减小会带来压缩产生的人工虚像。所以本文利用压缩感知技术求解高斯-牛顿方法的子问题, 以此代替传统共轭梯度法求解。在本文提出的方法中, 我们直接求解Born正演算子(优化理论中常称其为雅可比矩阵) 的逆。
对于大多数反演问题, 人们往往避免采用迭代法求解雅可比矩阵的逆, 因为迭代法在每次迭代时需要不停地计算其正传及其转置, 因而计算量巨大。此外, 在很多优化反演问题中, 雅可比矩阵往往是病态的(海森矩阵是奇异的)。然而与很多反演问题不同, 地震勘探中的海森矩阵是相对均衡的。因为在初始模型相对理想的情况下, 线性Born近似正演能够很好地匹配非线性波动方程正演, 在此情况下海森矩阵的逆可以用简单的对角矩阵近似代替[18]。
本文中, 我们利用压缩感知技术降低求解海森矩阵逆的计算量。同时利用L1范数正则化线性反演来计算“类似高斯牛顿”的迭代更新项, 如:
| $\begin{array}{*{20}{l}} {\delta {\boldsymbol{\tilde x}} = \mathop {{\rm{argmin}}}\limits_{\delta {\boldsymbol{x}}} {{\left\| {\delta {\boldsymbol{x}}} \right\|}_{{L_1}}}\;\;{\rm{s}}.{\rm{t}}.}\\ {{{\left\| {\delta \underline {\boldsymbol{P}} - {\boldsymbol{A}}\delta {\boldsymbol{x}}} \right\|}_2} \le \sigma } \end{array}$ | (6) |
式中: A :=RMJS *为Born近似正演矩阵(亦称雅可比算子, A′A为该问题的海森矩阵); S*为反曲波变换。该稀疏反演技术在曲波域寻找一个最稀疏的能够匹配观测数据的解。曲波变换表征地下层状介质非常有效, 所以利用公式(6) 求得的最稀疏解可以更容易反演得到接近地下构造的模型。降维技术结合稀疏反演既能解决二阶高斯-牛顿法计算量大的问题, 又能压制由于数据压缩导致的虚像影响。
波形反演存在局部极小点的问题, 即所谓的“周期跳跃”现象。人们提出了很多解决这一难题的方法, 比如在反演时引入高频信息和走时信息等[3, 5]。
本文中, 我们利用一个新的策略让模型迭代在曲波域中的L1范数逐渐地变大。这样让最接近真实地层构造信息先进入数据模型结果, 此方法称为算法2, 具体实现程序见图 2。

|
图 2 算法2的实现程序 |
综上所述, 通过降维处理, 我们可以极大地减少在全波形反演中所需要求解波动方程(偏微分方程) 的次数, 从而极大地减少计算量, 使求解二阶高斯-牛顿模型更新的计算量近似等于求一个梯度更新[17, 20]。本文方法利用了全波形反演模型更新中结构信息在曲波域是稀疏的, 而降维采样产生的人为虚像在曲波域不稀疏的性质, 在理论上对高斯-牛顿更新进行稀疏约束。在反演迭代过程中, 不相干的信息完全被曲波域稀疏约束压制, 该方法也可以用于最小二乘偏移[17.20]。本文给出的稀疏约束全波形反演技术不仅能够极大地减小计算量, 也能提高反演结果的分辨率[2, 17]。该技术具有以下优点:
1) 高斯-牛顿法的子问题是线性的, 而利用稀疏约束的方法求解线性问题正好符合压缩感知技术的基本理论。根据压缩感知理论[13, 21], 即压缩的信号可以显著低于尼奎斯特采样率下通过求解稀疏约束的方法恢复原来的信号。所以压缩感知技术结合随机选炮以及同时激发震源技术可以有效地减小计算量及去除降维采样带来的人工虚像。
2) 将曲波域的稀疏约束应用于全波形反演问题的高斯-牛顿更新项上, 并不会改变全波形反演优化问题的目标函数, 所有求解的过程也比较简单。而且高斯-牛顿法的子问题是线性的, 该问题是凸问题并且有全局极小点[22]。
3) 曲波变换表征地下层状结构非常有效[13-14], 所以波形反演以及地震成像中的层状同相轴形结构在曲波域可以用少量的稀疏表达, 该技术也可用于最小二乘偏移[20-21]。
2 北海模型数据测试为了评估波形反演在解决细节结构中的能力, 以及验证本文提出的基于压缩感知的稀疏约束高斯-牛顿法的有效性, 我们采用BG北海速度模型数据进行了测试。
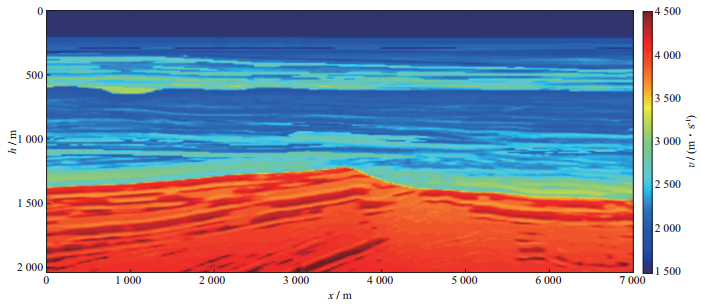
如图 3所示, 该速度模型包含了由实际地震、测井、地质等数据得到的地质构造信息。观测数据由时间域有限差分正演模拟产生, 采用15 Hz雷克子波。数据共350炮, 炮间距20 m, 每炮700道, 检波距10 m。
|
图 3 真实的BG速度模型 |
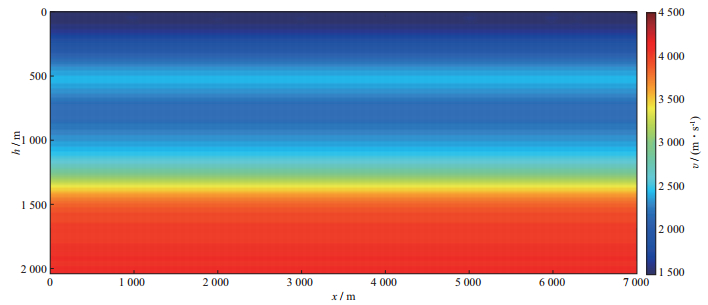
正演结果通过求解亥姆霍兹矩阵得到。图 4为初始速度模型, 可看出, 速度在横向上没有变化。
|
图 4 初始速度模型 |
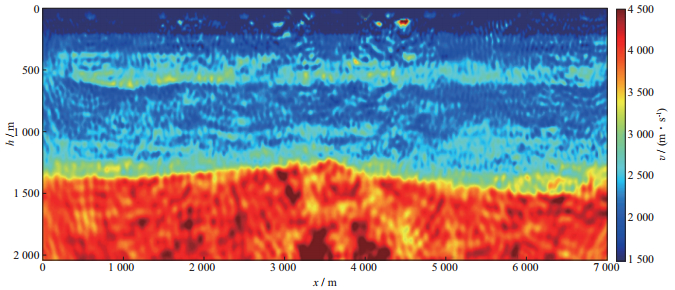
反演利用频率域方法从5 Hz开始, 为了避免局部极小点, 共反演了8个频带, 跨度从5 Hz到15 Hz, 每个频带选取20炮以及随机选取3个频率(每个频带总共10个频率), 进行稀疏约束下高斯-牛顿模型迭代计算(共10次)。对于每个高斯-牛顿法的子问题, 利用L1范数约束下谱梯度投影(SPGL1)[22-24]线性算法进行子迭代(10次)。图 5为传统高斯-牛顿算法反演结果, 图 6为稀疏约束下高斯-牛顿算法反演结果。对比图 5和图 6可以明显看出, 如果没有稀疏约束, 在采样率严重不足的情况下, 压缩数据会引入很多虚像噪声, 严重影响了反演结果; 利用稀疏
|
图 5 传统高斯-牛顿法波形反演结果(每次迭代随机利用1.7%的数据) |
|
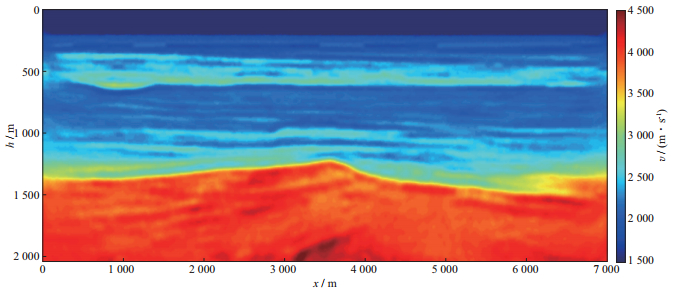
图 6 稀疏约束高斯-牛顿法反演结果(每次迭代随机利用1.7%的数据) |
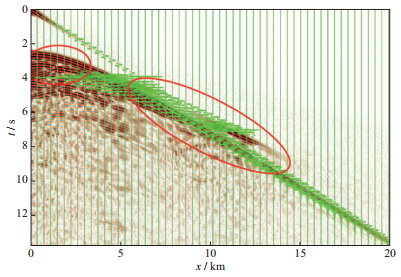
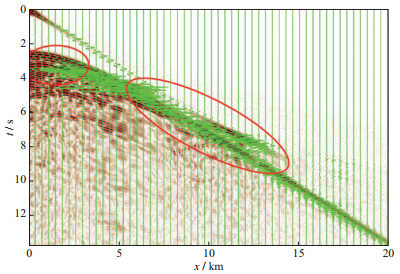
约束之后, 由降维采样带来的虚像明显减少, 反演结果更加真实可靠。图 7和图 8是数据匹配的结果, 背景为真实的单炮记录, 其中图 7中的波形图(绿色波形曲线) 为初始模型的正演结果, 图 8为全波形反演模型的正演结果(绿色波形曲线), 可见, 反演结果实现了更好的数据匹配。
|
图 7 初始模型正演纪录(背景为真实数据) |
|
图 8 全波形反演结果正演纪录(背景为真实数据) |
方法研究和应用实例表明:
1) 利用压缩降维技术, 可以极大地减小在反演过程中所用的数据量, 从而显著地减小计算量。
2) 将稀疏约束应用于反演中的模型更新, 不会改变波形反演的目标函数, 能够压制由欠采样产生的虚像噪声。
3) 曲波变换是个多尺度、多角度的可逆变换, 在表征地质模型上非常有效。所以将反演模型的迭代变换到曲波域, 更有利于稀疏约束算法。
压缩感知技术打破了传统尼奎斯特采样定理, 本文将其中的相关原理应用于全波形反演算法, 取得了较好的效果。该方法不仅可以用于地震波形反演, 也可用于偏移成像和地震数据采集。将压缩感知技术运用到数据采集, 可以极大地降低成本, 有了压缩采集的数据, 可直接利用本文方法进行数据处理, 将会更大地节省地震勘探成本。
| [1] | ASKAN A, AKCELIK V, BIELAK J, et al. Full waveform inversion for seismic velocity and anelastic losses in heterogeneous structures[J]. Bulletin of the Seismological Society of America, 2007, 97(6): 1990-2008 DOI:10.1785/0120070079 |
| [2] | HERRMANN F J, LI X, ARAVKIN A Y, et al. A modified, sparsity promoting, Gauss-Newton algorithm for seismic waveform inversion[J]. Proceedings of SPIE 8138, 2011: 1-20 |
| [3] | PRATT R G, SHIN C, HICKS G. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362 DOI:10.1046/j.1365-246X.1998.00498.x |
| [4] | SHIN C, JANG S, MIN D J. Improved amplitude preservation for prestack depth migration by inverse scattering theory[J]. Geophysical Prospecting, 2001, 49(5): 592-606 DOI:10.1046/j.1365-2478.2001.00279.x |
| [5] | VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26 DOI:10.1190/1.3238367 |
| [6] | TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266 DOI:10.1190/1.1441754 |
| [7] | MÉTIVIER L, BROSSIER R, VIRIEUX J, et al. Full waveform inversion and the truncated Newton method[J]. SIAM Journal on Scientific Computing, 2013, 35(2): B401-B437 DOI:10.1137/120877854 |
| [8] | GILBERT J C, NOCEDAL J. Global convergence properties of conjugate gradient methods for optimization[J]. SIAM Journal on Optimization, 1992, 2(1): 21-42 DOI:10.1137/0802003 |
| [9] | GRATTON S, LAWLESS A S, NICHOLS N K. Approximate gauss-newton methods for nonlinear least squares problems[J]. SIAM Journal on Optimization, 2007, 18(1): 106-132 DOI:10.1137/050624935 |
| [10] | HESTENES M R, STIEFEL E. Methods of conjugate gradients for solving linear systems[J]. Journal of Research of the National Bureau of Standards, 1952, 49(6): 409-436 DOI:10.6028/jres.049.044 |
| [11] | WARNER M, RATCLIFFE A, NANGOO T, et al. Anisotropic 3d full-waveform inversion[J]. Geophysics, 2013, 78(2): R59-R80 DOI:10.1190/geo2012-0338.1 |
| [12] | BAUSCHKE H H, COMBETTES P L, LUKE D R. Phase retrieval, error reduction algorithm, and fienup variants:a view from convex optimization[J]. Journal of the Optical Society of America A, 2002, 19(7): 1334-1345 DOI:10.1364/JOSAA.19.001334 |
| [13] | CANDÈS E J, DEMANET L, DONOHO D L, et al. Fast discrete curvelet transforms[J]. Multiscale Modeling and Simulation, 2006, 5(3): 861-899 DOI:10.1137/05064182X |
| [14] | KUMAR V.Incoherent noise suppression and deconvolution using curvelet-domain sparsity[D].Vancouver:University of British Columbia, 2009 |
| [15] | BUNKS C, SALECK F M, ZALESKI S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473 DOI:10.1190/1.1443880 |
| [16] | BURKE J V. A robust trust region method for constrained nonlinear programming problems[J]. SIAM Journal on Optimization, 1992, 2(2): 325-347 DOI:10.1137/0802016 |
| [17] | LI X, ARAVKIN A Y, VAN LEEUWEN T, et al. Fast randomized full-waveform inversion with compressive sensing[J]. Geophysics, 2012, 77(3): A13-A17 DOI:10.1190/geo2011-0410.1 |
| [18] | HORST R, PARDALOS P, VAN THOAI N. Introduction to global optimization[M]. New York: Springer, 2000: 1-353. |
| [19] | ABUBAKAR A, VAN DEN BERG P M. The contrast source inversion method for location and shape reconstructions[J]. Inverse Problems, 2002, 18(2): 495 DOI:10.1088/0266-5611/18/2/313 |
| [20] | TU N, ARAVKIN A Y, VAN LEEUWEN T. Fast least-squares migration with multiples and source estimation[J]. Expanded Abstracts of 75th EAGE Conference and Exhibition, 2013: 1-5 |
| [21] | HERRMANN F J, LI X. Efficient least-squares imaging with sparsity promotion and compressive sensing[J]. Geophysical Prospecting, 2012, 60(4): 696-712 DOI:10.1111/gpr.2012.60.issue-4 |
| [22] | HENNENFENT G, VAN DEN BERG E, FRIEDLANDER M P, et al. New insights into one-norm solvers from the Pareto curve[J]. Geophysics, 2008, 73(4): A23-A26 DOI:10.1190/1.2944169 |
| [23] | LI X, HERRMANN F J. Full-waveform inversion from compressively recovered model updates[J]. SEG Technical Program Expanded Abstracts, 2010: 1029-1033 DOI:10.1190/SEGEAB.29 |
| [24] | VAN DEN BERG E, FRIEDLANDER M P. Probing the pareto frontier for basis pursuit solutions[J]. SIAM Journal on Scientific Computing, 2008, 31(2): 890-912 |


