2. 湖南文理学院洞庭湖生态经济区建设与发展湖南省协同创新中心,湖南 常德 415000
2. Cooperative Innovation Center for The Construction & Development of Dongting Lake Ecological Economic Zone, Hunan University of Arts and Science, Changde 415000, China
大地电磁测深(Magnetotelluric,MT)方法是油气田普查勘探、岩石圈结构探测等领域的一种重要手段。在石油天然气勘探中,特别是在地震勘探困难区,电磁法勘探技术已成为首选的非地震勘探技术,被广泛用于石油综合地质调查,如勘查断裂破碎带、查明盆地边界、基底埋深和基本构造格架等,为油气田整体评价提供科学依据[1-2]。然而,大地电磁测深数据由于其信号自身的特点和日益严重的人文噪声的干扰,极易受到污染,影响响应参数的稳健估计[3-4]。如何有效消除噪声是大地电磁工作者关心的热点问题,国内外学者提出了一系列大地电磁信号的去噪方法,如:Robust处理[5-6]、远参考技术[7]、高阶统计量[8]、小波变换[4-9]和基于经验模态分解[10-12]的滤波方法等。其中,经验模态分解(empirical mode decomposition,EMD)方法由于具有良好的自适应特征,在大地电磁信号去噪领域得到广泛应用,但也存在模态混叠和端点效应等问题[10]。2009年,YAN等[13]提出的时频分析新技术——频率切片小波变换(Frequency Slice Wavelet Transform,FSWT),通过引入频率切片函数使传统傅里叶变换实现了时频分析功能。近年来,FSWT被应用到模式识别和爆破振动信号分析中,展示了其较好的时频分析和重构能力[13-15],但频率切片小波变换在大地电磁信号分析领域的应用鲜有报道。我们将频率切片小波变换的时频分析算法引入到大地电磁信号的时频特征分析中,探讨基于频率切片小波变换的大地电磁信号时频域去噪新方法。
1 基本原理基于频率切片小波变换的时频域去噪方法是先对信号进行频率切片小波变换,得到其时频分布,在时频域内进行阈值滤波后,再由频率切片小波变换的逆变换重构去噪后的信号。
1.1 频率切片小波变换假设信号f(t)∈L2(R),${\hat{p}}$(ω)为小波函数p(t)的傅里叶变换,则f(t)的频率切片小波变换为[13-14]:
| $W\left( t,\omega ,\sigma \right)=\frac{1}{2\pi }~\lambda \int_{-\infty }^{+\infty }{\hat{f}\left( u \right)~{{{\hat{p}}}^{*}}}\left( \frac{u-\omega }{\sigma } \right)~{{e}^{iut}}du$ | (1) |
式中:σ为尺度因子(σ≠0) ;λ为能量系数(λ≠0) ;σ和λ为ω和t的函数或常数; ${\hat{p}}$*(ω)为 ${\hat{p}}$(ω)的共轭函数。
设尺度因子σ=ω/k, k>0,则:
| $W\left( t,\omega ,k \right)=\frac{1}{2\pi }~\int_{-\infty }^{+\infty }{\hat{f}\left( u \right)~{{{\hat{p}}}^{*}}}\left( k\frac{u-\omega }{\sigma } \right)~{{e}^{iut}}du$ | (2) |
式中:k为时频分辨系数[14-15],用来调整时频域对变换的响应灵敏度,与ω,u无关。
通常,用频率分辨比率η和幅值期望响应比率ν这2个系数来评价分析信号,以获得较高的时频分辨率。
| $\begin{align} & \eta =(\Delta \omega )/\omega \\ & \nu =(\Delta W)/W \\ \end{align}$ | (3) |
对于f(t)=eiω0t,若|W(t,ω0+Δω,λ,σ)|/|W(t,ω0,λ,σ)|≤ν,则:
| $\left| \hat{p}\left( kv \right) \right|\le v\left| \hat{p}\left( 0 \right) \right|$ | (4) |
对于f(t)=δ(t-t0),若|W(t0+Δt,ω,λ,σ)|/|W(t0,ω,λ,σ)|≤ν,则:
| $\left| p\left( \frac{\mu }{k\eta } \right) \right|\le v\left| p\left( 0 \right) \right|$ | (5) |
式中:μ=ΔωΔt。若取 ${\hat{p}}$(ω)=e-0.5ω2,μ=0.5,可得解为ν=e-0.5ω2,k=0.707η。
1.2 频率切片小波变换的逆变换理论上,频率切片小波变换的时频域分解是冗余的,其逆变换也可以用不同的形式,其中最为简洁的一种可表示为:
| $f\left( t \right)=~\frac{1}{2\pi \lambda }~\int_{-\infty }^{+\infty }{\int_{-\infty }^{+\infty }{W\left( \tau ,\omega ,k \right){{e}^{i\omega (t-\tau )}}d\tau d\omega }}$ | (6) |
公式(6) 表明频率切片小波变换的逆变换只与参数k有关,而与函数p(ω)无关。当k为定值时,公式(6) 为傅里叶逆变换。f(t)的频率切片小波变换为W(t,ω,σ),则在时频区域(t1,t2,ω1,ω2)的信号分量为:
| ${{f}_{x}}\left( t \right)=~\frac{1}{2\pi \lambda }~\int_{{{\omega }_{1}}}^{{{\omega }_{2}}}{\int_{{{t}_{1}}}^{{{t}_{2}}}{W\left( \tau ,\omega ,k \right){{e}^{i\omega (t-\tau )}}d\tau d\omega }}$ | (7) |
显然,在f(t)的频率切片小波变换时频区间内,时频区域(t1,t2,ω1,ω2)即时频切片可任意选择。所以,可根据选择的时频切片在时频空间上随意提取所需的信号分量[13-15]。
1.3 去噪方法与步骤基于频率切片小波变换时频分析的大地电磁信号分析方法的实现过程如下。
1) 采用FSWT进行大地电磁信号分解,得到在全频带下的时频分布。
2) 对该时频谱进行时频域阈值滤波,即:
| $W\left( t,\omega ,k \right)=\left\{ \begin{matrix} W\left( t,\omega ,k \right) & \left| W\left( t,\omega ,k \right) \right|\ge {{t}_{n}} \\ 0 & \left| W\left( t,\omega ,k \right) \right|\le {{t}_{n}} \\ \end{matrix} \right.$ | (8) |
式中:
3) 对滤波后的时频区域进行逆变换重构分离出的有效MT信号。
4) 进一步对去噪后的MT信号进行功率谱计算和响应函数估计。
2 仿真实验为了验证上述时频滤波方法的正确性及其在处理MT信号方面的优势,我们对一组来自严家斌的仿真数据[9]进行了处理,噪声为类似工频干扰的正弦信号。在此,仿真信号表示为s(t),噪声是n(t),则含噪的仿真MT信号f(t)可表示为:
| $f({{t}_{i}})=s({{t}_{i}})+n({{t}_{i}})i=1,2,\cdots ,n$ | (9) |
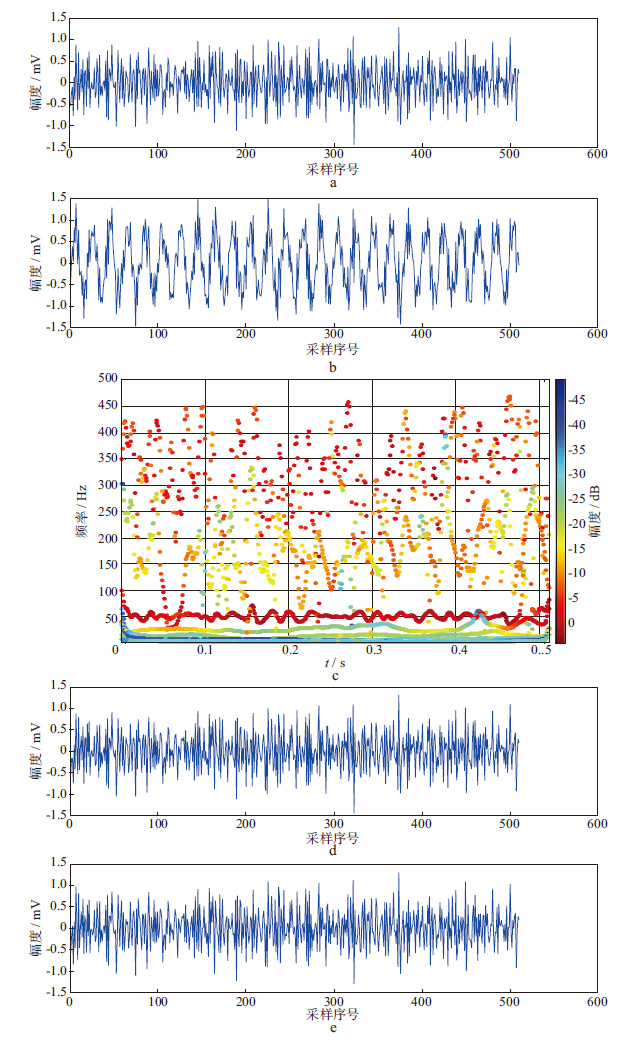
图 1a为无噪的原始仿真MT信号。图 1b为加噪后的信号(信噪比为-5 dB),由于加入的正弦信号的幅值较大,原始的仿真信号几乎被淹没。图 1c为采用函数${\hat{p}}$(ω)=e-0.5ω2对加噪信号进行FSWT后得到的时频分布,此时η=0.055。从频谱图中可明显看出50 Hz正弦波成分(带状)的能 量分布,用本文提出的时频域阈值滤波的方法对图 1c进行滤波,计算阈值为-8.4,滤波后,根据公式(7) 对时频域进行频率切片小波变换的逆变换,重构信号。图 1d为重构后的信号。为便于对比,图 1e给出了基于EMD分解的时空滤波方法去噪后的结果。从图 1中可以看出,两种方法都能有效地压制噪声,较好地恢复了信号的原貌,基于EMD分解的去噪方法丢失的信息更多些。为了评价这种时域滤波方法的良好效果,进一步将处理结果与基于EMD分解方法的结果进行了对比。并采用了一些评价参数(如:信噪比SNR,噪声抑制率NSR和信号失真比SDR)来对去噪效果进行评价,它们的定义为[18-19]:
| ${{S}_{NR}}=10\lg ({{P}_{S}}/{{P}_{n}})$ | (10) |
| ${{N}_{SR}}=1-~\frac{{{\left[ \sum\limits_{i=1}^{n}{{{\left| \hat{f}\left( {{t}_{i}} \right)-s\left( {{t}_{i}} \right) \right|}^{2}}} \right]}^{1/2}}}{{{\left[ \sum\limits_{i=1}^{n}{{{\left| f\left( {{t}_{i}} \right)-s\left( {{t}_{i}} \right) \right|}^{2}}} \right]}^{1/2}}}$ | (11) |
| ${{S}_{DR}}=~\frac{{{\left[ \sum\limits_{i=1}^{n}{{{\left| \hat{f}\left( {{t}_{i}} \right)-s\left( {{t}_{i}} \right) \right|}^{2}}} \right]}^{1/2}}}{{{\left[ \sum\limits_{i=1}^{n}{{{\left| s\left( {{t}_{i}} \right) \right|}^{2}}} \right]}^{1/2}}}$ | (12) |
|
图 1 仿真信号的去噪 a 仿真MT信号; b 加噪的仿真信号; c 加噪后的时频谱; d 本文方法去噪后的信号; e EMD时空滤波法去噪后的信号 |
式中:PS是信号s(t)的功率谱;Pn是噪声n(t)的功率谱; ${\hat{f}}$(ti)是估算的去噪后的MT信号;SNR反映了有用信号被噪声的污染程度,其值越小,说明噪声干扰越大。NSR越大,SDR越小,则说明去噪效果越好。
表 1给出了不同信噪比情况下几个参数的对比结果。从表 1中可以看出,在不同的SNR条件下,不管是本文提出的时频域去噪方法还是基于EMD的方法,信号失真比(SDR)都不大,且前者的SDR更低。就噪声抑制率来说,本文提出的时域方法也优于EMD去噪方法。在较高的SNR环境下,噪声很弱,所以NSR也相对较小(最大值仅是0.258 7) ,对应的SDR也很小(最大值仅是0.048 4) 。随着信噪比的增加,NSR也相对增大(从0.258 7增加到0.795 0) ,尽管SDR也增大了(从0.020 9增大到0.042 0) ,但是仍旧保持很小的值。这就说明本文提出的时域滤波方法有很好的去噪和信号细节保持能力。
| 表 1 评价参数比较 |
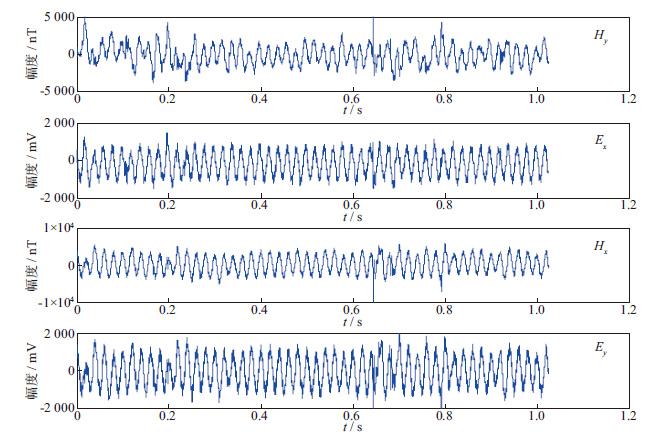
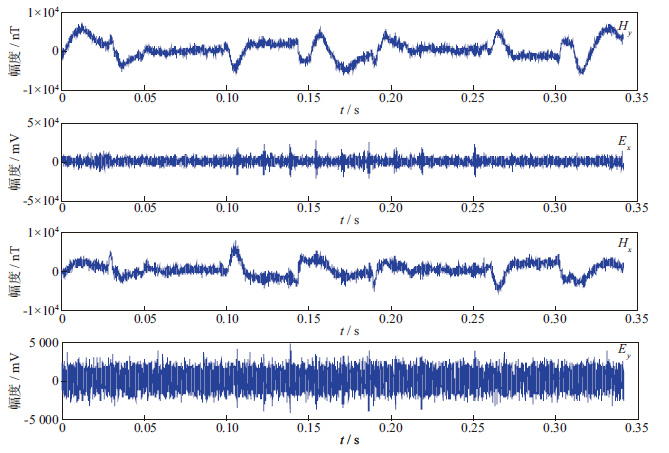
实测数据来自安徽,用EH-4仪器采集,采样频率是12 kHz。图 2给出了实测大地电磁信号4个分量的时域波形。由于勘测现场周围有高压电线经过,实测数据受到工频干扰的影响,其时域波形显示信号存在一个呈正弦波形态的干扰,且幅值很大。该50 Hz的工频干扰几乎淹没了电磁场信号,从时域几乎很难辨别出真实的电磁场信号。
|
图 2 受工频干扰的大地电磁信号 |
考虑到文章的篇幅,这里仅给出电场信号Ex分量的详尽处理过程。
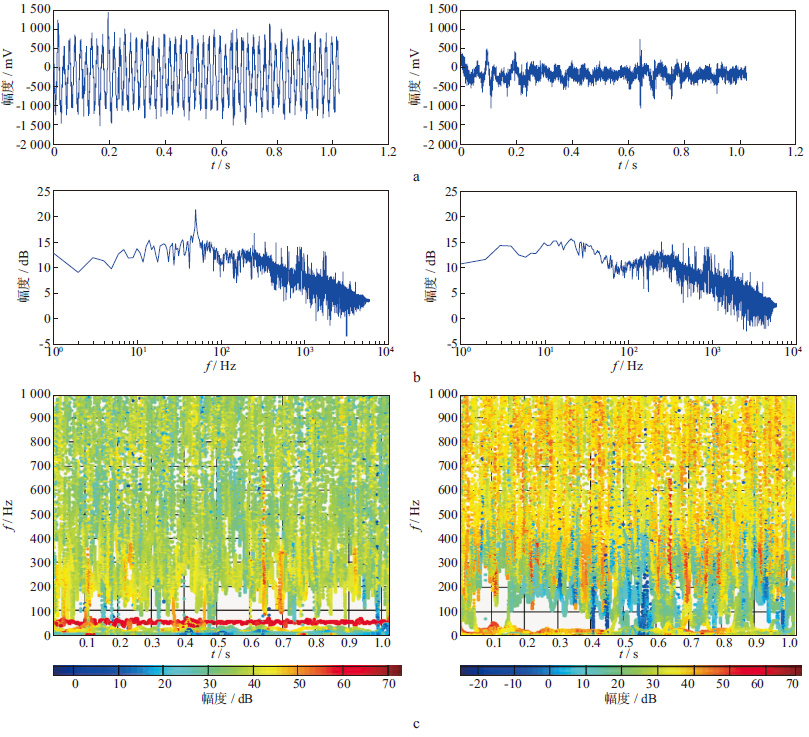
图 3a左图给出了Ex分量的时域信号,统计参数如下:最大值为1 760.136 mV,最小值为-1 508.098 mV,均值为-231.856 mV,能量为6.187×103 mV2,所用函数为${\hat{p}}$(ω)=e-0.5ω2。图 3b左图为信号的功率谱,可见在50 Hz处有个突出的异常值。对Ex分量进行FSWT后得到的时频分布图如3c左图所示,此时η=0.055。从频 谱图中也可明显看出50 Hz正弦波的能量分布。用本文提出的时频滤波方法对图 3c左图进行滤波,计算阈值为46,滤波后,根据公式(7) 对时频域进行频率切片小波变换的逆变换,重构信号。
|
图 3 大地电磁信号Ex分量去噪前(左)、后(右)的对比 a 信号的时间序列; b 信号的功率谱; c 信号的时频谱 |
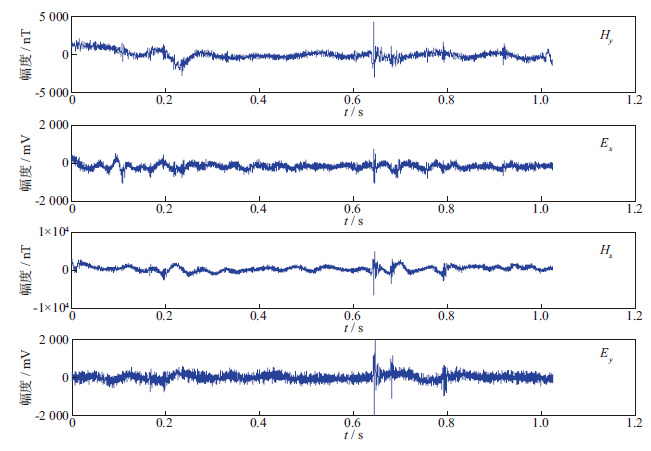
图 3a右图展示了去噪后的信号。图 3b右图为去噪后信号的功率谱 ,可以看出,去噪后信号变得平滑,50 Hz处的尖峰被消除。图 3c右图给出了重新对去噪后的Ex分量进行频率切片小波变换得到的时频分布图。从图 3中可以看出,去噪后信号变得平滑,正弦波干扰被消除,被噪声淹没的有用信号得到了显现。消噪后信号的统计参数如下:最大值为896.178 mV,最小值为-1 098.569 mV,均值为-104.007 mV,能量为1.706×102 mV2。比较图 3左、右两边的3幅图,可以清楚地看到,50 Hz 的干扰得到了有效抑制,时频谱中50 Hz的能量带也消失了,突出了有用信号的细节。用时频域滤波方法对受噪的其它3个分量做同样的处理,结果如图 4所示。从图 4可以看出,噪声均得到了有效的抑制,信号变得平稳。
|
图 4 压制工频干扰噪声后的大地电磁信号 |
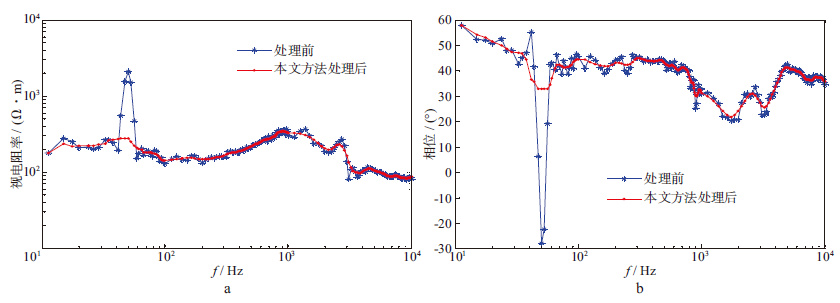
分别用去噪前、后的MT数据计算了视电阻率曲线和相位曲线(为节约篇幅这里仅给出视电阻率曲线ρxy及其对应的相位曲线Фxy,如图 5所示)。去噪前、后响应参数的平滑度用方差来衡量,它们的相似程度则用曲线相似度参数Ncc来评价。
|
图 5 ρxy曲线(a)和Фxy曲线(b)去噪前、后的对比 |
| ${{N}_{cc}}=1-~\frac{\sum\limits_{n=1}^{n}{f\left( n \right)\centerdot g\left( n \right)}}{\sqrt{\left[ \sum\limits_{n=1}^{n}{{{f}^{2}}\left( n \right)} \right]\left[ \sum\limits_{n=1}^{n}{{{g}^{2}}\left( n \right)} \right]}}$ | (13) |
式中:f(n),g(n)分别为两离散序列;Ncc的取值为-1~1,其中,-1代表变换前、后两数据波形反向,0代表两波形正交,1代表完全相同。
去噪前、后评价参数的对比结果如表 2所示。从前文给出的图和参数可以看出,这些曲线相似度Ncc都很大。这意味着去噪前、后得到的两条视电阻率参数曲线形态趋势一致。但去噪后曲线的方差减小了很多,曲线的奇异点得到了有效抑制(如在ρxy曲线的50 Hz频点,视电阻率的值由2 280 Ω·m降到了286 Ω·m)。对于所有的响应参数曲线,误差棒的平均值减小了,更多的细节信息得到了显现,曲线变得平滑和连续,估算的参数变得稳定。
| 表 2 去噪前、后评价参数的对比结果 |
单个三角波干扰或由多个三角波构成的干扰是大地电磁测深中常见的噪声,尤其是在矿集区,井下大功率设备的开停、开采带来的震动干扰等都会产生此类干扰。它们往往只出现在磁场信号中,且在时间域表示为明显的跳变,其形态为不规则的三角波。图 6所示是典型的受三角波干扰的MT数据。此类噪声通常在磁道观测信号中出现,且为磁场相关噪声,电道受其影响较小。噪声局部能量较强,将正常磁场信号完全湮灭。单个噪声幅值为正常信号幅值的数倍到数十倍。
|
图 6 受三角波干扰的MT数据 |
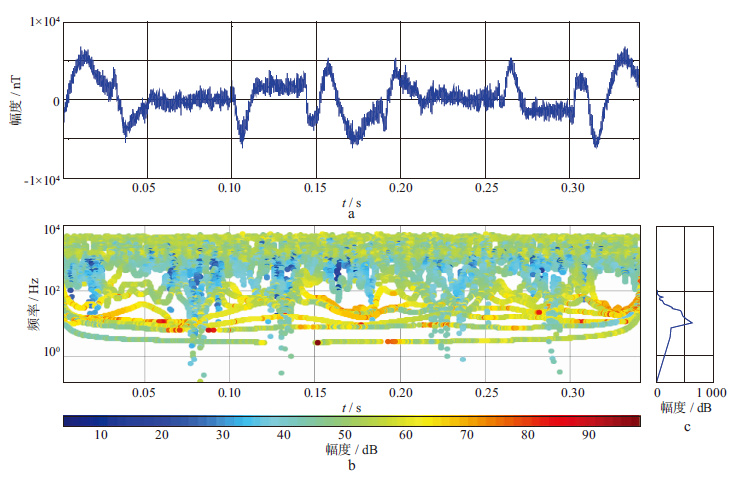
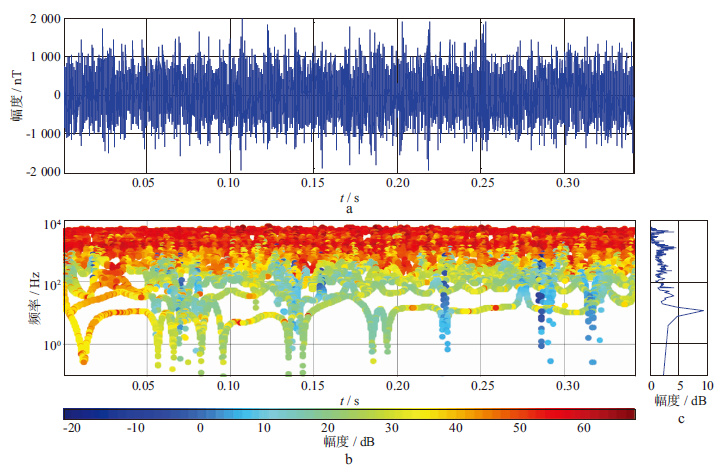
这里仅给出磁场信号Hy分量的详尽处理过程。图 7显示了Hy分量的时域信号(图 7a)、FSWT变换后得到的时频谱(图 7b)和功率谱(图 7c)。由时频谱和功率谱可见,含噪Hy分量的能量主要集中在低频段(100 Hz)以内,在相同的坐标轴刻度下,其它的信号能量几乎完全被抑制,这不符合正常大地电磁信号能量分布规律。用本文提出的时频域阈值滤波方法对图 7b进行滤波,滤波后再进行时频域频率切片小波变换的逆变换,重构信号,结果如图 8所示。从图 8可见,去噪后的信号,三角波形得到了有效抑制,信号表现为以0为均值的正态分布,信号的能量分布也变得合理。用时频域滤波的方法对含噪的另一个磁场分量Hx也做同样的处理,处理后的MT信号如图 9所示。从图 9可以看出,三角波干扰得到了有效的抑制,为后续的响应参数估算奠定了基础。
|
图 7 Hy分量的时域信号(a)、FSWT变换后得到的时频谱(b)和功率谱(c) |
|
图 8 Hy分量去噪后的时域信号(a)、FSWT变换后得到的时频谱(b)和功率谱(c) |
|
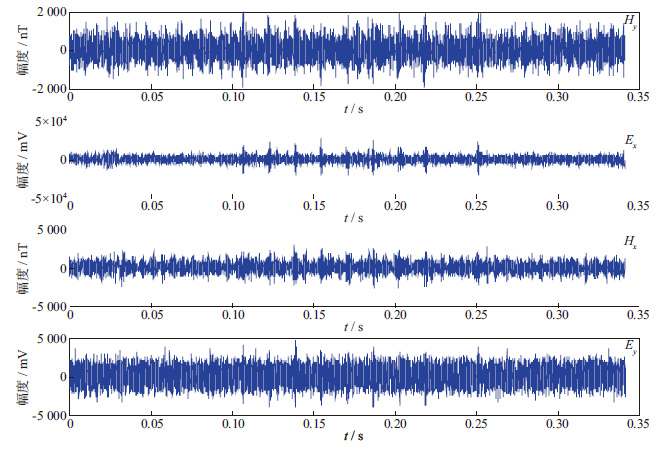
图 9 压制三角波干扰噪声后的MT数据 |
大地电磁勘测中,野外观测数据不可避免地会受到各种人文噪声的影响,且随着经济的发展而日趋严重。基于频率切片小波变换的时频分析能精确地呈现大地电磁信号的时频能量分布特征,在此基础上再对时频谱进行时频阈值滤波和逆变换重构,能分离出去噪后的MT信号,可以有效地滤除实测大地电磁信号中强噪声,为后续稳健的响应参数估计奠定了基础。应用本文所提方法对仿真数据和工程实践中常见的受工频干扰和三角波干扰的实测MT信号进行了分析,结果表明,这种方法可有效地消除强干扰;去噪后计算的响应参数曲线变得平滑、连续,提高了大地电磁测深数据的质量。当然,大地电磁噪声的来源和成分复杂,噪声的处理是一项重要而又艰巨的任务,下一步将研究其它类型噪声的时频特征及其处理方法,并讨论有效的去噪评价体系。
| [1] |
李晓昌. 大地电磁测深法在石油地质调查中的应用[J].
物探化探计算技术 , 2009, 31 (6) : 573-578 LI X C. Application of magnetotelluric sounding to petroleum investigation[J]. Computing Techniques for Geophysical and Geochemical Exploration , 2009, 31 (6) : 573-578 |
| [2] |
陈孝雄, 王友胜, 黄潜生. 大地电磁测深在库木库里盆地结构研究中的应用[J].
石油天然气学报 , 2007, 29 (6) : 78-82 CHEN X X, WANG Y S, HUANG Q S. Application of MT in structural study of kumukuli basin[J]. Journal of Oil and Gas Technology , 2007, 29 (6) : 78-82 |
| [3] |
王书明, 王家映. 高阶统计量在大地电磁测深数据处理中的应用研究[J].
地球物理学报 , 2004, 47 (4) : 928-934 WANG S M, WANG J Y. Application of higher-orderstatistics in magnetotelluric data processing[J]. Chinese Journal of Geophysics , 2004, 47 (4) : 928-934 |
| [4] |
严家斌, 刘贵忠, 柳建新. 小波变换在天然电磁场信号时间序列处理中的应用[J].
地质与勘探 , 2008, 44 (3) : 75-78 YAN J B, LIU G Z, LIU J X. Application of wavelet transform in processing nature electromagnetic fieldtime series[J]. Geology and Prospecting , 2008, 44 (3) : 75-78 |
| [5] | LARSEN J C, MACHIE R L. Robust smooth magnetotelluric transfer functions[J]. Geophysical Journal International , 1996, 124 (3) : 801-819 DOI:10.1111/gji.1996.124.issue-3 |
| [6] | EGBERT D, BOOKER R. Robust estimation of geomagnetic transfer function[J]. Geophysical Journal of the Royal Astronomical Society , 1986, 87 (1) : 173-194 DOI:10.1111/gji.1986.87.issue-1 |
| [7] | GAMBLE T M, GOUBAU W M, CLARKE J. Magnetotelluric with a remote magnetic reference[J]. Geophysics , 1979, 44 (1) : 53-68 DOI:10.1190/1.1440923 |
| [8] |
蔡剑华, 胡惟文, 任政勇, 等. 基于高阶统计量的大地电磁数据处理与仿真[J].
中南大学学报:自然科学版 , 2010, 41 (4) : 1556-1560 CAI J H, HU W W, Ren Z Y, et al. Magnetotelluric data processing and simulation based on higher-order statistics[J]. Journal of Central South University(Science and Technology) , 2010, 41 (4) : 1556-1560 |
| [9] |
严家斌.大地电磁信号处理理论及方法研究[D].长沙:中南大学, 2003
YAN J B.The study on theory and method of Mag- netotellurie signal proeessing[D].Changsha:Central South University, 2003 |
| [10] | CAI J H. A combinatorial filtering method for magnetotelluric time-series based on Hilbert-Huang transform[J]. Exploration Geophysics , 2014, 45 (2) : 63-73 DOI:10.1071/EG13012 |
| [11] | CAI J H. Magnetotelluric response function estimation based on hilbert-huang transform[J]. Pure and Applied Geophysics , 2013, 170 (11) : 1899-1911 DOI:10.1007/s00024-012-0620-3 |
| [12] |
蔡剑华, 王先春, 胡惟文. 基于经验模态分解与小波阈值的MT信号去噪方法[J].
石油地球物理勘探 , 2013, 48 (2) : 303-307 CAI J H, WANG X C, HU W W. De-noising of MT signal based on empirical mode decomposition and wavelet threshold method[J]. Oil Geophysical Prospecting , 2013, 48 (2) : 303-307 |
| [13] | YAN Z H, MIYAMOTO A, JIANG Z. Frequency slice wavelet transform for transient vibration response analysis[J]. Mechanical Systems and Signal Processing , 2009, 23 (5) : 1474-1489 DOI:10.1016/j.ymssp.2009.01.008 |
| [14] | YAN Z H, MIYAMOTO A, JIANG Z. An overall theoretical description of frequency slice wavelet transform[J]. Mechanical Systems and Signal Processing , 2010, 24 (2) : 491-507 DOI:10.1016/j.ymssp.2009.07.002 |
| [15] | YAN Z H, MIYAMOTO A, JIANG Z. Frequency slice algorithm for modal signal separation and damping identification[J]. Computers and Structures , 2011, 89 (1/2) : 14-26 |
| [16] |
尚帅, 韩立国, 胡玮, 等. 压缩小波变换地震谱分解方法应用研究[J].
石油物探 , 2015, 54 (1) : 51-55 SHANG S, HAN L G, HU W, et al. Applied research of synchrosqueezing wavelet transform in seismic spectral decomposition method[J]. Geophysical Prospecting for Petroleum , 2015, 54 (1) : 51-55 |
| [17] | DONOH D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory , 1995, 41 (3) : 613-627 DOI:10.1109/18.382009 |
| [18] |
段晨东, 高强. 基于时频切片分析的故障诊断方法及应用[J].
振动与冲击 , 2011, 30 (9) : 1-5 DUAN C D, GAO Q. Noval fault diagnosis approach using time-frequency slice analysis and its application[J]. Journal of Vibration and Shock , 2011, 30 (9) : 1-5 |
| [19] |
贾海青, 姜弢, 徐学纯, 等. 基于全方向波束定向的地震记录信噪比改善方法[J].
石油物探 , 2015, 54 (5) : 521-530 JIA H Q, JIANG T, XU X C, et al. The SNR improvement method based on omnidirectional beam-forming for vibrator seismic record[J]. Geophysical Prospecting for Petroleum , 2015, 54 (5) : 521-530 |


