凝灰质砂岩储层具有岩性复杂、非均质性强等特点, 储层中的凝灰质和泥质会影响孔隙度、饱和度和渗透率等参数的求取。准确计算出泥质和凝灰质含量, 是提高孔隙度等参数求取精度的关键。虽然计算泥质含量的方法较多, 但存在一定程度的使用局限性:如自然伽马法在只含有泥质地层时, 计算值较为准确, 但当地层中含有其它放射性物质时, 计算结果就会偏高;凝灰质含量的计算方法较少, 一般将其视为泥质的一部分来处理[1], 如ITOH等[2]在处理位于日本北部电阻率较低的凝灰质砂岩储层时指出, 由于凝灰质和泥质的导电特性相同, 可以将其视为泥质的一部分。上述方法求取凝灰质含量的前提条件是凝灰质和泥质的导电性相同, 但在海拉尔盆地许多凝灰质砂岩储层中, 这样的前提条件难以满足[3], 这就使得传统的测井解释方法很难准确求出该储层的参数。因此, 有必要建立一套适合于求取海拉尔盆地凝灰质砂岩储层参数的测井解释方法。
最优化测井解释方法可以对复杂岩性储层进行有效评价, 但其目标函数复杂, 对最优化算法的要求较高[4]。为提高精度, 许多学者从多方面对最优化测井解释中的算法进行了研究[5]。例如, 冯国庆等[6]将非时齐遗传算法引入复杂储层的最优化测井解释, 并且对潜山油藏测井资料进行了处理, 取得了较好的效果;段亚男[7]将细菌觅食算法引入最优化测井解释, 求取了苏里格致密砂岩储层参数, 取得了较准确的结果;曹旭光等[8]、肖亮等[9]在最优化算法方面也做了大量工作, 并且其文献具有很好的指导意义。前人虽然做了很多研究, 但是求取的储层参数种类较少;而对于凝灰质砂岩储层, 需要确定的参数较多。参数越多, 导致待求参数与各常规测井响应之间的非线性关系越强。萤火虫算法(GSO)[10]在处理这种非线性问题时, 具有很强的适应性。因此, 我们将萤火虫算法引入到基于岩石体积物理模型的最优化测井解释中, 并应用于海拉尔盆地凝灰质砂岩储层的参数求取, 较准确地计算出了处理层段的泥质、凝灰质和各骨架矿物含量以及孔隙度值。
1 最优化测井解释的基本原理最优化测井解释是以广义地球物理反演为理论依据, 结合最优化算法和统计概率理论, 充分利用多种测井信息, 对复杂储集层进行测井评价的一门技术[11]。它是以经过环境校正的测井值向量 α i=(φN, ρb, Δt)(φN为中子测井, ρb为密度测井, Δt为声波测井)为基础;以待求的储层参数为自变量x=(x1, x2, x3, …, xn);选取合理的测井响应方程和区域性解释参数z, 反演出相应的理论测井值fi(x, z), 理论值与实际测井值的误差为εi2;根据最小二乘法原理和误差理论, 当误差值趋于最小时, 理论值充分逼近实际测井值。在利用最优化算法不断使εi2趋于最小值的过程中, 自变量x的值会不断调整, 最终的x值即为最优化测井的解释结果[12]。
最优化测井解释的数学公式为:
| $\eqalign{ & \min F\left( {x,{\rm{ }}\alpha } \right) = \min \sum\limits_{i = 1}^m {{{{{\left[ {{\alpha _i} - {f_i}\left( {x,z} \right)} \right]}^2}} \over {{\sigma _i}^2 + {\tau _i}^2}}} \cr & \left\{ \matrix{ s.t. \to {h_k}\left( x \right) = 0\left( {k = 1,2, \cdots ,q} \right) \hfill \cr {g_j}\left( x \right) \ge 0\left( {j = 1,2, \cdots ,p} \right) \hfill \cr} \right. \cr} $ | (1) |
式中:F(x, α)为目标函数;αi为实际测井值;x为自变量;z为区域性解释参数;m为测井曲线个数;σi2与τi2分别为第i种测井值的测量误差和测井响应方程误差;gj(x)≥0与hk(x)=0分别为不等式约束和等式约束。
当确定好目标函数以及各种约束条件后, 即可用最优化算法求取自变量x, 本文将用萤火虫算法来寻求x的最优解。
2 萤火虫算法基本原理及最优化解释流程萤火虫算法是一种全局最优随机搜索算法, 其应用范围越来越广。关于萤火虫算法的应用, 国内外已有很多研究, SZYMON等[13]将萤火虫算法用于约束条件下的最优化问题寻优; JATI等[14]根据离散萤火虫算法理论求解了组合的优化问题, 并得到了较好的结果。研究结果表明, 无论是在解决连续空间还是离散空间的优化问题时, 萤火虫算法都具有较高的可靠性。
2.1 基本原理萤火虫算法是将萤火虫发光的生物学问题转化为数学问题的一种最优化算法[15], 算法的转化原理为:自然界中的每只萤火虫被视为搜索域中的点, 萤火虫因被吸引而产生移动的过程被视为搜索寻优的过程, 由吸引度来表示;萤火虫位于搜索域中的位置被视为目标函数, 由亮度来表示;萤火虫个体的优胜劣汰过程被视为最优解的替代过程。
根据仿生原理, 亮度和吸引度为萤火虫算法的两大要素。萤火虫发光特性数学化的主要公式如下[16]。
1) 相对荧光的亮度为:
| $I={{I}_{0}}\times {{e}^{-\lambda {{r}_{ij}}}}$ | (2) |
式中:I0为r=0处萤火虫的荧光亮度, 亮度越高, 目标函数值就越优;λ表示光强吸收系数, 为一常数, 表征荧光亮度的减弱程度;rij表示萤火虫i和j之间的距离。
2) 吸引度为:
| $\beta ={{\beta }_{0}}\times {{e}^{-\lambda r_{ij}^{2}}}$ | (3) |
式中:β0为r=0处的吸引度, 即最大吸引度。
3) 位置更新公式为:
| ${{x}_{i}}={{x}_{i}}+\beta ({{x}_{j}}-{{x}_{i}})+s({{R}_{nd}}-1/2)$ | (4) |
式中:s表示步长因子, 设为常数, 取值区间为[0, 1]; xi与xj分别表示萤火虫i和j的空间位置; Rnd表示随机因子, 取值区间为[0, 1]。
2.2 萤火虫算法最优化测井解释流程萤火虫个体的优劣程度以数值的大小作为指标进行描述, 数值的大小则是由f(x)决定。萤火虫算法中设定的适应度函数用来求取最大值。为满足最优化测井解释中的最小二乘原理, (1) 式中的目标函数F(x, α)可通过(5) 式转换成适应度函数, 转换公式为:
| $f\left( x \right)=1/\sum\limits_{i=1}^{m}{\frac{{{\left[ {{\alpha }_{i}}-{{f}_{i}}\left( x \right) \right]}^{2}}}{\tau _{i}^{2}+\sigma _{i}^{2}}}+\sum\limits_{j=1}^{m}{\frac{g_{j}^{2}\left( x \right)}{\delta _{j}^{2}}}$ | (5) |
式中:分母为目标函数;gj(x)与δj分别为第j种约束条件和约束条件下所允许的误差;gj2(x)/δj2为外部惩罚项。
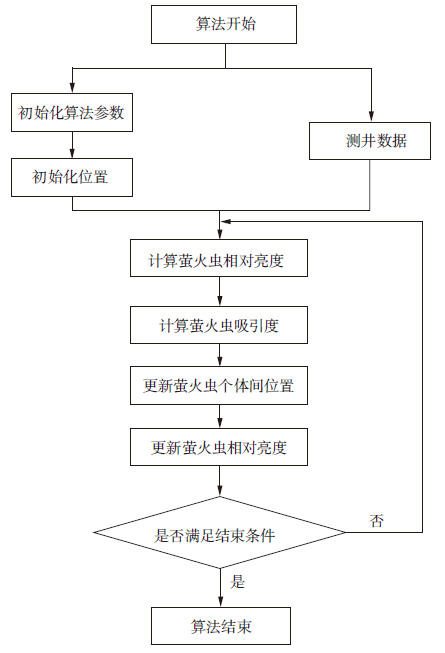
利用萤火虫算法对(5) 式中x进行最优化求解的主要步骤及流程(图 1)如下[17]:
|
图 1 萤火虫算法流程 |
1) 对萤火虫种群数目N, 光强吸收系数λ, 步长s, 最大迭代次数Im等参数进行初始化;
2) 对萤火虫种群位置进行随机初始化, 根据测井数据以及误差数据计算各位置的目标函数值, 并以此值作为各个位置的最大亮度;
3) 以步骤2) 中得出的最大亮度为初始亮度, 代入公式(2) 求出萤火虫的相对亮度;
4) 根据公式(3) 求出萤火虫的吸引度;
5) 根据公式(4) 求出萤火虫的新位置, 为避免陷入局部收敛, 利用随机因子对位置最好的萤火虫进行扰动;
6) 根据步骤5) 得出的新位置, 利用公式(2) 更新相对亮度的大小;
7) 当满足结束条件时, 执行步骤8) , 否则返回步骤3) 继续进行搜索与优化;
8) 输出最优的全局目标函数值以及个体值。
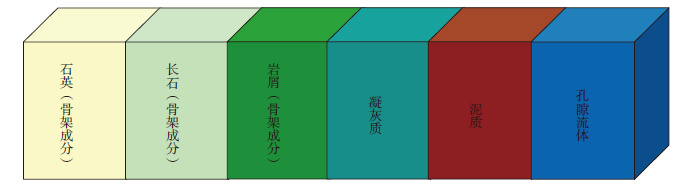
3 萤火虫算法的正反演模拟 3.1 测井响应方程的建立由于海拉尔盆地凝灰质砂岩储层中成分复杂, 为处理问题方便, 建立起岩石体积物理模型。该模型将凝灰质砂岩地层看作是由局部均匀的6部分构成, 分别为石英、长石、岩屑、凝灰质、泥质、有效孔隙流体(图 2)。本文选取的自变量x包括由石英、长石、岩屑组成的骨架矿物含量
|
图 2 岩石体积物理模型 |
根据岩石体积物理模型, 选择5条测井曲线来建立测井响应方程。由体积模型可知, 待求的未知数为6个, 由于引入萤火虫算法, 在响应方程与未知数的数量关系方面可以不作严格要求。5条测井曲线分别为:中子测井φN, 密度测井ρb, 声波测井Δt, 自然伽马测井γ, 岩石光电吸收截面U。各测井响应方程分别表示为:
| ${{\varphi }_{N}}={{\varphi }_{Nf}}\varphi +{{\varphi }_{Nsa}}{{V}_{sa}}+{{\varphi }_{Nsh}}{{V}_{sh}}+\sum\limits_{i=1}^{3}{{{\varphi }_{Nmai}}{{V}_{mai}}}$ | (6) |
| ${{\rho }_{b}}={{\rho }_{f}}\varphi +{{\rho }_{sa}}{{V}_{sa}}+{{\rho }_{sh}}{{V}_{sh}}+\sum\limits_{i=1}^{3}{{{\rho }_{mai}}{{V}_{mai}}}$ | (7) |
| $\Delta t=\Delta {{t}_{f}}\varphi +\Delta {{t}_{sa}}{{V}_{sa}}+\Delta {{t}_{sh}}{{V}_{sh}}+\sum\limits_{i=1}^{3}{\Delta {{t}_{mai}}{{V}_{mai}}}$ | (8) |
| $\gamma ={{\gamma }_{sa}}{{V}_{sa}}+{{\gamma }_{sh}}{{V}_{sh}}+\sum\limits_{i=1}^{2}{{{\gamma }_{mai}}{{V}_{mai}}}$ | (9) |
| $U={{U}_{f}}\varphi +{{U}_{sa}}{{V}_{sa}}+{{U}_{sh}}{{V}_{sh}}+\sum\limits_{i=1}^{3}{{{U}_{mai}}{{V}_{mai}}}$ | (10) |
由于体积模型中, 各个部分的体积和为1, 因而存在平衡方程, 其表达式为:
| $1=\varphi +{{V}_{sa}}+{{V}_{sh}}+\sum\limits_{i=1}^{3}{{{V}_{mai}}}$ | (11) |
按线性方程组的解法, 虽然利用(6) 式到(11) 式可以得出唯一解, 但是这组解很难满足实际条件, 会出现许多小于0或者大于1的值。由于未知数较多, 难以人为调整所求的解, 使之满足实际条件。用萤火虫算法求解上述方程组就能避免所求解不满足实际条件情况的发生, 在加入了误差项以及各种约束条件下对未知数进行搜索最优解, 结果会更加准确。
3.1.1 响应误差与测量误差的确定适应度函数((5) 式)的确定是最优化测井解释的基础条件。为了求得准确的最优解, 适应度函数中的响应方程误差τi和测量误差σi都需要考虑。由于各种测井方法原理、仪器的差异, 误差的公式也不一样。
1) 中子测井。
对于中子测井, 其响应方程误差为:
| $\tau _{{{\varphi }_{N}}}^{2}={{\left( E\varphi \right)}^{2}}+{{(\varphi \delta E)}^{2}}+{{({{V}_{sh}}\delta {{\varphi }_{Nsh}})}^{2}}+{{({{V}_{sa}}\delta {{\varphi }_{sa}})}^{2}}$ | (12) |
式中:E为挖掘效应因子, 误差约为1.3;δE为E的取值误差, 其值约为0.2;δφNsh为φNsh的取值误差, 其值约为0.02;δφsa为φsa的取值误差, 其值约为0.02。
中子测井的测量误差主要有核统计起伏误差、深度匹配误差、井径引起的误差, 其公式分别为:
| $\sigma _{{{\varphi }_{N}}}^{2}=\sum\limits_{k=1}^{3}{\sigma _{k}^{2}}$ | (13) |
| $\left\{ \begin{align} & {{\sigma }_{1}}=0.05{{\varphi }_{N}} \\ & {{\sigma }_{2}}=\left( \left| {{\varphi }_{N}}-{{\varphi }_{N-1}} \right|\text{+}\left| {{\varphi }_{N}}-{{\varphi }_{N+1}} \right| \right)/2 \\ & {{\sigma }_{3}}=0.005\left( \left| {{d}_{-1}}-d \right|+\left| d-{{d}_{+1}} \right| \right) \\ \end{align} \right.$ | (14) |
式中:σ1为核统计起伏误差;σ2为深度匹配误差;φN, φN-1与φN+1分别为当前及其前、后采样点的中子测井值;σ3为井径引起的误差;d, d-1与d+1分别为当前及其前、后采样点的井径值, 单位为in(1 in≈2.54 cm)。
2) 密度测井。
对于密度测井, 其响应方程误差为:
| $\tau _{{{\rho }_{b}}}^{2}={{(\varphi \delta {{\rho }_{h}})}^{2}}+{{({{V}_{sh}}\delta {{\rho }_{sh}})}^{2}}+{{({{V}_{sa}}\delta {{\rho }_{sa}})}^{2}}~$ | (15) |
式中:δρh, δρsh和δρsa分别为ρh, ρsh和ρsa的取值误差, 其值约为0.05 g/cm3, 0.02 g/cm3和0.02 g/cm3。
密度测井的测量误差主要有核统计起伏误差、深度匹配误差、井径校正误差、井壁不规则产生的误差, 其公式为:
| $\sigma _{{{\rho }_{b}}}^{2}=\sum\limits_{k=1}^{4}{\sigma _{k}^{2}}$ | (16) |
| $\left\{ \begin{align} & {{\sigma }_{1}}=0.01{{\rho }_{b}} \\ & {{\sigma }_{2}}=\left( \left| {{\rho }_{b-1}}-{{\rho }_{b}} \right|+\left| {{\rho }_{b}}-{{\rho }_{b+1}} \right| \right)/2 \\ & {{\sigma }_{3}}=\left\{ \begin{matrix} 0 & d\le 9 \\ 0.002\left( d-9 \right) & d>9且井径变化正常 \\ 10 & d>16且井径曲线饱和 \\ \end{matrix} \right. \\ & {{\sigma }_{4}}=0.1R_{ug}^{2} \\ \end{align} \right.$ | (17) |
式中:σ1为核统计起伏误差;σ2为深度匹配误差;ρb, ρb-1和ρb+1分别为当前及其前、后采样点的密度测井值;σ3为井径校正误差;σ4为井壁不规则产生的误差;Rug表示井壁的粗糙度, 可以用相邻7点处的井径值来进行估计:
| ${{R}_{ug}}=\sum\limits_{j=-3}^{3}{\left| {{d}_{j}}-2{{d}_{j+1}}+{{d}_{j+2}} \right|}$ | (18) |
3) 声波测井。
由于研究区均为压实地层, 所以未考虑压实校正系数, 声波测井的响应方程误差为:
| $\begin{align} & {{\tau }_{\Delta t}}^{2}=\text{ }{{\varphi }^{2}}+{{({{V}_{sh}}\delta \Delta {{t}_{sh}})}^{2}}+{{({{V}_{sa}}\delta \Delta {{t}_{sa}})}^{2}}+ \\ & \sum\limits_{i=1}^{3}{{{({{V}_{mai}}\delta \Delta {{t}_{mai}})}^{2}}} \\ \end{align}$ | (19) |
式中:δΔtsh为Δtsh的取值误差, 其值约为3 μs/ft(1 ft≈30.48 cm);δΔtsa为Δtsa的取值误差, 其值约为2 μs/ft;δΔtmai为Δtmai的取值误差, 其值为2~3 μs/ft。
声波测井的测量误差主要有仪器零点漂移误差、深度匹配误差, 公式为:
| ${{\sigma }_{\Delta t}}^{2}={{\sigma }_{1}}^{2}+{{\sigma }_{2}}^{2}$ | (20) |
| $\left\{ \begin{align} & {{\sigma }_{1}}=1 \\ & {{\sigma }_{2}}=(|~\Delta t-\Delta {{t}_{-1}}~\left| + \right|~\Delta t-\Delta {{t}_{+1}}~|)/2 \\ \end{align} \right.$ | (21) |
式中:Δt, Δt-1和Δt+1分别为当前及其前、后采样点的声波时差值。
4) 自然伽马测井。
对于自然伽马测井, 其响应方程误差为:
| ${{\tau }_{\gamma }}^{2}={{({{V}_{sh}}\delta {{\gamma }_{sh}})}^{2}}+{{({{V}_{sa}}\delta {{\gamma }_{sa}})}^{2}}+\sum\limits_{i=1}^{3}{{{({{V}_{mai}}\delta {{\gamma }_{mai}})}^{2}}}$ | (22) |
式中:δγsh, δγsa和δγmai分别为γsh, γsa和γmai的取值误差, 其值为1~3 API。
自然伽马测井测量误差主要有零点漂移误差、核统计起伏误差、深度匹配误差, 其公式为:
| ${{\sigma }_{\gamma }}^{2}=\sum\limits_{i=1}^{3}{{{\sigma }_{k}}^{2}}$ | (23) |
| $\left\{ \begin{align} & {{\sigma }_{1}}=1 \\ & {{\sigma }_{2}}=0.5{{\gamma }^{1/2}} \\ & {{\sigma }_{3}}=\left( \left| \gamma -{{\gamma }_{-1}} \right|+\left| \gamma -{{\gamma }_{+1}} \right| \right)/2 \\ \end{align} \right.$ | (24) |
式中:σ1, σ2与σ3分别为零点漂移误差、核统计起伏误差和深度匹配误差;γ, γ-1与γ+1分别为当前及其前、后采样点的自然伽马测井值, 单位为API。
5) 岩石体积光电吸收截面测井。
对于岩石体积光电吸收截面测井, 其响应方程的误差为:
| ${{\tau }_{U}}^{2}={{({{V}_{sh}}\delta {{U}_{sh}})}^{2}}+{{({{V}_{sa}}\delta {{U}_{sa}})}^{2}}+\sum \text{ }3\text{ }i=\sum\limits_{i=1}^{3}{{{({{V}_{mai}}\delta {{U}_{mai}})}^{2}}}$ | (25) |
式中:δUsh, δUsa和δUmai分别为Ush, Usa和Umai的取值误差, 其值为0.3~0.5 (b/cm3)。
岩石光电吸收截面测井的测量误差主要有核统计起伏误差、深度匹配误差, 公式为:
| $\left\{ \begin{align} & {{\sigma }_{1}}=0.02U \\ & {{\sigma }_{2}}=\left( \left| {{P}_{e}}-{{P}_{e-1}} \right|+\left| {{P}_{e}}-{{P}_{e+1}} \right| \right)/2 \\ \end{align} \right.$ | (26) |
式中:σ1与σ2分别为核统计起伏误差和深度匹配误差;Pe, Pe-1和Pe+1分别为当前及其前、后点的岩石光电吸收截面指数。
3.1.2 约束条件为了得到符合实际条件的最优解, 需要在对未知量x寻优的过程中, 加入一些限制条件, 即约束条件。GLOBAL程序[18]是将约束条件转化为惩罚项加入到目标函数中, 形成新的适应度函数(公式(5) )。约束条件主要有数学物理条件约束、地质条件约束和连续性条件约束。
1) 数学物理条件约束。
一般情况下, 凝灰质含量Vsa, 泥质含量Vsh, 孔隙度φ和各骨架矿物的相对体积含量都需要设定在 , 并且体积模型中各组分的含量和为1。本文用到的数学物理约束包括:
| $\left\{ \begin{align} & 0\le \varphi \le 1 \\ & 0\le {{V}_{sh}}\le 1 \\ & 0\le {{V}_{sa}}\le 1 \\ & 0\le {{V}_{mai}}\le 1i=1,2,3 \\ & \varphi +{{V}_{sh}}+{{V}_{sa}}+{{V}_{mai}}=1 \\ \end{align} \right.$ | (27) |
2) 地质条件约束。
地质条件约束是由地质资料与经验得出的约束, 本文用到的地质条件约束主要包括:
| $\left\{ \begin{matrix} \varphi \le {{\varphi }_{max}}{{(1-{{V}_{sh}}-{{V}_{sa}})}^{{{e}_{1}}}}{{e}_{1}}\approx 1.5 & {{\tau }_{j}}=0.01 \\ {{V}_{sa}}\le {{V}_{sa,~max}} & {{\tau }_{j}}=0.05 \\ {{V}_{mai}}\le {{V}_{mai,~max}} & {{\tau }_{j}}=0.05 \\ {{V}_{sh}}\le {{V}_{sh,~max}} & {{\tau }_{j}}=0.05 \\ \end{matrix} \right.$ | (28) |
3) 连续性条件约束。
在沉积地层的同一处理层段内, 储层性质一般都具有连续性变化的特点。因此, 两个相邻采样点之间的数据不会相差过大, 这种约束即为连续性条件约束, 本文用到的连续性条件约束包括:
| $\left\{ \begin{matrix} {{\varphi }_{j}}\approx {{\varphi }_{j-1}} & {{\tau }_{j}}=0.25{{\varphi }_{max}} \\ {{V}_{sh,\text{ }j}}\approx {{V}_{sh,\text{ }j-1}} & {{\tau }_{j}}=0.25 \\ {{V}_{sa,\text{ }j}}\approx {{V}_{sa,\text{ }j-1}} & {{\tau }_{j}}=0.25 \\ {{V}_{mai,\text{ }j}}\approx {{V}_{mai,\text{ }j-1}} & {{\tau }_{j}}=0.25 \\ \end{matrix} \right.$ | (29) |
为验证萤火虫算法程序的可行性, 首先在一定深度层段的各个深度点上, 人为的构造了凝灰质含量、泥质含量、骨架矿物含量以及孔隙度等6个储层参数, 将构造出的6种储层参数及相应的解释参数分别代入到(6) 式至(10) 式, 重构出5条测试曲线:φN, ρb, Δt, γ, U。
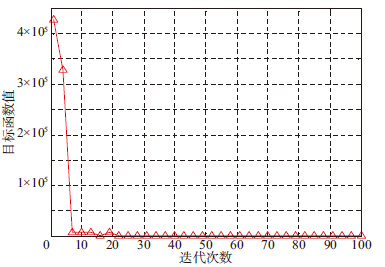
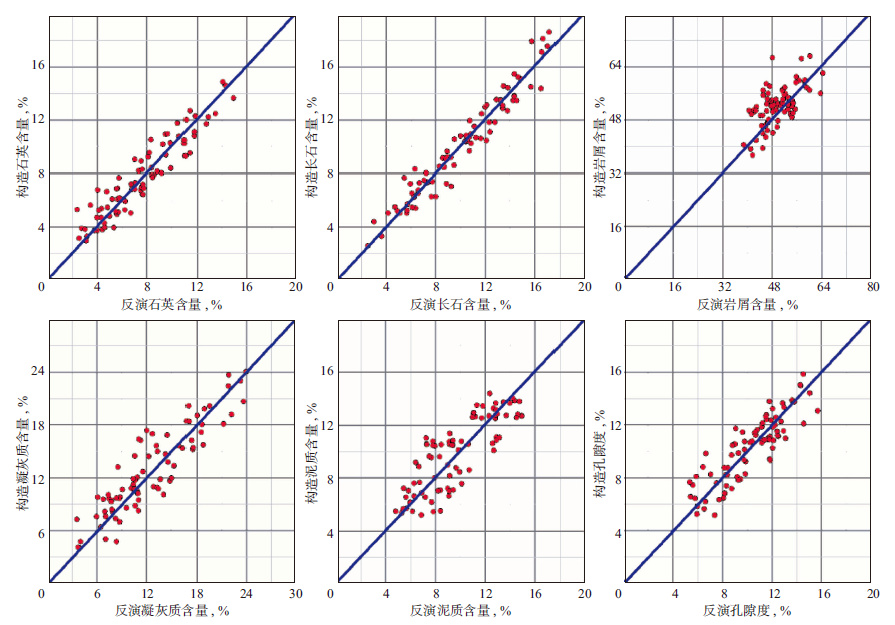
在考虑误差和约束项的条件下, 用萤火虫最优化算法结合最小二乘原理对构造的曲线值进行反演, 并对比反演出的储层参数值与构造值, 得出绝对误差和相对误差。图 3为程序运行过程中, 目标函数值随迭代次数变化图。由图 3可见, 由于误差和约束条件的加入, 使得初始的目标函数值较大, 随着迭代次数的增加, 目标函数值迅速下降, 并在迭代20次左右时, 达到平稳。图 4为反演出的储层参数与构造参数交会图。表 1为各储层参数的绝对误差与相对误差统计表。由图 4和表 1可以看出, 该程序计算的效果较好, 可以用其对实际测井数据进行处理。
|
图 3 目标函数值随迭代次数变化曲线 |
|
图 4 反演的储层参数与构造参数交会结果 |
| 表 1 反演的储层参数误差统计结果 |
利用萤火虫最优化测井解释程序对海拉尔盆地贝16井的凝灰质砂岩层段进行资料处理。主要步骤有:①程序参数的设置;②区域性解释参数的选取;③最优化测井解释成果的对比与分析;④最优化测井解释质量检验。
4.1 程序参数设置萤火虫算法程序的主要参数设置包括:萤火虫种群数目N=40;步长因子s=0.02;光强吸收系数λ=0.4;最大吸引度β0=5;感知半径rs=5;决策半径r0=3;最大迭代次数Im=100。
4.2 区域性解释参数的选取区域性解释参数选取的合理程度将直接影响到最优化测井解释的结果, 如果参数选择不合理, 将会导致解释结果与实际情况不吻合。本文需要确定的解释参数包括6种成分的5种测井响应值。由于所需参数较多, 并且很多参数并非常数, 因此, 需要根据岩心和测井数据, 并参照沉积岩主要矿物测井特征表[19]、岩石矿物手册[20]、火成岩岩石学[21]以及海拉尔盆地火山岩地层的测井响应特征[22]等资料来进行确定。
贝16井处理层段中的凝灰质砂岩属于火山碎屑沉积岩, 由薄片分析得出6种主要成分及其含量, 如图 5所示。
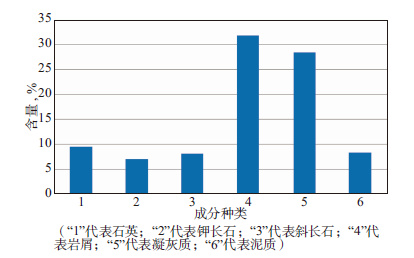
|
图 5 薄片中6种成分及其含量 |
根据贝16井的岩心和测井数据, 并结合文献资料得出处理层段的解释参数, 如表 2所示。
| 表 2 处理层段的解释参数 |
分别利用萤火虫最优化算法(GSO)和遗传算法(GA)计算出了贝16井1 347~1 360 m处的6种储层参数, 其绝对误差见表 3。图 6和图 7分别为GA和GSO算法最优化测井解释结果。图中第1道和第2道为原始曲线道, 第4道是根据计算结果绘制出的岩性剖面, 第5道至第9道分别为石英、长石、岩屑、凝灰质及泥质含量与薄片分析的含量对比, 第10道为最优化算法计算出的孔隙度与岩心孔隙度的对比, 第11道为单孔隙度测井泥质砂岩分析(POR)程序计算出的孔隙度与岩心孔隙度的对比。从图 6, 图 7和表 3可见, 两种优化算法计算出的孔隙度都优于POR程序的计算结果;与GA算法相比, GSO算法计算出的储层参数与岩心数据的吻合度更高, 并且曲线的毛刺较少。
| 表 3 GA和GSO算法绝对误差统计结果 |
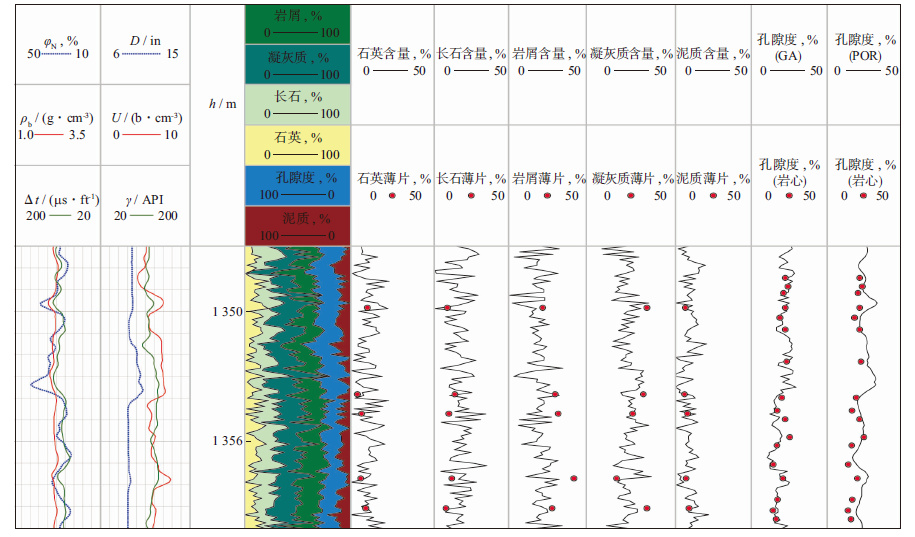
|
图 6 GA最优化测井解释结果(1 ft≈30.48 cm;1 in≈2.54 cm) |
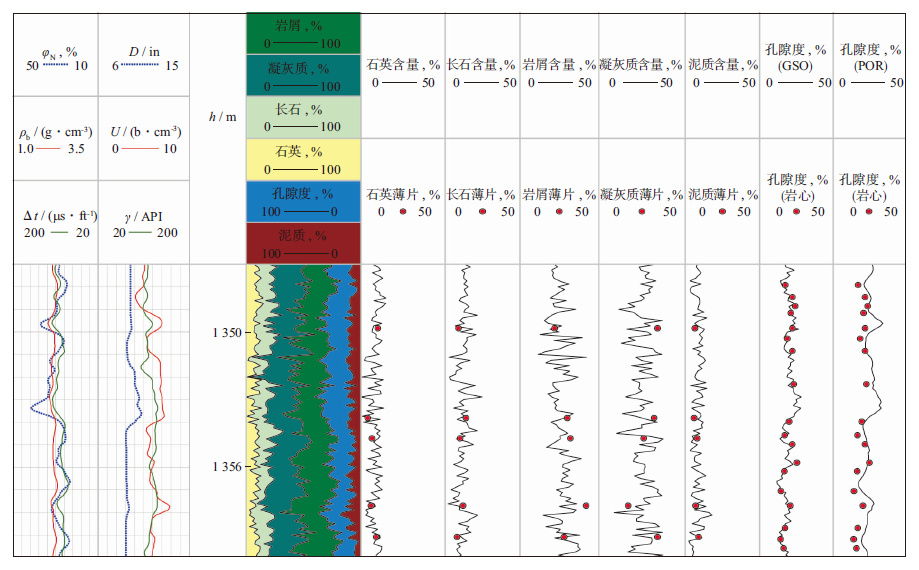
|
图 7 GSO最优化测井解释结果(1 ft≈30.48 cm;1 in≈2.54 cm) |
虽然GA和GSO算法都是以高等生物为模拟对象, 通过“生成+检验”的方式来寻求最优解, 但GSO算法中增加了方向信息, 提高了寻优的速度与精度。POR程序是一种常规计算孔隙度的方法, 对于复杂的非线性问题, 难以求解出准确的结果。
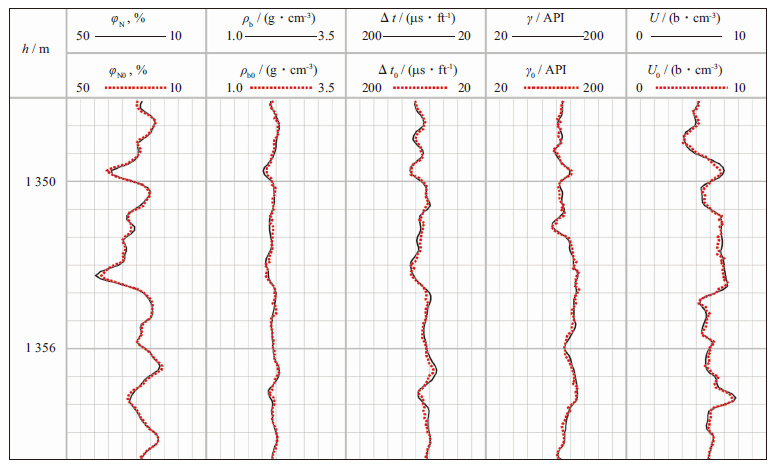
4.4 重构测井曲线质量检验图 8和图 9分别为GA算法和GSO算法重构测井曲线的质量检验图;表 4为两种算法重构测井曲线误差统计表。图 8和图 9中φN0, ρb0, Δt0, γ0, U0为重构曲线。GA和GSO算法都在符合实际地层条件的空间内进行最优解搜索, 并且需要满足目标函数中所加入的惩罚项及各种约束条件。在各种限制条件下, 重构曲线上会出现跳跃点, 这属于正常现象。从图 8, 图 9和表 4可见, 与GA算法相比, GSO算法的重构曲线与实际曲线吻合度更高, 跳跃点较少, 说明基于GSO算法的最优化测井解释结果更加合理、可信。
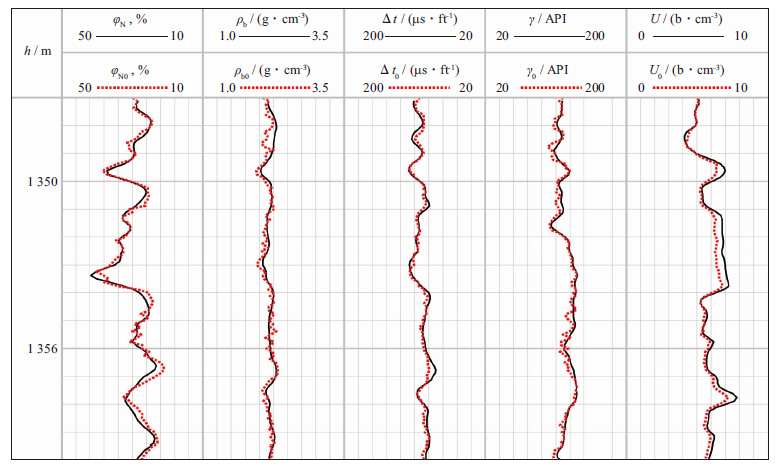
|
图 8 GA算法重构测井曲线质量检验结果(1 ft≈30.48 cm) |
|
图 9 GSO算法重构测井曲线质量检验结果(1 ft≈30.48 cm) |
| 表 4 重构测井曲线绝对误差统计结果 |
1) 利用萤火虫算法对海拉尔盆地凝灰质砂岩储层进行最优化测井解释时, 现有的地质和测井资料被充分利用, 并且一次性求取了既全面又较为准确的储层参数。
2) 萤火虫最优化算法成为计算砂岩储层泥质和凝灰质含量的一种可行方法, 可以减小泥质和凝灰质对储层有效孔隙度的影响。
3) 解释参数对最优化测井解释结果的影响较大, 需根据岩心和测井数据, 并结合文献资料来进行选取;为提高精度, 在处理同一地区不同井时, 解释参数需根据不同井的岩心和测井数据来进行适当调整。
4) 误差和约束条件的加入, 虽然会使得最优化算法的初始目标函数值很大, 但是这样能有效防止程序的过早收敛, 在很大程度上提高了储层参数的计算精度。
| [1] |
肖佃师.海拉尔盆地兴安岭群凝灰质砂岩储层物性解释方法研究[D].大庆:大庆石油学院, 2006
XIAO D S.Interpretation method study on physical property of the tuffaceous sands reservoir of Xing'anling group in Hailar Basin[D].Daqing:Daqing Petroleum Institute, 2006 |
| [2] | ITOH T, KATO S, MIYAIRI M.A quick method of log interpretation for very low resistivity volcanic tuff by the use of CEC data[C]//SPWLA 23rd Annual Logging Symposium.Corpus Christi, Texas:Society of Petrophysicists and Well-Log Analysts, 1982:SPWLA-1982-NN |
| [3] |
张晓峰, 潘保芝, 范晓敏, 等. 海拉尔盆地南屯组凝灰质砂岩储层含水饱和度计算方法[J].
测井技术 , 2009, 33 (4) : 345-349 ZHANG X F, PAN B Z, FAN X M, et al. Computational method of saturation of the tuffaceous sandstones reservoir of Nantun Group in Hailar Basin[J]. Well Logging Technology , 2009, 33 (4) : 345-349 |
| [4] |
潘保芝, 段亚男, 张海涛, 等. BFA-CM最优化测井解释方法[J].
地球物理学报 , 2016, 59 (1) : 391-398 PAN B Z, DUAN Y N, ZHANG H T, et al. BFA-CM optimization log interpretation method[J]. Chinese Journal of Geophysics , 2016, 59 (1) : 391-398 |
| [5] |
韩雪.梨树断陷砂砾岩储层GA-CM混合最优化测井解释方法研究[D].吉林:吉林大学, 2012
HAN X.Research on Glutenite reservoirs with GA-CM hybrid optimization log interpretation method in Lishu fault depression[D].Jilin:Jilin University, 2012 |
| [6] |
冯国庆, 陈军, 张烈辉, 等. 最优化测井解释的遗传算法实现[J].
天然气工业 , 2002, 22 (6) : 48-51 FENG G Q, CHEN J, ZHANG L H, et al. Algorithm of optimization log interpretation by genetic[J]. Natural Gas Industry , 2002, 22 (6) : 48-51 |
| [7] |
段亚男.苏里格致密砂岩储层BFA-CM混合最优化测井解释方法研究[D].吉林:吉林大学, 2015
DUAN Y N.Research on BFA-CM hybrid optimization log interpretation method in sandstone reservoirs of sulige area[D].Jilin:Jilin University, 2015 |
| [8] |
曹旭光, 翟慧杰, 刘传平, 等. 遗传算法计算储层参数研究[J].
长春理工大学学报 , 2007, 29 (4) : 59-61 CAO X G, ZHAI H J, LIU C P, et al. Research of genetic algorithm on computing reservoir parameter[J]. Journal of Changchun University of Technology , 2007, 29 (4) : 59-61 |
| [9] |
肖亮, 毛志强, 孙中春, 等. 最优化方法在复杂岩性储集层测井评价中的应用[J].
断块油气田 , 2011, 18 (3) : 342-345 XIAO L, MAO Z Q, SUN Z C, et al. Application of optimization method in log evaluation of complex lithologic reservoir[J]. Fault-Block Oil&Gas Field , 2011, 18 (3) : 342-345 |
| [10] | KRISHNANAND K N, GHOSE D.Detection of multiple source locations using a glowworm metaphor with applications to collective robotics[C]//Proceedings of IEEE Swarm Intelligence Symposium.Piscataway:IEEE Press, 2005:84-91 |
| [11] |
韩雪, 潘保芝, 张意, 等. 遗传最优化算法在砂砾岩储层测井评价中的应用[J].
测井技术 , 2012, 36 (4) : 392-396 HAN X, PAN B Z, ZHANG Y, et al. GA-optimal log interpretation applied in glutenite reservoir evaluation[J]. Well Logging Technology , 2012, 36 (4) : 392-396 |
| [12] |
雍世和.
最优化测井解释[M]. 北京: 石油大学出版社, 1995 : 1 -2.
YONG S H. Optimization log interpretation[M]. Beijing: Petroleum University Press, 1995 : 1 -2. |
| [13] | SZYMON L, SLAWOMIR Z.Firefly algorithm for continuous constrained optimization tasks[M]//Computational Collective Intelligence.Semantic web, social networks and multiagent systems.Berlin:Springer Berlin Heidelberg, 2009:97-106 |
| [14] | JATI G K. Evolutionary discrete firefly algorithm for travelling salesman problem[M]. Berlin: Springer Berlin Heidelberg, 2011 : 393 -403. |
| [15] |
杨娇, 叶春明. 应用新型萤火虫算法求解Job-shop调度问题[J].
计算机工程与应用 , 2013, 49 (11) : 217-219 YANG J, YE C M. New kind of firefly algorithm is applied to solve the problem of Job-shop[J]. Computer Engineering and Applications , 2013, 49 (11) : 217-219 |
| [16] |
刘长平, 叶春明. 一种新颖的仿生群智能优化算法:萤火虫算法[J].
计算机应用研究 , 2011, 28 (9) : 3295-3297 LIU C P, YE C M. Novel bioinspired swarm intelligence optimization algorithm:firefly algorithm[J]. Application Research of Computers , 2011, 28 (9) : 3295-3297 |
| [17] |
付强, 蒋睿奇, 王子龙, 等. 基于改进萤火虫算法的土壤水分特征曲线参数优化[J].
农业工程学报 , 2015, 31 (11) : 117-122 FU Q, JIANG R Q, WANG Z L, et al. Optimization of soil water characteristic curves parameters by modified firefly algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering , 2015, 31 (11) : 117-122 |
| [18] | MAYER C.Global, a new approach to computer-processed log interpretation[C]//SPE Annual Technical Conference and Exhibition.Dallas, Texas:Society of Petroleum Engineers, 1980:SPE-9341-MS |
| [19] |
雍世和, 张超谟.
测井数据处理与综合解释[M]. 东营: 石油大学出版社, 1996 : 202 -203.
YONG S H, ZHANG C M. Logging data processing and comprehensive interpretation[M]. Dongying: Petroleum University Press, 1996 : 202 -203. |
| [20] |
斯伦贝谢公司.测井解释常用岩石矿物手册[M].吴庆岩, 张爱军, 译.北京:石油工业出版社, 1998:151-159
SCHLUMBERGER CORP.Manual of normal rock and mineral in log interpreting[M].WU Q Y, ZHANG A J, translator.Beijing:Petroleum Industry Press, 1998:151-159 |
| [21] |
徐夕生, 邱检生.
火成岩岩石学[M]. 北京: 科学出版社, 2010 : 261 -278.
XU X S, QIU J S. Igneous petrology[M]. Beijing: Science Press, 2010 : 261 -278. |
| [22] |
张美玲, 邵阳, 高柏原, 等. 海拉尔盆地含火山岩地层主要岩性分布及测井响应分析[J].
中国石油勘探 , 2009, 14 (2) : 50-54 ZHANG M L, SHAO Y, GAO B Y, et al. Major lithological distribution and log response analysis of volcanic rock bearing strata in Hailar Basin[J]. China Petroleum Exploration , 2009, 14 (2) : 50-54 |



 ,
,