2. 成都理工大学能源学院,四川 成都 610059
2. College of Energy Resource, Chengdu University of Technology, Chengdu 610059, China
沉积盆地中, 岩石作为孔隙弹性介质[1], 其外部载荷受岩石骨架和孔隙流体共同影响, 这两者的合力即为有效应力。基于此, TERZAGHI[2]提出了著名的有效应力概念, 定义有效应力(σ′)为岩石所承受的总应力(σ)与孔隙压力(Pf)的差值, 即σ′=σ-Pf, 但该公式仅适用于未固结岩石或松散沉积物。
对于中等及强固结岩石, 考虑到颗粒支撑岩石内部存在较强的压实及胶结作用[3], 孔隙流体实际上未完全承担全部地层压力。因此, BIOT[4]提出了Biot理论(又称有效应力理论)公式, 该公式在TERZAGHI提出的公式基础上进行了修正, 定义有效应力σ′=σ-αPf, 其中, α被称为Biot系数或有效应力系数, 其取值范围在0~1.0, 定义为静态孔隙空间变形量与岩石总体积变化量的比值[5]。前人研究表明, Biot理论不仅适用于沉积岩体, 也适用于孔隙度低于1%的结晶岩体, 因此具有广阔的适用空间[6]。对于强固结致密岩石而言, 其α通常较小;随着岩石固结程度的降低, 其α逐渐增加;当岩石固结程度非常低或内部结构极为松散时, α接近1.0, 此时Biot理论公式中的σ和Terzaghi公式中的σ相同。
由Biot理论公式可以看出, Biot系数主要用于权衡地层压力对岩石有效应力的影响程度, 是控制地层岩石变形及流体渗流的内在因素。该参数是地震反演、压裂设计、出砂趋势预测、储层应力敏感性研究、井眼轨迹优化及井壁稳定性分析的重要输入参数[7], 在油气勘探、开发中均具有重要应用价值。
Biot系数可通过设计三轴实验测试方法获得[8]。具体方法为:首先保持岩石孔隙压力不变, 逐渐增加围压, 求得岩石体积压缩系数(Cb);然后, 在“不封套”条件下, 将围压和孔压同时以相同的速率增加。此时, 岩石孔隙压力与外部压力始终相等, 岩石的变形完全由颗粒引起, 求得岩石颗粒压缩系数(Cs)。最终, 岩石α可以表示为α=1-Cs/Cb。
该实验方法虽然可以较为准确地获得岩石Biot系数, 但存在费用高昂且数据离散的缺陷[9]。基于该问题, 很多学者试图利用岩石物性参数及声学参数等完成对岩石Biot系数的预测[10-11], 取得了一些重要成果, 但均存在一定问题, 例如在利用物性参数如孔隙度预测岩石Biot系数时, 所考虑的参数较少[10]。对于致密砂岩来说, Biot系数的降低机制除受压实减孔影响外, 还受强胶结作用的影响, Biot系数变化幅度较大(0.1~0.9) , 因而单依靠孔隙度对致密砂岩Biot系数进行预测, 可靠度相对较低[10];而利用声学参数预测岩石Biot系数虽然考虑的因素较为全面, 但仅代表一种动态结果, 与静态结果间具有一定差异, 需要进行相应校正[10]。同时, 对于同一岩性地层, 其中矿物组分、微组构及微裂缝发育程度均存在一定差异, 因此声学预测方法中定义岩石基质矿物参数为一定值的假设[12], 会使预测误差进一步扩大。
基于以上方法存在的不足, 本文以含气海陆过渡相致密砂岩储层为研究对象, 提出了一种新的Biot系数预测方法, 即利用自适应方法提取地层干岩石模量及基质矿物模量参数, 综合考虑孔隙度及静态力学参数对致密砂岩Biot系数的影响。我们将该方法获得的Biot系数预测结果与常规方法进行对比, 证明了该方法的有效性。
1 致密砂岩Biot系数常规预测方法 1.1 利用孔隙度预测岩石Biot系数(方法1)前人提出多种利用孔隙度(φ)预测砂岩Biot系数的方法, 对于未固结砂岩, 可以利用经验公式(1) [10];而对于强固结致密砂岩, 往往采用经验公式(2) [11]。从公式(1) 和公式(2) 均可看出, 砂岩α随φ的增加而增加。对于致密砂岩((2) 式), 当其孔隙度从0增加到10%时, 相应岩石α从0增加到0.33, 致密砂岩具有α较低的特征。
| $\alpha =\frac{-184.05}{1+\left( \frac{\exp \varphi +0.5646}{0.09425} \right)}+0.99494~$ | (1) |
| $\alpha =1-{{\left( 1-\varphi \right)}^{3.8}}$ | (2) |
利用声学参数预测岩石动态Biot系数的方法主要基于岩石和其中颗粒间压缩性的关系得来[13]。由于α=1-Cs/Cb, 因此, 岩石的α还可以表示为公式(3) 。公式(3) 中的各参数可以利用纵、横波波速进行计算, 见文献[9]和文献[14], 此时α计算结果为动态值。当Kd及Ko为静态值时, 所计算α结果为静态值[14]。
| $\alpha =1-\frac{{{K}_{d}}}{{{K}_{o}}}~$ | (3) |
式中:Kd为干岩石体积模量, 单位为GPa;Ko为基质矿物体积模量, 单位为GPa。
同时, 岩石动态α还可以根据公式(4) 进行计算[15]。
| $\alpha =1-\frac{\rho }{{{\rho }_{m}}~}\cdot \frac{3/\Delta {{t}_{c}}^{2}-4/\Delta {{t}_{s}}^{2}}{3/\Delta {{t}_{mc}}^{2}-4/\Delta {{t}_{ms}}^{2}}$ | (4) |
式中:ρ和ρm分别为岩石密度及岩石骨架密度, 单位为g/cm3;Δtc和Δts分别为岩石纵波时差及横波时差, 单位μs/m;Δtmc及Δtms分别为岩石骨架的纵波时差和横波时差, 单位为μs/m。公式(4) 中, 岩石骨架参数ρm, Δtmc及Δtms往往取常数。对于本文所研究的致密砂岩来说, 其骨架为石英矿物, 因而ρm取2.65 g/cm3, Δtmc取182 μs/m, Δtms取289 μs/m。
1.3 考虑孔隙空间变形的Biot系数预测方法(方法3)考虑孔隙空间变形的α预测方法主要基于Biot-Gassmann方程, 由于Biot-Gassmann方程是一个基于Biot理论的修正中-低频近似方程, 可用于地震及测井解释[16]。当考虑孔隙空间时[17], 多孔介质中纵波波速vP和横波波速vS分别满足公式(5) 和公式(6) 。
| $\rho {{v}_{P}}^{2}={{K}_{p}}+{{K}_{s}}+4{{\mu }_{s}}/3$ | (5) |
| $\rho {{v}_{S}}^{2}={{\mu }_{s}}$ | (6) |
式中:Kp为孔隙空间体积模量, 单位为GPa;μs为含流体岩石剪切模量, 单位为GPa。
将公式(5) 和公式(6) 作比可得:
| $\frac{{{v}_{P}}^{2}}{{{v}_{S}}^{2}}~~=\frac{{{K}_{p}}}{{{\mu }_{s}}}~~+\frac{{{K}_{s}}}{{{\mu }_{s}}}~~+\frac{4}{3}$ | (7) |
根据Biot理论, 孔隙空间体积模量Kp可近似表示为[7]:
| ${{K}_{p}}=\frac{{{\alpha }^{2}}}{\frac{\alpha -\varphi }{{{K}_{o}}}~}~+\frac{\varphi }{{{K}_{f}}}~$ | (8) |
式中:Kf为流体体积模量, 单位为GPa。
根据公式(7) 和公式(8) 即可求取地层岩石α, 同时可以看出, 由于考虑了Kf, 因此α不仅与岩石骨架参数有关, 而且与岩石中所含流体组分性质相关。由于公式(8) 中的Ks, μs及Ko参数均为静态值, 因而该方法最终所求得的α亦为静态结果。
2 自适应方法预测致密砂岩Biot系数利用自适应方法提取致密砂岩地层静态干岩石体积模量(Kd)及基质矿物体积模量(Ko)[18], 进而利用(3) 式完成地层岩石α的预测。
首先, 引入干岩样泊松比σd, 并定义Y:
| $Y=\frac{3(1-{{\sigma }_{d}})}{1+{{\sigma }_{d}}}$ | (9) |
对于致密砂岩而言, 参考本文研究区致密砂岩干岩样三轴实验测试结果, σd取值范围定义为0.10~0.25。
将Biot系数α引入Gassman-Biot-Geertsma方程, 得到关于α的一元二次表达式[19]:
| $\begin{align} & \left( Y-1 \right){{\alpha }^{2}}+\left[ Y\varphi \left( \frac{{{K}_{o}}~}{{{K}_{f}}}~-1 \right)-Y+\frac{M}{{{K}_{o}}} \right]~\alpha - \\ & \varphi \left( Y-\frac{M}{{{K}_{o}}} \right)\left( \frac{{{K}_{o}}~}{{{K}_{f}}}~-1 \right)=0 \\ \end{align}$ | (10) |
其中,
| $M=Y{{K}_{d}}+\frac{{{\alpha }^{2}}}{\frac{\alpha -\varphi }{{{K}_{o}}}+\frac{\varphi }{{{K}_{f}}}}$ | (11) |
由于待定参数较多, 先利用公式(4) 确定动态α。在上述σd定义取值区间内不断调整σd及Ko, 利用公式(10) 及测试数据对Kd进行计算, 将计算结果代入公式(12) , 完成岩石Ks的计算。将Ks计算结果与实测静态结果进行对比, 确定两者误差最小条件下的σd及Ko, 进而确定岩石Kd。可以看出, 该方法所确定的Ko及Kd均为静态值;同时, 计算结果Kd与Ko之间具有一定对应关系。将利用自适应方法获得的岩石Ko及Kd代入公式(3) , 从而获得地层岩石静态α。
| ${{K}_{s}}={{K}_{d}}+\frac{\left( 1-\frac{{{K}_{d}}}{{{K}_{o}}^{2}} \right)~}{\frac{\varphi }{{{K}_{f}}}~+\frac{1-\varphi }{{{K}_{o}}}-\frac{{{K}_{d}}}{{{K}_{o}}^{2}}}~$ | (12) |
式中:Ks为含流体岩石体积模量, 单位为GPa。
3 实例分析 3.1 研究区概述研究区位于沁水盆地南部樊庄区块煤层气井区, 目前以开发二叠系山西组煤层气(3号煤)为主。老井复查及气测录井资料显示, 该地区太原组、山西组及下石盒子组致密砂岩地层气测异常普遍, 具有巨大的致密气勘探、开发潜力。本文研究数据取自研究区10口单井(垂直井)的山西组及太原组地层, 地层埋深在500~800 m。对各单井岩心进行观察, 结合岩性归位后的测井资料提取致密砂岩物性及声学参数。所提取样本数N共计85组, 研究区致密砂岩静态模量参数与其它物理参数间的关系如图 1所示。图 1中, Ks和μs为实验校正后的静态结果。
|
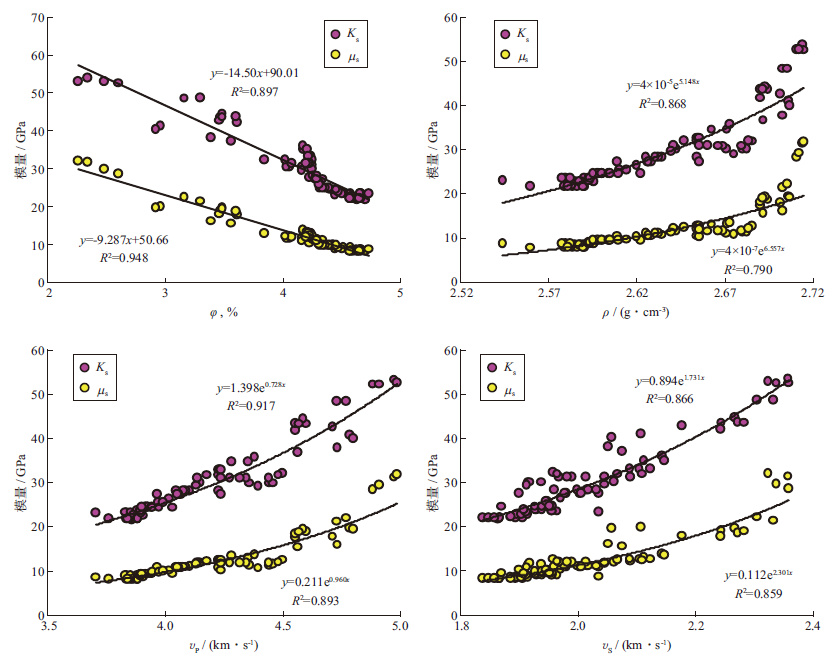
图 1 研究区致密砂岩静态模量参数与其它物理参数间的关系 |
从图 1可以看出, 目的层致密砂岩物性较差, 孔隙度分布在2.20%~4.75%, 密度分布在2.54~2.72 g/cm3, 具有明显的低孔、致密特征。该致密砂岩Ks主要分布在25~50 GPa, μs主要分布在10~30 GPa。这两个参数与岩石孔隙度均具有较好的负相关性, 而与岩石密度、vP及vS具有较好的正相关性。在岩石孔隙度φ<4.2%时, Ks和μs降低幅度较大, 之后逐渐变缓。对应密度曲线中, 当岩石密度ρ<2.67 g/cm3时, 岩石Ks和μs增加幅度较小, 之后增加幅度逐渐放大。
整体来看, 目的层致密砂岩可划分为两段:①φ>4.2%, ρ<2.67 g/cm3, vP<4.5 km/s, vS<2.2 km/s,这类致密砂岩具有相对较好的物性(孔隙度), 所占比例较大, 地层岩石Ks和μs变化幅度较小;②φ<4.2%, ρ>2.67 g/cm3, vP>4.5 km/s, vS>2.2 km/s,这类致密砂岩具有相对较差的物性(孔隙度), 被泥质等基质矿物严重充填, 其在地层中所占比例较小, 地层岩石Ks和μs变化幅度较大。
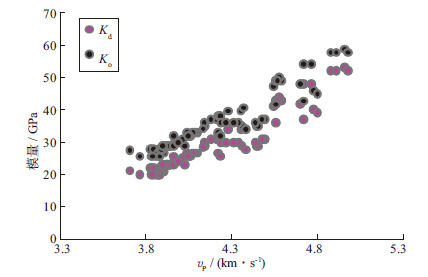
3.2 自适应方法参数提取结果分析利用本文方法提取了85组致密砂岩样本的Ko及Kd, 所提取致密砂岩地层Kd及Ko与纵波速度vP的关系如图 2所示。从图 2可以看出, 各组致密砂岩的Ko及Kd与vP均具有较好的正相关性, 同时, Ko>Kd。各组致密砂岩的Ko主要分布在25.9~50.9 GPa, 平均值为35.0 GPa;Kd主要分布在20.1~53.0 GPa, 平均值为29.0 GPa。
|
图 2 所提取致密砂岩地层Kd及Ko与纵波波速的关系 |
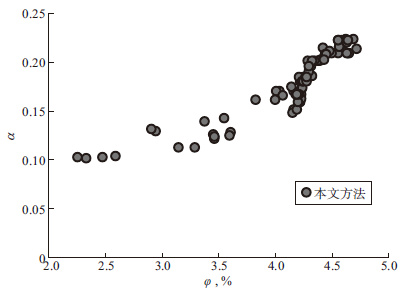
利用所提取的致密砂岩的Ko和Kd(图 2)及公式(3) 可以求取各组岩石相应α静态值, 结果如图 3所示。从图 3中可以看出, 所求取的85组致密砂岩的α与岩石孔隙度间具有非常好的正相关性, 在岩石孔隙度从2.20%增加到4.75%的过程中, 相应地层岩石的α从0.100增加到了0.224。由于目的层致密砂岩整体物性特征差异不大, 因而所求取的地层α变化亦不大, 这85组致密砂岩的φ平均值为4.11%, α平均值为0.179。
|
图 3 致密砂岩地层岩石孔隙度φ与所计算α的关系 |
该致密砂岩α较低的原因与其所经历的强压实及胶结作用有关[20]。图 4为Z1井致密砂岩(岩屑石英砂岩)显微图像, 可以看出, 其颗粒间多呈凹凸接触, 压实特征显著。所研究目的层致密砂岩中胶结物组分以硅质、钙质和绿泥石最为常见。硅质胶结物主要呈次生加大边、粒状自生石英和微晶-隐晶质玉髓3种形式产出; 钙质胶结物则呈泥晶、细粒状和连生结构3种形式产出;自生绿泥石多呈薄膜状, 多分布在碎屑颗粒周围, 应属成岩作用早期产物;自生高岭石多呈书册状或片状。这些充填组分及特征表明该区致密砂岩经历了强胶结作用。

|
图 4 Z1井岩屑石英砂岩显微图像 |
从前人获得的一些致密砂岩(φ<10.00%)及常规砂岩(φ>10.00%)α取值实验结果[21-25](表 1)可以看出, 第1~11组致密砂岩的φ主要分布在0.70%~7.70%, 平均值为4.26%;相应α主要分布在0.172~0.390, 平均值为0.242。第12~24组常规砂岩的φ主要分布在10.20%~20.10%, 平均值为15.20%;相应α主要分布在0.375~0.900, 平均值为0.637。中孔常规砂岩的φ和α均明显大于致密砂岩。
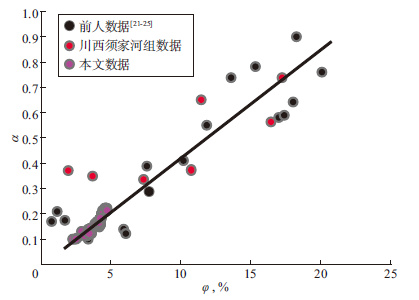
表 1中第1~11组致密砂岩的φ和α平均值与本文致密砂岩相差不大。将本文致密砂岩的φ和α与表 1中的结果进行相关性分析, 结果如图 5所示。从图 5可以看出, 本文数据与前人给出的数据变化趋势极为一致。向下延长这条拟合线(图 5)会经过坐标原点(0, 0) , 此时, 地层岩石孔隙度为0, 相应岩石的α和Biot理论公式中Pf均为0, 地层岩石有效应力(σ′)等于总应力σ。这些特征均能在一定程度上表明, 本文所计算的研究区致密砂岩Biot系数可靠, 所提出的方法有效可行。
|
图 5 砂岩孔隙度与Biot系数的关系 |
| 表 1 砂岩孔隙度及Biot系数取值结果 |
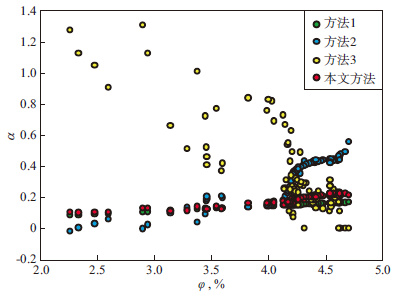
将本文所提出方法分别与前述孔隙度方法(方法1) 、声学参数方法(方法2) 及考虑孔隙空间变形方法(方法3) 进行对比。采用4种方法计算得到的研究区致密砂岩α值与孔隙度间关系见图 6。其中, 方法1采用公式(2) 计算, 方法2采用公式(4) 计算。
|
图 6 岩石孔隙度与采用不同方法计算的α的关系 |
从图 6中可以看出, 采用方法1,方法2和本文方法所计算的α均随孔隙度的增加而增加, 与实际情况相符。但采用方法3所计算的α随孔隙度的增加而降低, 部分α>1, 与实际情况明显不符;当φ<4.20%时该方法预测误差较大, 当φ>4.20%时, 预测误差略小, 但所计算的α离散度较大, 表明该方法应慎用。
当致密砂岩φ<4.20%时, 采用方法1,方法2和本文方法计算获得的α差别较小(图 6), 但采用本文方法的计算结果略大于采用方法1的计算结果, 而采用方法1的计算结果略大于采用方法2的计算结果。当岩石φ>4.20%时, 采用方法1,方法2和本文方法计算获得的α差别相对较大, 此时, 采用方法2计算的α最大, 采用本文方法的结果次之, 采用方法1的结果最小。
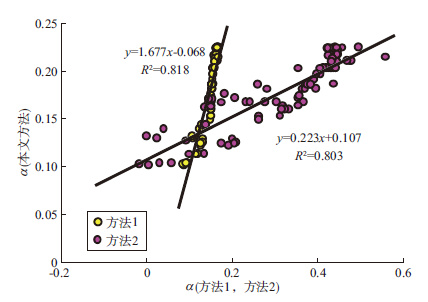
整体来看, 由于目的层致密砂岩物性变化较小, 所计算的α应具有较小的离散度。因此, 利用本文方法所计算的α最为合理。采用方法1和方法2计算的致密砂岩α值虽然具有一定误差, 但与采用本文方法计算的α具有较好的对应关系(图 7)。这一结果表明当采用方法1和方法2预测研究区致密砂岩α时, 可以利用该转换关系进行校正, 从而减小其预测误差。
|
图 7 采用不同方法计算的致密砂岩Biot系数校正结果 |
1) 以海陆过渡相致密砂岩储层为例, 提出基于自适应方法的Biot系数预测方法。提取的致密砂岩储层Ko主要分布在25.9~50.9 GPa, 平均值为35.0 GPa;Kd主要分布在20.1~53.0 GPa, 平均值为29.0 GPa;α平均值为0.179。α 值较低的原因与致密砂岩所经历的强压实及胶结作用有关。
2) 将本文方法分别与孔隙度方法、声学参数方法及考虑孔隙空间变形方法进行了对比。结果表明, 考虑孔隙空间变形方法在致密砂岩孔隙度φ<4.20%时误差较大;当孔隙度φ>4.20%时, 计算的α具有一定的离散度, 因此该方法应慎用。 对于另外两种方法(孔隙度方法和声学参数方法), 当孔隙度φ<4.20%时, 采用这两种方法与采用本文方法计算获得的α差别较小;当孔隙度φ>4.20%时, 采用声学参数方法计算的α值最大, 采用本文方法的结果次之, 采用孔隙度方法的结果最小。
3) 采用孔隙度和声学参数方法计算的α与采用本文方法的结果之间具有较好的对应关系, 该关系可以用于α的校正。
| [1] |
唐杰, 方兵, 孙成禹, 等. 基于各向异性流体替换的裂隙介质波传播特征研究[J].
石油物探 , 2015, 54 (1) : 1-8 TANG J, FANG B, SUN C Y, et al. Study of seismic wave propagation characteristics based on anisotropic fluid substitution in fractured medium[J]. Geophysical Prospecting for Petroleum , 2015, 54 (1) : 1-8 |
| [2] | TERZAGHI K. Erdbaumechanik auf bodenphysikalischer Grundlage[M]. Leipzig and Vienna: Franz Deuticke, 1925 : 1 -399. |
| [3] |
未晛, 王尚旭, 赵建国, 等. 致密砂岩纵、横波速度影响因素的实验研究[J].
石油物探 , 2015, 54 (1) : 9-16 WEI X, WANG S X, ZHAO J G, et al. Laboratory investigation of influence factors on vP and vS in tight sandstone[J]. Geophysical Prospecting for Petroleum , 2015, 54 (1) : 9-16 |
| [4] | BIOT M A. General theory of three dimensional consolidation[J]. Journal of Applied Physics , 1941, 12 (2) : 155-164 DOI:10.1063/1.1712886 |
| [5] | BIOT M A, WILLIS D F. The elastic coefficients of the theory of consolidation[J]. Journal of Applied Mechanics , 1957, 24 (4) : 594-601 |
| [6] | MAVKO G, MUKERJI T, DVORKIN J. The rock physics handbook:tools for seismic analysis in porous media[M]. London: Cambridge University Press, 1998 : 1 -339. |
| [7] | MOHANNAD M A, MAI K B, IDA L F, et al. Biot's coefficient as an indicator of strength and porosity reduction:calcareous sediments from Kerguelen Plateau[J]. Journal of Petroleum Scicence and Engineering , 2010, 70 (3/4) : 282-297 |
| [8] | CHARLEZ P A. Rock mechanics:theoretical fundamentals[M]. Paris: Editions Technip, 1991 : 1 -360. |
| [9] | LUO X, WERE P, LIU J F, et al. Estimation of Biot's effective stress coefficient from well logs[J]. Environment Earth Science , 2015, 73 (11) : 7019-7028 DOI:10.1007/s12665-015-4219-8 |
| [10] | LEE M W. Biot-Gassmann theory for velocities of gas-hydrate-bearing sediments[J]. Geophysics , 2002, 67 (6) : 1711-1719 DOI:10.1190/1.1527072 |
| [11] | WU B. Biot's effective stress coefficient evaluation:static and dynamic approaches[J]. Presented in ISRM-2nd Asian rock mechanics symposium , 2001 : 650 |
| [12] | LEE M W. Modified Biot-Gassmann theory for calculating elastic velocities for unconsolidated and consolidated sediments[J]. Marine Geophysical Researches , 2002, 23 (5) : 403-412 |
| [13] | CHENG H D. Material coefficients of anisotropic poroelasticity[J]. Intenational Journal of Rock Mechanics & Mining Science , 1997, 34 (2) : 199-205 |
| [14] | LEE M W.Velocity ratio and its application to predicting velocities . .http://pubs.usgs.gov/bul/b2197/B2197-508.pdf |
| [15] | CHRISTENSEN R S.Seismic velocities[C]//Carmichael RS.Handbook of physical properties of rocks, II.Florida:CRC Press, 1982:57-67 |
| [16] | GASSMANN F. Uber die elastizitat poroser medium[J]. Vierteliahrsschrift der Naturforschenden Gesellschaft in Zurich , 1951, 96 : 1-23 |
| [17] | BIOT M A. Theory of elastic waves in a fluid-saturated porous solid.I.Low frequency range[J]. Journal Acoustic Sac America , 1956, 28 : 179-191 DOI:10.1121/1.1908241 |
| [18] |
孙成禹, 李晶晶, 唐杰, 等. 基于测井资料的储层模量反演与地震反射特征分析[J].
石油物探 , 2015, 54 (3) : 350-357 SUN C Y, LI J J, TANG J, et al. Reservoir moduli inversion and seismic reflection characteristics analysis based on logging data[J]. Geophysical Prospecting for Petroleum , 2015, 54 (3) : 350-357 |
| [19] | BIRCH F. Compressibility;elastic constants, in Handbook of physical constants[M]. New York: Geological Society of America, 1966 : 97 -174. |
| [20] | KENNETH W W. Dispersion analysis of velocity and attenuation in Berea sandstone[J]. Journal of Geophysical Research , 1985, 90 (B8) : 6793-6800 DOI:10.1029/JB090iB08p06793 |
| [21] | HOU M Z, YOON J, KHAN I U, et al.Determination of the 3D primary stresses and hydromechanical properties of several strata in the Salzwedel reservoir area and multi-layer caprock reservoir 2D model for the Altensalzwedel test field for THMC coupled numerical modeling[R].BMBF project, Colorado, USA, Report 03G0704Q, 2009:5-10 |
| [22] | GUSTKIEWCZ J.Synoptic view of methane bahaviour of rocks under trixial compression[R].Pau, Balkema, Rotterdam, SPE, 1989:3-9 |
| [23] | FABER D. Poroelastic properties of limestones and sandstones under hydrostatic conditions[J]. Intenational Journal of Rock Mechanical and Mining Science , 1997, 34 (1) : 127-134 DOI:10.1016/S1365-1609(97)80038-X |
| [24] | QIAO L P, WONG R C K, AGUILERA R, et al. Determination of Biot's effective stress parameter for permeability of nikanassin sandstone[J]. Canadian International Petroleum Conference , 2009, 105 : 1-4 |
| [25] | TRAUTWEIN U.Poroelastische verformung and petrophysikalische eigenschaften von rotliegend sandsteinen[D].Berlin:Technische University Berlin, 2005 |



 ,
,