2. 中国石油化工股份有限公司胜利油田分公司物探研究院,山东 东营257022;
3. 中国石油大学(华东)地球科学与技术学院,山东 青岛266580
2. Geophysical Research Institute,Shengli Oilfield Company,SINOPEC,Dongying 257022,China;
3. School of Geosciences,China University of Petroleum,Qingdao 266580,China
目前, 地震速度反演主要经历了基于速度扫描的叠加速度分析、旅行时层析速度反演、基于成像道集的偏移速度分析和全波形反演等[1-2]。
基于速度扫描的叠加速度分析主要通过人机交互的方式进行, 而且只能适用于水平或者小倾角构造, 无法适应地层陡倾角带来的道集畸变以及叠前地震数据低信噪比等问题[3]。成像域速度反演的优势在于其全局收敛性、数据信噪比等方面, 成像域数据相关准则速度估计方法泛函凸性较好, 对地震数据的低频(小于3 Hz)成分没有要求, 适合进行背景速度的估计[4-5]。数据域波形反演是地震成像中精确的速度反演方法, 但是还存在一些问题:①影响地震波振幅的因素太多, 地震波振幅信息跟模型低波数成分呈较强的非线性;②地震子波未知, 地震数据空间不规则, 频带不完整, 尤其缺乏低频及大偏移距反射波;③实测数据和速度之间的非线性性很强, 反演问题构造的泛函的凸性不够[6-8]。目前, 层析速度反演方法是较为可行的、精度相对较高的速度建模方法, 引起了地球物理学家们的广泛研究。
另外, 由于模拟地震数据中地震波振幅的不确定性, 建立在传统最小二乘误差泛函基础上的波形反演严重受到了制约[9]。但是, 各种形式的波动方程遵循共同的程函方程, 其旅行时信息不会受到影响。故在反演中应当更注重旅行时信息或者相位信息[10]。数据域反射波互相关目标函数虽然在一定程度上受反射波振幅信息的影响, 但是它更侧重于反射波相位信息的匹配。反射波相位信息(或者旅行时信息)主要受背景速度的影响并对数据的频率成分不是很敏感[11]。建立在对互相关函数加权的目标泛函意义下的反演类似于波动方程偏移速度分析中衡量波场聚焦程度的思想, 在数据域衡量互相关面板的聚焦程度, 而波动方程偏移速度分析在成像域对成像道集进行惩罚, 使其达到最佳聚焦[6]。
由此, 我们构造了基于反射波波形互相关的目标泛函。这种基于波形互相关的反射波反演从反射波路径出发, 将反射波相位时差向反射波路径投影, 从而恢复速度模型中深层低波数成分。采用Marmousi速度模型对该方法进行了测试, 取得了一定效果。试验结果表明, 互相关的目标函数在一定程度上降低了波形反演对波动方程的依赖程度, 从而更好地克服了局部极值问题, 能够为全波形反演(FWI)提供一个很好的初始速度模型。
1 方法原理首先研究了时间互相关函数、空间互相关函数、空间-时间互相关函数对速度的敏感性[12-13]。为了衡量数据互相关的聚焦特性, 本文以时间加权的归一化互相关函数作为目标泛函, 求取了其梯度表达式。基于波动方程正问题的一阶Born近似推导了反射波场对背景速度的Fréchet导数, 并对比分析了反射波路径和透射波路径在反演中的不同梯度贡献。
1.1 地震记录的互相关函数给定两炮地震记录数据p(t, h)和q(t, h), t和h分别代表时间和偏移距, Δt和Δh分别代表时间移动量和空间移动量。定义其时间互相关函数Ct[p,q] 为:
| ${{C}_{t}}~\left( \Delta t,\text{ }h \right)=\int p\left( t,\text{ }h \right)q\left( t+\Delta t,\text{ }h \right)dt$ | (1) |
定义其空间互相关函数Ch[p,q] 为:
| ${{C}_{h}}~\left( t,\text{ }\Delta h \right)=\int p\left( t,\text{ }h \right)q\left( t,\text{ }h+\Delta h \right)dh$ | (2) |
定义其空间-时间互相关函数Ct, h[p,q] 为:
| $\begin{array}{*{35}{l}} {{C}_{t,\text{ }h}}~\left( \Delta t,\text{ }\Delta h \right)=\iint{p}\left( t,\text{ }h \right)q(t+\Delta h,\text{ }h+ \\ \Delta h)dtdh\text{ } \\ \end{array}$ | (3) |
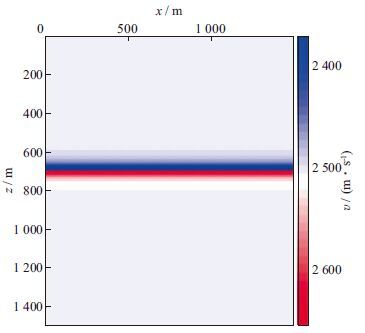
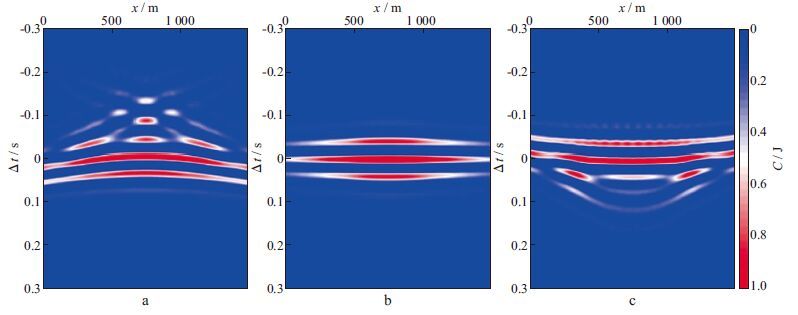
以存在单一反射体的常速背景(2 500 m/s)模型为例(图 1), 分析上述3种互相关函数对背景速度变化的敏感性。分别用不同的背景速度2 300, 2 500, 2 700 m/s将模型扰动进行映射(偏移-反偏移), 得到基于一阶Born近似的反射地震数据。分别对这3种速度下的映射数据与观测数据进行时间互相关, 结果如图 2a, 图 2b和图 2c所示。可以看出, 当速度正确时, 时间互相关面板在Δt=0处聚焦, 基本是拉平的;当速度偏小时, 其时间互相关面板是下弯的;当速度偏大时, 其时间互相关面板是上翘的。由于噪声的影响, 使得在非零时移处有效信号与噪声之间会出现“cross-talk”现象。本文正是利用数据域的这种聚焦特性进行速度分析。
|
图 1 存在单一反射体的常速背景(2 500 m/s)模型 |
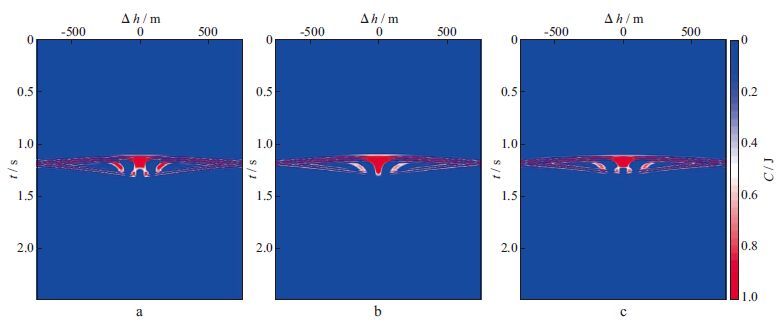
图 3a, 图 3b和图 3c显示了3种速度下的映射数据与观测数据的空间互相关面板。从图 3可以看到, 空间互相关面板的焦散性没有时间互相关面板明显, 不管速度是偏大还是偏小, 空间互相关面板几乎没有区别并有噪声存在;当速度不正确时, 空间互相关面板在Δh=0处未能聚焦;当速度准确时, 空间互相关面板在Δh=0处达到极大值, 但仍然没有达到最佳聚焦。所以, 本文在反演过程中尽量避免使用基于空间互相关的目标泛函。
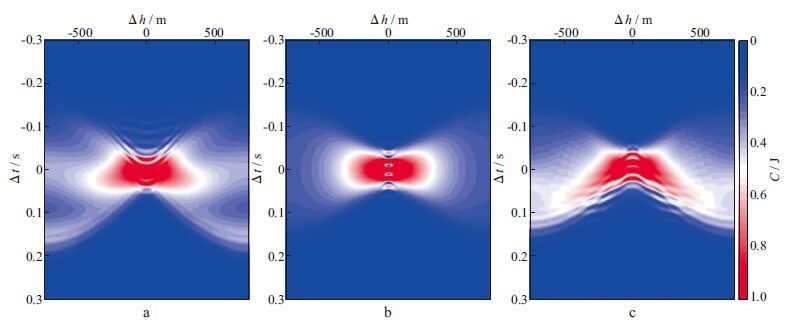
图 4a, 图 4b和图 4c分别显示了3种速度下的映射数据与观测数据的时间-空间互相关面板。可以看到, 时间-空间互相关面板的聚焦特性明显优于上述两种互相关面板。当速度准确时, 时间-空间互相关面板在Δt=0, Δh=0处聚焦, 达到极大值。 当速度不准确时, 时间-空间互相关面板是发散的。
从图 2, 图 3和图 4可以看出, 当速度正确时, 不管哪种互相关都是在移动量(Δt, Δh)为0处最佳聚焦;当速度偏小或偏大时, 互相关面板上都存在噪声。在适应性方面, 当地震记录缺失大偏移距数据时应避免使用空间互相关泛函;时间互相关泛函的焦散性要优于空间互相关泛函;但是地震记录受子波波形的影响。时间互相关面板往往会出现好几个聚焦同相轴, 不利于复杂模型的反演。时间-空间互相关泛函可以避免上述缺陷, 其焦散性受时间、空间两个变量影响, 可以有效降低互相关面板的噪声。
|
图 2 不同背景速度下的时间互相关面板 a 2 300 m/s; b 2 500 m/s; c 2 700 m/s |
|
图 3 不同背景速度下的空间互相关面板 a 2 300 m/s; b 2 500 m/s; c 2 700 m/s |
|
图 4 不同背景速度下的时间-空间互相关面板 a 2 300 m/s; b 2 500 m/s; c 2 700 m/s |
为了衡量数据互相关的聚焦特性, VAN LEEUWEN等[12]提出了一种加权的归一化互相关目标函数。其中, 加权函数应当放大互相关面板上零移动量处的能量, 减弱非零移动量处的能量[8]。针对时间互相关, 定义如下目标泛函Jt:
| ${{J}_{t}}=\text{ }\frac{1\text{ }}{{{S}_{t}}}~\int \int _{-\Delta {{t}_{max}}}^{\Delta {{t}_{max}}}W\left( \Delta t \right){{\text{ }\!\![\!\!\text{ }{{C}_{t}}\text{ }\!\![\!\!\text{ }p,q\text{ }\!\!]\!\!\text{ }\left( \Delta t,\text{ }h \right)]}^{2}}d\Delta tdh$ | (4) |
其中,
| ${{S}_{t}}=~\int \int _{-\Delta {{t}_{max}}}^{\Delta {{t}_{max}}}~{{\text{ }\!\![\!\!\text{ }{{C}_{t}}\text{ }\!\![\!\!\text{ }p,q\text{ }\!\!]\!\!\text{ }\left( \Delta t,\text{ }h \right)]}^{2}}d\Delta tdh~$ | (5) |
式中:h是偏移距;t和Δt分别为时间和时间移动量;Δtmax为最大时间移动量;St为归一化函数;W(Δt)是时间加权函数, W(Δt)主要有二次加权函数W1(Δt)= Δtmax)]2和高斯加权函数W2(Δt)= 1-e-αΔt2。高斯加权函数里, α控制着目标函数的“宽度”, α越小, 目标函数变化越平缓。类似地, 可以定义针对空间互相关和时间-空间互相关的目标泛函Jh, Jt, h。另外, 计算互相关时的滑动时窗的大小对减少“cross-talk”噪声具有重要作用。
在反演过程中采用了二次时间加权的归一化互相关目标泛函, 随着模型参数逐渐逼近真实值时, 目标函数(4) 式在互相关窗口范围内呈现下凸函数的形态。计算目标泛函(4) 式对观测记录的Fréchet导数, 便得到了基于互相关目标泛函的反射波反演的伴随源形式:
| $\begin{array}{*{35}{l}} {{f}^{adj}}= \\ \sum\limits_{\Delta t}{[W}\left( \Delta t \right)\frac{\text{ }\sum\limits_{t}{(p}\text{ }\left( \text{ }x{{~}_{s}},\text{ }x{{~}_{r}},\text{ }t,\text{ }v \right){{p}_{obs}}\left( \text{ }x{{~}_{s}},\text{ }x{{~}_{r}},\text{ }t+\Delta t \right)}{\left\| p\left( \text{ }x{{~}_{s}},\text{ }x{{~}_{r}},\text{ }t,\text{ }v \right) \right\|\text{ }\cdot \text{ }\left\| {{p}_{obs}}\left( \text{ }x{{~}_{s}},\text{ }x{{~}_{r}},\text{ }t+\Delta t \right) \right\|}\text{ }\cdot \\ \frac{{{p}_{obs}}\left( \text{ }x{{~}_{s}},\text{ }x{{~}_{r}},\text{ }t+\Delta t \right)}{\left\| p\left( \text{ }x{{~}_{s}},\text{ }x{{~}_{r}},\text{ }t,\text{ }v \right)\text{ }\cdot \text{ }{{p}_{obs}}\left( \text{ }x{{~}_{s}},\text{ }x{{~}_{r}},\text{ }t+\Delta t \right) \right\|}\text{ }] \\ \end{array}$ | (6) |
式中:p是模拟炮记录;pobs是观测炮记录; x s和 x r分别代表激发点和接收点的位置;v为当前迭代速度。
将该伴随源沿反射波路径进行投影, 便可得到基于互相关目标泛函的反射波反演的梯度, 从而更新速度场低波数成分, 最后代入梯度方法的迭代公式进行反演。
1.3 反射波路径的求取频率域的乘积相当于时间域的褶积。在频率域表达Born近似比较方便, 同时也易于推导计算。为便于在一阶Born近似基础上推导反射波路径, 本文首先在频率域推导反射波路径, 再将其转换到时间域进行计算。
介质散射模型中, 可以将地球介质分解为光滑的背景模型与模型扰动之和[14-15]:
| $m={{m}_{0}}+\delta m$ | (7) |
其中, 长波长背景模型m0决定了模型的透射响应, 短波长模型扰动δm决定了模型的反射响应。相应地, 将全波场分解为背景波场G0与扰动波场δG的和[16-17]:
| $G={{G}_{0}}+\delta G$ | (8) |
基于一阶Born近似理论, 本文可以得到一阶Born下的扰动波场:
| $\begin{align} & \delta G(\text{ }x{{~}_{r}},\text{ }\omega ;\text{ }x{{~}_{s}})=\text{ }{{\omega }^{2}}{{\int }_{V}}G(\text{ }x\text{ }\prime ,\text{ }\omega ;\text{ }x{{~}_{s}})\delta m\left( \text{ }x\text{ }\prime \right)\cdot \\ & G(\text{ }x{{~}_{r}},\text{ }\omega ;\text{ }x\text{ }\prime )d\text{ }x\text{ }\prime \text{ } \\ \end{align}$ | (9) |
式中: x s和 x r分别为炮点和检波点位置;δG是基于一阶Born近似的扰动场;ω是圆频率;V代表地下介质体;δm是速度扰动;G代表格林函数。下面分别研究数据扰动δG对δm及m0的Fréchet导数。
δG对δm的Fréchet导数是传统的Born算子:
| ${{\left. \frac{\partial \delta G}{\partial \delta m\left( \text{ }x\text{ }\prime \right)} \right|}_{{{m}_{0}}}}~={{\omega }^{2}}G(\text{ }x\text{ }\prime ,\text{ }\omega ;\text{ }x{{~}_{s}})G(\text{ }x{{~}_{r}},\text{ }\omega ;\text{ }x\text{ }\prime )$ | (10) |
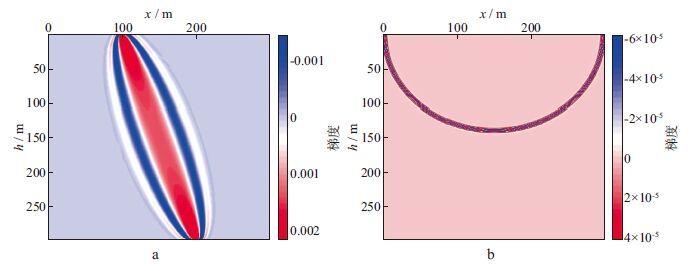
从(10) 式可以看出, 该梯度只与背景模型有关, 是经典的全波形反演过程, 是一阶Born近似问题[5-18], 同时也是一种偏移算子。对于透射波, 其响应是透射波路径, 代表透射波层析成像过程(图 5a), 只能反演浅层速度场的低波数成分[19]。利用透射波(一般在浅层传播)进行反演成像, 估计表层的速度, 建立表层模型。而对于反射波, 该梯度表达的是偏移算子的脉冲响应(图 5b), 只能反演速度场的高波数成分, 可以实现对中深层的反射波进行真振幅叠前深度偏移成像, 得到角度反射系数。由此也证实了全波形反演能恢复速度场浅层低波数成分和深层高波数成分。
XU等[17]推导了扰动波场对背景模型参数m0的Fréchet导数:
| $\begin{array}{*{35}{l}} {{\left. \frac{\partial \delta G}{\partial {{m}_{0}}\left( \text{ }x\text{ }\prime \right)} \right|}_{\delta m}}~=\text{ }{{\omega }^{2}}[\delta G(~x{{~}_{r}},\text{ }\omega ;\text{ }x\text{ }\prime )G\left( \text{ }x\text{ }\prime ,\text{ }\omega ;\text{ }x{{~}_{s}} \right)+ \\ \delta G\left( \text{ }x\text{ }\prime ,\text{ }\omega ;\text{ }x{{~}_{s}} \right)G\left( \text{ }x{{~}_{r}},\text{ }\omega ;\text{ }x\text{ }\prime \right)]~ \\ \end{array}$ | (11) |
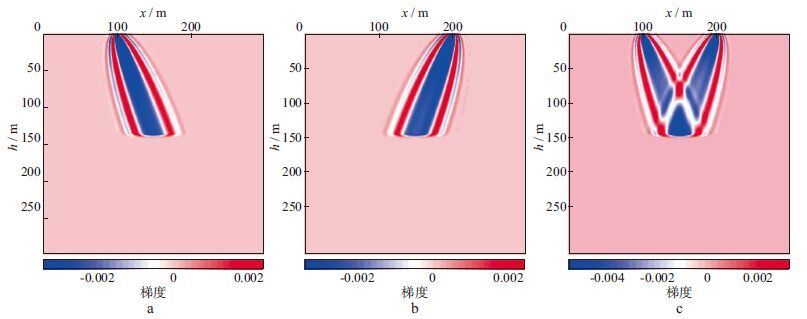
式中:δG( x ′, ω; x s), δG( x r, ω; x ′)分别是一阶Born近似下由模型扰动引起的反射波场;G( x ′, ω; x s), G( x r, ω; x ′)分别是炮点和检波点的入射背景波场。可以看出, 该梯度计算不仅与背景模型有关, 而且还与模型扰动有关。图 6a和图 6b分别显示了反射波路径的震源端和检波端部分。公式(11) 计算出的便是反射波路径[20-21](图 6c)。在反演过程中, 将利用二次散射波计算的积分核沿波路径进行残差波场的反传播。 可以看出, (11) 式进行的是反射波层析成像, 主要更新低波数的背景速度, 它由两部分构成:震源激发的入射场与检波点处逆时传播的一次反射伴随场的相关成像(炮点端梯度响应)以及震源激发的一次反射波场与检波点处逆时传播的入射伴随场的相关成像(检波点端梯度响应)[21-22]。
|
图 5 透射波与反射波的梯度贡献对比 a 透射波层析核函数; b 反射波对模型扰动的梯度贡献 |
(10) 式和(11) 式是现代勘探地震学中地震波反演成像的核心公式, 绝大部分方法技术都是在此基础上所做的展开和应用研究。
|
图 6 反射波对背景模型的梯度贡献 a 震源端; b 检波端; c 反射波路径 |
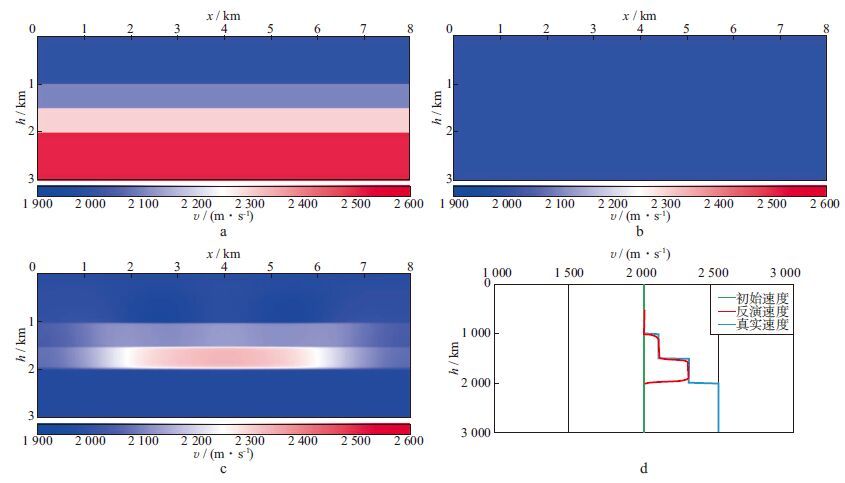
如图 7a所示, 该平层速度模型纵、横向采样点分别为300, 800, 采样间隔均为10 m。正演过程中共模拟101炮, 炮间距50 m, 每炮300道接收, 道间距10 m。震源为主频25 Hz的Ricker子波。在反演过程中, 将3个反射界面当做先验反射层信息来构建反射波梯度, 充分利用了反射波的低波数响应并改善了反演效果。其初始速度场为一个2 000 m/s的均匀速度场, 如图 7b所示。图 7c是迭代20次后得到的反演速度模型, 可以看出, 在2~6 km的速度场得到了很好的恢复, 由于照明不足, 速度场边缘处反演结果不准确。而2 km以下的速度场没有得到更新, 这是由于2 km以下没有反射界面, 故没有反射波产生, 因此这部分速度场没法得到改善。图 7d显示了横向4 km处的初始速度、反演速度与真实速度的对比结果, 可以看出, 速度场界面信息以及低波数成分基本都得到了很好的恢复, 从而验证了该方法的反演精度。
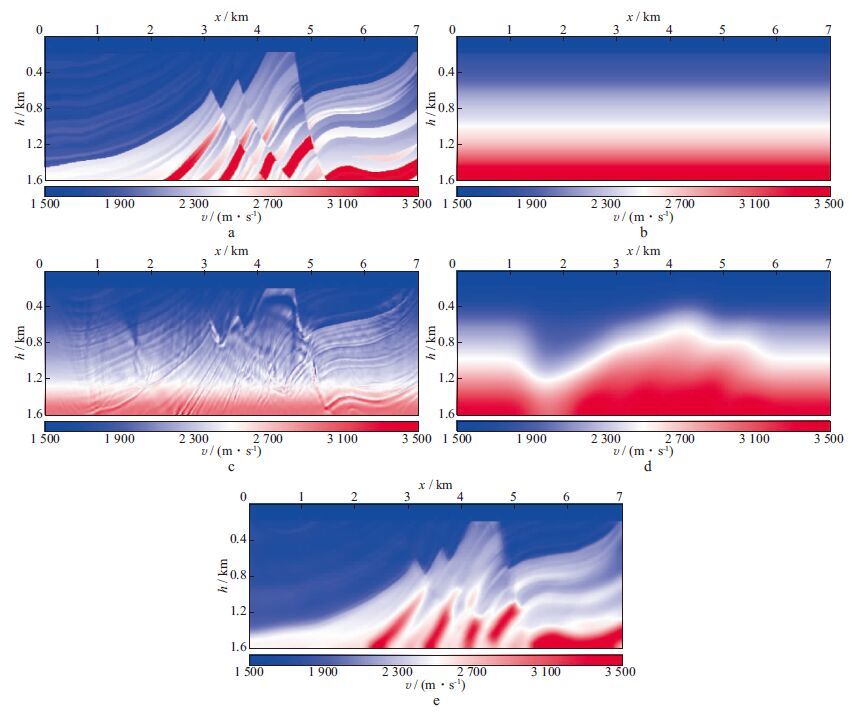
2.2 复杂构造模型采用Marmousi模型对本文方法进行测试, 结果如图 8所示。图 8a为一个纵、横向采样点数分别为200, 700的真实速度模型, 其采样间隔分别为8 m和10 m。本文模拟51炮数据进行测试, 每炮200道接收, 炮间距和道间距都为10 m。震源为15 Hz的Ricker子波。图 8b是一常梯度(其纵向速度梯度为一常数)速度模型。图 8c是图 8b所示速度模型的FWI结果, 可以看到, 由于速度场低波数成分的缺失, FWI结果陷入局部极小值。本文引入先验的反射层信息利用所述的方法以图 8b为初始速度模型进行波动方程反射波反演(WERI), 结果如图 8d所示, 可以看到, 速度场低波数成分有所改善。再在图 8d的基础上进行FWI, 结果如图 8e所示。与图 8c相比, 很明显, 采用本文方法更新的背景速度进行FWI, 可以有效改善中深层反演效果, 大大改善了全波形反演容易陷入局部极值的缺陷, 提高了反演的稳定性。由此可见, 尽管在速度模型较为复杂时, 互相关面板容易出现“cross-talk”现象, 但在反演背景速度方面仍然要优于最小二乘目标函数, 为全波形反演提供较好的初始速度场。
|
图 7 平层速度模型 a 真实速度模型; b 初始速度模型; c 最终迭代的速度模型; d 横向距离4 km处纵向速度对比曲线 |
|
图 8 Marmousi模型测试 a 真实速度模型; b 常梯度速度模型; c 以常梯度速度为初始速度模型的FWI结果; d 基于互相关的反射波反演(WERI)结果; e 以基于互相关的WERI结果为初始速度模型的FWI结果(WERI+FWI) |
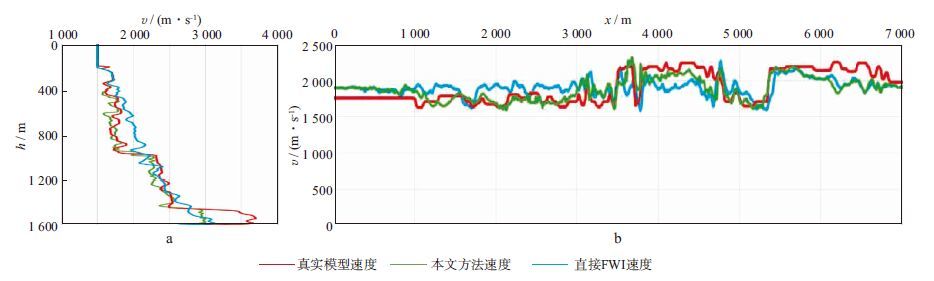
图 9a和图 9b分别显示了图 8a, 图 8c, 图 8e中横向位置2.5 km处纵向速度与深度0.6 km处横向速度对比曲线, 可以看到, 经过反射波反演后再做全波形反演, 速度曲线更加接近于真实速度曲线, 有效改善了速度场的低波数成分, 提高了全波形反演的效果。
|
图 9 Marmousi模型横向距离2.5 km处纵向速度(a)和深度0.6 km横向速度(b)对比曲线 |
我们提出了基于波形互相关的反射波反演方法, 实现了利用反射波来反演地下介质背景速度的过程。理论模型试算结果表明:
1) 基于加权互相关目标泛函的反射波反演主要利用了反射波的走时信息, 但是互相关函数在一定程度上受振幅信息的影响, 容易出现多层位反射“cross-talk”现象, 故该目标函数具有其局限性;
2) 相对于经典FWI, 本文提出的反射波反演通过求取反射波场对速度场低波数部分的Fréchet导数来更新背景速度模型, 能够提高FWI的收敛性;
3) 由于反射系数的估计受速度场低波数成分的影响, 当速度场低波数成分不准确时会形成高波数的噪声, 影响低波数梯度的更新方向。本文通过选取小偏移距数据, 对其进行偏移成像并将成像值作为其反射系数, 同时进行Laplace滤波, 从而减小反射系数的噪声。
在实际资料应用方面, 波形反演仍然面临着波动方程的准确性、地震子波的未知性、地震记录频带的完整性等诸多问题, 需要进一步探讨。本文所述方法的关键在于梯度的求取, 当背景速度不准确时, 互相关面板上会引入一些噪声, 再加之地震记录本身存在噪声问题, 这些因素都限制着反射波反演的进一步应用。
| [1] | CRASE E, PICA A, NOBLE M, et al. Robust elastic nonlinear waveform inversion:application to real data[J]. Geophysics , 1990, 55 (5) : 527-538 DOI:10.1190/1.1442864 |
| [2] |
王华忠, 冯波, 王雄文, 等. 地震波反演成像方法与技术核心问题分析[J].
石油物探 , 2015, 54 (2) : 115-125 WANG H Z, FENG B, WANG X W, et al. Analysis of seismic inversion imaging and its technical core issues[J]. Geophysical Prospecting for Petroleum , 2015, 54 (2) : 115-125 |
| [3] | GAROTTA R, MIEHON D. Continuous analysis of the velocity function and of the normal-moveout corrections[J]. Geophysical Prospecting , 1967, 15 (4) : 584-597 DOI:10.1111/gpr.1967.15.issue-4 |
| [4] | FAYE J P, JEANOT J P, DENELLE E. Prestack migration velocities from depth focusing analysis[J]. Expanded Abstracts of 56th Annual Internat SEG Mtg , 1986 : 438-440 |
| [5] | TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics , 1984, 49 (8) : 1259-1266 DOI:10.1190/1.1441754 |
| [6] | SYMES W W. Migration velocity analysis and waveform inversion[J]. Geophysical Prospecting , 2008, 56 (6) : 765-790 DOI:10.1111/gpr.2008.56.issue-6 |
| [7] | TARANTOLA A. Inverse problem theory and methods for model parameter estimation[M]. Paris,France: Albert Tarantola, 2005 : 1 -53. |
| [8] |
杨勤勇, 胡光辉, 王立歆. 全波形反演研究现状及发展趋势[J].
石油物探 , 2014, 53 (1) : 77-83 YANG Q Y, HU G H, WANG L X. Research status and development trend of full waveform inversion[J]. Geophysical Prospecting for Petroleum , 2014, 53 (1) : 77-83 |
| [9] |
张凯, 李振春, 陈永芮, 等. 一种新的用于全波形反演的能量加权梯度方法[J].
石油物探 , 2015, 54 (1) : 77-82 ZHANG K, LI Z C, CHEN Y R, et al. A new energy weighted gradient method for full waveform inversion[J]. Geophysical Prospecting for Petroleum , 2015, 54 (1) : 77-82 |
| [10] | ZHOU H, AMUNDSEN L, ZHANG G. Fundamental issues in full waveform inversion[J]. Expanded Abstracts of 75th Annual Internat SEG Mtg , 2005 : 1-5 |
| [11] |
李媛媛, 李振春, 张凯. 频率域多尺度弹性波全波形反演[J].
石油物探 , 2015, 54 (3) : 317-323 LI Y Y, LI Z C, ZHANG K. Multi-scale elastic full waveform inversion in frequency domain[J]. Geophysical Prospecting for Petroleum , 2015, 54 (3) : 317-323 |
| [12] | VAN LEEUWEN T. Correlation-based seismic velocity inversion[J]. Geophysics , 2010, 75 (6) : Z117 |
| [13] | VAN LEEUWEN T, MULDER W A. Waveform inversion with data correlation[J]. Expanded Abstracts of 70th EAGE Annual Conference , 2008 : 1-5 |
| [14] | BUNKS C, SALECK F M, ZALESKI S, et al. Multiscale seismic waveform inversion[J]. Geophysics , 1995, 60 (5) : 1457-1473 DOI:10.1190/1.1443880 |
| [15] | WANG Y, LUO W, HE Z, et al. Born approximation inversion for the marine CSEM data set[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg , 2008 : 1-5 |
| [16] | ALBERTIN U, SHAN G, WASHBOURNE J. Gradient orthogonalization in adjoint scattering-series inversion[J]. Expanded Abstracts of 83rd Annual Internat SEG Mtg , 2013 : 1-5 |
| [17] | XU S, WANG D, CHEN F, et al. Inversion on reflected seismic wave[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg , 2012 : 1-7 |
| [18] | WOODWARD M J. Wave-equation tomography[J]. Geophysics , 1992, 57 (1) : 15-26 DOI:10.1190/1.1443179 |
| [19] | MA Y, HALE D. Wave-equation reflection traveltime inversion with dynamic warping and full-waveform inversion[J]. Geophysics , 2013, 78 (6) : R223-R233 DOI:10.1190/geo2013-0004.1 |
| [20] | GAUTHIER O, VIRIEUX J, TARANTOLA A. Two-dimensional nonlinear inversion of seismic waveforms:numerical results[J]. Geophysics , 1986, 51 (7) : 1387-1403 DOI:10.1190/1.1442188 |
| [21] | WANG S, CHEN F, ZHANG H, et al. Reflection-based full waveform inversion(RFWI) in the frequency domain[J]. Expanded Abstracts of 83rd Annual Internat SEG Mtg , 2013 : 877-881 |
| [22] | MORA P. Inversion= migration+ tomography[J]. Geophysics , 1989, 54 (12) : 1575-1586 DOI:10.1190/1.1442625 |


