The parameter optimization analysis for the attenuation function in the perfectly matched layer
在地球物理学和地震学等研究领域, 完全匹配层(PML)被广泛应用于数值模拟无边界问题。在对电磁波、声波、弹性波等进行数值模拟的过程中, 受计算机内存和计算时间的限制, 通常会将无限区域截断, 从而产生无意义的人为边界反射。为了解决这一问题, 有关专家和学者提出了大量的吸收边界条件, 其中由BERENGER[1-2]提出的完全匹配层在理论上可以吸收来自各个方向、各种频率的波, 不产生任何边界反射。
完全匹配层最初是BERENGER于1994年针对电磁波问题的研究提出的一种有效吸收边界条件[1]。同年, CHEW等[3]将复伸展坐标应用在PML吸收边界条件中。之后又有许多专家学者将完全匹配层问题的研究扩展到了声波、弹性波等数值模拟中, 如HASTINGS等[4]将PML应用到一阶速度-应力声波方程中;COLLINO等[5], CHEW等[6]以及裴正林[7]将PML应用到弹性波的数值模拟中;DIMITRI等[8]提出了适用于二阶弹性波动方程分裂式的PML吸收边界条件;BECACHE等[9]在理论上证明了各向异性弹性波动方程PML吸收边界条件的稳定性。在完全匹配层问题的研究分析中, 产生了多种形式的PML, 主要有分裂式PML(Splitting PML, SPML)和非分裂式PML(Non-splitting PML, NPML)两种, 两者除在计算的复杂程度和计算量上有区别外, 对人工边界反射有相同的吸收效果, 在完全匹配层问题分析中都得到了广泛应用。
在地震波正演和波动方程偏移数值计算中, 边界处反射波的能量严重影响了计算结果的精确性。为了减小完全匹配层的边界反射, BERENGER[1], HASTINGS等[4], COLLINO等[5]分别针对一阶分裂Maxwell差分方程、一阶分裂式速度-应力声波方程和一阶分裂式速度-应力波动方程进行了完全匹配层问题的优化;VADIM[10]针对各向同性弹性波动方程提出了最优有限差分完全匹配层;COLLINO等[11]针对曲线坐标系下的Maxwell方程提出了最优完全匹配层;SHIMADA等[12]对有限元离散在完全匹配层边界上所产生的反射能量进行了研究。对于一阶分裂式和非分裂式完全匹配层的优化工作还有很多[13-19], 但关于二阶非分裂完全匹配层的优化研究很少。本文针对二阶弹性波动方程的非分裂PML吸收边界条件[20-21], 通过对最大反射系数的理论推导, 得出了该PML的反射机理, 对于非分裂完全匹配层问题的研究有一定的参考意义。
1 基本方程
考虑二维弹性半空间动力学问题, 用矩阵形式表示的弹性波基本方程如下:
|
${{L}^{~T\text{ }}}\sigma \text{ }+\text{ }f\text{ }=\rho \ddot{u}$
|
(1) |
|
$\sigma \text{ }=\text{ }C\varepsilon $
|
(2) |
|
$\varepsilon \text{ }=\text{ }Lu$
|
(3) |
其中,
|
$\begin{align}
& \sigma \text{ }=\left\{ \begin{array}{*{35}{l}}
{{\sigma }_{11}} \\
{{\sigma }_{33}} \\
{{\sigma }_{13}} \\
\end{array} \right\}~\varepsilon \text{ }=\left\{ \begin{array}{*{35}{l}}
{{\varepsilon }_{11}} \\
{{\varepsilon }_{33}} \\
{{\varepsilon }_{13}} \\
\end{array} \right\}u\text{ }=\left\{ \begin{array}{*{35}{l}}
~{{u}_{1}} \\
{{u}_{3}}~ \\
\end{array} \right\}f\text{ }=\left\{ \begin{array}{*{35}{l}}
~{{f}_{1}} \\
{{f}_{3}} \\
\end{array} \right\} \\
& C\text{ }=\left[ \begin{matrix}
\lambda +2\mu & \lambda & 0 \\
\lambda & \lambda +2\mu & 0 \\
0 & 0 & \mu \\
\end{matrix} \right]L\text{ }=\left\{ \begin{array}{*{35}{l}}
\frac{\partial }{\partial {{x}_{1}}} & 0 \\
0 & \frac{\partial }{\partial {{x}_{3}}} \\
\frac{\partial }{\partial {{x}_{3}}} & \frac{\partial }{\partial {{x}_{1}}} \\
\end{array} \right\} \\
\end{align}$
|
式中: σ 表示应力张量; ε 表示应变张量; u 表示位移矢量; f 表示外力矢量; C 表示弹性张量;λ和μ为拉梅系数;ρ表示弹性介质的密度;(¨ )表示对时间的二阶偏导; L 表示线性微分算子。
2 二阶非分裂PML吸收边界条件
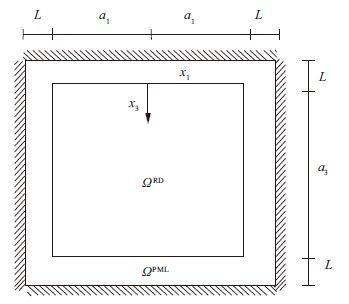
考虑弹性波在半空间无限平面区域Ω=(-∞, ∞)×[0,∞] 内传播,可将无限区域进行人为截断,计算区域限制为一个有限的矩形区域,所有弹性波的波源限制在矩形计算区域ΩRD=(-a1,a1)×(0,a3),(a1,a3>0)的内部。在ΩRD区域内,所有弹性波以任意角度向外传播,在ΩRD区域外侧,考虑波的传播速度不变,并在计算区域ΩRD的外围布置厚度为L的完全匹配层,用于吸收传出区域ΩRD的弹性波,如图 1所示。
联合(1) 到(3) 式可以得到由位移表示的方程:
|
$\left( \lambda +2\mu \right)\text{ }\frac{{{\partial }^{2}}{{u}_{1}}}{\partial {{x}_{1}}^{2}~}~+\left( \lambda +\mu \right)\text{ }\frac{{{\partial }^{2}}{{u}_{3}}~}{\partial {{x}_{1}}\partial {{x}_{3}}}~+\mu \text{ }\frac{{{\partial }^{2}}{{u}_{1}}}{\partial {{x}_{3}}^{2}}~~=\rho \text{ }\frac{{{\partial }^{2}}{{u}_{1}}~}{\partial {{t}^{2}}~}$
|
(4a) |
|
$\left( \lambda +2\mu \right)\frac{\text{ }{{\partial }^{2}}{{u}_{3}}}{\partial {{x}_{3}}^{2}~}~+\left( \lambda +\mu \right)\text{ }\frac{{{\partial }^{2}}{{u}_{3}}~}{\partial {{x}_{1}}\partial {{x}_{3}}}~+\mu \text{ }\frac{{{\partial }^{2}}{{u}_{3}}}{\partial {{x}_{1}}^{2}}~~=\rho \text{ }\frac{{{\partial }^{2}}{{u}_{3}}}{~\partial {{t}^{2}}}$
|
(4b) |
对时间变量t进行Fourier变换, 用 $\hat{u}$i来表示位移分量ui进行Fourier变换后的位移分量:
|
${{{\hat{u}}}_{i}}({{x}_{1}},\text{ }{{x}_{3}},\text{ }\omega )={{\int }_{-\infty }}^{\infty }{{e}^{i\omega t}}{{u}_{i}}({{x}_{1}},\text{ }{{x}_{3}},\text{ }t)dt$
|
(5) |
对(4) 式进行Fourier变换, 即将波动方程由时域变换到频域, 弹性波动方程可以改写为:
|
$\begin{array}{*{35}{l}}
\left( \lambda +2\mu \right)\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{\partial {{x}_{1}}^{2}}~~+\left( \lambda +\mu \right)\text{ }\frac{{{\partial }^{2}}~{{{\hat{u}}}_{3}}}{\partial {{x}_{1}}\partial {{x}_{3}}~}+\mu \text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{\partial {{x}_{3}}^{2}}~~= \\
-\rho {{\omega }_{1}}^{2}~ \\
\end{array}$
|
(6a) |
|
$\begin{array}{*{35}{l}}
\left( \lambda +2\mu \right)\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}~}{\partial {{x}_{3}}^{2}}~+\left( \lambda +\mu \right)\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{\partial {{x}_{1}}\partial {{x}_{3}}~}~+\mu \text{ }\frac{{{\partial }^{2}}~{{{\hat{u}}}_{3}}}{\partial {{x}_{1}}^{2}}~= \\
-\rho {{\omega }_{3}}^{2} \\
\end{array}$
|
(6b) |
引入复伸展坐标以及连续的衰减函数ζi:
|
${{{\tilde{x}}}_{i}}={{x}_{i}}+\text{ }\frac{1}{i\omega }\text{ }{{\int }_{0}}^{{{x}_{i}}}{{\zeta }_{i}}\left( x \right)d{{x}_{i}}~$
|
(7) |
复伸展坐标的偏微分形式为:
|
$\frac{\partial \text{ }}{\partial ~{{{\tilde{x}}}_{i}}~}=\text{ }\frac{i\omega }{i\omega +{{\zeta }_{i}}}\text{ }~\frac{\partial }{\partial {{x}_{i}}}$
|
(8) |
考虑在吸收层外时衰减函数ζi=0, 在吸收层内时, 衰减函数ζi为正。
利用公式(7) 对(6) 式进行复伸展坐标变换, 可以得到:
|
$\begin{array}{*{35}{l}}
\left( \lambda +\mu \right)\text{ }\left( \frac{{{\partial }^{2}}~{{{\hat{u}}}_{1}}}{\partial \tilde{x}{{~}_{1}}^{2}}~+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}}{\partial ~{{{\tilde{x}}}_{1}}\partial ~{{{\tilde{x}}}_{3}}~} \right)~+\mu \text{ }\left( \frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}~}{{{\partial }^{2}}{{{\tilde{x}}}_{1}}}~+\text{ }\frac{{{\partial }^{2}}~{{{\hat{u}}}_{1}}}{{{\partial }^{2}}\tilde{x}{{~}_{3}}~} \right)= \\
-\rho {{\omega }^{2}}{{{\hat{u}}}_{1}}~ \\
\end{array}$
|
(9a) |
|
$\begin{array}{*{35}{l}}
\left( \lambda +\mu \right)\text{ }\left( \frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}~}{\partial {{~}^{2}}{{{\tilde{x}}}_{3}}~}+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{\partial ~{{{\tilde{x}}}_{1}}\partial {{~}_{3}}}~ \right)~+\mu \left( \text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}~}{{{\partial }^{2}}{{{\tilde{x}}}_{1}}}~+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}~}{{{\partial }^{2}}{{{\tilde{x}}}_{3}}} \right)~= \\
-\rho {{\omega }^{2}}{{{\hat{u}}}_{3}}~ \\
\end{array}$
|
(9b) |
令
|
${{\gamma }_{j}}={{\gamma }_{j}}({{\zeta }_{j}},\text{ }i\omega ),\text{ }j=1,\text{ }3:\text{ }{{\gamma }_{j}}=1+\text{ }\frac{{{\zeta }_{j}}}{i\omega }$
|
(10) |
按照GROTE等[22]所给出的求解过程, 利用复伸展坐标的偏微分公式(8) 对(9) 式进行替换, 并在(9) 式两侧同时乘以γ1γ3, 可以得到:
|
$\begin{array}{*{35}{l}}
\left( \lambda +\mu \right)\text{ }\left( \frac{\partial }{\partial {{x}_{1}}}\text{ }~\frac{{{\gamma }_{3}}~}{{{\gamma }_{1}}~}\frac{\partial {{{\hat{u}}}_{1}}~}{\partial {{x}_{1}}}~+\text{ }\frac{\partial }{\partial {{x}_{1}}~}\text{ }\frac{{{\gamma }_{3}}~}{{{\gamma }_{3}}}~\frac{\partial ~{{{\hat{u}}}_{3}}~}{\partial {{x}_{3}}~} \right)+\mu \text{ (}\frac{\partial }{\partial {{x}_{1}}}\text{ }~\cdot \\
\frac{{{\gamma }_{3}}}{{{\gamma }_{1}}}~~\frac{\partial ~{{{\hat{u}}}_{1}}}{\partial {{x}_{1}}}~~+\text{ }\frac{\partial }{\partial {{x}_{3}}}\text{ }~\frac{{{\gamma }_{1}}}{{{\gamma }_{3}}}~~\frac{\partial \hat{u}{{~}_{1}}}{\partial {{x}_{3}}~})~=-\rho {{\omega }^{2}}{{{\hat{u}}}_{1}}{{\gamma }_{1}}{{\gamma }_{3}}~ \\
\end{array}$
|
(11a) |
|
$\begin{array}{*{35}{l}}
\left( \lambda +\mu \right)\text{ }\left( \frac{\partial \text{ }}{\partial {{x}_{3}}}~\frac{{{\gamma }_{1}}}{{{\gamma }_{3}}}\frac{\partial \hat{u}{{~}_{3}}}{\partial {{x}_{3}}~}+\text{ }\frac{\partial }{\partial {{x}_{1}}~}\text{ }\frac{{{\gamma }_{3}}~}{{{\gamma }_{3}}}~\frac{\partial ~{{{\hat{u}}}_{1}}~}{\partial {{x}_{3}}~} \right)~+\mu \text{ (}\frac{\partial }{\partial {{x}_{1}}~}\cdot \\
\frac{{{\gamma }_{3}}~}{{{\gamma }_{1}}~}\frac{\partial {{{\hat{u}}}_{3}}~}{\partial {{x}_{1}}}+\frac{\partial }{\partial {{x}_{3}}}\text{ }~\frac{{{\gamma }_{1}}}{{{\gamma }_{3}}}~~\frac{\partial \hat{u}{{~}_{3}}}{\partial {{x}_{3}}~})~=-\rho {{\omega }^{2}}{{{\hat{u}}}_{3}}{{\gamma }_{1}}{{\gamma }_{3}} \\
\end{array}$
|
(11b) |
根据(10) 式, 可以得到以下关系式:
|
$-{{\omega }^{2}}{{\gamma }_{1}}{{\gamma }_{3}}=-{{\omega }^{2}}+i\omega ({{\zeta }_{1}}+{{\zeta }_{3}})+{{\zeta }_{1}}{{\zeta }_{3}}$
|
(12a) |
|
${{\gamma }_{3}}~{{\gamma }_{1}}~=1+\text{ }\frac{{{\zeta }_{3}}-{{\zeta }_{1}}}{i\omega +{{\zeta }_{1}}}$
|
(12b) |
|
${{\gamma }_{1}}~{{\gamma }_{3}}~=1+\text{ }\frac{{{\zeta }_{1}}-{{\zeta }_{3}}~}{i\omega +{{\zeta }_{3}}~}$
|
(12c) |
将(12) 式代入(11) 式可以得到:
|
$\begin{array}{*{35}{l}}
\left( \lambda +\mu \right)\text{ }\left( \frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{\partial {{x}_{1}}^{2}}~~+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}}{~\partial {{x}_{1}}\partial {{x}_{3}}~} \right)+\text{ }\left( \lambda +2\mu \right)\text{ (}\frac{\partial }{\partial {{x}_{1}}}\text{ }~\frac{{{\zeta }_{3}}-{{\zeta }_{1}}~}{i\omega +{{\zeta }_{1}}~}\cdot \\
\frac{\partial ~{{{\hat{u}}}_{1}}~}{\partial {{x}_{1}}})~+\mu \text{ }\frac{\partial }{\partial {{x}_{3}}}\text{ }~\frac{{{\zeta }_{1}}-{{\zeta }_{3}}~}{i\omega +{{\zeta }_{3}}}~\frac{\partial \hat{u}{{~}_{1}}}{\partial {{x}_{3}}}~~+\mu \text{ }\left( \frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{\partial {{x}_{1}}^{2}}~~+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{~\partial {{x}_{3}}^{2}} \right)~= \\
\rho \hat{u}{{~}_{1}}~[-{{\omega }^{2}}+i\omega \left( {{\zeta }_{1}}+{{\zeta }_{3}} \right)~+{{\zeta }_{1}}{{\zeta }_{3}}]\text{ } \\
\end{array}$
|
(13a) |
|
$\begin{array}{*{35}{l}}
\left( \lambda +\mu \right)\text{ }\left( \frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}}{\partial {{x}_{1}}^{2}}~~+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{~\partial {{x}_{1}}\partial {{x}_{3}}~} \right)+\text{ }\left( \lambda +2\mu \right)\text{ (}\frac{\partial }{\partial {{x}_{3}}}\text{ }~\frac{{{\zeta }_{1}}-{{\zeta }_{3}}~}{i\omega +{{\zeta }_{1}}~}\cdot \\
\frac{\partial ~{{{\hat{u}}}_{3}}~}{\partial {{x}_{3}}})~+\mu \text{ }\frac{\partial }{\partial {{x}_{1}}}\text{ }~\frac{{{\zeta }_{3}}-{{\zeta }_{1}}~}{i\omega +{{\zeta }_{3}}}~\frac{\partial \hat{u}{{~}_{3}}}{\partial {{x}_{3}}}~~+\mu \text{ }\left( \frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}}{\partial {{x}_{1}}^{2}}~~+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}}{~\partial {{x}_{3}}^{2}} \right)~= \\
\rho \hat{u}{{~}_{3}}~[-{{\omega }^{2}}+i\omega \left( {{\zeta }_{1}}+{{\zeta }_{3}} \right)~+{{\zeta }_{1}}{{\zeta }_{3}}]\text{ } \\
\end{array}$
|
(13b) |
之后, 引入辅助函数 Φ ={ φ1 φ2 φ3 φ4 }T, φi的Fourier变换分量可以定义为:
|
${{{\hat{\varphi }}}_{1}}=\text{ }\frac{{{\zeta }_{3}}-{{\zeta }_{1}}}{i\omega +{{\zeta }_{1}}~}~\frac{\partial ~{{{\hat{u}}}_{1}}~}{\partial {{x}_{1}}~}$
|
(14a) |
|
${{{\hat{\varphi }}}_{2}}=\text{ }\frac{{{\zeta }_{1}}-{{\zeta }_{3}}}{~i\omega +{{\zeta }_{3}}}~\frac{\partial \hat{u}{{~}_{3}}}{\partial {{x}_{3}}}$
|
(14b) |
|
${{{\hat{\varphi }}}_{3}}=\text{ }\frac{{{\zeta }_{1}}-{{\zeta }_{3}}}{i\omega +{{\zeta }_{3}}}~~\frac{\partial \hat{u}{{~}_{1}}}{~\partial {{x}_{3}}}$
|
(14c) |
|
${{{\hat{\varphi }}}_{4}}=\text{ }\frac{{{\zeta }_{3}}-{{\zeta }_{1}}~}{i\omega +{{\zeta }_{1}}}~\frac{\partial \hat{u}{{~}_{3}}~}{\partial {{x}_{1}}}$
|
(14d) |
也可写成如下形式:
|
$(i\omega +{{\zeta }_{1}})~{{{\hat{\varphi }}}_{1}}=({{\zeta }_{3}}-{{\zeta }_{1}})\text{ }\frac{\partial ~{{{\hat{u}}}_{1}}~}{\partial {{x}_{1}}~}$
|
(15a) |
|
$(i\omega +{{\zeta }_{3}})~{{{\hat{\varphi }}}_{2}}=({{\zeta }_{1}}-{{\zeta }_{3}})\text{ }\frac{\partial \hat{u}{{~}_{3}}}{\partial {{x}_{3}}}$
|
(15b) |
|
$(i\omega +{{\zeta }_{3}})\hat{\varphi }{{~}_{3}}=({{\zeta }_{1}}-{{\zeta }_{3}})\text{ }\frac{\partial \hat{u}{{~}_{1}}}{~\partial {{x}_{3}}}$
|
(15c) |
|
$(i\omega +{{\zeta }_{1}})\hat{\varphi }{{~}_{4}}=({{\zeta }_{3}}-{{\zeta }_{1}})\frac{\partial \hat{u}{{~}_{3}}~}{\partial {{x}_{1}}}$
|
(15d) |
将(14) 式代入(13) 式可以得到:
|
$\begin{array}{*{35}{l}}
\left( \lambda +\mu \right)\left( \frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{\partial {{x}_{1}}^{2}}~+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}}{\partial {{x}_{1}}\partial {{x}_{3}}} \right)~~+\left( \lambda +2\mu \right)\text{ }\frac{\partial \hat{\varphi }{{~}_{1}}~}{\partial {{x}_{1}}}~+\mu \text{ }\frac{\partial \hat{\varphi }{{~}_{3}}~}{\partial {{x}_{3}}~}+ \\
\mu \text{ }\left( \frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{\partial {{x}_{1}}^{2}~}+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}~}{\partial {{x}_{3}}^{2}} \right)~=\rho \hat{u}{{~}_{1}}[-{{\omega }^{2}}+i\omega \left( {{\zeta }_{1}}+{{\zeta }_{3}} \right)~+{{\zeta }_{1}}{{\zeta }_{3}}] \\
\end{array}$
|
(16a) |
|
$\begin{array}{*{35}{l}}
\left( \lambda +\mu \right)\left( \frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}}{\partial {{x}_{3}}^{2}}~+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{\partial {{x}_{1}}\partial {{x}_{3}}} \right)~~+\left( \lambda +2\mu \right)\text{ }\frac{\partial \hat{\varphi }{{~}_{2}}~}{\partial {{x}_{3}}}~+\mu \text{ }\frac{\partial \hat{\varphi }{{~}_{4}}~}{\partial {{x}_{1}}~}+ \\
\mu \text{ }\left( \frac{{{\partial }^{2}}{{{\hat{u}}}_{1}}}{\partial {{x}_{1}}^{2}~}+\text{ }\frac{{{\partial }^{2}}{{{\hat{u}}}_{3}}~}{\partial {{x}_{3}}^{2}} \right)~=\rho \hat{u}{{~}_{3}}[-{{\omega }^{2}}+i\omega \left( {{\zeta }_{1}}+{{\zeta }_{3}} \right)~+{{\zeta }_{1}}{{\zeta }_{3}}] \\
\end{array}$
|
(16b) |
将(16) 式由频域转换到时域, 可以得到弹性波动方程的非分裂PML吸收边界条件的表达式:
|
$\begin{array}{*{35}{l}}
\left( \lambda +2\mu \right)\text{ }\frac{{{\partial }^{2}}{{u}_{1}}~}{\partial {{x}_{1}}^{2}}~+\left( \lambda +\mu \right)\text{ }\frac{{{\partial }^{2}}{{u}_{3}}~}{\partial {{x}_{1}}\partial {{x}_{3}}~}+\mu \text{ }\frac{{{\partial }^{2}}{{u}_{1}}~}{\partial {{x}_{3}}^{2}~}+ \\
\left( \lambda +2\mu \right)\text{ }\frac{\partial {{\varphi }_{1}}}{\partial {{x}_{1}}}~~+\mu \text{ }\frac{\partial {{\varphi }_{3}}}{\partial {{x}_{3}}~}~=\rho \text{ }\frac{{{\partial }^{2}}{{u}_{1}}~}{\partial {{t}^{2}}}~+\rho \left( {{\zeta }_{1}}+{{\zeta }_{3}} \right)\cdot \\
\frac{\partial {{u}_{1}}~}{\partial t}\text{ }+\rho {{\zeta }_{1}}{{\zeta }_{3}}{{u}_{1}}~ \\
\end{array}$
|
(17a) |
|
$\begin{array}{*{35}{l}}
\left( \lambda +2\mu \right)\text{ }\frac{{{\partial }^{2}}{{u}_{3}}~}{\partial {{x}_{3}}^{2}}~+\left( \lambda +\mu \right)\text{ }\frac{{{\partial }^{2}}{{u}_{3}}~}{\partial {{x}_{1}}\partial {{x}_{3}}~}+\mu \text{ }\frac{{{\partial }^{2}}{{u}_{3}}~}{\partial {{x}_{1}}^{2}~}+ \\
\left( \lambda +2\mu \right)\text{ }\frac{\partial {{\varphi }_{2}}}{\partial {{x}_{3}}}~~+\mu \text{ }\frac{\partial {{\varphi }_{4}}}{\partial {{x}_{1}}~}~=\rho \text{ }\frac{{{\partial }^{2}}{{u}_{3}}~}{\partial {{t}^{2}}}~+\rho \left( {{\zeta }_{1}}+{{\zeta }_{3}} \right)\cdot \\
\frac{\partial {{u}_{3}}~}{\partial t}\text{ }+\rho {{\zeta }_{1}}{{\zeta }_{3}}{{u}_{1}}~ \\
\end{array}$
|
(17b) |
同时, 将(15) 式转化到时间域, 可以得到辅助函数的控制方程:
|
$\frac{\partial {{\varphi }_{1}}}{\partial t}~\text{ }=-{{\zeta }_{1}}{{\varphi }_{1}}+({{\zeta }_{3}}-{{\zeta }_{1}})\text{ }\frac{\partial {{u}_{1}}}{\partial {{x}_{1}}}$
|
(18a) |
|
$\frac{\partial {{\varphi }_{2}}}{\partial t}\text{ }=-{{\zeta }_{3}}{{\varphi }_{2}}+({{\zeta }_{1}}-{{\zeta }_{3}})\text{ }\frac{\partial {{u}_{3}}}{\partial {{x}_{3}}}$
|
(18b) |
|
$\frac{\partial {{\varphi }_{3}}}{\partial t}\text{ }=-{{\zeta }_{3}}{{\varphi }_{3}}+({{\zeta }_{1}}-{{\zeta }_{3}})\text{ }\frac{\partial {{u}_{1}}}{\partial {{x}_{3}}}$
|
(18c) |
|
$\frac{\partial {{\varphi }_{4}}}{\partial t}\text{ }=-{{\zeta }_{1}}{{\varphi }_{4}}+({{\zeta }_{3}}-{{\zeta }_{1}})\frac{\text{ }\partial {{u}_{3}}}{~\partial {{x}_{1}}}$
|
(18d) |
在区域ΩRD的内部, 衰减函数ζi(i=1, 3) 和辅助矢量 Φ 会消失, 因此公式(17) 还原为公式(4) 。在弹性波动方程非分裂PML吸收边界条件的推导过程中, 只需引入4个标量辅助函数φ1, φ2, φ3, φ4, 即可将完全匹配层引入到弹性波动方程中, 而且在推导过程中不需要提高时间和空间的阶数, 形式简单, 易于实现。
3 完全匹配层反射系数的求解
基于二阶弹性波动方程的非分裂PML吸收
|
$\eqalign{
& \left[ \matrix{
\sigma {k^2}_1 + \mu {k^3}_2 + \sigma {k^2}_1{{\left( {{\zeta _3} - {\zeta _1}} \right)} \over {i\omega + {\zeta _1}}} + \mu _3^2{{\left( {{\zeta _1} - {\zeta _3}} \right)} \over {i\omega + {\zeta _3}}} \hfill \cr
\left( {\lambda + \mu } \right){\tan ^2}\theta k_3^2 \hfill \cr} \right. \cr
& {\left[ {{\omega ^2}\rho - i\omega \rho \left( {{\zeta _1} + {\zeta _3}} \right) - \rho {\zeta _1}\zeta } \right]_3}\left[ {\matrix{
{{D_1}} \cr
{{D_3}} \cr
} } \right] \cr} $
|
式中σ=λ+2μ.(23)式经过一系列的计算并整理边界条件, 考虑弹性波沿着x1方向和x3方向呈指数递减, 设纵波和横波的势函数分量形式为[4]:
|
${{u}_{1}}=\text{ }D{{~}_{1}}{{e}^{i(\omega t-{{k}_{1}}{{x}_{1}}-{{k}_{3}}{{x}_{3}})}}~$
|
(19a) |
|
${{u}_{3}}=\text{ }D{{~}_{3}}{{e}^{i(\omega t-{{k}_{1}}{{x}_{1}}-{{k}_{3}}{{x}_{3}})}}$
|
(19b) |
|
${{\varphi }_{1}}={{\varphi }_{1}}^{0}{{e}^{i(\omega t-{{k}_{1}}x-{{k}_{3}}{{x}_{3}})}}$
|
(19c) |
|
${{\varphi }_{2}}={{\varphi }_{2}}^{0}{{e}^{i(\omega t-{{k}_{1}}{{x}_{1}}-{{k}_{3}}{{x}_{3}})}}$
|
(19d) |
|
${{\varphi }_{3}}={{\varphi }_{3}}^{0}{{e}^{i(\omega t-{{k}_{1}}{{x}_{1}}-{{k}_{3}}{{x}_{3}})}}$
|
(19e) |
|
${{\varphi }_{4}}={{\varphi }_{4}}^{0}{{e}^{i(\omega t-{{k}_{1}}{{x}_{1}}-{{k}_{3}}{{x}_{3}})}}~$
|
(19f) |
式中:k1, k3和 D 1, D 3分别表示x1和x3方向上的波数和位移矢量;φ10, φ20, φ30, φ40表示势函数的幅值。
将(19) 式代入(17) 式可以得到方程:
|
$\begin{array}{*{35}{l}}
\left( \lambda +2\mu \right){{k}_{1}}^{2}~D{{~}_{1}}+\text{ }D{{~}_{3}}{{k}_{1}}{{k}_{3}}\left( \lambda +\mu \right)+\mu {{k}_{3}}^{2}~D{{~}_{1}}+ \\
i{{k}_{1}}\left( \lambda +2\mu \right){{\varphi }_{1}}^{0}+i{{k}_{3}}\mu {{\varphi }_{3}}^{0}={{\omega }^{2}}\rho \text{ }D{{~}_{1}}-i\omega \rho ({{\zeta }_{1}}+ \\
{{\zeta }_{3}})\text{ }D{{~}_{1}}-\rho {{\zeta }_{1}}{{\zeta }_{3}}~D{{~}_{1}} \\
\end{array}$
|
(20a) |
|
$\begin{array}{*{35}{l}}
\left( \lambda +2\mu \right){{k}_{3}}^{2}~D{{~}_{3}}+\text{ }D{{~}_{1}}{{k}_{1}}{{k}_{3}}\left( \lambda +\mu \right)+\mu {{k}_{1}}^{2}~D{{~}_{3}}+ \\
i{{k}_{3}}\left( \lambda +2\mu \right){{\varphi }_{2}}^{0}+i{{k}_{1}}\mu {{\varphi }_{4}}^{0}={{\omega }^{2}}\rho \text{ }D{{~}_{3}}-i\omega \rho ({{\zeta }_{1}}+ \\
{{\zeta }_{3}})\text{ }D{{~}_{3}}-\rho {{\zeta }_{1}}{{\zeta }_{3}}~D{{~}_{3}} \\
\end{array}$
|
(20b) |
再将(19) 式代入(18) 式可以得到位移和势函数幅值之间的转换关系:
|
${{\varphi }_{1}}^{0}=\text{ }\frac{-i{{k}_{1}}({{\zeta }_{3}}-{{\zeta }_{1}})\text{ }D{{~}_{1}}}{~i\omega +{{\zeta }_{1}}}$
|
(21a) |
|
${{\varphi }_{2}}^{0}=\text{ }\frac{-i{{k}_{3}}({{\zeta }_{1}}-{{\zeta }_{3}})\text{ }D{{~}_{3}}}{~i\omega +{{\zeta }_{3}}}$
|
(21b) |
|
${{\varphi }_{3}}^{0}=\text{ }\frac{-i{{k}_{3}}({{\zeta }_{1}}-{{\zeta }_{3}})\text{ }D{{~}_{1}}}{~i\omega +{{\zeta }_{3}}}$
|
(21c) |
|
${{\varphi }_{4}}^{0}=\text{ }\frac{-i{{k}_{1}}({{\zeta }_{3}}-{{\zeta }_{1}})\text{ }D{{~}_{3}}~}{i\omega +{{\zeta }_{1}}}$
|
(21d) |
将(21) 式代入(20) 式可以得到方程:
|
$\begin{array}{*{35}{l}}
\left( \lambda +2\mu \right){{k}_{1}}^{2}~D{{~}_{1}}+\text{ }D{{~}_{3}}{{k}_{1}}{{k}_{3}}\left( \lambda +\mu \right)+\mu {{k}_{3}}^{2}~D{{~}_{1}}+ \\
\left( \lambda +2\mu \right)\text{ }\frac{{{k}_{1}}^{2}\left( {{\zeta }_{3}}-{{\zeta }_{1}} \right)\text{ }D{{~}_{1}}}{i\omega +{{\zeta }_{1}}}~~+\mu \text{ }\frac{{{k}_{3}}^{2}\left( {{\zeta }_{1}}-{{\zeta }_{3}} \right)\text{ }D{{~}_{1}}~}{i\omega +{{\zeta }_{3}}}~= \\
{{\omega }^{2}}\rho \text{ }D{{~}_{1}}-i\omega \rho \left( {{\zeta }_{1}}+{{\zeta }_{3}} \right)\text{ }D{{~}_{1}}-\rho {{\zeta }_{1}}{{\zeta }_{3}}~D{{~}_{1}} \\
\end{array}$
|
(22a) |
|
$\begin{array}{*{35}{l}}
\left( \lambda +2\mu \right){{k}_{3}}^{2}~D{{~}_{3}}+\text{ }D{{~}_{1}}{{k}_{1}}{{k}_{3}}\left( \lambda +\mu \right)+\mu {{k}_{1}}^{2}~D{{~}_{3}}+ \\
\left( \lambda +2\mu \right)\text{ }\frac{{{k}_{3}}^{2}\left( {{\zeta }_{1}}-{{\zeta }_{3}} \right)\text{ }D{{~}_{3}}}{~i\omega +{{\zeta }_{3}}}~+\mu \text{ }\frac{{{k}_{1}}^{2}\left( {{\zeta }_{3}}-{{\zeta }_{1}} \right)\text{ }D{{~}_{3}}}{~i\omega +{{\zeta }_{1}}}~= \\
{{\omega }^{2}}\rho \text{ }D{{~}_{3}}-\rho \left( {{\zeta }_{1}}+{{\zeta }_{3}} \right)i\omega \text{ }D{{~}_{3}}-\rho {{\zeta }_{1}}{{\zeta }_{3}}~D{{~}_{3}} \\
\end{array}$
|
(22b) |
将(22) 式合并, 利用Snell定律k1/k3=sinθ/cosθ(θ为弹性波的入射角), 整理可得:
|
$\begin{align}
& \left[ \begin{matrix}
\sigma {{k}_{1}}^{2}+\mu {{k}_{3}}^{2}+\sigma \text{ }\frac{{{k}_{1}}^{2}\left( {{\zeta }_{3}}-{{\zeta }_{1}} \right)\text{ }}{i\omega +{{\zeta }_{1}}}~+\mu \text{ }\frac{{{k}_{3}}^{2}\left( {{\zeta }_{1}}-{{\zeta }_{3}} \right)}{i\omega +{{\zeta }_{3}}~} & \text{ta}{{\text{n}}^{2}}\theta {{k}_{3}}^{2}\left( \lambda +\mu \right) \\
\left( \lambda +\mu \right)ta{{n}^{2}}\theta {{k}_{3}}^{2} & \sigma {{k}_{3}}^{2}+\mu {{k}_{1}}^{2}+\sigma \text{ }\frac{{{k}_{3}}^{2}\left( {{\zeta }_{1}}-{{\zeta }_{3}} \right)}{i\omega +{{\zeta }_{3}}}\text{ }~+\mu \frac{\text{ }{{k}_{1}}^{2}\left( {{\zeta }_{3}}-{{\zeta }_{1}} \right)}{i\omega +{{\zeta }_{1}}} \\
\end{matrix} \right] \\
& \left[ \begin{matrix}
D{{~}_{1}} \\
D{{~}_{3}} \\
\end{matrix} \right] \\
& \left[ {{\omega }^{2}}\rho -i\omega \rho \left( {{\zeta }_{1}}+{{\zeta }_{3}} \right)-\rho {{\zeta }_{1}}{{\zeta }_{3}} \right] \\
& \left[ \begin{matrix}
D{{~}_{1}} \\
D{{~}_{3}} \\
\end{matrix} \right] \\
\end{align}$
|
(23) |
式中:σ=λ+2μ。(23) 式经过一系列的计算并整理后可得到两个控制方程:
|
$\mu [{\rm{ }}ta{n^2}\theta \left( {1 + a} \right) + \left( {b + 1} \right){\rm{ }}]{k_3}^2 - c = 0$
|
(24a) |
|
$\left( {\lambda + 2\mu } \right){\rm{ }}\left[ {ta{n^2}\theta \left( {1 + a} \right) + \left( {b + 1} \right){\rm{ }}} \right]{k_3}^2 - c = 0$
|
(24b) |
其中, 参数a, b, c的表达式为:
|
$a=\text{ }\frac{{{\zeta }_{3}}-{{\zeta }_{1}}~}{i\omega +{{\zeta }_{1}}}$
|
(25a) |
|
$b=\text{ }\frac{{{\zeta }_{1}}-{{\zeta }_{3}}}{~i\omega +{{\zeta }_{3}}~}$
|
(25b) |
|
$c=\left[ {{\omega }^{2}}-i\omega \left( {{\zeta }_{1}}+{{\zeta }_{3}} \right)-{{\zeta }_{1}}{{\zeta }_{3}} \right]\rho $
|
(25c) |
将(25) 式代入(24) 式, 并以P波的波数求解为例, 可以得到:
|
${{k}_{3}}=\pm \text{ }\frac{cos\theta }{{{v}_{P}}}\text{ }~i\text{ }\sqrt{\frac{{{(i\omega +{{\zeta }_{1}})}^{2}}{{(i\omega +{{\zeta }_{3}})}^{2}}~}{si{{n}^{2}}\theta {{(i\omega +{{\zeta }_{3}})}^{2}}+co{{s}^{2}}\theta {{(i\omega +{{\zeta }_{1}})}^{2}}}}$
|
(26) |
S波的波数求解过程与P波相同。为了简化(26) 式, 令二维函数f(ζ1, ζ3)为:
|
$f({{\zeta }_{1}},\text{ }{{\zeta }_{3}})=i\text{ }\sqrt{\frac{{{(i\omega +{{\zeta }_{1}})}^{2}}{{(i\omega +{{\zeta }_{3}})}^{2}}}{si{{n}^{2}}\theta {{(i\omega +{{\zeta }_{3}})}^{2}}+co{{s}^{2}}\theta {{(i\omega +{{\zeta }_{1}})}^{2}}}}~$
|
(27) |
应用一阶二维McLaughlin展式对(27) 式连续函数进行求解, 取频率项为正可以得到:
|
$f({{\zeta }_{1}},\text{ }{{\zeta }_{3}})=\omega -{{\zeta }_{1}}isi{{n}^{2}}\theta -{{\zeta }_{3}}ico{{s}^{2}}\theta $
|
(28) |
因此, 完全匹配层中P波的波数表达式为:
|
${{k}_{1}}=\text{ }\frac{sin\theta }{{{v}_{P}}}\text{ }~(\omega -{{\zeta }_{1}}isi{{n}^{2}}\theta -{{\zeta }_{3}}ico{{s}^{2}}\theta )$
|
(29a) |
|
${{k}_{3}}=\text{ }\frac{cos\theta }{{{v}_{P}}}~(\omega -{{\zeta }_{1}}isi{{n}^{2}}\theta -{{\zeta }_{3}}ico{{s}^{2}}\theta )$
|
(29b) |
S波的波数表达式为:
|
${{k}_{1}}=\frac{\text{ }sin\theta }{{{v}_{S}}}\text{ }~(\omega -{{\zeta }_{1}}isi{{n}^{2}}\theta -{{\zeta }_{3}}ico{{s}^{2}}\theta )$
|
(30a) |
|
${{k}_{3}}=\text{ }\frac{cos\theta }{{{v}_{S}}}\text{ }~(\omega -{{\zeta }_{1}}isi{{n}^{2}}\theta -{{\zeta }_{3}}ico{{s}^{2}}\theta )$
|
(30b) |
其中, $vP=\text{ }\sqrt{\frac{\lambda +2\mu }{\rho }}\text{ },vS=\text{ }\sqrt{\frac{\mu }{\rho }}\text{ }$。
将(30a)式、(30b)式代入(19a)式、(19b)式可以得到该吸收边界条件的位移表达式:
|
$\begin{array}{*{35}{l}}
{{u}_{1}}=\text{ }D{{~}_{1}}exp\text{ }\!\![\!\!\text{ }i\text{ }\left( \omega t-\text{ }\frac{sin\theta \omega }{{{v}_{S}}}\text{ }~{{x}_{1}}-\frac{\text{ }cos\theta \omega \text{ }}{{{v}_{S}}}~{{x}_{3}} \right)]\cdot \\
exp\text{ }\!\![\!\!\text{ }-\text{ }\frac{sin\theta }{{{v}_{S}}}\text{ }~\left( {{\zeta }_{1}}si{{n}^{2}}\theta +{{\zeta }_{3}}co{{s}^{2}}\theta \right){{x}_{1}}]\cdot \\
exp\text{ }-\text{ }\!\![\!\!\text{ }\frac{cos\theta }{{{v}_{S}}}\text{ }~\left( {{\zeta }_{1}}si{{n}^{2}}\theta +{{\zeta }_{3}}co{{s}^{2}}\theta \right){{x}_{3}}]\text{ } \\
\end{array}$
|
(31a) |
|
$\begin{array}{*{35}{l}}
{{u}_{3}}=\text{ }D{{~}_{1}}exp\text{ }\!\![\!\!\text{ }i\text{ }\left( \omega t-\text{ }\frac{sin\theta \omega }{{{v}_{S}}}\text{ }~{{x}_{1}}-\frac{\text{ }cos\theta \omega \text{ }}{{{v}_{S}}}~{{x}_{3}} \right)]\cdot \\
exp\text{ }\!\![\!\!\text{ }-\text{ }\frac{sin\theta }{{{v}_{S}}}\text{ }~\left( {{\zeta }_{1}}si{{n}^{2}}\theta +{{\zeta }_{3}}co{{s}^{2}}\theta \right){{x}_{1}}]\cdot \\
exp\text{ }-\text{ }\!\![\!\!\text{ }\frac{cos\theta }{{{v}_{S}}}\text{ }~\left( {{\zeta }_{1}}si{{n}^{2}}\theta +{{\zeta }_{3}}co{{s}^{2}}\theta \right){{x}_{3}}]\text{ } \\
\end{array}$
|
(31b) |
考虑衰减函数趋于0, (31) 式可以还原为以波数表示的弹性波在单相固体介质中传播的位移表达式。
考虑弹性波在进入吸收层时不产生任何反射, 进入吸收层后会发生衰减, 传至吸收层外边界时产生反射, 在吸收层内继续衰减直至分界面, 可得到反射系数的表达式[4]:
|
$\begin{array}{*{35}{l}}
{{R}_{P}}=exp\text{ }\!\![\!\!\text{ }-\text{ }\frac{sin\theta }{{{v}_{P}}}\text{ }\left( ~si{{n}^{2}}\theta {{\int }_{0}}^{L}{{\zeta }_{1}}d{{x}_{1}}+co{{s}^{2}}\theta {{\int }_{0}}^{L}{{\zeta }_{3}}d{{x}_{3}} \right)~{{x}_{1}}]\cdot \\
exp\text{ }\!\![\!\!\text{ }-\text{ }\frac{cos\theta }{{{v}_{P}}}\left( si{{n}^{2}}\theta {{\int }_{0}}^{L}{{\zeta }_{1}}d{{x}_{1}}+co{{s}^{2}}\theta {{\int }_{0}}^{L}{{\zeta }_{3}}d{{x}_{3}} \right)~{{x}_{3}}]\text{ } \\
\end{array}$
|
(32a) |
|
$\begin{array}{*{35}{l}}
{{R}_{S}}=exp\text{ }\!\![\!\!\text{ }-\text{ }\frac{sin\theta \text{ }}{{{v}_{S}}}~\left( si{{n}^{2}}\theta {{\int }_{0}}^{L}{{\zeta }_{1}}d{{x}_{1}}+co{{s}^{2}}\theta {{\int }_{0}}^{L}{{\zeta }_{3}}d{{x}_{3}}~ \right){{x}_{1}}]\cdot \\
exp\text{ }-[\frac{\text{ }cos\theta }{\text{ }{{v}_{S}}}~\left( si{{n}^{2}}\theta {{\int }_{0}}^{L}{{\zeta }_{1}}d{{x}_{1}}+co{{s}^{2}}\theta {{\int }_{0}}^{L}{{\zeta }_{3}}d{{x}_{3}} \right)~{{x}_{3}}]\text{ } \\
\end{array}$
|
(32b) |
式中:RP和RS分别表示完全匹配层中P波和S波的反射系数。
为进一步求解反射系数, 采用COLLINO等[11]提出的衰减函数形式:
|
${{\zeta }_{i}}({{x}_{i}})=\left\{ \begin{matrix}
0 & 其它 \\
\text{ }\frac{3v}{2L}\text{ }log{{r}^{-1}}~\left( \frac{{{x}_{i}}~}{L} \right){{~}^{2}} & ~0\le {{x}_{i}}\le Li=1,\text{ }3 \\
\end{matrix} \right.$
|
(33) |
式中:L为完全匹配层厚度;r为理论反射系数;v为弹性波的速度。
将(33) 式代入(32) 式任意一项可以得到:
|
${{R}_{P}}={{R}_{S}}=exp\text{ }\!\![\!\!\text{ }\frac{1}{2}(sin\theta {{x}_{1}}+cos\theta {{x}_{3}})logr]$
|
(34) |
完全匹配层的优化即是令PML最大反射系数为最小。通过对(34) 式分析可知, 当θ=0, π/2时, 最大反射系数Rmax表达式为:
|
${{R}_{max}}={{e}^{Llogr}}$
|
(35) |
分析(35) 式可知, 当完全匹配层厚度为0, 或者理论反射系数为1时, 完全匹配层处于全反射状态, 此时最大反射系数的值Rmax=1。
4 数值分析
为了更好地说明完全匹配层最大反射系数与完全匹配层厚度以及理论反射系数之间的关系, 也为了在完全匹配层数值模拟实验分析时能够确定衰减函数中参数的最优值, 对(35) 式进行了数值计算分析。
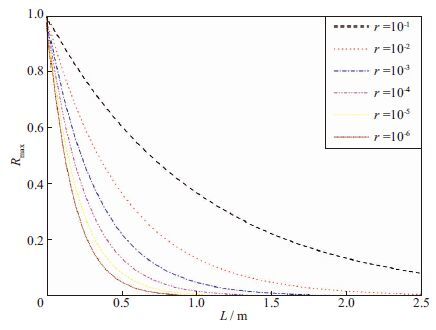
1) 在不同厚度、不同理论反射系数的情况下, 分析完全匹配层最大反射系数的变化。取完全匹配层厚度L在0~2.5 m变化, 理论反射系数r取10-j, j=1, 2, 3, 4, 5, 6, 由(35) 式可以得到最大反射系数Rmax的变化曲线, 如图 2所示。当理论反射系数r一定时, 完全匹配层的厚度L越大, 最大反射系数越小;当完全匹配层的厚度L一定时, 理论反射系数r取值越小, 最大反射系数越小。即理论反射系数取值越小, 完全匹配层厚度越大时, 完全匹配层的吸收效果越好。
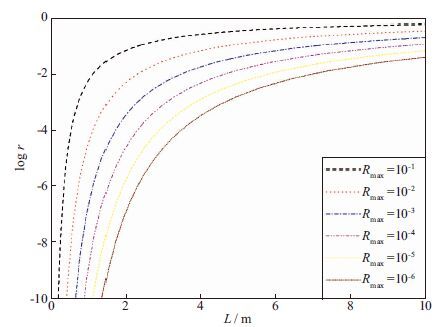
2) 在不同厚度、不同最大反射系数的情况下, 分析理论反射系数对数的变化。考虑完全匹配层厚度L在0~10 m变化, 最大反射系数Rmax取值为10-j, j=1, 2, 3, 4, 5, 6, 由(35) 式得到理论反射系数的对数logr的变化曲线, 如图 3所示。当最大反射系数Rmax一定时, 完全匹配层的厚度L越大, 理论反射系数的对数越大;当完全匹配层的厚度L一定时, 最大反射系数Rmax越大, 理论反射系数的对数越大。据此性质可对COLLINO等[11]提出的衰减函数中参数的取值进行优化。
5 结束语
本文基于复伸展坐标变换给出了一种适用于二阶弹性波动方程的非分裂吸收边界条件, 理论上推导了该完全匹配层的最大反射系数解析表达式。通过对最大反射系数进行理论分析和数值分析, 得出以下结论:①最大反射系数随着完全匹配层厚度的增加而减小, 随理论反射系数的减小而减小;②理论反射系数的对数随完全匹配层厚度以及最大反射系数的增加而增加。研究结果对于完全匹配层数值模拟实验分析中衰减函数的参数取值有一定的指导意义, 当衰减函数的参数取值适当时, 能够消除完全匹配层的边界反射。