2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东 青岛 266071
2. Laboratory for Marine Mineral Resources,Qingdao National Laboratory for Marine Science and Technology , Qingdao 266071 , China
常规一次反射波地震勘探受观测系统限制,对断层、盐丘侧翼等地下陡倾角构造照明不足,高陡构造精确成像困难[1-4]。高陡构造产生的棱柱波信息能够有效增加高陡构造的照明程度,改善高陡构造成像效果。棱柱波可视为二次反射波,波的传播路径主要分为3部分:震源激发入射到水平界面;水平界面反射传播到高陡构造;经过高陡构造反射被检波器记录。目前棱柱波应用尚不广泛,主要因为:①常规地震资料处理大多基于一次反射波,通常将棱柱波视为噪声滤除[5];②棱柱波能量与一次反射波能量相比更弱,成像结果通常被一次反射波成像值掩盖,很难体现棱柱波对成像结果的改善作用[6]。为了提高高陡构造的解释精度,作为常规成像剖面的补充,有必要对棱柱波进行单独成像。
近年来,关于棱柱波的研究逐渐成为热点。CAVALCA等[7]分析了棱柱波的运动学特征,并尝试在旅行时反演中加入棱柱波信息进行盐丘侧翼定位。MARMALYEVSKYY等[8]利用Kirchhoff法对棱柱波进行成像,从而刻画盐丘侧翼,成像之前需要从常规成像结果中提取水平反射界面信息。MALCOLM等[9]利用迭代单程波算法对棱柱波和多次波分步成像,各个阶段相互独立,不同阶段针对不同构造进行。JONES等[10]研究发现:将反射界面插入速度模型中即可借助常规逆时偏移算法对棱柱波进行成像。LIU等[11]指出,将陡倾角界面插入速度场时需要慎重,复杂的偏移速度场会产生复杂的波场,容易产生偏移假象;LI等[12]对常规逆时偏移算法加以改进,提出了针对复杂盐丘构造的棱柱波成像流程;DAI[6]提出了一种无需将反射界面插入速度场的棱柱波成像流程,避免拾取水平反射层。
本文在前人研究的基础上,推导了去除反射波后仅仅基于棱柱波的逆时偏移算子,使其在具有明确物理含义的基础上,排除了能量更强的一次反射波对棱柱波成像的影响,在成像过程中引入Poynting矢量[13-14]及平面波解构滤波算子[15-17]进行优化,通过典型的倒T及盐体边界陡倾角模型成像试算,验证了本文基于棱柱波逆时偏移优化算法对成像精度的改善作用以及算法本身的适应性。
1 逆时偏移棱柱波成像理论基础基于频率域波动方程,针对共炮点道集d(xg|xs)逆时偏移的成像公式可以表示为:
| $\begin{align} & {{m}_{mig}}(x|{{x}_{s}})=\underset{w}{\mathop{\sum }}\,\underset{g}{\mathop{\sum }}\,{{\omega }^{2}}{{W}^{*}}\left( \omega \right){{G}^{*}}(x|{{x}_{s}})\cdot \\ & {{G}^{*}}(x|{{x}_{g}})d({{x}_{g}}|{{x}_{s}}) \\ \end{align}$ | (1) |
式中:xs表示震源位置;mmig(x|xs)表示xs点炮集的成像值;W(ω)为震源频谱;xg表示检波点位置;“*”表示复数共轭。为了简化推导过程,假设格林函数G和数据d与角频率ω无关。
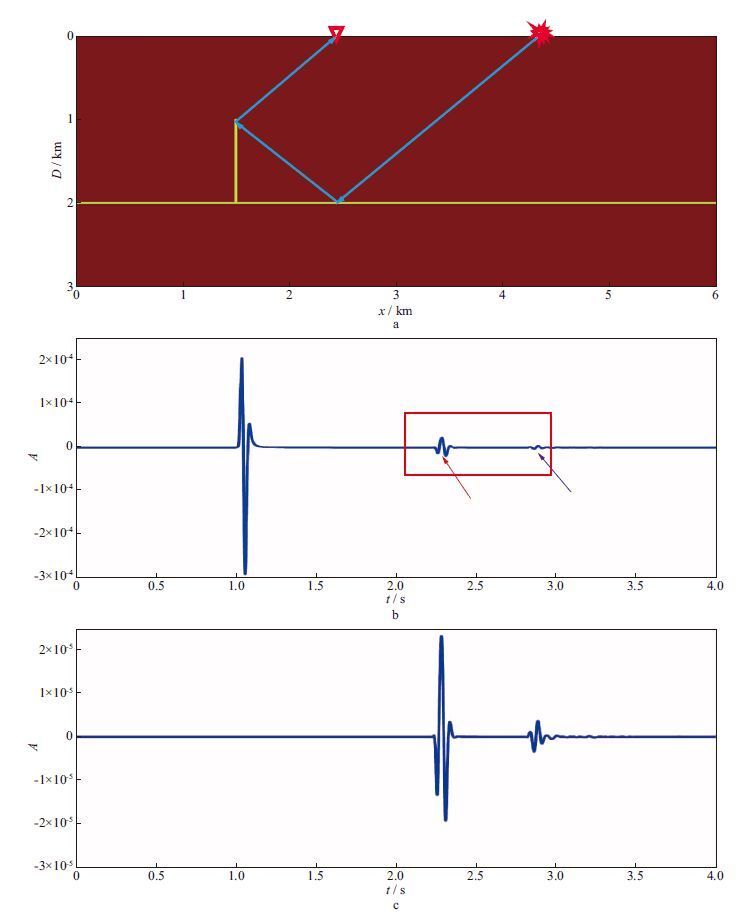
以图 1a所示模型为例,给出棱柱波偏移的基础原理。图 1a所示速度模型由嵌于均匀速度场的一个水平反射层和垂直反射层组成。背景速度大小为4000m/s,反射层速度为3500m/s。图 1a中蓝色箭头为棱柱波传播路径,其中激发点位置为(x,z)=(4500m,20m),检波点位置为(2500m,20m),震源子波为Ricker子波。接收到的全波场记录如图 1b所示,红色窗口中为接收到的一次反射波(红色箭头所指)和棱柱波(紫色箭头所指)。鉴于棱柱波能量较弱,为了更好的对棱柱波进行成像,本文将图 1b中的直达波切除,得到只包含一次反射波和棱柱波的记录,如图 1c所示。为了简化表达,本文将图 1c所示记录表达成:
|
图 1 倒T速度模型中的棱柱波反射路径及其单道记录 |
| $d({{x}_{g}}|{{x}_{s}})={{d}_{1}}({{x}_{g}}|{{x}_{s}})+{{d}_{2}}({{x}_{g}}|{{x}_{s}})$ | (2) |
其中,d1(xg|xs)和d2(xg|xs)分别表示一次反射波和二次反射棱柱波。
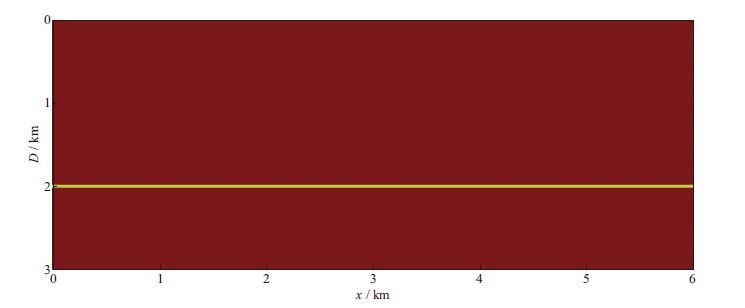
将水平反射层从常规偏移成像结果中拾取出来并加入偏移速度场(图 2)后,常规RTM算法可以正确成像棱柱波[10]。此时,采用图 2所示速度场计算得到的格林函数G(x|xs)可以分成两部分:直达波G0(x|xs)和水平界面的反射波G1(x|xs),即:
|
图 2 只包含一个水平反射层的速度模型 |
| $G(x|{{x}_{s}})={{G}_{0}}(x|{{x}_{s}})+{{G}_{1}}(x|{{x}_{s}})$ | (3) |
同理,可以得到检波点处的格林函数:
| $G(x|{{x}_{g}})={{G}_{0}}(x|{{x}_{g}})+{{G}_{1}}(x|{{x}_{g}})$ | (4) |
(3)式和(4)式中的G0代表下行波,G1代表上行波。
此时,整个偏移过程可以表示为:
| $\begin{align} & {{m}_{mig}}(x|{{x}_{s}})=\underset{\omega }{\mathop{\sum }}\,{{\omega }^{2}}{{W}^{*}}\left( \omega \right)[{{G}^{*}}_{0}(x|{{x}_{s}})+ \\ & {{G}^{*}}_{1}(x|{{x}_{s}})][{{G}^{*}}_{0}(x|{{x}_{g}})+{{G}^{*}}_{1}(x|{{x}_{g}})]\cdot \\ & [{{d}_{1}}({{x}_{g}}|{{x}_{s}})+{{d}_{2}}({{x}_{g}}|{{x}_{s}})]=\underset{\omega }{\mathop{\sum }}\,{{\omega }^{2}}{{W}^{*}}\left( \omega \right)\cdot \\ & {{G}^{*}}_{0}(x|{{x}_{s}}){{G}^{*}}_{0}(x|{{x}_{g}}){{d}_{1}}({{x}_{g}}|{{x}_{s}})+\underset{\omega }{\mathop{\sum }}\,{{\omega }^{2}}\cdot \\ & {{W}^{*}}\left( \omega \right){{G}^{*}}_{0}(x|{{x}_{s}}){{G}^{*}}_{0}(x|{{x}_{g}}){{d}_{2}}({{x}_{g}}|{{x}_{s}})+ \\ & \underset{\omega }{\mathop{\sum }}\,{{\omega }^{2}}{{W}^{*}}\left( \omega \right)G_{1}^{*}(x|{{x}_{s}})G_{0}^{*}(x|{{x}_{g}}){{d}_{1}}({{x}_{g}}|{{x}_{s}})+ \\ & \underset{\omega }{\mathop{\sum }}\,{{\omega }^{2}}{{W}^{*}}\left( \omega \right)G_{0}^{*}(x|{{x}_{s}})G_{1}^{*}(x|{{x}_{g}}){{d}_{1}}({{x}_{g}}|{{x}_{s}})+ \\ & \underset{\omega }{\mathop{\sum }}\,{{\omega }^{2}}{{W}^{*}}\left( \omega \right)G_{1}^{*}(x|{{x}_{s}})G_{0}^{*}(x|{{x}_{g}}){{d}_{2}}({{x}_{g}}|{{x}_{s}})+ \\ & \underset{\omega }{\mathop{\sum }}\,{{\omega }^{2}}{{W}^{*}}\left( \omega \right)G_{0}^{*}(x|{{x}_{s}})G_{1}^{*}(x|{{x}_{g}}){{d}_{2}}({{x}_{g}}|{{x}_{s}})+ \\ & others \\ \end{align}$ | (5) |
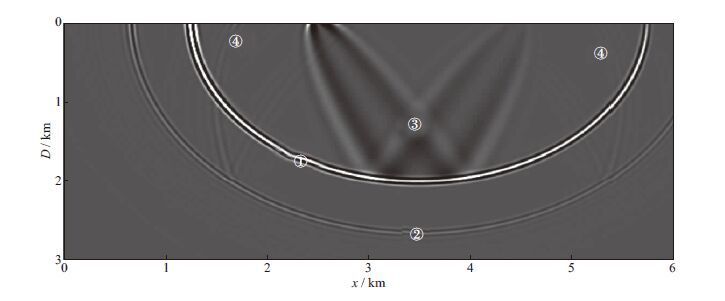
利用图 2所示的速度场对图 1c所示的道记录进行偏移成像,得到图 3所示的单道偏移结果。假设直达波的振幅为1,反射系数幅值为r,且与入射角度无关,则G0量级为O(1),G1,d1量级为O(r),d2量级为O(r2)。基于上述假设,对图 3进行如下分析。图 3中包含两个椭圆,内侧椭圆对应于公式(5)的第1项(图 3中标号①),振幅量级为O(r)。外侧椭圆对应于公式(5)的第2项(图 3中标号②),为棱柱波被当作一次反射波进行偏移后的成像值,属于偏移假象,振幅量级为O(r2)。公式(5)的第3项和第4项对应于图 3中的两个“兔耳”(图 3中标号③),振幅量级为O(r2)。公式(5)中的
|
图 3 非均匀速度模型逆时偏移成像结果 |
为了棱柱波单独成像,压制一次反射能量,本文直接利用公式(5)中的棱柱波成像项,计算棱柱波成像格林函数,进行棱柱波偏移。利用不含反射层的均匀速度场以及水平反射界面成像剖面,按照Born近似理论[18-19]计算格林函数:
| ${{G}_{1}}(x|{{x}_{s}})={{\int }_{x\prime }}{{\omega }^{2}}{{m}_{1}}\left( x\prime \right){{G}_{0}}(x\prime |{{x}_{s}})\cdot {{G}_{0}}\left( x\prime |x \right)dx\prime $ | (6) |
式中:m1(x')为水平反射层的反射率模型;G0为采用偏移速度场计算得到的格林函数。将(6)式代入(5)式的
| $\begin{align} & {{m}_{mig}}(x|{{x}_{s}})=\underset{\omega }{\mathop{\sum }}\,{{\omega }^{2}}{{W}^{*}}\left( \omega \right){{\int }_{x\prime }}{{\omega }^{2}}{{m}_{1}}\left( x\prime \right)\cdot \\ & G_{0}^{*}(x\prime |{{x}_{s}})G_{0}^{*}\left( x\prime |x \right)dx\prime G_{0}^{*}(x|{{x}_{g}}){{d}_{2}}({{x}_{g}}|{{x}_{s}}) \\ & =\underset{\omega }{\mathop{\sum }}\,{{\omega }^{2}}{{\int }_{x\prime }}{{\omega }^{2}}{{W}^{*}}\left( \omega \right)G_{0}^{*}(x\prime |{{x}_{s}}){{m}_{1}}\left( x\prime \right)\cdot \\ & G_{0}^{*}\left( x\prime |x \right)dx\prime G_{0}^{*}(x|{{x}_{g}}){{d}_{2}}({{x}_{g}}|{{x}_{s}}) \\ & =\underset{\omega }{\mathop{\sum }}\,{{\omega }^{2}}{{[{{P}_{1}}(x|{{x}_{s}})]}^{*}}[{{Q}_{0}}(x|{{x}_{s}})] \\ \end{align}$ | (7) |
其中,
| $\begin{align} & {{P}_{1}}(x|{{x}_{s}})={{\int }_{x\prime }}{{\omega }^{2}}{{W}^{*}}\left( \omega \right)G_{0}^{*}(x\prime |{{x}_{s}}){{m}_{1}}\left( x\prime \right)\cdot \\ & G_{0}^{*}\left( x\prime |x \right)dx\prime \\ & {{Q}_{0}}(x|{{x}_{s}})=G_{0}^{*}(x|{{x}_{g}}){{d}_{2}}({{x}_{g}}|{{x}_{s}}) \\ \end{align}$ | (8) |
波场P1(x|xs)可以在时间域通过两次有限差分模拟得到,这在一定程度上增加了计算量;波场Q0(x|xs)中的d2(xg|xs)项并未在炮记录中分离得到,成像过程中以全波场项d(xg|xs)代替。实际成像过程中,棱柱波波场值通过加权模拟原始波场与水平反射成像剖面得到,故在棱柱波成像剖面中会出现水平反射界面信息。(7)式以单道偏移为例,故未进行检波点叠加。同理,公式(5)中的第6项也可以按照相同的方法计算得到。从上面推导可以看出,相较于常规RTM成像,棱柱波成像共分为4个步骤:①获取水平反射界面成像剖面;②以第①步成像剖面为反射率模型通过Born近似模拟震源波场;③对震源波场和检波点波场进行相关成像;④将所有检波点的相关值叠加求和。我们引入Poynting矢量成像条件以及平面波解构算子对上述流程进行了优化,最终得到一套优化后的棱柱波成像流程(以公式(7)所示成像核为例):①利用上、下行波成像条件得到一次波成像的水平界面成像值m1(x');②利用步骤①得到的成像值进行Born正演得到波场值P1(x|xs),同时反传炮记录得到检波点波场Q0(x|xs),并利用左、右行波成像条件得到棱柱波成像的高陡界面成像值mmig(x|xs);③对所有炮点位置重复上述流程,叠加得到最终成像剖面;④对步骤③得到的成像值进行平面波解构滤波得到相应的倾角分布,利用该倾角分布对成像结果进行优化滤波得到最终成像结果。
2 Poynting矢量成像条件在优化后的棱柱波成像流程步骤①中,需要得到水平界面的成像值,因此我们借助Poynting矢量进行波场分离,然后对上行波场和下行波场进行单独成像。由于棱柱波主要由高倾角的反射体产生,因此在步骤③中,可借助Poynting矢量单独成像左、右行波,以压制水平反射界面能量,突出目标构造。Poynting矢量又称能流密度矢量,最初用在电磁学中[20]。YOON等[21]将其引入地震勘探中,并推导出一阶声波方程下Poynting矢量表达式:
| ${{P}^{y}}=pV=p({{v}_{x}},{{v}_{z}})=(p{{v}_{x}},p{{v}_{z}})=(P_{x}^{y},P_{z}^{y})$ | (9) |
式中:V=(vx,vz)表示质点的速度矢量,方向为质点振动方向;Pxy和Pzy为Poynting矢量的水平分量和垂直分量,方向与质点的运动方向一致。
随后,可借助下述准则对波场进行分离[13]:
| $\begin{align} & {{S}_{l}}=\left\{ \begin{matrix} S\left( x,z,t \right) & {{P}_{x}}\ge 0 \\ 0 & {{P}_{x}}<0 \\ \end{matrix} \right. \\ & {{S}_{r}}=\left\{ \begin{matrix} 0 & {{P}_{x}}\ge 0 \\ S\left( x,z,t \right) & {{P}_{x}}<0 \\ \end{matrix} \right. \\ & {{S}_{u}}=\left\{ \begin{matrix} S\left( x,z,t \right) & {{P}_{z}}\ge 0 \\ 0 & {{P}_{z}}<0 \\ \end{matrix} \right. \\ & {{S}_{d}}=\left\{ \begin{matrix} 0 & {{P}_{z}}\ge 0 \\ S\left( x,z,t \right) & {{P}_{z}}<0 \\ \end{matrix} \right. \\ \end{align}$ | (10) |
其中,Sl,Sr,Su和Sd分别代表左行波场、右行波场、上行波场和下行波场。此时,我们可以按照成像需求对不同波场分量求取相关值,对不同倾角的地下构造进行成像。
3 平面波解构滤波由于最终棱柱波成像剖面中仍含有水平反射界面以及不同倾角耦合的成像噪声,为了更好地突出棱柱波成像的垂直构造,引入倾角滤波思想滤除低倾角构造。本文采用FOMEL[15]提出的平面波解构滤波方法从全波场成像剖面中求取反射界面倾角信息,进而利用该倾角信息设计倾角滤波器,对成像剖面进行优化滤波。
平面波解构滤波器利用局部平面波叠加来表征地震数据,可以被看作频空域(F-X)预测误差滤波器的时空域(T-X)模拟,能较好地估计平滑连续同相轴的局部倾角信息。根据局部平面波物理模型,将公式(11)的局部平面波微分方程作为平面波解构滤波器的理论基础:
| $\frac{\partial P}{\partial x}+\sigma \frac{\partial P}{\partial t}=0$ | (11) |
式中:P(t,x)表示波场;σ为同相轴局部斜率。
当局部斜率σ为常数时,方程(11)的通解为:
| $P\left( t,x \right)=f\left( t-\sigma x \right)$ | (12) |
其中,f(x)可为任意波形。方程(12)为平面波的数学描述。
当局部斜率σ与t无关时,将(11)式变换到频率域可得频率域一般解:
| $R\left( x \right)\text{ }=\text{ }R\left( 0 \right){{e}^{i\omega \sigma x}}$ | (13) |
其中,R 是P的傅里叶变换项。在F-X域平面波可以通过如下的两项预测误差滤波器很好地预测出:
| ${{a}_{0~}}R\left( x \right)+{{a}_{1~}}R\left( x-1 \right)\text{ }=0$ | (14) |
其中,a0=1,a1=-eiωσ。将该滤波器表示为Z变换的形式,并进一步分解为多个两项滤波器的乘积:
| $A({{Z}_{x}})=\left( 1-\frac{{{z}_{x}}}{{{z}_{1}}} \right)\left( 1-\frac{{{z}_{x}}}{{{z}_{2}}} \right)\ldots \left( 1-\frac{{{z}_{x}}}{{{z}_{N}}} \right)$ | (15) |
当局部斜率σ随时间和空间都变化时,需重新变换到时间域寻找相移算子((13)式)和平面波预测滤波器((14)式)的类似表达。由于平面波传播的总能量保持不变,可以在时间域利用全通数字滤波器模拟该特性。在Z变换域,该过程表示为:
| ${{R}_{x\text{ }+\text{ }1~}}({{Z}_{t~}})\text{ }=\text{ }R{{~}_{x~}}({{Z}_{t~}})\frac{B({{Z}_{t~}})}{B\frac{1}{{{Z}_{t}}}}$ | (16) |
式中:R x (Zt )为相应地震道的Z变换;B(Zt)/B(1/Zt)为相移算子eiωσ的全通滤波近似。B(Zt)的系数可由相移滤波算子在低频时的频率响应拟合获得。(17)式为用Taylor级数展开求得的三点中心滤波器:
| $\begin{align} & {{B}_{3}}({{Z}_{t}})=\frac{\left( 1-\sigma \right)\left( 2-\sigma \right)}{12}Z_{t}^{-1}+\frac{\left( 2-\sigma \right)\left( 2+\sigma \right)}{6} \\ & +\frac{\left( 1+\sigma \right)\left( 2+\sigma \right)}{12}{{Z}_{t}} \\ \end{align}$ | (17) |
同时考虑时空两个方向上的变化,得到二维预测滤波器:
| $A({{Z}_{t}},{{Z}_{x}})=1-{{Z}_{x}}\frac{B({{Z}_{t~}})}{B\frac{1}{{{Z}_{t}}}}$ | (18) |
为了避免多项式除法,FOMEL将(18)式所示滤波器进行改进:
| $\begin{align} & C({{Z}_{t}},{{Z}_{x}})=A({{Z}_{t}},{{Z}_{x}})B(1/{{Z}_{t}}) \\ & =B(1/{{Z}_{t}})-{{Z}_{x}}B({{Z}_{t}}) \\ \end{align}$ | (19) |
由(17)式可知,C(Zt,Zx)可以表示为局部倾角σ的函数C(σ),C(σ)为预测误差算子。则局部倾角估计问题转化为如下的最小二乘问题:
| $C\left( \sigma \right)d\approx 0$ | (20) |
d为待预测倾角的地震数据,利用(20)式可从全波场成像结果中估计反射界面的倾角信息,进一步利用该倾角分布差异进行滤波处理。
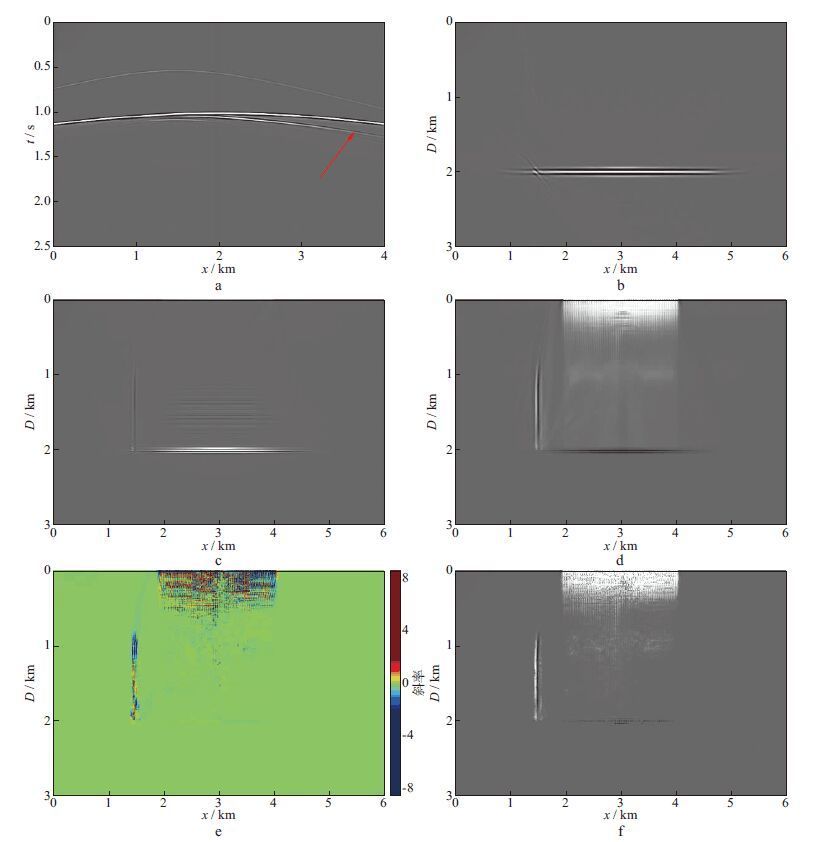
4 模型试算 4.1 倒T模型为了验证本文方法的正确性和有效性,采用图 1a所示的倒T速度模型对算法进行测试(图 4)。模型背景为4000m/s的均匀速度场,在模型中部存在两个3500m/s的棒状速度层,呈倒T状,横向601个采样点,纵向301个采样点,纵、横向采样间隔均为10m。采用中间放炮两边接收的观测系统,炮间距40m,最大偏移距2000m,道间距10m,共51炮,每炮401道接收,炮点位于CDP201~401。得到的第1炮单炮记录如图 4a所示,从图 4a中可以清晰地分辨出一次反射波、垂直反射层顶端的绕射波以及棱柱波(已切除直达波),棱柱波用箭头指出,相对于一次反射波,棱柱波能量较弱。
|
图 4 棱柱波成像结果 |
首先,以图 2所示速度场作为偏移速度场,利用Poynting矢量上、下行波成像条件对原始炮记录进行偏移,得到含有水平反射界面的RTM成像结果,如图 4b所示。随后,按照成像流程得到棱柱波成像结果。其中,图 4c为Laplace滤波后的常规棱柱波成像结果;图 4d为采用左、右行波成像条件得到的棱柱波成像结果;图 4e为经过平面波解构滤波器估计出的各个反射层的倾角斜率值,利用该斜率构建倾角滤波器,进一步压制水平反射层能量后垂直反射层能量得到凸显;图 4f为对图 4d进行平面波解构、倾角滤波后得到的仅含垂直反射层的成像剖面。对比图 4c和图 4d可知,采用左、右行波成像条件得到的垂直反射层能量更突出,水平反射界面的能量有所减弱。其中,图 4d,图 4e和图 4f中2000~4000m的垂直构造为偏移假象,由震源的激发效应产生,为Poynting矢量左、右行波成像条件所致。对比图 4中各成像结果可知:棱柱波单独成像可以提高垂直反射层的分辨率,有助于精确定位垂直反射层;Poynting矢量左、右行波成像条件可以进一步压制水平反射层能量并突出垂直反射层;平面波解构滤波器可以精确计算出成像剖面的同相轴倾角,从而利用其滤除水平反射层的能量,提高目标构造成像效果。应用棱柱波单独成像及其优化算子,先验模型中的垂直构造得到了较好的恢复,验证了本文棱柱波单独成像算法的正确性及优化算子的有效性。
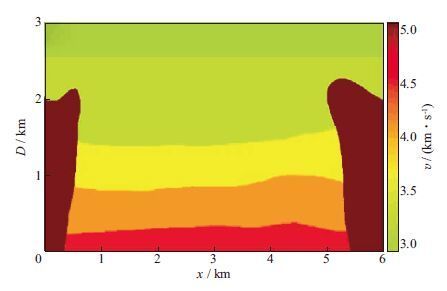
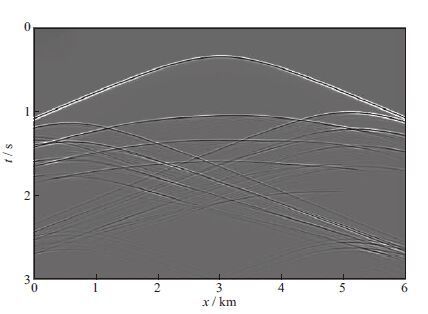
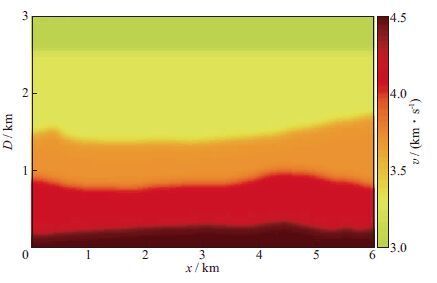
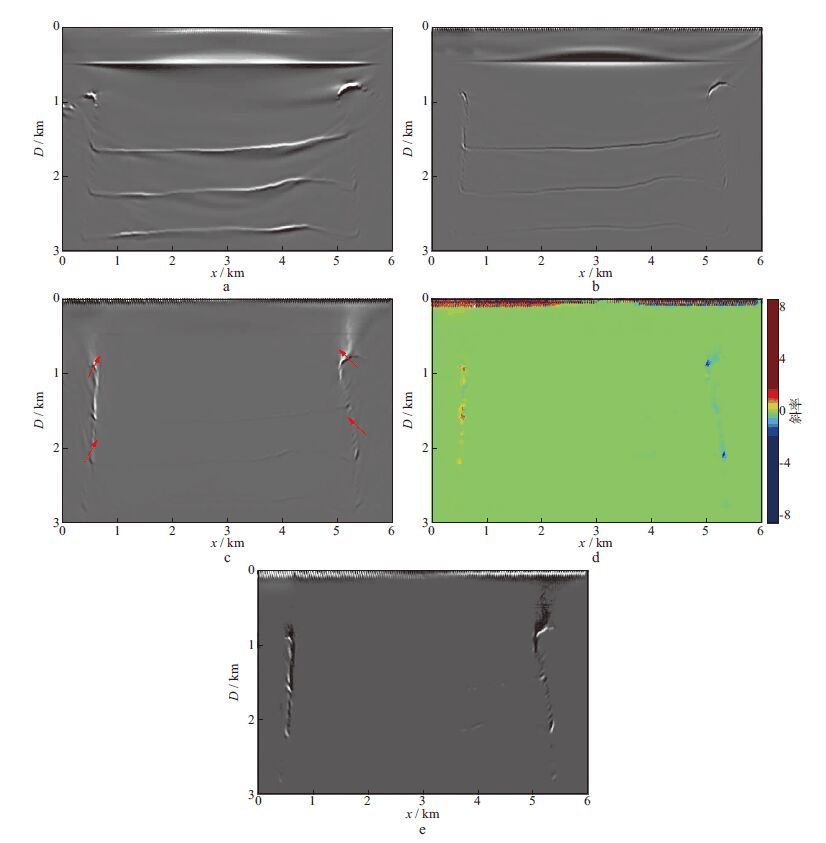
4.2 丘体边界模型为了进一步验证本文方法对复杂模型的适应性,针对棱柱波特点设计了更为复杂的丘体边界模型,如图 5所示。模型含有微弱起伏的水平层状构造,在模型左、右两侧各加入一含有陡倾角甚至负倾角的盐丘侵入体,该侵入体的高陡边界为主要成像目标区。模型横向601个采样点,纵向301个采样点,纵、横向间距均为10m。采用声波方程有限差分算法及多轴卷积完全匹配层(MC-PML)边界条件[22-23]得到正演记录。第1炮位于第10个CDP点处,炮间隔为40m,共146炮,每炮601个点接收。记录长度为3s,采样间隔为0.5ms,共6001个采样点。震源子波为Ricker子波,主频为30Hz。图 6为第298个CDP处的单炮记录,由于模型复杂,很难在炮记录上分辨出棱柱波同相轴。以图 7所示速度场(该速度场仅含平滑后的水平反射层信息)作为偏移速度场,采用Poynting矢量上、下行波成像条件对图 6所示单炮记录进行偏移成像,得到的RTM成像剖面如图 8a所示。由图 8a可见,常规RTM很难对盐丘边界等高陡倾角构造进行精确成像。图 8b为经过Laplace滤波后的常规棱柱波成像剖面,图 8c为采用Poynting左、右行波成像条件得到的棱柱波成像剖面。从图 8b和图 8c中均可观察到盐丘边界,说明棱柱波成像对盐丘边界成像效果改善明显。由于图 8c采用的是Poynting矢量分解得到的左、右行波进行成像,在一定程度上压制了水平反射层的能量,盐丘边界更加明显。图 8c对应的倾角估计值如图 8d所示,根据图 8d中的倾角分布,设定合适的阈值进行倾角滤波,倾角滤波后的结果如图 8e所示。由图 8e可见,经过平面波解构以及倾角滤波后,水平反射界面能量基本被滤除(只残留部分高陡倾角反射层),丘体边界得以清晰刻画,虚假成像构造(图 8c中红色箭头处)得到不同程度衰减,最大程度上突出了目标构造,剖面更加清晰。由此可见,棱柱波单独成像及其优化算子能有效提高对丘体边界等高陡构造的成像精度,有利于后期精确地质定位和构造解释。
|
图 5 丘体边界模型 |
|
图 6 对丘体边界模型正演得到的单炮记录 |
|
图 7 对丘体边界模型单炮记录进行偏移采用的速度场 |
|
图 8 丘体边界模型棱柱波成像结果 |
常规逆时偏移虽然可以对棱柱波进行成像,但是对速度场的要求较高,常规速度分析得到的速度场很难满足其要求。为了充分利用棱柱波信息,本文对棱柱波的产生以及数学表达进行了详细推导,最终形成了一套改进的更为有效的棱柱波成像流程:首先利用上、下行波成像水平同相轴,然后利用成像结果模拟波场(与最小二乘偏移方法类似),进而利用左、右行波成像条件加强高陡构造的成像能量,最后通过剖面倾角滤波进一步优化成像结果。简单倒T模型与复杂丘体边界模型的成像试算验证了本文棱柱波单独成像方法的正确性及优化算子(Poynting矢量及平面波解构滤波)的有效性。
棱柱波成像剖面可作为一次反射波成像剖面的辅助解释剖面,能在一定程度上提高解释的精度,尤其是高陡构造的精确刻画。单独成像棱柱波的优势在于降低了成像方法对初始速度场的依赖程度,无需速度场中包含高陡构造边界,仍然可以利用棱柱波所携带的陡倾角构造信息,对高陡构造进行正确成像。但是该方法仍然存在一些缺点:①计算时间与内存是常规逆时偏移的两倍,增加了计算量;②复杂构造区域波场过于复杂,Poynting矢量成像条件对高陡构造的改善效果有限(水平反射层压制不彻底);③本文方法属于常规成像范畴。下一步将引入反演思想及编码思想,进一步发展保幅且高效的棱柱波成像方法。
| [1] |
HALE D, HILL N R, STEFANI J. Imaging salt with turning seismic waves[J].
Geophysics , 1992, 57 (11) : 1453-1462 DOI:10.1190/1.1443213 ( 0) 0)
|
| [2] |
范贵良. 山前高陡构造区地震成图方法研究[J].
石油物探 , 2000, 39 (3) : 16-25 FAN G L. A study of seismic mapping in frontlands of hills with steeply dipping structures[J].
Geophysical Prospecting for Petroleum , 2000, 39 (3) : 16-25 ( 0) 0)
|
| [3] |
黄锐. 川东北碳酸盐岩地区地震勘探技术难点与对策[J].
石油物探 , 2008, 47 (5) : 476-482 HUANG R. Technical difficulties in and countermeasures for seismic exploration in the carbonate area of northeast Sichuan basin[J].
Geophysical Prospecting for Petroleum , 2008, 47 (5) : 476-482 ( 0) 0)
|
| [4] |
方伍宝, 张兵. 单程波外推高陡倾角反射成像技术的应用研究[J].
石油物探 , 2009, 48 (5) : 488-492 FANG W B, ZHANG B. Application of reflection imaging technology with one-way wave extrapolation in high and steep structure[J].
Geophysical Prospecting for Petroleum , 2009, 48 (5) : 488-492 ( 0) 0)
|
| [5] |
HAWKINS K. The challenge presented by North Sea central graden salt domes to all DMO algorithms[J].
First Break , 1994, 12 (6) : 327-343 ( 0) 0)
|
| [6] |
DAI W.Multisource least-squares migration and prism wave reverse time migration[D].America:The University of Utah,2012
http://utam.gg.utah.edu/UTAMtheses/Wei.Dai/WeiDai_Utah_dissertation_Nov19_2012.pdf ( 0) 0)
|
| [7] |
CAVALCA M, LAILLY P. Prismatic reflections for the delineation of salt bodies[J].
Expanded Abstracts of 75th Annual Internat SEG Mtg , 2005 : 2550-2553 ( 0) 0)
|
| [8] |
MARMALYEVSKYY N, ROGANOV Y, GORNYAK Z, et al. Migration of duplex waves[J].
Expanded Abstracts of 75th Annual Internat SEG Mtg , 2005 : 2025-2028 ( 0) 0)
|
| [9] |
MALCOLM A E, URSIN B, MAARTEN V. Seismic imaging and illumination with internal multiples[J].
Geophysical Journal International , 2009, 176 (3) : 847-864 DOI:10.1111/gji.2009.176.issue-3 ( 0) 0)
|
| [10] |
JONES I F, GOODWIN M C, BERRANGER I D, et al. Application of anisotropic 3D reverse time migration to complex North Sea imaging[J].
Expanded Abstracts of 77th Annual Internat SEG Mtg , 2007 : 2140-2144 ( 0) 0)
|
| [11] |
LIU F, ZHANG G, MORTON S A, et al. An effective imaging condition for reverse-time migration using wavefield decomposition[J].
Geophysics , 2011, 76 (1) : S29-S39 DOI:10.1190/1.3533914 ( 0) 0)
|
| [12] |
LI Y, AGNIHOTRI Y, DY T. Prismatic wave imaging with dual flood RTM[J].
Expanded Abstracts of 81st Annual Internat SEG Mtg , 2011 : 3290-3294 ( 0) 0)
|
| [13] |
CHEN T, HE B S. A normalized wavefield separation cross-correlation imaging condition for reverse time migration based on Poynting vector[J].
Applied Geophysics , 2014, 11 (2) : 158-166 DOI:10.1007/s11770-014-0441-5 ( 0) 0)
|
| [14] |
王保利, 高静怀, 陈文超, 等. 逆时偏移中用Poynting矢量高效地提取角道集[J].
地球物理学报 , 2013, 56 (1) : 262-268 WANG B L, GAO J H, CHEN W C, et al. Extracting efficiently angle gathers using Poynting vector during reverse time migration[J].
Chinese Journal of Geophysics , 2013, 56 (1) : 262-268 ( 0) 0)
|
| [15] |
FOMEL S. Applications of plane-wave destruction filters[J].
Geophysics , 2002, 67 (6) : 1946-1960 DOI:10.1190/1.1527095 ( 0) 0)
|
| [16] |
黄建平, 李振春, 孔雪, 等. 基于PWD的绕射波波场分离成像方法综述[J].
地球物理学进展 , 2012, 27 (6) : 2499-2510 HUANG J P, LI Z C, KONG X, et al. The review of the wave field separation method about reflection and diffraction based on the PWD[J].
Progress in Geophysics , 2012, 27 (6) : 2499-2510 ( 0) 0)
|
| [17] |
孔雪, 李振春, 黄建平, 等. 基于平面波记录的绕射目标成像方法研究[J].
石油地球物理勘探 , 2012, 47 (4) : 674-681 KONG X, LI Z C, HUANG J P, et al. Diffraction objective imaging based on plane wave record[J].
Oil Geophysical Prospecting , 2012, 47 (4) : 674-681 ( 0) 0)
|
| [18] |
BEYLKIN G. Imaging of discontinuities in the inverse scattering problem by inversion of a causal generalized Radon transform[J].
Journal of Mathematical Physics , 1985, 26 (1) : 99-108 DOI:10.1063/1.526755 ( 0) 0)
|
| [19] |
STOLT R H, BENSON A K. Seismic migration:theory and practice[J].
Acoustical Society of America Journal , 1987, 81 (5) : 1651-1652 ( 0) 0)
|
| [20] |
POYNTING J H. On the transfer of energy in the electromagnetic field[J].
Philosophical Transactions of the Royal Society of London , 1884, 175 : 343-361 DOI:10.1098/rstl.1884.0016 ( 0) 0)
|
| [21] |
YOON K, MARFURT K J. Reverse-time migration using the Poynting vector[J].
Exploration Geophysics , 2006, 37 (1) : 102-107 DOI:10.1071/EG06102 ( 0) 0)
|
| [22] |
黄建平, 杨宇, 李振春, 等. 几种自由边界实施方法在完全匹配层条件下的对比研究[J].
地震学报 , 2014, 36 (5) : 964-977 HUANG J P, YANG Y, LI Z C, et al. Comparative study among implementations of several free-surface boundaries with perefectly matched layer conditions[J].
Acta Seismologica Sinica , 2014, 36 (5) : 964-977 ( 0) 0)
|
| [23] |
田坤, 黄建平, 李振春, 等. 多轴卷积完全匹配层吸收边界条件[J].
石油地球物理勘探 , 2014, 49 (1) : 143-152 TIAN K, HUANG J P, LI Z C, et al. Multi-axial convolution perfectly matched layer absorption boundary condition[J].
Oil Geophysical Prospecting , 2014, 49 (1) : 143-152 ( 0) 0)
|


