2. 西南石油大学地球科学与技术学院, 四川 成都 610500;
3. 中国石油化工股份有限公司西南油气分公司, 四川 成都 610041;
4. 中国石油化工股份有限公司多波地震技术重点实验室, 四川 成都 610041
2. School of Geoscience and Technology,Southwest Petroleum University, Chengdu 610500, China;
3. Sinopec Southwest Company, Chengdu 610041, China;
4. Sinopec Key Laboratory of Multi Components Seismic Technology, Chengdu 610041, China
地震波在传播过程中, 转换波(P-SV)相对纵波(P-P)具有传播速度低、吸收衰减大、能量相对较弱、低速带厚度不一致、传播路径不相同等特点, 转换波的表层静校正量更大, 变化更加复杂, 导致P-SV波静校正量通常是相同位置P-P波静校正量的数倍, P-SV波静校正量难以准确估计; 转换波记录信噪比通常较低, 初至附近P-P波折射、P-SV波折射等信息混杂在一起, 使得P-SV波初至不易分辨, 难以拾取, 这些难点造成了转换波静校正处理问题突出。
在P-SV波静校正处理过程中, 由于炮点静校正量是通过P-P波静校正处理得到, 因此难点是求取P-SV波检波点静校正量。实际资料处理多利用P-P波静校正量中的检波点静校正量乘以一个系数来获取P-SV波检波点静校正量。虽然此方法能够提高转换波资料的成像质量, 但是, 由于求得的转换波检波点静校正量精度不够, 会导致转换波资料处理成果中经常出现假构造现象, 且在低信噪比地区还可能出现无法成像的情况。
针对转换波静校正的特点, 前人进行了大量研究, 并提出了很多方法。杨海申等[1]提出利用转换波与纵波初至的互相关函数叠加结果来推测转换波初至位置的算法为转换波初至拾取方法提供了新的思路。这种算法在转换波初至特别清晰的时候, 可以大体上确定出转换波初至的位置, 在这个大体位置附近使用手工拾取精确的转换波初至。潘树林等[2]总结出转换波初至判定的标准, 提出使用初至叠加法确定转换波初至, 并用τ-p变换自动拾取转换波初至的思路。该算法提出在CRP(共检波点)道集中使P-P-SV波(P波入射, 在折射界面上以P波速度滑行, 然后以SV波形式出射)同相折射初至能量通过叠加得到增强, 而其它信息能量被衰减, 从而分辨出P-P-SV波折射初至。
虽然转换波静校正方法较多[3-7], 但是, 目前仍然没有一套能够适用于实际生产的转换波表层静校正技术。基于此, 结合纵波和转换波的特点, 提出了一种新的多波联合的转换波折射静校正技术, 以求解转换波检波点静校正量。该方法利用成熟的纵波折射波(P-P-P波, 即P波入射, 在折射界面上以P波速度滑行, 然后以P波形式出射)静校正技术, 求取较准确的折射层厚度和纵波检波点延迟时, 并结合共检波点初至叠加技术和P-P-SV波延迟时差法, 求解转换波检波点静校正量[8-12]。该技术应用于转换波实际资料处理, 能够提高转换波检波点静校正量精度, 改善转换波资料成像质量, 构造形态更加真实[13-19]。
1 多波联合的转换波折射静校正基本方法分析P-P-P折射波初至延迟时法静校正技术、P-P-SV折射波共检波点初至叠加技术以及P-P-SV折射波延迟时差法的方法原理, 并以这3种方法为基础, 进行多波联合的转换波折射静校正。
1.1 P-P-P折射波初至延迟时法静校正技术延迟时是指地震波从激发点经折射界面滑行传播到接收点所用的时间相对于地震波从激发点直接以折射层速度传播到接收点所用的时间差。这个延迟时可以分解为炮点延迟时和检波点延迟时[3]。
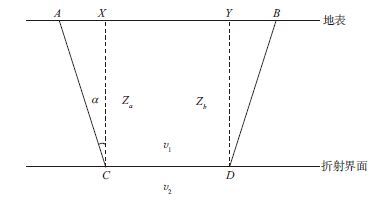
如图 1所示, 设A为炮点, B为检波点, A点和B点的表层厚度分别为Za和Zb, 临界角为α, 则A点激发, B点接收到的折射初至时间为:
| ${{T}_{AB}}=\frac{{{Z}_{a}}cos\alpha }{{{v}_{1}}}+\frac{\overline{AB}}{{{v}_{2}}}+\frac{{{Z}_{b}}cos\alpha }{{{v}_{1}}}$ | (1) |
|
图 1 折射模型 |
检波点延迟时间为:
| ${{d}_{P}}=\frac{{{Z}_{b}}cos\alpha }{{{v}_{1}}}$ | (2) |
对工区内有效的炮点-检波点对, 建立一个超大规模的、超定的方程组, 解这个方程组, 得到检波点延迟时(dP)、检波点处的折射层厚度(Zb, 即B点的表层厚度)和纵波折射波速度(v1)。
1.2 P-P-SV折射波共检波点初至叠加技术对多个水平层或倾斜界面情况下的P波和P-SV波的折射波时距曲线进行推导, 发现P-P-P折射波和P-P-SV折射波的时距曲线在同一构造下曲线斜率相同, 即在同一构造下两者相互平行。
基于以上发现, 利用共检波点初至叠加技术确定纵波初至与转换波初至时差(Δt), 具体过程为:
1) 首先将转换波记录所对应纵波分量的P-P-P折射初至波进行准确拾取;
2) 将拾取到的初至, 应用于对应的P-SV波记录上, 所有初至水平校正至某个时间点, 记录为T0;
3) 将P-SV波中的每一道使用对应的移动量进行校正, 移动量为P-P-P折射初至时间和某个固定时间与T0的差值;
4) 然后将改变位置之后的P-SV波CRP道集进行叠加;
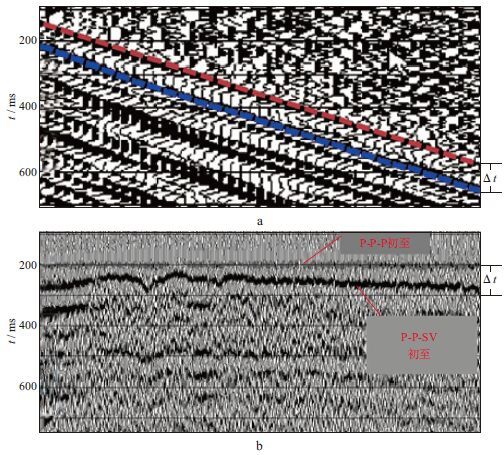
5) 拾取叠加道中能量最强的波峰所对应的时间位置作为P-P-SV折射初至与P-P-P折射初至的时间差。结果如图 2所示。
|
图 2 某地区转换波初至叠加 |
转换波延迟时差法[1]的原理为:转换波检波点延迟时等于转换波与纵波初至时差及纵波检波点延迟时之和。
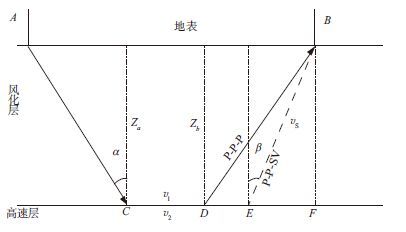
如图 3所示, 从激发点A到接收点B的纵波与转换波初至时间差为:
|
图 3 纵波和转换波初至传播路径 |
| $\begin{align} & \Delta t=[{{T}_{AC}}+{{T}_{CE}}+{{T}_{EB}}\left] - \right[{{T}_{AC}}+{{T}_{CD}}+{{T}_{DB}}] \\ & ={{T}_{DE}}+{{T}_{EB}}-{{T}_{DB}} \\ & ={{T}_{EB}}-{{T}_{EF}}+{{T}_{EF}}+{{T}_{DE}}-{{T}_{DB}} \\ & =\left( {{T}_{EB}}-{{T}_{EF}} \right)-\left( {{T}_{DB}}-{{T}_{DF}} \right) \\ \end{align}$ | (3) |
| ${{d}_{S}}=\Delta t+{{d}_{P}}$ | (4) |
| $\begin{array}{*{35}{l}} {{d}_{P}}={{T}_{DB}}-{{T}_{DF}} \\ {{d}_{S}}={{T}_{EB}}-{{T}_{EF}} \\ \end{array}$ | (5) |
式中:dP为纵波检波点延迟时; dS为转换波检波点延迟时; Δt为转换波与纵波的初至时差。
1.4 多波联合的转换波折射静校正技术 1.4.1 技术思路利用高质量的P-P-P折射波初至信息获得P-P波近地表模型, 以此为基础, 获取高质量的P-P-SV折射波初至信息, 通过建立检波点处P-P-P折射波与P-P-SV折射波的参数转换关系, 获得检波点处P-SV波近地表模型, 从而实现P-SV波基准面静校正。
1.4.2 基本原理利用P-P-P折射波初至延迟时法静校正技术、P-P-SV折射波共检波点初至叠加技术以及P-P-SV折射波延迟时差法分别得到每一折射层检波点处折射层厚度(Zb)、折射层速度(v1)、转换波检波点延迟时(dS)。基于这些信息, 采用多波联合的转换波折射静校正技术综合反演得到每一折射层相应的横波速度(vS)。
| $\frac{{{v}_{S}}}{{{v}_{1}}}=sin\beta $ | (6) |
| $\frac{{{Z}_{b}}cos\beta }{{{v}_{S}}}={{d}_{S}}$ | (7) |
式中:β为转换波折射角。
联合求解(6)式和(7)式, 可得:
| $tan\beta =\frac{{{Z}_{b}}}{{{d}_{S{{v}_{1}}}}}$ | (8) |
由公式(8), 可知β=arctan[Zb/(dSv1)], 代入(6)式即可求得vS。
当各检波点对应折射层的厚度和横波速度已知, 利用高程静校正技术就可以求解出各检波点转换波静校正量:
| $\Delta t=-\sum\limits_{i=1}^{n}{\frac{{{Z}_{bi}}}{{{v}_{Si}}}}+{{E}_{d}}-({{E}_{g}}-\sum\limits_{i=1}^{n}{{{Z}_{bi}}}){{v}_{c}}$ | (9) |
式中:vc为填充速度,通常根据工区特点给定一个常速度; zbi为第i层的检波点处折射层厚度; vSi为第i层的横波速度; Eg为物理点高程; Ed为固定基准面; Δt为检波点转换波静校正量。
1.4.3 实现方法方法的实现步骤为:
1) 精确拾取P-P波初至信息;
2) 利用P-P波初至信息, 采用纵波折射波静校正技术, 获得P-P-P折射波近地表模型参数, 包括检波点折射层厚度、P-P-P折射波检波点延迟时间、P-P-P折射波折射层速度;
3) 利用P-P波初至信息, 采用P-P-SV波共检波点初至叠加技术, 获得P-P-SV折射波初至与P-P-P折射波初至的时间差值;
4) 利用P-P-SV折射波初至与P-P-P折射波初至的时间差值和P-P-P折射波检波点延迟时间, 采用P-P-SV折射波延迟时差技术, 获得P-P-SV折射波的检波点延迟时间;
5) 结合检波点折射层厚度、P-P-P折射波检波点延迟时间、P-P-P折射波折射层速度、P-P-SV折射波的检波点延迟时间, 采用多波联合的转换波折射静校正技术, 获得P-SV波检波点处的横波速度;
6) 综合以上P-SV波的近地表结构, 利用基于近地表模型的静校正技术可以求解出P-SV波检波点基准面静校正量。
2 实际资料应用利用多波联合的转换波折射静校正技术对某工区3D3C资料进行转换波静校正处理, 该资料共10398炮, 每炮12个排列, 共35322个检波点。资料信噪比较低, 低降速带横向变化剧烈。具体处理过程如下:
1) 首先采用P-P-P折射波初至延迟时法静校正技术对纵波资料进行处理, 得到每个检波点对应折射层的厚度、速度和每个检波点的纵波延迟时间。
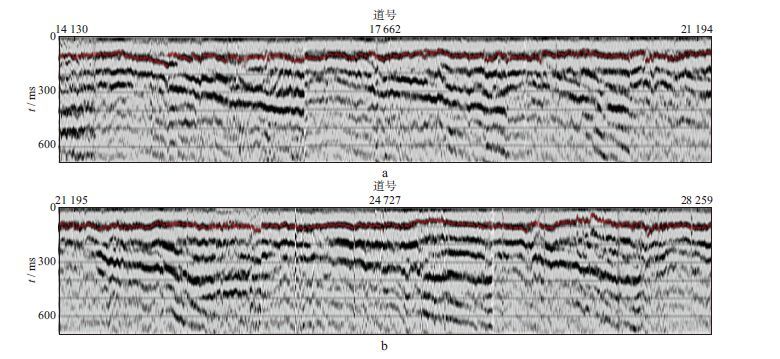
2) 采用P-P-SV折射波共检波点初至叠加技术确定每个检波点的转换波初至时差, 图 4为转换波资料CRP叠加剖面转换波初至时差拾取效果, 可以看出, 初至叠加效果较好, 拉平后的纵波初至时间下方明显出现强能量的转换波初至, 有利于初至拾取。
|
图 4 转换波资料CRP叠加剖面转换波初至时差拾取效果(红线为转换波初至) |
3) 对步骤2)得到的转换波初至时差和纵波检波点延迟时间, 采用P-P-SV折射波延迟时差法求取转换波检波点延迟时间。
4) 最后采用多波联合的转换波折射静校正技术, 结合每个检波点的转换波延迟时间, 及其对应折射层的厚度、速度, 计算出转换波检波点静校正量。
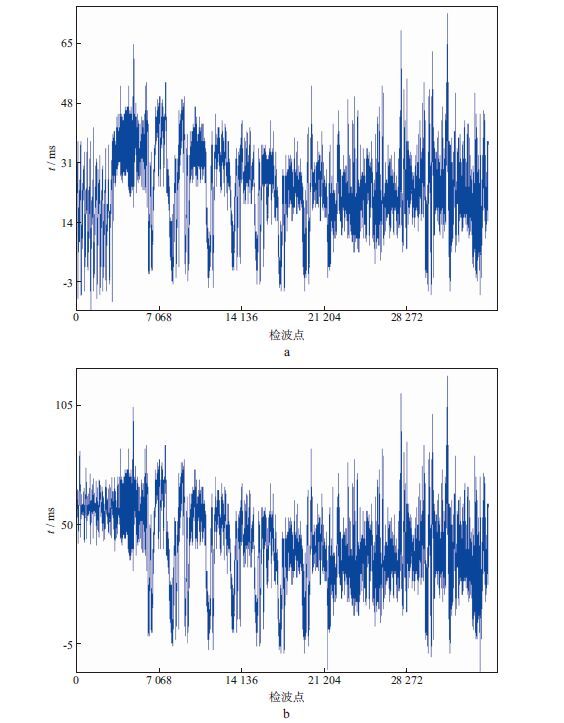
图 5对比了纵波和转换波检波点静校正量。可以看出, 计算出的转换波检波点静校正量分布范围为-19~109ms, 远大于纵波检波点静校正量分布范围(-12~70ms), 并且图 5中静校正量曲线特征与转换波初至时差大致相当, 也与近地表高程特征相符合, 因此可以认为计算出的转换波检波点静校正量正确。
|
图 5 纵波和转换波检波点静校正量对比 |
图 6分别为转换波资料施加转换波初至时差后的远、中、近偏移距炮集和转换波CRP叠加剖面对比图。可以看出, 当施加本方法计算的转换波静校正量后, 转换波炮集的初至更加平滑, 且深层的反射波呈现出双曲线特征, 与P-P-SV折射波基本原理相符, 说明计算出的转换波静校正量是正确的。

|
图 6 转换波资料施加转换波初至时差后的近(a)、中(b)、远(c)偏移距炮集和转换波CRP叠加剖面对比 |
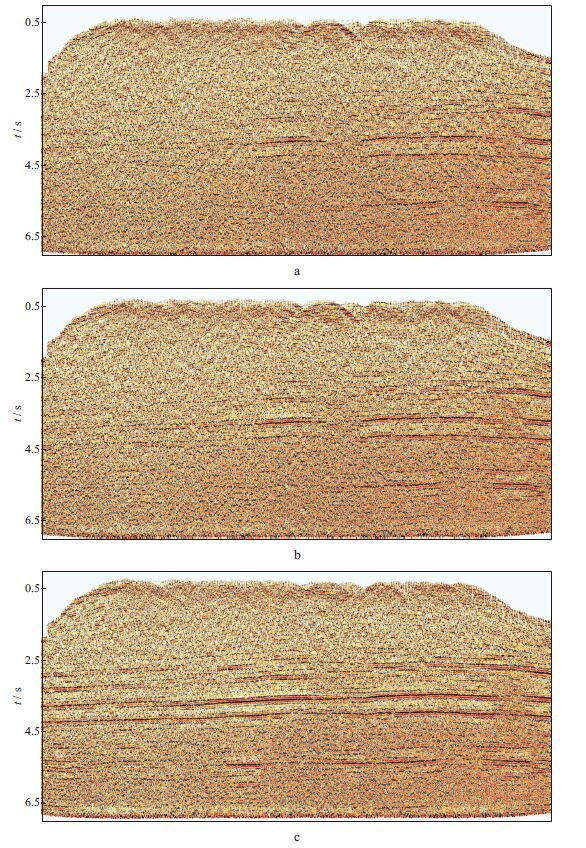
图 7a是施加纵波炮点静校正量的叠加剖面, 可看出, 剖面上构造起伏不大, 但信噪比较低, 成像质量不高; 图 7b是施加纵波炮点静校正量和纵波检波点静校正量的叠加剖面, 可看出, 加入纵波检波点静校正量后, 叠加剖面成像质量有所提高, 但改善程度不大; 图 7c是施加纵波炮点静校正量和转换波检波点静校正量的叠加剖面。比较图 7c和图 7b可以看出, 加入转换波检波点静校正量后的叠加剖面, 浅、中、深层成像质量均得到了改善, 构造特征更加清晰, 没有出现串相位现象, 说明转换波检波点静校正量比纵波检波点静校正量准确。
|
图 7 施加不同静校正量静校正后转换波叠加剖面对比 |
针对转换波静校正处理中转换波资料信噪比低、转换波初至不易分辨和转换波检波点静校正量大等难点, 充分利用纵波折射延迟时静校正、叠加法确定转换波初至时差和转换波延迟时差提取三项技术的优势, 建立了一种新的适用于实际资料处理的多波联合的转换波折射静校正技术。实际地震资料处理效果表明:转换波静校正问题得到了很好的解决, 单炮记录上转换波同相轴连续性增强; 叠加剖面上消除了串相位现象、信噪比明显提高、构造形态更加合理、成像效果显著改善。表明多波联合转换波折射静校正技术具有很好的应用前景。
| [1] |
杨海申, 李彦鹏, 陈海青. 转换波延迟时静校正[J].
石油地球物理勘探 , 2006, 41 (1) : 13-16 YANG H S, LI Y P, CHEN H Q. P-SV converted wave static corrections by delay times[J].
Oil Geophysical Prospecting , 2006, 41 (1) : 13-16 ( 0) 0)
|
| [2] |
潘树林, 高磊, 周熙襄, 等. 一种改进的P-SV转换波静校正方法[J].
石油物探 , 2007, 46 (2) : 143-146 PAN S L, GAO L, ZHOU X X, et al. An improved static correction method of converted P-SV wave[J].
Geophysical Prospecting for Petroleum , 2007, 46 (2) : 143-146 ( 0) 0)
|
| [3] |
MIKE C.反射波地震勘探静校正技术[M].李培明,柯本善,译.北京:石油工业出版社,2004:1-358
( 0) 0)
|
| [4] |
CARY P W, EATON W S. A simple method for resolving large converted wave (P-SV) statics[J].
Geophysics , 1993, 58 (3) : 429-433 DOI:10.1190/1.1443426 ( 0) 0)
|
| [5] |
马昭军, 唐建明. 基于构造时间控制的P-SV波静校正方法[J].
物探化探计算技术 , 2008, 30 (5) : 373-376 MA Z J, TANG J M. A P-SV wave static correction method based on controlling structure time[J].
Computing Techniques for Geophysical and Geochemical Exploration , 2008, 30 (5) : 373-376 ( 0) 0)
|
| [6] |
RICHARD R, VAN D I. Static correction for PS-wave surface seismic surveys,recent advances in shear wave technology for reservoir characterization[J].
SEG/EAGE Summer Research Workshop , 2000 : 233-235 ( 0) 0)
|
| [7] |
FJELLANGER J P, BOEN F, RONNING K J. Successful use of converted wave data for interpretation and well optimization on Grane[J].
Expanded Abstracts of 76th Annual Internat SEG Mtg , 2006 : 1138-1142 ( 0) 0)
|
| [8] |
EDME P, KRAGH E. Near-surface S-wave velocity estimation from P-wave polarization analysis[J].
Expanded Abstracts of 79th Annual Internat SEG Mtg , 2009 : 4289-4292 ( 0) 0)
|
| [9] |
DAVID W E, DON C L. P-SV stacking charts and binning periodicity[J].
Geophysics , 1992, 57 (5) : 745-748 DOI:10.1190/1.1443288 ( 0) 0)
|
| [10] |
ROTHMAN D H. Nonlinear inversion,statistical mechanics,and residual statics estimation[J].
Geophysics , 1985, 50 (12) : 2784-2796 DOI:10.1190/1.1441899 ( 0) 0)
|
| [11] |
RONEN J, CLAERBOUT J F. Surface-consistent residual statics estimation by stack power maximization[J].
Geophysics , 1985, 50 (12) : 2759-2767 DOI:10.1190/1.1441896 ( 0) 0)
|
| [12] |
STEWART R R, GAISER J E, Brown R J, et al. Converted-wave seismic exploration:application[J].
Geophysics , 2003, 68 (1) : 40-57 DOI:10.1190/1.1543193 ( 0) 0)
|
| [13] |
桑运云, 孙军晓, 焦淑萍, 等. 起伏地表下基于抛物插值的最短路径射线追踪[J].
石油物探 , 2014, 53 (2) : 142-148 SANG Y Y, SUN J X, JIAO Y P, et al. Shortest path raytracing based on parabolic traveltime interpolation in irregular topography[J].
Geophysical Prospecting for Petroleum , 2014, 53 (2) : 142-148 ( 0) 0)
|
| [14] |
陈海峰, 李向阳, 赵波, 等. 三维转换波处理技术研究及应用[J].
石油物探 , 2013, 52 (5) : 512-518 CHEN H F, LI X Y, ZHAO B, et al. 3D converted wave seismic data processing technology and its application[J].
Geophysical Prospecting for Petroleum , 2013, 52 (5) : 512-518 ( 0) 0)
|
| [15] |
刘财, 杨庆节, 耿美霞. 多波多分量地震资料速度扫描法转换波识别技术[J].
石油物探 , 2013, 52 (4) : 383-387 LIU C, YANG Q J, GENG M X. P-SV wave identification technique by velocity scanning for multiwave multi-component seismic data[J].
Geophysical Prospecting for Petroleum , 2013, 52 (4) : 383-387 ( 0) 0)
|
| [16] |
刘玉萍, 潘卫国, 丁飞浩, 等. 转换波组合静校正方法应用及效果[J].
地球物理学进展 , 2014, 29 (2) : 805-814 LIU Y P, PAN W G, DING F H, et al. Application and effect of combined static correction method of converted wave[J].
Progress in Geophysics , 2014, 29 (2) : 805-814 ( 0) 0)
|
| [17] |
查文锋, 于小磊. 浅表层结构复杂区静校正的优化选取及应用[J].
地球物理学进展 , 2014, 29 (2) : 958-965 CHA W F, YU X L. The optimal selection and comprehensive application of the static correction in the complex shallow surface structure areas[J].
Progress in Geophysics , 2014, 29 (2) : 958-965 ( 0) 0)
|
| [18] |
陈海峰, 李向阳, 钱忠平, 等. 联合纵波确定转换波接收点大的静校正量[J].
地球物理学进展 , 2014, 29 (1) : 306-311 CHEN H F, LI X Y, QIAN Z P, et al. Estimating C-wave receiver large statics associated with p-wave imaging[J].
Progress in Geophysics , 2014, 29 (1) : 306-311 ( 0) 0)
|
| [19] |
张正峰, 郭建, 韩立国, 等. 基于波场延拓的变换坐标转换波静校正[J].
地球物理学报 , 2013, 56 (5) : 1676-1685 ZHANG Z F, GUO J, HAN L G, et al. Transformation coordination converted wave static correction based on wave field continuation[J].
Chinese Journal of Geophysics , 2013, 56 (5) : 1676-1685 ( 0) 0)
|


