含流体储层地震岩石物理是建立储层物性参数与弹性参数之间关系的纽带, 可以用来指导地震流体识别, 同时也是定量表征含油气储层流体的重要理论基础[1-3]。岩石物理模型的构建有助于计算地下储层岩石的弹性参数, 提高岩石物性参数的反演精度, 进而更好地了解地下含油气储层特征及流体分布规律, 在储层岩性、物性分析以及流体识别分析中发挥着重要的作用[4-14]。
在岩石物理模型构建中, 等效介质理论(如Kuster & Toksöz(K-T)方程、微分等效介质理论等)是计算干岩石骨架等效弹性模量的重要方法。微分等效介质理论(DEM)[15]可以模拟双相混合物的影响, 由于其微分介质方程是耦合的, 一般通过迭代计算数值求解得到干岩石骨架等效弹性模量, 许多学者从不同的角度探讨了其解析解[16-20]。KUSTER等[21]从波散射理论出发, 考虑包裹体体积分数、弹性性质以及形状的影响, 确定了岩石的等效弹性模量, 可以模拟多重孔隙的影响, 但忽略了孔隙之间的相互作用。经过实验数据分析, HAN等[22]指出泥质砂岩的速度对孔隙度和泥质含量敏感。XU等[23]考虑了孔隙度与泥质含量的影响, 结合表征孔隙形状的砂岩与泥岩孔隙纵横比, 提出了一种适用于估算泥质砂岩纵、横波速度的岩石物理模型, 即Xu-White模型。Xu-White模型利用K-T方程[21]与微分等效介质理论[15]通过迭代求解计算干岩石的等效弹性模量, 结合Gassmann方程[24]估算纵、横波速度。KEYS等[19]假设干岩石的泊松比为常数, 在Xu-White模型的基础上得到了干岩石弹性模量的解析表达式, 称为干岩近似, 提高了计算效率, 但其给出的干岩石等效弹性模量表达式计算得到干岩石泊松比是随孔隙度变化的, 并不是常数。
从干岩石体积模量与剪切模量比和孔隙度的关系出发, 结合K-T方程和微分等效介质理论, 推导得到一个新的岩石物理模型。该模型避免了微分等效介质方程的迭代计算, 简化了K-T方程的求解过程。利用数值计算与实验数据对新模型的可行性与合理性进行了测试。应用结果表明, 新模型可以有效地估算泥质砂岩岩石的纵、横波速度。
1 岩石物理模型的构建以测井、实验分析资料为基础, 已知泥质砂岩的矿物组成与体积含量, 利用Voigt-Reuss-Hill(VRH)[25]平均计算岩石基质的体积模量或剪切模量:
| ${{M}_{VRH}}=\frac{{{M}_{V}}+{{M}_{R}}}{2}$ | (1) |
| $\begin{align} & {{M}_{V}}=\sum\limits_{i=1}^{N}{{{f}_{i}}{{M}_{i}}} \\ & \frac{1}{{{M}_{R}}}=\sum\limits_{i=1}^{N}{\frac{{{f}_{i}}}{{{M}_{i}}}} \\ \end{align}$ | (2) |
式中:MVRH为岩石基质的体积模量或剪切模量; MV, MR分别为Voigt上限和Reuss下限; fi和Mi分别为第i种组成成分的体积分数和体积(剪切)模量。
考虑泥质砂岩中孔隙的影响, 根据XU等[23], 将孔隙空间划分为孔隙纵横比较大的砂岩孔隙和孔隙纵横比较小的泥岩孔隙:
| $\varphi ={{\varphi }_{s}}+{{\varphi }_{c}}$ | (3) |
式中:φ表示总孔隙度; φs是砂岩孔隙度; φc是泥岩孔隙度。
利用K-T方程计算干岩石骨架的体积模量或剪切模量:
| ${{K}_{d}}-{{K}_{m}}=\frac{1}{3}({{K}^{'}}-{{K}_{m}})\frac{3{{K}_{d}}+4{{\mu }_{m}}}{3{{K}_{m}}+4{{\mu }_{m}}}\sum\limits_{l=s,c}{{{\varphi }_{l}}{{T}_{iijj}}}({{\alpha }_{l}})$ | (4) |
| $\begin{align} & {{\mu }_{d}}-{{\mu }_{m}}=\frac{{{\mu }^{'}}-{{\mu }_{m}}}{5}\cdot \\ & \frac{6{{\mu }_{d}}({{K}_{m}}+2{{\mu }_{m}})+{{\mu }_{m}}(9{{K}_{m}}+8{{\mu }_{m}})}{5{{\mu }_{m}}(3{{K}_{m}}+4{{\mu }_{m}})}\sum\limits_{l=s,c}{\varphi F({{\alpha }_{l}})} \\ \end{align}$ | (5) |
其中,
| $F\left( \alpha \right)={{T}_{ijij}}\left( \alpha \right)-\frac{{{T}_{iijj}}\left( \alpha \right)}{3}$ | (6) |
式中:Kd, Km和K′分别为干岩石骨架、岩石基质与孔隙包含物的体积模量; μd, μm和μ′分别为相应的剪切模量(对于干岩石, K′=μ′=0); αs和αc为砂岩孔隙与泥岩孔隙的孔隙纵横比; Tijij(α), Tiijj(α)和F(α)为孔隙纵横比α的函数[25]。
K-T方程要求φ/α$\ll $1, 砂岩孔隙与泥岩孔隙纵横比的典型值分别为0.120和0.035, 因此, K-T方程仅仅对低孔隙度适用。XU等[23]将微分等效介质方法应用到K-T方程中, 逐渐增大岩石的孔隙度, 使其满足K-T方程的要求。BERRYMAN[26-27]指出当增大的孔隙度趋于0时, 方程(4)和方程(5)收敛于:
| $\left( 1-\varphi \right)\frac{dK}{d\varphi }=\left( {{K}^{'}}-K \right)\sum\limits_{l=s,c}{{{\upsilon }_{l}}P({{\alpha }_{l}})}$ | (7) |
| $\left( 1-\varphi \right)\frac{d\mu }{d\varphi }=\left( {{\mu }^{'}}-\mu \right)\sum\limits_{l=s,c}{{{\upsilon }_{l}}Q({{\alpha }_{l}})}$ | (8) |
式中:K和μ分别是孔隙度为φ时的体积模量与剪切模量; υs和υc分别为砂和泥占岩石基质的体积分数, 与砂岩孔隙度、泥岩孔隙度有关。
极化因子P和Q通过标量A, B和R依赖于K, μ, 因此方程(7)和方程(8)是耦合的非线性微分方程, 其解要经过迭代过程数值计算得到。标量A, B和R的表达式为:
| $\begin{matrix} A=\frac{{{\mu }^{'}}}{\mu }-1 \\ B=13\left( \frac{{{K}^{'}}}{K}-\frac{{{\mu }^{'}}}{\mu } \right) \\ R=\frac{3\mu }{3K+4\mu } \\ \end{matrix}$ | (9) |
对于干岩石, 有K′=μ′=0, 则A=-1, B=0。
根据LI等[28], 干岩石模量比与孔隙度的关系为:
| $\frac{{{K}_{d}}}{{{\mu }_{d}}}=\frac{{{K}_{m}}}{{{\mu }_{m}}}\frac{{{\left( 1-\varphi \right)}^{a}}}{1+\frac{b}{a}\frac{{{K}_{m}}}{{{\mu }_{m}}}-\frac{b}{a}\frac{{{K}_{m}}}{{{\mu }_{m}}}{{\left( 1-\varphi \right)}^{a}}}$ | (10) |
式中:a, b分别为截距和梯度, 满足P-Q=a+bKd/μd。在φ=0处对(10)式进行泰勒展开, 取其一阶近似, 有:
| $\frac{{{K}_{d}}}{{{\mu }_{d}}}=m\varphi +n$ | (11) |
式中:m=-(Km/μm)[a+b(Km/μm)]为(10)式在φ=0处泰勒展开式的一阶系数, 与孔隙形状和岩石基质模量比有关; n=Km/μm; φ为孔隙度。以石英作为岩石基质, 体积模量为37GPa, 剪切模量为45GPa, 计算不同孔隙度与孔隙纵横比下干岩石模量比及其一阶近似值, 如表 1所示。孔隙纵横比较大时, 干岩石模量比与其近似值在较大孔隙度范围内吻合良好; 孔隙纵横比较小时, 其吻合程度在较小孔隙度范围内较好。对于实际地层来说, 对(11)式取一阶近似可以比较合理地描述干岩石模量比与孔隙度的关系。
| 表 1 不同孔隙度(φ)与孔隙纵横比(α)下干岩石模量比及其一阶近似值 |
根据李宏兵等[20], 当岩石中含有多种孔隙时, a和b可以表示为:
对于干岩石, 考虑双重孔隙, 令
| $\left( 1-\varphi \right)\frac{dK}{d\varphi }=-KP$ | (12) |
| $\left( 1-\varphi \right)\frac{d\mu }{d\varphi }=-\mu Q$ | (13) |
将(11)式代入极化因子P和Q的表达式, 经过一系列代数运算(见附录A), 可以得到极化因子P和Q近似表示式:
| $P={{P}^{0}}+{{P}^{1}}\varphi $ | (14) |
| $Q={{Q}^{0}}+{{Q}^{1}}\varphi $ | (15) |
将方程(14)和方程(15)分别代入方程(12)和方程(13)中, 由于极化因子P, Q与Kd, μd无关, 经过积分求解可以得到干岩石体积模量与剪切模量:
| ${{K}_{d}}={{K}_{m}}{{\left( 1-\varphi \right)}^{({{P}^{0}}+{{P}^{1}})}}{{e}^{{{P}^{1}}\varphi }}$ | (16) |
| ${{\mu }_{d}}={{\mu }_{m}}{{\left( 1-\varphi \right)}^{({{Q}^{0}}+{{Q}^{1}})}}{{e}^{{{Q}^{1}}\varphi }}$ | (17) |
式中:P0, P1, Q0, Q1为与孔隙度、孔隙纵横比有关的系数。当m=0时, P1=0, Q1=0, 此时得到的干岩石等效体积模量与剪切模量分别为K(φ)=Km·(1-φ)P0, μ(φ)=μm(1-φ)Q0。当m=0时, 干岩石模量比不随孔隙度变化, 即干岩石泊松比不随孔隙度变化, 此时得到的干岩石等效体积模量与剪切模量和KEYS等[19]给出的干岩石体积模量与剪切模量表达式一致。
得到干岩石骨架弹性模量后, 通过Gassmann方程[24]可以计算饱和岩石体积模量与剪切模量:
| ${{K}_{sat}}={{K}_{d}}+\frac{{{\left( 1-\frac{{{K}_{d}}}{{{K}_{m}}} \right)}^{2}}}{\frac{\varphi }{{{K}_{f}}}+\frac{1-\varphi }{{{K}_{m}}}-\frac{{{K}_{d}}}{K_{m}^{2}}}$ | (18) |
| ${{\mu }_{sat}}={{\mu }_{d}}$ | (19) |
式中:Ksat和μsat分别为饱和岩石体积模量与剪切模量; Kf为孔隙流体体积模量, 由Wood公式[25]给出, 即
首先以石英作为岩石基质, 假设包含物为两种不同形状的孔隙, 比较分析微分等效方程数值解与本文导出的解析解。基质石英的体积模量与剪切模量取为37GPa, 44GPa, 两种孔隙的纵横比设为0.12, 0.01。纵横比为0.01的孔隙体积分数分别为10%, 20%和40%, 分析其对岩石等效弹性模量的影响。微分等效方程(12)和方程(13)数值解采用四阶龙格-库塔法计算得到。数值模拟结果如图 1所示。
|
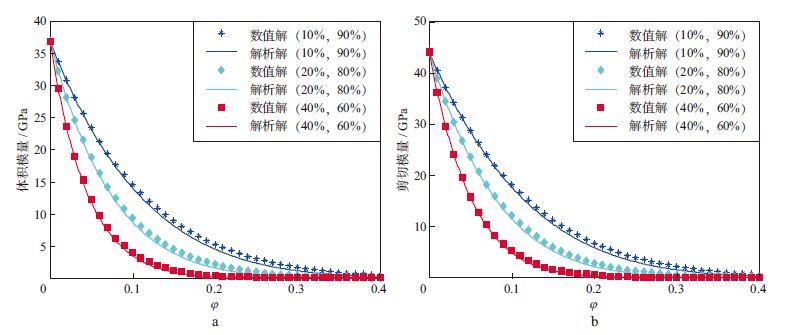
图 1 不同孔隙体积分数下体积模量(a)和剪切模量(b)的数值解与解析解结果对比 |
图 1中, 点线表示微分等效方程数值解, 实线表示由本文导出的新模型计算的解析结果。模拟结果显示, 对于干岩石体积模量和剪切模量, 在3种不同孔隙体积分数情况下, 本文导出的解析解与微分方程的数值解基本吻合, 干岩石的等效弹性模量随着低纵横比孔隙的体积分数增大而减小。
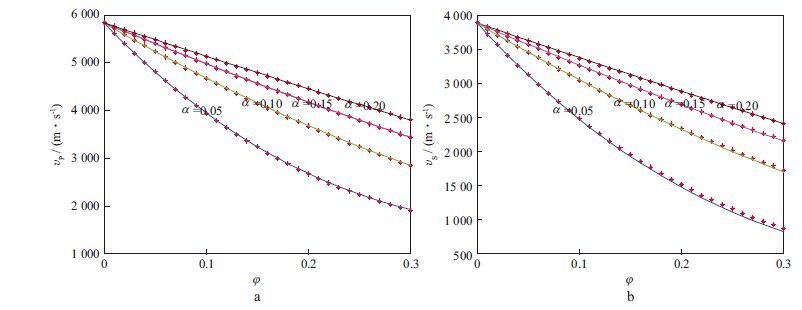
在上述岩石基质条件下, 假设包含物为单一形状的孔隙, 比较本文导出的岩石物理模型与常规Xu-White模型的精度, 模拟结果如图 2所示。不同孔隙纵横比下, 本文模型估算的纵、横波速度与Xu-White模型计算结果吻合良好。
|
图 2 不同孔隙纵横比下常规Xu-White模型(实线)与本文新模型(红色星号线)预测的纵(a)、横(b)波速度 |
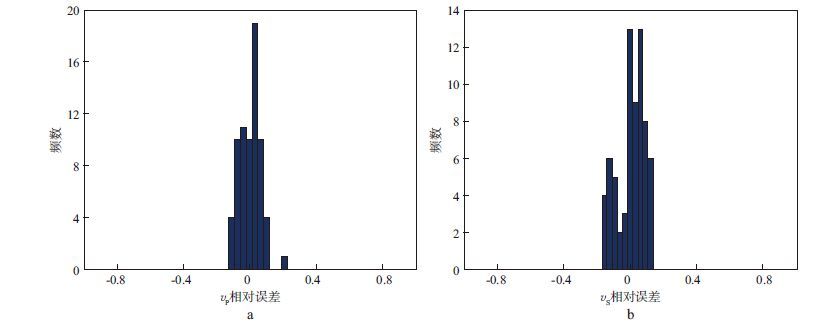
利用HAN等[22]在有效压力40MPa下测量的干燥岩石数据来分析新的岩石物理模型在速度估算方面的应用效果。砂岩样品的孔隙度为5%~30%, 粘土含量为0~50%。分析过程中, 石英矿物的剪切模量和体积模量分别为40GPa和44GPa, 粘土矿物的剪切模量和体积模量分别为7GPa和21GPa。采用Voigt-Reuss-Hill平均方法计算泥质砂岩岩石基质的体积模量与剪切模量[25]。图 3显示了计算的纵、横波速度与实测纵、横波速度的相对误差分布。从图 3可以看到, 纵、横波速度相对误差都在20%以内, 且集中分布在0附近, 说明新得到的岩石物理模型可以有效地计算泥质砂岩的纵、横波速度。
|
图 3 纵(a)、横(b)波速度计算值与实测值的相对误差分布 |
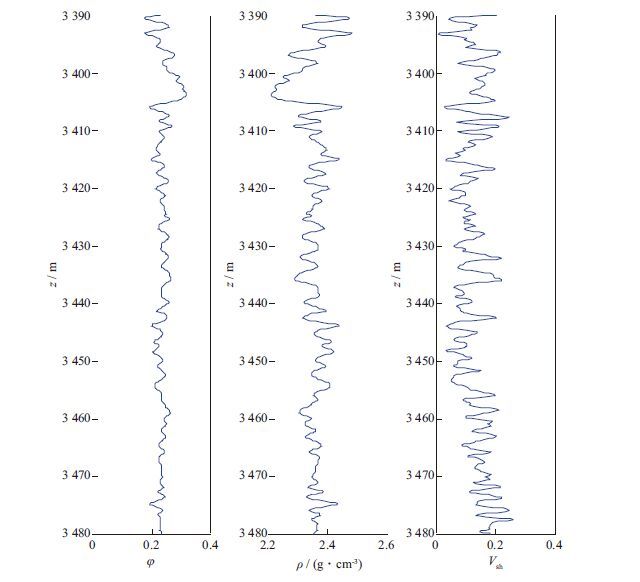
利用新的岩石物理模型对某口常规砂泥岩井资料进行横波速度估算。在已知的测井资料与实验室测量数据基础上, 利用新得到的岩石物理模型计算干岩石骨架弹性模量, 通过Gassmann方程进行流体替换得到饱和岩石弹性模量, 进而计算纵、横波速度。在计算过程中, 砂岩的体积模量与剪切模量分别为Ks=37GPa, μs=44GPa, 泥岩的体积模量与剪切模量分别为Ksh=21GPa, μsh=7GPa, 孔隙度(φ)、泥质含量(Vsh)与含水饱和度(Sw)等物性参数由测井曲线给出(图 4)。与实测纵波速度进行对比, 利用模拟退火算法调整输入参数, 迭代计算, 优化孔隙度, 最终得到横波速度。
|
图 4 孔隙度、密度与泥质含量测井曲线 |
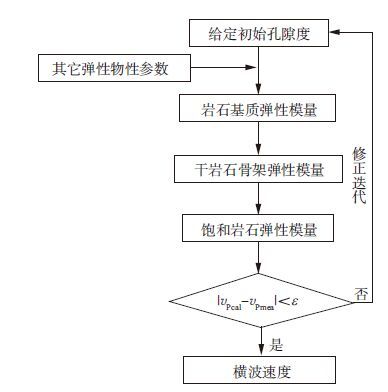
横波速度估算流程如图 5所示, 主要计算步骤如下。
|
图 5 横波速度估算流程 |
1) 给定初始孔隙度φ。
2) 结合砂岩与泥岩弹性模量和泥质含量、饱和度等物性参数, 利用VRH平均模型计算岩石基质弹性模量、Wood公式估算孔隙流体弹性模量。
3) 由新推导的岩石物理模型计算干岩石骨架弹性模量, 通过Gassmann流体替换计算饱和岩石弹性模量。
4) 计算纵波速度vPcal(Ks, μs, Ksh, μsh, φ, Vsh, Sw), 与实际测井纵波速度vPmea建立迭代格式, 即:|vPcal(Ks, μs, Ksh, μsh, φ, Vsh, Sw)-vPmea|<ε, ε为一极小的常数; 利用模拟退火算法逐渐修正孔隙度寻找最优解, 反演得到最优孔隙度。
5) 利用反演的孔隙度, 通过步骤2)和步骤3)计算横波速度。
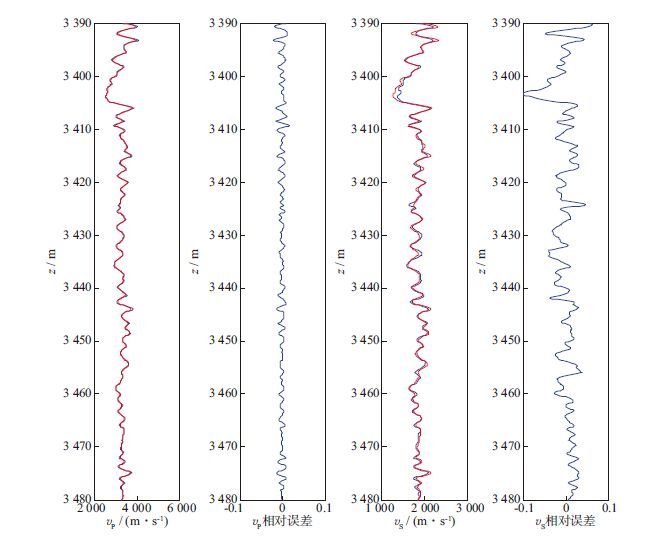
横波速度估算结果如图 6所示, 图中蓝色曲线为测井得到的纵、横波速度, 红色曲线为新模型估算得到的纵、横波速度。由图 6可见, 估算的横波速度与实测的横波速度吻合较好, 两者的变化趋势基本一致, 横波速度相对误差基本在5%以内, 表明新得到的岩石物理模型比较合理。
|
图 6 实测纵、横波速度(蓝色曲线)与预测纵、横波速度(红色曲线)及其相对误差 |
通过对干岩石模量比与孔隙度关系的近似简化, 得到极化因子与孔隙度的线性关系, 结合Kuster & Toksöz方程和微分等效介质理论, 推导得到一个新的岩石物理模型。该方法避免了微分等效介质方法的迭代计算, 简化了K-T方程的求解过程, 因此可以提高计算效率, 但要求孔隙满足稀疏分布条件。该模型综合考虑了泥质砂岩中矿物基质、孔隙度、孔隙纵横比与泥质含量对干岩石弹性模量的影响, 且与包含物添加的顺序无关。数值模拟分析结果表明, 新的岩石物理模型可以较准确地计算干岩石骨架的弹性模量。实验数据与实际资料应用结果表明, 该模型可以较好地估算泥质砂岩的纵、横波速度。
附录A 极化因子近似表达式的推导根据BERRYMAN[27], 极化因子P和Q的表达式为:
| $\begin{align} & P=\frac{1}{3}{{T}_{iijj}}=\frac{{{F}_{1}}}{{{F}_{2}}} \\ & Q=\frac{1}{5}\left( {{T}_{iijj}}-\frac{1}{3}{{T}_{iijj}} \right) \\ \end{align}$ | (A1) |
干岩石模量比与孔隙度之间的线性关系表示为:
| $x={{K}_{d}}/{{\mu }_{d}}=m\varphi +n$ | (A2) |
式中:φ为孔隙度。
极化因子P和Q对孔隙度φ的一阶导数为:
| ${{P}^{'}}=\frac{F_{1}^{'}{{F}_{2}}-{{F}_{1}}F_{2}^{'}}{F_{2}^{2}}$ | (A3) |
| $\begin{align} & {{Q}^{'}}=\frac{1}{5}\left[ \frac{-2F_{3}^{'}}{F_{3}^{2}} \right.+\frac{-F_{4}^{'}}{F_{4}^{2}}+\frac{F_{5}^{'}{{F}_{2}}-{{F}_{5}}F_{2}^{'}}{F_{2}^{2}}+\frac{F_{6}^{'}{{F}_{7}}+{{F}_{6}}F_{7}^{'}-F_{8}^{'}{{F}_{9}}-{{F}_{8}}F_{9}^{'}}{{{F}_{2}}{{F}_{4}}} \\ & -{{\left. \frac{({{F}_{6}}{{F}_{7}}-{{F}_{8}}{{F}_{9}})(F_{2}^{'}{{F}_{4}}+{{F}_{2}}F_{4}^{'})}{({{F}_{2}}{{F}_{4}})} \right]}^{2}} \\ \end{align}$ | (A4) |
对于干岩石, 式中F1′, F2′, F3′, F4′, F5′, F6′, F7′, F8′, F9′分别为F1, F2, F3, F4, F5, F6, F7, F8, F9对孔隙度的一阶导数, 其表达式为:
| $\begin{array}{*{35}{l}} ~{{F}_{1}}=\frac{3}{2}f+\frac{5}{2}\theta -\frac{4}{3}R+1-\frac{3}{2}f-\frac{3}{2}\theta \\ {{F}_{1}}^{\prime }=\left( \frac{3f+5\theta }{2}-\frac{4}{3} \right){{R}^{\prime }} \\ \end{array}$ | (A5) |
| $\begin{align} & {{F}_{2}}=(2f-2\theta +4{{\theta }^{2}}){{R}^{2}}+(2\theta -2f-3{{\theta }^{2}})R~ \\ & {{F}_{2}}\prime =(4f-4\theta +8{{\theta }^{2}})RR\prime +(2\theta -2f-3{{\theta }^{2}})R\prime \\ \end{align}$ | (A6) |
| $\begin{array}{*{35}{l}} {{F}_{3}}=-\left( f+\theta \right)R+\left( f+\frac{3}{2}\theta \right) \\ {{F}_{3}}\prime =-\left( f+\theta \right)R\prime \\ \end{array}$ | (A7) |
| $\begin{array}{*{35}{l}} {{F}_{4}}=\left( \frac{f-\theta }{4} \right)R+\left( 1-\frac{f+3\theta }{4} \right) \\ {{F}_{4}}\prime =\left( \frac{f-\theta }{4} \right){{R}^{'}} \\ \end{array}$ | (A8) |
| $\begin{array}{*{35}{l}} {{F}_{5}}=-\left( f+\theta -\frac{4}{3} \right)R+f \\ {{F}_{5}}\prime =\left( f+\theta -\frac{4}{3} \right){{R}^{'}} \\ \end{array}$ | (A9) |
| $\begin{array}{*{35}{l}} {{F}_{6}}=\left( f+\theta \right)R-f \\ {{F}_{6}}\prime =\left( f+\theta \right){{R}^{'}} \\ \end{array}$ | (A10) |
| $\begin{array}{*{35}{l}} {{F}_{7}}=\left( \frac{3f+5\theta }{4} \right)R+\left( 2-\frac{3f+9\theta }{4} \right) \\ {{F}_{7}}\prime =\left( \frac{3f+5\theta }{4} \right){{R}^{'}} \\ \end{array}$ | (A11) |
| $\begin{array}{*{35}{l}} {{F}_{8}}=\left( 2-\frac{f+5\theta }{2} \right)R+\left( \frac{3\theta +f}{2}-1 \right) \\ {{F}_{8}}\prime =\left( 2-\frac{f+5\theta }{2} \right)R\prime \\ \end{array}$ | (A12) |
| $\begin{array}{*{35}{l}} {{F}_{9}}=\left( \theta -f \right)R+f \\ {{F}_{9}}\prime =\left( \theta -f \right)R\prime \\ \end{array}$ | (A13) |
式中:R为干岩石模量比的函数; R′为其对孔隙度的一阶导数; f和θ为孔隙纵横比α的函数表达式。
| $\begin{align} & R=\frac{3\mu }{3K+4\mu }=\frac{3}{3x+4} \\ & {{R}^{\prime }}=\frac{-9}{{{\left( 3x+4 \right)}^{2}}}{{x}^{\prime }} \\ & {{x}^{\prime }}=m \\ \end{align}$ | (A14) |
| $\begin{array}{*{35}{l}} f=\frac{{{\alpha }^{2}}}{1-{{\alpha }^{2}}}\left( 3\theta -2 \right) \\ \theta =\frac{\alpha }{{{\left( 1-{{\alpha }^{2}} \right)}^{\frac{2}{3}}}}\left[ co{{s}^{-1}}\alpha -\alpha \right]{{\left( 1-{{\alpha }^{2}} \right)}^{\frac{1}{2}}} \\ \end{array}$ | (A15) |
式中:x′为干岩石模量比对孔隙度的一阶导数。
在φ=0处对极化因子P和Q取泰勒一阶近似, 最后得到:
| $\begin{array}{*{35}{l}} P={{P}^{0}}+{{P}^{1}}\varphi \\ Q={{Q}^{0}}+{{Q}^{1}}\varphi \\ \end{array}$ | (A16) |
式中:P0, Q0分别为φ=0时的极化因子值; P1, Q1分别对应于其一阶导数值。
| [1] |
YIN X Y, ZONG Z Y, WU G C. Research on seismic fluid identification driven by rock physics[J].
Science China Earth Sciences , 2015, 58 (2) : 159-171 DOI:10.1007/s11430-014-4992-3 ( 0) 0)
|
| [2] |
ZONG Z Y, YIN X Y, WU G C. AVO inversion and poroelasticity with P-and S-wave moduli[J].
Geophysics , 2012, 77 (6) : N17-N24 DOI:10.1190/geo2011-0214.1 ( 0) 0)
|
| [3] |
宗兆云, 印兴耀, 吴国忱. 基于叠前地震纵横波模量直接反演的流体检测方法[J].
地球物理学报 , 2012, 55 (1) : 284-292 ZONG Z Y, YIN X Y, WU G C. Fluid identification method based on compressional and shear modulus direct inversion[J].
Chinese Journal of Geophysics , 2012, 55 (1) : 284-292 ( 0) 0)
|
| [4] |
印兴耀, 李超, 张世鑫. 基于双相介质的地震流体识别[J].
中国石油大学学报(自然科学版) , 2013, 37 (5) : 38-43 YIN X Y, LI C, ZHANG S X. Seismic fluid discrimination based on two-phase media theory[J].
Journal of China University of Petroleum (Edition of Natural Science) , 2013, 37 (5) : 38-43 ( 0) 0)
|
| [5] |
叶端南, 印兴耀, 王璞, 等. 砂泥岩储层岩石物理交会模板构建[J].
地球物理学进展 , 2015, 30 (2) : 758-768 YE D N, YIN X Y, WANG P, et al. The build of rock physics cross plot template for sand shale reservoir[J].
Progress in Geophysics , 2015, 30 (2) : 758-768 ( 0) 0)
|
| [6] |
印兴耀, 孙瑞莹, 张广智, 等. 基于分形高频初始模型和低频先验信息的物性参数随机反演[J].
石油物探 , 2014, 53 (5) : 537-544 YIN X Y, SUN R Y, ZHANG G Z, et al. Stochastic inversion of reservoir physical property parameters based on high-frequency initial model from fractal and low-frequency prior information[J].
Geophysical Prospecting for Petroleum , 2014, 53 (5) : 537-544 ( 0) 0)
|
| [7] |
张永江, 轩义华, 秦成岗. 岩石物理分析在番禺天然气区含气性研究中的应用[J].
石油物探 , 2010, 49 (4) : 407-414 ZHANG Y J, XUAN Y H, QIN C G. The application of rock physics analysis in the study of hydrocarbon gas in panyu area[J].
Geophysical Prospecting for Petroleum , 2010, 49 (4) : 407-414 ( 0) 0)
|
| [8] |
谢月芳, 张纪. 岩石物理模型在横波估算中的应用[J].
石油物探 , 2012, 51 (1) : 65-70 XIE Y F, ZHANG J. The application of rock physics models in the shear wave velocity estimation[J].
Geophysical Prospecting for Petroleum , 2012, 51 (1) : 65-70 ( 0) 0)
|
| [9] |
印兴耀, 李龙. 基于岩石物理模型的纵?横波速度反演方法[J].
石油物探 , 2015, 54 (3) : 249-253 YIN X Y, LI L. P-wave and S-wave velocities inversion based on rock physics model[J].
Geophysical Prospecting for Petroleum , 2015, 54 (3) : 249-253 ( 0) 0)
|
| [10] |
曹丹平. 基于Backus等效平均的测井资料尺度粗化方法研究[J].
石油物探 , 2015, 54 (1) : 105-111 CAO D P. The upscaling method of the well logging data based on Backus equivalence average method[J].
Geophysical Prospecting for Petroleum , 2015, 54 (1) : 105-111 ( 0) 0)
|
| [11] |
胡起, 陈小宏, 李景叶. 基于各向异性岩石物理模型的页岩气储层横波速度预测[J].
石油物探 , 2014, 53 (3) : 254-261 HU Q, CHEN X H, LI J Y. S-wave velocity prediction of shale gas reservoir based on anisotropic rock physics model[J].
Geophysical Prospecting for Petroleum , 2014, 53 (3) : 254-261 ( 0) 0)
|
| [12] |
印兴耀, 刘欣欣, 曹丹平. 基于 Biot 相洽理论的致密砂岩弹性参数计算方法[J].
石油物探 , 2013, 52 (5) : 445-451 YIN X Y, LIU X X, CAO D P. Tight sandstone elastic parameters calculation method based on Biot-Consistent theory[J].
Geophysical Prospecting for Petroleum , 2013, 52 (5) : 445-451 ( 0) 0)
|
| [13] |
刘欣欣, 印兴耀, 张峰. 一种碳酸盐岩储层横波速度估算方法[J].
中国石油大学学报 (自然科学版) , 2013, 37 (1) : 42-49 LIU X X, YIN X Y, ZHANG F. An approach to predict S-wave velocity of carbonate rocks[J].
Journal of China University of Petroleum (Edition of Natural Science) , 2013, 37 (1) : 42-49 ( 0) 0)
|
| [14] |
郭栋, 印兴耀, 吴国忱. 横波速度计算方法与应用[J].
石油地球物理勘探 , 2007, 42 (5) : 535-538 GUO D, YIN X Y, WU G C. Methods of S-wave velocity computation and its application[J].
Oil Geophysical Prospecting , 2007, 42 (5) : 535-538 ( 0) 0)
|
| [15] |
NORRIS A. A differential scheme for the effective moduli of composites[J].
Mechanics of Materials , 1985, 4 (5) : 1-16 ( 0) 0)
|
| [16] |
LI H, ZHANG J. Elastic moduli of dry rocks containing spheroidal pores based on differential effective medium theory[J].
Journal of Applied Geophysics , 2011, 75 (4) : 671-678 DOI:10.1016/j.jappgeo.2011.09.012 ( 0) 0)
|
| [17] |
杨凤英, 印兴耀, 刘博. 可变干岩石骨架等效模型研究[J].
石油物探 , 2014, 53 (3) : 280-286 YANG F Y, YIN X Y, LIU B. The research of variable dry rock matrix equivalent model[J].
Geophysical Prospecting for Petroleum , 2014, 53 (3) : 280-286 ( 0) 0)
|
| [18] |
LI H, ZHANG J. Analytical approximations of bulk and shear moduli for dry rock based on the differential effective medium theory[J].
Geophysical Prospecting , 2012, 60 (2) : 281-292 DOI:10.1111/gpr.2012.60.issue-2 ( 0) 0)
|
| [19] |
KEYS R G, Xu S. An approximation for the Xu-White velocity model[J].
Geophysics , 2002, 67 (5) : 1406-1414 DOI:10.1190/1.1512786 ( 0) 0)
|
| [20] |
李宏兵, 张佳佳. 多重孔岩石微分等效介质模型及其干燥情形下的解析近似式[J].
地球物理学报 , 2014, 57 (10) : 3422-3430 LI H B, ZHANG J J. A differential effective medium model of multiple-porosity rock and its analytical approximations for dry rocks[J].
Chinese Journal of Geophysics , 2014, 57 (10) : 3422-3430 ( 0) 0)
|
| [21] |
KUSTER G T, TOKSZ M N. Velocity and attenuation of seismic waves in two-phase media,part I:theoretical formulations[J].
Geophysics , 1974, 39 (5) : 587-606 DOI:10.1190/1.1440450 ( 0) 0)
|
| [22] |
HAN D H, NUR A, MORGAN D. Effect of porosity and clay content on wave velocities in sandstones[J].
Geophysics , 1986, 51 (11) : 2093-2107 DOI:10.1190/1.1442062 ( 0) 0)
|
| [23] |
XU S, WHITE R E. A new velocity model for clay-sand mixtures[J].
Geophysical Prospecting , 1995, 43 (1) : 91-118 DOI:10.1111/gpr.1995.43.issue-1 ( 0) 0)
|
| [24] |
GASSMANN F. Elastic waves through a packing of spheres[J].
Geophysics , 1951, 16 (4) : 673-685 DOI:10.1190/1.1437718 ( 0) 0)
|
| [25] |
MAVKO G, MUKERJI J, DVORKIN J.
The rock physics handbook:tools for seismic analysis in porous media[M]. New York: Cambridge University Press, 2003 : 1 -329.
( 0) 0)
|
| [26] |
BERRYMAN J G. Single-scattering approximations for coefficients in Biots equations of poroelasticity[J].
The Journal of the Acoustical Society of America , 1992, 91 (2) : 551-571 DOI:10.1121/1.402518 ( 0) 0)
|
| [27] |
BERRYMAN J G. Long-wavelength propagation in composite elastic media II[J].
The Journal of the Acoustical Society of America , 1980, 68 (6) : 1820-1831 DOI:10.1121/1.385172 ( 0) 0)
|
| [28] |
LI H B, ZHANG J J. Modulus ratio of dry rock based on differential effective medium theory[J].
Geophysics , 2010, 75 (2) : N43-N50 DOI:10.1190/1.3360312 ( 0) 0)
|


