2. 中国地质大学(武汉)地球物理与空间信息学院, 湖北武汉 430074;
3. 中国石油化工集团公司华北分公司勘探开发研究院, 河南郑州 450006
2. Institute of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China;
3. Research Institute of Exploration and Development, North China Branch of SINOPEC, Zhengzhou 450006, China
随着地震勘探程度的不断提高和勘探工作的不断深入, 勘探对象逐渐趋于复杂化, 后续的地震资料处理与解释工作的难度也逐渐增大。地震资料的瞬时频率、瞬时振幅与瞬时相位(三瞬)信息在面对复杂地层构造时可以更全面地反映储层特性各方面的属性, 展示出更多的细节, 被广泛应用于天然气储层预测[1]。信号的瞬时相位会随界面的岩性和层序改变而变化; 瞬时振幅与储层的反射系数有关, 能够对储层的密度和孔隙度进行描述; 瞬时频率在遇到含气砂岩时高频成分会被削弱, 可以反映出储层的岩性特征。
实际地震信号是复杂的非平稳非线性信号, 采用基于平稳线性信号的传统处理技术求取的瞬时参数并不理想, 导致最终解释结果存在较大误差[2]。针对复杂地震信号的时频分析, HUANG[3]提出了一种新的信号处理技术, 即希尔伯特-黄变换(Hilbert-Huang transform, HHT)。该方法首先通过经验模态分解(EMD)方法将信号分解成有限个固有模态函数(IMF)分量之和, 然后对IMF分量进行Hilbert变换求取其瞬时参数[4-6]。HHT在提高地震资料分辨率、消除噪声以及提取地震瞬时属性等方面得到了广泛的应用, 并且取得了很好的效果。但是, HHT存在模态混叠和端点效应等问题, 导致解释结果中出现较大的误差, 严重制约了方法的实际应用范围[7]。
为了消除模态混叠与端点效应对HHT效果的影响, TORRES等[8]提出了完备总体经验模态分解法(CEEMD), 较好地解决了模态混叠问题[9]。目前CEEMD只在小波阈值去噪方面取得了较好的效果, 在求取地震瞬时参数领域的应用研究并未展开[10-12]。此外, 毕明霞等[13-14]利用自回归(AR)模型在信号两端预测出极值点进行拟合, 能够部分抑制端点效应。然而, 由于这些改进均基于EMD方法, 因而应用效果受到一定的限制。
为了进一步提高该方法的精度, 本文采用基于AR模型预测的CEEMD方法对HHT加以改进, 有效地抑制了模态混叠与端点效应, 提高了解释结果的精度。利用改进后的方法求取地震瞬时参数, 能够更加准确有效地反映含气储层信息。
1 HHT模态混叠和端点效应HHT由经验模态分解(EMD)与希尔伯特变换两部分组成[15]。对地震信号进行EMD后所得的IMF分量为单分量信号, 对其进行Hilbert变换后可得出信号的幅值函数与相位函数, 并求得IMF分量的瞬时频率。尽管在利用HHT求取地震记录的瞬时参数时, 能够获得比常规时频分析方法更准确的结果, 但因模态混叠与端点效应问题的存在, 导致所得结果中依然存在误差。
1.1 模态混叠问题模态混叠主要出现在EMD的过程中, 理想的EMD结果应该是按照由高频分量到低频分量的顺序依次从地震信号中分离, 所得IMF分量也是由高频到低频排列[16-17]。然而, 当遇到存在有间断高频振荡的信号时, 所得的IMF分量中会存在高频成分与低频成分混杂的问题, 相邻的分量中波形互相影响, 难以分离。
该问题的产生主要是因为EMD会自主选择并提取时间区域内频率最高的信号, 所以, 在不存在高频扰动的信号区间, EMD会把低频成分提取出来作为信号的最高频部分, 并与信号其余部分提取出来的高频扰动加以结合, 生成一阶IMF分量。这样的问题会逐渐传递下去。使得随后提取出来的IMF分量都存在高频成分与低频成分相互混杂的问题。
地震信号中往往存在随机噪声, 这些夹杂于信号中的不规则噪声会导致模态混叠问题的出现, 进行EMD时, 难以很好地分离噪声, 给解释工作带来干扰。
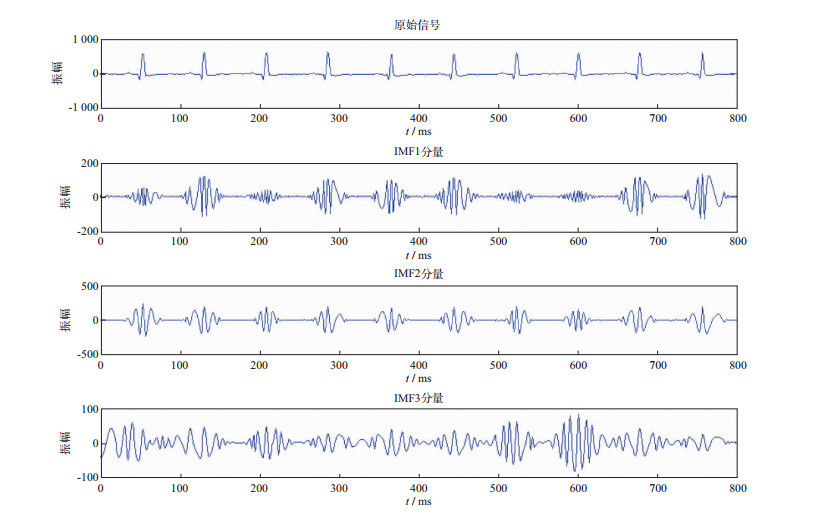
由图 1可以看出, 利用常规方法所求IMF的分量中, 本应为原始信号高频分量的IMF1中夹杂有低频成分, 高频部分未能很好地分离出来, 使得后面各阶的IMF分量都受到影响。对存在模态混叠的IMF分量进行瞬时参数求取时, 不同频率成分的混杂必然会导致较大的误差存在, 影响最终的解释结果。
|
图 1 模态混叠问题 |
端点效应出现在对信号进行包络线拟合的环节。上、下包络线采用3次样条插值的方法求取, 包络线形态由极值点位置决定。原始信号的两端通常并非极值点, 在拟合的时候如何对端点进行处理将会对拟合结果产生很大的影响。不当的处理方法会产生拟合误差, 使信号两端出现发散现象[18]。
EMD所采取的3次样条插值拟合的方法通常将信号的端点作为极值点[19], 信号端点不可能同时既是极大值也是极小值, 那么端点处究竟是作为极大值点还是作为极小值点来处理, 这个问题一直未能得到很好解决。端点效应并非只对信号端点附近产生影响, 在不断筛分的过程中, 每一次进行包络线的拟合都会产生这样的误差并代入下一次拟合。这种发散现象会逐渐向信号内部传播, 对整个信号造成污染, 使分解结果严重失真, 导致所求包络线的形态与实际信号不符。
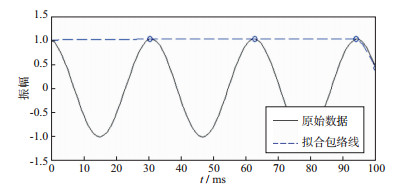
端点问题的处理直接影响到HHT的效果。从图 2可以看出, 原始信号的端点处明显不是极值点, 然而在拟合时将该点依然作为极值点来求取上包络线, 使得结果与实际情况出现较大的偏差。端点的误差会在EMD过程中不断地扩散, 以至于最终结果无法反映信号的真实特性。
|
图 2 端点效应 |
在处理地震信号的时候, 由于模态混叠和端点效应的缘故, 使得某些信号瞬时参数的求取结果存在较大的误差, 难以反映储层细节, 给实际解释工作带来极大的困扰。
2 HHT的改进 2.1 方法改进针对模态混叠与端点效应问题, 本文提出了基于AR模型的CEEMD方法对HHT进行改进。
首先, 利用AR模型对地震信号两端进行预测, 设x(n)之前的p个数据{x(n-p), x(n-p+1), …, x(n-1)}已知, 预测值为
| $ \begin{matrix} \rho =E\left\{ {{\left[x\left( n \right)-\widehat{x}\left( n \right) \right]}^{2}} \right\} \\ =E\left\{ {{\left[x\left( n \right)+\sum\limits_{k=1}^{p}{{{a}_{k}}}x\left( n-k \right) \right]}^{2}} \right\} \\ \end{matrix} $ | (1) |
其中, ρ在预测误差序列与原始序列正交时为最小值, 即:
| $ \begin{matrix} E\left\{ x\left( n-m \right)\left[x\left( n \right)-\widehat{x}\left( n \right) \right] \right\}=0 \\ m=1, 2, \cdots, p \\ \end{matrix} $ | (2) |
由(2)式可以导出线性预测的Wiener-Hopf方程, 其矩阵形式为:
| $ \begin{matrix} \left[\begin{array}{*{35}{l}} {{r}_{x}}\left( 0 \right) & {{r}_{x}}\left( 1 \right) & {{r}_{x}}\left( 2 \right) & \cdots & {{r}_{x}}\left( p \right) \\ {{r}_{x}}\left( 1 \right) & {{r}_{x}}\left( 0 \right) & {{r}_{x}}\left( 1 \right) & \cdots & {{r}_{x}}\left( p-1 \right) \\ {{r}_{x}}\left( 2 \right) & {{r}_{x}}\left( 1 \right) & {{r}_{x}}\left( 0 \right) & \cdots & {{r}_{x}}\left( p-2 \right) \\ \vdots & \vdots & \vdots & {} & \vdots \\ {{r}_{x}}\left( p \right) & {{r}_{x}}\left( p-1 \right) & {{r}_{x}}\left( p-2 \right) & \cdots & {{r}_{x}}\left( 0 \right) \\ \end{array} \right] \\ \left[\begin{matrix} 1 \\ \begin{matrix} {{\alpha }_{1}} \\ {{\alpha }_{2}} \\ \vdots \\ \end{matrix} \\ {{\alpha }_{p}} \\ \end{matrix} \right]=\left[\begin{matrix} {{\rho }_{\min }} \\ \begin{matrix} 0 \\ 0 \\ \vdots \\ \end{matrix} \\ 0 \\ \end{matrix} \right] \\ \end{matrix}\cdot $ | (3) |
(3)式即为P阶自回归模型的正则方程。求出系数{ak}后, 即可求出n+1时刻的预测值(n+1), 依次类推可以预测出往后任意时刻的值。
利用AR模型在原始信号两端分别预测出两个附加的极大值点和极小值点之后, 再加入k组正负成对的辅助白噪声, 可以得到2组IMF集合。
| $ \left[\begin{matrix} {{M}_{1}} \\ {{M}_{2}} \\ \end{matrix} \right]=\left[\begin{matrix} 1 & 1 \\ 1 &-1 \\ \end{matrix} \right]\left[\begin{matrix} S \\ N \\ \end{matrix} \right] $ | (4) |
式中:S为原始信号; N为辅助噪声; M1和M2分别是加入正、负成对噪声之后的信号。这样得到的集合信号的个数为2k。
然后, 对集合中的每一个合成信号都做EMD, 其中每次对信号进行三次样条插值拟合时, 都先通过AR模型在信号的两端分别预测出附加的极大值点和极小值点, 将信号的实际极值点与预测极值点相连组成信号的上下包络线。所得第i个信号的第j个IMF分量表示为cij, 对所有信号的相应IMF分量求取均值即可得出实际信号的第j个IMF分量cj:
| $ {{c}_{j}}=\frac{1}{2k}\sum\limits_{i=1}^{2k}{{{c}_{ij}}} $ | (5) |
最后, 选取合适的IMF分量进行HHT之后即可求出其瞬时参数。
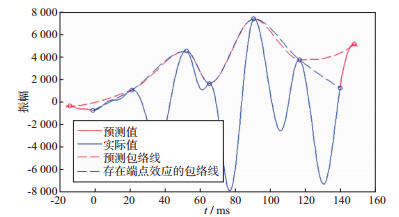
2.2 效果对比图 3中红色线条部分通过采用AR模型预测对信号端点进行延拓, 在信号两端预测出下一个极值点, 然后对其进行包络线拟合, 使得所求包络线更加符合信号自身的特点, 改善了端点效应对信号的影响。
|
图 3 改进后的方法对端点问题的处理 |
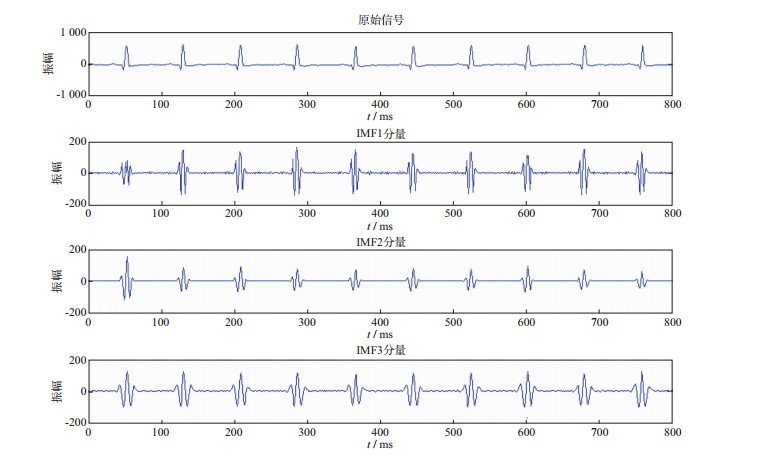
改进后的方法对模态混叠问题的抑制, 也取得了明显的效果(图 4)。对比图 4与图 1可以发现, 改进后的方法所求IMF分量中, IMF1中仅为信号的高频成分, 并没有夹杂低频成分, IMF2中以低频成分为主, IMF3的频率更低。各分量按照频率由高到低排列, 高频成分与低频成分得以很好地分离, 与预期结果相符。
|
图 4 改进后的方法对模态混叠的抑制 |
为了验证改进后方法的有效性, 对实际资料采用常规HHT与改进方法所得结果进行对比, 结合地震、测井、地质资料的综合解释, 对结果进行系统分析。
3.1 研究区特征以鄂尔多斯杭锦旗区块为例, 以岩性气藏为目标对目的层进行储层预测, 分析气藏特点及其分布规律, 并根据储层厚度变化、物性和含气性等特征对结果加以验证。
杭锦旗区块位于鄂尔多斯盆地伊陕斜坡北缘。主要目的层上古生界构造平缓, 仅有少量鼻状构造, 断裂不发育, 气藏以岩性控制为主。目的层段以冲积扇、辫状河沉积为主, 发育北北东向河道沉积、辫状水道沉积。东、中、西3个沉积水道, 东部最厚, 向西单层厚度减薄, 隔夹层增多。该区地震资料主频高, 频带宽, 具备了地震属性提取的基础条件。地震属性参数的提取, 对于地震相和地震反射结构综合分析、有利沉积相带、有利砂体发育区及有利含气密集区定性预测等工作尤为重要。
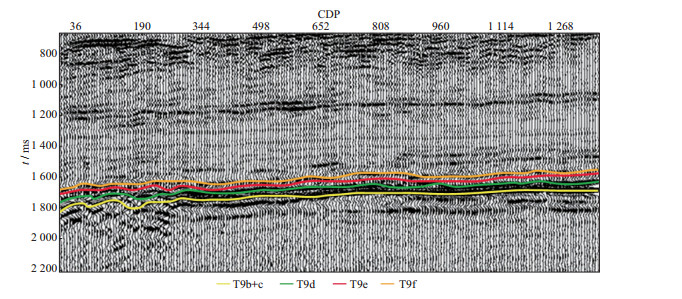
选择东西向的一条联井线作为试验线。在主要目的层山西组、太原组、石盒子组, 主要有4组反射同相轴, 分别为T9b+c, T9d, T9e及T9f, 其中T9b+c反射最强、同相轴清晰、连续性最好。测线西部局部地段反射杂乱、连续性差, 出现反射同相轴的合并、分叉现象, 反映了目的层的急剧变化(图 5)。
|
图 5 工区地震资料剖面 |
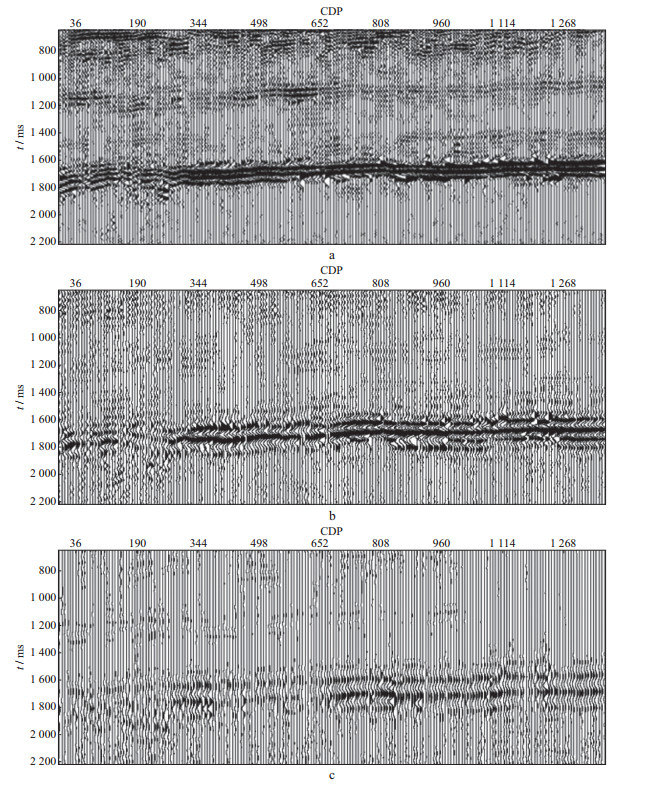
分别用常规HHT和改进后的HHT求取该剖面各道数据的IMF分量, 得到IMF分量剖面, 并对各个分量剖面的地质效果加以分析。常规HHT所得的3个IMF分量剖面(图 6)中, IMF1分量剖面质量最好。与原始数据相比, IMF1剖面中信号信噪比更高, 目的层与周围信号差异明显, 这说明该分量能够将目的层段信息较好地分离出来, 并包含了更少的噪声。在IMF2与IMF3分量剖面中噪声逐渐增多, 反射层逐渐模糊。因此在本文后续的分析中采用IMF1分量剖面。
|
图 6 常规HHT方法提取出的IMF分量剖面 a IMF1分量; b IMF2分量; c IMF3分量 |
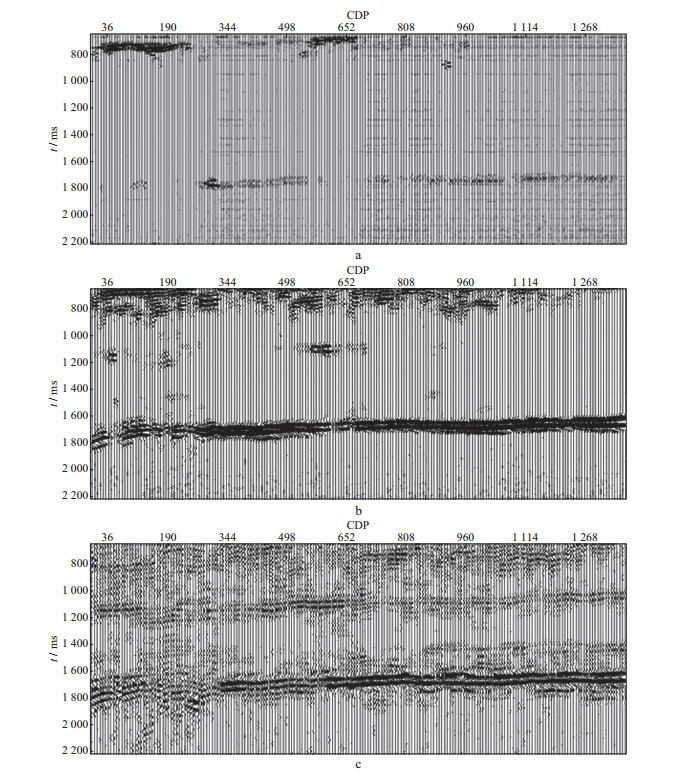
改进后的HHT所得的3个IMF分量剖面见图 7。由于在分解过程中加入了随机噪声, 所以IMF1分量只是分离了高频噪声。IMF2分量剖面效果最好, 剖面中包含了目的层段信息, 其主要反射层段与周围信号的振幅差异也较为明显。IMF3分量剖面中目的层有效信息较少, 噪声增多, 因此在本文后续的分析中采用IMF2剖面。
|
图 7 改进后的HHT方法提取出的IMF分量剖面 a IMF1分量; b IMF2分量; c IMF3分量 |
常规HHT所得IMF分量剖面中, 由于高低频分量混杂, 导致整体较为杂乱, 无法有效突出主要反射层信息; 改进后的方法提取的IMF分量能够较好地分离信号中的高频与低频部分, 且剖面中包含的噪声更少。因此改进后方法所得结果包含更多的目的层段信息, 能够准确分离目的层段信号。
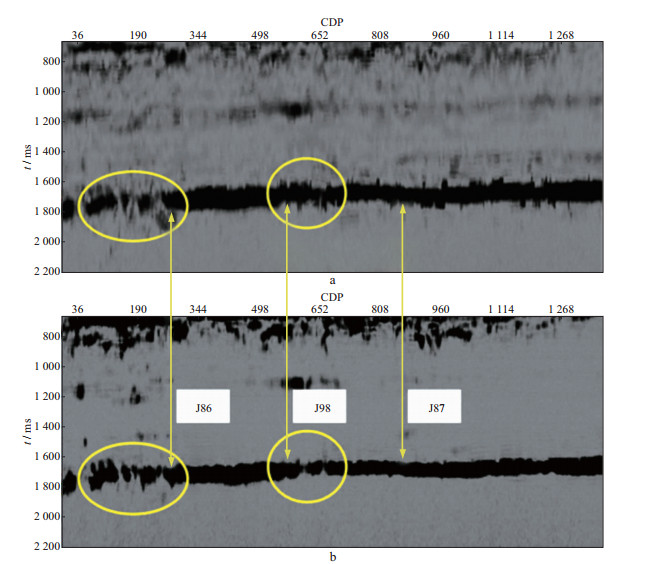
3.3 瞬时属性剖面对比分别对常规方法所得的IMF1分量剖面与改进后的HHT所得的IMF2分量剖面进行Hilbert变换, 求取瞬时振幅剖面。瞬时振幅是反射波组的包络线, 反映的是地震信号反射波能量的大小[20-21]。地震信号的瞬时振幅属性常用于确定地层的连续性以及储层中流体、岩性的横向变化, 强振幅区域往往与储层相对应。瞬时振幅剖面能够直观地反映出储层位置与形态。
图 8为两种方法计算的瞬时振幅剖面, 图中黄圈位置对应异常区域, 改进后的方法在该处的分辨率明显高于常规方法, 并包含了丰富的细节, 能够识别出常规方法所无法识别的精细构造。常规方法所得剖面中, 储层的上、下界面出现多处“毛刺”现象, 改进后的方法有效消除了这些误差。可见, 利用改进后的HHT方法求取地震信号的瞬时振幅属性能够更加准确地反映储层边界与储层的连续性。钻井结果表明, 西部异常区布设的J86井在该层段获得92224m3/d的天然气, 中部异常区布设的J98井产量为25602m3/d, 而东段布设的J87井没有试获天然气。可见改进后的方法对地层异常响应更为明显, 所获得的瞬时振幅信息是该区储层预测的有效参数。
|
图 8 常规HHT所得瞬时振幅剖面(a)和改进后的HHT所得瞬时振幅剖面(b)对比 |
瞬时频率反映的是地震目的层段瞬时主频, 瞬时频率会随着岩性的改变而变化[22]。地震波在传播过程中当遇到含气砂岩时, 其高频成分被吸收, 使得在瞬时频率剖面上出现低值异常, 因此瞬时频率剖面中的低值部分通常对应于储层位置。为此, 分别用常规方法与改进后的方法求取各道IMF分量的瞬时频率, 得到其瞬时频率剖面, 如图 9所示。对比可以看出, 常规方法所得结果整体比较模糊且杂乱, 目的层上对应的储层的上边界难以分辨, 而改进方法整体效果更为直观简洁。图 9中黄圈位置储层与围岩的差异更加明显, 对地层细节展示得更为细致, 对储层边界的刻画也更为精确。

|
图 9 常规HHT所得瞬时频率剖面(a)和改进后的HHT所得瞬时频率剖面(b)对比 |
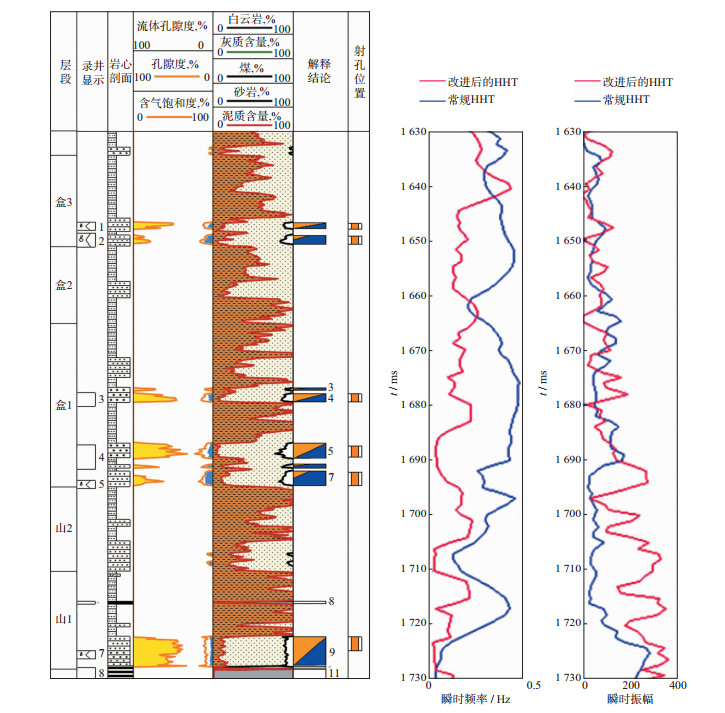
为了与测井资料解释结果对比, 本文选取J86井井旁地震道(第308道)数据进行详细比对分析, 该道位于西部沉积水道, 砂体厚度10m左右, 泥岩隔夹层和物性隔夹层都比较发育, 且厚度较大, 非常有利于砂体侧向尖灭形成岩性圈闭。对该道数据分别用改进前、后的HHT求得瞬时频率, 如图 10所示。可以看出瞬时频率与孔隙度存在明显的相关性, 高孔隙度的层段由于地震信号高频成分被吸收, 主要呈现为低频成分。含气层段与周围岩性的差异也能够通过瞬时频率直观地反映出来, 当信号传播至含气层时, 可以看出瞬时频率有明显降低, 经过含气层之后瞬时频率又开始增大。图 10中储层所对应的瞬时频率均存在先降低随后又增大的过程。可见通过求取信号的瞬时频率能够很好地反映地层孔隙度的变化及岩性的变化。改进后的HHT所求瞬时频率对地层变化更为敏感, 精确度也更高, 高孔隙度的层段均对应着瞬时频率的低值; 地层岩性改变时, 也能够看到瞬时频率存在明显的起伏波动。而在常规方法中这种对应关系同样存在但不明显, 有几处岩性变化并没有反应出来。
|
图 10 瞬时频率、瞬时振幅与测井资料对比 |
瞬时振幅与砂岩分布存在明显的相关性, 含气砂岩对应层段瞬时振幅明显增大。储层位置均对应着强振幅与低频率(图 10)。通过对两种方法的对比可以看出改进后的方法与测井资料所反映的储层信息更加吻合。
4 结论1) 针对HHT变换现存的模态混叠与端点效应问题, 提出了基于AR模型的CEEMD方法, 在一定程度上抑制了常规HHT中存在的模态混叠和端点效应。经过对比证明了改进后的方法比常规方法所得结果的精度更高, 提高了地震信号的分辨率。
2) 用改进后的HHT方法对鄂尔多斯杭锦旗区块实际地震资料进行处理后, 求得的地震信号瞬时参数与测井资料所反映的储层信息吻合度高, 证明了该方法的可行性和有效性。
| [1] |
杨占龙, 彭立才, 陈启林, 等. 地震属性分析与岩性油气藏勘探[J].
石油物探 , 2007, 46 (2) : 131-136 YANG Z L, PENG L C, CHEN Q L, et al. Seismic attributes analysis and lithological reservoir exploration[J]. Geophysical Prospecting for Petroleum , 2007, 46 (2) : 131-136 |
| [2] |
裴强, 胡波. Hilbert-Huang变换方法研究进展[J].
世界地震工程 , 2011, 27 (2) : 21-29 PEI Q, HU B. Progress of study on Hilbert-Huang transform[J]. World Earthquake Engineering , 2011, 27 (2) : 21-29 |
| [3] | HUANG N E.Computer implemented empirical mode decomposition method,apparatus,and article of manufacture for two-dimensional signals:U.S.Patent 6,311,130[P].2001-10-30 |
| [4] | HUANG N E, WU M C, LONG S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proceedings of the Royal Society Series A:Mathematical, Physical and Engineering Sciences , 2003, 459 (2037) : 2317-2345 DOI:10.1098/rspa.2003.1123 |
| [5] | HUANG N E, WU Z H. A review on Hilbert-Huang transform:method and its applications to geophysical studies[J]. Reviews of Geophysics , 2008, 46 (2) : RG2006 |
| [6] | HUANG N E, SHEN S S. Hilbert-Huang transform and its applications[M]. New York: World Scientific Publishing Company, 2005 : 1 -324. |
| [7] |
王姣.希尔伯特黄变换在地震数据处理中的应用[D].东营:中国石油大学,2013
WANG J.The application of the Hilbert-Huang transform in seismic data processing[D].Dongying:China University of Petroleum,2013 http://cdmd.cnki.com.cn/article/cdmd-10425-1015024743.htm |
| [8] | TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[J]. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing , 2011 : 4144-4147 |
| [9] |
刘爽.基于CEEMD的地震数据处理研究与应用[D].长春:吉林大学,2014
LIU S.A study and application of seismic data processing based on CEEMD[D].Changchun:Jilin University,2014 http://cdmd.cnki.com.cn/article/cdmd-10183-1014270542.htm |
| [10] |
王姣, 李振春, 王德营. 基于CEEMD的地震数据小波阈值去噪方法研究[J].
石油物探 , 2014, 53 (2) : 164-172 WANG J, LI Z C, WANG D Y. A method for wavelet threshold denoising of seismic data based on CEEMD[J]. Geophysical Prospecting for Petroleum , 2014, 53 (2) : 164-172 |
| [11] |
王维强, 杨国权. 基于EMD与ICA的地震信号去噪技术研究[J].
石油物探 , 2012, 51 (1) : 19-29 WANG W Q, YANG G Q. Random noise denoising technique based on EMD and ICA[J]. Geophysical Prospecting for Petroleum , 2012, 51 (1) : 19-29 |
| [12] |
孔庆丰. 基于Hilbert-Huang变换的面波压制方法研究[J].
石油物探 , 2012, 51 (5) : 446-450 KONG Q F. Surface wave supperressing method based on Hilbert-Huang transform[J]. Geophysical Prospecting for Petroleum , 2012, 51 (5) : 446-450 |
| [13] |
毕明霞, 黄汉明, 边银菊, 等. 基于经验模态分解的地震波特征提取的研究[J].
地球物理学进展 , 2012, 27 (5) : 1890-1896 BI M X, HUANG H M, BIAN Y J, et al. Study on seismic signal features extraction based on EMD[J]. Progress in Geophysics , 2012, 27 (5) : 1890-1896 |
| [14] |
张郁山.希尔伯特-黄变换(HHT)与地震动时程的希尔伯特谱[D].北京:中国地震局地球物理研究所,2003
ZHANG Y S.Hilbert-Huang transform and Hilbert spectrum of earthquake ground motion[D].Beijing:Institute of Geophysics,China Earthquake Administration,2003 http://www.oalib.com/references/18564807 |
| [15] | WU Z, HUANG N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis , 2009, 1 (1) : 1-41 DOI:10.1142/S1793536909000047 |
| [16] |
李斌, 陈学华, 贺振华, 等. 基于多尺度加窗希尔伯特变换的地震资料体边缘检测[J].
石油物探 , 2015, 54 (3) : 345-349 LI B, CHEN X H, HE Z H, et al. Seismic data 3D edge detection based on multi-scale windowed Hilbert transform[J]. Geophysical Prospecting for Petroleum , 2015, 54 (3) : 345-349 |
| [17] |
杨培杰, 印兴耀, 张广智. 希尔伯特-黄变换地震信号时频分析与属性提取[J].
地球物理学进展 , 2007, 22 (5) : 1585-1590 YANG P J, YIN X Y, ZHANG G Z. Seismic signal attributes time-frequency analysis and attribute extraction based on HHT[J]. Progress in Geophysics , 2007, 22 (5) : 1585-1590 |
| [18] |
薛雅娟.地震信号时频分析及其在储层含气性检测中的应用研究[D].成都:成都理工大学,2014
XUE Y J.Time-frequency analysis of seismic signals and its application in gas-bearing reservoir detection[D].Chengdu:Chengdu University of Technology,2014 http://cdmd.cnki.com.cn/article/cdmd-10616-1015530043.htm |
| [19] |
薛雪.地震属性中振幅和频率与油气层的关系[D].北京:中国地质大学,2014
XUE X.The relationship between amplitude and frequency with the oil and gas layer in seismic attributes[D].Beijing:China University of Geosciences,2014 http://cdmd.cnki.com.cn/article/cdmd-11415-1014238591.htm |
| [20] |
魏艳, 尹成, 丁峰, 等. 地震多属性综合分析的应用研究[J].
石油物探 , 2007, 46 (1) : 42-47 WEI Y, YIN C, DING F, et al. Synthetic analysis of seismic multi-attribute and its application[J]. Geophysical Prospecting for Petroleum , 2007, 46 (1) : 42-47 |
| [21] |
杨占龙, 彭立才, 陈启林, 等. 地震属性分析与岩性油气藏勘探[J].
石油物探 , 2007, 46 (2) : 131-136 YANG Z L, PENG L C, CHEN Q L, et al. Seisnuc attributes analysis and lithological[J]. Geophysical Prospecting for Petroleum , 2007, 46 (2) : 131-136 |
| [22] |
唐金炎.基于地震属性参数的地震相识别方法研究[D].成都:成都理工大学,2011
TANG J Y.Seismic fades identification based on the seismic attributes[D].Chengdu:Chengdu University of Technology,2011 http://cdmd.cnki.com.cn/article/cdmd-10616-1011235634.htm |



 ,
,