全波形反演方法(FWI)充分利用了叠前地震记录中的有效信息, 其反演精度比常规反演方法高。自20世纪80年代LAILLY首次在时间域尝试应用波形反演方法后[1], 很多学者对FWI理论进行了研究[2-10]。然而, 在实际应用中, 这种高精确度反演算法面临着很多问题, 其中主要问题之一就是该方法对初始模型和低频信息依赖严重, 容易出现周波跳跃现象。当理论波场和观测波场的相位差大于半个周期时, 就会出现周波跳跃现象。周波跳跃问题限制了全波形反演的实际应用, 由于全波形反演是一个局部优化过程, 当出现周波跳跃现象时, 全波形反演就会陷入局部极值点, 从而不能得到准确的速度模型。
解决这个问题的方法很多。最常用的方法是两步速度建模法[11-12], 即首先利用传统的层析成像方法得到一个平滑的速度模型, 然后以这个平滑模型为初始模型, 利用全波形反演得到一个分辨率更高的成像结果。另一个相似的方法是联合波动方程层析成像和全波形反演[13-14], 但上述两种方法计算量大。为了避免周波跳跃现象, CHOI等[15]提出了“相位缠绕”(phase wrapping)的频率域波形反演方法, 以减小地震数据的相位差异。BI等[16]提出了数据选择策略的全波形反演方法, 将相位差在半个周期之外的数据切除, 保证参与反演的数据都在半个周期之内。HU等[17]提出了通过2个相差不大的频率波场得到低波数成分的全波形反演方法。这些方法都在一定程度上改善了周波跳跃对全波形反演的影响。
本文在频率域全波形算法的基础上, 提出了波场相位相关时移FWI算法, 以此来改善周波跳跃现象对全波形反演的影响; 同时利用Curvelet变换的多尺度思想, 在反演过程中使用不同尺度的观测数据信息, 减小了全波形反演对初始模型的依赖。Marmousi模型数据测试表明方法有效。
1 全波形反演理论全波形反演方法充分利用了叠前地震记录中的走时和振幅信息, 其反演精度要比旅行时层析成像和偏移速度分析等常规方法高。全波形反演可以在时间域、频率域和Laplace域中进行, 各有其优点[18-19]。其中频率域全波形反演具有受地下介质复杂性影响较小、计算速度快、非线性问题影响小、只需要少量离散的频率就可以得到可靠的成像等优点, 在现有的计算机水平下是较容易实现的一种方法。
在反演问题中, 目标函数C(m)一般定义为实际地震数据dobs与模拟地震数据dcal之间的差, 用L2范数表示为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{C}}\left( m \right) = \frac{1}{2}{{\left[{{\mathit{\boldsymbol{d}}^{{\rm{obs}}}}-{\mathit{\boldsymbol{d}}^{{\rm{cal}}}}} \right]}^{\rm{T}}}\left[{{\mathit{\boldsymbol{d}}^{{\rm{obs}}}}-{\mathit{\boldsymbol{d}}^{{\rm{cal}}}}} \right]}\\ { = \frac{1}{2}\left\| {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} -{\mathit{\boldsymbol{d}}_{{\rm{sim}}}}} \right\|_2^2} \end{array} $ | (1) |
式中:上标T表示共轭转置; ‖·‖22表示L2范数; m是速度模型参数。反演的目的是求取目标函数的最小值, 得到最接近地下真实构造的模型。
全波形反演是一个不断迭代优化的过程, 更新后的模型m可表示成初始模型m0与模型更新量Δm之和:
| $ m={{m}_{0}}+\vartriangle m $ | (2) |
为了求取目标函数的最小值, 将方程(1)在m0处泰勒展开, 舍去高阶项, 两端对m求导并用矩阵形式表示, 得:
| $ \frac{{\partial \mathit{\boldsymbol{C}}\left( m \right)}}{{\partial m}} = \frac{{\partial \mathit{\boldsymbol{C}}\left( {{m_0}} \right)}}{{\partial m}} + \frac{{{\partial ^2}\mathit{\boldsymbol{C}}\left( {{m_0}} \right)}}{{\partial {m^2}}}\vartriangle m $ | (3) |
当
| $ \vartriangle m = - {\left[{\frac{{{\partial ^2}\mathit{\boldsymbol{C}}\left( {{m_0}} \right)}}{{\partial {m^2}}}} \right]^{ - 1}}\frac{{\partial \mathit{\boldsymbol{C}}\left( {{m_0}} \right)}}{{\partial m}} $ | (4) |
式中:
有很多种算法求解方程(1), 比如最速下降法、牛顿法、拟牛顿法等局部优化算法和Monte Carlo方法、遗传算法、模拟退火算法等全局优化算法[20-21]。在保证成像精度的前提下, 为了节约计算量和内存, 本文选用L-BFGS算法作为全波形反演的优化算法。
L-BFGS优化算法是一种拟牛顿算法, 是为了解决BFGS算法占用内存过大而提出的一种有限内存的BFGS算法[22-24]。与BFGS算法不同的是, L-BFGS算法不需要直接求取Hessian矩阵, 而是采用有限的梯度向量对对Hessian矩阵进行更新, 减少了存储量, 也提高了计算效率。其迭代更新公式为:
| $ {\mathit{\boldsymbol{m}}_{k + 1}} = {\mathit{\boldsymbol{m}}_k} - {\alpha _k}{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{g}}_k} $ | (5) |
式中:Hk为近似逆Hessian矩阵; αk为搜索步长; gk为目标函数的一阶导数。L-BFGS算法的优化更新只需要计算梯度, 因此大大节约了计算时间和存储量。其更新公式为:
| $ {\mathit{\boldsymbol{H}}_{k + 1}} = \mathit{\boldsymbol{V}}_k^{\rm{T}}{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{V}}_k} + {\rho _k}{\mathit{\boldsymbol{s}}_k}\mathit{\boldsymbol{s}}_k^{\rm{T}} $ | (6) |
式中:
| $ \begin{array}{*{20}{c}} {{\rho _k} = \frac{1}{{\mathit{\boldsymbol{y}}_k^{\rm{T}}{\mathit{\boldsymbol{s}}_k}}}}\\ {{\mathit{\boldsymbol{V}}_k} = \mathit{\boldsymbol{I}} - {\rho _k}{\mathit{\boldsymbol{y}}_k}\mathit{\boldsymbol{s}}_k^{\rm{T}}}\\ {{\mathit{\boldsymbol{s}}_k} = {\mathit{\boldsymbol{m}}_{k + 1}} - {\mathit{\boldsymbol{m}}_k}}\\ {{\mathit{\boldsymbol{y}}_k} = {\mathit{\boldsymbol{g}}_{k + 1}} - {\mathit{\boldsymbol{g}}_k}} \end{array} $ | (7) |
即Hk+1是利用有限个向量对{sk, yk}对Hk更新得到的, 通常只需要储存3~5个向量对就能隐式表达Hessian矩阵。相比较而言, L-BFGS算法在计算精度、收敛速度以及计算成本上要比其它的优化算法更适合于FWI, 而且基于L-BFGS算法的FWI具有一定的抗噪能力, 对初始模型的依赖程度较其它优化算法要低。
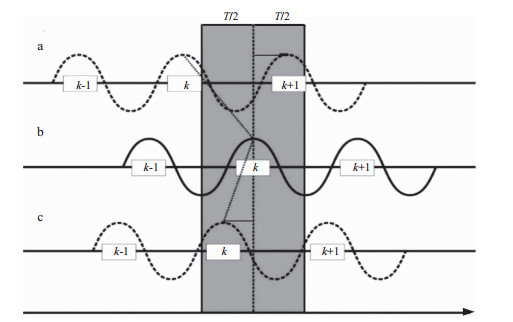
2 波场相位相关时移算法由于全波形反演是一个局部优化过程, 对初始模型和低频信息的依赖较高, 因此容易出现周波跳跃现象, 使反演陷入局部极小而得不到准确结果。周波跳跃问题是全波形反演在实际应用中的重要限制因素, 尤其是在实际资料缺少低频信息时, 由于强非线性性, 更容易出现周波跳跃现象。图 1为周波跳跃现象的示意图, 图 1a和图 1c表示理论波场, 图 1b表示观测波场。对比图 1b和图 1c, 可发现其波峰对应时刻之差小于半个周期, 即相位差小于π/2时, 就不会出现周波跳跃现象, 能够正确更新模型; 而对比图 1a和图 1b, 第k个波峰对应时刻之差大于半个周期, 即相位差大于π/2, 此时会出现周波跳跃现象。
|
图 1 周波跳跃现象示意 a理论波场1; b观测波场; c理论波场2 |
借鉴数字图像相关方法的思想, 模拟地震记录和观测地震记录之间的误差可以看做数字图像相关方法中基准图像和变形图像之间的变形, 在单道记录上只是单个方向上的平移。因此, 在全波形反演中, 由不准确的速度模型产生的波场扰动可以看作是一种偏离真实波场的“变形”, 而反演的目的可以看作是通过更新速度模型, 使这种变形逐渐减小, 使得模拟数据不断逼近观测数据。当变形过大时, 如果没有对得到模型大尺度构造有关键作用的低频信息, 反演就容易陷入局部极值点, 导致反演失败。因此, 我们可以使用相关方法估计模拟波场偏离真实波场的位置, 先将这种变形减小, 然后再进行反演, 将速度模型逐步逼近真实模型。根据周波跳跃产生的原因, 在反演之前, 先对观测地震记录和模拟地震记录的相位信息做互相关计算, 根据互相关系数的大小对模拟地震记录进行时移, 然后再进行全波形反演, 以此来改善低频信息不足时周波跳跃现象对全波形反演的影响。假设模型是无衰减的弹性介质, 且相位不随着波传播而改变。具体过程为:
1) 在反演之前, 首先对模拟数据与观测数据进行互相关运算, 考虑到偏移距的影响, 逐道求取互相关系数:
| $ \begin{array}{*{20}{c}} {{C_{ri}}\left( \tau \right) = \frac{1}{N}\sum\limits_{t = 0}^{N-1} {d_i^{{\rm{obs}}}\left( {x, t} \right)d_i^{{\rm{cal}}}\left( {x, t + \tau } \right)} }\\ {i = 1, 2, \cdots, N} \end{array} $ | (8) |
式中:Cr为互相关系数; i为道数; N为检波点数。
2)取相关系数最大时的τ值, 并对模拟波场进行时移:
| $ \widetilde d_i^{{\rm{cal}}}\left( {x, t} \right) = d_i^{{\rm{cal}}}\left( {x, t + \tau } \right) $ | (9) |
式中:
| $ \widetilde D_i^{{\rm{cal}}} = D_i^{{\rm{cal}}} \cdot {{\rm{e}}^{{\rm{i}}\omega \tau }} $ | (10) |
式中:
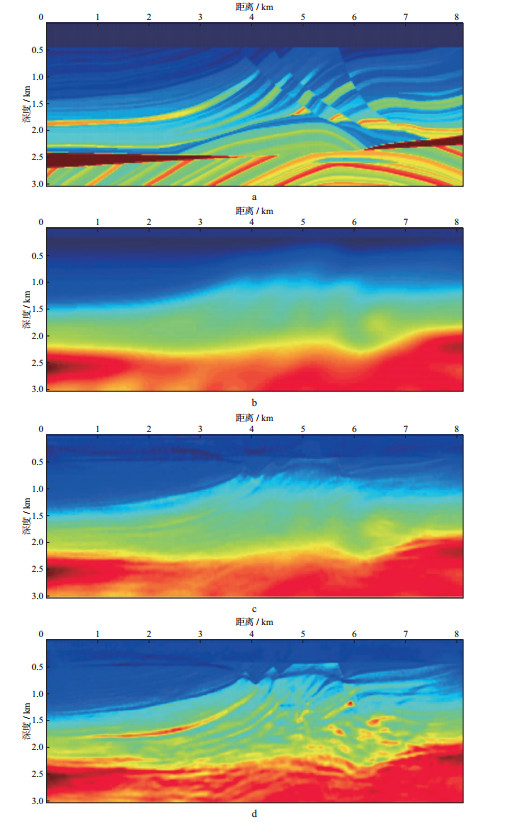
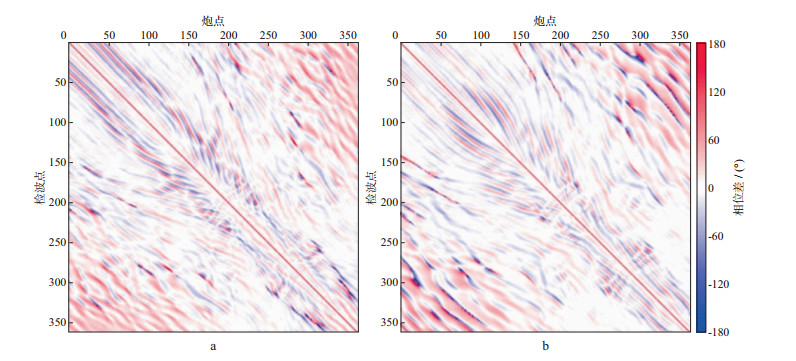
为证明方法的有效性, 利用Marmousi模型进行了测试, 图 2a和图 2b分别为Marmousi模型和初始速度模型。将反演起始频率选为7Hz, 终止反演频率为15Hz, 分别进行常规全波形反演和波场相位相关全波形反演, 反演结果分别为图 2c和图 2d。对比图 2c和图 2d可以看到, 由于缺少足够的低频信息, 常规全波形反演方法没有得到准确的结果, 而改进后的波场相位相关全波形反演方法反演结果的精度得到明显提高。以图 2b为速度模型进行正演模拟, 正演频率为7Hz, 得到模拟波场, 再将模拟波场进行波场相位相关时移得到时移后的波场, 将这2个波场分别与理论观测波场求相位差剖面, 如图 3所示。对比图 3a和图 3b可以发现, 经过时移后的波场与理论波场的匹配效果更好, 周波跳跃现象得到了明显改善, 说明了方法的有效性。
|
图 2 Marmousi模型(a), 初始速度模型(b), 常规FWI反演结果(c)以及波场相位相关FWI反演结果(d) |
|
图 3 两种波场与观测波场的相位差剖面 a 模拟波场; b 时移波场 |
近年来, Curvelet变换[25]由于其独特性而受到研究人员的日益关注。Curvelet变换由小波变换发展而来, 克服了小波变换在表达图像边缘的方向特性等方面的内在缺陷, 已经显示出其在图像处理中的发展潜力。Curvelet多尺度变换可以对时空信号进行最稀疏的表达, 能够获得最优的非线性逼近。在去噪方面, 根据Curvelet变换理论, 在含有噪声的信号中, 较大的Curvelet系数对应于有效信号, 反之为噪声[26]。因此Curvelet变换不仅可以很好地衰减随机噪声, 并且能较好地保持有效信号。Curvelet系数可表示为信号与小波函数的内积:
| $ C\left( {j, l, k} \right) = \left\langle {f, {\varphi _{j, l, k}}} \right\rangle = \int_{{R^2}} {f\left( x \right){\varphi _{j, l, k}}{\rm{d}}x} $ | (11) |
式中:j表示尺度; l表示方向; k表示位移; f为信号; φj, l, k为小波函数。
一个图像经过Curvelet变换后, 其系数可分为3个尺度层:第1层称为Coarse尺度层, 是由低频系数组成的一个矩阵; 第2层为Detail尺度层, 根据图像的大小又被分割为不同的方向, 是由中高频系数组成的矩阵; 第3层称为Fine尺度层, 是由高频系数组成的一个矩阵[27]。变换后第1层系数即Coarse层系数对应的是模型的大尺度构造, 随着层数的增加, 对构造的刻画越精细。
在全波形反演中, 多尺度方法是增加算法稳定性的常用方法, 常用的多尺度方法有分频反演法和变网格法等。结合Curvelet变换系数的多尺度特性, 本文提出了一种新的多尺度方法。在反演的不同阶段, 根据反演频率的大小, 结合Curvelet变换, 采用不同的模型(图 2a, 图 4a和图 4b), 分别提取地震资料不同尺度的数据。图 5a, 图 5b, 图 5c分别为由图 2a, 图 4a, 图 4b模型计算出的模拟地震记录, 图 5e, 图 5f分别为由观测地震记录中提取出的不同尺度的地震记录, 其中图 5d的尺度与图 5b对应, 图 5e的尺度与图 5c对应。

|
图 4 Marmousi模型的Coarse层系数对应的模型(a), Coarse+Detail层系数对应的模型(b) |

|
图 5 由图 2a所示Marmousi模型计算得到的模拟地震记录(a), 由Coarse层系数对应的模型计算得到的模拟地震记录(b), 由Coarse+Detail层系数对应的模型计算得到的模拟地震记录(c), 在图 5a中提取的大尺度数据(d), 在图 5a中提取的大尺度数据加中尺度数据(e) |
在全波形反演从低频到高频顺序反演的过程中, 地震数据的尺度选择不断精细, 即速度模型精度低时使用地震资料的大尺度数据, 即图 5e对应的数据, 并随着反演速度模型的精度不断提高, 逐渐加入地震资料的精细尺度信息, 过程如图 6所示。这样, 模拟地震记录能够更好的与实际地震记录进行匹配, 减小了周波跳跃的可能性, 得到满足全局最优解的反演结果。

|
图 6 Curvelet变换多尺度全波形反演示意 |
为验证Curvelet变换多尺度方法对改善全波形反演对初始模型依赖性的效果, 利用图 2a所示Marmousi模型进行测试。为说明方法的有效性, 将初始模型的精度降低, 如图 7a。在此基础上, 分别进行常规的频率域全波形反演和应用多尺度的频率域全波形反演。在初始反演时, 使用地震记录变换后的Coarse层系数对应的地震记录, 并随着反演精度的增大, 逐渐加入Detail层及Fine层系数对应的地震记录, 反演结果分别见图 7b到图 7e。可以看出, 由于初始模型的精度较差, 常规反演方法出现严重的周波跳跃现象, 不能得到准确的结果; 而利用Curvelet多尺度策略的方法通过对地震数据不同尺度的选取, 提高了模拟地震数据和观测数据的匹配精度, 减小了全波形反演对初始模型的依赖, 有效压制了周波跳跃的影响, 反演效果得到很大改善。

|
图 7 FWI初始模型(a), 常规频率域FWI反演结果(b), 应用Curvelet变换Coarse层数据的FWI反演结果(c), 应用Curvelet变换Coarse+Detail层数据的FWI反演结果(d), 应用完整数据的FWI反演结果(e) |
周波跳跃问题是限制全波形反演在实际应用中的重要因素。本文提出了波场相位相关时移算法, 在反演之前对模拟波场进行处理, 减小模拟波场和观测波场之间的相位差, 提高了波场匹配精度, 进而减小周波跳跃现象的影响。应用Curvelet变换多尺度方法, 在反演的不同阶段, 根据反演频率的大小, 分别提取观测地震数据不同尺度的数据, 在从低频到高频顺序反演的过程中, 地震数据的尺度选择不断精细, 随着反演速度模型的精度不断提高, 逐渐加入地震资料的精细尺度信息, 使模拟地震记录能够更好的与实际地震记录进行匹配, 减小了FWI对初始模型的依赖。对Marmousi模型进行全波形反演测试, 结果表明, 波场相位相关算法以及Cuevelet变换多尺度思想的全波形反演可以有效减少FWI对低频信息和初始模型的依赖, 为下一步全波形反演在实际数据中的应用提供了理论基础。
| [1] | LAILLY P. The seismic inverse problem as a sequence of before stack migrations[J]. Proceedings of the Conference on Inverse Scattering, Theory and Application Expanded Abstracts , 1983 : 206-220 |
| [2] | SONG Z M, WILLIAMSON P R, PRATT G. Frequency-domain acoustic wave modeling and inversion of crosshole data, part 2:inversion method, synthetic experiments and real-data results[J]. Geophysics , 1995, 60 (3) : 786-809 |
| [3] |
吕晓春, 顾汉明, 成景旺. 基于Huber函数的频率域全波形反演[J].
石油物探 , 2013, 52 (5) : 544-552 LV X C, GU H M, CHENG J W. Frequency domain full waveform inversion based on Huber function[J]. Geophysical Prospecting for Petroleum , 2013, 52 (5) : 544-552 |
| [4] | MA Y, HALE D. A projected Hessian matrix for full waveform inversion[J]. Expanded Abstracts of 81st Annual Internat SEG Mtg , 2011 : 2401-2405 |
| [5] | PRATT G, SHIN C. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International , 1998, 133 (2) : 341-362 DOI:10.1046/j.1365-246X.1998.00498.x |
| [6] | TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics , 1984, 49 (8) : 1259-1266 DOI:10.1190/1.1441754 |
| [7] |
王义, 董良国. L-BFGS法时间域全波形反演中初始矩阵的选择方法[J].
石油物探 , 2014, 53 (5) : 545-555 WANG Y, DONG L G. Selection strategy of the initial matrix for L-BFGS method in time domain full waveform inversion[J]. Geophysical Prospecting for Petroleum , 2014, 53 (5) : 545-555 |
| [8] | PRATT G. Seismic waveform inversion in the frequency domain, part 1:theory and verification in a physical scale model[J]. Geophysics , 1999, 64 (3) : 888-901 DOI:10.1190/1.1444597 |
| [9] | SHIN C, CHA Y H. Waveform inversion in the Laplace domain[J]. Geophysical Journal International , 2008, 173 (3) : 922-931 DOI:10.1111/gji.2008.173.issue-3 |
| [10] | GAROTTU R. Simultaneous recording of several vibroseis seismic lines[J]. Expanded Abstracts of 63rd Annual Internat SEG Mtg , 1983 : 308-310 |
| [11] | OPERTO S, RAVAUT C, IMPROTA L, et al. Quantitative imaging of complex structures from dense wide-aperture seismic data by multi-scale traveltime and waveform inversions:a case study[J]. Geophysical Prospecting , 2004, 52 (6) : 625-651 DOI:10.1111/gpr.2004.52.issue-6 |
| [12] | BRENDERS A, PRATT G. Efficient waveform tomography for lithospheric imaging:implications for realistic, 2D acquisition geometries and low-frequency data[J]. Geophysical Journal International , 2007, 168 (1) : 152-170 DOI:10.1111/gji.2007.168.issue-1 |
| [13] | SYMES W. Migration velocity analysis and waveform inversion[J]. Geophysical Prospecting , 2008, 56 (6) : 765-790 DOI:10.1111/gpr.2008.56.issue-6 |
| [14] | BIONDI B, ALMOMIN A. Tomographic full-waveform inversion (TFWI) by combining full waveform inversion with wave-equation migration velocity analysis[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg , 2012 : 1-5 |
| [15] | CHOI Y, ALKHALIFAH T. Frequency-domain waveform inversion using the unwrapped phase[J]. Expanded Abstracts of 81st Annual Internat SEG Mtg , 2011 : 2576-2580 |
| [16] | BI H, LIN T. Effective cycle skipping reduction through adaptive data selection for full waveform inversion[J]. Expanded Abstracts of 76th EAGE Conference and Exhibition , 2014 : 330-340 |
| [17] | HU W Y. FWI without low frequency data-beat tone inversion[J]. Expanded Abstracts of 84th Annual Internat SEG Mtg , 2014 : 1116-1120 |
| [18] | TEN BRINK U, BROCHER T M. Multichannel seismic evidence for a subcrustal intrusive complex under Oahu and a model for Hawaiian volcanism[J]. Journal of Geophysical Research:Solid Earth , 1987, 92 (B13) : 13687-13707 DOI:10.1029/JB092iB13p13687 |
| [19] | SINGH S C, HOBBS R W, SNYDER D B. Broadband receiver response from dual-streamer data and applications in deep reflection seismology[J]. Geophysics , 1996, 61 (1) : 232-243 DOI:10.1190/1.1443944 |
| [20] | GU H, CHEN J, CAI C, et al. Optimal towing depth for over/under streamer acquisition from deghosting operator analysis[J]. Expanded Abstracts of 83rd Annual Internat SEG Mtg , 2013 : 4387-4391 |
| [21] | VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics , 2009, 74 (6) : WCC127-WCC152 DOI:10.1190/1.3237087 |
| [22] | LIU D C, NOCEDAL J. On the limited memory BFGS method for large scale optimization[J]. Mathematical Programming:Series A and B , 1989, 45 (3) : 503-528 |
| [23] | MORALES J L. A numerical study of limited memory BFGS methods[J]. Applied Mathematics Letters , 2002, 15 (4) : 481-487 DOI:10.1016/S0893-9659(01)00162-8 |
| [24] |
邓武兵.基于混合采集技术的频率域全波形反演研究[D].长春:吉林大学, 2012
DENG W B.Study of blended acquisition based on frequency domain full waveform inversion[D].Changchun:Jilin University, 2012 http://cdmd.cnki.com.cn/article/cdmd-10183-1012365631.htm |
| [25] | CANDES E J, DONOHO D L. Curvelets:a surprisingly effective nonadaptive representation for objects with edges[M]. Stanford: Department of Statistics, Stanford University, 1999 : 1 -16. |
| [26] | NEELAMANI R, BAUMSTEIN A I, GILLARD D G, et al. Coherent and random noise attenuation using the curvelet transform[J]. The Leading Edge , 2008, 27 (2) : 240-248 DOI:10.1190/1.2840373 |
| [27] |
何劲, 李宏伟, 张群. 一种自适应阈值曲波图像去噪算法[J].
数据采集与处理 , 2010, 25 (3) : 336-340 HE J, LI H W, ZHANG Q. Curvelet transform algorithm with auto-adaptive threshold to image denoising[J]. Journal of Data Acquisition & Processing , 2010, 25 (3) : 336-340 |


