随着石油工业的发展和勘探开发程度的不断深入, 油气勘探开发从构造勘探阶段逐渐走向岩性勘探阶段。为此, 全波形反演(FWI)迅速发展起来, 并成为当今地球物理界的研究热点[1]。全波形反演是一个基于地震全波场模拟的数据拟合过程, 几乎使用了地震记录中所有的有效信息[2]。该方法利用优化算法不断进行搜索, 最终找到模拟数据与实际数据拟合差最小的模型[2]。20世纪80年代, TARANTOLA[3]提出了时间域全波形反演方法, 指出目标函数对模型参数的梯度可以通过残差反传波场和正传波场互相关运算得到, 该伴随状态法有效避免了求取Jacobi矩阵。20世纪90年代, PRATT[2]将全波形反演推广到了频率域, 提出只需要几个离散的频率就可以得到高精度的反演结果, 而且从低频到高频的反演策略可以很好地解决陷入局部极小值的问题。
TARANTOLA[3]给出了用最速下降法计算时间域二维声波方程参数的反演公式, 该方法结构简单, 计算量小, 但收敛速度慢。SHI等[4]用控制共轭梯度法和预条件共轭梯度法求解时间域波动方程参数, 并将该方法应用于实际地震数据处理, 得到了很好的反演剖面。GAO等[5]利用反褶积梯度法进行全波形反演, 但反演精度不高。PRATT等[6]给出全波形反演中近似Hessian矩阵和精确Hessian矩阵计算公式, 当利用基于Hessian矩阵的高斯-牛顿类优化方法进行全波形反演时, 计算量过大, 对存储的要求很高, 但当Hessian矩阵非正定或者高度病态时, 这种方法不能保证目标函数收敛。朱童等[7]将对角Hessian矩阵尺度化的梯度与粒子群算法联合, 降低了算法对初始模型的依赖性, 但计算效率较低。BROSSIER等[8]将L-BFGS方法应用到二维弹性波全波形反演中, 反演结果很好。LI等[9]提出修正高斯牛顿法, 并将其应用到稀疏约束全波形反演中, 减小了全波形反演对计算机内存的需求。全波形反演要求在高精度的前提下尽可能地提高计算效率, 而直接利用共轭梯度法进行全波形反演, 不能快速得到高精度的反演结果。
针对以上问题, 本文利用混合超记忆梯度法进行全波形反演。混合超记忆梯度法是将超记忆梯度法和固定步长超记忆梯度法二者组合来进行全波形反演, 目的是在保证具有超记忆梯度法反演精度的前提下提高计算效率。超记忆梯度法利用多步梯度信息来对当前梯度方向进行校正[10], 具有全局收敛性和超线性收敛速度, 该方法有效弥补了共轭梯度法只利用两步梯度信息的缺陷, 同时避免计算Hessian矩阵。固定步长超记忆梯度法利用梯度信息直接求取模型更新的步长[11], 不需要线性搜索, 节约了大量的计算时间。但固定步长超记忆梯度法在求取步长时没有利用Wolfe收敛准则来约束目标函数, 导致该方法在高频段反演结果不稳定。为了解决反演不稳定问题, 本文利用混合超记忆梯度法反演策略, 即固定步长超记忆梯度法先在低频段反演, 快速得到一个高精度初始模型, 再用超记忆梯度法在高频段反演, 最终得到高精度全波形反演结果。该策略结合了固定步长超记忆梯度法计算效率高的优势和超记忆梯度法反演精度高的优势。模型试算结果证明了本文方法可以很好地改善模型整体的反演效果并提高全波形反演的计算效率。
1 方法原理 1.1 频域全波形反演方法二维频率域声波波动方程可以表示为[12]:
| $ {\nabla ^2}\mathit{\boldsymbol{u}}\left( {x, w} \right) + \frac{{{w^2}}}{{v_{\rm{P}}^2}}\mathit{\boldsymbol{u}}\left( {x, w} \right) = \mathit{\boldsymbol{s}}\left( {x, w} \right) $ | (1) |
式中:w=2πf表示角频率, f表示频率; vP表示纵波速度; x表示震源位置; u(x, w)表示频率域单频波场; s(x, w)表示震源函数。利用有限差分离散算子, 则方程(1)可以表示为[13]:
| $ \mathit{\boldsymbol{A}}\left( {x, w} \right)\mathit{\boldsymbol{u}}\left( {x, w} \right) = \mathit{\boldsymbol{s}}\left( {x, w} \right) $ | (2) |
式中:A(x, w)表示阻抗矩阵。给定初始速度模型和震源子波函数, 根据(2)式即可求得频率为f时的单频地震波场u(x, w)。
频域全波形反演主要利用地震波的振幅、相位以及频率信息, 将采集的时间域地震数据通过傅里叶变换得到频域观测数据(dobs), 与正演模拟数据(dcal)做差, 得到残差数据。残差数据通过伴随算子作用得到残差反传波场, 并与正传波场互相关, 得到地下模型的更新梯度[7]。全波形反演是一个不断去拟合实际数据的过程(最终得到数据残差最小的反演结果), 它具有成像精度高、反演模型参数准确、复杂构造成像效果好等优点。
全波形反演目标函数定义为:
| $ C\left( \mathit{\boldsymbol{m}} \right) = \frac{1}{2}\left\| {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - {\mathit{\boldsymbol{d}}_{{\rm{cal}}}}} \right\| $ | (3) |
式中:m代表模型参数。目标函数两端对模型参数m求导, 即得到目标函数的梯度[7]:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{g = }}\nabla C\left( \mathit{\boldsymbol{m}} \right) = - {\mathop{\rm Re}\nolimits} \left[{\frac{{\partial {\mathit{\boldsymbol{d}}_{{\rm{cal}}}}}}{{\partial \mathit{\boldsymbol{m}}}}\left( {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}-{\mathit{\boldsymbol{d}}_{{\rm{cal}}}}} \right)} \right]}\\ { = - {\mathop{\rm Re}\nolimits} \left[{\frac{{\partial \mathit{\boldsymbol{A}}}}{{\partial \mathit{\boldsymbol{m}}}}{\mathit{\boldsymbol{u}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{A}}^{-1}}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}-{\mathit{\boldsymbol{d}}_{{\rm{cal}}}}} \right)} \right]} \end{array} $ | (4) |
式中:(A-1)T(dobs-dcal)为残差反传波场; (A-1)T为伴随算子; u代表正传波场。从(4)式可以看出, 目标函数的梯度可以利用正传波场与残差反传波场互相关得到。
1.2 混合超记忆梯度法 1.2.1 超记忆梯度法超记忆梯度法具有超线性收敛速度、内存需求小、反演精度高等特点。最速下降法只用当前梯度的信息, 在计算过程中目标函数收敛速度慢[14], 共轭梯度法用上一步梯度信息来对当前梯度方向进行校正, 目标函数收敛速度较最速下降法快[15]。准确的梯度方向可以加快目标函数的收敛速度, 超记忆梯度法则是利用多步梯度信息来校正当前梯度方向[10]。超记忆梯度算法具体步骤如下。
1) 给定初始模型参数m0, 允许误差ε, ρ∈(0, 1), σ∈(0, 2), 记忆度M(即记录梯度向量的个数)为正整数, 最大迭代次数为kmax, 令k=0。
2) 计算梯度gk=▽f(mk)和目标函数f(mk), 若‖gk‖≤ε, k≥kmax则停止计算; 否则转步骤3)。
3) 计算目标函数下降方向:
| $ {\mathit{\boldsymbol{d}}_k} = \left\{ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{g}}_k}}&{k < M}\\ { - {\beta _k}{\mathit{\boldsymbol{g}}_k} - \sum\limits_{i = 2}^M {{\beta _{k - i + 1}}{\mathit{\boldsymbol{g}}_{k - i + 1}}} }&{k \ge M} \end{array}} \right. $ | (5) |
其中,
| $ \begin{array}{*{20}{c}} {{\beta _{k - i + 1}} \in \left[{0, s_k^i} \right]\;\left( {i = 1, 2, \cdots, M} \right)}\\ {s_k^1 = 1}\\ {s_k^j = \frac{\rho }{{M - 1}}\frac{{{{\left\| {{\mathit{\boldsymbol{g}}_k}} \right\|}^2}}}{{{{\left\| {{\mathit{\boldsymbol{g}}_k}} \right\|}^2} + {{\left\| {\mathit{\boldsymbol{g}}_k^{\rm{T}}{\mathit{\boldsymbol{d}}_{k - i + 1}}} \right\|}^2}}}}\\ {\begin{array}{*{20}{c}} {i = 2, 3, \cdots, M}\\ {\sum\limits_{i = 2}^M {{\beta _{k - i + 1}}} = 1} \end{array}} \end{array} $ | (6) |
4) 利用强Wolfe收敛准则, 搜索步长αk, 更新模型参数mk+1=mk+αkdk, k=k+1, 并转步骤2)。
从步骤3)可以看出, 求取下降方向dk利用了多步梯度信息。在全波形反演过程中记忆梯度数目不同导致目标函数收敛速度及模型反演精度有差别, 记忆梯度数量过多则会导致梯度方向校正过度, 因为全波形反演的梯度是通过Born近似得到(非精确的一阶导数), 所以在全波形反演的过程中不能像数学理论描述的那样, 记忆梯度数目越多反演精度越高, 目标函数收敛速度越快[10]。当记忆过多梯度时, 目标函数值下降变慢, 计算速度变慢, 内存需求增大; 记忆梯度数量少则退化为共轭梯度法。
1.2.2 固定步长超记忆梯度法共轭梯度法和超记忆梯度法都需要进行线性搜索求模型更新步长, 在搜索合适步长过程中浪费了大量的计算时间。为此, 马巍[11]提出固定步长技术, 即在每次迭代中通过一个确定的公式来计算步长, 从而避免了每一步都进行线性搜索, 该方法大大节约了计算时间。固定步长超记忆梯度法具体步骤如下。
1) 给定初始模型m0, 允许误差ε, ρ∈(0, 1/M), σ∈(0, 2), 记忆度M为正整数, 最大迭代次数为kmax, 令k=0。
2) 计算梯度gk=▽f(mk)和目标函数f(mk), 若‖gk‖≤ε, k≥kmax则停止计算; 否则转步骤3)。
3) 计算目标函数下降方向:
| $ {\mathit{\boldsymbol{d}}_k} = \left\{ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{g}}_k}}&{k < M}\\ { - {\mathit{\boldsymbol{g}}_k} - \sum\limits_{i = 2}^M {\beta _k^i{\mathit{\boldsymbol{d}}_{k - i}}} }&{k \ge M} \end{array}} \right. $ | (7) |
其中,
4) 计算模型更新步长:
| $ {a_k} = - \frac{{\delta \mathit{\boldsymbol{g}}_k^{\rm{T}}{\mathit{\boldsymbol{d}}_k}}}{{{L_k}{{\left\| {{\mathit{\boldsymbol{d}}_k}} \right\|}^2}}} $ | (8) |
其中, Lk为Lipschitz常数, 有:
| $ {L_k} \approx \max \left\{ {{L_0},\frac{{\left\| {{\mathit{\boldsymbol{g}}_k} - {\mathit{\boldsymbol{g}}_{k - 1}}} \right\|}}{{\left\| {{\mathit{\boldsymbol{d}}_k} - {\mathit{\boldsymbol{d}}_{k - 1}}} \right\|}}} \right\} $ | (9) |
其中, L0是一个常数, 为了防止步长αk=0。
5) 更新模型参数mk+1=mk+αkdk, k=k+1, 转步骤2)。
可以看出, 固定步长超记忆梯度法无需进行线性搜索, 直接利用梯度和下降方向求出模型更新步长, 显著缩减了全波形反演的计算时间; 但由于未采用收敛准则约束目标函数, 导致高频段全波形反演结果不稳定。
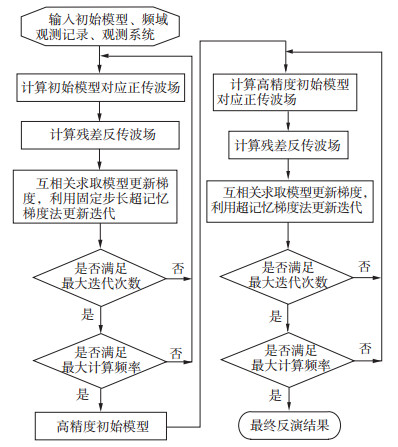
1.2.3 混合超记忆梯度法针对固定步长超记忆梯度法高频段反演不稳定问题, 本文提出混合超记忆梯度法反演策略, 即固定步长超记忆梯度法先在低频段反演, 快速得到一个高精度初始模型, 再利用超记忆梯度法在高频段反演, 最终得到高精度全波形反演结果。混合超记忆梯度法的实现流程如图 1所示, 给定初始模型通过正传波场与反传波场互相关求得模型更新梯度, 利用混合超记忆梯度优化算法进行迭代。在全波形反演过程中, 本文利用随机震源编码策略[16], 在一定程度上缩短了正演模拟所需要时间。
|
图 1 混合超记忆梯度法全波形反演流程 |
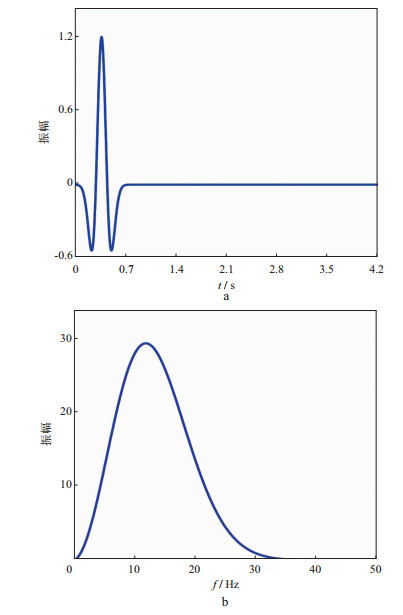
基于二维频率域声波波动方程, 对Marmousi速度模型用超记忆梯度类方法与共轭梯度法分别进行反演。模型横、纵网格大小为128×384, 网格间距均为50m。利用随机震源动态编码策略[16]压制超级炮内部的串扰噪声, 一个超级炮中含有38个震源。震源深度均为50m, 水平位置在模型表面随机分布。检波器沉放深度均为100m, 水平间隔均为50m, 共384个。震源为12Hz主频的雷克子波, 采样间隔为1ms, 采样总长度为4.2s, 反演频率为1~12Hz。图 2为雷克子波时间域波形及其频谱图。
|
图 2 雷克子波时间域波形(a)及其频谱(b) |
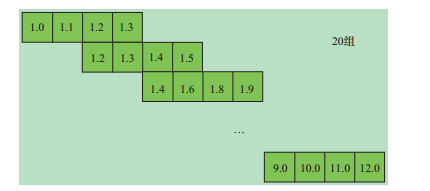
为了克服全波形反演过程中目标函数陷入局部极小和反演跳周问题, 利用组频重叠多尺度频率全波形反演。将反演频率(1~12Hz)分成20个组, 每个组包含4个频率, 频率间隔随着频率增加而增大, 相邻频率组之间重叠度为50%[17], 如图 3所示。每个频率迭代30次。
|
图 3 组频重叠多尺度示意(单位:Hz) |
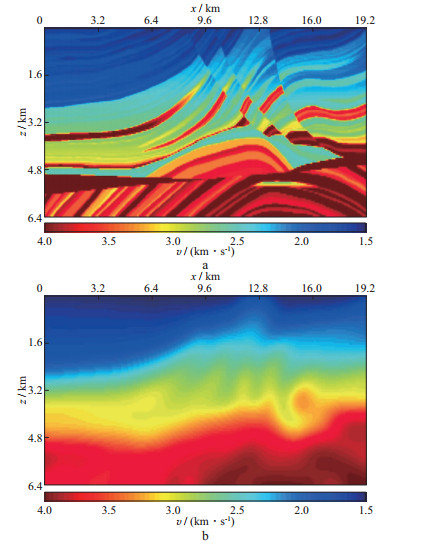
真实模型的速度范围是1.5~4.0km/s。全波形反演的初始模型是真实模型(图 4a)平滑后的结果如图 4b所示。
|
图 4 真实模型(a)和平滑初始模型(b) |
利用相同初始步长α0=0.5, 强Wolfe收敛准则搜索步长和相同组频分别采用共轭梯度法、超记忆梯度法和固定步长超记忆梯度法进行反演, 结果如图 5所示。从图 5可以看出, 超记忆梯度法具有更高的反演精度, 尤其是深层区域。

|
图 5 共轭梯度法(a)、超记忆梯度法(b)和固定步长超记忆梯度法(c)反演结果 |
从反演结果(图 5)中分别抽取第120道和第270道(模型中竖线标志)的速度值进行对比, 结果如图 6所示。从图 6可以看出, 共轭梯度法反演结果的速度曲线在深部偏离真实值, 而超记忆梯度类方法反演速度曲线与真实值几乎完全重合。可见, 超记忆梯度类反演方法得到的速度比较准确, 整体效果优于共轭梯度法, 尤其是深层区域的效果更好。

|
图 6 共轭梯度法(a)、超记忆梯度法(b)和固定步长超记忆梯度法(c)反演结果的第120道和第270道速度曲线对比 |
从图 5可以看出, 固定步长超记忆梯度法反演精度(图 5c)不如超记忆梯度法(但优于共轭梯度法), 根本原因在于固定步长超记忆梯度法无强Wolfe收敛准则约束目标函数, 导致反演结果不稳定, 这种现象越到高频越明显。本文利用混合超记忆梯度法反演策略很好地解决了高频反演不稳定问题。
混合超记忆梯度法反演结果如图 7所示, 可以看出, 固定步长超记忆梯度法反演结果只在低频段(1~4Hz)缺失很多细节信息(图 7a), 但在高频段有效避免了反演不稳定的问题。以该反演结果作为初始模型, 采用超记忆梯度法在高频段(4~12Hz)进行反演, 得到的反演结果(图 7b)与单独采用超记忆梯度法的反演结果几乎相同。

|
图 7 采用固定步长超记忆梯度法在低频段(1~4Hz)(a)和采用超记忆梯度法在高频段(4~12Hz)(b)的反演结果 |
从图 7b所示的反演结果中抽取第120道和第270道(模型中竖线标志)的速度值与真实速度值进行对比, 结果如图 8所示。由图 8可以看出, 混合超记忆梯度法反演速度曲线与真实值几乎完全重合, 反演精度与超记忆梯度法相同。

|
图 8 混合超记忆梯度法反演结果单道速度对比 |
在同一台机器(16G内存, CORETMi5, 4核处理器, windows7操作系统)上, 采用MATLAB编译, 并统计时间。表 1为梯度类不同优化方法的对比结果。
| 表 1 梯度类不同优化方法对比结果(迭代2400次) |
从表 1中可以看出, 共轭梯度法耗时最长, 原因是梯度方向与真实梯度方向有偏差, 使得在搜索步长的过程中浪费了大量的时间。在模型计算中, 超记忆梯度法的记忆度取M=5, 可以看出, 相比于共轭梯度法, 其反演精度得到了提高, 同时缩短了计算时间。固定步长超记忆梯度法的优势在于无需搜索步长, 直接根据之前梯度信息和下降方向计算出合适步长, 对模型进行更新迭代。混合超记忆梯度法的计算精度与超记忆梯度法的计算精度相同, 虽然其计算效率比不上固定步长超记忆梯度法的计算效率, 但相对于超记忆梯度法来说, 其计算时间减少了一半。
经过上述反演效率和反演模型误差的对比分析, 可以看出, 混合超记忆梯度法在计算效率和反演精度等方面具有明显的优势。本文提出的混合超记忆梯度法能够更好地适应求解大尺度全波形反演问题。
2.3 收敛稳定性分析 2.3.1 目标函数收敛速度分析采用图 4b所示结果作为初始模型进行测试, 反演频率为2Hz, 共迭代102次, 全波形反演目标函数如图 9所示。从图 9可以看出, 超记忆梯度法的记忆度(M)对目标函数下降幅度有一定的影响, 当记忆度M=4, 5时, 目标函数下降的幅度较大(图 9a), 随着记忆度的增加目标函数的下降幅度逐渐减小。可见, 当超记忆梯度法记忆梯度数量过多时, 则对当前梯度信息校正过度, 导致目标函数下降缓慢, 本文将记忆度M=5定为最优记忆度。固定步长超记忆梯度法目标函数因为没有约束条件的限制, 其下降幅度不稳定(图 9b), 但其整体下降幅度大于超记忆梯度法(图 9c)。

|
图 9 超记忆梯度法不同记忆度(a)、固定步长超记忆梯度法(b)和不同梯度法(c)的102次迭代目标函数 |
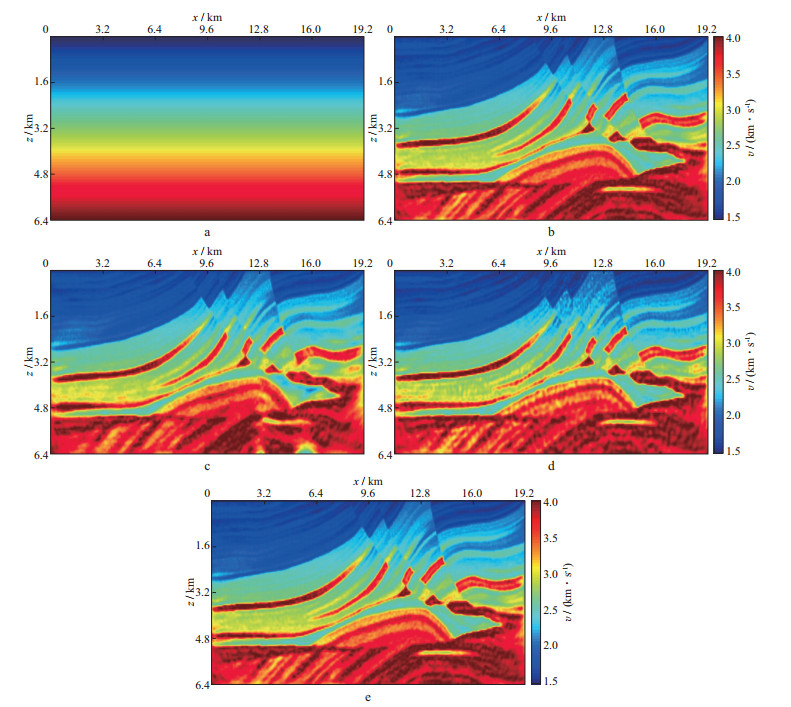
利用图 10a所示的线性初始速度模型测试梯度类优化算法反演时对初始模型的依赖程度, 反演结果如图 10b, 图 10c, 图 10d和图 10e所示。与真实模型(图 4a)对比可以看出, 线性初始速度模型与真实速度模型差距很大, 基本不含真实模型任何构造信息。从图 10可以看出, 当初始模型较差时, 4种方法都能很好地将Marmousi模型浅层构造反演出来, 随着深度的增加, 共轭梯度法反演结果出现了偏差, 在储层下方出现了一个实际上不存在的低速异常, 而且高速层位发生了错动(图 10c)。对比线性初始模型反演结果(图 10)和平滑初始模型反演结果(图 5)发现, 超记忆梯度类方法反演结果区别不大, 证明了超记忆梯度类方法在不缺失低频情况下基本不依赖初始模型, 而共轭梯度法对初始模型依赖较强。
|
图 10 线性初始模型(a)和超记忆梯度法(b)、共轭梯度法(c)、固定步长超记忆梯度法(d)、混合超记忆梯度法(e)的反演结果 |
利用图 4所示真实模型和平滑初始速度模型测试梯度类优化算法在反演中的抗噪能力。在真实模型上利用随机激发震源正演模拟观测数据, 并加入高斯噪声。地震记录信噪比SNR=10lg(dobs2/N2)=7(其中, dobs为观测数据, N为噪声), 除含噪之外, 其它条件均相同。图 11为加入高斯噪声和无噪声的随机震源单频波场对比结果, 可以看出, 高斯噪声对地震波场破坏非常严重。图 12为在地震观测记录中加入高斯噪声的反演结果。

|
图 11 加入高斯噪声(a)和无噪声(b)的随机震源单频波场 |
|
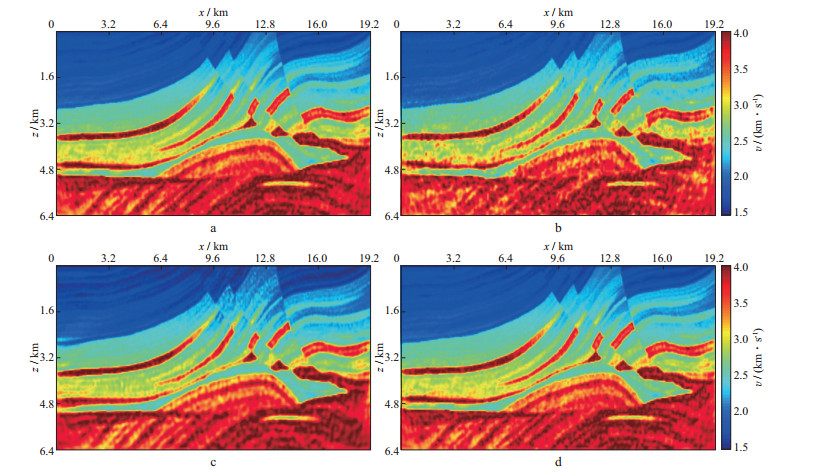
图 12 地震观测记录加入高斯白噪反演结果 a 超记忆梯度法; b 共轭梯度法; c 固定步长超记忆梯度法; d 混合超记忆梯度法 |
对比图 5与图 12发现, 高斯噪声对全波形反演结果影响较大, 虽然4种方法都可以基本反演出Marmousi模型, 但噪声使得模型反演结果不清晰, 影响了反演结果的稳定性。可以看出, 共轭梯度法反演结果受噪声影响最为严重, 尤其深部区域反演结果畸变严重。多次试验后发现, 逐渐增加噪声的强度, 当信噪比低于3时, 4种方法都无法得到正确的反演结果。
经过对梯度类优化方法收敛性的稳定性分析, 得出如表 2所示的结论。可以看出, 混合超记忆梯度法结合了超记忆梯度法和固定步长超记忆梯度法的优点, 相比于共轭梯度法具有明显的优势。
| 表 2 梯度类优化算法优、缺点分析 |
针对全波形反演的强非线性, 利用混合超记忆梯度法组频重叠多尺度反演策略, 增强了全波形反演的稳定性、可靠性和抗噪性, 并且一定程度上降低了对初始模型的依赖。
通过理论研究与模型试算得到以下认识。
1) 超记忆梯度法具有超线性收敛速度、反演精度高、基本不依赖初始模型、抗噪能力强等优点。将超记忆梯度法应用于全波形反演一定程度上提高了全波形反演的精度。
2) 在低频段利用固定步长超记忆梯度法进行全波形反演, 无需搜索步长, 节约大量计算时间, 可以快速为超记忆梯度法提供高精度的初始速度模型, 显著提高了全波形反演的计算效率。
3) 混合超记忆梯度法全波形反演结合了超记忆梯度类方法的高精度和高效等优点, 能够快速对复杂地下速度模型进行精细刻画, 满足当前地震成像对速度建模的高精度需求, 模型试算结果表明, 混合超记忆梯度法全波形反演, 在反演精度和计算效率方面均优于常规共轭梯度法。
| [1] |
胡光辉, 贾春梅, 夏洪瑞, 等. 三维声波全波形反演的实现与验证[J].
石油物探 , 2013, 52 (4) : 417-425 HU G H, JIA C M, XIA H R, et al. Implementation and validation of 3D acoustic full waveform inversion[J]. Geophysical Prospecting for Petroleum , 2013, 52 (4) : 417-425 |
| [2] | PRATT R G. Inverse theory applied to multi-source cross-hole tomography I:acoustic wave-equation method[J]. Geophysics Prospecting , 1990, 38 (3) : 287-310 DOI:10.1111/gpr.1990.38.issue-3 |
| [3] | TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics , 1984, 49 (8) : 1259-1266 DOI:10.1190/1.1441754 |
| [4] | SHI Y M, ZHAO W Z, CAO H. Nonlinear process control of wave-equation inversion and its application in the detection of gas[J]. Geophysics , 2007, 72 (1) : R9-R18 DOI:10.1190/1.2399450 |
| [5] | GAO F C, WILLIAMSON P, HOULLEVIGUE H. Full waveform inversion by deconvolution gradient method[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg , 2012 : 1-5 |
| [6] | PRATT R G, SHIN C, HICK G J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International , 1998, 133 (2) : 341-362 DOI:10.1046/j.1365-246X.1998.00498.x |
| [7] |
朱童, 李小凡, 汪文帅. 粒子群-梯度算法在频率域地震波形反演中的应用[J].
地球物理学进展 , 2013, 28 (1) : 180-189 ZHU T, LI X F, WANG W S. PSO-gradient algorithm and its application to seismic waveform inversion for velocity structure in frequency domain[J]. Progress in Geophysics , 2013, 28 (1) : 180-189 |
| [8] | BROSSIER R, OPERTO S, VIRIEUX J. Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion[J]. Geophysics , 2009, 74 (6) : WCC105-WCC118 DOI:10.1190/1.3215771 |
| [9] | LI X, ARAVKIN A, VAN LEEUWEN T, et al. Modified Gauss-Newton with sparse updates[J]. 12th International Congress of the Brazilian Geophysical Society & EXPOGEF , 2011 : 1412-1416 |
| [10] | SHI Z J, SHEN J. A new super-memory gradient method with curve search rule[J]. Applied Mathematics & Computation , 2005, 170 (1) : 1-16 |
| [11] |
马巍.无约束优化问题的超记忆梯度法的若干研究[D].海口:海南大学, 2013
MA W.Unconstrained optimization problem of super memory gradient method of research[D].Haikou:Hainan University, 2013 http://cdmd.cnki.com.cn/article/cdmd-10589-1013348552.htm |
| [12] | MARFURT K J. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J]. Geophysics , 1984, 49 (5) : 533-549 DOI:10.1190/1.1441689 |
| [13] | JO C H, SHIN C, SUH J H. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator[J]. Geophysics , 1996, 61 (2) : 529-537 DOI:10.1190/1.1443979 |
| [14] |
姚姚.
地球物理反演基本理论与应用方法[M]. 武汉: 中国地质大学出版社, 2002 : 17 -18.
YAO Y. Geophysics inversion of the basic theory and method application[M]. Wuhan: China University of Geophysics Press, 2002 : 17 -18. |
| [15] |
龚纯, 王正林.
精通MATLAB最优化计算[M]. 北京: 电子工业出版社, 2014 : 1 -416.
GONG C, WANG Z L. Proficient in MATLAB opti-mization calculation[M]. Beijing: Electronic Industry Press, 2014 : 1 -416. |
| [16] | BOONYASIRIWAT C, SCHUSTER G T. 3D multisource full-waveform inversion using dynamic random phase encoding[J]. Expanded Abstracts of 80th Annual Internat SEG Mtg , 2010 : 1044-1049 |
| [17] | LAURENT S, GERHARD P R. Efficient waveform inversion and imaging:a strategy for selecting temporal frequencies[J]. Geophysics , 2004, 69 (1) : 231-248 DOI:10.1190/1.1649391 |


