2. 中国石油天然气股份有限公司塔里木油田分公司勘探开发研究院, 新疆库尔勒 841000;
3. 中国石油天然气集团公司东方地球物理勘探有限公司研究院, 河北涿州 072750
2. Research Institute of Exploration and Development, Tarim Oilfield Company, PetroChina Company Limited, Korle 841000, China;
3. Bureau of Geophysical Prospecting INC., China National Petroleum Corporation, Zhuozhou 072750, China
由于地表变化、地表障碍以及人为施工等因素的影响, 造成原始陆上地震资料的炮点、检波点分布不规则, 给后续地震资料处理带来困难。
相干噪声是一种相对规则的干扰波, 目前常用的去噪方法有F-K滤波、拉东变换、f-x域滤波、基于小波变换分解和数据重构等[1]。国内许多学者进行了大量研究。王兆湖等[2]提出了一种利用频域自适应滤波的方法; 高少武等[3]提出了时间-空间域自适应相干噪声衰减技术; 鲁娥等[4]采用相似函数压制端点效应和截断效应的混合拉东变换从地震剖面中一次性分离面波等线性噪声, 再应用自适应滤波技术在拉东域识别并剔除噪声; 覃天[5]主要利用了小波变换的分频特性来压制相干噪声。上述压制相干噪声的原理主要基于两个基本假设:①相干噪声在地震记录上是线性的; ②相干噪声与有效信号的视速度不同。但是, 因地表条件限制, 炮、检点布设不规则等因素的影响, 实际地震资料中相干噪声是非线性的; 或者三维地震资料的远排列数据, 其相干噪声也不再是线性关系, 而呈现类双曲线关系, 因此压制相干噪声不理想。针对“远排列”去噪问题, 一些学者进行了相关研究, 如汪铁望等[6]、刘明乾等[7]、高秦等[8]针对地震采集资料中的二维弯线、非纵及三维测线中的非线性的相干噪声, 先进行时差校正或者时空校正使其线性化, 然后再进行线性噪声的去除; 田彦灿等[9]针对宽方位地震资料中的线性干扰的非线性化问题, 根据折射波的传播路径计算折射波时差, 并进行线性时差校正, 以消除横向炮检距变化对折射波旅行时的影响, 将各排列的道间距恢复为观测系统设计的道距, 可避免线性干扰波时距曲线形态双曲线化。上述方法解决“非纵观测”的非线性相干噪声的研究思路基本一致, 都采用时差校正的方法来尽量消除相干噪声的非线性化, 使相干噪声呈线性后再进行去噪处理, 但是时差校正的方法涉及到速度, 近地表速度的变化情况必然影响时差校正的效果, 同时该方法也没有考虑检波点间距或炮点之间距离不相等的问题。
针对上述问题, 我们提出了一种基于局部数据规则化的相干噪声压制技术, 通过在不规则观测系统局部区域利用五维插值技术构建规则化道集, 使噪声信号充分满足上述基本假设条件, 从而更好地获取相干噪声并进行压制, 山地实际地震资料的应用效果证实了该方法的有效性。
1 方法原理相干噪声的压制效果很大程度上依赖于噪声的相关程度。如果相干噪声具有数学意义上的相关性, 那么即使采用最简单的F-K滤波法, 其压制相干噪声、恢复有效信号的能力也是惊人的。然而, 陆上采集作业基本是人为施工, 操作的灵活性大、炮点和检波点的定位精度是由实际地表环境条件和采集作业的施工效率决定的, 相干噪声更多地呈现出“视相干”, 因此, 现有压制线性噪声的方法往往达不到预期效果。所以, 要想更好地压制相干噪声, 必须使相干噪声呈现严格的线性。
1.1 基于局部数据规则化的相干噪声压制技术针对非规则相干噪声, 我们提出了基于局部数据规则化的相干噪声压制技术思路。该方法的目标是使噪声信号尽量满足相干噪声压制技术的基本假设, 即相干噪声呈线性。采用十字交叉排列数据进行该技术基本原理说明, 其技术流程如图 1所示。
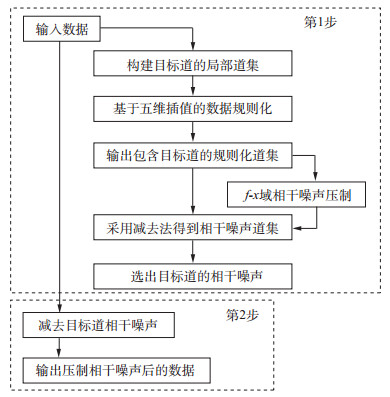
|
图 1 基于局部数据规则化的相干噪声压制技术流程 |
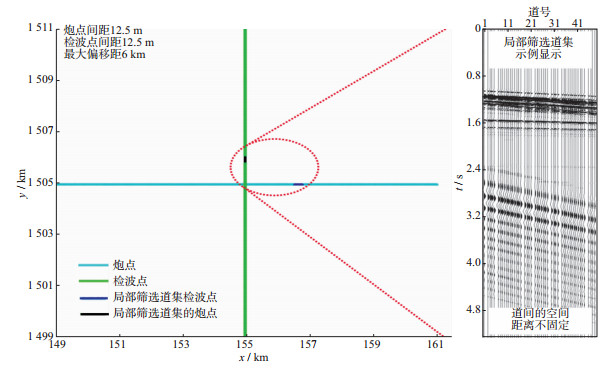
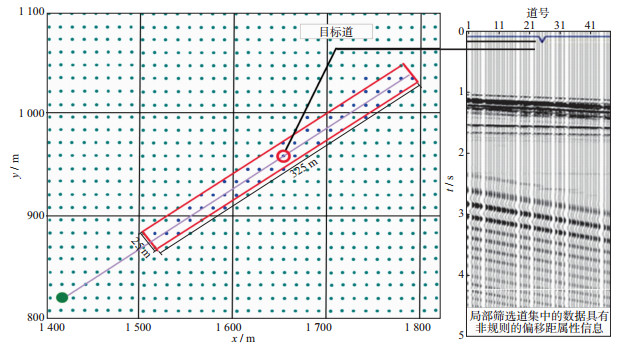
该方法的核心是第一步, 首先利用输入数据给每个地震道(称为目标道)构建一个“局部道集”, 需要确定“局部道集”的大小, 且该道集内的数据要具有相近的方位角信息(图 2, 图 3), 目标道的位置尽量在局部道集的中间位置。由于局部道集的道间距不同, 本文采用五维插值技术对局部道集进行规则化处理, 重新构建一个具有相同道间距的规则化道集(图 4)。这里需注意, 每个局部道集中的目标道是不进行任何处理的, 包括目标道本身和坐标。
|
图 2 十字交叉排列及局部筛选道集示意图解 |
|
图 3 数据规则化前局部筛选道集示意图解 |
|
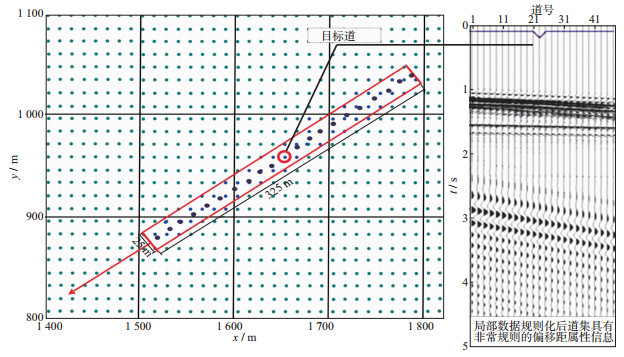
图 4 数据规则化后的局部筛选道集示意图解 |
如图 4所示, 数据规则化后的局部道集具有相同的道间距, 相干噪声基本呈现标准的线性, 然后利用F-K滤波法或者f-x域去噪技术对这种规则化的道集数据压制相干噪声, 最后选出目标道的噪声。因此如何实现“局部道集”的规则化处理, 是本文非规则相干噪声压制方法实现的关键环节, 我们研究了基于正交匹配追踪(OMP)算法的五维数据插值方法。
1.2 正交匹配追踪(OMP)算法OMP类算法是通过贪婪追踪算法每次迭代选择一个局部最优解来逐步逼近原始信号。该类算法均用匹配追踪(MP)算法[10-12]中的原子选择原则来选择原子更新支撑集, 并通过最小二乘法来获得最优解。各种算法的不同之处在于原子的选择方式不同。
通过余量r和观测矩阵A的每一列的内积计算来计算相关系数:
| ${g_n} = {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{r}}_{n - 1}}$ | (1) |
初始余量r0=y, y为观测向量。计算可得:
| $\mathit{\boldsymbol{u}} = \left\{ {{u_j}|{u_j} = |{\mathit{\boldsymbol{g}}_n}\left( j \right)|,j = 1,2, \cdots ,N} \right\}$ | (2) |
式中:uj=|gn(j)|表示由余量和观测矩阵内积得到的相关系数中的一个系数;u为uj组成的系数向量。
从相关系数向量中选择原子索引集J(选取原则一般是选相关系数最大的值, 即选取使得argmaxj=1, 2, …, d|〈y, uj〉|成立的索引), 更新支撑集Sn=Sn-1∪J(S0一般为空集)及原子向量Asn, 并用最小二乘法求得近似解:
| ${\mathit{\boldsymbol{\theta }}_n} = \mathit{\boldsymbol{A}}_{{s_n}}^ + \mathit{\boldsymbol{y}}$ | (3) |
其中, Asn+=(AsnTAsn)-1AsnT表示用观测矩阵A中选取的原子向量Asn的最小二乘矩阵, 与y相乘得到的结果θn即为压缩后的信号, 再用压缩后的信号更新余量为:
| ${\mathit{\boldsymbol{r}}_n} = \mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{A}}_{{s_n}}}{\mathit{\boldsymbol{\theta }}_n}$ | (4) |
OMP算法首先采用相关性原则, 选择和迭代余量最匹配的原子, 然后将已选择的原子进行Gram-Schmidt正交化处理, 再将信号投影到这些正交原子构成的空间上, 得到信号在已选原子上的分量和迭代余量, 然后用相同的方法分解余量[13]。
OMP算法由于进行了Gram-Schmidt正交化处理, 保证了每次迭代的最优性, 减少了迭代的次数。但是该算法也存在两个问题:①每次用最小二乘法迭代, 计算量和存储复杂度都很高; ②在每次迭代中仅选取一个原子来更新支撑集,重构时间代价大。随着迭代次数的增加, 运行时间也会增加, 对于一些数据量很大的信号, OMP算法甚至无法应用。因此后续出现了一系列改进算法, 例如针对计算量问题, 本文采用共轭梯度方法(CG)计算最小二乘最小化公式; 针对重构时间, 在每次迭代中选取一个原子来更新支撑集, 即傅里叶扩展函数集。
1.3 基于OMP算法的数据规则化技术一般来说, 实现地震数据规则化和插值是先将不规则网格点的时间域数据进行傅里叶变换到空间频率域, 再进行规则网格点的数据规则化和插值, 最后经过傅里叶反变换变换到时间域。数据规则化和插值时需要进行数据和维度的选择, 即如何选择和排列数据, 在什么样的维度上进行数据规则化和插值, 同样是数据规则化和插值的关键[11-13]。
基于OMP的数据规则化技术基于傅里叶展开式表示输入数据以及用展开式的因子在任何期望的空间位置来进行数据重建。为更清楚地解释其原理, 这部分插值的扩展用二维地震数据来说明。
假定f(xj)表示对于给定频率的空间频率域地震数据, 其中, j=0, 1, …, Nx-1, Nx是地震道数, xj(0≤xj≤xmax)是空间坐标, 则输入数据的傅里叶扩展形式为:
| $f\left( {{x_j}} \right) \approx \sum\limits_l {\tilde f\left( l \right)} {{\rm{e}}^{{\rm{i2 \mathsf{ π} }}l{x_j}/{x_{\max }}}}$ | (5) |
其反变换为:
| $\tilde f\left( l \right) \approx \sum\limits_{j = 0}^{{N_x} - 1} {f\left( {{x_j}} \right)} {{\rm{e}}^{{\rm{ - i2 \mathsf{ π} }}l{x_j}/{x_{\max }}}}$ | (6) |
公式(5)和公式(6)通过不规则快速傅里叶变换得到。
空间波数kl与指数l的关系为:kl=2πl/xmax, l=-Nk/2, -Nk/2+1, …, Nk/2-1, Nk表示空间频率的个数。假定最大波数为固定值, 增加xmax的值会导致波数域的过采样和冗余扩展空间; 反之, 则会提高插值计算效率。通常xmax选用最大偏移距的4倍。
OMP算法在公式(5)扩展时每增加一个分量, 经过m步后, 误差可以写成:
| ${R^m}\left( {{x_j}} \right) = f\left( {{x_j}} \right) - \sum\limits_{l = 0}^{m - 1} {\tilde f\left( {{P_l}} \right)} {{\rm{e}}^{{\rm{i2 \mathsf{ π} }}{P_l}{x_j}/{x_{\max }}}}$ | (7) |
式中:Pl是在第l步系数的指数。
OMP算法可以大致总结为以下几步:
首先, 构造一个元素为e-i2πlxj/xmax的索引为l×j(即l行, l > sum{-Nk/2, -Nk/2+1, …, Nk/2-1};j列, j=0, 1, …, Nx-1)的冗余字典为观测矩阵A, 观测向量y={f(xj):j=0, 1, …, Nx-1)}T。
然后, 初始化。设定m=0, R0(xj)=f(xj), 迭代过程如下。
1)通过公式(6)计算傅里叶变换系数如下:
| $\tilde R\left( l \right) = \sum\limits_{j = 0}^{{N_x} - 1} {{R^m}\left( {{x_j}} \right)} {{\rm{e}}^{{\rm{ - i2 \mathsf{ π} }}l{x_j}/{x_{\max }}}} = \mathit{\boldsymbol{Ay}}$ | (8) |
| $l = - {N_k}/2, - {N_k}/2 + 1, \cdots ,{N_k}/2 - 1$ |
然后找到量级最大系数的索引集Pm, 更新支撑集Sn=Sn-1∪Pm, 那么选取的原子向量就是Asn。
2)那么由选取的原子得到的傅里叶系数矩阵就为Asny, 令
| $\varphi \left( {m + 1} \right) = {\sum\limits_j {\left[ {f\left( {{x_j}} \right) - \sum\limits_{l = 0}^m {\tilde f\left( {{P_l}} \right)} {{\rm{e}}^{{\rm{i2 \mathsf{ π} }}{P_l}{x_j}/{x_{\max }}}}} \right]} ^2}$ | (9) |
注意这一步骤与前文所述的OMP算法稍有不同, 前文是直接由选取的原子向量进行最小二乘再与观测矩阵相乘得到压缩信号, 此步骤是先将选取的原子向量与观测信号相乘得到相应的傅里叶系数, 再对此傅里叶系数进行反变换得到时间域信号, 用此时间域信号跟原始信号做最小二乘最小化, 相当于每迭代一次都重新计算一遍先前得到的傅里叶系数以得到最优结果。这里的φ表示基于最小二乘最小化原理构造的目标函数, 最后得到最优傅里叶系数
3)将
4)当‖Rm+1‖变得足够小时或者当达到所允许系数的最大个数时, 终止。
步骤2)是采用共轭梯度法计算, 虽然共轭梯度的解需要大量正向和反向的不规则傅里叶变换, 但是减少了共轭梯度迭代次数, 因此提高了总的计算效率。
1.4 基于OMP算法的五维数据规则化的实现目前, 国内基于OMP算法的数据规则化主要应用于三维数据处理[14-15], 而五维数据规则化是将所有数据放在一起, 考虑三维不同面元数据本身所包含的五维信息:主测线(inline)、联络测线(crossline)、偏移距(offset)、方位角(azimuth)和时间, 其规则化过程与二维、三维数据规则化类似[16-18]。
三维叠前地震数据可由时间(t)、主测线(I)、联络测线(X)、偏移距(O)以及方位角(A)为自变量的五维函数f(t, Im, Xn, Op, Aq)完整表示, 其中, m, n, p, q分别为I, X, O, A的索引。其频率空间域表示为F(Im, Xn, Op, Aq), 因此五维插值就是在频率域中对其它4个维度插值。
基于傅里叶正交基的扩展, F(Im, Xn, Op, Aq)的离散傅里叶变换的扩展式为:
| $\begin{array}{l} F\left( {{I_m},{X_n},{O_p},{A_q}} \right) = \sum\limits_{{k_{{I_m}}} = 0}^{{K_{{I_m}}}} {{\beta _{{k_{{I_m}}}}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ {{\rm{i}}2{\rm{ \mathsf{ π} }}{k_{{I_m}}}{I_m}/\left( {{K_{{I_m}}}{D_{{I_m}}}} \right)} \right] \end{array}$ | (10) |
其离散傅里叶系数为:
| $\begin{array}{l} {\beta _{{k_{{I_m}}}}} = \frac{1}{{{K_{{I_m}}}{D_{{I_m}}}}}\sum\limits_{{k_{{I_m}}} = 0}^{{K_{{I_m}}}} F \left( {{I_m},{X_n},{O_p},{A_q}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ {{\rm{ - i}}2{\rm{ \mathsf{ π} }}{k_{{I_m}}}{I_m}/\left( {{K_{{I_m}}}{D_{{I_m}}}} \right)} \right] \end{array}$ | (11) |
对βkIm函数中的Xn进行离散傅里叶变换得到βkIm的扩展式:
| $\begin{array}{l} {\beta _{{k_{{I_m}}}}}\left( {{X_n},{O_p},{A_q}} \right) = \sum\limits_{{k_{{X_n}}} = 0}^{{K_{{X_n}}}} {\chi {k_{{I_m}}}{k_{{X_n}}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ {{\rm{i}}2{\rm{ \mathsf{ π} }}{k_{{X_n}}}{X_n}/\left( {{K_{{X_n}}}{D_{{X_n}}}} \right)} \right] \end{array}$ | (12) |
其离散傅里叶系数为:
| $\begin{array}{l} \chi {k_{{I_m}}}{k_{{X_n}}} = \frac{1}{{{K_{{X_n}}}{D_{{X_n}}}}}\sum\limits_{{k_{{X_n}}} = 0}^{{K_{{X_n}}}} {{\beta _{{k_{{I_m}}}}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ {{\rm{ - i}}2{\rm{ \mathsf{ π} }}{k_{{X_n}}}{X_n}/\left( {{K_{{X_n}}}{D_{{X_n}}}} \right)} \right] \end{array}$ | (13) |
对χkImkXn函数中的Op进行离散傅里叶变换得到χkImkXn的扩展式:
| $\begin{array}{l} \chi {k_{{I_m}}}{k_{{X_n}}}\left( {{O_p},{A_q}} \right) = \sum\limits_{{k_{{O_p}}} = 0}^{{K_{{O_p}}}} {{\xi _{{k_{{I_m}}}{k_{{X_n}}}{k_{{O_p}}}}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ {{\rm{i}}2{\rm{ \mathsf{ π} }}{k_{{O_p}}}{O_p}/\left( {{K_{{O_p}}}{D_{{O_p}}}} \right)} \right] \end{array}$ | (14) |
其离散傅里叶系数为:
| $\begin{array}{l} {\xi _{{k_{{I_m}}}{k_{{X_n}}}{k_{{O_p}}}}} = \frac{1}{{{K_{{O_p}}}{D_{{O_p}}}}}\sum\limits_{{k_{{O_p}}} = 0}^{{K_{{O_p}}}} {\chi {k_{{I_m}}}{k_{{X_n}}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ {{\rm{ - i}}2{\rm{ \mathsf{ π} }}{k_{{O_p}}}{O_p}/\left( {{K_{{O_p}}}{D_{{O_p}}}} \right)} \right] \end{array}$ | (15) |
同理, 对ξkImkXnkOp函数中的Aq进行离散傅里叶变换得到ξkImkXnkOp的扩展式:
| $\begin{array}{*{20}{l}} {{\xi _{{k_{{I_m}}}{k_{{X_n}}}{k_{{O_p}}}}}\left( {{A_q}} \right) = \sum\limits_{{k_{{A_q}}} = 0}^{{K_{{A_q}}}} {\alpha {k_{{I_m}}}{k_{{X_n}}}{k_{{O_p}}}{k_{{A_q}}}} \exp \cdot }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\left[ {{\rm{i}}2{\rm{ \mathsf{ π} }}{k_{{A_q}}}{A_q}/\left( {{K_{{A_q}}}{D_{{A_q}}}} \right)} \right]} \end{array}$ | (16) |
其离散傅里叶系数为:
| $\begin{array}{*{20}{l}} {\alpha {k_{{I_m}}}{k_{{X_n}}}{k_{{O_p}}}{k_{{A_q}}} = \frac{1}{{{K_{{A_q}}}{D_{{A_q}}}}}\sum\limits_{{k_{{A_q}}} = 0}^{{K_{{A_q}}}} {{\xi _{{k_{{I_m}}}{k_{{X_n}}}{k_{{O_p}}}}}} \cdot }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ {{\rm{ - i}}2{\rm{ \mathsf{ π} }}{k_{{A_q}}}{A_q}/\left( {{K_{{A_q}}}{D_{{A_q}}}} \right)} \right]} \end{array}$ | (17) |
前述公式中的KIm, KXn, KOp, KAq分别表示Im, Xn, Op, Aq维度中相应的采样数; DIm, DXn, DOp, DAq分别表示Im, Xn, Op, Aq维度中相应的采样间隔。
将公式(11)代入到公式(13)得到:
| $\begin{array}{l} \chi {k_{{I_m}}}{k_{{X_n}}} = \frac{1}{{{K_{{X_n}}}{D_{{X_n}}} \cdot {K_{{I_m}}}{D_{{I_m}}}}}\sum\limits_{{k_{{X_n}}} = 0}^{{K_{{X_n}}}} {\sum\limits_{{k_{{I_m}}} = 0}^{{K_{{I_m}}}} F } \left( {{I_m},} \right.{X_n},\\ \;\;\;\;{O_p},\left. {{A_q}} \right)\exp \left[ { - {\rm{i}}2{\rm{ \mathsf{ π} }}\left( {\frac{{{k_{{I_m}}}{I_m}}}{{{K_{{I_m}}}{D_{{I_m}}}}} + \frac{{{k_{{X_n}}}{X_n}}}{{{K_{{X_n}}}{D_{{X_n}}}}}} \right)} \right] \end{array}$ | (18) |
同理, 将公式(18)代入到公式(15), 再代入公式(17), 简化可表示为:
| $\begin{array}{l} \alpha {k_{{I_m}}}{k_{{X_n}}}{k_{{O_p}}}{k_{{A_q}}} = \frac{1}{{{K_{{I_m}}}{D_{{I_m}}} \cdot {K_{{X_n}}}{D_{{X_n}}} \cdot {K_{{O_p}}}{D_{{O_p}}} \cdot {K_{{A_q}}}{D_{{A_q}}}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{{k_{{A_q}}} = 0}^{{K_{{A_q}}}} {\sum\limits_{{k_{_{{O_p}}}} = 0}^{{K_{_{{O_p}}}}} {\sum\limits_{{k_{{X_n}}} = 0}^{{K_{{X_n}}}} {\sum\limits_{{k_{{I_m}}} = 0}^{{K_{{I_m}}}} F } } } \left( {{I_m},{X_n},{O_p},{A_q}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( { - {\rm{i}}\mathit{\Phi }} \right) \end{array}$ | (19) |
式中:αkImkXnkOpkAq为离散傅里叶变换系数。公式(19)即为五维地震数据的离散傅里叶变换。
最后, 基于傅里叶正交基的扩展, F(Im, Xn, Op, Aq)离散傅里叶变换的反变换可表示为:
| $\begin{array}{l} F\left( {{I_m},{X_n},{O_p},{A_q}} \right) = \\ \;\;\;\;\;\;\;\;\sum\limits_{{k_{{A_q}}} = 0}^{{K_{{A_q}}}} {\sum\limits_{{k_{_{{O_p}}}} = 0}^{{K_{_{{O_p}}}}} {\sum\limits_{{k_{{X_n}}} = 0}^{{K_{{X_n}}}} {\sum\limits_{{k_{{I_m}}} = 0}^{{K_{{I_m}}}} {\alpha {k_{{I_m}}}{k_{{X_n}}}{k_{{O_p}}}{k_{{A_q}}}} } } } \exp \left( {{\rm{i}}\mathit{\Phi }} \right) \end{array}$ | (20) |
其中,
| $\begin{array}{l} \mathit{\Phi } = \frac{{2{\rm{ \mathsf{ π} }}}}{{{K_{{I_m}}}{D_{{I_m}}}}}{k_{{I_m}}}{I_m} + \frac{{2{\rm{ \mathsf{ π} }}}}{{{K_{{X_n}}}{D_{{X_n}}}}}{k_{{X_n}}}{X_n} + \frac{{2{\rm{ \mathsf{ π} }}}}{{{K_{{O_p}}}{D_{{O_p}}}}} \cdot \\ \;\;\;\;\;\;\;{k_{{O_p}}}{O_p} + \frac{{2{\rm{ \mathsf{ π} }}}}{{{K_{{A_q}}}{D_{{A_q}}}}}{k_{{A_q}}}{A_q} \end{array}$ | (21) |
依次计算“主测线、联络测线、偏移距、方位角”每一维度的傅里叶扩展函数的系数, 执行1.3节中步骤1)至步骤4)迭代过程, 依次得到该扩展函数的最小化误差函数。获得扩展函数系数的方法与常规方法的主要区别是加入一个新的扩展项后, 重新计算所有扩展函数的系数; 而常规方法保持先前计算的扩展项系数不变的情况下, 依次选取一个额外的扩展函数和其系数。
常规三维数据规则化是进行主测线、联络测线和时间3个维度的数据规则化和插值, 忽略了数据在不同偏移距和不同方位角之间的联系, 不能很好地保真保幅以及保持偏移距和方位角信息, 而本文中的五维数据规则化技术很好地解决了这个问题。
2 应用效果分析为了检验本文方法在压制相干噪声方面的有效性和适应性, 采用山地实际地震资料进行效果测试。
图 5为单炮记录对比结果。图 5a是原始单炮记录, 是一个远炮点接收排列的共炮点道集, 受野外地表条件的限制, 很难实现规则观测系统采集, 可以看出, 资料的信噪比非常低, 相干噪声在单炮记录上呈现非线性关系, 有明显的扭曲现象。图 5b是常规f-x域去噪后的单炮记录, 可以看出, 噪声压制效果不理想, 并且去噪后地震记录上有明显的线性噪声, 根本原因在于非规则观测系统导致相干噪声相干性变差。图 5c是采用本文方法的去噪结果, 可以看出, 地震记录上没有明显的线性噪声遗留现象, 整个地震记录的波场特征较常规去噪结果更自然, 去噪结果比较理想。
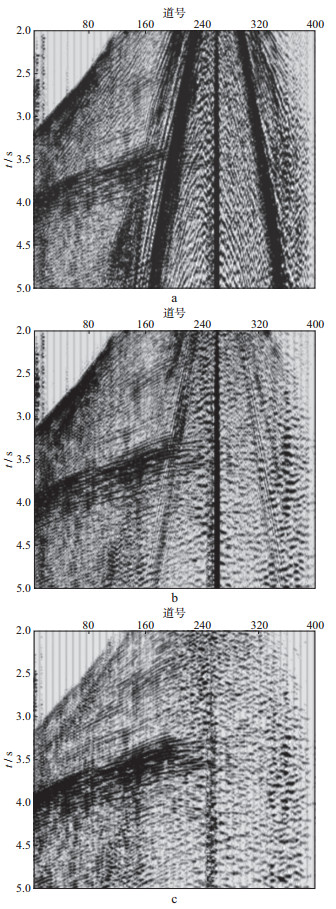
|
图 5 不规则观测系统去噪前、后单炮记录对比 a原始单炮记录; b常规f-x域去噪后的单炮记录; c本文方法去噪后的单炮记录 |
图 6为叠加剖面对比结果。图 6a是去噪前的叠加剖面, 资料的信噪比非常低, 隐约见到地震有效反射。图 6b是常规f-x域去噪结果, 可以看出, 剖面线性噪声压制总体效果比较好, 但剖面右侧区域噪声压制效果不尽理想, 有残余噪声。图 6c是采用本文方法的压制结果, 与图 6b相比, 噪声压制效果更好, 尤其是压制了剖面右侧的异常噪声, 整个剖面背景自然。图 7为采用不同方法去掉的噪声记录及噪声叠加剖面。在图 7a的噪声单炮记录和图 7c噪声叠加剖面中, 红色箭头指示处能看到有效信号, 而在图 7b和图 7d中难以见到有效信号。图 7b噪声单炮记录形态与图 5a单炮记录中的噪声形态更接近。
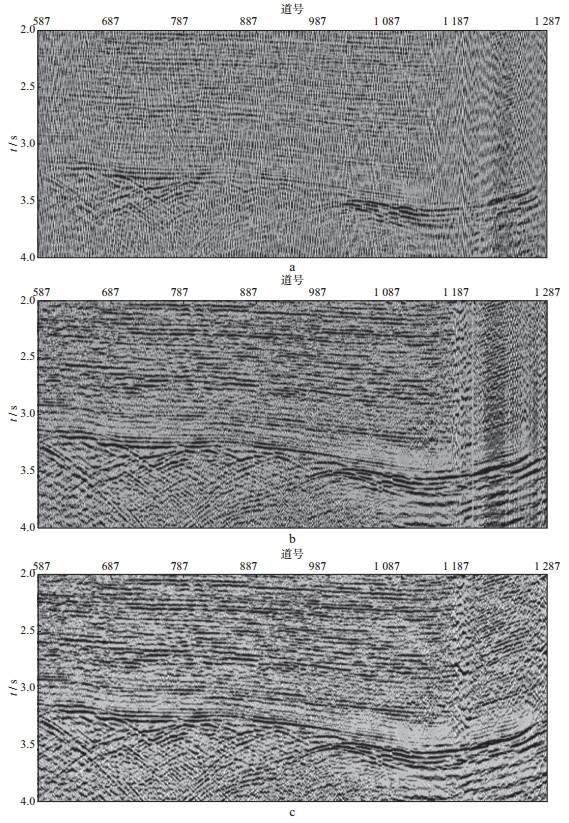
|
图 6 不规则观测系统去噪前、后叠加剖面对比 a去噪前叠加剖面; b常规f-x域去噪后的叠加剖面; c本文方法去噪后的叠加剖面 |
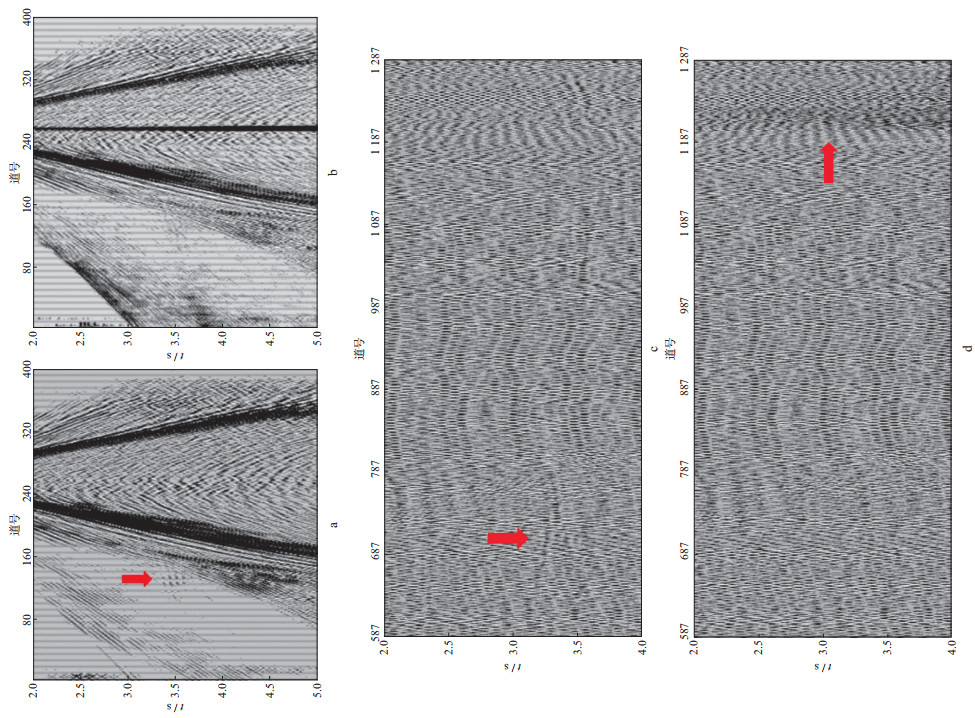
|
图 7 采用不同方法去掉的噪声及噪声叠加剖面 a常规f-x域去掉的单炮噪声记录; b本方文法去掉的单炮噪声记录; c常规f-x域去掉的噪声叠加剖面; d本文方法去掉的噪声叠加剖面 |
实际资料应用效果证明, 该方法可以更好地压制非规则相干噪声。
3 结论与认识相干噪声的压制效果不理想, 往往不是去噪方法或技术本身的不足, 而是由于地震数据不能满足去噪方法的假设条件。野外采集环境的限制、人为施工的误差都有可能导致相干噪声发生扭曲或者畸变。因此, 我们提出了在局部区域利用五维插值技术构建规则化的道集, 使噪声信号满足相干的假设条件后再进行压制的新思路。
在构建规则化道集时, 本文采用了基于OMP的五维数据规则化技术, 一方面在计算过程中采用共轭梯度法, 提高了计算效率; 另一方面充分考虑了三维地震数据在主测线、联络测线的时间域振幅与偏移距和方位角之间的联系, 更好地保真保幅并保持偏移距和方位角信息。
我们提出的相干噪声压制技术是基于地震数据真实坐标驱动的, 可以有效压制因不规则观测造成的同相轴扭曲的相干噪声, 即使在严重的非规则几何关系观测系统的地震数据也可能得到较理想的去噪结果。山地实际地震资料的应用效果证明了该方法的优越性和实用性。
| [1] |
杨宁, 贺振华, 黄德济. 基于系数相关性阈值的波原子域叠前地震资料信噪分离方法[J].
石油地球物理勘探 , 2011, 46 (1) : 53-57 YANG N, HE Z H, HUANG D J. Signal and noise separation method for pre-stack seismic data in wave atomic domain based on coefficient correlation threshold[J]. Oil Geophysical Prospecting , 2011, 46 (1) : 53-57 |
| [2] |
王兆湖, 王建民, 高振山, 等. 叠前自适应f-x域相干噪音衰减技术及应用[J].
地球物理学进展 , 2013, 28 (5) : 2605-2610 WANG Z H, WANG J M, GAO Z S, et al. Pre-stack self-adapting f-x domain coherent noise attenuation technique and application[J]. Progress in Geophysics , 2013, 28 (5) : 2605-2610 |
| [3] |
高少武, 赵波, 周兴元. 自适应相干噪声衰减技术[J].
石油地球物理勘探 , 2003, 38 (3) : 242-246 GAO S W, ZHAO B, ZHOU X Y. Self-adaptive coherent noise attenuation technique[J]. Oil Geophysical Prospecting , 2003, 38 (3) : 242-246 |
| [4] |
鲁娥, 李庆春. 混合Radon变换地震噪声压制的应用[J].
物探与化探 , 2013, 37 (4) : 706-710 LU E, LI Q C. The application of seismic noise attenuation based on hybrid radon transform[J]. Geophysical & Geochemical Exploration , 2013, 37 (4) : 706-710 |
| [5] |
覃天. 基于小波分频叠前相干噪声压制方法[J].
地球物理学进展 , 2009, 24 (4) : 1426-1430 QIN T. Prestack coherent noise attenuation based on wavelet frequency-division[J]. Progress in Geophysics , 2009, 24 (4) : 1426-1430 |
| [6] |
汪铁望, 于相海, 胡浩, 等. 弯曲测线地震资料相干噪声压制[J].
地球物理学进展 , 2010, 25 (3) : 946-950 WANG T W, YU X H, HU H, et al. Attenuation of coherent noise in seismic data coith crooked line geometry[J]. Progress in Geophysics , 2010, 25 (3) : 946-950 |
| [7] |
刘明乾, 于相海, 周夏丽, 等. 非纵测线地震资料相干噪声压制[J].
石油物探 , 2011, 50 (3) : 307-309 LIU M Q, YU X H, ZHOU X L, et al. Coherent noise attenuation in broadside seismic data[J]. Geophysical Prospecting for Petroleum , 2011, 50 (3) : 307-309 |
| [8] |
高秦, 田子奇, 王智茹, 等. 时空变换在地震数据处理中的应用[J].
石油地球物理勘探 , 2011, 46 (1) : 48-52 GAO Q, TIAN Z Q, WANG Z R, et al. Application of time-space transformation in seismic data processing[J]. Oil Geophysical Prospecting , 2011, 46 (1) : 48-52 |
| [9] |
田彦灿, 王西文, 彭更新, 等. 宽方位地震资料噪声压制技术[J].
石油地球物理勘探 , 2011, 46 (2) : 187-191 TIAN Y C, WANG X W, PENG G X, et al. Noise attenuation technology on wide azimuth seismic data[J]. Oil Geophysical Prospecting , 2011, 46 (2) : 187-191 |
| [10] |
李建卓. 匹配追踪算法在振动信号去噪中的应用[J].
计算机与数字工程 , 2013, 41 (12) : 1918-1919 LI J Z. Application of matching pursuit algorithm in vibration signal de-noising[J]. Computer & Digital Engineering , 2013, 41 (12) : 1918-1919 |
| [11] |
赵天姿, 宋炜, 王尚旭. 基于匹配追踪算法的时频滤波去噪方法[J].
石油物探 , 2008, 47 (4) : 367-371 ZHAO T Z, SONG W, WANG S X. Time-frequency filtering de-noise method based on matching pursuit algorithm[J]. Geophysical Prospecting for Petroleum , 2008, 47 (4) : 367-371 |
| [12] |
蔡涵鹏, 贺振华, 高刚, 等. 基于混合优化算法的地震数据匹配追踪分解[J].
中南大学学报(自然科学版) , 2013, 44 (2) : 687-694 CAI H P, HE Z H, GAO G, et al. Seismic data matching pursuit using hybrid optimization algorithm and its application[J]. Journal of Central South University (Science and Technology) , 2013, 44 (2) : 687-694 |
| [13] |
杨真真, 杨震, 孙林慧. 信号压缩重构的正交匹配追踪类算法综述[J].
信号处理 , 2013, 29 (4) : 486-496 YANG Z Z, YANG Z, SUN L H. A survey on orthogonal matching pursuit type algorithms for signal compression and reconstruction[J]. Journal of Signal Processing , 2013, 29 (4) : 486-496 |
| [14] |
高建军, 陈小宏, 王芳芳, 等. 不规则地震道数据规则化重建方法研究[J].
地球物理学进展 , 2011, 26 (3) : 983-991 GAO J J, CHEN X H, WANG F F, et al. Study on regularized reconstruction of uneven seismic traces[J]. Progress in Geophysics , 2011, 26 (3) : 983-991 |
| [15] |
唐刚.基于压缩感知和稀疏表示的地震数据重建与去噪[D].北京:清华大学, 2010
TANG G.Seismic data reconstruction and denoising based on compressive sensing and sparse representation[D].Beijing:Tsinghua University, 2010 http://cdmd.cnki.com.cn/article/cdmd-10003-1011280421.htm |
| [16] | NIMSAILA K, WANG P. Fast progressive sparse Tau-P transform for regularization of spatially aliased seismic data[J]. Expanded Abstracts of 76th EA-GE Annual Conference , 2014 : 230-234 |
| [17] | POOLE G, HERMANN P. Multi-dimensional data regularization for modern acquisition geometries[J]. Expanded Abstracts of 69th EAGE Annual conference , 2007 : 70-75 |
| [18] | XU S, ZHANG Y, LAMBARE G. Anti-leakage Fourier transform for seismic data regularization practice in higher dimensions[J]. Geophysics , 2010, 70 (4) : 87-95 |


