2. 金陵科技学院 机电工程学院, 南京 210000
2. School of Electrical Engineering, Jinling Institute of Technology, Nanjing 210000, China
物质在外力作用下, 发生的常见形变主要分为弹性形变与黏性流动, 但也有相当数量的物质同时存在弹性和黏性共有的黏弹性流变学特征, 如聚合物溶液、凝胶等。流变学是研究物质在外力作用下流动和变形规律的科学, 是一门介于物理、化学、力学和工程科学之间的交叉学科[1]。传统流变学对获取复杂物质力学特性和参数起到了重要作用, 在涉及复杂黏弹性材料的不同行业得到了广泛应用。随着"软物质"概念的建立[2]和微纳流动实验技术的发展, 基于显微定量观测技术的微流变学(Microrheology)被提出, 已成为一门与传统流变学显著不同的独立的流变学分支。与传统流变学实验方法不同, 微流变学在显微尺度上探测复杂物质的局部黏弹性, 从而实现工业领域、生物医学和现代日常生活中普遍存在的各种复杂流体/软物质在微米乃至分子尺度下的力学表征, 对一些非均质性液体局部流变特征分布、高分子凝胶液-固转变特性测量以及一些量少、稀有样品流变特性的研究发挥着重要作用[3-5]。微流变学将测量物质黏弹性的方法从宏观、平均、粗粒化水平跨越到了微观、局部、精细化水平, 极大地拓展了人们认识复杂流体/软物质力学特性的能力, 它所涉及的各类技术成为研究各种复杂流体/软物质微观黏弹特性的强有力方法。
根据探针颗粒驱动方式的不同, 微流变学的研究方法主要分为两类:被动微流变方法(Passive microrheology technique)和主动微流变方法(Active microrheology technique)。前者源于探针颗粒受到被测流体分子热运动作用产生的不规则热运动, 后者则是通过某种特殊技术在探针颗粒上施加作用力使其产生位移[6]。被动微流变方法主要分为光散射微流变技术(Light Scattering Microrheology, LSM)、颗粒追踪微流变技术(Particle Tracking Microrheo-logy, PTM)两类, 其动力学基础为粒子布朗运动。被动微流变方法始于Mason[7]和Gittes[8]等开创性的研究。Mason等发现探针颗粒在介质中的热运动与样品的黏弹特性有关, 从而引入了广义Stokes-Einstein(Generalized Stokes-Einstein, GSE)关系研究其黏弹特性。主动微流变方法中, 探针颗粒通常由恒定或振荡的外力场驱动(磁场、电场、光场等), 所以常用的探针颗粒是具有磁性、带电或具有高折射系数的颗粒[9]。目前, 主动微流变方法以磁镊、光镊和原子力显微镜为代表。
随着高分子物理、化学、生物医学工程、材料科学以及溶胶/凝胶等软物质力学的发展, 微流变学在表征复杂溶液和软物质微观材料力学性质方面发挥着重要作用。Larsen等[10]利用多颗粒追踪微流变方法(Multi-Particle Tracking, MPT)从探针颗粒动力特征中识别出聚合物凝胶液-固转变的凝胶点、临界松弛指数和动态缩放指数, 表明微流变学可用于在凝胶化转变中提取整个流变特征谱。Gambini等[11]对水母注射胺修饰荧光微球悬浮液, 通过MPT方法研究了水母下伞面细胞外基质(Extracellular Matrix, ECM)的机械性质及其老化过程中力学性能的演变, 通过和宏观微流变仪所得结果比较发现, ECM在宏观尺度上表现为黏弹性凝胶特性, 而在微观尺度下则表现为更柔软和非均匀的黏弹特性。Abdala等[12]使用扩散波谱法(Diffusing-Wave Spectroscopy, DWS)探测梳状疏水改性的碱溶胀性缔合(HASE)聚合物的动力学特征。Xu等[13]通过视频荧光显微镜监测分散良好的微球的热驱动位移, 研究了高黏度燕麦β-葡聚糖溶液的微观结构异质性和微观流变性, 发现微观结构的不均匀性和微流变性质的变化都发生在β-葡聚糖的小浓度范围之间。Cohen等[14]使用MPT方法, 将蜂蜜的经典宏观流变与其热波动颗粒追踪微观流变进行了比较, 证明了使用颗粒追踪微流变方法可以准确表征高黏度样品。Moschakis等[15-18]使用MPT方法研究了含有黄原胶的稳定酪蛋白乳液和酪蛋白的凝胶化以及葡聚糖多糖的结构动力学。Nath等[19]使用荧光相关光谱法和单粒子跟踪(SPT)实验方法获得分散在简单各向同性液体和聚氧化乙烯(PEO)溶液中的纳米粒子探针的均方位移, 对"陷(captured)"在高分子聚合物"笼(cage)"中探针颗粒的运动进行实验分析, 研究了纠缠聚合物溶液中纳米粒子的动力学。van Zanten等[20]使用扩散波谱法测量了25 ℃时不同浓度的PEO溶液的动力学。
目前, 对于固定温度下聚合物溶液的微观流变特性研究较为常见, 但不同温度下聚合物溶液微流变特性的实验研究并不多见。本文采用单颗粒追踪方法, 对温度变量下不同浓度的PEO溶液的微流变特性进行了测量和分析。开展了不同温度下(25 ℃、35 ℃和45 ℃), 浓度为0.4 wt%、0.6 wt%、0.8 wt%和1.0 wt%的PEO溶液的微流变特性的实验研究。
1 基本原理在简单流体中, 探针颗粒受到水分子等的热运动作用而发生自由布朗运动。但在链状高分子溶液中, 颗粒被链状分子构成的网状结构限制, 颗粒的自由布朗运动强度被削弱。图 1为颗粒在高分子溶液中所受链状分子网络限制的示意图, 图中大圆(球体)表示布朗颗粒, 灰色的小圆代表水分子, 细长曲线表示链状分子。由于受到链状分子网络的限制, 颗粒布朗运动规律比简单流体更为复杂。

|
| 图 1 颗粒在高分子溶液中受链状分子网络限制的示意图 Fig.1 Schematic diagram of the limitation of a macromolecular chain network on particles in a polymer solution |
在简单流体(牛顿流体)中, 探针颗粒受周围液体分子热涨落运动的作用, 其布朗运动可以用Langevin方程来描述。而在非牛顿流体中, 亚微米/纳米颗粒布朗运动规律则需要采用广义Langevin方程来描述[7, 21-22]:
 (1)
(1)
其中, m为布朗颗粒质量; V(t)为球体布朗颗粒的速度时间函数, 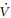
由涨落-耗散理论〈F(t)F(t')〉=6kBTξ(t-t')[23]在频域上处理记忆函数和黏度的关系, 在傅里叶域有:
 (2)
(2)
或在拉普拉斯域有:
 (3)
(3)
其中, 〈〉表示系综平均值, kB为玻尔兹曼常数, T为绝对温度, a为颗粒半径, η为流体黏度, η*(ω)、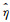
将式(2)或(3)代入上述涨落-耗散理论公式中, 可以得到探针颗粒在复杂流体内的均方位移〈Δr2(t)〉在傅里叶域的表达式:
 (4)
(4)
以及在拉普拉斯域的表达式:
 (5)
(5)
式(4)和(5)即为广义Stokes-Einstein关系(GSER)。
在微流变学理论中, 复合黏弹性模量G*与复合黏度η*之间的关系为G* (ω)=iωη* (ω)。代入式(4)和(5), 得出黏弹性流体复合黏弹性模量与均方位移的关系[7, 24-25]:
 (6)
(6)
或
 (7)
(7)
则储能(弹性)模量和损耗(黏性)模量可以通过以下关系得出:
 (8)
(8)
其中G'称为储能模量, 取G*的实部; G″称为损耗模量, 取G*的虚部。材料的储能模量和损耗模量需要通过微流变学的实验方法获得。
2 实验系统及材料制备 2.1 实验系统微流变实验平台主要由倒置显微平台(Lavison)、显微物镜(Zeiss)、电子倍增CCD相机(EMCCD, ANDOR)、连续激光器(1.5 W, λ=532 nm)以及工作站组成。实验选用直径0.49 μm荧光染色聚苯乙烯微球(Thermo Scientific)作为探针颗粒, 该粒径颗粒的布朗运动明显, 能够准确反映复杂溶液的微流变规律。实验前, 荧光微球原溶液与去离子水按体积比1:2000配制, 因此溶液中的探针颗粒密度足够低, 不会因少量探针颗粒的加入而改变被测溶液的微流变特性。实验系统如图 2所示, 532 nm连续激光通过显微物镜照射待测液体中的荧光探针颗粒, 颗粒受激发后发射的荧光(波长约610 nm)由EMCCD实时采集, 由此获得布朗运动的图像。相机帧率10.664帧/s, 每2帧之间的时间间隔Δt为0.09377 s。考虑探针颗粒长时间运动会偏离平面观测视场, 单次实验中连续拍摄帧数取为600, 采集时长为56.26 s。

|
| 图 2 颗粒追踪实验平台示意图 Fig.2 Schematic diagram of particle tracking experimental platform |
为开展温度变量下的微流变研究, 本文设计了一套对被测样品温度进行控制的方案。温度装置如图 3所示, 分为恒温加热和水浴保温两部分。图 3(a)为恒温加热箱(上海一恒, 温度分辨率/波动值:0.1 ℃/±0.5 ℃), 图 3(b)是由包覆了保温层的特制玻璃方缸制成的水浴保温装置。图 3(c)是待测溶液载玻片, 使用凹槽载玻片(凹槽半径7 mm, 槽深0.4~0.6 mm)与PDMS键合制作而成。实验时, 首先向载玻片内注入制备好浓度的待测溶液, 然后使用硅橡胶黏合剂将进出口密封。接下来, 将盛有待测溶液的载玻片放入保温玻璃方缸中进行水浴加热, 加热时将载玻片与玻璃方缸一同放入已达设定温度值的恒温加热箱内, 静置20 min后取出方缸, 置于倒置显微平台观测区进行探针颗粒布朗运动的图像采集。

|
| 图 3 温控装置硬件图 Fig.3 Diagram of temperature control device |
实验采用单颗粒追踪技术, 该方法具有颗粒识别容易、追踪准确等优势, 可以精确追踪每个时刻的颗粒位置。通过对原始图像进行图像预处理、颗粒识别和追踪、数据处理等, 计算出颗粒布朗运动均方位移。图 4(a)所示为实验采集的探针颗粒原始图像, 经过平滑、噪点清除等预处理后, 获得高质量的颗粒图像, 如图 4(b)所示。以上图像处理是基于Java语言的开源软件ImageJ进行的。

|
| 图 4 探针颗粒的原始图像及图像处理结果 Fig.4 Original image and image processing results of probe particles |
颗粒的识别和追踪采用开源软件Video Spot Tracker v07.02。得到探针颗粒运动轨迹和单步位移之后, 均方位移(MSD)采用下式进行计算:
 (9)
(9)
其中, ri表示颗粒在i时刻的位置, N为拍摄得到的颗粒运动总步数, k表示时间间隔Δt的整数倍。因此上式表示颗粒在k个时间间隔内的均方位移, 即MSD-t的关系。考虑误差等因素, 实验取1~400个时间间隔, 即k=1~400。
为确保实验平台和测量方法的有效性, 首先针对颗粒在去离子水中的布朗运动进行了验证实验。实验在室温条件下(20 ℃)进行, 使用63倍物镜对探针颗粒连续采集500帧布朗运动图像, 在对颗粒布朗运动轨迹追踪的基础上, 利用式(9)计算得到均方位移(MSD), 绘制MSD-t曲线并进行直线拟合, 结果如图 5所示。从图中可以看出, 探针颗粒均方位移随时间呈线性增长。根据牛顿流体布朗运动理论可知, 二维情况下拟合曲线斜率为4Dex:
 (10)
(10)

|
| 图 5 去离子水中MSD-t曲线及拟合直线图 Fig.5 MSD-t curve and fitting straight line in deioned water |
当温度T=293.15 K(20 ℃)时, 去离子水的动力黏性系数ηth=1.002 (mPa·s), 由Stokes-Einstein关系可以计算得出对应理论扩散系数Dth。将实验值与理论值对比, 计算实验偏差ε=(Dex-Dth)/Dth×100%, 相关数据由表 1给出。从表中可以看到, 扩散系数的实验结果与理论值相对偏差仅为3.24%, 表明实验具有较高测量精度, 为接下来开展复杂流体实验奠定了基础。
| ηth/(mPa·s) | Dth/ (μm2·s-1) | Dex/ (μm2·s-1) | ε |
| 1.002 | 0.8527 | 0.8813 | 3.24% |
本文针对一类典型的高分子溶液——聚氧化乙烯(PEO)水溶液开展微流变特性实验研究, 见图 6。PEO固体是一种白色粉末状非离子型线性高分子聚合物(图 6(a)), 具有良好的水溶性和热塑性, 其水溶液可用作水相减阻剂、胶黏剂、增稠剂等, 无毒无刺激性, 化学性质稳定[26]。PEO水溶液为透明黏稠状(图 6(b)), 能够通过光学图像采集设备(如本文采用的EMCCD)获取探针颗粒布朗运动的图像, 在此基础上对其微流变特性进行研究。本文所选PEO的相对分子质量为106, 其相关参数由表 2给出。实验的溶液与探针颗粒尺寸可以采用GSE方程进行分析[24]。

|
| 图 6 聚氧化乙烯及其水溶液 Fig.6 Polyethylene oxide and its aqueous solution |
| 分子式 | 软化点 | 熔点 | 密度 (at 25 ℃) | 水溶液PH值 (0.5 wt%) |
| CH2CH2O | (65~67) ℃ | (87~140) ℃ | 0.93 g/mL | 中性 |
图 7给出了浓度为0.4 wt%、0.6 wt%、0.8 wt%和1.0 wt%的PEO溶液在温度为25 ℃、35 ℃和45 ℃时的布朗运动轨迹。从图中可以看到探针颗粒的布朗运动呈现无规则随机运动状态。从图 7(a)~(d)的横向比较(如比较图 7(a1)~(a3)等)来看, 随着温度的升高, 相同浓度溶液中探针颗粒布朗运动逐渐增强, 其布朗运动范围明显扩大; 从图 7(a)~(d)的纵向比较(如比较图 7(a1)~(d1)等)可以看到, 在相同温度下, 随着溶液浓度的升高, 探针颗粒的整体运动范围逐步缩小, 表明探针颗粒布朗运动受限程度逐渐加大, 其原因可以从图 1中颗粒受到链状分子网络的约束得到定性解释。

|
| 图 7 布朗运动轨迹图 Fig.7 Brownian motion trajectory |
在对被测溶液中探针颗粒布朗运动进行追踪后, 得到颗粒运动轨迹和600个单步位移。本文取k个时间间隔(k=1~400), 计算得出均方位移与间隔时间的函数曲线, 即MSD-t曲线。图 8给出了对数坐标系下不同浓度PEO溶液的MSD-t曲线, 其中, 每个工况下绘制了3个不同温度(25 ℃、35 ℃和45 ℃)的曲线。从图中可以看到, PEO溶液的均方位移随着温度升高而增大, MSD-t也随温度升高呈现平滑递增趋势。特别地, 从图 8(d)中可以看到, 1.0 wt%的PEO溶液在25 ℃时均方位移曲线斜率明显减小, 表明在该温度和浓度条件下, 溶液中的高分子对探针颗粒布朗运动的限制作用显著增加, 黏弹性流体的弹性行为开始有所体现[1]。随着温度升高至35 ℃, 均方位移曲线形状恢复平滑上升特征, 其连续400步的MSD均值在数值上接近0.8 wt%(25 ℃)时的数值。图 9给出了对数坐标系下3个不同温度的MSD-t曲线。可以看到, 相同温度下, 探针颗粒布朗运动的均方位移随着浓度的升高而减小。

|
| 图 8 相同浓度不同温度下MSD-t曲线 Fig.8 MSD-t curves at the same concentration and different temperatures |

|
| 图 9 相同温度不同浓度下的MSD-t曲线 Fig.9 MSD-t curves at the same temperature and different concentrations |
为进行定量比较, 表 3列出了k取400时, PEO溶液在不同浓度、不同温度下均方位移的平均值。可以看到, 45 ℃时浓度为0.4 wt%的PEO溶液中探针颗粒的布朗运动最为剧烈, 均方位移均值最大; 25 ℃时浓度1.0 wt%的PEO溶液中探针颗粒的布朗运动最为微弱, 其均方位移均值最小。本文实验所测MSD-t曲线与文献采用扩散波谱法针对PEO溶液浓度从0.2 wt%到1.0 wt%所获均方位移结果在趋势上具有一致性, 表现出微弱的亚扩散现象, 类似于探针颗粒在水中的扩散。
| 25 ℃ | 35 ℃ | 45 ℃ | |
| 0.4 wt% | 25.18 | 35.29 | 57.10 |
| 0.6 wt% | 10.95 | 26.19 | 41.30 |
| 0.8 wt% | 9.46 | 21.20 | 31.69 |
| 1.0 wt% | 2.17 | 8.76 | 21.23 |
得到均方位移数据后, 根据对广义Stokes-Einstein关系估算黏弹性模量, 采用与频率相关的指数函数模型[27], 计算得出被测样品的微观黏弹性模量G'、G″, 模量曲线如图 10所示。其中, G'为弹性模量, 也称储能模量(Storage Modulus), 反映物质的弹性特性; G″为黏性模量, 也称损耗模量(Loss Modulus), 反映物质的黏性特征。

|
| 图 10 不同工况下的PEO溶液黏弹性模量曲线 Fig.10 Viscoelastic modulus curves of PEO solutions at different conditions |
图 10中(a~d)分别给出了浓度为0.4 w t%、0.6 wt%、0.8 wt%、1.0 wt%的PEO溶液在不同温度(25 ℃、35 ℃和45 ℃)下的黏弹性模量图。可以看到, 本文实验条件下的PEO溶液以黏性模量为主, 弹性模量相对较弱。从图 10的纵向比较来看, 随着浓度的增加, 溶液黏弹性模量G'和G″同时增大; 从横向比较来看, 随着温度的升高, 被测溶液表现为黏性模量增强, 弹性模量减弱; 同时可以注意到, 25 ℃时, 1.0 wt%的PEO溶液弹性模量在0.3~3.0 Hz之间表现较为明显, 出现了与黏性模量曲线趋近的状态, 如图 10(d1)所示; 而随着温度升高至35 ℃, 弹性模量骤降, 此时黏性模量明显占主导, 如图 10(d2)所示。为定量比较, 表 4和5分别列出了12个工况下的弹性模量和黏性模量的最大值, 可以看出, 随着温度的升高, 溶液黏弹性模量G'和G″都有所减小, 但弹性模量下降趋势更为明显。
| 25 ℃ | 35 ℃ | 45 ℃ | |
| 0.4 wt% | 0.0135 | 0.0049 | 0.0035 |
| 0.6 wt% | 0.0455 | 0.0096 | 0.0321 |
| 0.8 wt% | 0.1136 | 0.0239 | 0.0172 |
| 1.0 wt% | 0.1582 | 0.1749 | 0.0746 |
| 25 ℃ | 35 ℃ | 45 ℃ | |
| 0.4 wt% | 0.1011 | 0.0804 | 0.0648 |
| 0.6 wt% | 0.2134 | 0.1611 | 0.1376 |
| 0.8 wt% | 0.3585 | 0.2849 | 0.1794 |
| 1.0 wt% | 0.5499 | 0.3365 | 0.3055 |
对每种工况各10组实验数据进行了误差分析, 并采用均方位移标准差σ作为误差来源, 标准差按下式计算:
 (11)
(11)
式中, xi表示第i个MSD值; N为样本个数, 本实验同一工况重复性实验次数10次, 即N=10;μ为样本算术平均值。
图 11给出了以0.8 wt%PEO溶液为例(其余浓度有类似结果)显示标准差区间的MSD-t图。从图中可以看到, 均方位移标准差区间随间隔时间kΔt的增加呈现加宽的趋势, 说明随着时间的推移, 测量误差有所增加。由式(9)可知, 随着时间推移, k值逐渐增大, 则求解均方位移的测量样本数量N-k(等号右侧的分母)逐渐减小, 由此推知测量精度降低(根据误差理论, 被测样本数量越大, 平均值越接近真值), 可以定性地解释均方位移的测量误差随着时间推移呈现递增的原因。图 12给出了相同浓度不同温度情况下均方位移标准差随时间定量变化的曲线。从图中可以看到, 相同浓度下, 标准差随着颗粒追踪时长的增加而增大, σ-t曲线呈上升趋势; 同时, 标准差随温度的升高而呈现增大趋势。

|
| 图 11 0.8 wt%PEO溶液MSD-t误差带曲线 Fig.11 MSD-t error band curves for 0.8 wt% PEO solution |

|
| 图 12 不同工况下的PEO溶液MSD标准差(σ-t)曲线 Fig.12 MSD standard deviation curves (σ-t) of PEO solution under different conditions |
本文基于单颗粒追踪方法, 研究了不同温度和浓度下聚氧化乙烯(PEO)溶液的微流变特性, 结果表明:
(1) 相同温度下, 探针颗粒布朗运动随着浓度的升高而减弱; 相同浓度下, 探针颗粒布朗运动随温度的升高而增强。随着温度的升高, 相同浓度的PEO溶液中探针颗粒布朗运动的均方位移MSD增大。其中, 在25 ℃时, 浓度为1.0 wt%的PEO溶液MSD最大值为2.17 μm2, MSD-t曲线斜率显著降低, 布朗运动受限明显, 溶液弹性行为开始有所体现。
(2) PEO溶液中黏性模量G″(ω)明显占主导, 弹性模量G'(ω)较弱; 相同温度下, PEO溶液黏弹性模量G'(ω)、G″(ω)都随着浓度增加而增大; 随着温度的升高, 黏弹性模量G'(ω)、G″(ω)都随之减小, 其中, 弹性模量G'(ω)减小速率更快, 黏性模量G″(ω)的主导趋势更明显。
(3) 标准差分析表明, 相同浓度下, 标准差随着颗粒追踪时长的增加而增大, σ-t曲线呈上升趋势; 同时, 标准差随温度的升高而呈现增大趋势。
| [1] |
FURST E M, SQUIRES T M. Microrheology[M]. Oxford: Oxford University Press, 2017.
|
| [2] |
王振东, 姜楠. 软物质漫谈[J]. 力学与实践, 2014, 36(2): 249-252. |
| [3] |
MACKINTOSH F C, SCHMIDT C F. Microrheology[J]. Current Opinion in Colloid & Interface Science, 1999, 4(4): 300-307. |
| [4] |
WAIGH T A. Microrheology of complex fluids[J]. Reports on Progress in Physics, 2005, 68(3): 685-742. DOI:10.1088/0034-4885/68/3/R04 |
| [5] |
MANSEL B W, KEEN S, PATTY P J, et al. A practical review of microrheological techniques[M]. Croatia: Intech, 2013.
|
| [6] |
YANG N, LYU R H, JIA J J, et al. Application of microrheology in food science[J]. Annual Review of Food Science and Technology, 2017, 8(1): 493-521. DOI:10.1146/annurev-food-030216-025859 |
| [7] |
MASON T G, WEITZ D A. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids[J]. Physical Review Letters, 1995, 74(7): 1250-1253. DOI:10.1103/PhysRevLett.74.1250 |
| [8] |
GITTES F, SCHNURR B, OLMSTED P D, et al. Microscopic viscoelasticity:shear moduli of soft materials determined from thermal fluctuations[J]. Physical Review Letters, 1997, 79(17): 3286-3289. DOI:10.1103/PhysRevLett.79.3286 |
| [9] |
KIMURA Y. Microrheology of soft matter[J]. Journal of the Physical Society of Japan, 2009, 78(4): 1005. |
| [10] |
LARSEN T H, FURST E M. Microrheology of the liquid-solid transition during gelation[J]. Physical Review Letters, 2008, 100(14): 146001. DOI:10.1103/PhysRevLett.100.146001 |
| [11] |
GAMBINI C, ABOU B, PONTON A, et al. Micro-and macrorheology of jellyfish extracellular matrix[J]. Biophysical Journal, 2012, 102(1): 1-9. |
| [12] |
ABDALA A A, AMIN S, VAN ZANTEN J H, et al. Tracer microrheology study of a hydrophobically modified comblike associative polymer[J]. Langmuir, 2015, 31(13): 3944-3951. DOI:10.1021/la504904n |
| [13] |
XU J Y, CHANG T S, INGLETT G E, et al. Micro-heterogeneity and micro-rheological properties of high-viscosity oat β-glucansolutions[J]. Food Chemistry, 2007, 103(4): 1192-1198. DOI:10.1016/j.foodchem.2006.10.024 |
| [14] |
COHEN I, WEIHS D. Rheology and microrheology of natural and reduced-calorie Israeli honeys as a model for high-viscosity Newtonian liquids[J]. Journal of Food Engineering, 2010, 100(2): 366-371. DOI:10.1016/j.jfoodeng.2010.04.023 |
| [15] |
MOSCHAKIS T, MURRAY B S, DICKINSON E. Particle tracking using confocal microscopy to probe the microrheology in a phase-separating emulsion containing nonadsorbing polysaccharide[J]. Langmuir, 2006, 22(10): 4710-4719. DOI:10.1021/la0533258 |
| [16] |
MOSCHAKIS T, MURRAY B S, DICKINSON E. On the kinetics of acid sodium caseinate gelation using particle tracking to probe the microrheology[J]. Journal of Colloid and Interface Science, 2010, 345(2): 278-285. DOI:10.1016/j.jcis.2010.02.005 |
| [17] |
MOSCHAKIS T, LAZARIDOU A, BILIADERIS C G. Using particle tracking to probe the local dynamics of barley β-glucan solutions upon gelation[J]. Journal of Colloid and Interface Science, 2012, 375(1): 50-59. DOI:10.1016/j.jcis.2012.02.048 |
| [18] |
MOSCHAKIS T, LAZARIDOU A, BILIADERIS C G. A micro-and macro-scale approach to probe the dynamics of sol-gel transition in cereal β-glucan solutions varying in molecular characteristics[J]. Food Hydrocolloids, 2014, 42(1): 81-91. |
| [19] |
NATH P, MANGAL R, KOHLE F, et al. Dynamics of nanoparticles in entangled polymer solutions[J]. Langmuir, 2018, 34(1): 241-249. DOI:10.1021/acs.langmuir.7b03418 |
| [20] |
VAN ZANTEN J H, AMIN S, ABDALA A A. Brownian motion of colloidal spheres in aqueous PEO solutions[J]. Macromolecules, 2004, 37(10): 3874-3880. DOI:10.1021/ma035250p |
| [21] |
KUBO R. The fluctutation-dissipation theorem[J]. Reports on Progress in Physics, 1966, 29: 255-284. DOI:10.1088/0034-4885/29/1/306 |
| [22] |
ZWANZIG R, BIXON M. Hydrodynamic theory of the velocity correlation function[J]. Physical Review A, 1970, 2(5): 2005-2012. DOI:10.1103/PhysRevA.2.2005 |
| [23] |
DOI M. Soft matter physics[M]. New York: Oxford University Press, 2013.
|
| [24] |
MASON T G, GANESAN K, VAN ZANTEN J H, et al. Particle tracking microrheology of complex fluids[J]. Physical Review Letters, 1997, 79(17): 3282-3285. DOI:10.1103/PhysRevLett.79.3282 |
| [25] |
MASON T G, GANG H, WEITZ D A. Diffusing-wave-spectroscopy measurements of viscoelasticity of complex fluids[J]. Journal of the Optical Society of America A:Optics Image Science and Vision, 1997, 14(1): 139-149. DOI:10.1364/JOSAA.14.000139 |
| [26] |
崔凤霞, 郭春梅, 王开林, 等. 聚氧化乙烯(PEO)的合成及应用[J]. 精细石油化工, 1999, 16(6): 41-44. |
| [27] |
MASON T G. Estimating the viscoelastic moduli of complex fluids using the generalized Stokes-Einstein equation[J]. Rheologica Acta, 2000, 39(4): 371-378. DOI:10.1007/s003970000094 |



